Constructing Matched Groups in Dental Observational Health Disparity Studies for Causal Effects

Abstract

Introduction:

Electronic health record (EHR) systems provide investigators with rich data from which to examine actual impacts of care delivery in real-world settings. However, confounding is a major concern when comparison groups are not randomized.

Objectives:

This article introduced a step-by-step strategy to construct comparable matched groups in a dental study based on the EHR of the Willamette Dental Group. This strategy was employed in preparation for a longitudinal study evaluating the impact of a standardized risk-based caries prevention and management program across patients with public versus private dental insurance in Oregon.

Methods:

This study constructed comparable dental patient groups through a process of 1) evaluating the need for and feasibility of matching, 2) considering different matching methods, and 3) evaluating matching quality. The matched groups were then compared for their average ratio in the number of decayed, missing, and filled tooth surfaces (DMFS + dmfs) at baseline.

Results:

This systematic process resulted in comparably matched groups in baseline covariates but with a clear baseline disparity in caries experience between them.

The weighted average ratio in our study showed that, at baseline, publicly insured patients had 1.21-times (95% CI: 1.08 to 1.32) and 1.21-times (95% CI: 1.08 to 1.37) greater number of DMFS + dmfs and number of decayed tooth surfaces (DS + ds) than privately insured patients, respectively.

Conclusion:

Matching is a useful tool to create comparable groups with EHR data to resemble randomized studies, as demonstrated by our study where even with similar demographics, neighborhood and clinic characteristics, publicly insured pediatric patients had greater numbers of DMFS + dmfs and DS + ds than privately insured pediatric patients.

Knowledge Transfer Statement:

This article provides a systematic, step-by-step strategy for investigators to follow when matching groups in a study—in this case, a study based on electronic health record data. The results from this study will provide patients, clinicians, and policy makers with information to better understand the disparities in oral health between comparable publicly and privately insured pediatric patients who have similar values in individual, clinic, and community covariates. Such understanding will help clinicians and policy makers modify oral health care and relevant policies to improve oral health and reduce disparities between publicly and privately insured patients.

Introduction

Randomized controlled trials (RCTs) are a research gold standard but are challenging to deploy in real-world applications. Electronic health record (EHR) data from a large dental accountable care organization, the Willamette Dental Group (WDG), provide an opportunity to examine the effects of a standardized caries prevention program on reducing socioeconomic oral health disparities among publicly insured (Oregon Health Plan/Medicaid) and privately insured (commercial plan) pediatric populations in Oregon. When the gold standard of an RCT is not feasible in the real world to evaluate a treatment effect, an alternative approach to resemble an RCT is the use of matched cohorts. This approach requires the assumption of no unmeasured confounders when given observed variables; therefore, investigators need to evaluate if the assumption is reasonable in their study (see Assessing the Assumptions section). This article describes and evaluates the methodology to create a matched cohort to assess clinical patient-level outcomes, and it calculates the baseline health disparities between matched sets of publicly insured and privately insured pediatric patients aged 0 to 18 y under a standardized preventive care protocol. The matching process discussed here can be used in cohort, case-control, and other nonrandomized studies for group comparisons.

The WDG caries prevention program was developed to improve the quality and effectiveness of clinical care across a large dental health system by implementing highly standardized, diagnosis-driven, risk- and evidence-based, clinical decision–supported care, documented in an EHR (axiUm; Exan Corp). The program contains all chronic care model elements in oral health, including self-management support, decision support, delivery system design, clinical information systems, and community resources and policies (Wagner et al. 1996). A large multifaceted study was designed with the US Centers for Disease Control and Prevention’s (2018) program evaluation process framework and based on the Fisher-Owens et al. (2007) conceptual framework of children’s health, which acknowledges the multilevel factors that influence children’s health outcomes. This framework provides the context within which to measure changes in health outcomes and evaluate disparities, including factors affecting the intervention at the provider/organizational level and the policy/systems level (Tomar and Cohen 2010; Creswell et al. 2018).

Evaluation of Standardized Preventive Care to Reduce Dental Disparities in Children

Study Sample

Pediatric patients eligible for inclusion in the baseline cohort were residents of Oregon who were ≤18 y old, enrolled in the WDG with capitated commercial plan insurance (private) or Oregon Health Plan/Medicaid insurance (public), and were examined (Current Dental Terminology code D0120, D0145, or D0150) at any WDG clinic between 2014 and 2016. Pediatric patients who moved into the state of Oregon or qualified for insurance after their first examination visit in the period were not included in the study. A total of 34,173 privately insured and 32,497 publicly insured pediatric patients qualified for inclusion between 2014 and 2016. In the final data set—which merged EHR, clinic (merged by site of care), and community census (merged by home zip code) data—pediatric patients were clustered by neighborhood and dental clinic, making the matching more complicated. This article systematically demonstrates the utilization of propensity score (PS) matching with clustered data in a large pediatric patient cohort for a future longitudinal outcomes study.

Evaluating the Need for and Feasibility of Matching

When a randomized assignment design is not feasible for a research study, because of ethical, financial, or temporal issues, investigators must decide if matching is preferred to other methods, such as regression analysis with adjustment on baseline covariates. Variables occurring after the baseline, called intermediate variables, are intermediate outcomes of the exposure, program, or treatment and are therefore not considered in baseline matching.

Covariate Balance between Comparison Groups

The first step of group comparisons is to check baseline covariate distributions for balance. Covariates that are not balanced between groups may confound evaluating the study exposure, program, or treatment on outcomes of interest (Heckman et al. 1997) and therefore should be addressed by matching or regression adjustment or a combination thereof.

The Appendix Table shows summary statistics on WDG participants’ demographics, clinical conditions, and neighborhood and clinic characteristics by the insurance groups and the standardized mean difference (SMD) between the groups. The SMD is the group mean divided by the standard deviation of the difference of a random variable from 2 groups, measuring the difference between groups in the variable. A large SMD value (<–0.25 or >0.25) means a big difference in effect size and hence distribution between groups. The SMD between the insurance groups was as high as 0.552, indicating unbalanced covariate distributions between the groups.

As compared with the privately insured group, the publicly insured group had many differences, such as a higher proportion of continuing patients; more representation of racial/ethnic minorities; higher likelihood to live in urban areas, live closer to the dental clinic, and visit an urban dental clinic; higher mean caries risk; and a higher likelihood to live in communities with fewer Whites and more Blacks and Pacific Islanders, more people below the poverty line, and more people with lower education level. Because the 2 groups differed in many baseline covariates, methods should account for the group differences at baseline. When there are many variables requiring adjustment, regression modelers often need to consider different covariate adjustment models utilizing the outcome data and examining estimated effects. When a complex model (e.g., a multilevel mixed effect model) is needed, as in analyzing dental outcomes, the model adjusting for many covariates may sometimes fail to converge or meet model assumptions. In contrast, matching has the advantage of requiring only baseline covariate data and comparison group status; moreover, matching can be performed multiple times to establish matched groups without examining and modeling outcome data so that the matching process avoids possible selection bias toward desired results (Rubin 2007; Stuart 2010; Kang et al. 2016).

Overlap of Baseline Covariate Distributions between Comparison Groups

Heckman et al. (1997) showed that nonoverlapping support and different distributions of covariates between groups contribute most to the total bias in treatment estimation in observational studies. If the distributions of baseline covariates have sufficient overlap across comparison groups (common support), regression adjustment is often used to remove the bias due to imbalanced covariate distributions between groups. However, when the covariate distributions of comparison groups only slightly overlap, regression adjustment will heavily rely on extrapolation and may perform poorly without checking the overlap (Dehejia and Wahba 1999, 2002). In such cases, matching can be used to check and ensure that covariate distributions overlap between the groups.

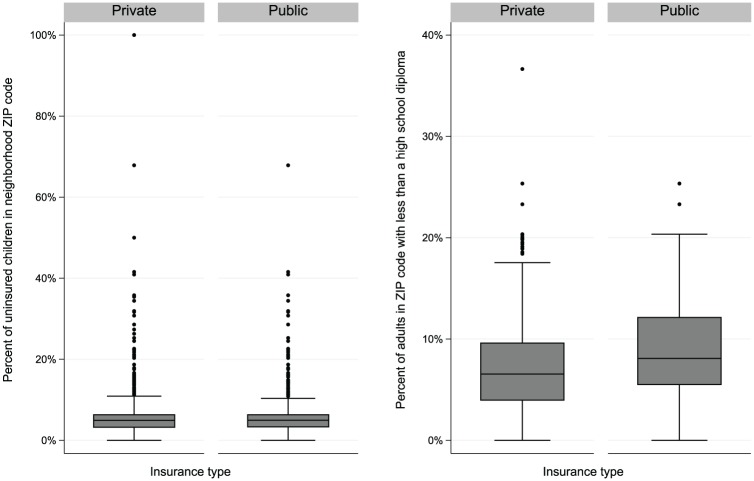
Figure 1 shows boxplots of 2 variables used for matching that describe socioeconomic aspects of the communities where patients lived: percentages of children without health insurance and adults with less than a high school diploma in participants’ communities, as stratified by dental insurance group. Although the publicly insured group had higher or similar medians and first and third quintiles, a few “extreme” communities where privately insured pediatric patients lived had higher percentages of children without health insurance and adults lacking a high school diploma than any community where publicly insured pediatric patients lived, indicating that no publicly insured pediatric patients were comparable to those privately insured pediatric patients in those variables. In this case, a regression model adjusting for those variables will rely on extrapolation, whereas matching can check and ensure that those covariate distributions overlap between the matched insurance groups. In matching, some unmatched patients would be excluded from the analysis to avoid extrapolation.

Figure 1.

Boxplots of percentages of children without health insurance and adults lacking a high school diploma in the participants’ communities, by dental insurance group. Values are presented as median, interquartile range (IQR), 1.5xIQR and outliers.

Analysis Methods for Causal Effects

In some studies, the evaluation of causal effects may need special methods. For example, the outcome may not follow any known parametric distribution, so nonparametric methods will be considered in the analysis. In those studies, even when the covariate distributions sufficiently overlap between comparison groups, matching has the advantage that, after the matched groups are constructed, any analysis methods (including nonparametric methods) can analyze the matched groups directly—in this case, to test the program’s effect on the final outcome differences between the privately and publicly insured groups.

The primary outcomes of interest in the dental disparities study are children’s number of decayed, missing, and filled primary and permanent tooth surfaces (dmfs + DMFS) and number of untreated decayed primary and permanent tooth surfaces (ds + DS). The DMFS + dmfs histogram by insurance group (Fig. 2) shows that the DMFS + dmfs distribution is highly skewed, where 53.5% of privately insured pediatric patients and 44.6% of publicly insured pediatric patients had 0 dmfs. The untreated DS + ds had a similar pattern as the DMFS + dmfs. Discrete data such as these, with excessive zeros, are called zero-inflated count data. While analytic methods have been developed for zero-inflated count data, matching provides flexibility to permit the use of semiparametric and nonparametric analytic methods.

Figure 2.

Histogram of the dental outcome (DMFS + dmfs) by insurance group. DMFS + dmfs, decayed, missing, and filled tooth surfaces.

What Data Are Needed for Sufficient Matching?

A well-designed observational study with successful matching can resemble a randomized study so that comparison groups have balanced distributions of all baseline covariates known from the literature to be relevant factors to the study outcomes of interest (Rubin and Thomas 1996). Including variables unassociated with the outcome will slightly increase the variance, but excluding a potentially important confounder could yield a biased result (Stuart 2010). EHR data and even the best-designed observational study will not be able to measure all possible baseline confounders, but by including an array of baseline covariates, any unmeasured baseline covariates that are correlated with baseline covariates used in matching would be less likely to be substantially associated with comparison groups.

Fisher-Owens et al. (2007) described child-, family-, and community-level factors associated with childhood dental caries. This conceptual framework informed our selection of factors for a balanced distribution between the publicly and privately insured pediatric patients to be included in our PS model. That is, important predictors (individual-, clinic-, and community-level baseline variables) for having public versus private insurance were included in the PS model so that pediatric patients with similar PS values had similar covariate values. Interactions of predictors were examined but did not contribute significantly to the model and therefore were not included in the PS model. The Appendix includes the list of baseline variables in the PS model.

In summary, in our evaluation of whether to use matching, the baseline covariate imbalances and insufficient covariate overlap between privately and publicly insured groups, as well as the highly skewed zero-inflated count dental outcome in the WDG EHR, make matching appealing as compared with the covariate adjustment in regression models for creating a matched cohort in this study.

Matching Methods

Multiple matching methods have been developed to construct matched groups based on the distance between someone in the comparison group and someone in the intervention group. Various distance measures have been proposed to measure the difference between people (e.g., exact, Mahalanobis, PS, linear PS, and combined; see Appendix). Note that when many covariates—especially categorical variables (say >8)—need to be matched, the exact and Mahalanobis distance measures do not work well (Stuart 2010). Hansen (2008) proposed a prognosis score: the predicted outcome for someone in 1 group. Different from PS for the likelihood of being in a comparison group independent of outcome, the prognosis score requires modeling the relationship between the outcome and covariates, and it can be helpful especially when external data or a subset of the study data is available to model the covariate-outcome relationship.

In this study, we considered matching on covariates only at the design stage, so prognosis scores were not used in our matching process. Because dozens of individual-, clinic-, and community-level baseline covariates needed to be balanced at baseline in the dental disparity study, exact and Mahalanobis distances would not work well either. Therefore, PS was the distance measure used for this study, and the baseline multilevel covariates discussed earlier were included in the model to estimate the PS of being publicly insured for each pediatric patient. The study examines whether a baseline oral health disparity exists between insurance groups; the follow-up study will assess whether the disparity is reduced over time. Therefore, baseline dental outcomes were excluded from the PS model and not balanced. Different matching methods were tried and assessed, and the one best balancing covariates between insurance groups was selected to construct matched sets (subclasses) for the final analysis. A detailed introduction to each method is included in the Appendix but is briefly summarized here with results of testing WDG data.

Exact matching matches each pediatric patient in the publicly insured group to all possible pediatric patients in the privately insured group who have the same values on all the covariates to be balanced. Because of the relatively large number of multilevel baseline covariates to be balanced in the dental disparity study, exact matching could match only 1,203 publicly insured pediatric patients with 1,354 privately insured pediatric patients, discarding >30,000 patients from each group.

Nearest neighbor (NN) matching selects 1 (1:1) or more (m:1) privately insured pediatric patients best matched to each pediatric patient in the publicly insured group, where “best match” is defined as that with the smallest difference in covariate values between publicly and privately insured groups. In the study, 34,173 privately insured pediatric patients and 32,497 publicly insured pediatric patients had a baseline visit between 2014 and 2016. A 1:1 NN matching would have limited ability to balance the covariates for selecting 32,497 privately insured pediatric patients to match the 32,497 publicly insured pediatric patients. For example, the SMD in covariates between privately and publicly insured pediatric patients after NN matching was still as high as 0.48, which is considered unacceptably high; SMD values less than or equal to an absolute value of 0.25 (|SMD| ≤ 0.25) are typically deemed to represent acceptable covariance balance between groups. Without compromising the balance quality, NN matching would likely be able to match only a small fraction of the sample and consequently result in a significantly reduced sample size.

Optimal matching considers all pediatric patients when choosing individual matches to minimize the mean absolute distance across all matched pairs. Gu and Rosenbaum (1993) showed that simple NN matching and optimal matching usually end with choosing the same referent group of pediatric patients so that the overall balance is the same, but by assigning them to a different comparison group of pediatric patients, optimal matching performs better in minimizing the distance within each pair. So, as suggested by Stuart (2010), simple NN matching is sufficient to construct well-matched groups, but optimal matching is preferable to construct well-matched pairs. Unfortunately, optimal matching programming did not work for the disparity study, because of the large number of variables and sample members.

Subclassification is considered a type of broadly defined matching to balance the covariate distributions between comparison groups. Based on some arbitrary cutoffs (e.g., quantiles of the estimated PS distribution), the subclassification method groups subjects who are similar in covariate distributions into subclasses so that the publicly and privately insured groups are largely comparable within a subclass. The disparity effect can be estimated within each subclass, and the overall disparity effect was estimated as a weighted average of subclass-specific disparity effects. Cochran (1968) and Rosenbaum and Rubin (1985) showed that using only 5 subclasses removes >90% of the bias in the estimated disparity effect with initial unbalanced groups.

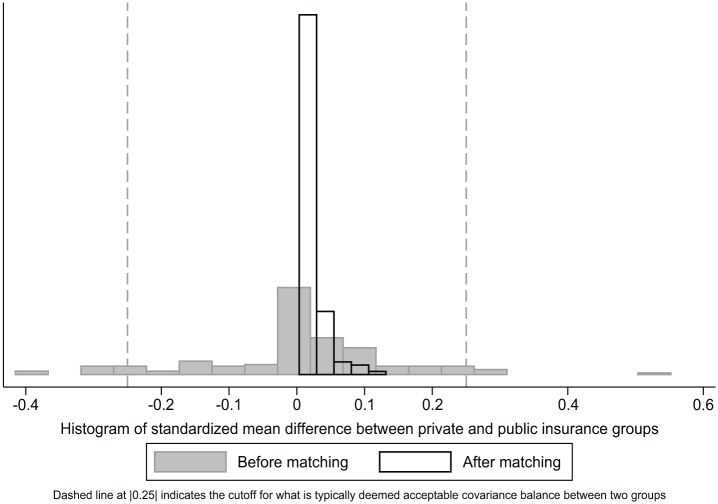
Subclassification was able to classify 31,603 publicly insured pediatric patients and 33,189 privately insured pediatric patients into 6 subclasses based on estimated PS. Each subclass had 5,267 publicly insured pediatric patients and 654 to 16,650 matched privately insured pediatric patients with similar estimated PSs. Figure 3 shows the SMDs between the publicly and privately insured pediatric patients before and after subclassification matching, where the overall SMDs across subclasses are the weighted averages of subclass-specific SMDs. Before-matching SMDs ranged from −0.421 in distance to clinic to 0.551 in percentage of publicly insured patients at a clinic, but after-matching SMDs diminished—ranging from 0.035 in brushing teeth to 0.132 in percentage of publicly insured patients at a clinic)—indicating big improvements in covariate balance between publicly and privately insured pediatric patients within each subclass.

Figure 3.

Covariate balance between insurance groups before and after matching.

Full matching is a special type of subclassification that creates the subclasses in an automatically optimal way by minimizing the weighted average of the distances between publicly and privately insured pediatric patients within each matched set (Rosenbaum 1991, 2002; Hansen 2004). Unfortunately, because of the large number of variables and patients in the WDG data, as in the optimal matching method, the full matching method could not be successfully implemented.

Evaluation of Matching

To evaluate different matching methods, we assessed the common support (or overlap) and covariate balance between matched publicly and privately insured groups to establish the best method of finding groups with similar distributions.

Common Support

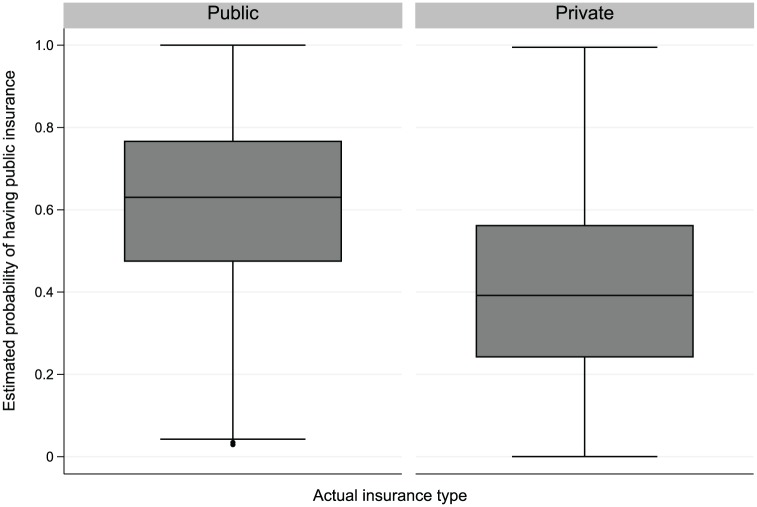
The common support is the region of a covariate value for both groups (publicly and privately insured). Caliper matching uses pediatric patients within a user-specified maximum permitted difference, thus automatically leading to matched pediatric patients with good common support, while subclassification uses all pediatric patients. With many covariates, we assessed the overlap of PS distributions between the groups. When there is inadequate PS distribution overlap between the groups, subjects with PSs outside the range of another group may be discarded because the disparity effect for them cannot be accurately estimated with the given data without relying on extrapolation. Figure 4 contains boxplots of the final estimated PSs. For almost every publicly insured pediatric patient, there was a comparable privately insured pediatric patient with a similar combination of covariate values, indicating good common support between the groups.

Figure 4.

Boxplot of the estimated propensity score by insurance groups. Values are presented as median, interquartile range (IQR), 1.5xIQR, and outliers.

Covariate Balance

The goal of matching is to approximate a randomized study without incorporating the outcome data in the process; matching should be repeated with different methods until well-balanced covariate distributions result. Different measures and guidelines have been proposed (Rubin 2001), including the SMD, the variance ratio of the PS, and the variance ratio of the residuals orthogonal to the PS. The Kolmogorov-Smirnov test can also be used for checking the similarity of a covariate distribution between the groups. Figure 3 shows the plot of the SMDs for the baseline covariates before and after subclassification matching in the WDG study population. SMDs substantially decreased after matching for each covariate with a postmatching maximum of 0.132, indicating much improved and sufficient covariate balance.

Analyses after Matching

Matching creates comparable groups with balanced covariate distributions at baseline; however, it does not provide estimates of disparity effects. Therefore, after matching, the matched groups will be compared with appropriate statistical methods. In some cases, when there is some residual covariate imbalance between the groups (e.g., SMD >0.25), the covariate(s) can be included in the analysis model for further adjustment on residual confounding.

For 1:n matching, there has been discussion whether the analysis should use individual matched pairs as in a traditional matched case-control study. Researchers argue that although groups of individuals will have similar covariate distributions if they have similar PSs, individual pairs matched by PS may not be well matched on all the individual covariates. Therefore, an analysis within individual matched pairs may not be necessary, but using the groups as a whole for the analysis should be sufficient (Ho et al. 2007; Schafer and Kang 2008; Stuart 2008).

For a matched cohort constructed by subclassification, such as the 6 subclasses formed in the dental disparity study, we estimated the difference between the groups within each subclass and then computed the weighted average across subclasses (Rosenbaum and Rubin 1984), using the number of individuals in each subclass as the weight for the average disparity effect in all pediatric patients (overall average disparity effect) or the number of publicly insured pediatric patients in each subclass as the weight for the average disparity effect in the publicly insured group. Comparison groups will usually be well balanced in covariate distributions after subclassification, so nonparametric methods can be used in analysis without covariate adjustments. In rare cases, when a model is needed to further adjust residual covariate imbalance, separate models can be fitted within each subclass while adjusting residual covariates within the subclass (Lunceford and Davidian 2004). When the sample size is too small within each subclass, a joint model across subclasses can be fitted with subclass and subclass × insurance type interaction as fixed effects while controlling for covariates.

The Table shows the average DMFS + dmfs and DS + ds at baseline within each subclass and the weighted average across subclasses between publicly and privately insured pediatric patients. The average ratio in DMFS + dmfs and DS + ds at baseline between publicly and privately insured pediatric patients and its 95% CI were computed within each subclass, assuming a negative binomial distribution. The overall average ratio (publicly insured:privately insured) was calculated as a weighted average ratio across subclasses, with the weight proportional to the number of subjects within a subclass. We can see from the Table that, at baseline, publicly insured pediatric patients had 1.21-times (95% CI: 1.08 to 1.32) and 1.21-times (95% CI: 1.08 to 1.37) greater numbers of DMFS + dmfs and DS + ds than privately insured pediatric patients, respectively.

Table.

Dental Health Status at Baseline among Matched Publicly and Privately Insured Pediatric Patients: DMFS + dmfs and DS + ds.

	Estimated PS Range	Publicly Insured		Privately Insured		Ratio (Public:Private) (95% CI)
Subclass		n	Mean ± SD	n	Mean ± SD
DMFS + dmfs
1	0.62 to 1.00	5,267	3.0 ± 6.0	16,650	2.5 ± 5.3	1.19 (1.10 to 1.27)
2	0.49 to 0.64	5,267	3.8 ± 7.1	7,218	3.0 ± 5.7	1.27 (1.18 to 1.37)
3	0.39 to 0.49	5,267	4.4 ± 7.6	4,275	3.7 ± 6.7	1.20 (1.10 to 1.30)
4	0.29 to 0.39	5,267	5.0 ± 8.3	2,663	3.9 ± 7.1	1.27 (1.16 to 1.39)
5	0.19 to 0.30	5,267	5.8 ± 8.9	1,729	4.5 ± 7.1	1.27 (1.16 to 1.40)
6	0.00 to 0.19	5,268	6.7 ± 9.6	654	6.2 ± 8.1	1.07 (0.55 to 1.22)
Overall weighted	0.00 to 1.00	31,603	4.8 ± 0.1a	33,189	4.0 ± 0.1a	1.21 (1.08 to 1.32)
DS + ds
1	0.62 to 1.00	5,267	0.6 ± 2.1	16,650	0.5 ± 1.7	1.27 (1.13 to 1.43)
2	0.49 to 0.64	5,267	0.9 ± 2.8	7,218	0.8 ± 2.2	1.26 (1.13 to 1.40)
3	0.39 to 0.49	5,267	1.2 ± 3.1	4,275	1.0 ± 2.8	1.06 (0.99 to 1.24)
4	0.29 to 0.39	5,267	1.5 ± 3.6	2,663	1.2 ± 2.8	1.23 (1.09 to 1.38)
5	0.19 to 0.30	5,267	1.9 ± 4.0	1,729	1.4 ± 3.0	1.32 (1.16 to 1.50)
6	0.00 to 0.19	5,268	2.5 ± 4.8	654	2.6 ± 4.7	0.95 (0.81 to 1.12)
Overall weighted	0.00 to 1.00	31,603	1.2 ± 0.0a	33,189	1.0 ± 0.0a	1.21 (1.08 to 1.37)

DMFS + dmfs, decayed, missing, and filled tooth surfaces; DS + ds, decayed tooth surfaces; PS, propensity score.

^aMean ± SE.

Assessing the Assumptions

The key assumption for matching is that there is no unmeasured confounding. Evaluating this assumption requires both statistical and clinical considerations. Statistically speaking, Durbin (1954), Wu (1973), and Hausman (1978) independently proposed a test of unmeasured confounding using an instrumental variable, called the Durbin-Wu-Hausman endogeneity test (DWH test). However, Brookhart et al. (2010) noted that if the DWH test rejects the null hypothesis, there is still uncertainty whether it is due to unmeasured confounding or to disparity effect heterogeneity. Guo et al. (2014) developed a test that distinguishes whether the rejection is due to unmeasured confounding or to disparity effect heterogeneity for some types of unmeasured confounding.

Note that the DWH and Guo et al. (2014) tests both require availability of a valid instrumental variable. When one is not available in a study, investigators may assess the assumption of no unmeasured confounding from scientific or clinical point of views. In the dental disparity study, we have not identified an adequate instrumental variable that affected publicly versus privately insured status and was independent of confounding, so we did not test for unmeasured confounding. However, the good balance between the insurance groups at baseline in the dozens of multilevel variables after matching (Appendix Table) provides some reassurance, though not with 100% certainty, that insurance group is less likely to be substantially associated with unmeasured confounding in the study (Imbens 2004). The reassurance comes from the fact that the dozens of individual-, clinic-, and community-level variables in the dental disparity study included almost all known important factors associated with childhood oral health (Fisher-Owens et al. 2007). If investigators are concerned about a particular confounder unobserved in their study, a sensitivity analysis can be performed to assess how sensitive the conclusions are to a plausible violation of the “no unmeasured confounding” assumption. Rosenbaum and Rubin (1983) and Rosenbaum (2002) discussed the sensitivity analysis approach to assess the robustness of the results to unobserved confounders. If investigators have some idea on the associations of the unmeasured confounder with treatment and outcome in a study, then they can consider a sensitivity analysis similar to that of Rosenbaum and Rubin.

Conclusion

RCTs are the gold standard for treatment evaluation but are not always feasible in practice. This article provides a systematic, step-by-step strategy to create matched comparison groups to resemble a randomized study so that the comparison groups are similar in the distributions of known baseline covariates applied to health disparities research. It also gives advice on ways to check matching adequacy. In the dental disparity study, we constructed 6 subclasses so that the privately and publicly insured groups were comparable in dozens of multilevel variables within each subclass. The weighted average causal effect reveals that publicly insured pediatric patients had 1.21-times (95% CI: 1.08 to 1.32) and 1.21-times (95% CI: 1.08 to 1.37) greater numbers of DMFS + dmfs and DS + ds, respectively, than privately insured pediatric patients, who were comparable in multilevel baseline demographics, behaviors, and clinical and socioenvironmental covariates.

For studies with matching as an option, we suggest that investigators 1) carefully evaluate the need and feasibility of matching; 2) decide on the candidate matching methods; 3) evaluate the quality of different matching methods in their study; 4) use appropriate analytic methods incorporating matching to estimate treatment effects of interest, and, finally; 5) include the appropriate methods (matching and analysis methods, as well as corresponding evaluation of quality and assumptions) and results in the reports and/or manuscripts.

Author Contributions

J. Cheng, contributed to conception, design, data acquisition, analysis, and interpretation, drafted and critically revised the manuscript; S.E. Gregorich, contributed to conception, design, data acquisition, and interpretation, critically revised the manuscript; S.A. Gansky, contributed to conception, design, and data interpretation, critically revised the manuscript; S.A. Fisher-Owens, J.M. White, contributed to conception and data interpretation, critically revised the manuscript; A.M. Kottek, contributed to data acquisition and analysis, critically revised the manuscript; E.A. Mertz, contributed to conception, design, data acquisition, and interpretation, drafted and critically revised the manuscript. All authors gave final approval and agree to be accountable for all aspects of the work.