Abstract
A major goal of analyzing retinal optical coherence tomography (OCT) images is retinal layer segmentation. Accurate automated algorithms for segmenting smooth continuous layer surfaces, with correct hierarchy (topology) are desired for monitoring disease progression. State-of-the-art methods use a trained classifier to label each pixel into background, layer, or surface pixels. The final step of extracting the desired smooth surfaces with correct topology are mostly performed by graph methods (e.g. shortest path, graph cut). However, manually building a graph with varying constraints by retinal region and pathology and solving the minimization with specialized algorithms will degrade the flexibility and time efficiency of the whole framework. In this paper, we directly model the distribution of surface positions using a deep network with a fully differentiable soft argmax to obtain smooth, continuous surfaces in a single feed forward operation. A special topology module is used in the deep network both in the training and testing stages to guarantee the surface topology. An extra deep network output branch is also used for predicting lesion and layers in a pixel-wise labeling scheme. The proposed method was evaluated on two publicly available data sets of healthy controls, subjects with multiple sclerosis, and diabetic macular edema; it achieves state-of-the art sub-pixel results.
Keywords: Retina OCT, Deep learning segmentation, Surface segmentation
1. Introduction
Optical coherence tomography (OCT), which uses light waves to rapidly obtain 3D retina images, is widely used in the clinic. Retinal layer thicknesses change with certain diseases [15] and the analysis of OCT images improves disease monitoring. Manually segmenting the images and measuring the thickness is time consuming, and fast automated retinal layer segmentation tools are routinely used for this purpose.
The goal of layer segmentation is to obtain smooth, continuous retina layer surfaces with the correct anatomical ordering; these results can then be used for thickness analysis or registration [14]. State-of-the-art methods use a trained classifier (e.g, random forest (RF) [13] or deep network [5]) for coarse pixel-wise labeling and then level set [2] or graph methods [3,5,6,13] for surface estimation. Deep networks, which can learn features automatically, have been used in retina layer segmentation. ReLayNet [18] uses a fully convolutional network (FCN) to segment eight layers and edema by classify each pixel into layer or background classes. The main problem with this pixel-wise labeling scheme is that the layer topology is not guaranteed and final continuous and smooth surfaces are not always obtained. Ben-Cohen et al. [1] extract the boundaries from the layer maps using a Sobel filter and then use a shortest path algorithm to extract the surfaces. Other work focuses on classifying the pixels into surface pixels or background. Fang et al. [5] use a convolutional neural network (CNN) and Kugelman et al. [12] use a recurrent neural network (RNN) to classify the center pixel of a patch into boundary pixel or background; then a graph method is used to extract the final surfaces. In order to build a topologically correct graph [6,13], surface distances and smoothness constraints, which are spatially varying, must be experimentally assigned and an energy minimization must be solved outside the deep learning framework. A simpler shortest path graph method [3] was used by [5,12]; however, the shortest path extracts each surface separately, thus the hierarchy is not guaranteed compared to [6,13], especially at the fovea where surface distances can be zero.
The aforementioned graph method cannot be integrated into a deep network, and it needs special parameter settings, which make the method harder to optimize. He et al. [7,9] use a second network to replace the graph method to obtain the smooth, topology-guaranteed surfaces, but this requires much more computation.
In this paper, we propose a new method for obtaining smooth, continuous layer surfaces with the correct topology in an end-to-end deep learning scheme. We use a fully convolutional network to model the position distribution of the surfaces and use a soft-argmax method to infer the final surface positions. The proposed fully convolutional regression method can obtain sub-pixel surface positions in a single feed forward propagation without any fully-connected layer (thus requiring many fewer parameters). Our network has the benefit of being trained end-to-end, with improved accuracy against the state-of-the-art, and it is also light-weight because it does not use a fully-connected layer for regression.
2. Method
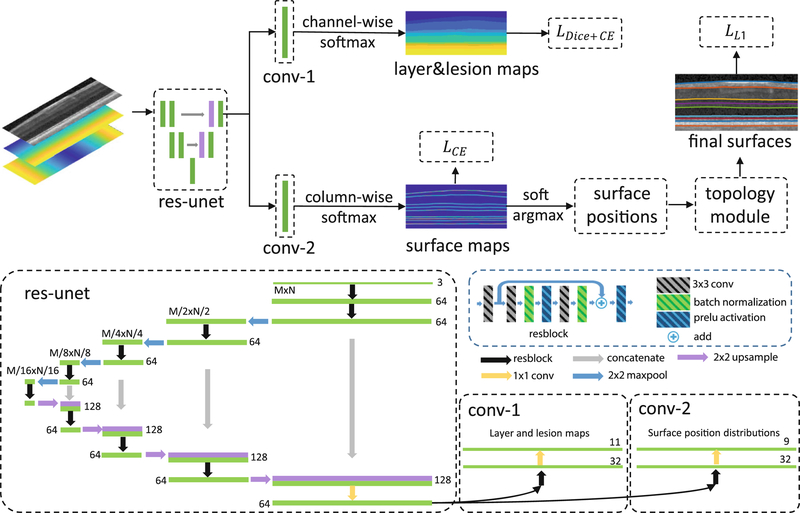
Our framework is shown in Fig. 1, we provide a description below for each step. The network has two output branches: the first branch outputs a pixel-wise labeling segmentation of layers and lesions and the second branch models the distribution of surface positions and outputs the positions of each surface at each column. These two branches share the same feature extractor, a residual U-Net [17]. The input to the network is a three-channel image. One channel is the original flattened OCT image [13], and the other two images are the spatial x and y positions (normalized to the interval [0,1]) of each pixel to provide additional spatial information.
Fig. 1.
A schematic of the proposed method (top) and network structure (bottom).
Preprocessing.
To reduce memory usage, we flatten a retinal B-scan image to the estimated Bruch’s membrane (BM) using an intensity gradient method [13] and crop the retina out.
Surface Position Modeling.
Given an image I and a ground truth surface represented by row indexes across N columns (correspondingly N A-scans), a conventional pixel-wise labeling scheme builds a surface probability map H, where and zero else where. A U-Net [17] takes I as input and learns to generate H. Ideally, the surface should be continuous across the image and intersect each column only once. However, the generated probability map may produce zero or multiple positions with high prediction probability in a single column, thus breaking the continuity. Extreme class imbalance between the one-pixel-wide boundary and non-boundary pixels may also cause problems.
In contrast to the pixel-wise labeling scheme, we want to model the surface position distribution by approximating it with . For an input image I, the network generates N independent surface position distributions at each column. θ are the network parameters to be trained by minimizing the K-L divergence between the data distribution p and q. This idea has similarities with Variational Bayesian methods. The direct inference of each xi from the joint distribution p is hard but it is easier given the simpler independent qi’s. To train the network by minimizing the K-L divergence using the input image I and ground truth ’s, we have
| (1) |
| (2) |
| (3) |
The is a vector of surface positions at N columns and is sampled from data distribution p. In a stochastic gradient descent training scheme, the expectation in Eq. (3) can be removed with a training sample and the position of the ith column is on the image grid which can only be an integer from 1 to the image row number R. So the loss becomes,
| (4) |
is the indicator function where and zero elsewhere. Equation (4) is the cross entropy loss for a single surface. In multiple surfaces segmentation, we use the network to output M feature maps (each map has the same size as the input image) for M surfaces. A column-wise softmax is performed independently on these M feature maps to generate surface position probabilities for each column and each surface. An intuitive explanation of the proposed formulation is: instead of classifying each pixel into surfaces or backgrounds, we are selecting a row index at each column for each surface.
Soft-argmax.
The deep network outputs marginal conditional distributions for each column i, so the exact inference of the boundary position at column i from qi can be performed independently. The differentiable soft-argmax operation (5) used in keypoint localization [10] is used to estimate the final surface position at each column i. Thus, we directly obtain the surface positions from the network with soft-argmax,
| (5) |
We further regularize qi by directly encouraging the soft-argmax of qi to be the ground truth, with a smooth L1 loss,
| (6) |
Topology Guarantee Module.
The layer boundaries within the retina have a strict anatomical ordering. For M surfaces s1,...,sM from inner to outer retina, the anatomy requires where sj(i) is the position of the jth surface at the ith column. The soft-argmax operation produces exact surfaces s1,...,sM but may not satisfy the ordering constraint. We update each iteratively to guarantee the ordering. We implement this as the deep network output layer to guarantee the topology both in the training and testing stages.
Layer and Lesion Pixel-Wise Labeling.
Our multi-task network has two output branches. The first branch described above outputs the correctly ordered surfaces whereas the second branch outputs pixel-wise labelings for both layers and lesions. A combined Dice and cross entropy loss [18] is used for the output of this branch. C is the total number of classes, gc(x) and pc(x) are the ground truth and predicted probability that pixel x belongs to class c, and Ωc is the number of pixels in class c and our combined loss is,
Here, ϵ = 001 is a smoothing constant and wc(x) is a weighting function for each pixel [18]. The final network training loss is
3. Experiments
The proposed method was validated on two publicly available data sets. The first data set [8] contains 35 (14 healthy controls (HC) and 21 subjects with multiple sclerosis (MS)) macula Spectralis OCT scans, of which nine surfaces are manually delineated. Each scan has 49 B-scans of size 496 × 1024. We train on the last 6 HC and last 9 MS subjects and test on the other 20 subjects. The second data set [4] contains 110 B-scans (496 × 768) from 10 diabetic macular edema patients (each with 11 Bscans). Eight retina surfaces and macular edema have been manually delineated. We train on the last 55 B-scans and test on the challenging first 55 B-scans with large lesions. The network is implemented with Pytorch and trained with an Adam optimizer with an initial learning rate of 10−4, weight decay of 10−4, and a minibatch size of 2 until convergence. The training image is augmented with horizontal flipping and vertical scaling both with probability 0.5.
HC and MS Data Set.
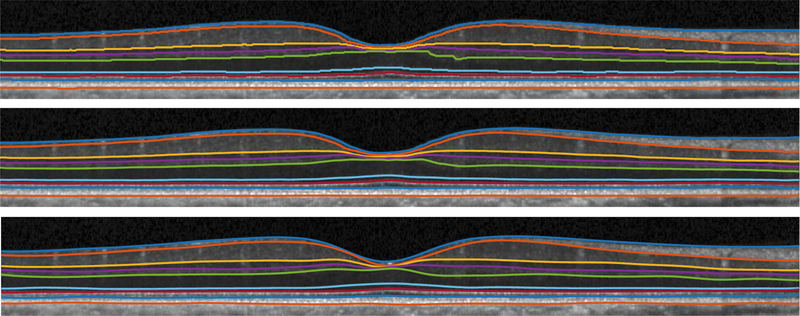
We compare our proposed method with several baselines. The AURA tool [13] is a graph based method and it is the state-of-the-art compared to other publicly available tools as shown in [19]. The RNet [9] is a regression deep network that can obtain smooth surfaces from layer segmentation maps. ReLayNet [18] is a variation of U-Net and only outputs layer maps; we obtain the final surface positions by summing up the output layer maps in each column. The shortest path (SP) algorithm [3,5,12] is also compared. We extract the final surfaces using SP on our predicted qi’s (the surface map as shown in Fig. 1). All the baseline methods are retrained on the same data as our proposed method. The mean absolute distances (MADs) for each method are shown in Table 1 (Fig. 2).
Table 1.
Mean absolute distance (MAD) and standard deviation (Std. Dev.) in μm evaluated on 20 manually delineated scans of 9 surfaces, comparing AURA toolkit [13], R-Net [9], ReLayNet [18], SP (shortest path on our surface map), and our proposed method. Depth resolution is 3.9 μm. Numbers in bold are the best in that row.
| Boundary | MAD (Sth. Dev.) |
||||
|---|---|---|---|---|---|
| AURA | R-Net | ReLayNet | SP | Our’s | |
|
| |||||
| ILM | 2.37 (0.36) | 2.38 (0.36) | 3.17 (0.61) | 2.70 (0.39) | 2.41 (0.40) |
| RNFL-GCL | 3.09 (0.64) | 3.10 (0.55) | 3.75 (0.84) | 3.38 (0.68) | 2.96 (0.71) |
| IPL-INL | 3.43 (0.53) | 2.89 (0.42) | 3.42 (0.45) | 3.11 (0.34) | 2.87 (0.46) |
| INL-OPL | 3.25 (0.48) | 3.15 (0.56) | 3.65 (0.34) | 3.58 (0.32) | 3.19 (0.53) |
| OPL-ONL | 2.96 (0.55) | 2.76 (0.59) | 3.28 (0.63) | 3.07 (0.53) | 2.72 (0.61) |
| ELM | 2.69 (0.44) | 2.65 (0.66) | 3.04 (0.43) | 2.86 (0.41) | 2.65 (0.73) |
| IS-OS | 2.07 (0.81) | 2.10 (0.75) | 2.73 (0.45) | 2.45 (0.31) | 2.01 (0.57) |
| OS-RPE | 3.77 (0.94) | 3.81 (1.17) | 4.22 (1.48) | 4.10 (1.42) | 3.55 (1.02) |
| BM | 2.89 (2.18) | 3.71 (2.27) | 3.09 (1.35) | 3.23 (1.36) | 3.10 (2.02) |
|
| |||||
| Overall | 2.95 (1.04) | 2.95 (1.10) | 3.37 (0.92) | 3.16 (0.88) | 2.83 (0.99) |
Fig. 2.
Visualization of shortest path (top), our result (middle), and manual segmentation (bottom) from a healthy subject.
DME Data Set.
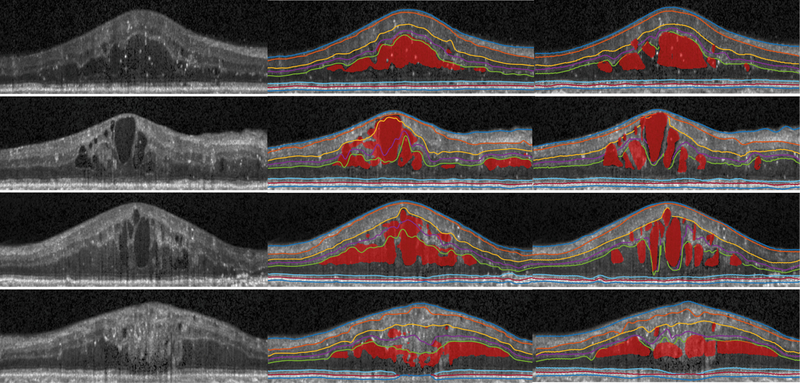
We compare our results with three graph based methods (for final surface extraction): Chiu et al. [4], Rathke et al. [16], and Karri et al. [11]. Since ReLayNet layer surfaces cannot be obtained by simply summing up layer maps (due to lesions), we compare the lesion Dice scores with it. We ignore the positions where Chiu et al. [4]’s result or manual delineation are NaN. The boundary MAD is shown in Table 2. Our network has an extra branch for lesion prediction; however, Rathke’s and Karri’s method can only output layer surfaces. The Dice score of diabetic macular edema for Chiu’s method [4], ReLayNet [18] and ours are 0.56, 0.7, 0.7 respectively. Qualitative results are shown in Fig. 3.
Table 2.
Mean absolute distance (MAD) in μm for eight surfaces (and the mean of those eight surfaces) evaluated on 55 manually delineated scans comparing Chiu et al. [4], Karri et al. [11], Rathke et al. [16], and our proposed method. Numbers in bold are the best in that column.
| Mean | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | |
|---|---|---|---|---|---|---|---|---|---|
| Chiu | 7.82 | 6.59 | 8.38 | 9.04 | 11.02 | 11.01 | 4.84 | 5.74 | 5.91 |
| Karri | 9.54 | 4.47 | 11.77 | 11.12 | 17.54 | 16.74 | 4.99 | 5.35 | 4.30 |
| Rathke | 7.71 | 4.66 | 6.78 | 8.87 | 11.02 | 13.60 | 4.61 | 7.06 | 5.11 |
| Ours | 6.70 | 4.51 | 6.71 | 8.29 | 10.71 | 9.88 | 4.41 | 4.52 | 4.61 |
Fig. 3.
Visualization of original image (left), our results (middle), manual segmentation (right) of four B-scans from diabetic macular edema subjects.
4. Discussion and Conclusion
In this paper, we proposed a new way for retina OCT layer surface and lesion segmentation without using handcrafted graph based methods. The direct modeling of surface position and the fully differentiable soft-argmax operation generates sub-pixel surface positions in a single feed forward propagation. The generated sub-pixel accuracy surface is smooth and continuous and guarantees correct layer ordering, thus overcoming conventional pixel-wise labeling problems. The topology module affects the network training and thus is not simply a post-processing step. Currently the algorithm works on each B-scan individually, and future work will consider context among different B-scans.
Acknowledgments.
This work was supported by the NIH/NEI under grant R01EY024655.
References
- 1.Ben-Cohen A, et al. : Retinal layers segmentation using fully convolutional network in OCT images. In: RSIP Vision (2017) [Google Scholar]
- 2.Carass A, et al. : Multiple-object geometric deformable model for segmentation of macular OCT. Biomed. Opt. Express 5(4), 1062–1074 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chiu SJ, et al. : Automatic segmentation of seven retinal layers in SDOCT images congruent with expert manual segmentation. Opt. Express 18(18), 19413–19428 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chiu SJ, et al. : Kernel regression based segmentation of optical coherence tomography images with diabetic macular edema. Biomed. Opt. Express 6(4), 1172–1194 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fang L, et al. : Automatic segmentation of nine retinal layer boundaries in OCT images of non-exudative AMD patients using deep learning and graph search. Biomed. Opt. Express 8(5), 2732–2744 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Garvin MK, et al. : Automated 3-D intraretinal layer segmentation of macular spectral-domain optical coherence tomography images. IEEE Trans. Med. Imag 28(9), 1436–1447 (2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.He Y, et al. : Towards topological correct segmentation of macular OCT from cascaded FCNs In: Cardoso MJ, et al. (eds.) FIFI/OMIA −2017. LNCS, vol. 10554, pp. 202–209. Springer, Cham; (2017). 10.1007/978-3-319-67561-923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.He Y, et al. : Retinal layer parcellation of optical coherence tomography images: data resource for multiple sclerosis and healthy controls. Data Brief 22, 601–604 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.He Y, et al. : Topology guaranteed segmentation of the human retina from OCTusing convolutional neural networks. arXiv preprint arXiv:1803.05120 (2018) [Google Scholar]
- 10.Honari S, et al. : Improving landmark localization with semi-supervised learning. In: The IEEE Conference on Computer Vision and Pattern Recognition (2018) [Google Scholar]
- 11.Karri S, et al. : Learning layer-specific edges for segmenting retinal layers with large deformations. Biomed. Opt. Express 7(7), 2888–2901 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kugelman J, et al. : Automatic segmentation of oct retinal boundaries using recurrent neural networks and graph search. Biomed. Opt. Express 9(11), 5759–5777 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lang A, et al. : Retinal layer segmentation of macular OCT images using boundary classification. Biomed. Opt. Express 4(7), 1133–1152 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lee S, et al. : Atlas-based shape analysis and classification of retinal optical coherence tomography images using the functional shape (fshape) framework. Med. Image Anal 35, 570–581 (2017) [DOI] [PubMed] [Google Scholar]
- 15.Medeiros FA, et al. : Detection of glaucoma progression with stratus OCT retinal nerve fiber layer, optic nerve head, and macular thickness measurements. Invest. Ophthalmol. Vis. Sci 50(12), 5741–5748 (2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rathke F, Desana M, Schnörr C: Locally adaptive probabilistic models for global segmentation of pathological OCT scans In: Descoteaux M, Maier-Hein L, Franz A, Jannin P, Collins DL, Duchesne S (eds.) MICCAI 2017. LNCS, vol. 10433, pp. 177–184. Springer, Cham; (2017). 10.1007/978-3-319-66182-721 [DOI] [Google Scholar]
- 17.Ronneberger O, Fischer P, Brox T: U-Net: convolutional networks for biomedical image segmentation In: Navab N, Hornegger J, Wells WM, Frangi AF (eds.) MICCAI 2015. LNCS, vol. 9351, pp. 234–241. Springer, Cham; (2015). 10.1007/978-3-319-24574-428 [DOI] [Google Scholar]
- 18.Roy AG, et al. : Relaynet: retinal layer and fluid segmentation of macular optical coherence tomography using fully convolutional networks. Biomed. Opt. Express 8(8), 3627–3642 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tian J, et al. : Performance evaluation of automated segmentation software optical coherence tomography volume data. J. Biophotonics 9(5), 478–489 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]