Recent Advances in Computational Modeling of Fibrin Clot Formation: A Review

Abstract

The field of thrombosis and hemostasis is crucial for understanding and developing new therapies for pathologies such as deep vein thrombosis, diabetes related strokes, pulmonary embolisms, and hemorrhaging related diseases. In the last two decades, an exponential growth in studies related to fibrin clot formation using computational tools has been observed. Despite this growth, the complete mechanism behind thrombus formation and hemostasis has been long and rife with obstacles; however, significant progress has been made in the present century. The computational models and methods used in this context are diversified into different spatiotemporal scales, yet there is no single model which can predict both physiological and mechanical properties of fibrin clots. In this review, we list the major strategies employed by researchers in modeling fibrin clot formation using recent and existing computational techniques. This review organizes the computational strategies into continuum level, system level, discrete particle (DPD), and multi-scale methods. We also discuss strengths and weaknesses of various methods and future directions in which computational modeling of fibrin clots can advance.

Introduction

Hemostasis is a natural process of preventing excessive bleeding in the event of injury[1]. In contrast, thrombosis is often related to pathological states and results in the formation of blood clots (thrombi) within the vasculature unintentionally, obstructing the flow of blood, leading to morbidity. In pathological states, thrombosis can often lead to rupturing, forming embolisms that engender arterial embolisms, strokes, myocardial infarction, venous thromboembolisms[2] (VTE), and pulmonary embolisms.

Despite advancements in blood clot studies by researchers, our understanding of the blood clotting process is still incomplete and continually evolving[3, 4]. Knowledge about the mechanical processes behind these events is of significant importance to develop more effective thrombolytic therapies. In comparison with physical experimental studies, computational modeling studies can provide insights about nanoscale properties of biochemical processes which may affect the mechanical properties at the macroscale. For example, results from studies on fibrinogen mechanical behavior and elasticity from molecular simulations[5] can be scaled up to the macroscale to understand the bulk behavior of fibrin clots.

In addition, the vast amount of literature in thrombosis experiments identifies the risk factors associated with the VTE formation; however, the root cause underlying this pathological state has not yet been determined. To unveil the origin and mechanisms for why such diseases develop and progress, it is necessary to establish the relationship of thrombus formation and rupture with dynamic mechanical properties. This necessitates an understanding of the molecular basis and mechanisms by which fibrin clot mechanical properties are governed. Developments in computational methods such as molecular simulations, mesoscopic methods, and continuum theories promise a synergetic solution to these problems. Toward achieving this goal, we will summarize the advancements in the area of blood clot computational modeling studies and simulations of thrombus formation.

In the past two decades, an exponential increase in the number of publications related to understanding the formation of blood clots under various conditions and physical locations has been observed. Figure 1 shows the results of Web of Knowledge search results of number of publications related to computational modeling of thrombus formation and experimental investigations of blood clot formation mechanisms. This indicates a growing interest in the field of thrombosis and hemostasis for using computational modeling efforts to understand blood clot formation. The studies range from molecular level to large scale continuum level and incorporate constituents, to include: fibrinogen[6], erythrocytes, platelets, hemoglobin[7], and fibrin[8]. A short review on this field is given by [9] and a review on discrete particle methods used for blood simulation is given by [10].

Figure 1.

Total number of publications over the past 15 years with different keywords related to thrombus formation modeling. (a) Computational studies related to thrombus formation (b) Publications related to the study of blood clot formation.

Advancements in experimental investigations of the blood clotting process is well established; however, computational modeling and theoretical understanding of the clotting process has been limited. In this review, we consolidated computational modeling tools and strategies used by researchers to study blood clot formation. The emphasis of the review is focused on direct modeling techniques to simulate clot formation and its dynamic behavior, rather than focusing on computational methods that are used to evaluate images from experimental assays [11, 12].

Biological Background

Hemostasis[13] is the natural process for preventing excessive blood loss from a damaged blood vessel and for preventing hemorrhagic events[1]. When injury to the endothelial lining occurs, endothelial cells stop secretion of coagulation and aggregation inhibitors and instead secrete von Willebrand factor[14], which initiates the maintenance of hemostasis subsequent to injury. Hemostasis consists of three major steps: 1) vasoconstriction, 2) temporary blockage of an injury by a platelet plug, and 3) blood coagulation, or formation of a fibrin clot[15]. This series of processes is necessary for sealing the site of injury until wound healing occurs and tissues are repaired. Blood coagulation consists of a cascade of events, in which a number of blood factors participate in the biochemical reactions that lead to the formation of a stable blood clot. In normal physiological conditions, when there is no injury, endothelial cells of intact (healthy) vessels prevent blood clotting with production of prostacyclin, secretion of plasminogen activator, cell surface heparin containing proteoglycans that stimulate certain coagulation factor inhibitor, and thrombomodulin, an endothelial cell surface glycoprotein that promotes protein C activation[16].

Coagulation Cascade

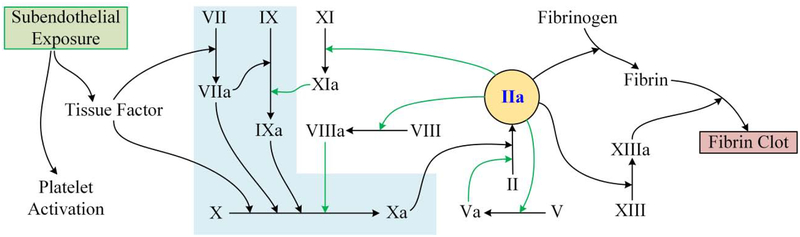
The classical coagulation cascade [17] consists of an intrinsic path, an extrinsic path, and a common pathway. Over the past few decades, our understanding of the coagulation cascade has evolved and is continually improving[17–19]. The modern coagulation cascade consists of an i) Initiation phase, ii) Amplification phase, and iii) Propagation phase.

The initiation phase begins with the exposure of tissue factor (TF), present in sub-endothelial cells in contact with the blood stream during an event of vascular injury. TF binds with factor VIIa (FVIIa) and cleaves FIX and FX to form FIXa and FXa, respectively. The suffix a after the blood factors indicates that they are in the activated state and the prefix F stands for factor. FXa facilitates in the conversion of FII (prothrombin) to FIIa (thrombin). This is followed by the amplification phase, in which FIIa plays a central conversion role (Fig. 2). FIIa converts FV to FVa, FXI to FXIa and FVIII to FVIIIa. These parallel processes accelerate the production of FIIa and are thus termed the amplification phase. In the propagation phase, FXIa also converts FIX into FIXa, which along with FVIIIa catalyzes the formation of FXa. In the final stages, FXIIIa catalyzes the formation of a cross linked fibrin network. In regard to the classical coagulation cascade, when FXII binds to negatively charged surfaces, this leads to the initiation of the intrinsic pathway of blood plasma in-vivo and eventually cleaving leading to form FXIIa [20]. It is also well established that tenase is instrumental as a key component of the intrinsic pathway (involving FIXa, FVIIIa, phospholipid, and calcium) and is responsible for converting FX to FXa. In this intrinsic pathway, once FX is converted to FXa, a complex is developed with FVa, phospholipid, and calcium to create the pro-thrombinase complex, which converts FII to FIIa. In many disease states, tenase of the extrinsic pathway (by the complex of tissue factor (TF)-FVIIa) engenders activation of FX to FXa and FIX to FIXa in vivo [21].

Figure 2.

Coagulation cascade (modern-day) (Light blue shade indicates the initiation phase and green arrows show amplification phase.) The blood factors and their names are listed in the nomenclature section. Note that this cascade does not show clot inhibiting factors, such as protein C.

A detailed explanation of the coagulation cascade and other sub processes can be found in the literature[18] and a brief review about fibrinolysis is provided by Longstaff [22].

Thrombosis and Thrombus Formation

Thrombosis is the process of the formation of a blood clot inside a blood vessel, obstructing the flow of blood through the circulatory system, which is different from the natural hemostasis process. Even in the absence of injury to a blood vessel, blood clots may form in the body undesirably and this occurs mainly because of pathological conditions. A clot, or a fragment of the clot, that dislodges and travels to a distal site in the body is known as an embolus. In platelet-poor conditions such as in veins, emboli can travel to the lungs and form a pulmonary embolism, or can cause a number of other conditions such as deep vein thrombosis or renal vein thrombosis. In the case of arterial thrombosis, the embolus can lead to a stroke, or myocardial infarction (heart attack). Insights about the mechanical properties of blood clots can be useful for the development of advanced thrombolytic therapies[23]. In their study, Weisel et al. have observed that fibrin clots are composed of interconnecting fibrin strands with numerous branches and crosslinking. However, these long fiber strands do not exhibit any loose ends and are viscoelastic. They also examined the effects of FXIIIa on viscoelastic properties, strain hardening, sensitivity of viscoelastic properties to small changes in polymerization, and network strand dissociation[23]. In a different study, Ryan[24] suggested that fibrin diametrical growth is directly related to the branching of the fibrin monomers, and the chances reduce with an increased number of fiber branch points. Fibrin network stiffness is directly related to an increase in fibrinogen concentration, thickness of the fiber, and branch point frequency. Their study also suggests that FXIIIa induced ligation increases the rigidity and stability of the fibrin clot.

There are a plethora of biochemical processes that occur during blood clotting. In addition, fibrin aggregation is influenced by blood flow conditions and other environmental factors. Thus, the study of thrombus formation, its growth, and eventual rupture is a challenging topic. Experimental investigations are often limited or focused on singular macroscopic properties. For example, many experimental studies are focused on rheological properties under various chemical compositions and pathological states, rate of coagulation, or effects of specific enzymes. In these situations, computational resources can be very helpful and insightful for studying multiple processes and components simultaneously. However, there is a lack of computational studies revealing the molecular basis for the mechanical properties as well as the dynamics of clot formation using a single and unified approach.

The processes involved in the clotting process can be broadly classified based on length and time scales. The associated enzymatic proteolysis reactions and their associations and dissociations due to the hydrophobic and electrostatic interactions can be classified as molecular level processes. Dynamic clot formation and lysis of larger particles such as platelets, vWF, fibrin, and erythrocytes can be classified as microscopic processes. Top level polymerization of fibrin and its attachment/detachment with vascular chamber walls and RBCs can be classified as macroscopic and continuum level process. In order to simulate these processes at different spatiotemporal scales, appropriate computational tools must be employed. Mathematical and computational methods have advanced greatly in the last century and the computational resources have become cheaper, faster, and more readily accessible. In addition, one can make use of open source software and powerful languages such as LAMMPS[25], NAMD[26], GROMACS[27], Open-Foam[28], Octave[29], Python[30] to simulate these processes at different length and time scales.

Mathematical Background

Many of the computational studies conducted in the area of fibrin and blood clots utilize a standard set of methods that will be detailed in this section. Our goal is to provide a brief introductory concept of the various techniques, and the length and time scales in which they are applicable. A detailed demonstration or explanation of such methods are beyond the scope of this review and readers are advised to refer to the appropriate cited references. In addition, the authors in [31] have devoted a book to modeling fluid-structure interactions in biomedical systems, with a specific focus on cell-based mathematical models of blood coagulation. Similarly, an entire book has been written on mathematical aspects of blood [32], with particular emphasis on mathematical aspects of hemorheology and hemodynamics, and blood coagulation.

Navier-Stokes Equations

The Navier-Stokes (NS) equations[33] are one of the most highly used set of mathematical equations and are used to describe the motion of viscous fluid substances. Some of the applications of the NS equations include: modeling the weather, ocean currents, water flow in pipes, combustion, and air flow around an aircraft wing. Recently, NS equations have also been employed to simulate blood flow in the human body under various physiological conditions. The differential form of the NS equations in convective form is (Eq. 1):

$$\partial u/\partial t+(u.\nabla )u=v{\nabla }^{2}u-\nabla w+g$$ (1)

Here, u is the velocity of the fluid, t is time, v is the kinematic viscosity, g is gravity (or external body force), and w = P/ρ, where P is the pressure and ρ is the mass density. The left-hand side terms of the equation represent local variation of the velocity field and its convection. The terms on the right represent the diffusion term, pressure (or internal source term), and gravity in conjunction with external sources respectively. NS equations are often solved with the assumption of incompressibility, given mathematically as ∇. u = 0.

As of today, there exists no exact general solution for the NS equations, but one can obtain analytical solutions for simple geometries with assumptions of incompressibility and laminar flow. For complex geometries, one can numerically differentiate NS equations to determine approximate solutions. The solution of the NS equations provides the velocity field and other properties such as stream functions, vorticity, and pressure gradient. When the geometry is simplified with two flat plates separated at a distance or in a pipe, the flow is characterized as Poiseuille flow[33]. Often, blood flow in narrow vascular chambers is simulated using the Poiseuille flow assumption.

Convection Diffusion Reaction Equations

Convection diffusion reaction (CDR) equations are analogous to NS equations in mathematical form, but are used to define the transport behavior of a chemical species, electric current, or temperature. These equations are termed advection-diffusion equations, drift diffusion equations[34], or scalar transport equations[35], depending on the context of application. A general form of the CDR equations is (Eq. 2):

$$\partial c/\partial t=D{\nabla }^{2}c-u.\nabla c+R$$ (2)

Here, c is the variable of interest, and could represent the concentration for chemical species transport or temperature for heat transfer. u is the velocity vector of the medium, D is the mass or thermal diffusivity, and R is the source or sink. For a chemical species, R is the chemical reaction creating more or less species of c. The first term of Eq. 2 represents the time dependent variation of the species with time. The second term describes the diffusion of the species based on the concentration difference. The third term represents the convection or advection, which describes the change in species concentration due to the flow of the surrounding medium. The solution of the CDR equation is the variation of concentration c with respect to space and time. This formulation is very useful in the context of simulating chemical reactions coupled with flow for fibrin polymerization simulations.

Dissipative Particle Dynamics

Dissipative Particle Dynamics (DPD) is a relatively new stochastic simulation technique for simulating the dynamic and rheological properties of simple and complex fluids[36]. DPD is considered as a mesoscopic version of MD simulations and has the capability for representing larger time and length scales[37]. DPD techniques possess powerful capabilities and are being employed for simulating complex fluid systems[38], such as fibers in viscous media, dispersion of nanofluids, nanocomposites, and surfactants.

The DPD method treats the fluid system as a collection of particles (beads), which interact with each other using soft repulsive potentials. The DPD system is governed by Newton’s second law and the force acting on an i^th bead is the sum of internal and external forces, given by $f_i=f_i^{int}+f_i^{ext}$. Here, $f_i^{ext}$ represents the external forces on the system by gravity and other body forces. The internal force is given by the mutual interactions:

$$f_i^{int}={\sum }_{j\ne i}\left(F_{ij}^C+F_{ij}^D+F_{ij}^R\right)$$ (3)

Eq. 3 consists of a soft repulsive conservative force $F_{ij}^C$, a dissipative force $F_{ij}^D$, and a random force $F_{ij}^R$. This allows for simulation of many properties of the fluid, including its density, diffusivity, and surface tension. The details of implementation, estimation of variables for a specific system, and validation are discussed in detail in[37]. One advantage of DPD simulations is the ability to compensate for non-Newtonian flow properties of a fluid,[39] which makes it attractive in the case of blood flow modeling[10].

Cellular Potts Model

The Cellular Potts model (CPM) is a computational model that allows for simulation of the collective behavior of cellular structures. CPM is also known as the Extended Potts model and is modeled as an extension of the large-q Potts model[40]. It allows simulation of many biological phenomena, such as cell migration, clustering, and growth by considering environment sensing as well as volume and surface-area constraints [41, 42].

Other Computational Methods

Apart from the aforementioned methods, there exists many newly developed methods to model blood flow. Lattice Boltzmann methods (LBM) and Smooth Particle Hydrodynamics (SPH) are among them. LBM are a class of computational fluid dynamics (CFD) models in which the flow of the fluid is simulated by solving the discrete Boltzmann equation with collision models such as Bhatnagar-Gross-Krook[43] (BGK). LBM have advantages of simulating complex, coupled flow with heat transfer and chemical reactions. SPH is a computational method employed for simulating the dynamics of continuum media, such as solid mechanics and fluid flow[44]. SPH has several benefits over traditional grid-based techniques in simulating fluid flow. First, SPH guarantees conservation of mass without extra computation since the particles themselves represent the mass of the system. Second, SPH computes pressure from weighted contributions of neighboring particles rather than by solving a linear system of equations. Finally, unlike grid-based techniques which must track fluid boundaries, SPH creates a free surface for two-phase interacting fluids directly since the particles represent the denser fluid (usually water) and empty space represents the lighter fluid (usually air). This implementation makes it an attractive choice for fluid simulation.

Computational Modeling of Blood Clots

Modeling and simulation of blood and its clot formation is a complex process [45]. Due to the involvement of a large number of proteolysis reactions, polymerization processes, and different length and time scales, there is difficulty with simulating such processes with a single method. In this section, we classify various methods used for hemostasis and thrombosis based on length scale, time scale, and class. For brevity, we will limit our discussions related to modeling and simulation of blood or fibrin clot formation and also their mechanics. First, we will list out the simulation methods focused on the flow of blood and clot formation and then we will discuss the methods to study the mechanics of such formed clots.

System Level Methods

System level methods involve modeling of blood flow and coagulation from a larger scale and include the development of mathematical relationships to reproduce experimental results. These are generally modeled using CDR equations and the constants are estimated empirically from the experimental results. The advantage in employing these models is that with less complexity we can simulate the qualitative behavior of events related to blood clotting. However, due to the assumptions made when developing the model, the finer details of the processes are compromised. A simple example of this type of method is the simulation of fibrin clotting time using simple ordinary differential equations[46] (ODEs). Blood coagulation factors are modeled as time dependent concentrations and chemical reactions are simulated using ODEs. Finally, clotting time of fibrin from fibrinogen in the presence of thrombin is simulated and matched with the experimental results.

An established method that can be used to simulate enzyme reaction kinetics and associated products is Michaelis-Menten kinetics[47], which relates reaction rate to substrate concentration. This method enables one to define enzymatic product formation using a relationship such as: $E+S\stackrel{k_f,k_r}{\leftrightarrow }ES\stackrel{k_{cat}}{\to }E+P$. Here, an enzyme (E) binds to a substrate (S) to form a complex (ES), which eventually releases a product (P). The reaction occurs at a forward rate of k_f, reverse rate of k_r and a catalytic rate of k_cat and are collectively called reaction rate constants, or simply rate constants[48]. These equations can be written as a system of nonlinear ODEs[49] that define the rate of change of reactants. Using this technique, blood clot formation can be simulated[50], wherein the blood factors involved in the coagulation cascade are modeled as a system of Michaelis–Menten equations. Based on the physiologically observed concentrations and rate constants, the kinetics of the reactions can be simulated. One of the drawbacks of these methods is the dependence on empirical models and experimental values for rate constants, which makes the method susceptible to incorrect kinetics assumptions. In order to utilize the power of this method, one must thoroughly validate the rate constants with experimental results.

Weisel[11] developed a kinetic model that can simulate the formation of the fibrin clot from individual monomers. They modeled the various stages of fibrin polymerization using simple rate equations. To account for the observed lag period observed in experiments, they modified the model to account for additional fibrin geometric parameters. One drawback, as they point out, is the lack of accurate rate constants for the many reactions considered, so they were chosen arbitrarily and later adjusted to align with experimental results. However, a qualitative reasoning of the dependence of concentration and other factors on clotting rate was provided.

System level reaction kinetics can be combined with spatial information to simulate a more realistic system. In one such study, researchers combined the NS equations and CDR equations to study blood clot formation and lysis[51]. The enzymatic reactions were described using 25 CDR equations and coupled with NS equations to account for flow conditions. The initiation and lysis of clot formation was defined using threshold limits for fibrinogen concentrations. To initiate the CDR equations, platelet activation conditions were employed using an exponential function with a complex set of conditions.

Continuum Methods

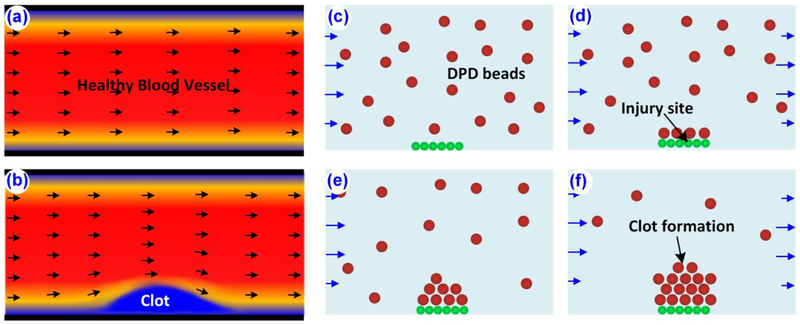
While system level methods can be used to determine the rate at which clotting or lysis occurs in a particular hemostatic event, the shortcomings lie in the inability to simulate clotting and lysis at physical length scales and geometries. This becomes important when studying blood clots in complex geometries[52] and under various mechanical and environmental factors. Figure 3a represents a schematic of a simulation of blood clot formation using continuum methods. In this model, blood is modeled as an incompressible Newtonian fluid, flowing between two parallel flat plates. This leads to Poiseuille flow conditions and the velocity across the flow cross section takes on a parabolic form[33]. The flow profile is disrupted when the thrombus (semi solid formation) forms near the walls as shown in Fig. 3b. The complexity of the models depends on the level of details of the blood constituents considered. A basic continuum model is a combination of NS equations for flow dynamics and CDR equations for species spatiotemporal concentration evolution [53–55]. Most of the available continuum models assume blood vessels are rigid walls and blood constituents as massless particles. This enables one to model the equations by forward coupling NS equations’ solution to CDR equations and neglecting the effect of particles back on flow velocity.

Figure 3.

Schematic of continuum and DPD modeling of a blood clot. Solution of NS equations for (a) a normal blood vessel and (b) blood vessel with thrombus formation. (c-f) Blood constituents, walls and plasma are modeled using DPD particles and used to simulate rule-based clot formation. Often, DPD simulations are coupled with NS and CDR equations.

Fogelson [56] modeled blood in a two-dimensional (2-D) domain as an incompressible fluid, and the flow was simulated using NS equations. The transport of platelets and adenosine diphosphate (ADP) in the blood stream was modeled using a particulate CDR equation. The solution of the NS equation for the Poiseuille flow was determined and then coupled with the CDR equations to estimate the impact of flow velocity on ADP and platelets. The mesh point velocities were interpolated to the particle positions using a 2-D delta function. The activation of platelets and the release of ADP by them were simulated using threshold values of ADP in contact. The platelets interacted with each other using a force function which caused adherence to the injured wall, sticky among themselves, or simply in an inactivated state. In the study, the researchers captured the effects of platelet aggregation at an injured site.

These types of studies were further extended by Govindarajan[57] to accommodate thrombus formation at a site of injury. The flow was simulated using NS equations, and spatiotemporal platelet concentrations using CDR equations. The platelets and other factors were modeled as continuum entities with varying concentrations, and the thrombus growth was simulated by comparing the increased local concentration of fibrin. The effect of the formed thrombus on blood flow was simulated by including an additional porous medium term into the NS equations, which increases the viscosity locally at regions of high fibrin concentrations and such methods are termed two-way coupled modeling.

There are many studies aimed at applying the continuum level methods to specific cases of blood clots, namely aortic dissection [58, 59] and cerebral aneurysms [60, 61]. Simulations on these complex geometries can be performed by defining the NS equations for flow with appropriate boundary conditions such as pulsating flow and two-way coupling of the NS equations with CDR equations using a momentum source term in the NS equation. This allows specification of the growing thrombus as a region with high resistance to flow and hence simulates a solid obstruction (thrombus) to the flow. The authors in [62] used a continuum based method to model thrombus formation under shear flow, influenced by platelet aggregation and adhesion. In a recent review by researchers in [63], the researchers focused on modeling of thrombi using methods at the macroscopic scale, under flow based conditions.

So far, we have observed modeling of thrombus formation as an increase in the concentration of platelets, fibrin, or other blood constituents. Thrombus formation can also be modeled as a volume fraction of platelet deposition in the region of thrombus formation[64]. Their study also accounted for a large number of blood constituents and their reactions through CDR equations. The activation and deposition of the platelets, thrombus propagation, erosion, inhibition, stabilization and thrombus-fluid interactions were captured in this study.

Discrete Particle Methods

Due to versatile fluid simulation capabilities at both the nano and micro scales, DPD methods have been employed more recently by researchers to model blood flow[65–69]. Platelets are usually modeled as DPD particles or beads and fibrin fibers as polymer chain beads connecting to each other by harmonic springs. A typical particle based or DPD simulation setup for blood flow resembles what is observed experimentally (Fig. 3c–f).

When only platelets are considered for simulation, the DPD system constitutes only loosely distributed beads interacting with each other. Pressure or velocity boundary conditions are often applied to the system via external forces. These external forces can be a solution of a simple Poiseuille flow or by coupling with NS equations. Filipovic [65] used CDR equations to estimate the local concentrations of blood constituents and NS equations to solve the velocity field. The walls were considered as rigid and a velocity bounce-back criterion was used to simulate the interaction between beads and the wall. In this study, NS equations were solved to obtain the flow field as an input to CDR and for DPD beads, a known solution of the Poiseuille flow (parabolic profile) velocity was provided as the inlet and outlet boundary conditions.

One challenge with the DPD simulation is the modeling of dynamic bead adhesion to the wall (thrombus formation). Filipovic[65] used an additional force based model to capture this: $F_w^a=k_{bw}\left(1-L_w/L_{max}^{\mathit{\text{wall}}}\right)$. Here, $F_w^a$ is the attractive force between a bead and wall, L_w is the distance of the bead from the wall, and $L_{max}^{\mathit{\text{wall}}}$ is the size of the domain. The density distribution of blood factors obtained from the CDR solution was compared with the experimental results and the effective spring constant, k_bw, was iteratively modified to match the results. This method was modified by Tosenberger[66], to include time dependent bead adhesion force. The results from their study has demonstrated that the formed thrombus ruptures at higher flow due to induced forces. Both of these studies did not account for blood constituents such as fibrinogen and other important coagulation factors. This model was improved by adding CDR equations for fibrin concentration[67], thrombin concentrations [68], and basic coagulation pathway model using CDR equations [69].

Multiscale Methods

In multi-scale methods, two or more computational methods are coupled together at different length or time scales, which is different from hybrid methods which couple two or more methods at the same scales. A typical scenario of multi-scale modeling as shown in Fig. 4, is the modeling of blood factors’ biochemical reactions using MD simulations, their spatiotemporal concentrations through CDR equations, and blood flow using NS equations. Using this method, one can capture the macroscopic behavior of clot formation without losing nanoscale characteristics.

Figure 4.

Schematic of multiscale blood clot modeling approach. (a) In continuum length and time scales, NS equations are solved to obtain the velocity field. (b) CDR equations provide the solutions as the concentration of various blood factors and their reactions. (c) Clot formation using mesoscopic methods such as DPD, CGMD or CPM. (d) MD simulations or Ab-Initio methods used to capture atomic level biomolecular interactions.

Xu et al.[70] developed a 2-D multi-scale model with fluid flow simulated using NS equations, spatiotemporal thrombin concentration using CDR equations, and a discrete CPM model for platelet activation, migration and binding behavior. The fibrin concentration in the system was modeled using a rate equation related to the concentration of the activated platelet. The simulation results were compared with thrombus growth rates and sizes. More blood cells were employed in the model and a Lagrangian coherent structure[71] (LCS) was used to capture more details of blood clot formation[72]. The NS equations were coupled with the CPM model to capture the effects of cell adhesion on blood flow and vice versa. However, smaller particles (cells) were not coupled with NS, in an effort to reduce computational expense. The model was further improved by adding CDR equations to accommodate for surface mediated clot formation based on the coagulation cascade[73]. As a variation, fibrin polymerization was modeled by introducing additional differential equations and a fibrin element sub model[74], which also extends a 3-D version of LBM coupled with sub cellular element model (SCEM) to simulate blood flow.

Instead of using CPM and CDR equations, Moreno[75] formulated the multi-scale blood flow using a coupled NS equation, variational multi-scale method and smooth dissipative particle dynamics[76] (SDPD). However, this method needs improvement, like including blood factors and other criteria. A brief review about the particle based modeling methods for blood flow, application of Stokesian dynamics with a discrete element method, Particle semi-implicit method and DPD is discussed by Yamaguchi[10].

Modeling of Clot Mechanics

In the previous sections we have discussed the methods and models used to simulate the flowing blood and formation of a thrombus and here we focus on the models which are used to study the mechanical properties of fibrin or blood clots. The study of the structure and mechanics behind the thrombus is of great importance since it can predict the physiological or pathological conditions at which it can fracture and dislodge, leading to VTE or other states. A brief review of interfacial mechanics of biomaterials is available in literature[77]. Many experimental investigations and empirical models are focused on predicting the compression-decompression behavior of blood clots[78, 79]. There exists modular models to simulate the stress strain behavior of fibrin fibers[6], which can be scaled up and combined with other models to predict the bulk behavior of fibrin clots.

Discussion and Future Trends

The trend of computational modeling over the years indicates that the simpler models like single component continuum models are becoming redundant and increasingly replaced with discrete particle methods (DPD) and emerging techniques such as multiscale modeling. The continuum level methods are still suitable for predicting the top-level behavior based on empirical data, limiting them to use NS equations coupled with CDR equations and investigation of the blood flow dynamics. Two-way coupling of NS equations with CDR or other methods is superior to one-way coupling in many aspects like accurate flow distribution of blood and thrombus deformations due to high shear flow.

DPD is a powerful method for simulating fluid mechanical behavior, which currently is being utilized in many biological simulations. The base requirements for using DPD in blood flow simulations are put forward by many[10, 36, 65, 67, 69] and is continually improving. One of the advantages of DPD is that one can model many of the complex blood components like WBCs, RBCs, platelets and plasma as simple beads. These properties render DPD as a better choice compared to boundary element methods, LBM, and discrete element methods. One of the biggest challenges that the field still experiences is the modeling of blood as a non-Newtonian fluid, where DPD shows some promise[80–82]. However, one has to be careful in introducing additional potentials in DPD to simulate polymer chains, solid walls, dynamic bond formation and breaking, since DPD was originally developed for fluids with only three main soft interactive forces. Any modification on them will alter the dynamics and the parameters must be validated with experimental values.

Multiscale blood clot models (Fig. 4), can be used to simulate blood clotting dynamics, biochemical reactions, and factor concentrations effectively. The model will have cascading submodels which can serve as independent models to predict a few specific characteristics like thrombin cleaving fibrinogen, and attachment of fibrin to vWF to submodels which can predict thrombus solid-liquid interactions. A good multiscale model will have the characteristics of simulating the bulk behavior of the blood such as diffusivity and viscosity, mechanical properties of the thrombus under shear flow, and dynamic properties to simulate lysis and thrombus rupture based on molecular level mechanics. With the development of more accurate models for subcomponents of blood constituents, it will be promising to develop and simulate realistic blood clot formation and lysis. Erythrocyte multiscale models[83, 84] can predict the behavior of RBCs in the plasma flow and fibrin submodels[85–87] can be used to simulate atomic level[88] to mesoscale properties. The mathematical modeling of the overall coagulation process is advancing with capturing more and more factors and conditions[89–93]. These advancements in different scales will enable us to develop new accurate multiscale models to predict both the blood clotting process and its mechanics. In Table 1, some of the strengths and weaknesses of different scales of modeling is provided.

Table 1.

Strengths and Weaknesses of Various Methods

Method	Advantage	Weakness
System level	Good agreement with experiments	Missing spatiotemporal information
Continuum	Easy to setup Less computational power	Molecular and microscopic details are missing Need CDR equations to account for blood factors
DPD	Can work with complex geometries	Computationally expensive for big systems
Multiscale	Detailed information of system included Fine-tuned information at any scale can be included to improve the modeling Reliable simulation results of system under consideration	Complex to model Needs careful designing of algorithms to solve at different scales Computationally expensive

Conclusion

In this paper we have reviewed the recent developments in the area of computational modeling of blood clot formation using various methods at different length and time scales. From continuum level methods, we discussed the usage of NS equations coupled with CDR equations and mesoscopic methods like CPM, DPD and SPH are reviewed. A promising newly developed class of multiscale methods which utilizes the power of methods at different length and time scales is discussed in detail. The trend and the future direction leads to more multiscale methods to be evolved. We have also critically analyzed some of the strengths and weaknesses of the methods and suggested which ones can be used to simulate fibrin polymerization and mechanics.

Highlights.

• Computational strategies at various length scales are crucial for the field of thrombosis and hemostasis

• Continuum methods alone cannot describe thrombosis and hemostasis physically

• Hematological pathologies can be elucidated using various computational techniques

• Complex multiscale methods will be necessary for understanding thrombosis and hemostasis in the future

Nomenclature

I

Fibrinogen

II

Prothrombin

III

Tissue Thromboplastin

IV

Calcium

V

Proaccelerin

VII

Proconvertin

VIII

Antihemophilic factor A

IX

Antihemophilic factor B

X

Thrombokinase

XI

Plasma thromboplastin antecedent

XII

Hageman factor

XIII

Fibrin-stabilizing factor

MD

Molecular Dynamics