Multi-layer Fast Level Set Segmentation for Macular OCT

Abstract

Segmenting optical coherence tomography (OCT) images of the retina is important in the diagnosis, staging, and tracking of ophthalmological diseases. Whereas automatic segmentation methods are typically much faster than manual segmentation, they may still take several minutes to segment a three-dimensional macular scan, and this can be prohibitive for routine clinical application. In this paper, we propose a fast, multi-layer macular OCT segmentation method based on a fast level set method. In our framework, the boundary evolution operations are computationally fast, are specific to each boundary between retinal layers, guarantee proper layer ordering, and avoid level set computation during evolution. Subvoxel resolution is achieved by reconstructing the level set functions after convergence. Experiments demonstrate that our method reduces the computation expense by 90% compared to graph-based methods and produces comparable accuracy to both graph-based and level set retinal OCT segmentation methods.

1. INTRODUCTION

Ophthalmological assessment of retinal disease and neurological disorders often includes a segmentation of retinal cellular layers [1] from optical coherence tomography (OCT) images. Eight retinal layers are commonly segmented: retinal nerve fiber (RNFL), ganglion cell layer and inner plexiform layer (GCIP), inner nuclear layer (INL), outer plexiform layer (OPL), outer nuclear layer (ONL), inner segment (IS), outer segment (OS), and the retinal pigment epithelium (RPE) complex. Automatic segmentation of the retinal layers from OCT images has been accomplished using deep learning methods [2], graph methods [3], level set methods [4], and other methods [5–7].

Deformable models have been widely used in image segmentation [8,9]. Methods that use implicit representations of curves or surfaces [8] are often called geometric deformable models (GDMs) [10]. GDMs are typically based on the solution of partial differential equations (PDEs), which makes them computational expensive. As the closed curve or surface is represented as the zero level set, it requires frequent reinitialization, which further complicates its computation. Narrow band methods have been widely used to restrict the computation within a set distance of the zero level set [9]. Shi and Karl developed a fast level set method in a discrete domain that does not need to solve a PDE [11]; our work is inspired by their method, extending and adapting it for OCT retinal layer segmentation.

Since the initial introduction of GDMs, there have been modifications to handle topology and multiple-objects though all of these compound the computational burden. In this paper, we propose a multi-layer fast level set segmentation algorithm that can segment retinal layers in 3D. Our work extends fast level set methods to the specific case of OCT segmentation.

2. METHODS

Shi and Karl [11] represent a boundary as two lists of inside, L_I, and outside, L_O, voxels:

$$\begin{gathered} L_{\mathrm{I}}=\left\{x|\varphi (x)<0\text{and}\exists y\in {\mathcal{N}}_x\text{with}\varphi (y)>0\right\} \\ \text{and} \\ {L}_{\mathrm{O}}=\left\{x|\varphi (x)>0\text{and}\exists y\in {\mathcal{N}}_x\text{with}\varphi (y)<0\right\} \end{gathered}$$

where ϕ(x) is the level set function at voxel location x, and ${\mathcal{N}}_x$ are the 26-connected neighbors of x. The fast level set methods of Shi and Karl use −3 for voxels that are inside objects that are not in L_I, −1 for voxels in L_I, +1 for voxels in L_O, and +3 for voxels outside the object and not in L_O. With this definition, a positive force will switch a voxel from L_I to L_O and a negative force will switch a voxel from L_O to L_I. During each iteration, the fast level set method identifies all voxels with a negative force in L_I or a positive force in L_O, then L_I and L_O are updated to reflect the forces. The explicit level set function is required for removing idle points that are produced when switching voxels between L_I and L_O.

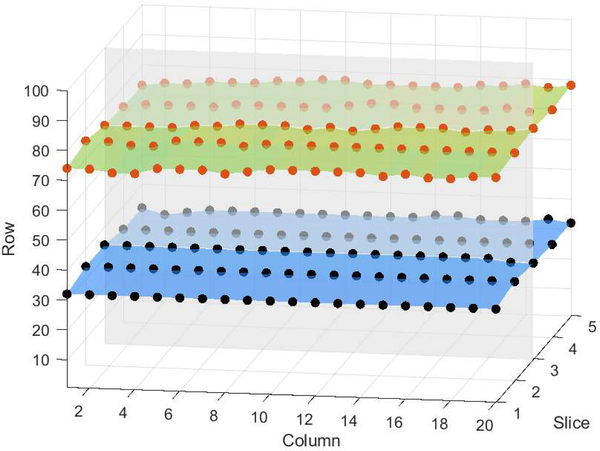
OCT retinal layers in either their original space or a “flat space” (wherein the A-scans are shifted and, perhaps, stretched or compressed), occupy a single voxel in each vertical column of the data. This is the case because, biologically, retinal layers cannot fold over on themselves. Thus, we can describe a boundary in 2D as a 1D list or a boundary in 3D as a 2D matrix as shown in Fig. 1. The size of this representation is determined by the size of image. Thus, for OCT data we can make three simplifications to the Shi and Karl fast level set method:

1. We switch voxels between L_I and L_O exclusively in the vertical direction.

2. Evolving in this manner means that no stationary voxels will be generated and thus no explicit computation or storage of level set functions is required.

3. Either L_I or L_O is needed, not both.

Fig. 1.

Boundary representation showing two boundaries in a five-slice, 3D image.

Our segmentation method is performed in the computational domain of flat space [4], where each layer is approximately flat. This allows a simple initialization and is suitable for our vertical direction only, voxel level evolution process. An example of an OCT image in flat space is shown in Fig. 2(a). A boundary, b, is represented in flat space by the value L_b(c, s) which is the height of the boundary at column c and slice s of the 3D image. Thus in each position (c, s) of this representation, we can apply either,

$$\begin{gathered} \text{Expand}(c,s):L_b(c,s):=L_b(c,s)+1 \\ \text{or} \\ \text{Shrink}(c,s):L_b(c,s):=L_b(c,s)-1 \end{gathered}$$

to update L_b(c, s). We apply Expand(c, s) if the net forces at (L_b(c, s),c, s) are positive and apply Shrink(c, s) if the net forces at (L_b(c, s),c, s) are negative.

Fig. 2.

Shown are a region of (a) an original OCT image transformed to flat space, the results of (b) Algorithm C, and (c) Algorithm N. The blue and red are the vitreous and choroid, respectively, with the eight layers of interest shown in shades of gray.

The primary “force” (actually a speed function in the context of a GDM) we use to drive our approach is the inner product of the gradient vector flow (GVF) [12] field computed from a specific boundary probability map with the gradient of the associated signed distance function. Nine GVF fields are computed, one for each retinal boundary, which ensures a large capture range—i.e., the entire computational domain—for each boundary we wish to identify. The boundary probabilities come from a trained random forest (RF) [13].

Given the layered nature of the tissues under consideration within the retina, there is a topological requirement for OCT images. Specifically, we must preserve the ordering of the eight layers from vitreous to choroid. Consider boundaries b and c with boundary b always above boundary c. Assuming appropriate initialization, we can enforce this topology constraint by performing a simple topology check before either of our two basic operations—i.e., Shrink or Expand. A point (c,s) will fail the topology check if the basic operation to be performed will cause L_b(c, s) ≤ L_c(c, s). Pseudo code for our algorithm is shown in Algorithm 1.

Algorithm 1.

Main Function

Initial boundaries

loop:

// Shrink Boundaries

for each boundary do

identify points that pass the topology check

if a point has negative force then

Shrink(c, s)

// Expand Boundaries

for each boundary do

identify points that pass the topology check

if a point has positive force then

Expand(c, s)

if no change was made to all boundaries then

break

Shi and Karl [11] Gaussian filter the signed distance function to provide smoothness regularization. We describe two alternative approaches: Algorithm C uses a fast curvature force estimation method [14], which requires no level set function to compute it and is therefore readily incorporated in our total force. It encourages flat surfaces, and is therefore quite appropriate for flat space. A result is shown in Fig. 2(b). Algorithm N uses an intuitive approach based on modifying the topology check: to perform Expand(c, s) to a boundary point, its neighbor points cannot be both two voxels above; to perform Shrink(c, s) to a boundary point, its neighbor points cannot be both two voxels below. In general, this condition disables operations that yield three-voxel peaks or valleys on boundaries. A more complex and boundary specific constraint can be imposed, but we used this simple method for computational efficiency. Also, this regularization method may actually speed up the evolution since we perform the check before we shrink or expand the boundaries. A result of Algorithm N is shown in Fig. 2(c).

The output of our algorithm is the voxel locations of all nine boundaries. The corresponding force map of each boundary voxels has positive forces for all of these locations and negative forces at one voxel below. Subvoxel boundary locations can be obtained by interpolating a zero-force location between these voxels. A result of subvoxel boundary location is shown in Fig. 3(d).

Fig. 3.

A magnified region in native space is shown in (a) with manual delineation (b). The segmentation result from Algorithm C in voxel resolution is shown in (c), while the result in (d) is the subvoxel resolution generated by interpolation.

3. RESULTS

To evaluate the accuracy of our fast multi-layer segmentation algorithm we compare it to the multi-object geometric deformable model (MGDM) [4] approach and a graph-based method (RF+Graph) [15]. We used the same random forest boundary probability map for MGDM, RF+Graph, and our method to allow for a direct, unbiased comparison. Our algorithm is implemented in Matlab and run on a single core 3.4 GHz computer. Data from the right eyes of 37 subjects were obtained using a Spectralis OCT system (Heidelberg Engineering, Heidelberg, Germany): 16 healthy controls and 21 multiple sclerosis patients were used, each mapped to flat space [4]. The GVF fields are precomputed, and the mean execution times for each volume is 218.5 seconds for Algorithm C and 8.4 seconds for Algorithm N, compared to over 2 hours for MGDM and approximately 5 mins for RF+Graph. The Dice coefficients [16] of MGDM, RF+Graph, Algorithm C, and Algorithm N are shown in Table 1. Almost no difference can be observed in the mean Dice coefficient between our two algorithms and MGDM; these three have larger Dice coefficient than RF+Graph for all eight layers. We used a paired Wilcoxon rank sum test to compare the distributions of the Dice coefficients. The p-values indicate that three out of the eight layers for Algorithm C and one out of the eight layers for Algorithm N are statistically better than MGDM (α level of 0.001). The average Hausdorff distance for nine boundaries between our two regularization methods and the manual delineation are calculated. Compared with 4.495μm without regularization, we observed 4.269μm for Algorithm C and 4.536μm for Algorithm N. Thus, using curvature as a regularization force improves the results, while Algorithm N results are visually more satisfying compared with no regularization but introduces more error. We also report a 7% reduction of average Hausdorff distance in subvoxel results.

Table 1.

The mean (and std. dev.) Dice Coefficient for MGDM [4], RF+Graph [15], Algorithm C, and Algorithm N over 37 subjects.

	RNFL	GCIP	INL	OPL	ONL	IS	OS	RPE
MGDM	0.903 (±0.028)	0.911 (±0.029)	0.812 (±0.034)	0.860 (±0.024)	0.927 (±0.016)	0.805 (±0.022)	0.845 (±0.030)	0.900 (±0.027)
RF+Graph	0.877 (±0.053)	0.892 (±0.053)	0.806 (±0.026)	0.855 (±0.016)	0.909 (±0.019)	0.751 (±0.030)	0.816 (±0.032)	0.884 (±0.023)
Algorithm C	0.903 (±0.026)	0.912* (±0.030)	0.826* (±0.031)	0.865 (±0.023)	0.927 (±0.017)	0.815* (±0.021)	0.846 (±0.027)	0.901 (±0.028)
Algorithm N	0.900 (±0.027)	0.910 (±0.031)	0.817* (±0.033)	0.857 (±0.025)	0.924 (±0.018)	0.806 (±0.023)	0.841 (±0.028)	0.899 (±0.027)

Statistically significant improvement based on a paired Wilcoxon rank sum test between MGDM and either Algorithm C or Algorithm N is denoted by *, with an α level of 0.001 and no multiple comparison correction.

4. CONCLUSION

The Dice coefficient and average execution time suggest that our method with both smoothness regularization approaches produce competitive segmentation results compared with MGDM and the RF+Graph method while significantly reducing the computational cost compared with MGDM and producing subvoxel resolution results that the RF+Graph method cannot. Our evolution strategy enforces correct layer topology at a very low computational complexity.