Diabetes and Diet: Purchasing Behavior Change in Response to Health Information

Abstract

Individuals with obesity and related conditions are often reluctant to change their diet. Evaluating the details of this reluctance is hampered by limited data. I use household scanner data to estimate food purchase response to a diagnosis of diabetes. I use a machine learning approach to infer diagnosis from purchases of diabetes-related products. On average, households show significant, but relatively small, calorie reductions. These reductions are concentrated in unhealthy foods, suggesting they reflect real efforts to improve diet. There is some heterogeneity in calorie changes across households, although this heterogeneity is not well predicted by demographics or baseline diet, despite large correlations between these factors and diagnosis. I suggest a theory of behavior change which may explain the limited overall change and the fact that heterogeneity is not predictable.

1. Introduction

In many health contexts, individuals appear resistant to undertaking costly behaviors with health benefits. Examples include resistance to sexual behavior change in the face of HIV (Caldwell et al., 1999; Oster, 2012) and lack of regular cancer screening (DeSantis et al., 2011; Cummings and Cooper, 2011). Among the most common examples of this phenomenon is resistance to dietary improvement among both obese individuals and those with conditions associated with obesity (Ogden et al., 2007).

The context for this paper is the change in diet in response to diabetes diagnosis. Type 2 diabetes is a serious complication of obesity which affects approximately 29 million Americans, and an estimated 422 million people worldwide.¹ It is well known - based on a considerable medical literature and clinical practice that the prognosis of individuals with Type 2 diabetes is improved with better diet and resulting weight loss. It is also well known - consistent with the overall behavior change literature - that many diabetics struggle to adhere to recommended behavioral changes (e.g. Delamater, 2006; Broadbent, Donkin and Stroh, 2011; Ponzo et al, 2017; Raj et al, 2017).

However, we have relatively little sharp evidence on how behavior changes after diabetes diagnosis. Among the limited examples, Feldstein et al. (2008) use medical records to show that, on average, weight loss after diagnosis is fairly limited. At the same time, that paper shows considerable heterogeneity, with some individuals losing more weight and having better clinical outcomes than others. Whether these patterns are a result of changes in diet, exercise or some other factor remains unclear.² To the extent this heterogeneity is observed in other data, and reflects differences in behavior change, it may be crucial to understanding why behavior change is limited.

The primary goal of this paper is to estimate how diet responds to a diabetes diagnosis. This estimation requires a data source with both detailed panel data on diet and information on health. Standard health data sets contain the latter, but not the former.³ The initial task of the paper is, therefore, to begin with a source with detailed diet data, and develop a method for generating health information.

The data used in this paper is the Nielsen HomeScan panel, a dataset which is commonly used in industrial organization and marketing applications. Household participants in the panel are asked to scan the Universal Product Codes (UPC) of purchases including all grocery and drug store item purchases (the UPC is encoded in the barcode).⁴ These data provide very detailed information about food purchases, which allows for tracking a measure of dietary choices with very fine timing. I merge these data with a second dataset which provides calorie information and that can therefore be used to estimate calorie purchases over time. Given information on timing of disease diagnosis, these data are well-suited to estimate household-level dietary response to disease using a household fixed-effect framework.⁵

The primary HomeScan data does not contain health information. For a subset of households, a secondary survey provides some information on health conditions. This survey does not, however, provide precise information on diagnosis timing. The key empirical strategy innovation in this paper is to infer diagnosis from purchase behavior. I do this using a machine learning approach.

This is discussed in detail in Section 4. I begin by using purchases of diabetes-specific products (primarily glucose testing products), after a period of exclusion, as a marker for diabetes diagnosis. This is straightforward to implement but I show (using the subset of individuals with known diagnosis in the data) that it generates a large share (about 70%) of false positives. The primary issue is that many long-standing diabetics only occasionally purchase these products. Assuming that only the newly diagnosed diabetics change their behavior, any effects estimated with this measure of diagnosis will be substantially attenuated.

The primary analysis therefore relies on combining the purchase data with information from the subset of households with diagnosis information. I use a machine learning algorithm to identify purchase patterns that are indicative of new diagnoses. Intuitively, this approach relies on the possibility that some combinations of products or product purchase timing may be more predictive of a new diagnosis. Identifying these combinations by hand would be impractical and subject to bias.

The learning approach is a random forest. In this method the algorithm is trained on the subset of the data for which we have known diagnosis timing. The inputs are a large number of characteristics of households and information about purchases of diabetes testing products. Purchase information includes what households purchased, the timing of the purchases, the combination of the purchases, etc. The random forest optimizes the use of these for prediction. The output is a predicted probability of a correctly identified diagnosis for each individual. The prediction model is generated from the households for which we observe the diagnosis, but the predictions are generated for all households, including those where diagnosis is unknown.

I use this probability directly in the analysis. First, I regress the outcome on the predicted probability directly, which will yield the treatment effect of interest in a linear model. Second, I estimate on a sample limited to those with higher predicted probability of new diagnosis, and scale the effects. I show these give very similar results.

Using this method, I document the response of overall calories and by food group. I find a statistically significant decrease in calories in the two months around diagnosis - this is about 6.4%. In the year following diagnosis there is also a reduction relative to the pre-period, but it is smaller (2.5%) and not significant. Using some simple scaling assumptions, I show this predicts weight loss in the same range seen in other data (Feldstein et al., 2008; data from the Health and Retirement Study).

The overall changes in calories reflect some improvements in diet quality. Households significantly reduce calories from non-whole grains, soda and red meat. Even in the longer term - the year following diagnosis - there are significant reductions in calories from non-whole grains, soda and whole milk products. These are partially offset in the overall calculation by increases in calories from nuts. Aggregating these together, I conclude there is some small improvement in diet, even in the long term, which is not fully captured in the calorie counts.

A natural question is whether the small changes on average mask larger changes for some individuals and, if so, if the larger changes are predictable. On the first question, I do find evidence that some households are more responsive. More specifically, using quantile regression I show that a subset of households show quite large changes; a similar analysis on the non-diagnosed households shows this is not a mechanical effect.

Turning to predictability, I find first that the diabetic households are systematically different from the non-diagnosed in predictable ways - less educated, lower income, older, worse diets. In addition, there is some heterogeneity in responsiveness to diagnosis. However, these do not line up. The variables which are correlated with diabetes are not the ones which predict heterogeneity in response.

From the standpoint of theory, I suggest these results present two puzzles. First, overall limited behavior change is at odds with large medical incentives to improve diet. Second, the predictable heterogeneity is at odds with the baseline heterogeneity. The baseline heterogeneity suggests - for example - that more educated people must have better diets, and yet within this sample they do not respond more.

In the final section of the paper I develop a simple theory which accommodates these facts and may shed light on the general observation that behavior change is limited in many interventions. The theory highlights the limits to learning about population behavior from a sample like this. The results rely on the extremely simple point that in this setting, like other progressive lifestyle diseases, there are many opportunities for warnings which head off disease development. On the way to being diagnosed with diabetes, most individuals have been given many instructions to lose weight and improve their lifestyle. The sample of individuals who arrive at a diagnosis are, therefore, selected to have not responded to these arguments.

The theory has several implications. First, it suggests that limited behavior change after diagnosis may not be surprising and, importantly, may not be informative about behavior in the overall population. Second, the theory speaks to heterogeneity in response. This shows that the strongest correlates of behavior change in the overall population may be completely uncorrelated with behavior change in the selected sample.

The theory may have implications for understanding why lifestyle interventions (diet studies, for example) are so often unsuccessful. In many of these settings, the population on which the intervention is run is extremely selected relative to the overall population. Their lack of success may not be informative and, moreover, analyzing the correlates of success in the studies may say little about the population overall.

This paper’s primary contribution is to our understanding of resistance to health behavior change. A secondary contribution is to illustrate a new way that household scanner data might be used by health researchers and, in particular, how it may be possible to use machine learning techniques to take advantage of data like this in which we see detailed purchase data for many people, along with some health data for a limited subset of those people. These scanner data are commonly used in industrial organization and marketing applications, but they have been less often used to evaluate questions in health.

2. Background on Diabetes

This paper explores the issue of behavior change in the context of diabetes. Diabetes is a medical condition in which the body does not process insulin correctly. There are two types. In Type 1 diabetes, the pancreas cannot make any insulin. This disease typically manifests in childhood and individuals with the illness must manage it with insulin injections to replace pancreatic function. In Type 2 diabetes, the pancreas produces some insulin, but the body does not process it correctly and glucose levels rise too much. This illness more commonly manifests in adulthood and is very often a complication of obesity. Medical treatment of Type 2 diabetes includes oral medication and, if the disease progresses, injected insulin. Our empirical strategy will allow for inclusion of both groups, but the vast majority of the diagnoses identified in this paper will be Type 2 diabetes diagnoses, given that only about 4% of diabetics are Type 1 diabetics.⁶

The health consequences of Type 2 diabetes result from the possible buildup of glucose in the blood. This buildup can damage blood vessels, leading to a variety of problems. Complications from poorly managed diabetes include blindness, kidney failure, amputation of extremities (feet in particular), heart attack and stroke. Even with treatment, Type 2 diabetics have significantly elevated mortality risk compared to non-diabetics (Taylor et al., 2013). Similar to other complications of obesity, Type 2 diabetes is on the rise in the US. An estimated 29 million Americans live with the disease, and 1.7 million new cases are diagnosed each year (CDC, 2014). The vast majority of these are Type 2 diabetes. Estimates from 2012 put the annual cost of diabetes to the US health care system at $176 billion, with $69 billion in further costs from reduced productivity (American Diabetes Association, 2013).

A central component of diabetes treatment is changes in diet and exercise behavior. Diet recommendations are made by the American Diabetic Association (American Diabetes Association, 2013; Franz et al., 2002) and have several components. The most important one is weight loss. A very large majority of Type 2 diabetics are overweight or obese, and the ADA recommends weight loss through a deficit of 500 to 1000 calories per day relative to what would be required for weight maintenance. The ADA also makes recommendations on the makeup of these calories: roughly 60–70% should be from carbohydrates, 15–20% from protein, and less than 10% from saturated fat. Although, in general, a diet rich in whole grains and vegetables is recommended, the ADA has, in recent periods, noted that the total calorie intake is more important than the source.

It is important to note that the diagnosis of diabetes in most individuals follows a period of warning. Many individuals are diagnosed as pre-diabetic in the period before developing diabetes. The benefits of weight loss for individuals at risk of diabetes, but not yet diagnosed, are well known and lifestyle interventions in this period have had some success in delaying onset (Lindstrom et al., 2006; Diabetes Prevention Program et al., 2002).

3. Data: Consumer Purchases

The primary outcome data used in this paper is expenditures based on consumer purchases. These data are collected through the Nielsen HomeScan panel. I merge these with calorie data, also described below. This section describes how I use these data to create an overall measure of diet for individuals in the panel. The first subsection describes the data sources and the second discusses some data limitations.

3.1. Consumer Purchase Data

Nielsen HomeScan

The Nielsen HomeScan panel tracks consumer purchases using at-home scanner technology. Individuals who are part of the HomeScan panel are asked to scan their purchases after all shopping trips; this includes grocery and pharmacy purchases, large retailer and super-center purchases, as well as purchases made online and at smaller retailers. The Nielsen data records the UPC of items purchased and panelists provide information on the quantities, as well as information on the store. Prices are recorded by the panelists or drawn from Nielsen store-level data, where available. Einav, Leibtag and Nevo (2010) have a validation of the reliability of the HomeScan panel. I use Nielsen data available through the Kilts Center at the University of Chicago Booth School of Business. This data covers purchases from 2004 through 2014.

In addition to purchase data, Nielsen records demographic information on individuals. This includes household size, structure, income, education of the household heads and age of household heads and children. The data also include information on zip code of residence. I merge in data from the USDA on “food deserts” by zip code; these are defined as low income census tracts more than 1 (10) miles away from a supermarket in urban (rural) areas.

I calculate a measure of household size in the Nielsen data that takes into account the ages of household members and their relative calorie needs. The outcome measures are all calculated based on this adjusted household size and can be thought of as per-adult-equivalents.

The analysis will rely on a balanced panel of households for whom I infer a diabetes diagnosis during the panel (this inference is described in detail in Section 4.1). There are 857 households in this group. Panel A of Table 1 shows demographic summary statistics for this group.

Table 1:

Summary Statistics

Panel A: Panelist Demographics
	Mean	Standard Deviation	Sample Size
HH Head Age	59.5	12.1	4656
HH Head Years of Education	14.1	2.26	4682
HH Income	$61,888	$50,614	4666
White (0/1)	0.82	0.37	4645
In Food Desert (0/1)	0.36	0.48	4684
Panel B: Panelist Shopping Behavior
Avg. Number of Trips/Month	11.5	7.3	112,416
Shopping Behavior:
Calories (person/month)	46,672	29,589	112,416
Expenditures (person/month)	$126.70	$92.19	112,416
Expenditures Shares on:
Whole Grains	2.0%	3.3%	112,340
Non Whole Grains	16.5%	9.2%	112,340
Potato Products	1.66%	2.3%	112,340
Dark Green Vegetables	1.41%	2.4%	112,340
Orange Vegetables	0.50%	1.1%	112,340
Beans, Lentils, Peas	0.29%	0.9%	112,340
Other Vegetables	2.71%	3.4%	112,340
Whole Fruits	4.06%	5.5%	112,340
Fruit Juices	1.63%	3.1%	112,340
Whole Milk Products	3.13%	4.3%	112,340
Low Fat/Skim Milk Products	3.11%	4.6%	112,340
All Cheese	4.96%	4.8%	112,340
Beef, pork, veal, lamb, game	5.55%	5.8%	112,340
Chicken, Turkey	0.59%	2.0%	112,340
Fish	1.48%	3.2%	112,340
Bacon, Sausage, lunch meats	2.19%	5.9%	112,340
Nuts, Nut butters, Seeds	3.67%	4.8%	112,340
Eggs and egg mixtures	1.16%	1.8%	112,340
Fats, condiments	2.42%	3.2%	112,340
Coffee, tea	1.99%	4.1%	112,340
Soft Drinks, Soda	7.54%	10.8%	112,340
Sugar, sweets, candy	19.1%	11.1%	112,340
Soups	3.17%	3.9%	112,340
Frozen Entrees	9.07%	9.2%	112,340

Notes: This table reports summary statistics on demographics (Panel A) and panelist shopping behavior (Panel B). Household age, income and education are computed at the median of reported categories. Quantity and expenditure data come from Nielsen data directly. Calories are generated by merging the Nielsen panel with Gladson data.

Nielsen Ailment Panel

The Nielsen Ailment Panel (hence, “Ailment Panel”) is collected by Nielsen as a supplemental data product, which can be merged into the HomeScan data. I was able to access these data for 2010. The Ailment Panel survey covers approximately 35,000 Nielsen households and asks questions about a wide variety of health conditions and about the timing of diagnosis. In some households all family members complete the survey, although in others it is only a subset. The information on diagnosis timing is yearly: individuals are asked if they were diagnosed within the last year, 1 to 2 years ago, 3 to 4 years ago or further in the past. The survey includes diabetes as one of the conditions; this is the data I will use below. I will use all diabetic categories (type 1, type 2, pre-diabetes) since newly diagnosed members of all groups will want to change their diet and, in practice, differentiating these groups is very difficult to do with the diagnosis strategy detailed below. However, given the shares in the population we expect about 95% of cases to be Type 2 diagnosis.

Gladson Product Information Data

I merge the Nielsen data with nutrient information from Gladson. Gladson maintains a database of information on consumer products, including virtually all information available on the packaging. The primary objects of interest are total calories and nutrient breakdown. I use a single pull of the Gladson data as of 2010.

The Gladson data does not contain a UPC match for every code in HomeScan. I undertake a sequential match procedure similar to what is used in Dubois, Griffith and Nevo (2014). There is a direct UPC match for about 60% of purchases. For products which do not have a match in the Gladson data, I impute nutrition values based on the type of product (e.g. “tortilla chips”, “chocolate candy”), brand and size. I calculate average nutrition per size from the matched products and multiply this by the product sizes of the unmatched products to obtain the imputed values. Approximately 3.7% of purchases remain unmatched.⁷

Outcome Measures

The first outcome measure is overall calories of the purchases. The second aggregate outcome measure is total expenditures. As I will note below, it is not obvious that these will move in parallel. Recommendations for dietary changes focus on calories and not price, so total expenditures may go up or down, or not move at all. However, alongside calories they provide a useful overall measure.

Diet quality is based on the share of calories or expenditures in food categories, as defined by the USDA Thrifty Food Plan (TFP). The TFP is one of four USDA-designed food plans specifying foods and amounts of foods that provide adequate nutrition. The TFP is used as the basis for designing Food Stamp Program benefits. TFP groups include whole grains, non-whole grains, sugars, fats and condiments, vegetables, etc. I generate measures of the share of calories or expenditures in each group. These measures of diet quality have been used in previous literature, most notably by Handbury et al. (2015) in a study on food deserts and differences in diet by SES, and Volpe et al. (2013) on the effect of supercenter-format stores on the healthfulness of grocery purchases.

The focus on shares here has the advantage of giving a measure of diet quality which is independent of the size of the basket purchased.

Panel B of Table 1 shows averages of these outcome measures for the household-months in the sample. Of particular note is that the average household records purchases of 1480 calories per adult-equivalent per day. This indicates that we miss some calories, an issue which is discussed in the next section. We can also see expenditure shares by food group in Panel B of Table 1. The two most heavily purchased groups are non-whole grains and sugars, sweets and candies. This does not suggest a very high quality diet. One thing to note is that fruits and vegetables will be under-represented in these data since this includes only UPC coded items. This issue is discussed in more detail below.

3.2. Data Limitations

These data have some significant advantages in addressing the questions posed here. Households are not enrolled in a study of diet, so they are unlikely to feel that the healthfulness of their diet is being monitored. This leads to less concern about Hawthorne effects than in a study more directly focused on diet. I observe food choices before and after diagnosis for the same household, which has not been possible in large-scale data before. Finally, the data is available at a very detailed food level. However, there are a number of limitations in the data which deserve discussion.

A first central issue is that I observe only a subset of what households buy and consume. This is true for two reasons. First, Nielsen panelists do not scan food purchased outside the home. Second, even within the subset of food at home, it is very likely that individuals do not record all purchases. Einav et al. (2010) validate the HomeScan data using a match with records from a retailer and suggest slightly less than half of trips are not recorded at all; among trips which are recorded, they find a high level of accuracy.

To get a sense of the magnitude of this issue, I compare with food diary data from the National Health and Nutrition Examination Survey (NHANES). Although the food diaries recorded in the NHANES are also subject to under-reporting, the issue is likely to be less significant. Using the 2007–2008 NHANES (the date is chosen as the midpoint of the Nielsen sample) I find adults report approximately 1862 daily calories in total. The calorie levels in HomeScan therefore represent approximately 80% of total calories (taking the NHANES as a baseline). An alternative baseline is to evaluate this relative to the calorie level which an average diabetic would require to maintain weight. I do a calculation in this spirit in Appendix A and conclude this figure is approximately 2194. Using this baseline, HomeScan records about 68% of calories.

It is further worth noting that we observe only purchases, not consumption, and it seems likely that there is at least some wastage. If this is the case then we see a smaller share of the diet than suggested above, since we see purchases amounting to (say) 80% of calories but less than 100% of these calories are consumed.

These issues could bias our results in either direction. On the one hand, if the pattern of calorie changes on the full diet are the same as the patterns on the items we observe, and wastage does not change with diagnosis, then we can simply scale up the effects we observe based on our estimate of under-reporting. However, this would over-state the degree of change if there is (for example) a greater change in grocery purchases relative to food away from home. It could under-state the degree of change if the opposite is true - if people substitute away from food outside the home towards groceries, we may see a smaller change here than in truth. Further, if the patterns of wastage across food change with diagnosis - perhaps people waste fewer vegetables after diagnosis - then our purchase results will not reflect consumption results.

These issues are most salient when we think about the results on calorie changes. When we analyze the share of purchases in healthy and unhealthy food we may be less concerned, at least about the issue of levels. Nevertheless, these biases do influence the likely precision of these results.

A second issue is that this analysis will be done at the household level. Ideally, we would limit the analysis to single-person households, but this is infeasible. I will show robustness in which I limit to this group, but in general the changes observed represent the household overall. It is therefore not possible to directly attribute these changes to the particular diagnosed individual.

Finally, non-UPC coded items are recorded only by a subset of households (called Magnet households). These items do not have calorie measures. I will show overall price responses of these households separately, although, as I note below, the expected impact on price is ambiguous. In general, missing the non-UPC coded items may mute the response on fruits and vegetables.

One implication of all of these issues is that the levels of consumption are difficult to interpret. When I report results, I will generally also report changes in terms of percentages, which may have an easier interpretation.

4. Empirical Strategy

The primary goal in this paper is to estimate how diet responds to a health event. In existing datasets - say, a health survey with a food diary - it is often feasible to observe a lot of detail about health events but without the detailed dietary data over time. In the HomeScan data I have the detailed diet information over time, but the data does not contain detailed measures of health event timing. The key empirical challenge in the paper is that we do not observe this event directly and would like to infer it from purchase behavior.

Broadly, the solution I use is to infer diagnosis based on purchases of diabetes-related products. I do this using a machine learning approach, which is described below. This approach relies on the fact that I observe some true diagnosis information for a subset of individuals. Among other things, this illustrates how such techniques might be productively used in settings like this.

The first subsection below describes the machine learning approach to diagnosis identification. The second subsection details the empirical strategy following this diagnosis identification.

4.1. Identifying Diabetic Diagnosis

4.1.1. Nielsen Ailment Panel

For a subset of households we have information on disease diagnosis timing.

In principle, these data could be used directly. However, there are two issues. The first issue is sample size. Although there are many households covered, in most cases the survey includes only a subset of household members, and I was able to access only a single year of data. Second, the data on diagnosis timing is extremely coarse. Individuals are asked only if they were diagnosed within the last year, 1 to 2 years ago, 3 to 4 years ago or further in the past. Given issues of memory, it seems unrealistic to make precise inferences from most of these categories. Further, if we think that response to diagnosis is immediate, but perhaps not sustained, seeing diagnosis at a yearly level may not be sufficient.

4.1.2. Random Forest Regression Approach

Setup and Problem

I attempt to learn about diagnosis directly from purchase behavior. In the HomeScan data I observe purchases of diabetes-related products. Broadly, the goal is to use these products to infer diagnosis timing. Because we see these data for all households, and we see the exact date of purchase, this avoids two of the issues in using the Ailment survey.

I begin by identifying a set of candidate diabetes-related products. I use products which are specific to diabetes (e.g. testing strips, glucose monitors). These are straightforward to identify. I take the sample of all products in the blood and urine testing product module, and identify any for which the UPC description contains a set of diabetic keywords.⁸

I first use these data to identify individuals as newly diagnosed if they are observed purchasing one of these diabetes-related items after some exclusion period in which there are no purchases. There are two potential errors here. First, this will miss anyone who does not purchase one of these items. Second, it may mis-classify individuals as newly diagnosed who are either (a) not diabetic or (b) were diagnosed in the past and have never purchased products before in the HomeScan data. The first of these problems is an issue only for the external validity of the estimates, but the second is an issue even for internal validity. In particular, if the errors result in the inclusion of many non-diagnosed individuals, the estimated effects will be attenuated.

I can evaluate the extent of these problems by using the Ailment Panel data for validation. I merge the inferred diagnosis data with the Ailment Panel, limiting to households who have all members observed in the Ailment Panel, to ensure we are not missing diagnosis due to missing people. I use the Ailment Panel diagnosis timing to identify whether the inferred diagnosis is plausibly a new diagnosis. For example, I identify an inferred diagnosis in 2008 or 2009 as accurate if the household reports a diagnosis of diabetes either within the last year or one-to-two years prior.⁹

The error rate is large. Of the 1679 diagnoses in the panel, 1141 are missed by this procedure. This suggests many diagnosed people do not appear in the sample purchasing testing products. As noted, this may affect the external validity of the estimates, although it should not affect the internal validity.

This procedure also identifies a large number of false positives. There are 246 true positives identified this way, and 512 false positives. In the sample of individuals identified as newly diagnosed, therefore, only 30% of them would be true new diagnoses. Most of these households (80%) do contain a diabetic household member, so the error is largely a result of cases where the household was diagnosed sometime in the past and does not frequently purchase these products.

Estimation using the identified households will lead to attenuated effects, assuming there are no impacts for non-diagnosed households. To improve this procedure it is necessary to better separate the true from the false positives. I do this using a machine learning approach which uses an algorithm to identify - among the set of diabetic candidate products - those which are most indicative of a new diabetes diagnosis. I use the Ailment Panel data on diagnosis accuracy as the outcome of interest to predict.

To be more specific: I begin with the sample of households which are identified as newly diagnosed based on purchasing some diabetes-related items after the exclusion period in either 2008 or 2009. This is 758 households. For these households I observe the purchase event that triggers my diagnosis coding, and (in addition) patterns of purchases over the following period. I define the initial purchase event as a “correct” diagnosis if this household reports a new diagnosis in 2008 or 2009. Our hope is to separate these true positives from false positives by using information about the baseline purchase and subsequent purchases.

One possibility is that some particular products are very diagnostic of a new diagnosis (for example, a glucose monitoring set). It may also be that some timing of purchases is very diagnostic - for example, a households who consistently buys testing products following the baseline purchase may be more likely to be a new diagnosis, given that this represents a large change in behavior from the exclusion period. Finally, it may also be that new diagnoses are frequently characterized by a constellation of purchases - testing system plus testing lancets (needles) together, for example.

To allow for all of these factors to enter, and possibly to enter in combination with each other, I use an approach based on regression trees and a random forest algorithm. I will describe this briefly here, but interested readers can find more details about machine learning in general in Friedman, Hastie and Tibshirani (2009) and about random forests in particular in Breiman (2001).

Trees and Random Forest

Tree-based methods work by partitioning the households based on the products they buy into groups which are as similar as possible on the outcome (in this case, whether they are a new diagnosis or not). I use an approach based on a popular method called CART. The procedure works by generating a series of binary splits of the data. This begins by identifying the product and the split level that is the best fit to the data. Think, for example, of as series of regressions of whether a household is newly diagnosed on a dummy for whether you buy at least $1 of product 1, at least $2 of products 1, at least $3 of product 1, at least $1 of product 2, etc, etc. The procedure then picks the best fit version of this regression and segments the data into two groups. Then within each group this is done again. This can be continued until some desired stopping point.

The result is a tree where each “leaf” is a group of households which share the features of each binary split, and are as similar as possible. The hope in a case like this would be to end up with some leaves in which a large share of households are new diagnoses, and then we would use this prediction to apply to the full dataset.

It is well know that producing a single tree - while generating intuitive results - generates a lot of out-of-sample variance in prediction. Put simply, the tree is fit to a particular draw of the data, and may therefore be overly reflective of that particular data draw. We can think of this problem as over-fitting. To address this, there are a number of options which involve growing multiple trees and averaging them; I will use a common approach called a random forest.¹⁰ The random forest draws a bootstrapped sample of the data, and then also draws a random sample of the full set of variables used (in this case, the products). With these inputs a tree is created. The procedure is repeated to build many trees, and then the trees are averaged to create a prediction for each household. As noted in Friedman, Hastie and Tibshirani (2009), the random forest preforms well in many settings and is computationally tractable.

The choice of the number of trees to build and average is a trade-off between the value of increasing the number of trees and the computational cost. Friedman, Hastie and Tibshirani (2009) note in a number of applications that performance stabilizes around 200 trees. I use 250 trees, and run this procedure using the randomForest package in R.

The random forest procedure takes feature inputs from the data. These include (a) household demographics, (b) information on testing product purchases, including the initial purchase and subsequent purchases over the following year. Appendix B discusses the full variable list and tuning details of the random forest.

Results:

Importance and Fit

When fitting a single tree it is straightforward to visualize the classification, since it is possible to see the splits at each branch and the characteristics of the leaves. It is difficult to visualize the output of a random forest. However, we can generate an importance measure for each variable. This importance value is based on the out-of-sample error with and without the variable included. Table 2 lists the top 15 variables in order of importance.¹¹

Table 2:

Random Forest Importance Results

Feature Description	Importance Measure
Test Strips, Baseline Visit	6.48
Time to First Purchase after Baseline	5.32
Max Time between Purchases	4.58
Avg. Time between Purchases	4.28
Min. Time between Purchases	3.72
Lancet Purchase, Baseline Visit	3.62
Household Income	2.87
System + Lancet + Test Strips, Baseline Visit	2.73
# Purchase Dates	2.49
Testing System Purchase, Baseline Visit	2.42
Maximum Purchase of Same Item	1.86
Lancet + Test Strip, Baseline Visit	1.78
Test Strips, End of Year	1.65
Baseline Purchase in August	1.55
Household Head Education	1.49

Notes: This table shows the top 15 UPC-codes in the random forest based on the importance function. Column (1) gives the feature description and Column (2) shows the average reduction in node impurity for this variable.

Purchase of test strips at the baseline visit is the highest importance measure. But importance also loads on the timing of purchases and their frequency, as well as combinations of purchases. These importance measures do not indicate direction - they do not tell us that these correlate positively with the outcome, just that they contribute importantly to the outcome.

The output of the random forest is a predicted probability of the identified event being a true diagnosis event. I will use this probability directly in the analysis, as described in Section 4.2 below. In addition, in robustness analysis I will use subsets of the data defined by having predicted probabilities of diagnosis greater than some cutoff c. Increasing the cutoff c lowers the false positive rate at the expense of sample size.

Final Sample

The final sample contains all individuals with possible new diagnosis, merged with their probability of diagnosis. Note that this sample includes many people for whom we do not see Ailment Panel data, but we use the algorithm that was trained on the merged data to predict for the sample for whom we see only purchase data.

It is important to be clear on what the learning algorithm is predicting. The starting sample is individuals who have a purchase of a diabetes product after an exclusion period. We are predicting whether that purchase occurs in a diagnosis year. The coarse aspect of the ailment data means we cannot pinpoint whether this is the diagnosis month. Effectively, we need to assume that the first purchase we see in a diagnosis year is the first purchase; this introduces some noise into the data, which could attenuate our effects.

Related to this, the use of purchase data means there is very likely to be a delay between diagnosis and related purchases. We will observe a reflection of this in the data, where the effects begin in the month prior to the purchase. I will consider this month prior as a “diagnosed” month, to reflect the fact that the diagnosis will occur before the purchases. The figures with results will show the precise timing.

I focus on a balanced sample of households which are observed for a year before and a year after identified diagnosis. I will show robustness to including households outside of the balanced panel. The final sample contains 4,684 households. This sample includes any household with a positive probability of being a new diagnosis (effectively, any household with testing product purchases following the exclusion period). In Appendix D I show all of the results using a balanced panel of 579 households with a predicted probability of diagnosis greater than 50%. In Appendix C I also show the robustness of the main calorie results using varying cutoffs.

The machine learning approach is designed to deal with the issue of false positives. However, there are many people that are newly diagnosed who are missed by this approach. These may be individuals who receive their testing supplies for free, for example. The direction of the external validity bias is not obvious. If a purchase of diabetes products signals a seriousness in disease management, then this would suggest our estimates are upward biased as a measure of the overall population effect. On the other hand, if people with better insurance coverage are more likely to get their testing supplies through their insurer, this probably suggests a downward bias.

To get a sense of whether this group differs systematically from the group we can identify, we can again use the validation data and compare those who are identified as newly diagnosed by the algorithm to those who are missed. Appendix Table C1 compares the two groups on some baseline demographics, as well as some characteristics of their diet. The samples are well-matched on demographics; the identified sample is significantly more educated but the differences are small. In terms of diet, the identified households purchase slightly more calories, but there is no difference in diet composition on several of the major food groups. The larger number of calories may reflect differences in scanning behavior, with identified households scanning more of their purchases (which would be consistent with scanning testing products). Overall, this table provides some confidence that this sample is similar on observables, although of course they may differ on unobservables.

4.2. Event Study Approach

Define D_it as indicators for months relative to identified diagnosis month for individual i. Given this, I can construct an event study method within the household to estimate the average response to diagnosis timing. For outcome Y_it this regression would be:

$$Y_{it}=\sum _t{\beta }_t{D}_{it}+{\gamma }_i+{\tau }_t+{\epsilon }_{it}$$ (1)

where γ_i is a household fixed effect and τ_t is a fixed effect for the month-year. The inclusion of τ_t means the regression controls for common non-diagnosis time effects.

In this setting, our “diagnosis month” event contains some true diagnosis events, and some false events. The values of β_t above will be attenuated in the stated regression.

This attenuation will be a function of the share of diagnoses events that are false positives. Given that this share is known for each household, based on the random forest output, I consider two approaches.

First, I use the probability directly. Specifically, note that we observe the predicted probability p_i that the event is a true diagnosis event. Given this linear model, I can therefore estimate

$$Y_{it}=\sum _t{\beta }_t\left(p_i{D}_{it}\right)+{\gamma }_i+{\tau }_t+{\epsilon }_{it}$$ (2)

and identify the true coefficients β_t.¹²

Second, I estimate Equation (1) for both the overall sample (with a false positive rate of about 68%) and for the sample with predicted probability greater than 0.5 (with a false positive rate of 40%). I scale the estimates based on the expected attenuation, under the assumption that the effect is zero for the false positives.

The former analysis will be more efficient as it uses all of the data, so I will largely focus on this but will show all of the results using the restricted sample of high probability individuals in Appendix D.

Diabetes Product Purchases

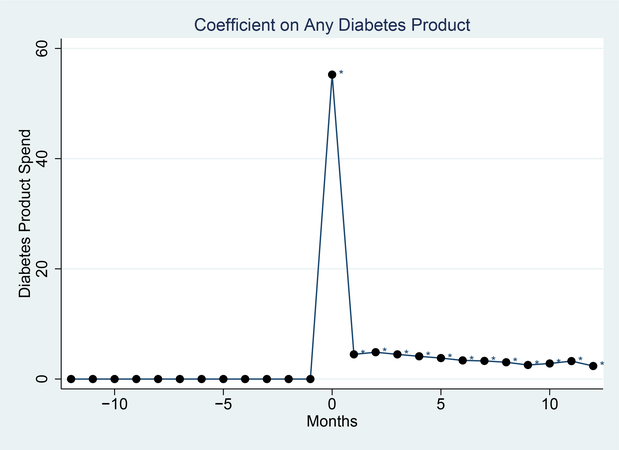
To illustrate this approach, Figure 1 shows the spending on the diabetes-related products around the identified diagnosis. Prior to diagnosis there are no purchases (by definition). In the month identified as the diagnosis there is a large spike up - this is mechanical since everyone must purchase in this period. There is then a decline, but the spending in subsequent months on these products is positive and significantly different from zero.

Figure 1: Testing Supply Purchases.

Notes: This figure shows data on purchasing diabetes-related products around the inferred diagnosis timing. These represent average spending on such products by month, in a balanced panel of households. * indicates significantly different from 0 at the 5% level.

The fact that the subsequent purchases are lower reflects the approach to identification here. Everyone buys something in the first month - this is how they are defined as diagnosed - and often these purchases are of multiple things. In later months people do continue purchasing, but they do not purchase many things together as often. Moreover, some do not purchase anything in a given month. These facts together drive the lower purchases in later months.

Empirical Issues: Crowd Out and Diagnosis Timing

There are four remaining issues in the analysis, related to the procedure used for inference here.

The first relates to shopping trip crowd out. By construction, households must have undertaken a shopping trip when they purchased the products I use to define diagnosis. It seems likely that such a shopping trip would include other purchases. This will lead to a mechanically higher purchase amount in the diagnosis period. This is a downside of using purchase data rather than consumption data.

To avoid this, I would like to exclude this period. One option would be to exclude only the trip at which the purchases are made. However, this will artificially depress the purchase amount in this period. Instead, I attempt to exclude a period around the purchase data, with the length of the period chosen to reflect the serial correlation in shopping. Using the data, I estimate the propensity to shop by day around a particular shopping trip. I find, not surprisingly, that shopping occurs on a weekly cycle. If people shop on day 1, then shopping is lower for days 2–7 and higher again at day 8.¹³ I therefore exclude the entire two-week shopping cycle: the day of the trip and one week on either side, and count months from there. This means that, for example, the month after diagnosis is in fact the 4 weeks starting at 1 week after diagnosis and going to 5 weeks after diagnosis, the second month is 6 to 9 weeks and so on.¹⁴

A second issue is that we will measure diagnosis at least some time after the actual diagnosis. It seems unlikely that everyone responds to a diagnosis by immediately going out and purchasing testing supplies that day. Therefore the definition of the “pre-period” is somewhat complicated since clearly there is scope for some response shortly prior to when we see purchases. I will largely allow the data to inform this and, in practice, the figures give a clear sense that there is a response in the month immediately before the measured purchase.

Third, we may be concerned that there is some mechanical reason we observe a response, related to the data construction. To alleviate this concern, I use a sample of control individuals with no diabetes-related purchases as a placebo. I define a “diagnosis date” for this group as some arbitrary purchase date within their data.

A final concern is that the timing of diagnosis may be endogenous. Individuals may decide to visit the doctor, at which time they are diagnosed, and simultaneously devote themselves to getting healthier in other ways. I show that there is no evidence of a pre-trend leading up to the changes, which rules out some of this concern. However, it is important to keep in mind that this empirical strategy cannot rule out some other change which drives both diagnosis and diet changes at the same time.

5. Results

5.1. Aggregate Changes in Calories

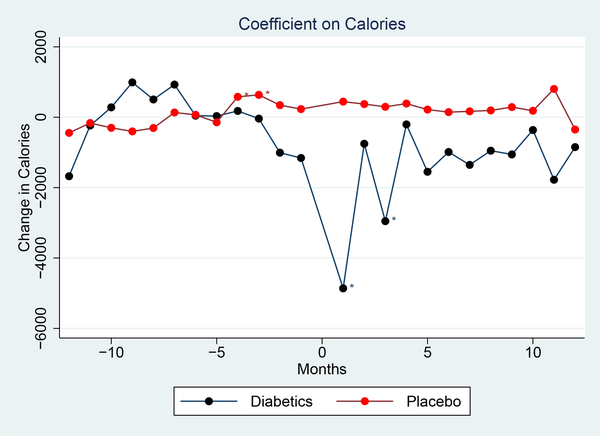
Figure 2 shows the primary result: changes in calories over time around diagnosis. This figure is estimated based on Equation (2), using the entire sample and interacting the timing with the predicted probability. The black line shows the diabetic sample. The red line illustrates the placebo.

Figure 2: Impact of Diagnosis on Calories.

Notes: This graph shows changes in calories after the inferred diagnosis. The graph shows coefficients from a regression of calories on time from diagnosis with household and year-month fixed effects; the coefficients are relative to the mean in the pre-period. The red line shows the trend over time for a placebo group of household without diagnosis. “Diagnosis” timing is defined randomly for this set. The outcome is calories per household member.

This figure shows the impact of diagnosis on calories purchased. There is some decline in calories in the month before we observe diabetes-related purchases in the data, consistent with the fact that diagnosis must precede these purchases and then a sharp decline in the first month after. The effect diminishes after this.

The period prior to diagnosis shows no noticeable trend, and the placebo group shows no changes around “diagnosis”. This provides confidence that the changes we observe in the diagnosed group are real.

Table 3 shows the primary results in regression form. Motivated by the patterns in Figure 2, I define two “post” periods. The first is the two months around the initial purchase. The second is the year following this. These definitions are, of course, somewhat arbitrary. The full pattern of changes over time can be seen in Figure 2. The goal here is simply to provide a way to summarize these changes.¹⁵

Table 3:

Behavior Change After Inferred Diabetes Diagnosis

	Calories			Expenditures	Expenditures, Magnet HH
	Prob. Interaction	All TS Purchase	Predict Diab >=50%	Prob. Interaction	Prob. Interaction
	(1)	(2)	(3)	(4)	(5)
Month Before, Month After	−3019.6***	−590.3**	−1797.5**	−2.37	−6.52
	(937.5)	(296.9)	(828.2)	(2.49)	(3.97)
		[−2951.5]	[−2869.9]
2–12 Months After	−1189.3	216.7	−468.6	−0.40	−4.41
	(841.1)	(321.0)	(914.5)	(2.54)	(4.04)
		[1083.8]	[−748.2]
Household Fixed Effects	YES	YES	YES	YES	YES
Year-Month FE	YES	YES	YES	YES	YES
R-squared	0.49	0.49	0.51	0.66	0.675
Number of Obs	112,416	112,416	13,896	112,416	64,680
Number of HHs	4684	4684	579	4684	2695

Notes: This table shows the evidence on calories and expenditure changes. The omitted category is the year before diagnosis, not including the month before. In Columns (1), (5) and (6) the independent variables are timing interacted with the probability of being diabetic, as inferred from the machine learning approach. These coefficients can be interpreted as the impact of diagnosis. In Columns (2) and (3) the independent variables are timing alone, and the sample is either the overall sample, or limited to households with higher predicted probability. Standard errors are in parentheses. The figures in square brackets in Columns (2) and (3) show the estimated impact scaled up to 100% diagnosis. This should be comparable with the coefficient in Column (1). Regressions include controls for household fixed effects and year-month fixed effects. Magnet households are those who also scan and report prices for non-UPC coded goods

^*significant at 10% level

^**significant at 5% level

^***significant at 1% level.

Column 1 shows the results corresponding to Figure 2 using the diabetes probability interaction as the independent variable. There is a decline of approximately 3000 calories per person/month in the first two months around diagnosis, and an (insignificant) decline of about 1000 calories per person/month in the year following. These figures are, respectively, 6.4% and 2.5% of the pre-period mean.

Columns 2 and 3 show the non-interacted effects. Column 2 includes all households; for this sample the estimated share of true diagnosis is 20%.¹⁶ The figure in square brackets show the coefficients scaled up by this share. The re-scaled effect is quite close to the estimate in Column 1. Column 3 includes only those households with predicted probability greater than 50%; the true positive rate in this sample is 60%. The estimated effect is larger here, and the re-scaled effect is now very similar to the Column 1 effect. The effects on the 2 to 12 month period are very imprecise; we cannot reject the re-scaled effects are the same across columns, although this is due to noise.

Columns 2 and 3 are only two examples of possible cutoff values. For any given cutoff we can run regressions of the form in these columns, and re-scale to generate an overall effect. These effects should be similar to each other, and similar to the effect in Column 1 of Table 3. Appendix Figure C1 shows this analysis for the first two month effect. Indeed, the effect sizes are quite similar at most cutoff levels; at very high levels, the data become spare and the effects are noisier, but even at that point these are within statistical precision of the effect in Column 1 of Table 3.

In the remaining text, I will focus on the analysis using the predicted probabilities, as in Column 1 of Table 3. However, Appendix D shows all of these results using the sample in Column 3 of Table 3. This produces similar qualitative patterns, with the coefficients scaled down.

Columns 4 and 5 of Table 3 show the impact on expenditures (overall and in the magnet sample only). Expenditures decline, although not significantly. This is perhaps not surprising. Healthy calories tend to be more expensive than unhealthy calories, so a decrease in total calories need not be accompanied by a decrease in expenditures and, indeed, could be accompanied by an increase.¹⁷

In Table 4 I present a number of robustness checks for these primary results on calories. These all use the probability regression, so the magnitudes are comparable to Column 1 of Table 3. Columns 1, 2 and 3 limit to subsets of households. Column 1 focuses only on two person households, and Column 2 focuses on single person households. These results are in similar direction – the effects are larger for single person households, smaller for two person – but less precise given the loss in sample size. Column 3 excludes households in the bottom 25% of the distribution in terms of pre-period purchases. Other literature (i.e. Einav et al. (2010)) has suggested a lower error rate when limiting to more regular purchasers. The results in this sample are larger and more significant; the larger magnitude is due to the larger number of calories purchased overall in this group.

Table 4:

Robustness Checks

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
	Two Person	Single Person	Exclude Low	Total HH	Adjust for	Remove Time	Additional	Unbalanced
	Households	Households	Spenders	Calories	Pretrends	Controls	Post-Period	Panel
Month Before, Month After	−1415.0	−3725.1	−4446.0***	−5753.0***	−2902.9***	−5942.7***	−2647.6**	−3411.4***
	(1204.8)	(2461.1)	(1152.1)	(1895.8)	(937.4)	(920.8)	(1006.8)	(809.9)
2–12 Months After	638.4	−4276.1**	−2006.7**	−3197.4**	−950.9	−4988.9***	−737.3	−1916.3***
	(943.8)	(2137.1)	(1021.2)	(1472.7)	(841.0)	(721.8)	(869.9)	(728.2)
13–18 Month After							−45.3
							(1172.7)
Household FE	YES	YES	YES	YES	YES	YES	YES	YES
Year-Month FE	YES	YES	YES	YES	YES	NO	YES	YES
R-squared	0.50	0.590	0.40	0.59	0.48	0.50	0.48	0.48
Number of Obs.	59,826	21,623	84,312	112,416	112,416	112,416	120,240	162,398
Number of HH	2795	1009	3513	4684	4684	4684	4008	7207

Notes: This table replicates the results in Columns (1) Table 3, under varying robustness checks. Column (1) includes only two person households; Column (2) includes only single person households; Column (3) excludes the top 25% of spenders based on the pre-period; Column (4) uses as the outcome the total calories in the household; Column(5) adjusts for estimated pre-trends in calories; Column (6) removes the year-month controls; Column (7) includes an additional post-period; Column (8) does not limit to the balanced panel. Standard errors are in parentheses.

^*significant at 10% level

^**significant at 5% level

^***significant at 1% level.

In Column 4 I use as the outcome the total household calories, rather than calories per person. Since there is only one person diagnosed in the household, it is not obvious one needs to take into account the size differences across households. The effects here are larger - they are scaled up by the average household size.

Column 5 adjusts the data for a trend in the pre-period; that is, I estimate trends in the calories using the period prior to diagnosis, and adjust the later period for a continuation of this trend. This makes little difference to the results, likely because (as can be seen in Figure 2) there is limited pre-period trend. Column 7 of Table 4 excludes time controls, with larger results.

Column 7 adds an additional post-period, extending to 18 months after diagnosis. I now restrict this analysis to a balanced panel of households which are observed for 12 months before and for 18 months after; this slightly limits the number of households in the sample. The changes seem to tail off in this later period, suggesting the total effects are short-lived. Column 8 returns to the primary time frame but includes all observed household-months, not just the balanced panel. The results are a bit larger and more significant. In general, these columns suggest the results are robust.

Magnitudes

Overall, the main results in this section suggest relatively small but significant reductions in calories following diagnosis. Commenting on the magnitude of this change in terms of weight loss is challenging given the structure of the data. In particular, the fact that we observe only household level purchases and do not observe food away from home presents a problem.

If we are willing to assume that the percent change in foods we observe are reflective of overall changes, and to make some assumptions about the role of the diagnosed individual in the household overall, it is possible to scale these results to weight loss. Appendix A provides details of this calculation. Overall, we conclude these changes are sufficient to lose around 0.5 to 1.1 pounds per month. This is broadly consistent with the degree of weight loss seen in other data (Feldstein et al. 2008; data from the Health and Retirement Survey).

5.2. Changes in Diet Composition

A significant advantage of these data is that they allow me to look in detail at which foods contribute to the changes in calories. This is useful both to get a sense of which behaviors are most responsive, and also because it is possible that increases in consumption of good foods - fruit, vegetables - mask larger calorie reductions in less healthy foods. There is good evidence that even conditional on caloric intake, some dietary patterns are better than others (see, for example, Estruch et al. (2013) on the Mediterranean diet) so such changes could matter for health.

Diet quality is measured based on expenditure shares in the “Thrifty Food Plan” (TFP) food groups defined by the USDA. I look at both calorie and expenditure shares by group.¹⁸

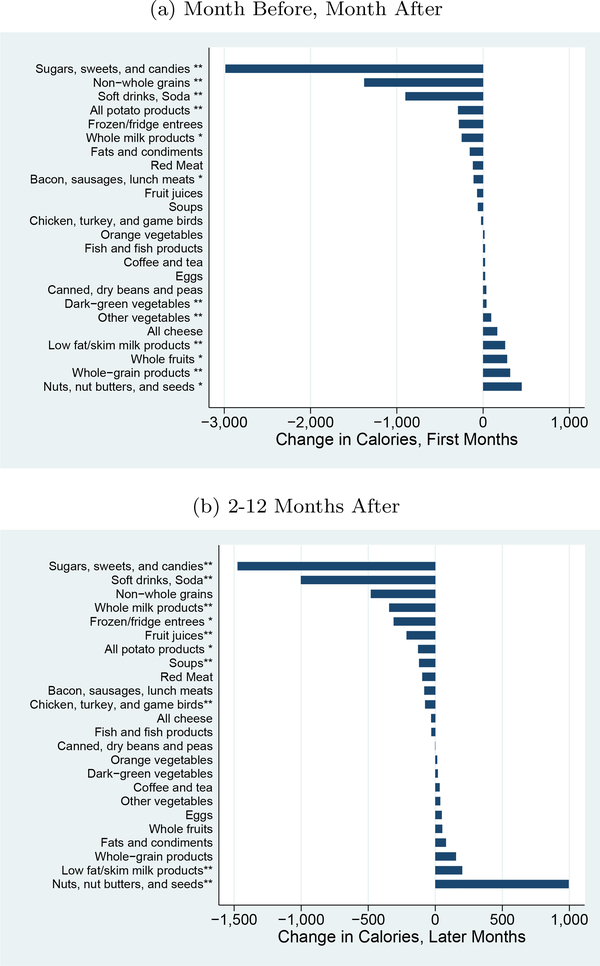
Figures 3a and b show the changes in calories by TFP group in the early period (first two months) and the later period.¹⁹ These figures shows changes which are consistent with some dietary improvements. The groups with the largest declines are non-whole grains, sweets and soda. These show significant declines in the early period. Perhaps more notable, when we look at the later period, the evidence here shows dietary improvements even though the overall reduction in calories was insignificant. In particular, there are reductions in non-whole grains, soda and whole milk products. These reductions are offset by some increases in nuts, but these overall changes are toward a healthier diet, even if the calorie declines are muted.

Figure 3: Changes by Food Group, Calories.

Notes: This graph shows the impact on calories by food group, using the USDA Thrifty Food Plan (TFP) groups. Results are generated by regressing the calories in each group on dummies for time from diagnosis (first months, later months, with year prior as the excluded category), year-month fixed effects and household fixed effects. ^∗indicates significance at 5% level;^∗∗ indicates significance at the 1% level.

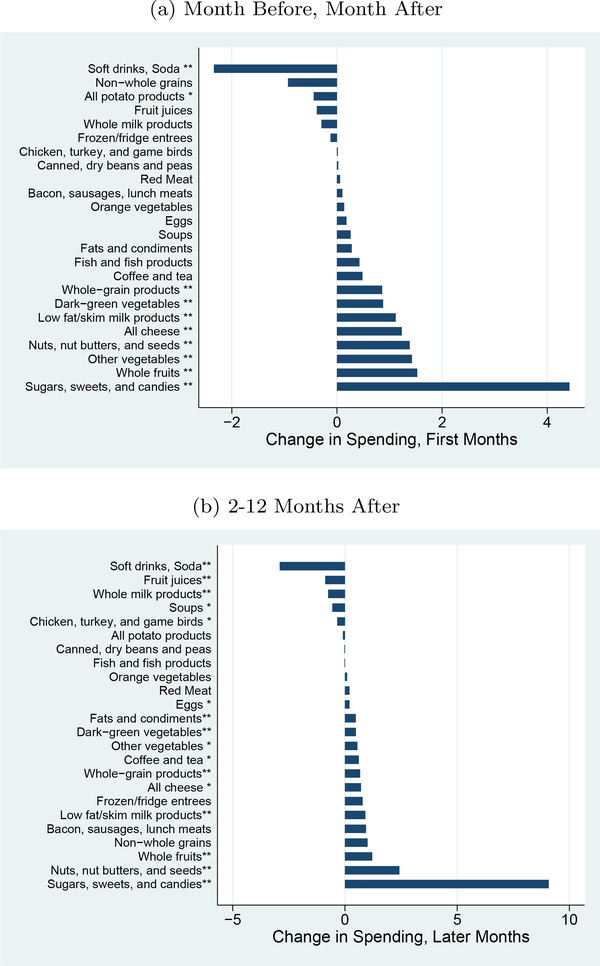
Figures 4a and b show the same changes using expenditures rather than calories. The patterns here are mostly similar. The only major difference is in the sugars, sweets and candies group. In this case, the spending actually goes up in the later period. This may reflect purchases of fewer, but more expensive, calories.

Figure 4: Changes by Food Group, Expenditures.

Notes: This graph shows the impact on expenditures by food group, using the USDA Thrifty Food Plan (TFP) groups. Results are generated by regressing the calories in each group on dummies for time from diagnosis (first months, later months, with year prior as the excluded category), year-month fixed effects and household fixed effects. ^∗indicates significance at 5% level;^∗∗ indicates significance at the 1% level.

Appendix D shows the results are similar with the analysis using only timing and restricting to those with a predicted probability greater than 0.5.

6. Heterogeneity in Response

The previous section focused on responses of the average individual. A natural following question is how much heterogeneity there is across individuals. Although the average household does not change very much, it may be that some households change much more than others. Going further, identifying correlates of greater behavior change may suggest directions for policy.

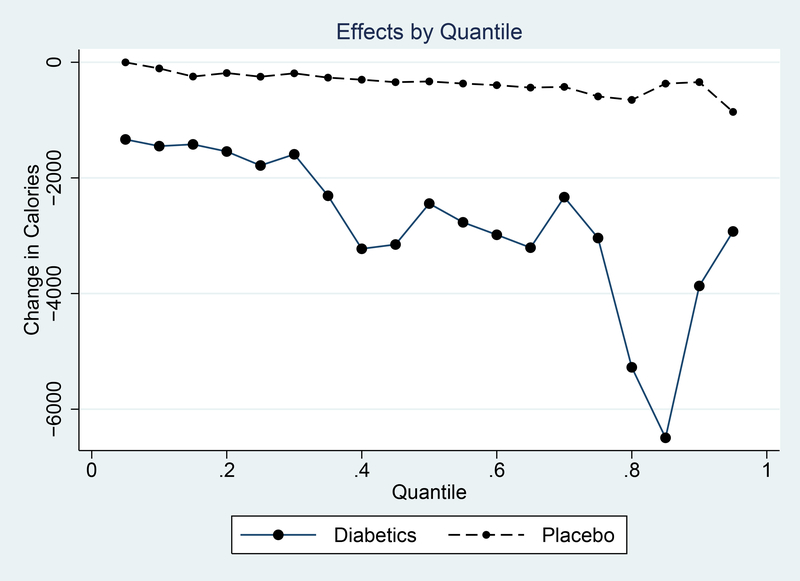
I begin by estimating heterogeneity in calorie changes across the population using a quantile regression. I estimate a version of Equation (2) using a quantile regression approach, with 20 quantiles. I aggregate the entire post-period into a single period so the coefficient represent the average per-month decline over the entire year following diagnosis for each quantile.

The solid line in Figure 5 illustrates the effects by quantile. Most notable is the fact that the effects are reasonably large for the most responsive quantiles. The calorie reduction in the uppermost quantiles is around 5000 calories per household member per month; this is about an 11% decline in calories, which is actually quite large.

Figure 5: Heterogeneity Across Distribution.

Notes: This graph shows the excess change in calories relative to the non-diabetic sample across the distribution. The distribution is measured in 20 groups, so the value for group “1” is the excess percent change in calories among the bottom 5% of the diabetic distribution relative to the bottom 5% of the non-diabetic distribution.

One potential issue is that there is likely to be some general heterogeneity in calorie changes which occurs independent of diagnosis and can be observed in the non-diabetic population. That is: between any two periods there will be some households which change more, and some which change less - this could reflect mean-reversion or simple noise. To evaluate this issue, I use the control sample (generated with the fake diagnosis dates) and run a similar regression. This is shown in the dotted line in Figure 5. We do not see the same heterogeneity.

This analysis suggests there is some substantial heterogeneity in behavior change and, in particular, there are some individuals who do seem to effect substantial changes. In the top quantile the observed reductions would be sufficient to lose a substantial amount of weight. In light of the evidence from, for example, Feldstein et al. (2008) this suggests that at least part of the heterogeneity in weight loss is a result of heterogeneity in dietary changes.

Correlates of Heterogeneity in Behavior Change

From a policy standpoint, this heterogeneity is most valuable if it is predictable. To explore this, I begin by illustrating the demographic and behavioral differences which are correlated with appearing in the diabetic sample. That is, I look at the baseline difference between the diabetic sample and the controls.

Table 5 shows demographic differences across the samples. Note that this analysis includes all the households in the diabetic sample - regardless of their diagnosis probability - since nearly all of them are diabetics either at or before the predicted diagnosis time (since the false positives are largely earlier diagnoses). We are interested here in the difference between diabetics and non-diabetics, not in the diagnosis event per se.

Table 5:

Demographic, Baseline Diet Differences: Diabetics versus Comparisons

	Diabetics	Comparison
Household Head Age	59.7***	57.1
Household Income	$64,043***	$72,255
Household Head Education	14.15***	14.5
Share White	81.5%*	84.3%

Notes: This table shows differences in demographics for those in the diabetic sample versus the control individuals.

^*significant at 10% level

^**significant at 5% level

^***significant at 1% level.

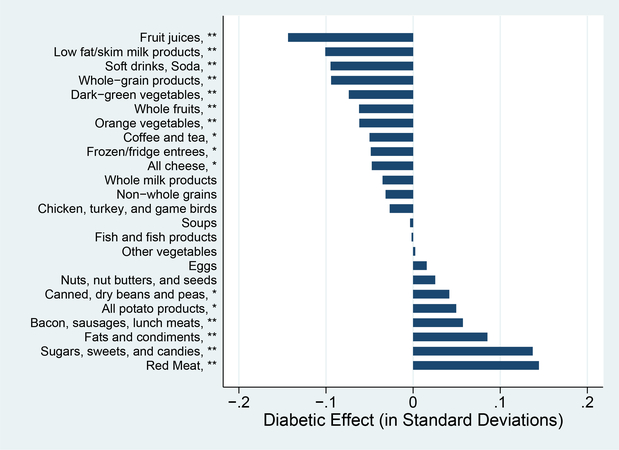
These differences line up with what is known from other evidence on diabetics. This group is lower income and has less education than the control sample. It is also older, and less likely to be white. Not surprisingly, the group’s diet prior to diagnosis is also on average worse. This is shown in Figure 6, which illustrates the standardized differences in diet shares across groups. Diabetics eat more meat products, more fats, and more sugars and sweets than the comparison group. They consume less fruit juice and lower rates of low fat milk products. Many of these differences are significant.

Figure 6: Baseline Food Group Shares (Calories).

Notes: This graph shows the baseline shares by food group for the diabetic group and the controls. Shares are measured as shares of total calories. ^∗∗ difference significant at 1% level; ^∗difference significant at 5% level.

A natural question is whether these same elements of heterogeneity will predict behavior change after diagnosis. I explore this by aggregating the post-periods, and estimating regressions of the form of Equation (2) but interacting the treatment with demographics and baseline diet characteristics. To address the possibility that some purchase patterns lead to changes in calories even absent diagnosis, I include the control group in this analysis and further interact the timing with this group. The analysis therefore asks whether the change is mitigated by the baseline characteristics relative to what would be expected in a placebo sample.

The effects are illustrated in Figure 7, which shows the impact of moving from the 25th to the 75th percentile in each of these variables. Each effect comes from a separate regression since multivariate analysis would be difficult to interpret given the correlation across variables.

Figure 7: Determinants of Heterogeneity in Calorie Changes.

Notes: This graph shows the relationship between baseline characteristics and the extent of behavior change. This figure shows the heterogeneity in behavior change by baseline levels of these variables for diabetics. The changes are relative to the changes for nondiabetics, to avoid any mechanical relationship. The effects are shown as the effect of moving from the 25th to the 75th percentile in each variable. ^∗∗ difference significant at 1% level; ^∗difference significant at 5% level.

There are some significant differences here. Households with fewer purchases of non-green vegetables, coffee and tea and canned beans are predicted to decrease more.²⁰ Those who purchase more bacon and whole milk are predicted to decrease less. We also see white households decrease calories less than minority households.

Although there are significant interactions here, it is notable that they do not seem related to the baseline correlations in Figure 6 or Table 5. White households are much less likely to be diabetic, but they actually change behavior less. Households who are diabetic eat many more sugars, sweets and candies but this category has no predictive power for change heterogeneity.

This is somewhat puzzling, since on average we might expect these to line up. The next section discusses this in the context of a model.

7. Model of Behavior Change

The evidence above shows three things. First, behavior change in response to diabetes diagnosis is limited on average. Second, there is substantial heterogeneity in this change, with a tail of individuals who decrease their calories substantially more. Finally, this heterogeneity appears to be largely unrelated to the demographic or diet characteristics which correlate with being in the diabetic sample.

The lack of behavior change and the limited heterogeneity in response to this information shock are both somewhat puzzling. In general, health would be improved and mortality decreased by improved diets in this population, which is why we expect behavioral response. This fact alone could, however, be rationalized by simply assuming people put a high value on their preferred diet relative to their health.

More puzzling, perhaps, is the observation that the characteristics which are associated with appearing in the diabetic sample are not predictive of behavior change. This suggests there must be some heterogeneity across the population, which correlates with health, but that is not being reflected in the behavior in the sample.

In this section I present a simple theory of behavior change which rationalizes this disconnect and may extend to other similar settings. The key assumption is that disease diagnosis is not an isolated event but, in most cases, one which is preceded by a set of warning periods in which people are told to change their behavior and some people do so. The model develops intuition about when results in a sample may be informative about a population, and when they may not be.

Setting and Notation

Consider a setting in which individuals can engage in either a healthy or unhealthy behavior. In the context of obesity and diabetes, for example, the healthy behavior would be eating a low calorie diet and the unhealthy behavior would be eating a high calorie diet. If we consider something like smoking, the behavior would be smoking or not smoking.

There are hedonic reasons to engage in the unhealthy behavior - people enjoy eating junk food, for example. Absent a reason not to, people will behave in an unhealthy way. There is a set of measure 1 of individuals who initially engage in unhealthy behavior.

There is a public health actor in the model - a doctor, a policy maker - who provides arguments in favor of healthy behaviors. These arguments could be information on why it is good to change behavior, suggestions of particular behavior change strategies, or other things. An argument is simply something which could potentially induce behavior change. In each period t = 1, .., T the public health actor sends one message out. This message may or may not be received by each individual.

Each individual j in the model is characterized by a vector of characteristics Ω_j = {p_1j,⋯,p_Nj,q_1j,⋯,q_Nj}. The value p_ji ∈ [0,1] indicates the probability that individual j sees each message i. This reflects the fact that some people may pay more attention to public health messages, or may visit the doctor more often. For each argument i there is a value q_ij ∈{0,1} which indicates whether individual j will be persuaded by argument i; they will be persuaded if q_ij = 1. There are at most N possible arguments.

Denote the average of q_ij as ${\overline{q}}_i$ which is a measure of the share of individuals who are persuaded by argument i. Assume that we can order the arguments such that $\overline{q_1}>\overline{q_2}>\dots >\overline{q_N}$. That is, argument “1” is the argument that convinces the largest share of people, followed by argument 2 and so on. Further, assume the arguments are independent: those who are convinced by argument 1 are equally likely to be convinced by argument 2 as those who are not convinced by argument 1. This delivers the observation that $\overline{q_2}$ is the same among those for whom q_ij = 1 as for those for whom q_ij = 0.

In addition, denote the average of p_ij as $\overline{p_i}$ which is the share of people who see message i. For simplicity, we will assume that there is no systematic relationship between p_ij and q_ij - that is, people are no more likely to see messages that they find convincing. Finally, assume that ${\overline{p}}_1={\overline{p}}_2=\dots =\overline{p}$ so the same share of people see each message on average.

Timing and Public Health Strategy

In each period of the game the public health actor announces one argument. If an individual sees the message and if that argument is convincing to them, they switch to the healthy behavior. Once an individual is engaging in the healthy behavior they do not return to the unhealthy behavior. We denote the behavior of individual j after period t as h_jt ∈ 0,1. Note that h_j0 = 0 for all j.

The goal of the public health actor is to change as many people’s behavior as quickly as possible. Trivially, then, their optimal strategy is to begin with argument 1, followed by argument 2 and so on.

Results

These results focus on a setting in which we observe individual behavior change at some period $\widehat{t}$. At this point the population has been exposed to messages at periods 1 through $\widehat{t}$ − 1. I will ask what we learn about the overall effectiveness of messages 1 through $\widehat{t}$-1 by observing the response at $\widehat{t}$.

Extent of Behavior Change

Proposition 1 The share of individuals who switch to a healthy diet at $\widehat{t}$ is smaller than the share who are affected by messages sent in periods 1 through $\widehat{t}$ − 1.

Proof 1 Consider first the share of individuals whose behavior is changed by messages in periods 1 through $\widehat{t}$ − 1. In a given period i the share of unhealthy individuals whose behavior is changed is $\overline{p{q}_i}$. This simple formulation follows from the fact that the success of the arguments are independent. We can therefore write the total share healthy after $\widehat{t}$ − 1 periods as:

$$\overline{p{q}_1}+\left(1-\overline{p{q}_1}\right)\overline{p{q}_2}+\sum _{i=3}^{\widehat{t}-1}\left(\left({\Pi }_{ii=1}^{i-1}\left(1-\overline{p{q}_{ii}}\right)\right)\overline{p{q}_i}\right)$$

and the share who change in period $\widehat{t}$ as $\overline{p{q}_{\widehat{t}}}$. The behavior change up to this point is greater than the change after. To see this, note that by definition $\overline{q_1}>\overline{q_{\widehat{t}}}$ and $\left(1-\overline{p{q}_1}\right)\overline{p{q}_2}+{\sum }_{i=3}^{\widehat{t}-1}\left(\left({\prod }_{ii=1}^{i-1}\left(1-\overline{p{q}_{ii}}\right)\right)\overline{p{q}_i}\right)\ge 0$. This completes the result.

This first result shows that behavioral response to any particular messaging - for example, to a disease diagnosis - will be lower than the overall share of people responsive to any messaging. Effectively, in this model people who are more responsive are “harvested”, and by the time we arrive at a later period, there are fewer susceptible respondents.

A natural follow-on question is in what circumstances this difference is larger or smaller. This result is summarized in the propositions below.

Proposition 2 All else equal, the gap between the behavior change in the sample and the behavior change in the population is decreasing in the number of periods before $\widehat{t}$.

Proof 2 This follows trivially from the above. The total behavior change prior to $\widehat{t}$ is smaller if $\widehat{t}$ is smaller. Further, $\overline{p{q}_{\widehat{t}}}$ is larger when $\widehat{t}$ is smaller.

Proposition 3 The gap between behavior change in the sample and behavior change in the population may be increasing or decreasing in $\overline{p}$. It will be increasing in $\overline{p}$ when $\overline{p}$ and $\overline{q_i}$∀ i are small.

Proof 3 The gap in behavior change is equal to

$$\overline{p{q}_1}+\left(1-\overline{p{q}_1}\right)\overline{p{q}_2}+\sum _{i=3}^{\widehat{t}-1}\left(\left({\Pi }_{ii=1}^{i-1}\left(1-\overline{p{q}_{ii}}\right)\right)\overline{p{q}_i}\right)-\overline{p{q}_{\widehat{t}}}$$

We can write the derivative with respect to $\overline{p}$ as

$$\sum _{i=1}^t{q}_i-\sum _{i=1}^{t}p{q}_i\sum _{j\ne i}{q}_j+\sum _{i=1}^t{p}^2{q}_i\sum _{j\ne i}{q}_j\sum _{k\ne i,j}{q}_k-\sum _{i=1}^t{p}^3{q}_i\sum _{j\ne i}{q}_j\sum _{k\ne i,j}{q}_k\sum _{l\ne i,j,k}{q}_l+terms-q_{\widehat{t}}$$

where terms continues the series through the term with $p^{(\widehat{t}-2)}$. If $\overline{p}$ is small, and if any given argument does not change many people’s behavior, this will be positive. As these grow very large, the derivative may become negative.

Proposition 2 suggests that the degree of behavior change in the population and the sample will be closer if the sample is observed after fewer messages have been sent. Proposition 3 suggests that, in particular for cases with relatively limited behavior change, the gap between population and sample will be smaller if people are less likely to see messages. Both of these point in the same direction. When there is widespread messaging about behavior change in a particular context, or there has been a long period for messages to be delivered, the sample will be increasingly less representative of the population.

Heterogeneity in Sample and Population

I turn now to results on the heterogeneity in the sample and population. Consider first an example with just two periods. In the first period, argument 1 is presented. Anyone who receives the message and is responsive to argument 1 will change their behavior. Anyone who either (a) does not receive the message or (b) is not responsive to argument 1 will not change their behavior.

Entering period 2, when we observe the population we will observe that healthy people are much more likely to be responsive to argument 1. To see why, observe that all people with healthy behavior are responsive to argument 1. In contrast, only some of those who are unhealthy are susceptible to the argument: the share susceptible to argument 1 in this unhealthy population is $\frac{(1-\overline{p})\overline{q_1}}{\left(1-\overline{p{q}_1}\right)}<1$.

However, when we then look at predictors of response in period 2, we will not see any difference in response among those who are responsive to argument 1 and those who are not.

This result becomes even more extreme as $\overline{p}$ goes toward 1. If everyone receives the message in period 1 then the unhealthy group in period 2 will contain no one who is responsive to argument 1. This point is summarized formally below.

Proposition 4 Consider behavior change at period $\widehat{t}$. Heterogeneity in responses to arguments 1 through $\widehat{t}$ − 1 will not be reflected in behavior change at period $\widehat{t}$. However, they will be reflected in differences between healthy and unhealthy populations overall as observed before period $\widehat{t}$.

Proof 4 At period $\widehat{t}$ behavior change is in response to the message delivered in that period. Heterogeneity in response to this message across people will be reflected in the observed behavior change. Since messages are independent, however, there is no correlation between this heterogeneity and heterogeneity in response to earlier messages.

It is worth noting that this model does not suggest we cannot learn anything from heterogeneity in the sample, but instead that what we learn may not be representative of the population. The model can rationalize the patterns in the data. Consider the particular example here, involving the reasons to change diet. A natural first argument would be that individuals should change their behavior so they live longer. Economic theory (and some results, see Oster, 2012) suggests this argument will be most compelling to individuals with high value of life - higher income, higher education, etc. A signature of the success of this argument overall would be observing changes in behavior which are larger in these high value of life groups.

In the end, this will manifest in observing better health for these groups at visit $\widehat{t}$. Indeed, we expect to find they are less likely to be diagnosed at this point. This is consistent with our cross-sectional comparisons between diabetics and others. However, under this model we will not see this heterogeneity among the diagnosed population since individuals who are compelled by this argument do not arrive at the diagnosis event. This is again consistent with what we observe in the data.

This may help rationalize the results above. I noted that although there is some heterogeneity in behavior change, the dimensions on which heterogeneity loads is different from the dimensions which differ on average between diabetics and non-diabetics. If people who consume a lot of sugars, sweets and candies see a lot of messages about decreasing this, then those who are diagnosed may be more heavily selected on lack-of-responsiveness to this message than others. Similarly, on race, if whites see more messages of this type than minorities - perhaps due to better health care access - then those who are diagnosed may be selected to be relatively unresponsive.

A simple extension of this model would be one in which messages can be sent multiple times.

Proposition 5 Consider a case where message 1 is sent for a second time at visit $\widehat{t}$. The response will be smaller in period $\widehat{t}$ than in period 1. The excess response in period 1 is increasing in $\overline{p}$.

Proof 5 In period 1, when message 1 is sent, the share of the population who responds is $\overline{p{q}_1}$. As noted above, the share who are still responsive to argument 1 is $\frac{(1-\overline{p})\overline{q_1}}{\left(1-\overline{p{q}_1}\right)}$. Since the other messages are independent, this share will be the same at period $\widehat{t}$. If message 1 is sent again, the share who respond will be $\overline{p}\frac{(1-\overline{p})\overline{q_1}}{\left(1-\overline{p{q}_1}\right)}$. This is less than $\overline{p{q}_1}$. The excess response in period 1 is equal to $\frac{{\overline{p}}^2\overline{q_1}\left(1-\overline{q_1}\right)}{\left(1-\overline{p{q}_1}\right)}$. This is increasing in $\overline{p}$, showing that as the message is more likely to be received, the selection is greater.

This extension demonstrates that as the public health actor sends the same message over and over again, its effectiveness wanes, since the individuals who are responsive to the message are being siphoned off. This issue is more extreme when more people are reached by the message each period.

Discussion

At the core, this model makes a very simple point. It is common to observe very limited behavior change in response to lifestyle interventions (for example: diet studies or efforts to encourage smoking cessation). This often seems at odds with the very large incentives to change this behavior. This model suggests that this may not be surprising in light of the selection procedure which identifies these samples. Individuals who (in this particular case) get a diabetes diagnosis, or (in other contexts) those who enter research studies on diet or smoking cessation, have likely already failed at repeated attempts to change behavior. It is therefore perhaps not surprising if they show limited behavior change and, moreover, the average behavior change in this population is likely not informative about the overall behavior change potential in the population. Further, it may be difficult to use these selected populations to test predictions of economic theory about who is susceptible to behavioral response. In fact, lack of heterogeneity in response along some dimension may suggest that this dimension has already been successfully used as an argument for behavior change.

The model has further implications, which are not testable in these data. One is that if we track a population at risk for some unhealthy behavior over time, we should observe greater behavior change at initial attempts to alter behavior, and less as time goes on. Second, heterogeneity in behavior change should be more predictive early on when fewer arguments have been exhausted. Finally, over time the characteristics of the healthy and unhealthy populations should diverge, even as the predictability of behavior change becomes more limited. These are implications which could be tested in future work with this or similar populations.

8. Conclusion

This paper analyzes behavioral response to health news, specifically the response of diet to news about diabetes. I find that the response is on average fairly small, although it exhibits some heterogeneity. I provide a simple theory to discuss the extension of these results out of sample. This exercise is relevant to a much larger literature which would like, for example, to draw conclusion about what interventions work in the population overall based on a randomized evaluation in a sample. The theory suggests that this extension may be difficult in this and related contexts since the sample in this case is selected to be individuals who have continued to engage in unhealthy behavioral despite (likely) repeated warnings.

This paper also makes methodological contribution. Broadly, I suggest researchers may find more uses for scanner data in health applications, especially when it is possible to learn about health directly from the purchase behavior. More specifically, I show this general approach can be improved by the application of basic machine learning algorithms, which are not yet in frequent use within applied economics.