Optical characterization of marine phytoplankton assemblages within surface waters of the western Arctic Ocean

Abstract

An extensive data set of measurements within the Chukchi and Beaufort Seas is used to characterize the optical properties of seawater associated with different phytoplankton communities. Hierarchical cluster analysis of diagnostic pigment concentrations partitioned stations into four distinct surface phytoplankton communities based on taxonomic composition and average cell size. Concurrent optical measurements of spectral absorption and backscattering coefficients and remote‐sensing reflectance were used to characterize the magnitudes and spectral shapes of seawater optical properties associated with each phytoplankton assemblage. The results demonstrate measurable differences among communities in the average spectral shapes of the phytoplankton absorption coefficient. Similar or smaller differences were also observed in the spectral shapes of nonphytoplankton absorption coefficients and the particulate backscattering coefficient. Phytoplankton on average, however, contributed only 25% or less to the total absorption coefficient of seawater. Our analyses indicate that the interplay between the magnitudes and relative contributions of all optically significant constituents generally dampens any influence of varying phytoplankton absorption spectral shapes on the total absorption coefficient, yet there is still a marked discrimination observed in the spectral shape of the ratio of the total backscattering to total absorption coefficient and remote‐sensing reflectance among the phytoplankton assemblages. These spectral variations arise mainly from differences in the bio‐optical environment in which specific communities were found, as opposed to differences in the spectral shapes of phytoplankton optical properties per se. These results suggest potential approaches for the development of algorithms to assess phytoplankton community composition from measurements of seawater optical properties in western Arctic waters.

The Arctic environment has proven to be extremely sensitive to changes in climate and is currently exhibiting the most rapid transformation on Earth. The most visible evidence of change is the dramatic reduction in the annual extent (Comiso et al. 2008), thickness (Kwok and Rothrock 2009; Comiso 2012) and seasonal persistence of sea ice (Markus et al. 2009) observed over recent decades, which are anticipated to continue throughout the century (Wang et al. 2018). These changes are accompanied by alterations of the pelagic environment in terms of seawater physical and chemical properties and hydrographic circulation, all of which can influence the marine biota (Wassmann et al. 2011). Reduced sea ice cover increases penetration of light into open water, which satellite‐based models suggest have led to significant increases in overall primary production and changes in its seasonal phenology (Arrigo and van Dijken 2011; Kahru et al. 2011). However, in many regions of the Arctic Ocean, phytoplankton growth appears to be limited by nutrients, particularly nitrogen (Tremblay and Gagnon 2009), and increased water column stability owing to intensified stratification could further reduce the supply of new and regenerated nutrients to surface waters.

The effects of these multiple perturbations on the taxonomic composition and seasonal or spatial distribution of Arctic Ocean phytoplankton communities is unknown but of paramount importance to predicting impacts of climate change in this region. The taxonomic composition and size structure of phytoplankton communities exerts a strong impact on biogeochemical cycling and ecological processes (Hood et al. 2006; Ardyna et al. 2011). Perturbations to the physical environment may potentially alter the distribution of biomass among different taxonomic groups of phytoplankton, which would strongly influence rates of primary production and its subsequent utilization by higher trophic levels. There have been previous reports that the community composition of the Canadian Beaufort Sea may be transitioning to a prevalence of smaller phytoplankton (Li et al. 2009) and that changes in the timing of sea ice distribution influences phytoplankton community structure (Fujiwara et al. 2014). However, as these studies are based on limited shipboard observations, it is difficult to make large‐scale generalizations regarding the spatial and temporal extent of such changes.

Both active and passive optical measurements obtained from sensors deployed on either in situ or above sea‐surface platforms provide a means to significantly expand observations of phytoplankton biomass and community composition over extended spatial and temporal scales. The absorption and scattering of light by phytoplankton cells has a direct influence on the optical properties of seawater, and thus there is a growing effort to develop approaches to identify phytoplankton taxonomic composition from optical measurements, including satellite ocean color observations (see recent reviews by IOCCG [2014] and Mouw et al. [2017]). These approaches are collectively referred to as phytoplankton functional type (PFT) algorithms, with the understanding that functional type can be interpreted broadly in relation to a community's biogeochemical or ecological role. Despite explicit linkages between phytoplankton cell size and pigmentation with the inherent optical properties (IOPs) of seawater such as the spectral absorption coefficient or volume scattering function, this is a challenging problem because phytoplankton are only one of multiple optically significant constituents of seawater.

The development and application of such approaches to the Arctic Ocean and surrounding seas are further hindered by the optical complexity of these waters, as nonphytoplankton materials that do not covary with algal abundance often exert a dominant influence on the IOPs. The presence of colored dissolved organic material (CDOM) and nonalgal particles (NAP), including those derived from terrigenous sources or resuspended in shallow environments, limits the accuracy in which the concentration of chlorophyll a (Chla), a common proxy for algal biomass, can be estimated using standard empirical algorithms (IOCCG 2015). This degrades the performance of abundance‐based approaches, which relate phytoplankton community composition to overall phytoplankton biomass (Uitz et al. 2006; Brewin et al. 2010; Hirata et al. 2011). Similarly, the dominant contribution of these nonphytoplankton constituents can also mask the influence of phytoplankton contributions to measured optical signals, hindering approaches that relate changes in phytoplankton composition to the magnitude or spectral shape of ocean color (Sathyendranath et al. 2004; Alvain et al. 2012; Li et al. 2013). As a result, most studies that employ PFT algorithms to examine regional or global phytoplankton community dynamics have explicitly excluded the Arctic Ocean and surrounding seas from their analysis.

A primary requirement in the development of any optically based approach to discriminate phytoplankton community composition is characterization of the IOPs associated with different phytoplankton assemblages and an understanding of the extent to which other optically significant constituents can influence ocean optical properties. In this study, we utilize an extensive set of observations from the Chukchi and Beaufort Seas to characterize both the IOPs of seawater (spectral absorption and backscattering coefficients) and apparent optical properties (spectral remote‐sensing reflectance) associated with different phytoplankton communities. An approach utilizing phytoplankton diagnostic pigment concentrations is used to classify stations based on the contributions of three phytoplankton size classes to the total Chla, and the average magnitude, spectral shape, and relative contribution of different optically significant constituents to the spectral absorption or backscattering coefficient of seawater is quantified for each phytoplankton assemblage. The results of these IOP measurements are compared with independent radiometric measurements of the average spectral shape of the remote‐sensing reflectance associated with each community.

Materials and methods

Study area

Field observations were obtained on three expeditions to the western Arctic Ocean. The MALINA (MAckenzie LIght aNd cArbon) cruise surveyed the southeastern Beaufort Sea during the period 31 July to 24 August 2009 on the CCGS Amundsen (e.g., Matsuoka et al. 2012). The station grid encompassed the outflows of the Mackenzie River, with transects extending from the delta to the southernmost limit of the pack ice outside the continental shelf. Two cruises associated with the NASA Impacts of Climate on EcoSystems and Chemistry of the Arctic Pacific Environment (ICESCAPE) program utilized the USCGC Healy to sample the Chukchi Sea and western Beaufort Sea during two successive years—from 18 June 2010 to 16 July 2010 and from 28 June 2011 to 24 July 2011 (Arrigo 2015). Sampling on these cruises included transects where measurements were done from open water across the ice edge to several kilometers within fully consolidated pack ice.

In situ measurements of seawater optical properties were measured immediately before or after collection of discrete water samples to characterize the oceanic phytoplankton community and suspended particle assemblage. The instrumentation and methodology used for the collection and processing of data were similar among all cruises, with only minor exceptions as noted in the following sections.

Phytoplankton pigments and particulate assemblage composition

Water samples for the determination of phytoplankton pigment concentrations and other properties of the suspended particle assemblage were collected at each station using a CTD‐Rosette equipped with Niskin bottles. In this study, our ultimate interest is in remotely sensed water properties, and we restrict our analysis to samples collected at near‐surface depths (~ 1 to 3 m nominal depth). Samples obtained with the CTD‐Rosette were drained into 20 liters carboys by opening the bottom closure of each Niskin bottle, facilitating collection of all particles. Subsamples for all analyses were withdrawn from the carboys after mixing to ensure homogeneity among measurements. Filtration volumes for each measurement were adjusted based on observed particle concentration and optimized for each individual analysis, with values ranging from 30 mL to 11 liters.

Duplicate or triplicate samples for phytoplankton pigments were filtered on 25‐mm GF/F filters under low light and flash frozen in liquid nitrogen for transport back to the laboratory. Pigment concentrations were determined by high‐performance liquid chromatography (HPLC). MALINA samples were analyzed using the analytical procedure described in Ras et al. (2008), and ICESCAPE samples were determined using the method of Van Heukelem and Thomas (2001). In this study, we use the HPLC‐determined concentration of total chlorophyll a as the measure of Chla, which represents the summed concentrations of monovinyl and divinyl chlorophyll a, chlorophyllide‐a, and the allomeric and epimeric forms of chlorophyll a.

Additional samples for determination of particle dry mass and organic carbon concentration were used to further characterize the bulk particle assemblage. A detailed description of the methodology is provided in Reynolds et al. (2016). Briefly, the mass concentration of suspended particulate matter (SPM) per unit volume of water was determined gravimetrically by measuring the dry weight of particles collected on a GF/F filter. The concentration of particulate organic carbon (POC) was determined on GF/F filters through standard CHN analysis involving high temperature combustion of dried filters. Two to three replicate samples of each of these measurements were taken at each station and averaged.

Spectral absorption and backscattering coefficients

At each station, the spectral absorption properties of seawater constituents were measured on discrete surface water samples obtained from the CTD‐Rosette. Measurements of spectral backscattering were collected in situ through vertical profiling with a submersible instrument package.

The spectral absorption coefficient of particles, a _p(λ), where λ indicates light wavelength in vacuum, was determined on samples collected on 25‐mm GF/F filters and stored in liquid nitrogen until analysis. Thawed filters were scanned at 1 nm intervals over the spectral range 300–800 nm (MALINA) or 300–850 nm (ICESCAPE) in a dual‐beam spectrophotometer (Lambda 18, Perkin Elmer) equipped with a 15 cm integrating sphere (Labsphere). Both blank and sample filters were placed inside the integrating sphere for measurement and scanned in multiple orientations to subsample different portions of the filter. Following subtraction of the blank, the absorption coefficient was calculated and a correction for the pathlength amplification factor was applied to the data (Stramski et al. 2015).

Additional absorption measurements were made on the sample filters following pigment extraction with methanol in order to partition a _p(λ) into the contributions of phytoplankton, a _ph(λ), and NAP, a _nap(λ), components (Kishino et al. 1985). The partitioning approach failed to provide reliable estimates of a _ph(λ) in a few cases where pigment extraction was incomplete or when the phytoplankton contribution to particle absorption was extremely small. All other spectra of a _p(λ) and a _nap(λ) were smoothed using a moving average filter with size ranging between 3 and 9 nm depending on the general spectral shape. For purposes of this study, spectra of absorption by nonalgal particles were further fit to an exponential relationship a _nap(λ) = a _nap(λ _ο) exp[S _nap(λ − λ _ο)] using data between 380 and 730 nm, excluding the 400–480 and 620–710 nm ranges, in order to minimize residual pigment absorption effects.

The spectral absorption coefficient of CDOM, a _cdom(λ), was measured with an UltraPath instrument on samples passed through a 0.2 μm filter (Matsuoka et al. 2012). The UltraPath provided measurements of a _cdom(λ) with sufficient signal‐to‐noise ratio in the spectral region below 550 nm; at longer wavelengths, artifacts in measured spectra were often observed that were likely related to variations in the baseline absorption of pure water. To avoid these experimental artifacts, the measured spectral values from 400 to 550 nm were fitted to an exponential function of wavelength and extrapolated to provide values for wavelengths exceeding 550 nm.

In contrast to spectral absorption measurements, the spectral backscattering coefficient, b _b(λ), was determined in situ using a combination of Hydroscat‐6 and a‐βeta sensors (HOBI Labs). Sensors were calibrated by the manufacturer immediately before or after each cruise. For MALINA, a single multispectral Hydroscat‐6 was paired with two single wavelength a‐βetas to yield measurements in eight spectral bands. For the ICESCAPE cruises, two Hydroscat‐6 instruments with complementary wavelength sets were deployed to provide estimates in 11 spectral bands spanning the UV/VIS/NIR spectral region. The processing of these data and the calculation of both b _b(λ) and the particulate backscattering coefficient, b _bp(λ) = b _b(λ) − b _bw(λ) where b _bw is the backscattering coefficient of water molecules, are described in detail in Reynolds et al. (2016).

Spectral remote‐sensing reflectance

The spectral remote‐sensing reflectance, R _rs(λ), is defined as the ratio of the upwelling (i.e., photons traveling along the vertical from nadir toward zenith direction) water‐leaving radiance, L _w(λ), to the surface downward plane irradiance, E _s(λ), where all quantities are just above the sea surface. On all cruises, L _w(λ) and E _s(λ) were determined from underwater measurements obtained with in situ spectral radiometers and extrapolated to values above the sea surface. A free‐falling Biospherical Instruments compact‐optical profiling system (MALINA; Antoine et al. 2013) or profiling reflectance radiometer (ICESCAPE; Lewis et al. 2016) was used to provide vertical radiometric profiles of spectral upwelling radiance and downwelling plane irradiance in 18 spectral bands. The radiometric measurements, data processing, and subsequent determination of R _rs(λ) are fully described in Zheng et al. (2014).

Pigment‐based phytoplankton community composition

The pigment chlorophyll a is found in nearly all photosynthetic algae and cyanobacteria and thus Chla is commonly used as a proxy for algal biomass in aquatic ecosystems. Phytoplankton accessory pigments and their ratios to chlorophyll a vary among taxa (Jeffrey and Vesk 1997; Roy et al. 2011), and these variations are useful for inferring the general taxonomic composition of phytoplankton communities (Mackey et al. 1998; IOCCG 2014). Because many taxonomic groups tend to be associated with specific ranges of cell size, these accessory pigment observations can also be used to partition Chla into the relative contributions of different phytoplankton size classes.

In this study, we employ the approach of Uitz et al. (2006) to partition the measured Chla into the fractional contributions of three phytoplankton size classes; picophytoplankton (f _pico; D < 2 μm), nanophytoplankton (f _nano; D = 2 to 20 μm), and microphytoplankton (f _micro; D > 20 μm), where D indicates the approximate cell diameter. The concentrations of seven diagnostic pigment biomarkers of specific phytoplankton taxa are employed, which are assigned to one of the three size classes (Vidussi et al. 2001). The seven diagnostic pigments utilized in this approach are fucoxanthin (Fuco), peridinin (Peri), 19′‐hexanoyloxyfucoxanthin (Hex), 19′‐butanoyloxyfucoxanthin (But), alloxanthin (Allo), total chlorophyll b (TChlb, sum of monovinyl and divinyl forms), and zeaxanthin (Zea). The fractional contribution of each pigment‐derived size class to Chla is calculated as

$$f_{\text{micro}}=\left(1.41\text{Fuco}+1.41\text{Peri}\right)/\mathrm{\sum DP}$$

$$f_{\text{nano}}=\left(0.60\text{Allo}+0.35\mathrm{But}+1.27\mathrm{Hex}\right)/\mathrm{\sum DP}$$

$$f_{\text{pico}}=\left(0.86\mathrm{Zea}+1.01\text{TChl}b\right)/\mathrm{\sum DP}$$

where ∑DP is the sum of the weighted concentrations of all seven diagnostic pigments,

$$\mathrm{\sum DP}=1.41\text{Fuco}+1.41\text{Peri}+0.60\text{Allo}+0.35\mathrm{But}+1.27\mathrm{Hex}+0.86\mathrm{Zea}+1.01\text{TChl}b$$

The weighting coefficients used here represent average ratios between the concentrations of chlorophyll a and each diagnostic pigment and were obtained by multiple regression analysis of a global HPLC‐derived pigment database (Uitz et al. 2006). There are inherent limitations of this method that have been noted previously, for example, certain diagnostic pigments can be shared by multiple phytoplankton groups and some phytoplankton groups may encompass a wide size range. Taxonomic resolution is limited to the level of algal classes and does not reveal potential changes occurring at the species level. This model is also based on a global data set and not tuned specifically to the Arctic. Despite these limitations, prior studies have used similar pigment‐based approaches successfully in the region of our study (Hill et al. 2005; Coupel et al. 2012, 2015; Fujiwara et al. 2014).

Hierarchical cluster analysis of pigment‐derived size classes

Hierarchical cluster analysis (HCA) was used to group stations on the basis of input data representing the values of the three pigment‐derived size class contributions to Chla, i.e., f _pico, f _nano, and f _micro. Various clustering methods based on different algorithms are available (e.g., Legendre and Legendre 2012). In this study, we applied an unsupervised agglomerative clustering approach using Ward's (1963) minimum variance method and paired Euclidean linkage distances (Neukermans et al. 2016).

The results of this analysis were used to identify groups of stations with generally similar surface phytoplankton communities in terms of relative accessory pigment concentrations and dominant cell size. Following classification, the mean and variance of particle characteristics and seawater optical properties were computed for each group of stations. Statistical significance between cluster means was determined using a one‐way analysis of variance, with Tukey's Honestly Significant Difference test used to identify significant differences in the mean between individual clusters.

Analysis of spectral shapes for constituent optical properties

Measurements of the particulate and dissolved absorption coefficients were obtained at high spectral (1‐nm) resolution, and for the purposes of this study, we restrict our analysis to the visible light spectral range of 400–700 nm. The summed measurements of individual constituent absorption coefficients allow estimation of the total absorption coefficient of seawater at hyperspectral resolution,

$$a\left(\lambda \right)=a_{\mathrm{w}}\left(\lambda \right)+a_{\text{cdom}}\left(\lambda \right)+a_{\mathrm{p}}\left(\lambda \right)=a_{\mathrm{w}}\left(\lambda \right)+a_{\text{cdom}}\left(\lambda \right)+a_{\mathrm{ph}}\left(\lambda \right)+a_{\mathrm{nap}}\left(\lambda \right)$$

where a _w(λ) is the spectral absorption coefficient of pure water. For these calculations, we used the values of a _w tabulated in the IOCCG Protocol Series (2018), interpolated to 1‐nm resolution, and ignored temperature and salinity dependencies.

To characterize the spectral shapes of each constituent, absorption spectra were normalized to the integral over the wavelength range 400–700 nm,

$$a_{\mathrm{x},\mathrm{n}}\left(\lambda \right)=a_{\mathrm{x}}\left(\lambda \right)/{\int }_{400}^{700}{a}_{\mathrm{x}}\left(\lambda \right)\mathrm{d}\lambda$$

where the subscript n indicates a normalized spectrum and the subscript x is replaced by the constituent symbol of interest (i.e., w, p, ph, nap, and cdom) or their additive contributions (e.g., p + w).

For comparison with hyperspectral absorption measurements, the multispectral values of the spectral backscattering coefficient were interpolated to 1‐nm resolution by fitting measured values to a power law function of the form

$$b_{\mathrm{b}}\left(\lambda \right)=b_{\mathrm{b}}\left({\lambda }_{\mathrm{o}}\right){\left[\lambda /{\lambda }_{\mathrm{o}}\right]}^{\eta }$$

where λ _ο represents a reference wavelength and η is the dimensionless slope of the spectral backscattering coefficient. This model was applied to measurements of both b _b(λ) and b _bp(λ), and provides a good fit to the measured data with generally small residuals (Reynolds et al. 2016). The normalized spectral shapes of b _b and b _bp were calculated in the same manner as absorption. We note that because this fitting procedure removes any potential spectral features associated with the backscattering coefficient, the spectral slope η is the sole distinguishing characteristic in shape analysis.

The radiometric measurements used in the determination of R _rs(λ) were also multispectral, consisting of 18 discrete bands over the range 320–710 nm. The normalized spectral shape R _rs,n(λ) was calculated by using a shape‐preserving piecewise cubic polynomial function to interpolate the data of R _rs(λ) to 1‐nm resolution (MATLAB pchip function) and using this interpolation to compute the value of the integral over 400–700 nm solely for the purpose of normalization.

Results

Phytoplankton community clusters based on diagnostic pigments

Surface concentrations of phytoplankton pigments obtained at 136 stations were used as input to HCA in order to group stations of similar community composition. The dendrogram resulting from the data set consisting of three values representing the fractions f _pico, f _nano, and f _micro at each station is illustrated in Fig. 1. Objective analyses of the linkage distance diagram suggest that four to seven distinct clusters can be considered with this dendrogram. In this study, we chose a linkage distance cutoff of 1.6, dividing the 136 stations into four clusters. This choice leads to clusters that are more easily interpreted in terms of the dominant differences in phytoplankton community composition and does not result in clusters with fewer than 10 stations. For convenience, we assign an alphabetical letter (N, P, O, or M) as a label for each cluster.

Figure 1.

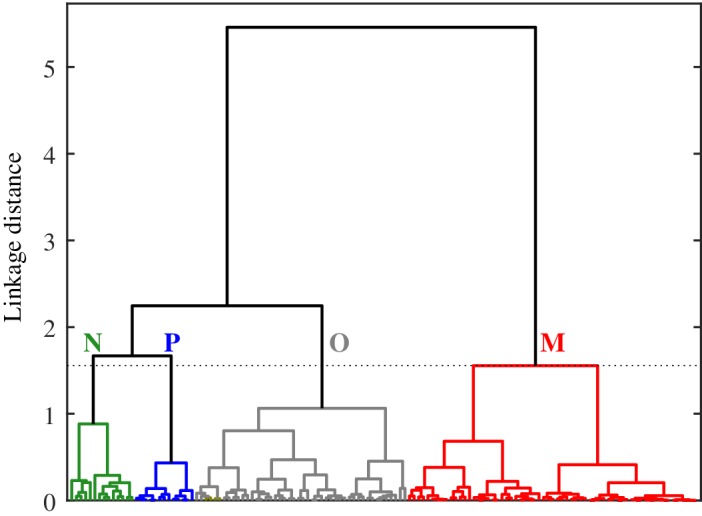
Dendrogram of stations obtained from HCA using as input the fractional contributions of three pigment‐based phytoplankton size classes to Chla. The input data represent near‐surface measurements obtained from 136 stations in the western Arctic. The dashed line corresponds to a linkage distance of 1.6, dividing the data set into the four clusters denoted as N, P, O, and M.

Figure 2 depicts the cluster assignment of each station with regards to the relative contributions of the three pigment‐based size fractions to Chla. Cluster M contains the largest number of stations (n = 63) and is characterized by communities having a predominant contribution of microphytoplankton to Chla (84% ± 13%, mean ± SD) and correspondingly the lowest average contributions of both picophytoplankton and nanophytoplankton (Table 1). In contrast, cluster P contains the fewest number of stations (n = 13), and for these stations, picophytoplankton contribute > 50% to Chla (60% ± 7%). These stations also comprise the lowest overall values of f _micro. Stations associated with cluster N contain the largest values of f _nano, ranging from 45% to 90% with an average value of 61% ± 14%. Similar to the P cluster, this cluster contains a relatively small number of stations (n = 14) in our data set. Cluster O, the second largest cluster, represents the stations for which there is no predominant contribution to Chla from a single size class but instead two or three size classes contribute about equally to Chla. For this cluster, the average contributions are 34%, 25%, and 41% for f _pico, f _nano, and f _micro respectively.

Figure 2.

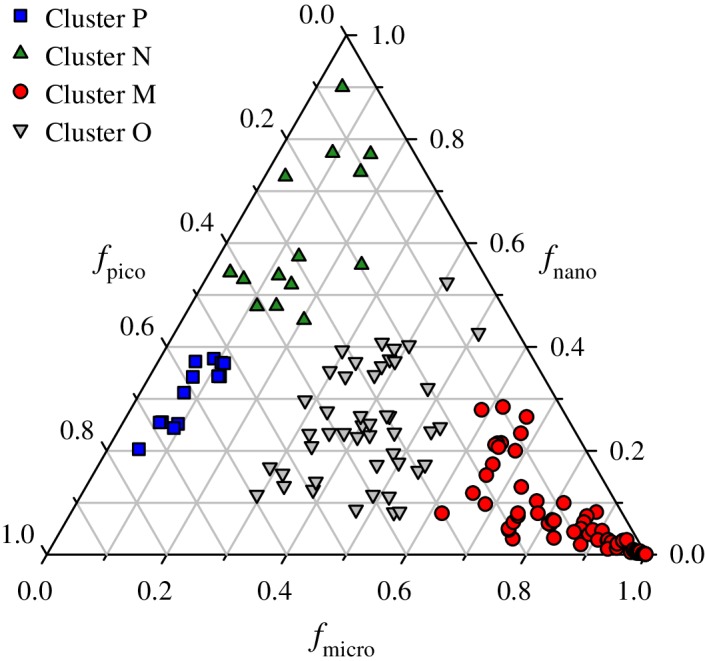
Ternary diagram illustrating the fractional contributions of picophytoplankton, nanophytoplankton, and microphytoplankton size classes to Chla for the four clusters illustrated in Fig. 1.

Table 1.

Values for the mean and standard deviation of pigment and particle characteristics associated with each cluster derived from the pigment‐based size classification.

	P	N	M	O
Number of stations	13	14	63	46
Chla (mg m−3)	0.08 ± 0.03	0.49 ± 0.74	2.80 ± 6.0	0.40 ± 0.64
f micro	0.09 ± 0.02	0.12 ± 0.06	0.84 ± 0.13	0.41 ± 0.08
f nano	0.31 ± 0.06	0.61 ± 0.14	0.07 ± 0.08	0.25 ± 0.11
f pico	0.60 ± 0.07	0.27 ± 0.13	0.09 ± 0.07	0.34 ± 0.11
Diagnostic pigments (g g −1 )
Fuco	0.019 ± 0.005	0.028 ± 0.020	0.374 ± 0.149	0.150 ± 0.066
Peri	0.016 ± 0.005	0.028 ± 0.023	0.033 ± 0.051	0.027 ± 0.039
Allo	0.029 ± 0.011	0.020 ± 0.016	0.016 ± 0.020	0.033 ± 0.029
But	0.064 ± 0.036	0.046 ± 0.046	0.011 ± 0.014	0.037 ± 0.026
Hex	0.110 ± 0.024	0.275 ± 0.122	0.026 ± 0.031	0.098 ± 0.059
Zea	0.041 ± 0.009	0.032 ± 0.020	0.019 ± 0.018	0.033 ± 0.018
TChlb	0.313 ± 0.046	0.126 ± 0.070	0.043 ± 0.038	0.177 ± 0.061
Other particle properties
SPM (g m−3)	0.50 ± 0.92	16.43 ± 41.68	1.24 ± 2.15	1.22 ± 3.41
POC (g m−3)	0.06 ± 0.01	0.31 ± 0.43	0.25 ± 0.24	0.10 ± 0.10
POC/SPM (g g−1)	0.23 ± 0.10	0.20 ± 0.10	0.31 ± 0.14	0.27 ± 0.13

Diagnostic pigment concentrations are reported relative to the HPLC‐derived Chla.

Table 1 also summarizes the average Chla and diagnostic pigment concentrations relative to Chla associated with each cluster. Stations comprising the microphytoplankton‐dominated cluster M exhibit the highest average concentration and overall variation of Chla (2.8 ± 6 mg m⁻³), the largest relative contributions of the pigments Fuco and Peri, and the lowest cluster averages of the other four diagnostic pigments. Fuco and Peri are generally considered indicators of diatom and dinoflagellate abundance, respectively. As the ratios of Peri to Chla in this cluster are on average low (3%), we consider this cluster to represent primarily phytoplankton communities dominated by diatoms.

In contrast to cluster M, the picophytoplankton‐dominated cluster P exhibits the smallest average Chla (0.08 ± 0.03 mg m⁻³) and normalized values of Fuco and Peri but is associated with the highest relative contributions of the pigments TChlb, Zea, and But. Based on the presence of these pigments and historical observations of species distributions, green algae such as the prasinophyte Micromonas sp. are likely the dominant phytoplankton constituent of this community.

The nanophytoplankton‐dominated cluster N is characterized by the highest relative concentration of the accessory pigment Hex, which is associated with the presence of nanoflagellate haptophytes (e.g., Phaeocystis sp.). The average value of Chla (0.49 ± 0.64 mg m⁻³) was intermediate between clusters P and M.

As expected from Fig. 2, the cluster O was intermediate to the three other clusters for nearly all pigment concentrations. The only exception was a slightly elevated contribution of Allo, a pigment generally associated with the presence of cryptophytes, which is significantly higher than cluster M but not for the other clusters. We interpret this cluster to represent stations with a mixture of various phytoplankton communities.

The spatial distribution of cluster locations is illustrated in Fig. 3. Surface communities dominated by picophytoplankton and nanophytoplankton (clusters P and N, respectively) were only observed in the eastern Beaufort Sea, with cluster P associated with the least turbid waters as indicated by the lowest average values of Chla, SPM, and POC (Table 1). In contrast, cluster N tended to be found in the most turbid waters of the study in which mineral particles contributed strongly to particle mass concentration as evidenced by low values of the POC/SPM ratio. Stations in which microphytoplankton (cluster M) provided the dominant contribution to surface Chla as well as the mixed communities (cluster O) were found throughout the study area. It should be noted that the sampling in the eastern Beaufort Sea during MALINA occurred later in the season than that of the Chukchi and western Beaufort Sea (ICESCAPE), which also could influence these spatial patterns.

Figure 3.

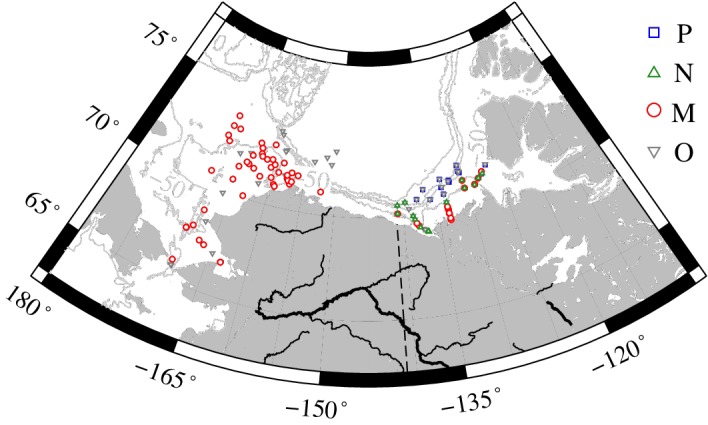
Map depicting locations of cluster membership. Isobaths depict depth in meters.

In the following sections, for each cluster we summarize the average spectral shape of various seawater constituents and their relative contributions to the IOPs of seawater.

Spectral shapes for IOPs of seawater constituents

Phytoplankton absorption coefficient

Conceptually, the spectral absorption coefficient of phytoplankton is the seawater optical property most directly linked to the phytoplankton community, and spectral shape variations among differing taxa form the basis of several PFT discrimination approaches. Figure 4a depicts the mean normalized spectral shape of the phytoplankton absorption coefficient, a _ph,n(λ), obtained for each cluster. All four spectra exhibit features characteristic of phytoplankton absorption, including major maxima located in the blue and red spectral regions near chlorophyll a absorption bands (~ 440 and ~ 675 nm) and a broad minimum in the region 550–650 nm. Differences in shape among the clusters are evident in the range 415–505 nm, a spectral region which encompasses the Soret band of chlorophyll a absorption as well as the absorption peaks of accessory light‐harvesting and photoprotective pigments. The values of a _ph,n(λ) increase in this spectral region from the lowest values associated with cluster M through intermediate values for cluster N to the highest values for clusters O and P. At 443 nm, the cluster M value is 10% lower than clusters P and O and 6% lower than cluster N. The opposite trend among clusters is observed for the spectral values of a _ph,n(λ) in the red spectral bands associated with chlorophyll a absorption. At 675 nm, the average values decrease 15% from the maximum value associated with cluster M to the minimum value associated with cluster P.

Figure 4.

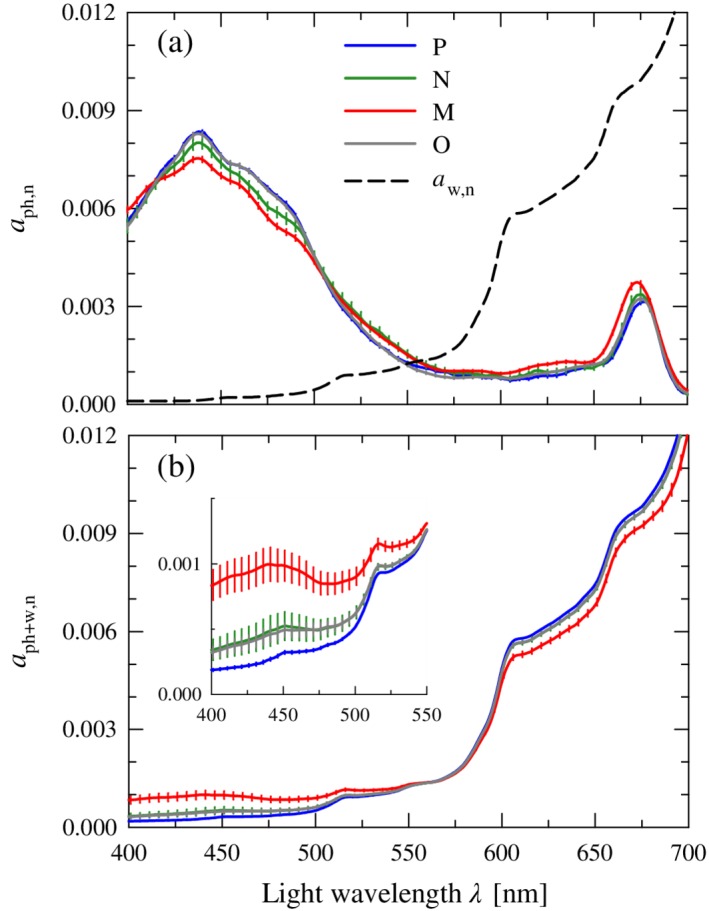
(a) Normalized mean spectra of the phytoplankton absorption coefficient, a _ph,n(λ), for each of the four clusters. Error bars depicting the standard error of the mean (= SD/√n) are provided at 5‐nm intervals. The normalized spectrum of the water absorption coefficient, a _w,n(λ), is also shown for comparison. All spectra are normalized to the integral over the wavelength range 400–700 nm and therefore dimensionless. (b) Similar to (a) but for the summed absorption coefficient of phytoplankton and water, a _ph+w,n(λ), for each of the four clusters. The inset provides an expanded view of the wavelength range 400–550 nm.

The observed flattening of the phytoplankton absorption spectra associated with the trend going from smaller to larger phytoplankton size classes (i.e., pico → nano → micro) has been reported in numerous other oceanic studies (e.g., Bricaud et al. 2004; Uitz et al. 2015) and is generally interpreted in terms of the so‐called pigment packaging effects in algal cells. The package effect is controlled by both cell size and intracellular pigment concentration (Duysens 1956; Morel and Bricaud 1981). With an increase in cell size, intracellular pigment concentration, or both, the magnitude of the chlorophyll‐specific absorption coefficient tends to decrease and the absorption spectra become flatter. The highest blue‐to‐red absorption ratio (i.e., the weakest package effect) is observed in the spectra belonging to cluster P, consistent with the expectation based on the predominance of small‐sized picophytoplankton. We note that the contributions of accessory pigments, especially photoprotective carotenoids, can also play a role in determining the spectral shape of a _ph,n(λ). For example, an enhanced absorption in the blue in the spectra from cluster P may also be partly associated with the presence of picoplankton‐specific carotenoids such as zeaxanthin.

The mean spectrum of the phytoplankton absorption coefficient for cluster O is markedly similar and statistically indistinguishable to that of cluster P. Although statistical effects related to small and unequal sample size between clusters cannot be ruled out, it may suggest that in mixed communities, the weighted contribution to absorption by different phytoplankton assemblages differs from their contribution to Chla, with picophytoplankton having a proportionally higher influence on the bulk a _ph,n(λ). A similar observation has been reported in results from a modeling study examining the contributions of various planktonic components to seawater IOPs (Stramski et al. 2001).

Although the observed differences in spectral shape among clusters at a given wavelength are relatively small, absorption band ratio differences are enhanced by the flattening of spectral shape. Band ratios are also independent of the normalization process. The average difference in the band ratio a _ph(443)/a _ph(555) between clusters P and M is 22% and increases to 38% for the ratio 443/670 nm (Table 2). Both of these differences are statistically significant (p < 0.005), suggesting that multispectral measurements of the phytoplankton absorption coefficient can provide a means to discriminate at least some of the assemblages in this region.

Table 2.

Average optical band ratios and spectral dependencies computed from the normalized spectral shape of each constituent or combination of constituents.

		P	N	M	O
a ph,n	443/555	7.1 ± 1.0 (10)	6.3 ± 2.2 (10)	5.9 ± 1.7 (54)	8.4 ± 2.8 (42)
	443/670	3.0 ± 0.2	2.7 ± 0.6	2.1 ± 0.6	2.8 ± 0.4
a ph+w,n	443/555	0.21 ± 0.0 (10)	0.37 ± 0.3 (10)	0.72 ± 0.7 (54)	0.35 ± 0.3 (42)
	443/670	3.0 ± 0.2	2.7 ± 0.6	2.1 ± 0.6	2.8 ± 0.4
a nap,n	443/555	1.9 ± 0.1 (12)	2.0 ± 0.1 (13)	2.4 ± 0.4 (60)	2.0 ± 0.3 (46)
	443/670	2.8 ± 0.3	3.1 ± 0.3	3.9 ± 0.9	3.1 ± 0.7
	S nap	−0.006 ± 0.001	−0.006 ± 0.000	−0.008 ± 0.001	−0.007 ± 0.001
a cdom,n	443/555	11.0 ± 2.9 (7)	8.2 ± 3.5 (11)	6.9 ± 1.4 (61)	9.6 ± 5.1 (45)
	443/670	142.0 ± 80.3	85.0 ± 97.2	51.0 ± 24.6	133.0 ± 192
	S cdom	−0.020 ± 0.001	−0.020 ± 0.000	−0.018 ± 0.002	−0.019 ± 0.002
b bp,n	443/555	1.3 ± 0.2 (2)	1.5 ± 0.4 (3)	1.3 ± 0.1 (57)	1.4 ± 0.2 (40)
	443/670	1.7 ± 1.8	2.2 ± 1.1	1.6 ± 0.2	1.8 ± 0.5
	η bbp	−1.3 ± 0.6	−1.7 ± 1.1	−1.1 ± 0.3	−1.4 ± 0.6
a n	443/555	0.67 ± 0.05 (6)	2.0 ± 0.7 (10)	1.7 ± 0.7 (59)	1.3 ± 0.8 (45)
	443/670	0.11 ± 0.01	0.78 ± 0.87	0.45 ± 0.47	0.42 ± 0.63
b b,n	443/555	1.9 ± 0.2 (2)	1.6 ± 0.3 (3)	1.5 ± 0.2 (57)	1.7 ± 0.4 (41)
	443/670	3.4 ± 0.5	2.5 ± 0.9	2.1 ± 0.5	2.8 ± 1.1
	η bb	−2.9 ± 0.4	−2.1 ± 0.9	−1.7 ± 0.6	−2.3 ± 0.9
(b b/a)n	443/555	2.7 ± nd* (0)	0.6 ± 0.2 (3)	1.1 ± 0.5 (54)	2.1 ± 1.4 (41)
	443/670	29.7 ± nd* (0)	2.0 ± 1.6 (3)	9.3 ± 6.6 (54)	24.2 ± 21.5 (41)
R rs,n	443/555	2.9 ± 0 (1)	0.4 ± 0.2 (3)	1.1 ± 0.5 (46)	1.8 ± 1.2 (36)
	443/670	29.5 ± 0 (1)	1.4 ± 2.1 (3)	10.3 ± 7.3 (46)	19.1 ± 16.5 (36)

For a _nap and a _cdom, the spectral slope parameter S (nm⁻¹) of an exponential model fit to the data is provided. For b _bp and b _b, the dimensionless spectral slope parameter η of a fitted power law function to the data is listed. The values represent the mean and standard deviation of each cluster, with the number of samples in parentheses for the first band ratio.

^* For the P cluster, no single station included measurements of every constituent. A single value for the cluster was calculated by combining the cluster means of each constituent to estimate a mean b _b/a spectrum, which was then normalized prior to calculating the band ratio.

Absorption coefficients of nonphytoplankton constituents

Even within an idealized hypothetical ocean consisting solely of phytoplankton, the contributions to absorption by water molecules will influence the spectral shape of the absorption coefficient in addition to any observed differences in the spectral shape of phytoplankton absorption. The normalized absorption spectrum of water, a _w,n(λ), in the visible spectral region spans more than two orders of magnitude and has a substantially different shape from that of the other major categories of absorbing constituents of seawater including a _ph,n(λ), with minimal values of absorption at 419 nm but increasing rapidly with increasing wavelength (Fig. 4a).

Figure 4b depicts the resulting normalized mean spectral shapes of the summed absorption coefficient a _ph+w,n(λ), calculated by first computing the sum a _ph(λ) + a _w(λ) at each station followed by subsequent normalization to the integral. These calculations thus integrate both the station‐specific differences in a _ph(λ) as well as differences in the relative contributions of a _ph(λ) and a _w(λ) to the sum. Following the addition of water absorption, differences in the mean spectral shape of a _ph+w,n(λ) among clusters are still observed, but the direction of phytoplankton size‐related trends is reversed to that observed for the phytoplankton absorption coefficient alone. In the blue spectral region, the absorption coefficient of water is minimal and exhibits relatively little spectral variation, thus differences in phytoplankton absorption among clusters have the most impact. Figure 4b indicates that the relative differences between clusters in this region are increased relative to a _ph,n(λ) alone, for example, the value of a _ph+w,n(443) for cluster M is 3.6‐fold higher than that observed for cluster P. Differences among communities and the reversal of the size trend are also still observed in the red band despite the increased absorption contribution of water, but the range of variation is reduced compared to the blue (< 6% at 675 nm). This range of variation is even smaller in the middle of the spectrum (< 2% at 555 nm) where phytoplankton absorption is weak. These results highlight that changes in the relative contribution to absorption by phytoplankton and other optically significant constituents is also an important determinant in the ability to discriminate planktonic assemblages based on spectral shape.

In natural environments, additional contributions to the absorption coefficient from both dissolved substances and nonalgal particulate material are always present to some degree. The Arctic in particular is a challenging environment, because these nonphytoplankton components are often the dominant contributor to absorption and their concentrations generally do not covary with phytoplankton abundance (IOCCG 2015). Figure 5 illustrates the average normalized spectral shapes of the absorption coefficient of CDOM, a _cdom,n(λ), and nonalgal particles, a _nap,n(λ), associated with each cluster. We recall that in our treatment of these data, a fitted exponential model is used in order to minimize measurement artifacts.

Figure 5.

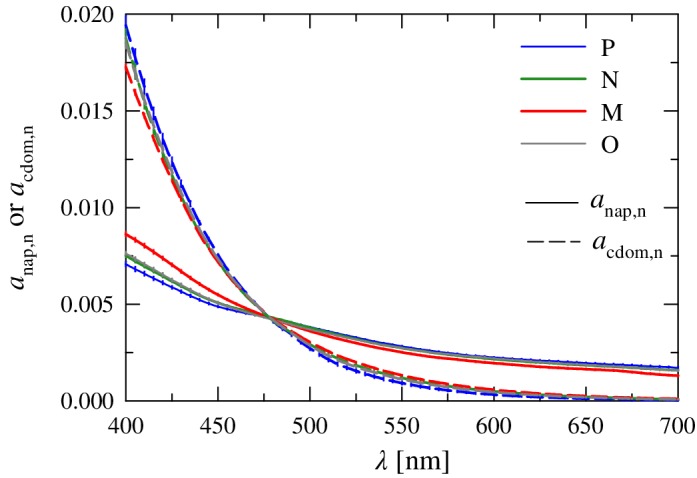
Normalized mean spectra of the absorption coefficient for nonalgal particles, a _nap,n(λ), and colored dissolved organic matter, a _cdom,n(λ), for each of the four clusters. Error bars as in Fig. 4.

The spectral shape of a _cdom,n in the blue exhibits the largest normalized values and steepest slope of all absorbing constituents (Fig. 5). Minimum variation in the values between clusters occurs near a wavelength of 470 nm, with only small differences in the overall spectral shape among clusters observed in our data set. The absorption coefficient of CDOM is steep with an average spectral slope S _cdom = −0.0184 ± 0.002 nm⁻¹ (Table 2), similar to the seasonally averaged value of −0.0180 ± 0.004 nm⁻¹ reported for this region by Matsuoka et al. (2011) and also consistent with values reported for various coastal waters around Europe (Babin et al. 2003). This steepness results in very high spectral band ratios of 7 to 11 for the 443/555 nm band ratio and values exceeding 50 for the 443/670 nm ratio.

Values of a _nap,n are smaller than a _cdom,n for wavelengths less than 475 nm, but show a similar convergence in the blue with the minimal variation among clusters occurring at about 480 nm. The overall spectral shape is much flatter than that observed for a _cdom,n, but similarly the among cluster variability is small with an average value of S _nap = −0.0071 ± 0.001 nm⁻¹ (Table 2). This slope parameter also falls within the range of previously reported values for this region (Matsuoka et al. 2011).

Spectral backscattering coefficient

Measurements of the spectral backscattering coefficient were partitioned into the summed contributions of molecular water and particles, i.e., b _b(λ) = b _bw(λ) + b _bp(λ). There are theoretical linkages between the spectral dependence of the particle backscattering coefficient, η _bbp, and the total particle size distribution (Morel 1973), and results from modeling studies (Stramski et al. 2001; Woźniak and Stramski 2004; Kostadinov et al. 2009) as well as field and satellite observations of the ocean are consistent with this notion (Reynolds et al. 2001; Loisel et al. 2006; Slade and Boss 2015). This has led to the development of backscattering‐based (Hirata et al. 2008; Kostadinov et al. 2010, 2016) or combined backscattering and absorption (Fujiwara et al. 2011; Neukermans et al. 2016) approaches to discriminating phytoplankton size classes. However, as the particulate backscattering represents the summed contributions of all particles in suspension, including but not limited to algal cells, there is a less direct linkage with the phytoplankton community. In addition to the particle size distribution, other characteristics such as particle shape, composition, and internal structure can also influence b _bp(λ), further complicating this linkage.

In the present data set, differences in the normalized spectral shapes of b _bp,n(λ) among the four clusters exhibit a 10–15% range in the blue and red spectral regions, with reduced variations of < 5% in the green. We recall that because of our use of a fitted spectral power law for extending multispectral measurements of both b _b(λ) and b _bp(λ), differences in the fitted spectral slope parameters (η _bb and η _bbp, respectively) are the sole basis for comparing spectral shapes among clusters and any finer spectral structures, such as features associated with backscattering in the presence of strong absorption, are ignored. Measured values of η _bbp vary over the range −2.98 to −0.20 for this data set, with a mean value of −1.20 ± 0.52 (n = 102). Consistent with expectations based on an increased proportion of large particles, cluster M has the flattest average spectral slope of all clusters (Table 2). The steepest average slope was found for cluster N. The values of η _bbp are not statistically different, however, among the four clusters. This result is also consistent with the analysis of Reynolds et al. (2016) for a larger portion of this same data set, in which a lack of strong correlation between the spectral slope of b _bp(λ) and metrics of the particle size distribution was observed.

The molecular backscattering coefficient of water molecules, b _bw(λ), exhibits a much steeper spectral shape than particles, with an average wavelength dependency of ~ λ ^−4.1 calculated for the stations in the present data set (Fig. 6). In contrast to water absorption, the contribution to spectral backscattering from water is greatest in the blue spectral region and decreases strongly with increasing wavelength. As is the case of the total absorption coefficient, the differences in both spectral shapes and the relative contributions of water and nonwater constituents dictate the final spectral shape of b _b(λ).

Figure 6.

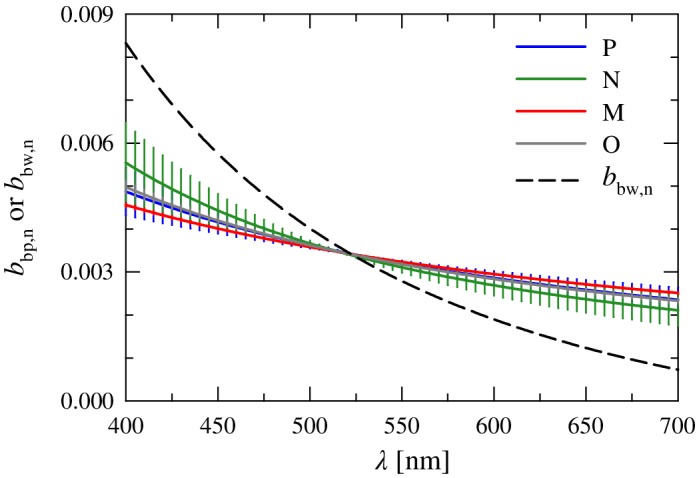
Normalized mean spectra of the particulate backscattering coefficient, b _bp,n(λ), for each of the four clusters. The mean normalized spectrum of the pure seawater backscattering coefficient, b _bw,n(λ), is also depicted. Error bars as in Fig. 4.

Magnitudes and relative contributions of optical constituents

Apparent optical properties of the ocean, such as ocean color, are closely linked to the overall magnitudes of IOPs. To first approximation, the spectral remote‐sensing reflectance is directly proportional to the backscattering coefficient and inversely proportional to the absorption coefficient, R _rs(λ) ∝ b _b(λ)/a(λ) (Gordon and Morel 1983; Gordon et al. 1988). In addition to differences in the characteristic spectral shapes associated with individual absorbing or scattering constituents, the relative contribution of each constituent to the overall magnitude of a(λ) or b _b(λ) will also have a strong influence on the magnitude and spectral shape of R _rs(λ).

For each cluster, Fig. 7 depicts the cluster‐averaged magnitude and relative contribution of individual constituents to the absorption and backscattering coefficients of seawater for wavelengths in the blue (443 nm) and green (555 nm) portion of the spectrum. Quantitative values for both these spectral bands and for an additional red wavelength (670 nm) are also provided in Table 3. Average values of a(443) for the four clusters vary nearly fourfold over the range 0.05–0.19 m⁻¹. The lowest average value is associated with cluster P and the highest value with cluster M. For all clusters, CDOM provided the dominant contribution to absorption at this wavelength (46–69%), a commonly observed feature of Arctic waters (Matsuoka et al. 2011; IOCCG 2015). For three of the four clusters, nonalgal particles are the second largest contributor to absorption, with the sole exception of cluster M in which the contribution of phytoplankton is comparable. Despite generally elevated values of Chla in cluster M, for this cluster the average phytoplankton contribution to absorption was less than 25% in the blue spectral region and exceeded 50% only for stations where Chla was generally 5 mg m⁻³ or higher. For the other clusters, the average phytoplankton contribution to a(443) was much smaller (9–13%). The contributions of molecular water to absorption range from 5% to 13% among clusters, with the highest relative contribution observed in cluster P.

Figure 7.

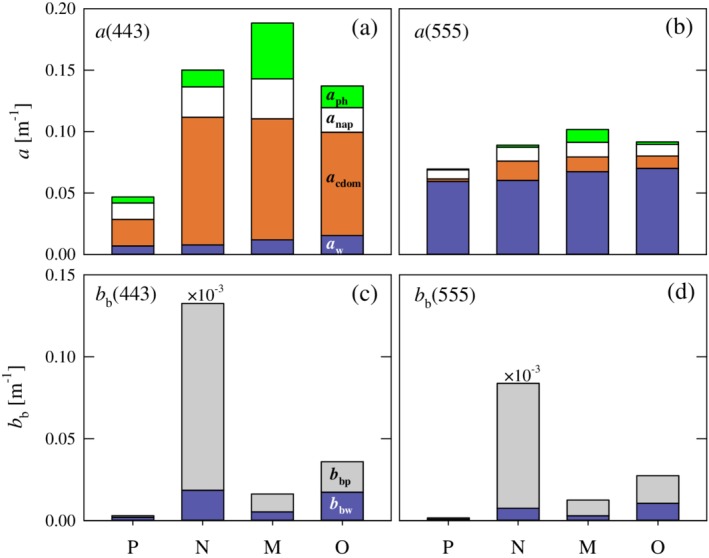
(a, b) Cluster mean values of the total absorption coefficient of seawater, a(λ), at light wavelengths of 443 and 555 nm. The height of each stacked bar indicates the mean value of the absorption coefficient, which is partitioned to depict the mean relative contribution of four absorbing constituents as indicated. (c, d) Similar to a and b but for the total backscattering coefficient of seawater, b _b(λ), with the relative partitioning between pure seawater and particulate matter. The values for cluster N have been multiplied by 1 × 10⁻³ to allow display on the same scale as the other clusters.

Table 3.

Average magnitudes of the spectral absorption and backscattering coefficients associated with individual constituents for each cluster.

Cluster	λ (nm)	a w	a cdom	a nap	a ph	a	b bw	b bp	b b
P	443	0.007	0.022	0.013	0.005	0.047	0.0020	0.0010	0.0030
		(15.0)	(46.3)	(28.4)	(10.3)		(67.5)	(32.5)
	555	0.060	0.002	0.007	0.001	0.070	0.0008	0.0015	0.0015
		(85.7)	(3.0)	(10.4)	(0.9)		(53.0)	(47.0)
	670	0.439	0.0002	0.005	0.002	0.446	0.0003	0.0009	0.0009
		(98.5)	(0.04)	(1.1)	(0.4)		(36.1)	(63.9)
N	443	0.007	0.109	0.023	0.011	0.150	0.0017	132.58	132.59
		(5.3)	(69.2)	(16.5)	(9.1)		(14.0)	(86.0)
	555	0.060	0.017	0.011	0.002	0.089	0.0007	83.81	83.81
		(67.8)	(17.7)	(12.7)	(1.8)		(8.9)	(91.1)
	670	0.439	0.002	0.008	0.004	0.453	0.0002	58.83	58.83
		(96.9)	(0.5)	(1.7)	(0.9)		(3.7)	(96.3)
M	443	0.007	0.085	0.040	0.057	0.188	0.0020	0.0143	0.0163
		(6.4)	(52.3)	(17.2)	(24.1)		(32.4)	(67.6)
	555	0.060	0.014	0.015	0.013	0.102	0.0009	0.0116	0.0125
		(66.5)	(11.6)	(11.9)	(10.1)		(23.1)	(76.9)
	670	0.439	0.002	0.010	0.036	0.487	0.0003	0.0098	0.0101
		(91.3)	(0.4)	(1.8)	(6.4)		(14.0)	(86.0)
O	443	0.007	0.085	0.029	0.016	0.137	0.0020	0.0340	0.0360
		(11.3)	(61.2)	(14.7)	(12.8)		(48.2)	(51.8)
	555	0.060	0.015	0.014	0.003	0.092	0.0009	0.0265	0.0274
		(76.7)	(10.7)	(10.3)	(2.3)		(38.3)	(61.7)
	670	0.439	0.003	0.009	0.007	0.458	0.0004	0.0216	0.0219
		(96.2)	(10.3)	(1.9)	(1.4)		(27.7)	(72.3)

All coefficients are in units of m⁻¹. The values within parentheses indicate the average contribution in percentage of individual constituents to either a(λ) or b _b(λ).

Cluster‐averaged values of a(555) are markedly less variable than observed in the blue spectral bands, ranging only from 0.07 to 0.10 m⁻¹ among the four clusters (Fig. 7). This is attributable to the observation that the constant value of molecular water is the dominant contributor to absorption in this spectral band (66–86%), with other constituents having only a minor contribution to absorption. This trend is further strengthened in the red portion of the spectrum, where average values of a(670) between clusters vary by < 4% as a consequence of the water absorption contribution generally exceeding 95% (Table 3).

The average magnitudes of b _b(λ) and the relative partitioning between water and particle contributions exhibit even larger differences among the four clusters. The most striking difference consists of the extremely high values of b _b(λ) associated with cluster N, with an average value more than three orders of magnitude higher than the other clusters. Unfortunately, only 3 of the 14 stations in this cluster have measurements of backscattering, and all 3 occur on a transect sampling the main MacKenzie River plume. The two stations closest to the MacKenzie River mouth exhibit extremely high turbidities in which measured values of b _bp(λ) exceeded 100 m⁻¹, whereas a third station at the seaward end of the transect had much smaller values. We thus caution that the extremely high average values of b _bp(λ) and b _b(λ), as well as the mean spectral shapes, obtained for this cluster result from a very limited sample size. Because of the high particulate load associated with these MacKenzie River plume stations, water has only a small contribution to b _b (< 15%) in the blue spectral region, and this contribution decreases with increasing wavelength.

Apart from cluster N, there is still a greater than 10‐fold difference in the average magnitude of b _b(λ) among the three clusters P, M, and O. Cluster P has the smallest average values of b _b of all clusters (0.0030 ± 0.00003 m⁻¹ at 443 nm), and in accordance the relative contribution of water to backscattering is greatest (> 50%) in both the blue and green spectral bands. Similar to cluster N, measurements of backscattering for this cluster are available only on a limited number of samples. Both clusters M and O have a significantly higher average values of b _b(λ) compared to cluster P, with the contribution of b _bp(λ) to b _b(λ) having intermediate values between that of cluster P and N. Interestingly, the average magnitudes of both b _bp(λ) and b _b(λ) are more than twofold higher for cluster O than those observed for cluster M, despite the latter having much higher average values of Chla and POC but similar SPM. These results imply significant differences in the average mass‐specific backscattering coefficients among clusters.

Spectra of total absorption and backscattering coefficients

The interplay between variations in the spectral shapes of constituent absorption and backscattering coefficients among clusters as well as cluster‐specific differences in the relative contributions of these constituents is integrated in the spectral shapes of a(λ) and b _b(λ). The average normalized spectral shapes of these IOPs for each cluster are depicted in Fig. 8.

Figure 8.

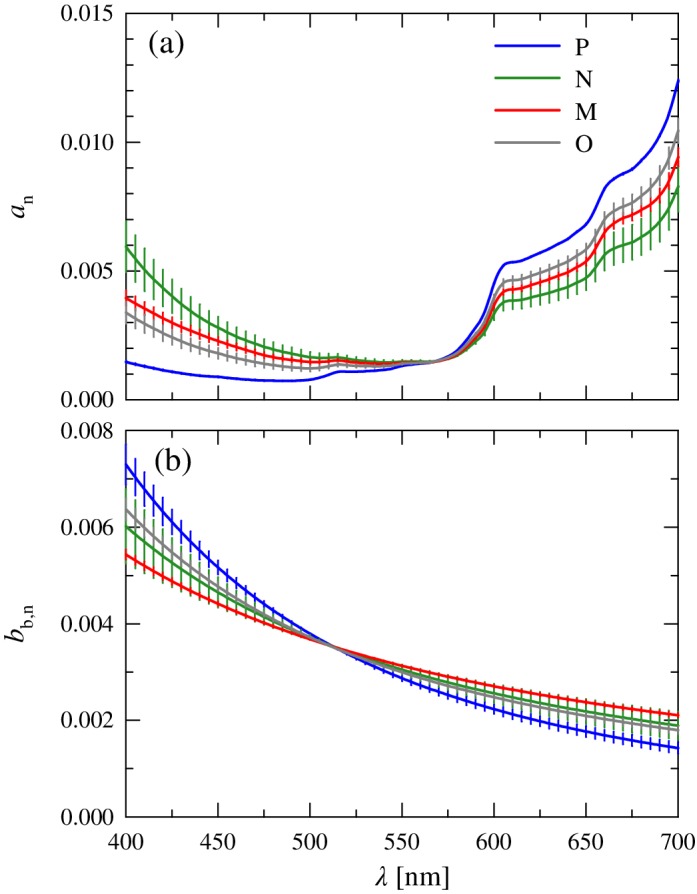
Normalized mean spectra of the (a) absorption, a _n(λ), and (b) backscattering, b _b,n(λ), coefficients for each of the four clusters. Error bars as in Fig. 4.

In the blue spectral domain, the main contributions to absorption are CDOM, nonalgal particles, and water; these three components contribute > 75% to a(443) for all clusters. Although the spectral shapes of these constituents differ from one another, the within cluster variability is relatively constrained (< 15% at 443 nm). Even in a region of maximal pigment absorption, phytoplankton generally contribute only 10–25% to a(443) and exhibit only ~ 10% variation in shape among clusters at this wavelength.

Despite limited variability in constituent spectral shapes between clusters, the mean normalized spectral shapes of a(λ) exhibit large differences among the four clusters (Fig. 8a). The largest variations are at the short wavelength region of the visible spectrum, exceeding threefold at 443 nm. The spectra of a _n(λ) all show a mostly featureless decrease in absorption throughout the blue spectral region with no evident absorption peaks associated with phytoplankton pigments, consistent with the dominant contribution of nonphytoplankton constituents. The highest values in the blue are associated with cluster N, reflecting that stations in this cluster have the highest average contribution of CDOM, the constituent with the steepest spectral slope, to absorption. In contrast, cluster P exhibits the lowest relative absorption in the blue associated with the lowest relative contribution of CDOM and highest contribution of water absorption. For clusters P and O, the minimum in the normalized absorption coefficient occurs below 500 nm, whereas for the other two clusters, this minimum is shifted to longer wavelengths (~ 540 nm).

Minimal variation (< 5%) in the spectral shape of a _n(λ) is observed among the clusters in the spectral region 550–580 nm. This convergence in the green occurs where water becomes the dominant contribution to absorption. With increasing wavelength, the mean cluster spectra diverge again despite the increasing dominance of water absorption, with a 1.5‐fold variation among spectra observed at 700 nm. The cluster order is, however, opposite to that observed in the blue. Despite overall lower absorption compared to the Soret blue bands, difference in a _ph(λ) among clusters has greater influence on variations of a(λ) in the red region of the spectrum because of the minimal contributions of a _cdom(λ) and a _nap(λ) coupled with a constant value of a _w(λ). This pattern is generally similar to that observed in Fig. 4b for the spectral shapes of a _ph+w,n(λ), confirming the dominant role of water and phytoplankton. The cluster differences result from a combination of phytoplankton spectral differences in the red coupled with small differences in a _ph(λ)/a(λ). Although among cluster variability at a _ph,n(670) is twice greater than at 443 nm, the variations in the spectral shape of phytoplankton absorption at 670 nm are still relatively small (~ 24%). This suggests the perhaps counterintuitive result that for the total absorption coefficient of seawater, the red spectral region is better than the blue for detecting variability in phytoplankton absorption.

With regards to the backscattering coefficient, the differences in the normalized mean spectral shape b _b,n(λ) among clusters are generally smaller than observed for a _n(λ) (Fig. 8b). The minimal variation among clusters occurs around 515 nm, blue‐shifted ~ 50 nm relative to a _n(λ). The normalized spectra diverge outside this range with differences between clusters < 15% throughout the visible spectrum. The spectral slope values of b _b(λ) associated with each cluster, η _bb, are steeper than those observed for b _bp,n(λ) because of the added contribution of molecular water scattering but exhibit a similar range of variation (1.7‐fold) as that of η _bbp (Table 2). Cluster M has the flattest spectral dependency similar to that observed for b _bp,n(λ), but as a consequence of having the greatest contribution of water cluster P exhibits the steepest spectral slope of all clusters.

Spectra of the backscattering‐to‐absorption ratio and remote‐sensing reflectance

The spectral backscattering‐to‐absorption ratio, b _b(λ)/a(λ), provides a proxy for the influence of subsurface IOPs of water on the spectral remote‐sensing reflectance, R _rs(λ). Although a principal factor driving the spectral shape of R _rs(λ), this approximation does not account for spectral variations associated with directional effects of radiative transfer across the sea surface. It is also important to note that this approximation ignores any spectral alterations to the subsurface and water‐leaving light fields arising from inelastic radiative transfer processes, such as contributions from the Raman scattering by water molecules or fluorescence from dissolved or particulate compounds. These influences are always present to some extent in natural waters and can be considerable in the portion of the visible spectrum beyond 500 nm (Stavn and Weidemann 1988; Li et al. 2016, 2018).

Figure 9a illustrates the mean normalized spectral shapes of the backscattering‐to‐absorption ratio, (b _b/a)_n(λ), computed for each cluster. We recall that for each station, the spectrum of b _b was obtained from the measured multispectral values fitted to a power function, a(λ) was computed as the sum of a _w(λ) + a _cdom (λ) + a _p(λ) [≡ a _w(λ) + a _cdom(λ) + a _nap(λ) + a _ph(λ)], and the resulting ratio b _b(λ)/a(λ) was normalized to the integral over the visible spectrum. For cluster P, there was no single station which had concomitant measurements of all constituent absorption and backscattering coefficients, so for this cluster a single composite spectrum of (b _b/a)_n(λ) was calculated by using the mean spectrum of each individual constituent IOP. This single spectrum is identified by the dashed line in Fig. 9a.

Figure 9.

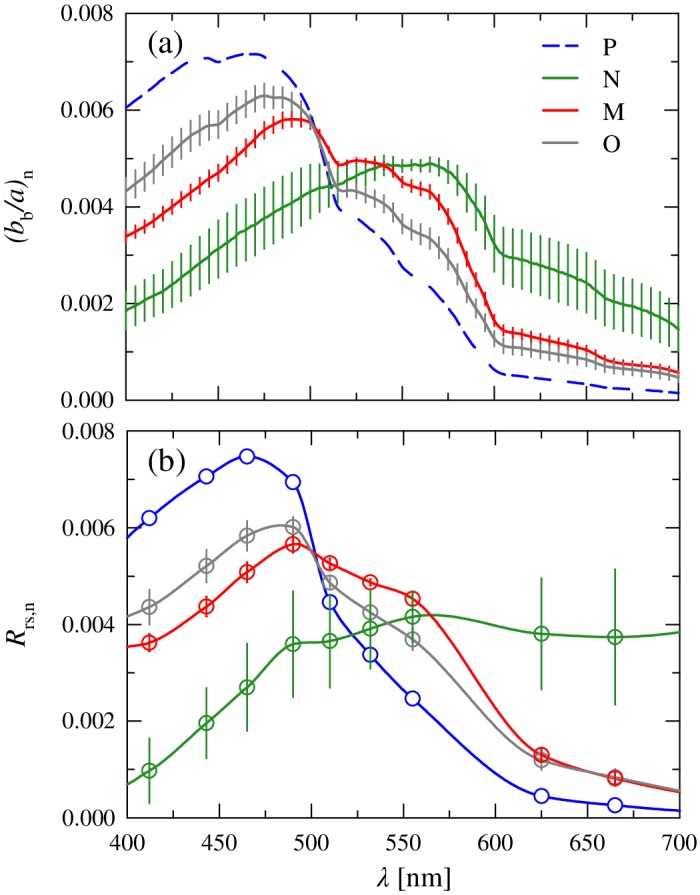
(a) Normalized mean spectra of the backscattering‐to‐absorption ratio, (b _b/a)_n(λ), for each of the four clusters. Error bars as in Fig. 4. The spectra for cluster P was calculated using the cluster mean values of all absorption and backscattering constituents. (b) Similar to (a) but for independent radiometric measurements of the remote‐sensing reflectance spectra, R _rs,n(λ).

The results indicate that the variation between clusters in (b _b/a)_n(λ) is greater than that observed for any of the individual absorbing or backscattering constituents. The cluster mean values of (b _b/a)_n at 443 nm vary more than twofold over the range 0.003 to 0.007. Cluster N exhibits the flattest spectral shape of all clusters with the lowest values in the blue spectral region and the highest values in the red and a broad peak in the spectrum centered near 555 nm. Such behavior is typical of coastal or inland waters that feature high scattering of particles and strong absorption in the blue, generally arising from terrestrial sources (e.g., Sathyendranath et al. 1989; Lubac and Loisel 2007).

In contrast to cluster N, the remaining three clusters exhibit peak values of (b _b/a)_n(λ) in the blue spectral region and generally decline with increasing wavelength. These clusters also show some features associated with absorption of phytoplankton pigments, although the location of these peaks varies between clusters. The order of clusters in the blue (P > O > M) is similar to that observed for a _ph,n(λ). The shape of cluster P is the most similar to clear oceanic waters, with a maximal value of (b _b/a)_n(λ) at 465 nm and a steep decrease with increasing wavelength and lowest values of (b _b/a)_n(λ) in the red. Both clusters O and M are intermediate between the two extremes of clusters P and N. Compared to cluster P, these spectra are characterized by lower values in the blue with the main peak shifted toward longer wavelengths, a convergence with cluster P near 500 nm, and higher values for cluster M relative to cluster O at longer wavelengths.

The observed trends in the spectral shape of the ratio b _b(λ)/a(λ) were confirmed through comparison with independent radiometric measurements obtained at each station in conjunction with IOP measurements (Fig. 9b). The results of this comparison indicate remarkably good agreement in the cluster trends observed for (b _b/a)_n(λ) and R _rs,n(λ). The general pattern in cluster trends for (b _b/a)_n(λ) is reproduced in R _rs,n(λ), and the normalized values of R _rs,n(λ) and the observed range of variation within the visible spectrum are similar to (b _b/a)_n(λ). For a given cluster, the shape of R _rs,n(λ) also corresponds well to that observed for (b _b/a)_n(λ), with generally only small deviations which are likely related to the caveats of the R _rs(λ) ∝ b _b(λ)/a(λ) approximation as described earlier. These results lend a high level of confidence to the individual IOP constituent measurements and suggest that the average values and overall trends among cluster IOPs are adequately captured despite the sometimes low or unequal number of samples between clusters. Importantly, the large separation among clusters in the spectral shape of both b _b(λ)/a(λ) and R _rs(λ) suggests that they can be discriminated from these optical measurements.

Discussion

Our study utilizes measurements of phytoplankton biomarker pigments to estimate the relative contributions of three phytoplankton size classes to overall chlorophyll a concentration. Chemotaxonomic methods based on diagnostic pigments have become one of the most common approaches to characterizing oceanic phytoplankton community composition and can be routinely applied on shipboard surveys without requiring the detailed taxonomic training that is required for more labor‐intensive microscopic analyses. In that regard, these benefits can outweigh the well‐known limitations of these approaches, in particular, the lack of information on changes occurring at smaller taxonomic levels such as species.

There are alternative pigment‐based approaches to classify phytoplankton taxonomic composition (Mackey et al. 1998; Hill et al. 2005; Fujiwara et al. 2014) but all require knowledge or assumptions about the mean and variance of diagnostic pigments ratios to chlorophyll a. We chose the Uitz et al. (2006) model for size class composition as it condenses information from multiple diagnostic pigments into a limited number of categories based upon average cell size, facilitating the ecological interpretation of the clusters identified for optical characterization. Reconstructed values of Chla using the original weighting coefficients of the Uitz et al. (2006) model are highly correlated with measured Chla (R = 0.99) but overestimate measured values on average by 36%. Despite this departure from the globally derived pigment ratios, the overall partitioning of stations and patterns among clusters is similar to those based on raw pigment ratios and thus has no influence on the results of this study.

We recognize that the partitioning analysis results in some clusters comprising a small number of stations, which are not necessarily representative of the relative abundance of these phytoplankton groups either spatially or temporally in the study region. This limitation is further exacerbated in that even smaller subsets of stations within a cluster have a complete suite of concomitant optical measurements, and the unequal sample sizes among clusters make it challenging to adequately characterize within‐cluster variation or to unequivocally establish statistical differences among clusters. The difficulties associated with obtaining a complete set of particle and optical characteristics at each station is a common challenge in ocean optical studies and not limited to the Arctic. There is a continued need for the collection of such comprehensive datasets in order to identify the best approaches and to provide evaluation data sets for algorithms to discriminate phytoplankton communities from optical measurements.

Implications for optical approaches to discriminate phytoplankton communities

Variations in the spectral shape of the phytoplankton absorption coefficient, a _ph(λ), associated with changes in phytoplankton community composition arise from taxon‐specific changes in pigmentation and average cell size and form the basis of several approaches for PFT discrimination. Our results indicate significant differences in the spectral shape of a _ph(λ) related to phytoplankton community composition in the study area. The statistical significance between cluster means varies spectrally (e.g., weaker significance at 555 nm as opposed to 443 or 670 nm), and not all clusters were significantly different from one another at all wavelengths. For example, in many spectral regions, cluster M was statistically different from clusters P and O but did not differ significantly from cluster N. Although the variability in the normalized shape of a _ph(λ) at a single wavelength between communities is small (e.g., ~ 10% at 443 nm), the observed flattening in overall spectral shape associated with the transition from a microphytoplankton‐ to picophytoplankton‐dominated community enhances differences in spectral band ratios. This suggests that simple approaches based on multispectral measurements of a _ph(λ) in key spectral bands can be used to discriminate at least some phytoplankton communities in this region, as has been suggested in previous studies (Fujiwara et al. 2011; Zhang et al. 2018). If hyperspectral data are available, these approaches can be enhanced through the derivative analysis of phytoplankton absorption spectra (Torrecilla et al. 2011; Uitz et al. 2015).

Our analysis also indicates that some classes, such as the picophytoplankton (cluster P) and the mixed communities (cluster O), are statistically indistinguishable in terms of the shape of a _ph(λ) and will be difficult to separate solely on that basis. This limitation can likely be mitigated by the inclusion of additional optical information, such as the magnitude of a _ph(λ) and a _ph+w(λ) or the magnitudes of the total absorption and backscattering coefficients.

Current techniques that use chemical extraction for estimating phytoplankton absorption are not well suited for autonomous or remote observations. There is, however, an increasing capability to obtain measurements of the spectral absorption coefficient from in situ instrumentation (Slade et al. 2010; Wollschläger et al. 2013) or to estimate it through the use of inverse models applied to observations obtained from air or spaceborne ocean color sensors (Werdell et al. 2018). Recent work suggests that these latter inversion models can perform with reasonable accuracy in the Arctic (Zheng et al. 2014; Loisel et al. 2018). In parallel, there has been recent progress in the development of mathematical approaches to partitioning data of the absorption coefficient into the separate contributions of various seawater constituents, including phytoplankton (Lee et al. 2002; Ciotti and Bricaud 2006; Zheng and Stramski 2013).

The findings of this study also emphasize that in the Arctic, phytoplankton generally have only a small and variable contribution to the absorption coefficient of seawater. Phytoplankton were the dominant contribution to absorption in only 11 of the 136 stations, and these represented stations with high phytoplankton biomass in the surface (Chla generally > 5 mg m⁻³). This contribution is substantially smaller in other regions of the visible spectrum. The predominance of nonphytoplankton contributions to the absorption coefficient implies that PFT approaches which rely on specific signatures or spectral anomalies in reflectance related to phytoplankton pigment absorption are likely to have limited application in these waters, except perhaps in specific bloom conditions where the phytoplankton contribution to seawater optical properties can be significant.

Despite the limited contribution of phytoplankton to the total absorption coefficient, strong differences were observed in the average spectral shape of both the backscattering‐to‐absorption ratio, b _b(λ)/a(λ), and the remote‐sensing reflectance, R _rs(λ), among the four clusters. In the visible spectral region, these variations are substantially larger than those observed for any of the individual absorbing or scattering constituents. The separation in spectral shape among clusters arises mainly from differences in the bio‐optical environment in which the specific communities tend to be found and thus have a basis in phytoplankton ecology. In our study, picophytoplankton‐dominated communities (cluster P) were primarily found in the clearer waters of the eastern Beaufort Sea where nutrients limit phytoplankton biomass and terrigenous influences are reduced. Although CDOM and nonalgal particles still comprise the dominant contribution to absorption in the blue, water has its greatest contribution of all clusters to both spectral absorption and backscattering. In contrast, the nanophytoplankton‐dominated communities (cluster N) were generally located in very turbid waters of shallow coastal regions near river sources, which exhibit a high particle load and associated particle scattering as well as the greatest contribution of CDOM to absorption. The microphytoplankton‐dominated communities (cluster M), which exhibit a spectral shape intermediate of these two end members, have the highest average Chla and the greatest phytoplankton contribution to absorption of all clusters, with intermediate values of particle scattering.

The large differences observed in the spectral shape of b _b(λ)/a(λ) and R _rs(λ) associated with these different phytoplankton assemblages suggest that relatively simple algorithms, utilizing either multispectral band ratios or spectral shape matching approaches, may serve as a means to discriminate them from either in situ or remotely obtained observations of ocean optical properties. Similarly, approaches based on optical water type classification may also provide a basis for discrimination (Moore et al. 2009; Neukermans et al. 2016). Because within‐cluster variability in the spectral shape of R _rs(λ) can be large, the development of such algorithms would benefit from additional data, particularly for clusters with low number of stations, collected in different seasons in order to better quantify the uncertainties in cluster assignment.

The conceptual basis of this approach, however, would not be based upon differences in the specific optical properties of phytoplankton per se, as is the case in many extant PFT algorithms. Instead, it reflects the fact that different phytoplankton communities tend to inhabit specific optical environments that have differing magnitudes of IOPs and varying contributions of optically significant constituents. On that basis, the discrimination approach is indirect in the sense that it relies upon phytoplankton assemblages occupying specific ecological roles or niches that tend to be associated with certain pelagic habitats or environments with different characteristics in terms of abiotic and biotic factors. This classical concept is similar in nature to approaches that estimate the distribution of PFTs based on environmental considerations (Raitsos et al. 2008; Palacz et al. 2013) and is also consistent with numerical modeling studies examining phytoplankton community composition and size structure in the ocean (Le Quéré et al. 2005; Ward et al. 2012). Exceptions to the covariation between environmental factors and phytoplankton community composition observed within our data set may exist or may not persist under current trends regarding climate change and planktonic community evolution. For these reasons, a more mechanistic approach using discrimination based on phytoplankton absorption shapes may provide a more robust algorithmic approach, despite the smaller variance observed between phytoplankton classes and potentially larger uncertainties associated with the inversion of R _rs(λ) to absorption and subsequent partitioning of a(λ) into the contribution of phytoplankton. These types of analyses will be the subject of future work.

Our results indicate that measurements of seawater optical properties can offer a new window on observing phytoplankton community diversity in the Arctic. Such measurements cannot discriminate at the level of individual species or assess genetic diversity, and there are additional limitations to the use of data obtained from satellite optical remote sensing such as the restriction of measurements to the ocean surface layer coupled with a frequent lack of observations in many regions of the Arctic owing to cloud cover and sea ice. Despite these limitations, because of their suitability to a variety of sensor platforms (both above‐surface and in situ), optical measurements currently provide the only means to obtain information about oceanic planktonic community composition and size structure over synoptic, multidecadal spatial and temporal scales. The development and demonstration of these capabilities through algorithm development and application to remote ocean color imagery would enable the investigation of trends in the biogeography and temporal succession of distinct phytoplankton assemblages, which can provide baseline information for monitoring future changes within the Arctic Ocean and guide future targeted studies. These observations can also provide an independent data set for the development and validation of coupled physical‐biogeochemical numerical models which include or assimilate information on multiple classes of PFT or size structure (Ward et al. 2012; Bopp et al. 2013; Ciavatta et al. 2018). Such capabilities represent marked improvements over the sole use of bulk Chla as an indicator of phytoplankton abundance and primary production.

Conflict of Interest

None declared.