Sequence Effects on Size, Shape, and Structural Heterogeneity in Intrinsically Disordered Proteins

Abstract

Intrinsically disordered proteins (iDPs) lack well-defined three-dimensional structures, thus challenging the archetypal notion of structure—function relationships. Determining the ensemble of conformations that IDPs explore under physiological conditions is the first step toward understanding their diverse cellular functions. Here, we quantitatively characterize the structural features of IDPs as a function of sequence and length using coarse-grained simulations. For diverse IDP sequences, with the number of residues (N_T) ranging from 20 to 441, our simulations not only reproduce the radii of gyration (R_g) obtained from experiments, but also predict the full scattering intensity profiles in excellent agreement with small-angle X-ray scattering experiments. The R_g values are well-described by the standard Flory scaling law, $R_{\text{g}}=R_{\text{g}}^0{N_{\text{T}}}^{\nu },\text{with}\nu \approx 0.588,$ making it tempting to assert that IDPs behave as polymers in a good solvent. However, clustering analysis reveals that the menagerie of structures explored by IDPs is diverse, with the extent of heterogeneity being highly sequence-dependent, even though ensemble-averaged properties, such as the dependence of R_g on chain length, may suggest synthetic polymer-like behavior in a good solvent. For example, we show that for the highly charged Prothymosin-α, a substantial fraction of conformations is highly compact. Even if the sequence compositions are similar, as is the case for α-Synuclein and a truncated construct from the Tau protein, there are substantial differences in the conformational heterogeneity. Taken together, these observations imply that metrics based on net charge or related quantities alone cannot be used to anticipate the phases of IDPs, either in isolation or in complex with partner IDPs or RNA. Our work sets the stage for probing the interactions of IDPs with each other, with folded protein domains, or with partner RNAs, which are critical for describing the structures of stress granules and biomolecular condensates with important cellular functions.

graphical abstract

INTRODUCTION

The discovery that a large fraction of eukaryotic protein sequences are not ordered in isolation^1–7 has produced a paradigm shift in the commonly held view of structure—function relationship. Such sequences, referred to as intrinsically disordered proteins (IDPs), play key functional roles in diverse cellular processes, such as signal transduction^2,8 and vesicular transport,⁹ and are also implicated in neurodegenerative disorders and other diseases.^3,10 Experimental realizations of folding coupled to binding partners and the more recent discovery of intracellular liquid—liquid phase separation¹¹ have further resulted in a concerted effort in describing the intramolecular and intermolecular interactions involving IDPs.^12–17 Recent estimates indicate that between 30 and 40% of eukaryotic proteomes are either intrinsically disordered or contain intrinsically disordered regions in otherwise folded proteins.^17,18 Despite the importance of IDPs, characterization of the sequence-dependent conformational properties of IDPs in isolation as well as their phase behavior remains largely qualitative.^14,16,19 Biologically relevant forms of IDPs do not fold into unique tertiary structures but explore a large number of distinct conformational states. In this sense, they are like synthetic polymers, whose conformations can only be characterized in statistical terms, such as the distribution of the radius of gyration, R_g, from which its dependence on the number of residues, N_T, can be calculated.^17,20 Two decades of experiments indicate that isolated IDPs typically behave as polymers in a good solvent based on the scaling of R_g with N_T.^21–23 However, the conformational ensembles of IDPs, which are instrumental in modulating their in vivo functionalities, strongly depend on the precise sequence, in addition to other external conditions, such as pH, temperature, and salt concentration.^24,25 Therefore, scaling laws alone cannot provide a faithful description of the physicochemical properties of IDPs. The complex sequence dependence poses a great challenge to purely theoretical approaches^26,27 and raises the need for computational models that can quantitatively account for the experimental data.

Small-angle X-ray scattering (SAXS) and single-molecule Förster resonance energy transfer (smFRET) have found the greatest applicability in the study of IDP conformational properties. ^21,28 In addition, nuclear magnetic resonance (NMR) and fluorescence correlation spectroscopy (FCS)^24,28–31 have been used to characterize the structural ensembles and conformational dynamics of IDPs. SAXS experiments, which measure structure factors, could be used to calculate the global conformational properties of IDPs, such as R_g and shape, whereas smFRET experiments are used to probe distances between specific labeled residues along the polypeptide chain. With SAXS, the measured structure factor, I(q), as a function of the wave vector q, at small values of q is often used to estimate R_g using the Guinier approximation.³² However, the sequence-specific conformational ensembles are not directly available from SAXS experiments, and usually, techniques based on ensemble optimization are invoked to map scattering profiles to representative structures.³³

A complementary approach involves computer simulations that employ force fields to generate IDP ensembles, which embody the key experimental observables. It is tempting to exploit an all-atom representation for IDPs and the surrounding environment in order to characterize their conformations. Indeed, great progress is being made in devising new force fields, which make systematic updates to the existing water models or protein interaction potentials.^34–38 Systematic benchmarking has revealed that although all-atom force fields provide the much needed microscopic insight into the conformational dynamics of IDPs, the associated ensembles often tend to depend on the details of the parameterization.^39,40 A simpler description of the protein molecule based on systematic coarse graining often provides a complementary route toward probing the conformational dynamics of IDPs. ^15,41,42 We and others have previously exploited coarse-graining strategies with great success in applications of protein folding and kinetics^43–45. In this work, we introduce a self-organized polymer (SOP) coarse-grained model for IDPs (SOP-IDP), which not only recapitulates the wealth of experimental SAXS data, but also delineates the complex interplay between sequence, structure, and aspects of conformational heterogeneity that have been largely unexplored in much of the previous studies.

We show that for IDPs of varying lengths and sequence composition, the R_g values are in accord with Flory’s scaling law. The calculated R_g values from simulations are generally in good agreement with those extracted from SAXS data. The simulations accurately reproduce the measured SAXS profiles, thus allowing us to provide insights into the shape and conformational fluctuations, which govern their functions. The ensembles of conformations of all the IDPs are heterogeneous, with sequence being a key determinant of the relative populations of different substates. Our findings using SOP-IDP simulations suggest that the phases of IDPs cannot be predicted solely based on sequence compositional properties but require complete statistical characterization of the IDP ensembles.

METHODS

Development of the Model.

In the SOP-IDP model, except for glycine and alanine, the amino acid residues are represented using a backbone and a side-chain (SC) bead. We use the C_α atoms to model glycine and alanine owing to their small SCs. The radii of the individual beads are given in Table S1 of the Supporting Information. The energy function in the SOP-IDP model is

$$\begin{gathered} E=-\sum _{i=1}^{N_B}\frac{k}{2}{R}_0^2\log \left(1-\frac{{\left(r_i-r_{ref,i}\right)}^2}{R_0^2}\right)+\sum _{i=1}^{N_{\text{loc}}}{ϵ}_{\text{loc}}{\left(\frac{{\sigma }_i}{r_i}\right)}^6 \\ +\sum _{i,j}^{\prime }\frac{e_i{e}_j\exp \left(-\kappa r_{ij}\right)}{\epsilon r_{ij}}+\sum _{i=1}^{N_{\text{BB}}}{ϵ}_{\text{BB}}\left[{\left(\frac{{\sigma }_i}{r_i}\right)}^{12}-2{\left(\frac{{\sigma }_i}{r_i}\right)}^6\right] \\ +\sum _{i=1}^{N_{\text{BS}}}{ϵ}_{\text{BS}}\left[{\left(\frac{{\sigma }_i}{r_i}\right)}^{12}-2{\left(\frac{{\sigma }_i}{r_i}\right)}^6\right]+\sum _{i=1}^{N_{\text{SS}}}{ϵ}_{\text{SS}}\left|{ϵ}_i-0.7\right| \\ \left[{\left(\frac{{\sigma }_i}{r_i}\right)}^{12}-2{\left(\frac{{\sigma }_i}{r_i}\right)}^6\right] \end{gathered}$$ (1)

The first term in eq 1, for a chain with N_B bonds, represents bonded interactions, which are described using a finitely extensible nonlinear elastic (FENE) potential. The purely repulsive second term acts only between bead pairs (total number N_loc) that are not covalently bonded but belong to residues separated by ≤2 along the polypeptide chain. It represents the excluded volume interactions that prevent unphysical bond crossing between pairs of beads that closely follow one another along the polymer chain. The third term is a screened Coulomb potential that accounts for electrostatic interactions between all pairs of charged residues. The charge corresponding to a residue is assigned to the SC. The titratable residue histidine is treated as neutral in the model, unless it is experimentally determined to be in the protonated state. The parameters κ and ε in the third term in eq 1 are the inverse Debye length and the dielectric constant, respectively. These three terms were previously used in protein folding and related studies,^43,44,46 where the justifications for their choices are given.

The final three terms in eq 1 represent interactions between backbone—backbone (BB), backbone—side-chain (BS), and side-chain—side-chain (SS) beads. The total numbers of such BB, BS, and SS pairs are, respectively, N_BB, N_BS, and N_SS. Interactions between the SCs depend only on the identities of the amino acids without bias toward any specific structure. The parameter ${ϵ}_i$ in the final term in eq 1 is obtained from the Betancourt—Thirumalai statistical potential.⁴⁷ The ${ϵ}_i$ values are unique to each pair of amino acid residues, and hence, depend explicitly on the IDP sequence. In eq 1, the three parameters ${ϵ}_{\text{BB}},{ϵ}_{\text{BS}},\text{and}{ϵ}_{\text{SS}}$ set the energy scales corresponding to the nonlocal interactions and are the only free parameters in the energy function. We determine the initial values of ${ϵ}_{\text{BB}},{ϵ}_{\text{BS}},\text{and}{ϵ}_{\text{SS}}$ in a top-down fashion by using the SAXS data (R_g and I(q)) for only three short IDPs (24 ≤ N_T ≤ 131) as constraints in the parameterization scheme. Subsequently, to find the optimum values of the parameters, only the experimental R_g estimates for three long IDP sequences (202 ≤ N_T ≤ 441) were used as constraints in the parameterization scheme. Further details of this learning procedure are provided in the Supporting Information.

Comments on the Parameter Values.

The values of the parameters, which were obtained using a learning procedure described in the Supporting Information, in the SOP-IDP model are

$${ϵ}_{\text{BB}}=0.12\text{kcal}/\text{mol},{ϵ}_{\text{BS}}=0.24\text{kcal}/\text{mol},{ϵ}_{\text{SS}}=0.18\text{kcal}/\text{mol}$$ (2)

which in units of k_BT (T = 298 K) are ${ϵ}_{\text{BB}}=0.2,{ϵ}_{\text{BS}}=0.4,{ϵ}_{\text{SS}}=0.3$ These values differ from the ones used to describe globular proteins,⁴⁸ which were obtained in order to describe their folding thermodynamics at zero denaturant concentration ([C]). As [C] increases, the stability of the folded states decreases, which we accounted for phenomenologically using transfer free energies, thus creating the SOP-molecular transfer model (MTM).⁴⁸ The effective interaction parameters ${ϵ}_{\text{BB}},{ϵ}_{\text{BS}},\text{and}{ϵ}_{\text{SS}}$ are expected to decrease as [C] increases, so that at high [C], the statistical properties of the denatured state ensemble (DSE) of globular proteins and IDPs, such as R_g, would exhibit the scaling $R_{\text{g}}\approx 0.20{\text{N}}_{\text{T}}^{\nu },\text{with}\nu \approx \mathrm{0.588.}$ ⁴⁹ Because the R_g scaling of DsEs of globular proteins at high denaturant concentrations is statistically equivalent to those for IDPs (hence the plausible relevance of IDPs to the SAXS-FRET controversy), it is not surprising that the optimal values for the SOP-IDP model (eq 2) differ from the [C] = 0 values.⁴⁸ The values of ${ϵ}_{\text{BB}},{ϵ}_{\text{BS}},\text{and}{ϵ}_{\text{SS}}$ for globular proteins in water, respectively, are 4.6, 1.7, and 1.7 times larger than the values for IDPs (eq 2).

If the above reasoning is correct, then we ought to obtain reasonably accurate R_g values for globular proteins at high denaturant concentrations using the parameters given in eq 2. After all, at high [C], the unfolded states of globular proteins are statistically equivalent to IDPs. To this end, we simulated the sequence corresponding to the highly charged ubiquitin (PDB ID: 1UBQ) molecule using the current SOP-IDP force field. The estimated R_g for ubiquitin using the SOP-IDP model is 2.51 and 2.55 nm at 150 and 1000 mM monovalent salt concentrations, respectively. These values compare well with the R_g for the DSE of ubiquitin (≈2.56 nm, see, e.g., Figure 4A in Gates et al.⁴⁹ and Figure 2A in Reddy et al.⁵⁰ at high denaturant concentration). The simulations described in Reddy et al.⁵⁰ were carried out using the parameters described in Liu et al.⁴⁸ and taking into account the effect of denaturants using MTM. These new simulations for ubiquitin using the SOP-IDP model are gratifying because the SOP-MTM⁵⁰ and the current model were developed using entirely different methods for different purposes. This shows that the parameters for the IDP model describe well the properties of globular proteins at high denaturant concentrations (8 M GdmCl), in line with the expected statistical equivalence of their ensembles with IDPs. However, as pointed out in the Discussion section, the parameters will not be accurate in the sense found for IDPs for real globular proteins.

Figure 4.

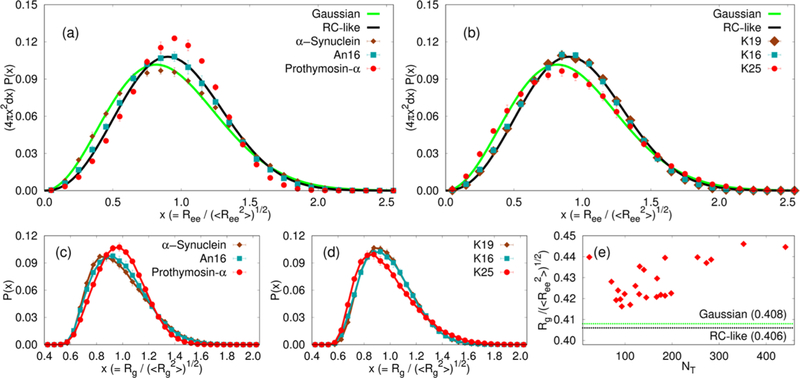
Distributions of the end-end distance (R_ee), scaled by ${\langle R_{\text{ee}}^2\rangle }^{1/2}.$ In order to compare with results for Gaussian chains (solid green line) and RCs (solid black line), we show 4πx²P(x), where $x=R_{\text{ee}}/{\langle R_{\text{ee}}^2\rangle }^{1/2}.$ (a,b) show the distributions for representatives from the sets of non-Tau IDP sequences and Tau sequence constructs, respectively. If a particular IDP behaves strictly as a RC (Gaussian chain) in terms of end-end distance distribution, then the corresponding distribution should coincide exactly with the theoretical result in black (green). (c,d) Distributions of R_g for IDPs described in (a,b) respectively. (e) Ratio of R_g to root-mean-square R_ee for all 24 IDPs described in the article. The dashed horizontal lines in green and black show the ratio for a Gaussian chain and a RC, respectively.

Figure 2.

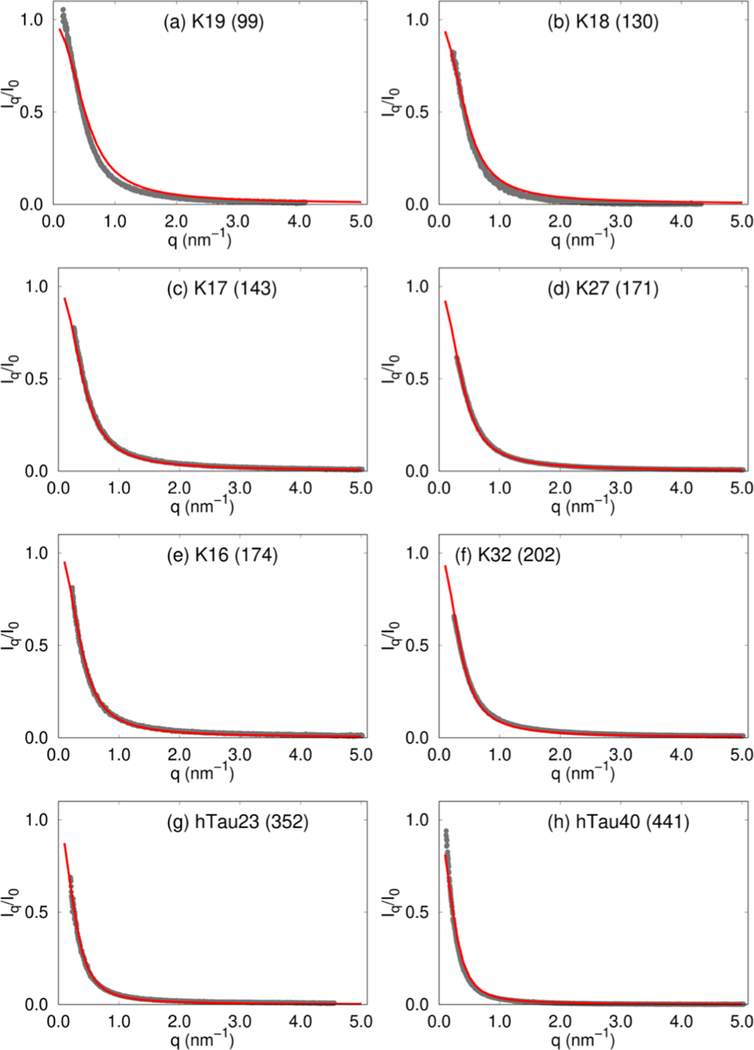
Comparison of SAXS profiles for eight Tau protein constructs. The lengths of the sequences are shown in parentheses in each figure. The color coding is the same as in Figure 1.

Simulations.

We used the LAMMPS molecular dynamics simulator for all the simulations,⁵¹ which were performed using underdamped Langevin dynamics.⁵² The equations of motion were integrated with a time step of 30 fs. To obtain statistically meaningful results, we carried out 10 independent simulations for each system, which we ascertained are sufficient to obtain converged results. Each trajectory was equilibrated for 10⁸ simulation steps, following which the production runs were carried out for 2 × 10⁸ simulation steps for sequence lengths <130 and 5 × 10⁸ simulation steps for longer sequences. Visual molecular dynamics (VMD) was used for visualization, as well as some data analyses.⁵³

In our simulations, all the nonbonded interaction terms in eq 1 were implemented in their truncated and shifted forms, with the cutoff separation for short-range interactions set at 2.4 nm. The cutoff separation for the screened Coulomb potential was consistently chosen to be greater than 4κ⁻¹. The inverse Debye length (κ) was determined from the corresponding monovalent salt concentrations employed in the simulations. We set the dielectric constant, ε = 78.

Data Analyses.

The simulated SAXS profiles were computed using the Debye formula

$$I(q)=\sum _{i=1}^{N_{\mathit{\text{tot}}}}\sum _{j=1}^{N_{\mathit{\text{tot}}}}{f}_i(q)f_j(q)\frac{\sin \left(q{r}_{ij}\right)}{q{r}_{ij}}$$ (3)

with q-dependent structure factors (f(q)), which were reported elsewhere.⁵⁴ In eq 3, N_tot is the total number of beads in a given IDP.

Hydrodynamic Radius, R_h.

Dynamic light scattering and FCS experiments^9,55–57 are routinely used to measure R_h. The value of R_h for a polymer is calculated as the radius of a hard sphere that has the same effective diffusive behavior as the polymer. We computed R_h from the simulations using

$$\frac{1}{R_{\text{h}}}=\frac{1}{N_{\text{tot}}^2}\langle \sum _{i\ne j}\frac{1}{r_{ij}}\rangle$$ (4)

where N_tot is the total number of beads in the IDP model and r_ij is the distance between beads j and i. The angular brackets denote the ensemble average.

Shape Parameters.

We use △ and S to characterize the shapes offolded and unfolded proteins,^58,59 which are defined as

$$\mathrm{\Delta }=\frac{3}{2}\frac{{\sum }_{i=1}^3{\left({\lambda }_i-\overline{\lambda }\right)}^2}{{(3\overline{\lambda })}^2},s=\frac{{\prod }_{i=1}^3\left({\lambda }_i-\overline{\lambda }\right)}{{\overline{\lambda }}^3}$$ (5)

where λ_i are the eigenvalues of the gyration tensor and $\overline{\lambda }=({\lambda }_1+{\lambda }_2+{\lambda }_3)/3.$ ⁵⁸ By definition, $R_{\text{g}}^2=3\overline{\lambda }.$ The △ parameter characterizes the asphericity of conformations and is bound between 0 (perfectly spherical) and 1 (linear). The shape parameter S, which is negative (positive) for oblate (prolate) ellipsoids, satisfies the bound −1/4 ≤ S ≤ 2.⁶⁰

Hierarchical Clustering.

To identify representative conformations populating the IDP ensembles as well as characterize their structural heterogeneity, we performed hierarchical clustering⁶¹ using a pairwise distance metric D_ij, defined as

$$D_{ij}={\left(\frac{1}{N_{\text{pairs}}}\sum _{a,b}|\left(r_{a,b}^i-r_{a,b}^j\right){|}^2\right)}^{1/2}$$ (6)

where r_a,bⁱ and r_a,b^j are the pairwise distances between the C_α atoms a and b in snapshots i and j, respectively, and N_pairs is the total number of C_α pairs. The terminal C_α atoms were excluded in the evaluation of the distance matrix. The Ward variance minimization criterion,⁶² as available within the scipy module, was employed to identify the distinct clusters. The hierarchical organization of clusters was visualized in the form of dendrograms. The structure exhibiting the lowest root-mean-square-deviation with respect to all the other members is identified as the representative structure of a given cluster.

RESULTS

SOP-IDP Model Accurately Reproduces Experimental SAXS Profiles.

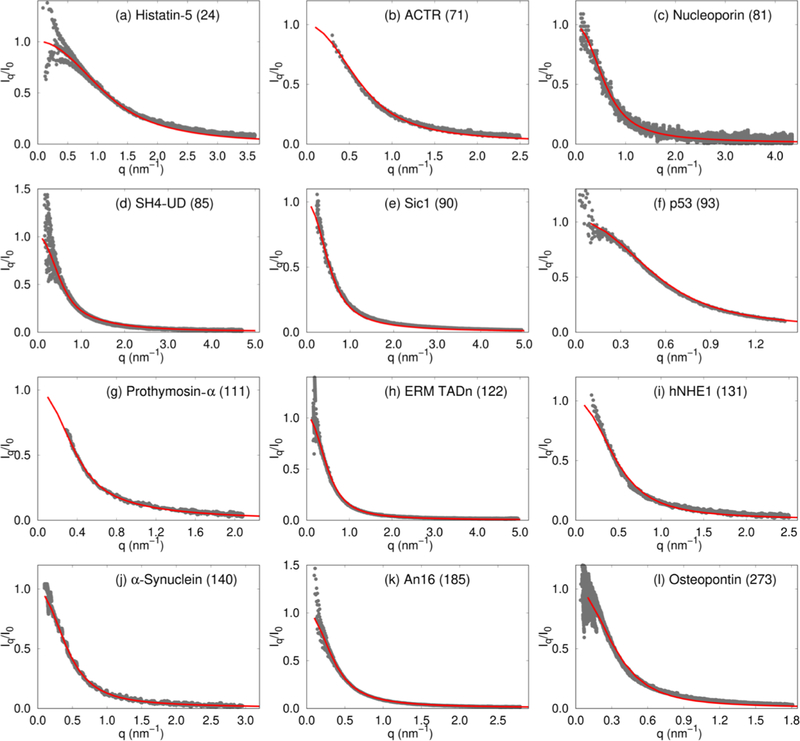
We used the SOP-IDP model (see Methods and Supporting Information for details) to calculate a variety of measurable structural properties for different IDP sequences. Twelve of these, including the initial training set consisting of Histatin-5, ACTR, and hNHE1, are sequences with lengths ranging from 24 to 273 that are unrelated in composition and biological functions.^63,74 The computed scattering profiles, I(q), as a function of the scattering vector q, bear close resemblance to those obtained from SAXS experiments, particularly in the low q regime, which describes the global structure of IDPs (Figure 1). The scattering profiles depicted in the Kratky representation (q²I(q)/I(0) vs q, Figures S1 and S2) are also accurate at low q values. The level of agreement between our simulations and experiment is further quantified by calculating the normalized squared deviation, δ² (Table S2). The δ² values conclusively show that for most sequences, the overlap between the calculated and experimental SAXS profiles remains good up to qR_g ≈ 3, well beyond the range of validity of the Guinier approximation, normally taken to be qR_g ≈ 1.3. Hence, the SOP-IDP model not only accurately describes the global shapes of IDPs, but also likely captures the structural details on smaller length scales. In some cases, the agreement with experimental profiles deteriorates at qR_g > 3, perhaps owing to a combined effect of the increased experimental noise and the coarse-grained nature of the model.

Figure 1.

Comparison of SAXS profiles for 12 IDPs, labeled in the panels. The experimental profiles^63–73 are shown using gray dots and those obtained from simulations are depicted using red curves. The number in parentheses in each figure is N_T, which indicates the number of residues in each IDP. Histatin-5 (a), ACTR (b), and hNHE1 (i) are part of the initial training set.

Wild-Type Tau Proteins and Their Variants.

In notable SAXS experiments, Svergun and co-workers measured the structure factors of the wild-type (WT) 441 residue human Tau protein, as well as artificial sequence constructs generated through truncation and merger of segments.⁷⁵ We simulated 11 such artificial constructs (Supporting Information contains the sequences), in addition to the full length WT sequence using the SOP-IDP model, thus covering the full range of sequence lengths (99 ≤ N_T ≤ 441) considered in the experiments. The scattering profiles for the Tau sequences are shown in Figure 2.

As is evident from the δ² values (Table S2), the simulated and experimental profiles are in good agreement. It should be emphasized that we used only 5 (Histatin-5, ACTR, hNHE1, K32, and hTau40) of the 20 IDPs shown in Figures 1 and 2 to learn the parameters in the model (described in the Supporting Information). Of these, we used only the R_g values for K32 and hTau40 as a constraint to determine a single parameter and not the SAXS profiles. Therefore, the good agreement between the simulated and experimental SAXS profiles, across the sample set, which is diverse in terms of sequence composition, length, and charge densities, is truly an emergent property of our model. In addition, we also show in the Supporting Information that the calculated I(q) as a function of q for the 24-residue RS peptide is in excellent agreement with experiments as are the results based on one of the recently introduced atomically detailed force fields.³⁸ Because of its predictive power over a wide range of sequence space, we anticipate that the SOP-IDP model will be efficacious in applications that require a faithful description of conformational ensembles, among other properties. We have predicted I(q) for two other IDPs in the Supporting Information, which await future validation.

Dependence of Radius of Gyration and Hydrodynamic Radius on Sequence Length.

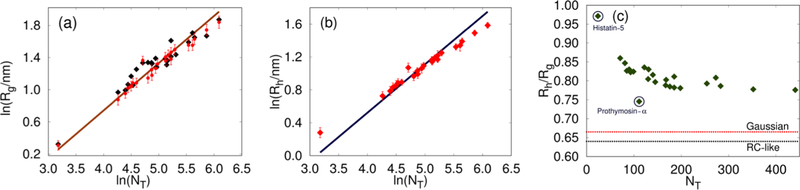
Given the accurate reproduction of the SAXS profiles (Figures 1 and 2) for most IDPs, it is not surprising that the R_g values computed from simulations are also in accord with the experimental values (Figure S3). The scaling of R_g with sequence length (N_T), fitted using the calculated or experimental R_g values, follows $R_{\text{g}}\approx 0.20N_{\text{T}}^{\nu }\text{nm,}\text{with}\nu \approx 0.588$ (Figure 3a), which naively suggests that in the experimental conditions, the IDPs might be in a good solvent. However, this is not the case (see below).

Figure 3.

(a) Values of R_g from simulations (red circles) in comparison with the experimental estimates (black squares).The brown solid line is a fit to the power law: $R_{\text{g}}=R_{\text{g}}^0{N}^{\nu },\text{with}{R}_{\text{g}}^0=0.2\text{nm}\text{and}\nu =\mathrm{0.588.}$(b) Hydrodynamic radii, R_hs, of the IDPs computed from the simulation trajectories (red symbols). The solid blue line is a power law fit: $R_{\text{h}}=R_{\text{h}}^0{N}^{\nu },\text{with}{R}_{\text{h}}^{\widehat{0}}=0.16\text{nm}\text{and}\nu =0.588.$ Both R_g and R_h follow the Flory random coil predictions. (c) Ratio of the hydrodynamic radius to the radius of gyration R_h/R_g obtained from simulations. The outliers, Histatin-5 and Prothymosin-α, are marked with circles. The theoretical limits are marked as dotted lines. Note that there are substantial deviations from the theoretical predictions for an ideal chain and a polymer in a good solvent.

We also calculated the hydrodynamic radii, R_h, from the conformational ensemble using eq 4. The computed values of R_h are shown in Figure 3b and are tabulated in Table S3 of the Supporting Information. Though not equal in magnitude, both R_g and R_h (measurable from NMR for example) should show the same scaling with N_T with identical values of $\nu$ (Figure 3a,b).⁷⁶ However, this scaling behavior does not imply that these IDPs behave as random coils (RC).³² Indeed, the R_h/R_g ratios from simulations deviate substantially from the established theoretical limits, which are 0.665 and 0.640 for an ideal chain and a polymer in a good solvent, respectively (Figure 3c). As N_T increases beyond 300, R_h/R_g becomes insensitive to sequence length (Figure 3c), indicating that the observed deviations may not be due to finite size effects.

Distributions of Radius of Gyration (R_g) and End-End Distances (R_ee).

If the solution conditions used in experiments are good solvents for IDPs, as the R_g and R_h scaling with N_T imply (Figure 3), then it should be reflected in the distribution P(R_ee) of the end-end distance (R_ee), which is rigorously known for a polymer and an ideal chain in a good solvent. Therefore, comparing the simulated distributions to the rigorous functional forms provides a stringent test of the solvent quality. The P(R_ee) distributions, with R_ee measured as the separation between the backbone atoms at the termini, are shown in Figure 4a,b (see also Figures S12 and S13 in the Supporting Information). As a general rule, we find that the P(R_ee) for IDPs closely resemble the theoretical result for a RC. However, for specific sequences, the distributions are more skewed toward the ideal or the Gaussian chain limit.^32,77 The deviations from the RC limit based on the theoretical predictions are likely due to nonlocal electrostatic interactions and sequence composition (see below). Figure 4a shows that the P(R_ee) distribution for Prothymosin-α differs substantially from both the theoretical limits. The deviation can be attributed to the high fraction of charged residues (~58%).

Sequence Matters.

Interesting sequence-specific effects on the P(R_ee)s are also observed for the Tau protein constructs, in spite of their common parent sequence. The P(R_ee)s for the majority of the Tau protein constructs show excellent agreement with the theoretical P(R_ee) for a RC (see Figure 4b for K19 and K16 and also Figure S11 in the Supporting Information) and deviate substantially from that for an ideal chain. Deviations from the RC behavior are found for 5 out of the 12 Tau sequence constructs, namely, K25 (Figure 4b), K23, K44, hTau23, and the WT sequence, hTau40 (Figure S13 in the Supporting Information). The P(R_ee)s for these sequences show increased propensities for smaller R_ee, as can be seen from Figure 4b for the K25 Tau construct. These sequence-specific deviations from average RC-like behavior are also discernible in the distributions of R_g values, as shown in Figure 4c,d. In Figure 4e, the ratio of R_g to root-mean-square R_ee is shown as a function of N_T. This ratio is 0.406 for a RC and 0.408 for a Gaussian chain.³² Interestingly, even for those IDPs, whose P(R_ee) coincides with the theoretical predictions for RCs, the $R_{\text{g}}/{\langle R_{\text{ee}}^2\rangle }^{1/2}$ values deviate from the theoretical limits. This deviation becomes particularly pronounced as N_T increases, most notably for the longer Tau protein constructs.

The Tau sequences, which do not conform to standard polymer behavior, namely, K25, K23, K44, hTau23, and hTau40, do not differ appreciably from the rest of the sequence constructs in terms of conventional sequence compositional parameters that are often used to rationalize their shapes (Table S4 in the Supporting Information). This apparent incongruity could be rationalized in terms of ensemble-averaged contact maps obtained from simulations (see the Discussion section). We document below that the deviation from the theoretical RC limit is in fact a direct manifestation of the sequence-dependent conformational heterogeneity.

Shape Parameters Are Sequence-Dependent.

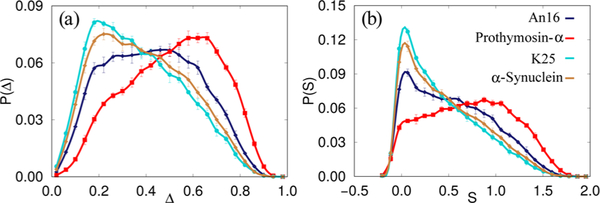
The sequence-specific shape fluctuations of IDPs can be gleaned from the distributions of their shape parameters, Δ and S (see eq 5 in Methods). The calculated values of Δ and S indicate that the conformations of IDPs can be described as prolate ellipsoids (Table S3 in the Supporting Information). In Figure 5, we show the distributions for four IDP sequences, and the rest are included in the Supporting Information (Figures S6-S9).

Figure 5.

Comparison of the distributions of shape parameters (a) Δ and (b) S for An16 (blue, diamonds), α-Synuclein (brown, diamonds), Prothymosin-α (red, squares), and K25 construct of the Tau protein (cyan, circles). Note that the average values of Δ and S for Gaussian chains are 0.52 and 0.87, respectively, and the corresponding estimates for an equivalent polymer in a good solvent are 0.55 and 0.91, respectively. The mean values of both Δ and S for the IDPs are drastically different from the expected theoretical values for standard polymer models.

Figure 5a shows that Prothymosin-α has a high preference for extended conformations, while the structural ensembles for the K25 construct and α-Synuclein are closer to being spherical. In contrast, the shape parameters for An16 are homogeneously distributed, suggesting that elongated and spherical conformations are equally probable. This systematic trend is also reflected in the distributions of S (Figure 5b), where the bias toward prolate conformations is maximal for Prothymosin-α and minimal for K25. The large dispersions in P(Δ) and P(S) make the calculation of the mean values, listed in Table S3 of the Supporting Information, not meaningful (see Supporting Information for elaboration). For comparison, the average values of Δ and S for Gaussian chains are 0.52 and 0.87, respectively, and the corresponding estimates for an equivalent polymer in a good solvent are 0.55 and 0.91, respectively.⁷⁸ Overall, the shape fluctuations of the IDPs allude to a sequence-dependent heterogeneity of conformational ensembles. This aspect, which seems characteristic of the conformations of the IDPs explored here, is discussed in more detail below.

IDP Conformations Are Structurally Heterogeneous.

The distributions of R_g and R_ee, as well as their deviations from RC-like behavior for certain IDPs, suggest that the equilibrium populations of different conformations populating the IDP ensemble depend on the sequence. To illustrate the importance of conformational fluctuations in determining the statistical properties of IDPs, we consider representative examples: Prothymosin-α, α -Synuclein, An16, and the K25 construct from the family of Tau proteins.

To obtain insights into the structural ensembles and reveal their heterogeneous nature, we performed hierarchical clustering of the IDP conformations. Hierarchical clustering not only provides a means to quantify the contrasting features of the structural ensembles, which are evident from the Δ and S distributions, but also aids in visualizing the extent of the underlying conformational heterogeneity. We note that several authors have used “heterogeneity” as a concept to underscore the differences between homopolymers and IDPs.^79–81 More recently, this idea has also been suggested to explain the apparent lack of agreement between the R_g values measured using SAXS and those inferred from FRET experiments.^82–84

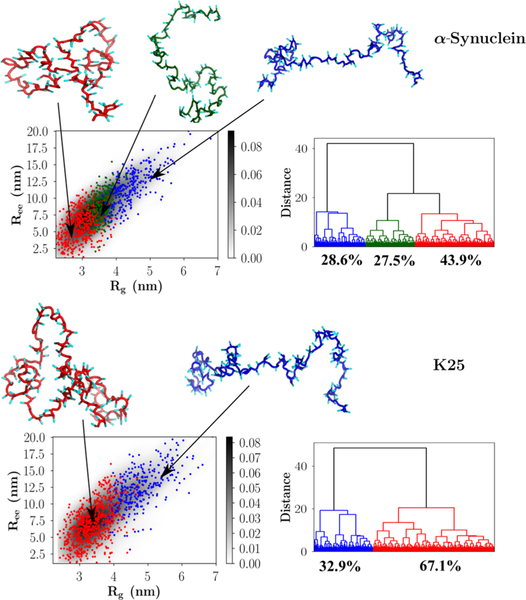
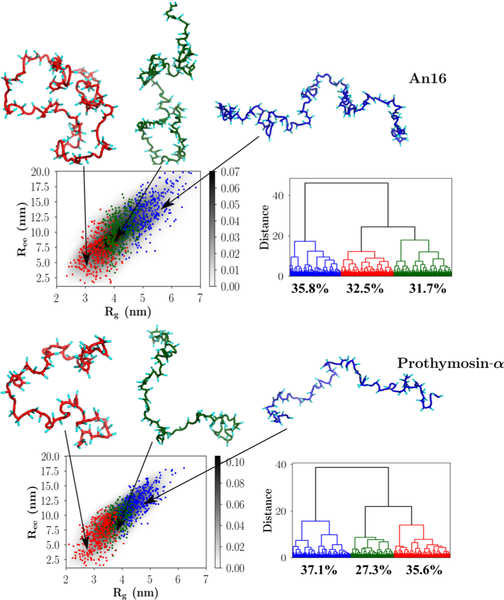
The results from the clustering analyses of α-Synuclein and the K25 Tau construct are shown in Figure 6. The conformational ensembles corresponding to An16 and Prothymosin-α are depicted in Figure 7. The appropriate number of clusters for each sequence was determined by evaluating the largest distance jumps in the corresponding dendrograms using the elbow method.⁸⁵ Figures 6 and 7 show that our clustering scheme is robust, and the various families are clearly demarcated on a two-dimensional projection of the conformational landscape onto the R_g and R_ee coordinates.

Figure 6.

Hierarchical clustering of the IDP conformational ensembles using the Ward variance minimization algorithm. Upper panel: α-Synuclein; lower panel: K25. The conformational landscapes (depicted as probability density plots) projected onto R_g and R_ee are shown on the left of each figure, and the corresponding dendrograms are shown on the right. Representative snapshots from each family, with their backbones rendered in different colors, are shown superposed on the conformational landscape. The same color-coding is used to classify clusters within the dendrograms and the two-dimensional plots. The relative cluster populations are marked below the appropriate dendrogram branches.

Figure 7.

Upper panel: An16; lower panel: Prothymosin-α. The conformational landscapes projected onto R_g and R_ee are shown on the left of each figure, and the corresponding dendrograms are shown on the right. Representative snapshots from each family, with their backbones rendered in different colors, are shown superposed on the conformational landscape. The same color-coding is used to classify clusters within the dendrograms and the two-dimensional plots. The relative cluster populations are marked below the appropriate dendrogram branches.

α-Synuclein and K25.

The equilibrium ensemble of α -Synuclein (Figure 6) partitions into at least three clusters and consists of a large population of relatively compact structures (43.9%). Both semiextended and fully extended structures are populated to a lesser extent, with occupation probabilities of 27.5% and 28.6%, respectively. As is evident from the dendrogram (Figure 6), the equilibrium ensemble of the K25 Tau protein construct is overwhelmingly dominated by relatively compact structures, with the overall contribution being 67.1% to the net population. This trend is also reflected in the two-dimensional conformational landscape, where the region with small R_g and R_ee values is associated with the highest density. The shape of the conformational landscapes for both α-Synuclein and K25, as well as the relative cluster sizes, is commensurate with the observed deviations from a RC-like behavior.

An16 and Prothymosin-α.

The equilibrium ensemble of An16 (Figure 7) consists of approximately equal contributions from relatively compact, semiextended, and extended structures, with the populations being 32.5%, 31.7%, and 35.8%, respectively. The relative populations suggest that no specific conformation is particularly favored for An16, which is consistent with a RC-like behavior.

For the Prothymosin-α sequence, the ensemble of conformations partitions into at least three clusters (Figure 7). Although naively, we expect that, due to the high value of net charge, there would be an overwhelmingly large population of extended structures for Prothymosin-α, clustering of conformations shows otherwise. While conformations exhibiting high R_g and R_ee values contribute maximally to the equilibrium population (37.1%), relatively compact conformations constitute the second largest cluster and account for as much as ≈35.6% of the conformational ensemble. Configurations having intermediate values of R_g and R_ee or the semiextended structures have the lowest occupation probability (27.3%).

Overall, the systematic variations in the heterogeneity of sampled conformations for the different IDP sequences provide a structural explanation for the calculated distributions of R_ee and R_g, which are clearly masked if only their mean values are analyzed. It is indeed remarkable that although the mean values of R_g and R_h adhere to Flory scaling laws for good solvents, there is considerable fine structure in the IDP ensembles, as the clustering analyses demonstrate. It is likely that the plasticity of the conformational ensembles makes it possible for IDPs to carry out diverse functional roles in a bewildering array of metabolic pathways.

DISCUSSION

Enhancements in Local Contact Probability Lead to Deviation from RC Behavior.

Ahallmark of polymers in good solvents (RCs) is that the P(R_ee) must obey the theoretical distribution obtained using polymer theory (see the Supporting Information). The statistical properties of the ensemble of conformations of RCs are purely determined only by chain entropy. Interestingly, we find that although the dependence of R_g on N_T for all the IDPs is consistent with the Flory scaling law (Figure 3), there are deviations in P(R_ee) from the expected theoretical predictions for RCs. For example, we observed such deviations for α-Synuclein, Prothymosin-α, as well as the Tau sequences K25, K23, K44, hTau23, and hTau40, but not for An16. The apparent conundrum can be understood from the dendrograms, which reveal clearly the sequence-dependent conformational heterogeneity. As a result, the conformational ensembles are determined not only by entropy, but also sequence-dependent energy, resulting in higher Boltzmann weights for certain classes of conformations relative to others.

To further illustrate the origin of deviation from the RC behavior, we calculated ensemble-averaged contact maps from simulations using the SOP-IDP energy function, as well as the corresponding RC limit. We define the difference contact maps as

$$\mathrm{\Delta }C(i,j)=C_{\text{IDP}}(i,j)-C_{\text{RC}}(i,j)$$ (7)

where C_IDP(i,j) is the contact probability between residues i,j of an IDP obtained from simulations and C_RC(i,j) is the same contact probability obtained by specifically neglecting the contributions because of the last four terms in eq 1 (see the Methods section). Thus, Δ C(i,j) is a measure of the increased or decreased probability of contact between two residues, compared to an equivalent RC. Both C_IDP(i,j) and C_RC(i,j) were computed using the coordinates of the SC beads, including glycine and alanine. We assume that a contact exists if the distance between two residues is ≤0.8 nm.

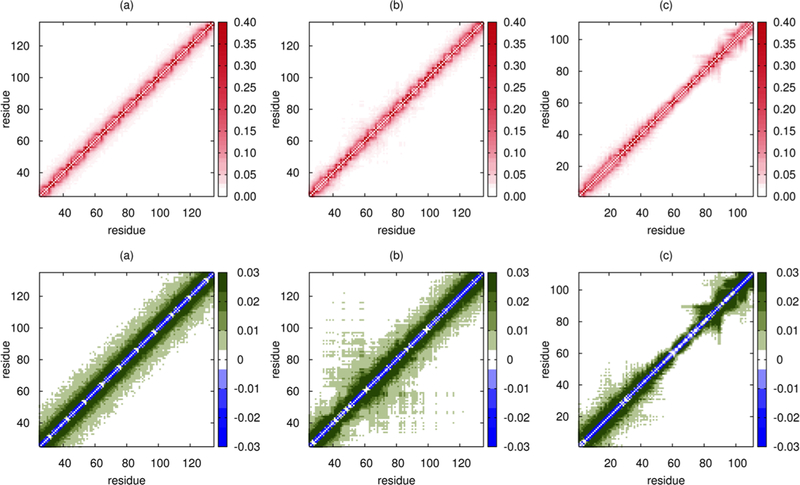
The three contact maps shown in Figure 8 represent characteristically divergent scenarios.

Figure 8.

Contact maps for (a) An16, (b) K25 Tau construct, and (c) Prothymosin-α. The top panel shows the contact maps for the three IDPs calculated using the SOP-IDP simulations. To illustrate the deviations from the corresponding RC contact map, we plot the difference map using eq 7 (bottom panel). While the contact map for An16 reveals no sequence-driven propensities for local structures, the latter two clearly highlight the presence of local domains that are more compact compared to the rest of the sequence. The nearly RC-like behavior of the mid-segment of Prothymosin-α, in stark contrast to the other IDPs studied (see also Figures S14–S16 in the Supporting Information), rationalizes the peripheral contribution of compact conformations observed for it in the hierarchical clustering of the conformational ensemble. Each of the contact maps depicts a segment of 111 residues (N_t for Prothymosin-α) for optimal visual comparison. The full ranges for (a) and (b) are shown in Figure S16 in the Supporting Information.

An16.

The contact map for An16 (Figure 8a) shows a uniform enhancement in contacts between residues proximate along the sequence over the entire sequence length compared to an equivalent RC polymer. This can readily be understood as a consequence of the nonspecific attractive interactions between nonbonded residues, with sequence-specific interactions (final term in eq 1) playing a relatively minor role. Without the formation of stable local structures, such enhanced contacts do not alter the RC-like nature of the polymer, as also evidenced by the RC-like P(R_ee) distribution for An16 (Figure 4).

K25.

The results in Figure 8b show that the K25 Tau construct contains a locally compact segment, with preferentially enhanced contacts compared to the rest of the sequence. The segment with locally enhanced contacts is also present in the WT Tau sequence (hTau40), as well as the K25, K23, K44, and hTau23 constructs (shown in Figures S15 and S16). We infer that the presence of this region, which results in the formation of the locally preferred structures, leads to the observed deviations from the RC-like behavior for the five sequence constructs.

Prothymosin-α.

In this IDP (Figure 8c), the two termini adopt locally compact structures, while the mid-segment of the IDP closely conforms to the RC limit. For this IDP, electrostatic interactions dominate the conformational properties, and the termini, with both positively and negatively charged residues, undergo local compaction. However, both the termini are overall negative, leading to unfavorable local electrostatic interactions. Both these effects together lead to the predominance of extended as well as relatively compact conformations in the conformational ensemble (Figure 7).

Structural Ensemble of a-Synuclein.

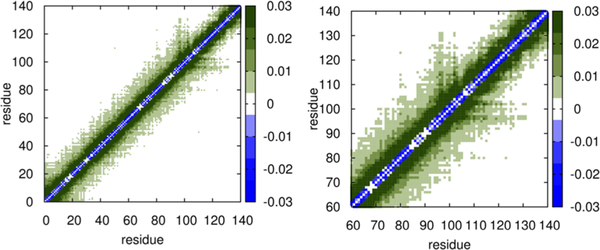
Our simulations provide considerable insights into the structural details of α-Synuclein, which has been extensively investigated using a variety of experimental methods. The calculated hydrodynamic radius reported in Table S3 (R_h = 2.89 ± 0.17 nm) is in very good agreement with the experimental value (R_h = 2.74 ± 0.04 nm) obtained using pulse field gradient NMR.⁸⁶ Similarly, the calculated R_g value is in close agreement with the experimental estimate (see Table S3), with the difference between simulation and experimental estimates being about 12%. More importantly, our simulations provide a complete characterization of the subtle structural details that are difficult to glean from experiments. First, the segregation of the conformational landscape for α-Synuclein is in accord with recent experimental works ^87–90 that hinted at the presence of distinct conformational states in the structural ensemble, with compact structures having the highest population at equilibrium. Specifically, the difference contact map (Figure 9) reveals that there are long-range tertiary interactions between residues in the acidic C-terminal region and the nascent polypeptide-associated complex (NAC) domain in α-Synuclein. Previous works^91,92 suggest that such interactions, which protect the NAC region against fibrillation, play a key role in impeding aggregation. Interestingly, tertiary contacts between residues in the neighborhood of 74 and 94, first noted in experiments using electron transfer,^93,94 are captured in the contact maps presented in Figure 9. Because of large conformational fluctuations of such tertiary interactions, which could serve as initiating nucleation sites for aggregation, the probability of forming such contacts is not substantial but detectable.

Figure 9.

Difference contact maps for α-Synuclein. Left: whole sequence; Right: zoomed-in view highlighting the contacts between the C-terminal and the NAC regions.

Sequence-specific deviations from the RC limit highlight the heterogeneity in the population of IDPs. We reiterate that it cannot be trivially ascertained that water (or solution conditions used in experiments) acts uniformly as a good solvent over the entire peptide sequence of an IDP. To classify IDP sequences as polymers in a good solvent, based solely on estimates of the Flory exponent $\nu$ with modest variations in N_T, is erroneous, which severely undermines the heterogeneity of their conformations.

Limitations of the SOP-IDP Model.

Although the SOP-IDP model is remarkably successful in capturing many aspects of the structural ensembles of even large IDPs, like all other empirical potentials, it is not without limitations. The SOP-IDP force field does reproduce quantitatively the radius of gyration of globular proteins at high denaturant concentrations, thus showing that the model is accurate in describing statistical properties of disordered states. It is unlikely that the model could predict the folding properties of even small globular proteins (e.g., the heat capacity) as a function of denaturant concentration as accurately as we have done here for I(q) for IDPs.

Recently, the goal^35,37,38 of creating a transferable force field, which yields highly accurate results for both globular proteins and IDPs from essentially sequence alone, has been a motivating factor to drastically alter the currently popular force fields. Although laudable, achieving this goal is a daunting task because it is tantamount to solving all aspects of the protein folding problem and issues in IDPs in one fell swoop. In these studies,^35,37,38 which use three entirely different empirical energy functions, the calculated I(q)s for the 24-residue RS peptide (see the Supporting Information for details) and the 71-residue ACTR IDPs are in very good agreement with experiments. In addition, the R_g values for a few IDPs calculated using a force field³⁷ that differs greatly from the ones used by others^35,38 agree with experimental measurements. However, for foldable peptides and miniproteins, the agreement between simulations and experiments is not satisfactory, which means the stated goal of creating a transferable force field has not been accomplished. This illustrates the difficulty in building a truly “universal” potential within the limitations inherent in additive classical force fields, as articulated elsewhere.³⁸ With the possible exception of a recent study of IDPs,³⁷ applications (especially to globular proteins) are restricted to small N_T values, thus leaving open the question of the extent of transferability for longer N_T, even when restricted to IDPs. It is indeed the case that a large number of energy functions, at all levels of coarse graining, could be constructed for successful applications to possibly only a certain class of proteins.

The SOP-IDP force field is not designed to be a universal potential that can simultaneously describe accurately the measurable properties of both IDPs and globular proteins. We have shown that the SOP-IDP force field is unique in its accuracy for IDPs, and provides a new perspective for describing their sequence-specific properties (and by statistical equivalence the DSE of globular proteins at high denaturant concentrations). However, for structural characterization of folded proteins under physiological conditions, as well as studies of various aspects of protein folding, the parameters described in Liu et al.⁴⁸ are appropriate. The one advantage is that the SOP model has only three independent parameters, and hence, a broad range of applications could be explored to assess its limitations.

Additional Tests.

We have taken advantage of the availability of experimental data and results from atomic detailed simulations of Wu et al.³⁸ to carry out simulations for the 24-residue RS peptide using the SOP-IDP model. Wu et al.³⁸ used the RSFF2+/TIP4P-D force field to calculate the scattering profile (I(q) vs q) for the RS peptide and found it to be in excellent agreement with SAXS experiments. We used the current model to simulate the RS peptide and find that the I(q)s from the SOP-IDP model, the all-atom simulations, and the measured SAXS profile nicely overlap with each other (see Figure S4 in the Supporting Information). In the Supporting Information, we also illustrate additional applications to the 20-residue GS10 and the 26-residue HIV-1 Rev peptides for which R_g values (but not SAXS profiles) have been reported by Wu et al.³⁸ The results using coarse-grained and RSFF2+/TIP4P-D force fields are in good agreement. It should be pointed out that a similar level of accuracy could be obtained using the Flory formula given in the caption of Figure 3a, without the need for any simulations, which shows that the success of a force field can only be assessed by comparing the simulated and measured SAXS profiles. The predictions in the Supporting Information as well as the results in the main text show vividly that the proposed SOP-IDP energy function is highly efficacious in obtaining statistical properties of 27 IDPs of which 5 were used in the training set.

CONCLUSIONS

Given the multifarious roles that IDPs play in a variety of cellular functions, there is an urgent need to decipher the physical principles governing IDP structure, and dynamics, at the molecular level. We have introduced a robust coarse-grained model for IDPs (SOP-IDP), which quantitatively reproduces the SAXS profiles for a diverse range of sequences and length varying from 24 to 441 residues. The parameters of the force field were calibrated via a learning procedure, using a few test sequences, and once optimized they were unaltered for 24 other IDP sequences of varying composition, charge densities, and sequence lengths.

Although globally the sizes of the IDPs follow the well-known Flory scaling law obtained for synthetic polymers, equilibrium populations of different substates strongly depend on the precise IDP sequence. In the conformational substates of IDPs, we find evidence for specific weak intramolecular interactions between certain residues, giving rise to population of conformations with local structures. We also show that the adaptability of IDPs arising from their conformational plasticity, which cannot be anticipated using sequence characteristics (such as fraction of positively and negatively charged residues) alone,²⁷ is important in their ability to interact with a multitude of partners to form fuzzy complexes stabilized by specific intermolecular interactions. Our work lends further credence to an existing viewpoint that the observed sequence-dependent conformational heterogeneity determines the functions of IDPs. The accuracy of the computations in describing the equilibrium ensemble of a number of IDPs sets the stage for describing IDP- RNA interactions, which is needed to understand ribonucleo-protein stress granule formation in eukaryotes, as well as quantitative descriptions of the formation of biomolecular condensates at the molecular level.