Summary
Much of survival analysis is concerned with absorbing events, i.e., subjects can only experience a single event such as mortality. This article is focused on non-absorbing or recurrent events, i.e., subjects are capable of experiencing multiple events. Recurrent events have been studied by many; however, most rely on the restrictive assumptions of linearity and proportionality. We propose a new method for analyzing recurrent events with Bayesian Additive Regression Trees (BART) avoiding such restrictive assumptions. We explore this new method via a motivating example of hospital admissions for diabetes patients and simulated data sets.
Keywords: Bayesian Additive Regression Trees, Cumulative intensity, Electronic health records (EHR), Machine learning, Non-proportional, Variable selection
1. Introduction
Survival analysis is typically concerned with absorbing events, i.e., subjects can only experience a single event such as mortality. This article is focused on non-absorbing or recurrent events, i.e., subjects are capable of experiencing multiple events such as hospital admissions. We advocate using all of the events rather than restricting to the first event, if any; the first event will produce a valid inference, but only at the cost of lost power and estimation inefficiency.
In this article, we follow the precedent of the recurrent events literature by using the term intensity instead of hazard, but note that the terms are generally interchangeable. Recurrent events have been studied by many; however, most rely on the Cox proportional intensity model with its precarious restrictive assumptions of linearity and proportionality (Andersen and Gill, 1982; Wei and others, 1989; Kalbfleisch and Prentice, 2002; Hosmer and others, 2008); i.e., the intensity is 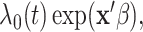 where
where 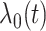 is the non-parametric baseline intensity multiplied by the term
is the non-parametric baseline intensity multiplied by the term 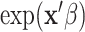 stipulating both linearity in the covariates and multiplicative proportionality of the baseline intensity. We propose a new method for recurrent events that does not rely on such restrictive assumptions. We explore this new method via a motivating example of hospital admissions for diabetes patients.
stipulating both linearity in the covariates and multiplicative proportionality of the baseline intensity. We propose a new method for recurrent events that does not rely on such restrictive assumptions. We explore this new method via a motivating example of hospital admissions for diabetes patients.
Excess health care utilization is a cause of concern in the United States. For example, the World Bank estimates that health care expenditures in the United States were approximately 17% of Gross Domestic Product in 2014 while no other developed country was above 12% (World Bank, 2015). Even so, the US health care system is prone to extremes: some patients receive too much care while others, not enough (Fisher and others, 2009; Smith and others, 2013). Concerns such as these triggered the Affordable Care Act of 2010 (ACA) with provisions such as the Medicare Hospital Readmissions Reduction Program (Singh and others, 2014; Zuckerman and others, 2016).
Our purpose in studying health care utilization is to determine if there are ways to reduce unneeded services via preventive measures. In this undertaking, we look at the entire record of health care utilization with all hospital admissions (including readmissions) to distinguish prudent and excessive health care utilization. In this investigation, we are not disputing whether a given patient should have been admitted or not, i.e., admission practices are not assumed to have been inappropriate or unnecessary. Rather, we want to identify risk factors that foreshadow preventable or avoidable hospital admissions; these factors could be prudently managed via outpatient clinical care. Not taking advantage of these mitigation opportunities will most likely lead to excessive utilization such as future admissions.
We focus on the collected electronic health records (EHR) for a cohort of diabetes patients in a unified health care system including a network of hospitals and affiliated outpatient clinics. EHR databank systems have been used by hospitals for decades. More recently, the American Recovery and Reinvestment Act of 2009 (ARRA) incentivized the usage of EHR systems in outpatient clinics and physician offices (Blumenthal and Tavenner, 2010) transforming the EHR into a near-complete health ledger for patients cared for by a single health care system.
The modern EHR is an omnibus of current and historical digital health information. EHR data are often paired with digital billing information; therefore, we use the term EHR in the widest possible sense. We intend to estimate the relative intensity, or relative risk, of a hospital admission based on data routinely available in the EHR such as demographics (age, gender, and race), body size (height, weight, and body mass index), primary insurance provider (if any), billing, vital signs, comorbidities/complications, procedures/surgeries, and pharmaceutical prescriptions; note that some of these covariates are static like race while most are longitudinally dynamic.
In Section 2, we discuss our new Bayesian Additive Regression Trees (BART) methodology for recurrent events and our motivating example. Section 3 displays the results of our application. Section 4 discusses our findings and conclusions. The last section summarizes the supplementary materials to this article.
2. Methods
Hospital admissions can be handled by survival analysis, specifically via recurrent events. Recurrent events have traits of time-to-event data such as right censoring; the main difference being that rather than potentially experiencing a single absorbing event, each patient is free to experience multiple events during their observation period. For this application, we considered extending random survival forests (Ishwaran and others, 2008) to recurrent events. Although, random survival forests do not suffer from restrictive assumptions, they do not naturally provide uncertainty estimates for quantities of interest such as the cumulative intensity. Conversely, informed by earlier research with BART on survival analysis (Sparapani and others, 2016), we concluded that extending BART to recurrent events is a more natural choice.
The observation period can be terminated by an absorbing event like death or with right censoring at the end of follow-up. With respect to the recurrent event of interest, a death may be either independent or dependent: independent deaths can be considered independent censoring while dependence is more challenging (Cook and Lawless, 1997; Ghosh and Lin, 2000; Wang and others, 2001; Ghosh and Lin, 2003). When likely dependent deaths are relatively rare, we make the simplifying assumption that deaths are independent of the event: often a reasonable approximation since their impact will likely be small. When dependent deaths are more common, then it will be more appropriate to base the analysis on the competing risks paradigm; for a brief discussion of recurrent events and competing risks with BART, see Appendix F of the of the Supplementary material available at Biostatistics online.
2.1. Bayesian Additive Regression Trees (BART)
In this article, we propose to model hospital admissions with a new non-parametric recurrent events framework based on BART extending earlier work on survival analysis of absorbing events with BART (Sparapani and others, 2016). BART is a Bayesian non-parametric, ensemble sum of trees predictive model for continuous, dichotomous, categorical, and time-to-event outcomes. Furthermore, BART is a machine learning black-box model of the outcome via an arbitrary random function, 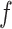 , of the covariates. So-called black-box models generate functions of the covariates so complex that interpreting the internal details of the fitted model is generally abandoned in favor of assessing it by evaluations of the fitted function,
, of the covariates. So-called black-box models generate functions of the covariates so complex that interpreting the internal details of the fitted model is generally abandoned in favor of assessing it by evaluations of the fitted function, 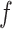 , at chosen values of the covariates.
, at chosen values of the covariates.
Evaluating predictive modeling often entails comparisons of predictive performance for in-sample vs. out-of-sample data elements; in-sample refers to elements that are members of the training data used to fit the model while out-of-sample are not. The term over-fitting is used when the model fits the training data too well at the expense of generalizability to unseen out-of-sample data, e.g., over-fitting can be accomplished by over-parameterizing the model. BART’s out-of-sample predictive performance is generally equivalent to, or exceeds that, of alternatives like lasso or other black-box models such as gradient boosting, neural nets with one hidden layer and random forests (Chipman and others, 2010). BART is in the class of ensemble predictive models that typically do not over-fit to the training data (Kuhn and Johnson, 2013); more details of the BART prior are provided in Section 2.1.1 below.
Essentially, BART is a Bayesian non-linear model with all the advantages of the Bayesian paradigm such as posterior inference including point and interval estimation. Conveniently, BART is scalable to a large number of covariates and naturally incorporates variable selection (Linero, 2016); it does not require the covariates to be re-scaled; neither does it require pre-specifying the functional relationship of the covariates nor their interactions.
The BART prior specifies a flexible unknown function, 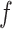 , which is a randomly generated fit to the data via the posterior. BART relies on Markov chain Monte Carlo (MCMC) to sample
, which is a randomly generated fit to the data via the posterior. BART relies on Markov chain Monte Carlo (MCMC) to sample 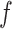 . As with other Bayesian methods employing MCMC, posterior convergence diagnostics are recommended for BART especially with large data sets; see Appendix E of the Supplementary material available at Biostatistics online for a primer on convergence diagnostics with BART.
. As with other Bayesian methods employing MCMC, posterior convergence diagnostics are recommended for BART especially with large data sets; see Appendix E of the Supplementary material available at Biostatistics online for a primer on convergence diagnostics with BART.
2.1.1. Introduction to trees and the BART prior
A binary tree is a type of directed acyclic graph consisting of nodes and the edges connecting nodes. We describe binary trees, which we simply call trees hereafter, by allusion to leafy trees. The direction of tree growth is up as indicated by the numerical progression of node numbering, 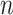 , and tier height,
, and tier height, 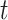 . Each node is either a terminal leaf node, or it is a parent branch node that bifurcates into two child nodes connected by limb edges. All trees have a root node,
. Each node is either a terminal leaf node, or it is a parent branch node that bifurcates into two child nodes connected by limb edges. All trees have a root node, 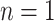 , at tier
, at tier 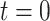 ; the root is either a degenerate tree consisting only of a leaf or a branch leading up to the next tier,
; the root is either a degenerate tree consisting only of a leaf or a branch leading up to the next tier, 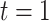 , with a left node,
, with a left node, 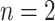 , and a right node,
, and a right node, 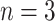 . The nodes are uniquely numbered at tier
. The nodes are uniquely numbered at tier 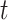 as
as 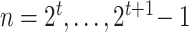 . At tier
. At tier 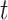 , a branch at
, a branch at 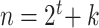 leads upward to tier
leads upward to tier 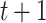 to the left,
to the left, 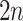 , and to the right,
, and to the right, 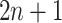 . We can completely describe a tree as
. We can completely describe a tree as 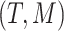 where the set of branches is denoted by
where the set of branches is denoted by 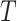 and the set of leaves by
and the set of leaves by 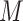 . See the diagram below where we have a tree with two branches at nodes
. See the diagram below where we have a tree with two branches at nodes 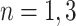 and three leaf nodes:
and three leaf nodes: 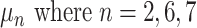 .
.
To turn a tree into a regression function, each branch is associated with a decision rule and each leaf with an outcome value, e.g., in Figure 1, 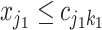 , is a branch decision at node
, is a branch decision at node 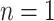 : if true go up to the left; otherwise, go up to the right. The decision rules partition the covariate space such that for each set of covariates a corresponding outcome value is defined. Let the function
: if true go up to the left; otherwise, go up to the right. The decision rules partition the covariate space such that for each set of covariates a corresponding outcome value is defined. Let the function  assign an outcome value such that
assign an outcome value such that 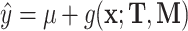 based on a vector of covariates,
based on a vector of covariates, 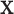 , and the tree,
, and the tree, 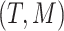 , where
, where 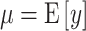 .
. 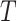 represents a branch decision rule of the form
represents a branch decision rule of the form 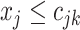 ; if true take the left branch up to the next tier, otherwise the right. So,
; if true take the left branch up to the next tier, otherwise the right. So,  is composed of ordered triples,
is composed of ordered triples,  :
:  for the node,
for the node,  for covariate
for covariate 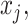 and
and 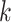 for the cutpoint
for the cutpoint 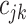 .
. 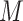 represents leaves and is composed of ordered pairs,
represents leaves and is composed of ordered pairs, 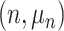 :
: 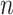 for the node and
for the node and 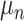 for the outcome value.
for the outcome value.
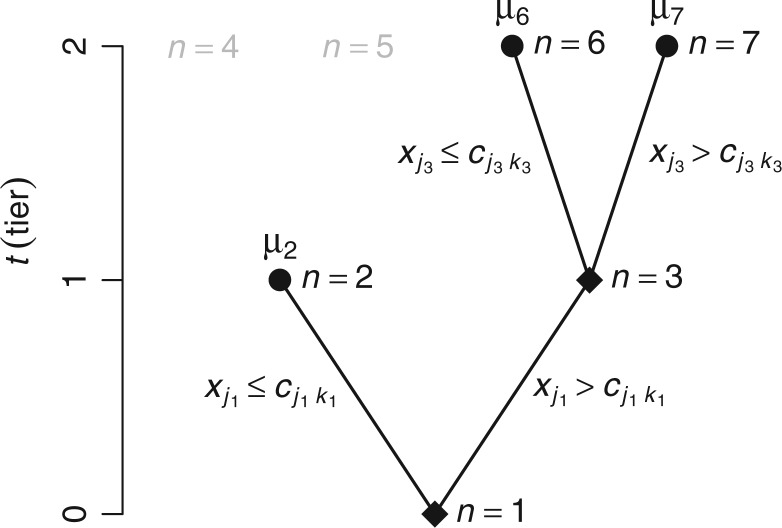
Fig. 1.
This is a diagram of a binary regression tree. On the vertical axis, we have the tier, 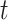 , i.e., in each tier, we may have nodes
, i.e., in each tier, we may have nodes 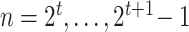 . This tree has branch decisions (diamonds) at nodes
. This tree has branch decisions (diamonds) at nodes 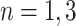 and terminal leaf nodes (circles) at
and terminal leaf nodes (circles) at 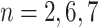 with corresponding output values of
with corresponding output values of 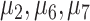 . At branches
. At branches 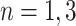 , the splitting variable is
, the splitting variable is 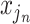 and the cutpoint is
and the cutpoint is  , i.e., if
, i.e., if 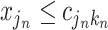 , then go to node
, then go to node 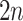 , otherwise,
, otherwise, 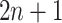 . Note that nodes
. Note that nodes 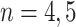 (in gray) do not appear since node
(in gray) do not appear since node 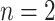 is a leaf. This tree is denoted by
is a leaf. This tree is denoted by 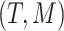 and a corresponding regression function
and a corresponding regression function 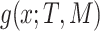 where
where 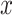 is a vector of covariates,
is a vector of covariates, 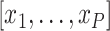 .
. 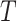 represent the branch decision rules of the form
represent the branch decision rules of the form 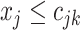 and is composed of ordered triples,
and is composed of ordered triples, 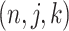 :
: 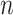 for the node,
for the node, 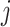 for covariate
for covariate 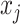 and
and 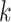 for the cutpoint
for the cutpoint 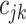 . So, here we have
. So, here we have 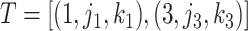 .
.  represents leaves and is composed of ordered pairs,
represents leaves and is composed of ordered pairs, 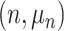 :
: 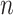 for the node and
for the node and 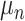 for the outcome value. So,
for the outcome value. So, 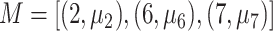 . The regression function,
. The regression function, 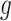 , climbs the tree. For example, suppose
, climbs the tree. For example, suppose 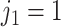 and
and  , then
, then 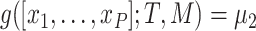 .
.
BART is an ensemble sum of regression trees: 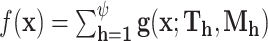 where
where 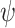 is a prior parameter that is often chosen to be either 50, 100, or 200; to avoid over-fitting, 50 is recommended (Bleich and others, 2014). For a continuous outcome, we have the following BART regression on the covariates:
is a prior parameter that is often chosen to be either 50, 100, or 200; to avoid over-fitting, 50 is recommended (Bleich and others, 2014). For a continuous outcome, we have the following BART regression on the covariates: 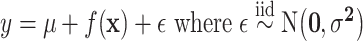 ;
; 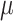 is a prior parameter centering
is a prior parameter centering 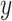 usually set to
usually set to 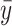 ; the unknown random function and the error variance follow the BART prior expressed as
; the unknown random function and the error variance follow the BART prior expressed as 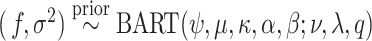 (N.B. the BART prior parameters are discussed below except
(N.B. the BART prior parameters are discussed below except 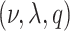 for
for 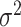 ; for these, see Chipman and others, 2010). For a binary outcome, the BART regression model is:
; for these, see Chipman and others, 2010). For a binary outcome, the BART regression model is:
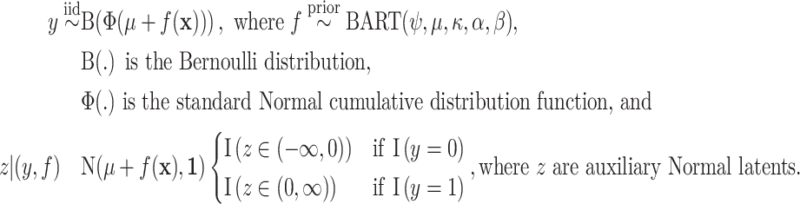 |
We employ an efficient Normal latent sampling technique (Albert and Chib, 1993; Robert, 1995); or an alternative Logistic latent formulation (Holmes and Held, 2006; Gramacy and Polson, 2012) as discussed in Appendix E of the Supplementary material available at Biostatistics online. The parameter 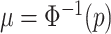 is used to center the latents,
is used to center the latents, 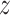 , around the probability of an event
, around the probability of an event 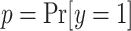 , e.g.,
, e.g., 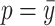 .
.
To describe the BART prior, we employ generic bracket notation (Gelfand and Smith, 1990) for densities/mass functions, e.g., suppose that 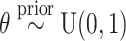 , then
, then 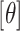 represents the prior density that is standard uniform,
represents the prior density that is standard uniform, 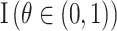 ; similarly,
; similarly, 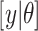 is the likelihood function and
is the likelihood function and 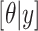 is the posterior density/mass function. We decompose the BART prior into the tree prior,
is the posterior density/mass function. We decompose the BART prior into the tree prior, 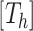 , the leaf prior,
, the leaf prior, 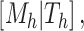 and the error variance prior,
and the error variance prior, 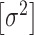 (but
(but 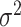 is for continuous outcomes only and not considered further). We assume that the joint tree/leaf priors are i.i.d., i.e.,
is for continuous outcomes only and not considered further). We assume that the joint tree/leaf priors are i.i.d., i.e., 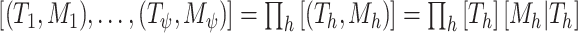 .
.
There are three components for 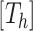 . The first is a regularity component for the probability that any node
. The first is a regularity component for the probability that any node 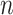 is a branch, denoted by
is a branch, denoted by 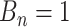 , rather than a leaf,
, rather than a leaf, 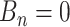 , given tier,
, given tier, 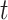 ; the prior is:
; the prior is: 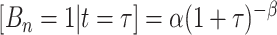 where the default parameter settings are
where the default parameter settings are 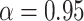 and
and 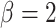 (for a discussion of these parameters, see Chipman and others, 1998). Due to the regularity tree-branching penalty, in prior probability, the branch total for a single tree is likely just 1 or 2, i.e., each tree has few parameters (branches and leaves) playing a small part in the overall fit as desired. Next there is a component for the choice of a splitting variable,
(for a discussion of these parameters, see Chipman and others, 1998). Due to the regularity tree-branching penalty, in prior probability, the branch total for a single tree is likely just 1 or 2, i.e., each tree has few parameters (branches and leaves) playing a small part in the overall fit as desired. Next there is a component for the choice of a splitting variable, 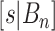 ; this prior is discrete uniform given a branch, otherwise no splitting variable is necessary (denoted
; this prior is discrete uniform given a branch, otherwise no splitting variable is necessary (denoted 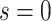 ):
): 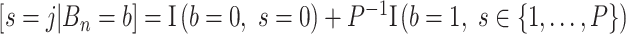 , where
, where 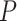 is the number of covariates (note that a Dirichlet prior is worth considering especially when
is the number of covariates (note that a Dirichlet prior is worth considering especially when  is large; see Linero, 2016). The last tree component,
is large; see Linero, 2016). The last tree component, 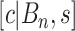 , selects a cutpoint,
, selects a cutpoint, 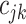 ; this prior is discrete uniform given a branch, otherwise no cutpoint is necessary (denoted
; this prior is discrete uniform given a branch, otherwise no cutpoint is necessary (denoted 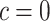 ):
): 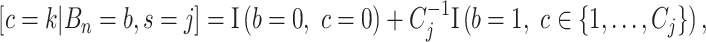 where
where 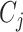 is the number of cutpoints for variable
is the number of cutpoints for variable 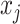 . To summarize, the tree prior is
. To summarize, the tree prior is 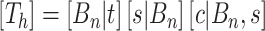 .
.
Given a tree, 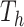 , there is a prior on its leaf values,
, there is a prior on its leaf values, 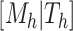 . We assume a priori the leaves are i.i.d. given
. We assume a priori the leaves are i.i.d. given 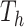 , i.e.,
, i.e., 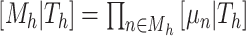 . Let
. Let 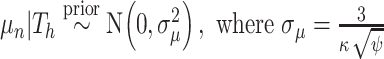 and
and 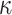 is recommended to be between 1 and 3 with 2 being the default (this setting can chosen by cross-validation; for more, see Chipman and others, 2010). That finalizes the description of the BART prior. Based on this prior, posterior sampling of
is recommended to be between 1 and 3 with 2 being the default (this setting can chosen by cross-validation; for more, see Chipman and others, 2010). That finalizes the description of the BART prior. Based on this prior, posterior sampling of 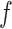 given the data are performed via MCMC, however, those details are beyond the scope of this discussion (see Chipman and others, 1998, 2010).
given the data are performed via MCMC, however, those details are beyond the scope of this discussion (see Chipman and others, 1998, 2010).
2.2. Recurrent events and BART
Consider recurrent events data in the form: 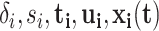 where
where 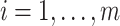 indexes subjects;
indexes subjects; 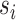 is the end of the observation period (due to death,
is the end of the observation period (due to death, 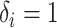 , or censoring,
, or censoring, 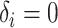 ) for subject
) for subject 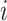 ;
; 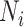 is the number of events experienced by subject
is the number of events experienced by subject 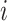 ;
; 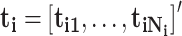 , and
, and 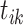 is the event start time of the
is the event start time of the 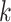 th event (let
th event (let 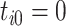 );
); 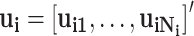 and
and 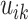 is the event end time of the
is the event end time of the 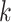 th event (let
th event (let 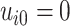 ); and
); and 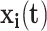 is a vector of time-dependent covariates. Both start and end times of events are necessary to define risk set eligibility for non-absorbing events like readmissions since, by definition, patients currently hospitalized cannot be readmitted. Events that are instantaneous (or nearly so) are a special case where the end times are simply ignored.
is a vector of time-dependent covariates. Both start and end times of events are necessary to define risk set eligibility for non-absorbing events like readmissions since, by definition, patients currently hospitalized cannot be readmitted. Events that are instantaneous (or nearly so) are a special case where the end times are simply ignored.
We denote the 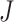 collectively distinct event start and end times for all subjects by
collectively distinct event start and end times for all subjects by
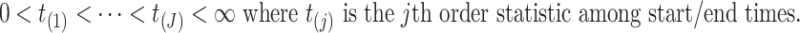 |
For convenience, 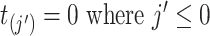 . Note that
. Note that 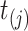 are constructed from all event start/end times for all subjects, but for some subjects they may be censoring times.
are constructed from all event start/end times for all subjects, but for some subjects they may be censoring times.
Now consider binary event indicators 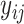 for each subject
for each subject 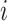 at each distinct time
at each distinct time 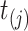 up to the subject’s last observation time
up to the subject’s last observation time 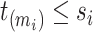 with
with 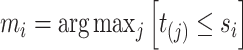 , i.e.,
, i.e., 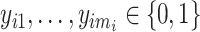 . At time
. At time 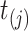 , we intend to model the probability of an event,
, we intend to model the probability of an event, 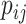 , by the covariates,
, by the covariates, 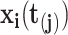 , the number of previous events experienced for subject
, the number of previous events experienced for subject 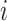 , denoted by
, denoted by  , and the time since the last event, if any, or sojourn time, for subject
, and the time since the last event, if any, or sojourn time, for subject 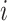 ,
, 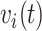 . Let
. Let  be the number of events for subject
be the number of events for subject 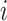 just prior to time
just prior to time 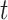 and note that
and note that 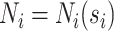 . Let
. Let 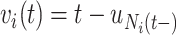 be the sojourn time. Notice that we can replace
be the sojourn time. Notice that we can replace 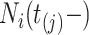 with
with 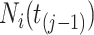 since, by design, the state of information available at time
since, by design, the state of information available at time 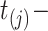 is the same as that available at
is the same as that available at 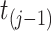 . We then denote
. We then denote 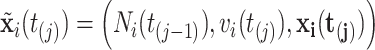 . Assuming constant values for covariates,
. Assuming constant values for covariates, 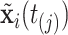 , and constant intensity in the interval
, and constant intensity in the interval 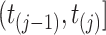 , we define the cumulative intensity process as:
, we define the cumulative intensity process as:
 |
(2.1) |
where 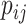 is modeled in (2.5).
is modeled in (2.5).
With absorbing events, we need not consider the conditional independence of future events since there won’t be any; but, with recurrent events, we need to address it. Conditional independence holds by conditioning on the entire event history, 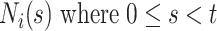 . However, conditioning on the entire event history can be problematic as it would be here. Instead, we condition on the most recent prior event, if any, via
. However, conditioning on the entire event history can be problematic as it would be here. Instead, we condition on the most recent prior event, if any, via 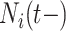 and
and 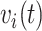 , giving a reasonable expectation of conditional independence.
, giving a reasonable expectation of conditional independence.
Consider a non-parametric probit regression model for 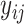 on
on 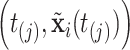 that is analogous to parametric models of the discrete-time intensity (Thompson, 1977; Arjas and Haara, 1987; Fahrmeir, 1998). We define a sequence of longitudinal binary events as follows:
that is analogous to parametric models of the discrete-time intensity (Thompson, 1977; Arjas and Haara, 1987; Fahrmeir, 1998). We define a sequence of longitudinal binary events as follows:
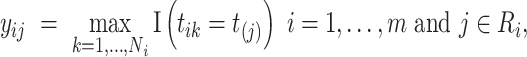 |
(2.2) |
where 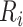 is the risk set of time points for subject
is the risk set of time points for subject 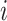 as defined in (2.4). The construction of binary indicators,
as defined in (2.4). The construction of binary indicators, 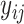 , and the risk set,
, and the risk set, 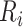 , is illustrated by a vignette (2.3) and a diagram (see Figure S22 of the Supplementary material available at Biostatistics online). We have two subjects with the following values:
, is illustrated by a vignette (2.3) and a diagram (see Figure S22 of the Supplementary material available at Biostatistics online). We have two subjects with the following values:
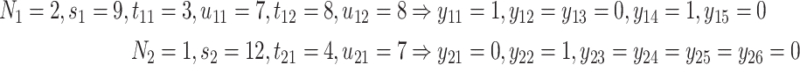 |
(2.3) |
creating the grid of time points: 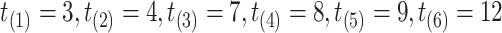 . For subject 1 (2), notice that
. For subject 1 (2), notice that 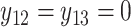 (
(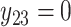 ) as it should be since no event occurred at time(s) 4 or 7 (7). However, no event could occur because their first event had not ended yet, i.e., these time points do not contribute to the likelihood (2.6) since these subjects are not chronologically at risk for an event.
) as it should be since no event occurred at time(s) 4 or 7 (7). However, no event could occur because their first event had not ended yet, i.e., these time points do not contribute to the likelihood (2.6) since these subjects are not chronologically at risk for an event.
Therefore, we define the risk set for subject 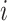 as
as
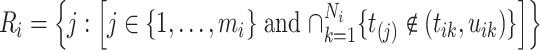 |
(2.4) |
i.e., the risk set contains 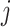 if
if 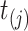 is during the observation period for subject
is during the observation period for subject 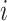 , and
, and 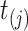 is not contained within an already ongoing event for this subject. Therefore, the only
is not contained within an already ongoing event for this subject. Therefore, the only 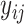 that contribute to the likelihood (2.6) are those corresponding to
that contribute to the likelihood (2.6) are those corresponding to 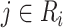 .
.
Putting it all together, we arrive at the following recurrent events discrete-time model (N.B. although we choose BART for its desirable properties, any Bayesian or frequentist method generating a sufficiently flexible 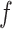 function could be substituted in its place below).
function could be substituted in its place below).
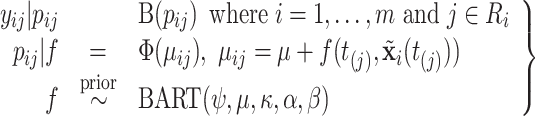 |
(2.5) |
For computational efficiency, we carry out the probit regression via truncated Normal latent variables 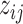 to recast it as a continuous outcome BART model (Albert and Chib, 1993). Thus
to recast it as a continuous outcome BART model (Albert and Chib, 1993). Thus 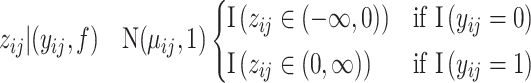 . Therefore, our recurrent events model (2.5) corresponds to the following likelihood.
. Therefore, our recurrent events model (2.5) corresponds to the following likelihood.
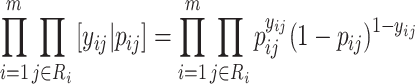 |
(2.6) |
Here, we center the latents, 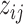 , by
, by 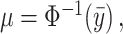 where
where 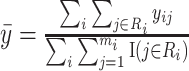 .
.
2.3. Targets for inference
With the data prepared as described in the above vignette (2.3), the BART model for binary data treats the probability of an event as a non-parametric function of time, 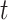 , and covariates,
, and covariates, 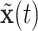 . Conditioned on the data, BART provides samples from the posterior distribution of
. Conditioned on the data, BART provides samples from the posterior distribution of 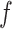 . For any
. For any 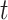 and
and 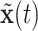 , we obtain the posterior distribution of
, we obtain the posterior distribution of 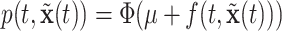 .
.
With survival analysis, survival is typically of interest. Conversely, many applications of recurrent events have relatively few absorbing events like mortality. Therefore, recurrent events inference is typically interested in other quantities like the cumulative intensity function [as presented in formula (2.1)] rather than survival. With these estimates, one can accomplish inference from the posterior via means, quantiles or other functions of 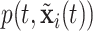 or
or 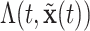 as needed such as the relative intensity, i.e., RI
as needed such as the relative intensity, i.e., RI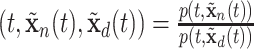 , where
, where 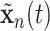 and
and 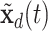 are two settings we wish to compare like two treatments. Also, the cumulative intensity could be calculated for arbitrary intervals on the grid, i.e.,
are two settings we wish to compare like two treatments. Also, the cumulative intensity could be calculated for arbitrary intervals on the grid, i.e., 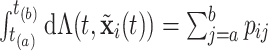 .
.
2.4. Marginal effects
Our model, (2.5), does not directly provide a summary of the marginal effect of a single covariate, or a subset of covariates, on the outcome. Marginal effect summaries are generally a challenge for non-parametric regression and/or black-box models. We use Friedman’s partial dependence function (Friedman, 2001) with BART to summarize the marginal effect due to a subset of the covariates,  , by aggregating over the complement covariates,
, by aggregating over the complement covariates, 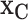 , i.e.,
, i.e., 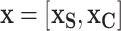 . The marginal dependence function is defined by fixing
. The marginal dependence function is defined by fixing 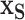 while aggregating over the observed settings of the complement covariates in the cohort:
while aggregating over the observed settings of the complement covariates in the cohort: 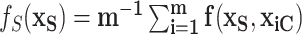 . For example, consider the cumulative intensity function:
. For example, consider the cumulative intensity function: 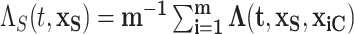 . Other marginal functions can be obtained in a similar fashion. Marginal estimates can be derived via functions of the posterior samples such as means, quantiles, etc.
. Other marginal functions can be obtained in a similar fashion. Marginal estimates can be derived via functions of the posterior samples such as means, quantiles, etc.
2.5. Variable selection
Various methods for variable selection have been proposed for BART (Chipman and others, 2010; Bleich and others, 2014; McCulloch and others, 2015; Linero, 2016). We utilize the computationally friendly approach of Decoupling Shrinkage and Selection (DSS) as proposed by Hahn and Carvalho (2015) for Bayesian linear models and extended to BART by McCulloch and others (2015). For continuous outcomes, DSS attempts to find the best subset of variables,  , which describe the mean function,
, which describe the mean function, 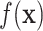 , i.e., identify the best subset,
, i.e., identify the best subset, 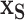 , by regressing
, by regressing 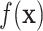 on
on 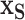 (rather than regressing
(rather than regressing 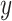 on
on 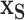 ). In our case, we substitute
). In our case, we substitute 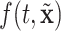 for
for 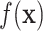 and
and 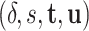 for
for 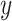 ; however, we stick with the continuous notation for brevity. Step 1 consists of fitting
; however, we stick with the continuous notation for brevity. Step 1 consists of fitting 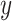 by
by 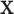 with BART as proposed resulting in
with BART as proposed resulting in 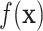 . Step 2 fits
. Step 2 fits 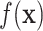 by
by 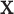 via a non-linear method of choice. In Step 2, over-fitting is not an issue, i.e., we can’t over-fit to
via a non-linear method of choice. In Step 2, over-fitting is not an issue, i.e., we can’t over-fit to 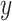 since
since 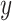 itself does not appear (McCulloch and others, 2015). Therefore, we select an undemanding computational method since repeated fits may be necessary to find the best subset,
itself does not appear (McCulloch and others, 2015). Therefore, we select an undemanding computational method since repeated fits may be necessary to find the best subset, 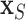 . We choose the method of Classification and Regression Trees (CART) and the criteria of
. We choose the method of Classification and Regression Trees (CART) and the criteria of 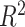 following the lead of McCulloch and others (2015). Step 3 is optional: we may choose to re-fit
following the lead of McCulloch and others (2015). Step 3 is optional: we may choose to re-fit 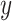 by
by 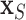 with BART arriving at
with BART arriving at 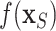 ; otherwise, we simply compute the marginal effect,
; otherwise, we simply compute the marginal effect, 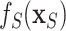 , as described in Section 2.4.
, as described in Section 2.4.
2.6. Handling missing data with BART
BART can handle missing data (Kapelner and Bleich, 2016; Xu and others, 2016). We utilize the missing data framework developed by Xu and others (2016) that they call Sequential BART. Sequential BART assumes that the missing covariates are missing at random, i.e., missingness only depends on what has been observed and not the missing value itself. Missing at random is a deliberate assumption in our case; the missingness of vital signs and laboratory values in this study is mainly driven by what is available at a given time rather than what the value might have been (see the description of missing covariates in Appendix G of the Supplementary material available at Biostatistics online). Specifically, sequential BART assumes that a missing covariate can be imputed by BART from the rest of the covariates, and so on, sequentially for all missing covariates. A brief description of this method can be found in Appendix C of the Supplementary material available at Biostatistics online.
2.7. Motivating example
We explored the hospital admissions in a cohort of patients with diabetes in a unified health care network comprised of 3 hospitals and 16 primary care sites. These patients were identified via their EHR. This human subjects research was approved by the Medical College of Wisconsin and Froedtert Hospital joint Institutional Review Board. To maintain patient privacy, roughly one-fourth of patients were randomly sampled for inclusion.
We identified likely incident diabetes mellitus type 2 patients by diagnosis codes; see Table 1 for the codes used. We tabulated their first coding of primary diabetes in 2006 or 2007, i.e., no such codes were found prior to 2006 for as far back as each patient’s records go. Unfortunately, there are no type 2 specific codes; based on the diabetes population at large, we assume that around 90% of our cohort are type 2. We restricted the population to adults aged 21 to 90 by January 1, 2008. Among the patients treated in this network, the vast majority were racially self-identified as either white or black so our inclusion criteria is restricted to these groups. Finally, we restricted to a geographic area that we refrain from divulging in the interest of patient privacy.
Table 1.
Cohort overview
| Patients | Comment | |
|---|---|---|
| Inclusion and exclusion criteria | ||
| Primary diabetes diagnosis in 2006–2007 | 6000 | Estimate |
| (ICD-9-CM diagnoses: 250.x0, 250.x2) | 1495 | Random sample |
| Age: 21 to 90 | 1471 | |
| Race: White or Black | 1341 | |
| ZIP code in region | 927 | |
| E&M visit in 2006–2007 | 791 | |
| E&M visit in 2012–2013 | 520 | |
| or deceased with E&M visit within 1 year of death | ||
| Excluding secondary diabetes (ICD-9-CM diagnosis: 249.xx) | 488 | Cohort total |
| and gestational diabetes (ICD-9-CM diagnoses: 648.8, V12.21) | ||
| Deceased | Patients | % |
| Yes | 30 | 6.1 |
| No | 458 | 93.9 |
| Hospital admissions | Patients | % |
| 0 | 308 | 63.0 |
| 1 | 79 | 16.2 |
| 2–3 | 50 | 10.3 |
| 4–6 | 37 | 7.6 |
| 7–16 | 14 | 2.9 |
We identify a cohort of patients suffering diabetes via their collected electronic health records (EHR) to determine which covariates are related to the risk of hospital admission. Herein, we provide the details of the inclusion and exclusion criteria for this study. In addition, we summarize mortality and hospital admissions in this cohort.
E&M, Evaluation and Management; ICD-9-CM, International Classification of Diseases, Ninth Revision, Clinical Modification.
We want to identify those who are primarily cared for by this health care network (rather than those who may have been admitted to a network hospital, but were clinically treated elsewhere) so that the collected EHR are a near-census of their health care experience for a 5-year window from 2008 to 2012. Therefore, we required that they have an Evaluation and Management (E&M) physician office visit as a new or established patient in 2006 or 2007; as well as a later visit in 2012 or 2013; for those who passed away before December 31, 2012, their second E&M visit had to be within 1 year prior to death. Since our interest is in patients with primary diabetes, we excluded those patients who were diagnosed with either secondary diabetes or gestational diabetes.
For this cohort, we identified every hospital admission between January 1, 2008 and December 31, 2012. For convenience, follow-up begins on January 1, 2008, rather than from each patient’s incident diagnosis date that obviously varies. Following patients concurrently allows us to temporally adapt for seasonal/epidemic hospital admissions such as the A/H1N1 swine influenza pandemic that inundated the United States from April to June 2009 (Jain and Kamimoto, 2009); note that diabetes is a risk factor for severe complications of the flu that often require a hospital admission.
We investigated the following risk factors: gender, race, age, insurance status (commercial, government, or other), anti-diabetic therapy (insulin, metformin, and/or sulfonylurea), health care charges, relative value units (RVU), vital signs, laboratory values, comorbidity/complication diagnoses, and procedures/surgeries (we will refer to vital signs and laboratory values collectively as signs; and comorbidity/complication diagnoses and procedures/surgeries collectively as conditions). In total, we considered 85 covariates; 82 are external factors as described above and three are temporal factors: time, 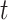 , the number of previous events,
, the number of previous events, 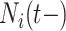 , and the sojourn time,
, and the sojourn time, 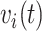 . Among these potential predictors only gender, race, and age are time-independent; age was calculated once at study start and truncated at a maximum of 85 years old so elderly patients cannot be identified. The rest are defined as last value carried forward. More details on the motivating example can be found in Appendix G of the Supplementary material available at Biostatistics online.
. Among these potential predictors only gender, race, and age are time-independent; age was calculated once at study start and truncated at a maximum of 85 years old so elderly patients cannot be identified. The rest are defined as last value carried forward. More details on the motivating example can be found in Appendix G of the Supplementary material available at Biostatistics online.
3. Results
Here, we summarize the results of our new BART method based on simulated data sets (the full details are contained in Appendix D of the Supplementary material available at Biostatistics online). Then, we apply our method to the motivating example of hospital admissions among newly diagnosed diabetes patients.
3.1. BART vs. Cox comparison
We use the term proportional setting to mean a simulated data scenario where the relative intensity is constant with respect to time. For the proportional setting, in-sample comparisons were performed between our new BART method and the counting process Cox (CPC) model (Kalbfleisch and Prentice, 2002; Hosmer and others, 2008) based on simulated data sets (as described in Appendix D of the Supplementary material available at Biostatistics online). We based this comparison on the following metrics: root mean squared error, bias, and interval coverage (credible intervals for BART and confidence intervals for Cox). These comparisons were done overall and within realms of the true cumulative intensity quantiles: [0.00, 0.10), [0.10, 0.25), [0.25, 0.50), [0.50, 0.75), [0.75, 0.90), [0.90, 1.00]. For Cox, the proportional setting is advantageous since it assumes proportionality; however, there is an important caveat: discrete-time tied events are incompletely controlled for diminishing the efficiency of the Cox model (given the sample sizes considered, an adequate treatment is computationally infeasible). Generally, BART is very competitive with Cox in the proportional setting for all metrics and in all realms; see Figures S3:S6 of the Supplementary material available at Biostatistics online. Notably, BART uniformly achieves nominal or near nominal 95% interval coverage while Cox does not. As shown in Table S3 of the Supplementary material available at Biostatistics online, the overall in-sample 95% interval coverage for BART is 96.5% while for Cox it is only 71.4%.
3.2. BART in-sample vs. out-of-sample comparison
We use the term proportional (non-proportional) setting to mean a simulated data scenario where the relative intensity is constant (varies) with respect to time. For proportional and non-proportional settings, comparisons were performed between our new BART method’s in-sample and out-of-sample predictions based on simulated data sets (as described in Appendix D of the Supplementary material available at Biostatistics online). We based this comparison on the same metrics and realms as above. Since BART is in the class of ensemble predictive models, theoretically, BART’s performance on in-sample vs. out-of-sample predictions should be quite similar. The results of the comparison show that BART’s out-of-sample performance is only slightly worse than in-sample as expected; for the proportional (non-proportional) setting, see Figures S8:S12 (15:18) of the Supplementary material available at Biostatistics online. As shown in Table S3 of the Supplementary material available at Biostatistics online for the proportional setting, the overall in-sample 95% interval coverage for BART is 96.5% while for out-of-sample it is 97.8%; cross-validation improved out-of-sample coverage to 94.4%. A shown in Table S3 of the Supplementary material available at Biostatistics online for the non-proportional setting, the overall in-sample 95% interval coverage for BART is 88.6% while for out-of-sample it is 91.1%.
3.3. Motivating example results
Utilizing all 85 temporal and external covariates is a challenge for traditional methods but is rather routine for BART. Nevertheless, it is difficult to tabulate information on all 82 external covariates in a convenient manner for the readers of this article. Therefore, we mainly restrict our attention to the covariates that were deemed to be the most important by variable selection with BART and DSS (see Section 3.3.2): insulin therapy, peripheral vascular disease (PVD), and the number of prior hospitalizations (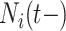 ). We tabulate these important external covariates and a select few others in Table 2.
). We tabulate these important external covariates and a select few others in Table 2.
Table 2.
Patient characteristics and hospital admissions
| Characteristics | Beginning of follow-up | End of follow-up | Hospital admissions | Unadjusted relative intensity | ||||
|---|---|---|---|---|---|---|---|---|
| Gender | 488 | 488 | 525 | |||||
| M | 216 | (44.3) | 216 | (44.3) | 228 | (43.4) | 0.98 | (0.69, 1.40) |
| F | 272 | (55.7) | 272 | (55.7) | 297 | (56.6) | 1.00 | Reference |
| Race | 488 | 488 | 525 | |||||
| Black | 174 | (35.7) | 174 | (35.7) | 265 | (50.5) | 1.85 | (1.30, 2.63) |
| White | 314 | (64.3) | 314 | (64.3) | 260 | (49.5) | 1.00 | Reference |
| Age | 488 | 488 | 525 | |||||
| Mean, SD | 56.0 | 15.1 | 60.9 | 15.0 | 60.3 | 15.7 | ||
| Min, Max | 21.0 | 89.0 | 26.0 | 94.0 | 24.0 | 92.0 | ||
| 21–44 | 104 | (21.3) | 66 | (13.5) | 87 | (16.6) | 1.00 | Reference |
| 45–54 | 127 | (26.0) | 94 | (19.3) | 99 | (18.9) | 0.90 | (0.50, 1.62) |
| 55—64 | 116 | (23.8) | 137 | (28.1) | 115 | (21.9) | 0.85 | (0.48, 1.53) |
| 65–74 | 78 | (16.0) | 92 | (18.9) | 100 | (19.0) | 1.21 | (0.65, 2.28) |
| 75+ | 63 | (12.9) | 99 | (20.3) | 124 | (23.6) | 1.48 | (0.83, 2.64) |
| ZIP area | 488 | 488 | 525 | |||||
| Urban | 378 | (77.5) | 378 | (77.5) | 454 | (86.5) | 1.90 | (1.19, 3.05) |
| Suburb | 110 | (22.5) | 110 | (22.5) | 71 | (13.5) | 1.00 | Reference |
| Insurance | 488 | 488 | 525 | |||||
| Government 65+ | 141 | (28.9) | 191 | (39.1) | 224 | (42.7) | 1.00 | Reference |
Government 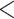 65 65 |
134 | (27.5) | 138 | (28.3) | 208 | (39.6) | 1.08 | (0.73, 1.59) |
Commercial 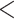 65 65 |
192 | (39.3) | 143 | (29.3) | 71 | (13.5) | 0.31 | (0.20, 0.48) |
Other 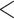 65 65 |
21 | ( 4.3) | 16 | ( 3.3) | 22 | ( 4.2) | 0.77 | (0.45, 1.32) |
| Insulin | 488 | 488 | 525 | |||||
| Yes | 191 | (39.1) | 206 | (42.2) | 391 | (74.5) | 4.56 | (3.35, 6.21) |
| No | 297 | (60.9) | 282 | (57.8) | 134 | (25.5) | 1.00 | Reference |
| Metformin | 488 | 488 | 525 | |||||
| Yes | 176 | (36.1) | 176 | (36.1) | 168 | (32.0) | 0.76 | (0.53, 1.08) |
| No | 312 | (63.9) | 312 | (63.9) | 357 | (68.0) | 1.00 | Reference |
A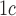 (%) (%) |
389 | 416 | 488 | |||||
| Mean, SD | 7.1 | 1.7 | 7.1 | 1.6 | 6.9 | 1.7 | ||
| Min, Max | 4.4 | 18.5 | 4.5 | 15.6 | 4.1 | 16.4 | ||
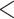 9 9 |
355 | (91.3) | 366 | (88.0) | 437 | (89.5) | 1.00 | Reference |
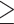 9 9 |
34 | ( 8.7) | 50 | (12.0) | 51 | (10.5) | 1.25 | (0.83, 1.88) |
| Missing | 99 | 72 | 37 | |||||
| Calcium(mg/dL) | 415 | 435 | 520 | |||||
| Mean, SD | 9.3 | 0.5 | 9.4 | 0.6 | 8.9 | 0.7 | ||
| Min, Max | 7.2 | 10.9 | 7.2 | 11.6 | 6.2 | 11.6 | ||
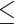 9.1 9.1 |
151 | (36.4) | 125 | (28.7) | 334 | (64.2) | 7.35 | (5.67, 9.51) |
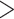 9.1 9.1 |
264 | (64.6) | 310 | (71.3) | 186 | (35.8) | 1.00 | Reference |
| Missing | 73 | 53 | 5 | |||||
| PVD | 488 | 488 | 525 | |||||
| Yes | 172 | (35.2) | 272 | (55.7) | 488 | (93.0) | 16.16 | (11.19, 23.34) |
| No | 316 | (64.8) | 216 | (44.3) | 37 | ( 7.0) | 1.00 | Reference |
| PUD | 488 | 488 | 525 | |||||
| Yes | 239 | (49.0) | 333 | (68.2) | 480 | (91.4) | 7.49 | (5.09, 11.01) |
| No | 249 | (51.0) | 155 | (31.8) | 45 | ( 8.6) | 1.00 | Reference |
We identified a cohort of patients suffering diabetes via EHR to determine which covariates are related to the risk of hospital admission. In the first column, we provide a selection of the covariates. In the second (third) column, we summarize these covariates at the beginning (end) of follow-up where the unit of analysis is the subject. In the fourth column, we summarize these covariates for hospital admissions where the unit of analysis is an admission. In the fifth column, we provide unadjusted relative intensities (and 95% CI) computed via a counting process Cox model.
3.3.1. Aggregate description and unadjusted relative intensity
We describe the Table 2 summary as follows: in the first (second) column of numbers, we have summarized the covariates as they appear at the beginning (end) of follow-up; and in the third column, as they appear at the beginning of hospital admissions. For the fourth column, we summarize via a simple unadjusted CPC model of time (we describe this model in Appendix B of the Supplementary material available at Biostatistics online) by providing relative intensity and its corresponding 95% confidence interval. As we have previously discussed, the CPC model has the disadvantage of restricting to proportionality, and it is only one of several possible Cox model choices. However, it is computationally convenient that we can calculate the CPC model on the same grid that we employ for BART allowing us to use the same data including time-dependent covariates like insulin therapy. And, we can easily incorporate our risk set definition.
The first thing to notice is the relatively high admission rate: 525 admissions for 488 patients in roughly 5 years of follow-up. In this cohort, there are more women than men, roughly a 56:44 split and a similar hospital admission rate with an estimated relative intensity near 1. There are about twice as many whites as blacks; however, the hospital admission rate is about 50:50 with whites under, and blacks over, represented and a statistically significant relative intensity of 1.85.
Among the oldest members of the population, there is a non-significant trend towards more hospital admissions. About 78% of this cohort resided in an urban area poorer than the surrounding suburbs where about 22% resided. Urban residents had a higher hospital admission rate than the suburbs with a significant relative intensity of 1.9.
Virtually everyone in the cohort aged 65 and older was enrolled in the Medicare insurance program and that increased throughout the study from roughly 29% to 39%. About 28% of the cohort was under 65 and had public health insurance, mainly the Medicaid safety net for the low income and disabled. Over the course of the study, commercial health insurance coverage of those under 65 dropped from roughly 39% to 29%. Public health insurance for those under 65 had the highest rate of hospital admissions, but only commercial insurance for those under 65 had a statistically significant relative intensity of 0.31.
During the course of the study, insulin therapy increased slightly. Insulin recipients were much more likely to have a hospital admission than those not taking insulin; a statistically significant relative intensity of 4.56. Metformin therapy was constant: 50 patients added Metformin, and 50 patients dropped it resulting in the same rate. Patients taking metformin had a non-statistically significant relative intensity of 0.76 as opposed to those not taking metformin.
Glycohemoglobin A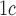 levels
levels 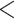 9% vs.
9% vs. 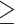 9% did not produce a statistically significant relative intensity. Serum calcium levels
9% did not produce a statistically significant relative intensity. Serum calcium levels 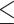 9.1 mg/dL vs.
9.1 mg/dL vs. 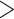 9.1 mg/dL produced a statistically significant relative intensity of 7.35. PVD and peptic ulcer disease (PUD) both produced a statistically significant increase in hospital admissions with estimated relative intensities of 16.2 and 7.5, respectively.
9.1 mg/dL produced a statistically significant relative intensity of 7.35. PVD and peptic ulcer disease (PUD) both produced a statistically significant increase in hospital admissions with estimated relative intensities of 16.2 and 7.5, respectively.
3.3.2. Model-based analysis with BART
In order to minimize false positives, we randomly divided our data set into two parts: a training cohort with 235 patients and a validation cohort with 253 patients. We fit both cohorts independently and then performed variable selection on each via DSS. We started out with 82 external covariates and 3 temporal variables. In the training cohort, the important covariates are PVD, insulin treatment, the number of prior hospitalizations (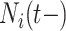 ), PUD, and serum calcium. In the validation cohort, the important covariates are PVD, insulin treatment, the number of prior hospitalizations, and hypertension. Therefore, we conclude that the intersection of these two sets (in italics) are very likely risk factors. However, we do not proceed to the optional Step 3 of DSS, i.e., re-fitting
), PUD, and serum calcium. In the validation cohort, the important covariates are PVD, insulin treatment, the number of prior hospitalizations, and hypertension. Therefore, we conclude that the intersection of these two sets (in italics) are very likely risk factors. However, we do not proceed to the optional Step 3 of DSS, i.e., re-fitting 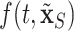 where
where 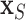 consists of just the three important variables. Rather, we choose to perform marginal inference adjusting for all covariates due to potential confounding. For example, since our patients were not randomized to insulin therapy vs. no insulin, it may be that patients treated with insulin are more likely to possess other possible risk factors such as low serum calcium, PUD, and/or hypertension. So, while we will restrict ourselves to assessing the effects of just the important covariates identified, we have the comforting reassurance that the analysis is adjusted for the rest.
consists of just the three important variables. Rather, we choose to perform marginal inference adjusting for all covariates due to potential confounding. For example, since our patients were not randomized to insulin therapy vs. no insulin, it may be that patients treated with insulin are more likely to possess other possible risk factors such as low serum calcium, PUD, and/or hypertension. So, while we will restrict ourselves to assessing the effects of just the important covariates identified, we have the comforting reassurance that the analysis is adjusted for the rest.
Having fit this full model to the data, we now use it to understand the data via the model’s consequences. In order to evaluate the effects of the important covariates, we estimate our marginal function of interest at chosen settings, 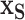 , while marginally aggregating over the other covariates,
, while marginally aggregating over the other covariates, 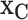 via Friedman’s partial dependence function (see Section 2.4 for a complete description). For a binary covariate like insulin, the chosen settings are easy to enumerate: 1 for being present (treated) and 0 for absent (not treated). However, for
via Friedman’s partial dependence function (see Section 2.4 for a complete description). For a binary covariate like insulin, the chosen settings are easy to enumerate: 1 for being present (treated) and 0 for absent (not treated). However, for 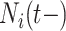 , it is not so simple.
, it is not so simple.
First, we describe the relative intensities by Friedman’s partial dependence function for the important binary variables; the relative intensities are for present vs. absent and are aggregated over all 60 months since they did not appear to vary temporally. The relative intensity (and 95% credible interval) for PVD is 2.90 (2.00, 3.89) and for insulin therapy, 2.39 (1.56, 3.25). Notice the dramatic difference between the relative intensity estimate when adjusting for other covariates vs. the unadjusted relative intensity shown in Table 2; from this, we conclude that patients who have PVD, and/or are taking insulin, likely have other risk factors for hospital admission. Nevertheless, there is a clearly significant increase in risk due to these two important factors.
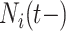 is more challenging since
is more challenging since 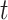 ,
, 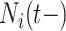 and
and 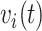 are intimately related. To explore the relative risk of
are intimately related. To explore the relative risk of 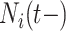 , we create low, medium, and high risk profiles. The low risk profile consists of patients who are not on insulin nor have PVD throughout; and, they do not have a hospital admission so
, we create low, medium, and high risk profiles. The low risk profile consists of patients who are not on insulin nor have PVD throughout; and, they do not have a hospital admission so  and
and 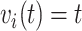 . Medium risk patients are on insulin without PVD throughout while being admitted to the hospital once at 24 months with
. Medium risk patients are on insulin without PVD throughout while being admitted to the hospital once at 24 months with 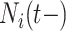 and
and 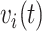 set accordingly. High risk patients are on insulin with PVD and hospital admissions at 12, 24, 36, and 48 months with
set accordingly. High risk patients are on insulin with PVD and hospital admissions at 12, 24, 36, and 48 months with 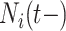 and
and 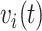 set accordingly. In Figure S21 of the Supplementary material available at Biostatistics online, Friedman’s partial dependence function shows that
set accordingly. In Figure S21 of the Supplementary material available at Biostatistics online, Friedman’s partial dependence function shows that 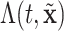 fall in the predetermined order from low, to medium, to high risk. Furthermore, the cumulative differential intensity, CDI
fall in the predetermined order from low, to medium, to high risk. Furthermore, the cumulative differential intensity, CDI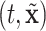 , shows that the high (medium) risk patients will, on average, have 2 (0.5) more hospital admissions than low risk patients over 5 years.
, shows that the high (medium) risk patients will, on average, have 2 (0.5) more hospital admissions than low risk patients over 5 years.
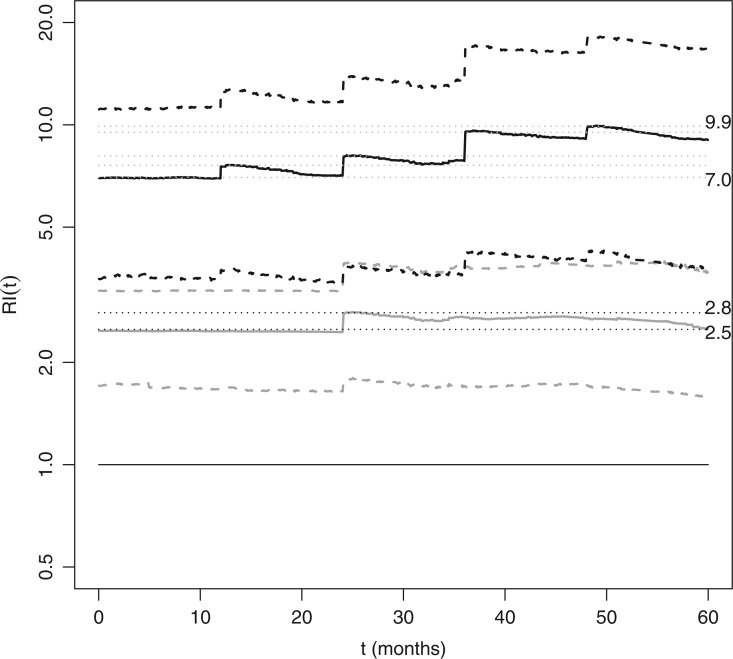
In Figure 2, Friedman’s partial dependence function shows that the previous hospital admissions increase the risk of new hospital admissions; however, not to the same extent as insulin or PVD. Also note the sawtooth pattern, i.e., the increased risk due to a recent hospital admission appears to dissipate as the sojourn time,  , increases; although, the credible intervals are wide the pattern is notable for its consistency after each new hospital admission.
, increases; although, the credible intervals are wide the pattern is notable for its consistency after each new hospital admission.
Fig. 2.
We studied a cohort of patients suffering diabetes to determine the covariates related to the risk of hospital admissions. Based on a recurrent events analysis with BART, we determined that there are three important risk agonists for a new hospital admission: peripheral vascular disease (PVD), receiving insulin treatment, and the number of previous hospital admissions. The effect of binary covariates like PVD and insulin are relatively easily summarized. However, the number of previous hospital admissions is more difficult because it is time-dependent. To explore these risk factors, we present the estimated relative intensities, RI(t): medium vs. low (solid gray) and high vs. low (solid black). In these profiles, PVD and insulin are set to either present or absent throughout the 5-year observation period. For low risk subjects, PVD and insulin are absent and there are no hospital admissions. For medium risk subjects, PVD is absent, insulin is present and there is one hospital admission at 24 months. For high risk subjects, PVD and insulin are present and they are admitted to the hospital at 12, 24, 36, and 48 months. The estimated relative intensities displayed are the effects of the risk profiles marginalizing over all other covariates with Friedman’s partial dependence function. Dashed lines represent 95% credible intervals. Previous hospital admissions increase the risk of new hospital admissions; however, not to the same extent as PVD or insulin. Also note the sawtooth pattern, i.e. the increased risk due to a recent hospital admission appears to dissipate as the sojourn time, 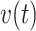 , increases; although, the credible intervals are wide the pattern is notable for its consistency after each new hospital admission. The horizontal line at 1.0 (solid black), the lines of 2.5 and 2.8 (dotted black), and 7.0 to 9.9 (dotted gray), are plotted for reference.
, increases; although, the credible intervals are wide the pattern is notable for its consistency after each new hospital admission. The horizontal line at 1.0 (solid black), the lines of 2.5 and 2.8 (dotted black), and 7.0 to 9.9 (dotted gray), are plotted for reference.
3.3.3. Cox model comparison
Let’s compare the BART results to a CPC model. As noted, there are several possible CPC choices: which model should we fit? The sawtooth of Figure 2 empirically suggest the CPC model should be based on sojourn time, rather than study time, stratified by prior events. These two models generate similar results for the relative intensity while the corresponding 95% confidence (credible) intervals for CPC (BART) are wider for CPC. The relative intensity for PVD is: CPC 3.07 (1.61, 5.85) and BART 2.90 (2.00, 3.89). The relative intensity for insulin therapy: CPC 2.62 (1.74, 3.96) and BART 2.39 (1.56, 3.25).
4. Discussion
Here, we have outlined our new methodology for recurrent events, and we have applied it to a motivating example of the hospital admissions experienced by diabetes patients. For investigations such as this, we are advocates for using as much information as is practically available. For example, with recurrent events we can employ all of the hospital admissions; if we had restricted to only the first admission in this cohort, we would have been limited to only 182 (34.7%) admissions rather than the 525 total that we actually analyzed. In the same vein, we brought in a variety of data from the EHR.
Observational studies have limitations: for example, the patients in this study were not randomized to insulin therapy vs. no insulin. However, our inferences are causal if we can assume that all confounders are measured due to BART’s uncanny capability to account for treatment heterogeneity (Hill, 2011); an assumption that we feel has some merit due to the omnibus of health care data enlisted from the EHR in this study. But, the causal inference assertion must be tempered for several reasons. (i) Although we went to great lengths to include a wide variety of EHR data (as described in Section 2.7), we employed only a portion of the EHR data available in this study, e.g., we ignored imaging, notes written by physicians/nurses/etc. (ii) We assumed the information available to us was complete and accurate. (iii) We assumed that the patients had equal access to, and received, high quality health care. Nevertheless, we strongly recommend mitigating the likely causal elevated risk of hospital admission that we foresee for the following groups of diabetes patients (by closely monitoring them in the outpatient clinic setting): those suffering from PVD, treated with insulin, and/or previously admitted to the hospital especially a recent admission.
Supplementary Material
Acknowledgments
Thanks to the associate editor, the reviewers, and Brent Logan for their insightful comments. Conflict of Interest: None declared.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
Advancing Healthier Wisconsin Research and Education Program (in part); and the NIH National Center for Advancing Translational Sciences (Grant Number UL1TR001436). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.
Disclaimer
The motivating example data have been supplied by the Clinical and Translational Science Institute of Southeast Wisconsin’s Clinical Research Data Warehouse at the Medical College of Wisconsin. The interpretation and reporting of these data are the responsibility of the authors and in no way should be seen as an official policy of, or interpretation by, the Medical College of Wisconsin.
References
- Albert J. and Chib S. (1993). Bayesian analysis of binary and polychotomous response data. Journal of the American Statistical Association 88, 669–679. [Google Scholar]
- Andersen P. K. and Gill R. D. (1982). Cox’s regression model for counting processes: a large sample study. Annals of Statistics 10, 1100–1120. [Google Scholar]
- Arjas E. and Haara P. (1987). A logistic regression model for hazard: asymptotic results. Scandinavian Journal of Statistics 14, 1–18. [Google Scholar]
- Bleich J., Kapelner A., George E. I. and Jensen S. T. (2014). Variable selection for BART: an application to gene regulation. Annals of Applied Statistics 8, 1750–1781. [Google Scholar]
- Blumenthal D. and Tavenner M. (2010). The “meaningful use” regulation for electronic health records. NEJM 363, 501–504. [DOI] [PubMed] [Google Scholar]
- Chipman H. A., George E. I. and McCulloch R. E. (1998). Bayesian CART model search (with discussion). Journal of the American Statistical Association 93, 935–960. [Google Scholar]
- Chipman H. A., George E. I. and McCulloch R. E. (2010). BART: Bayesian Additive Regression Trees. Annals of Applied Statistics 4, 266–298. [Google Scholar]
- Cook R. J. and Lawless J. F. (1997). Marginal analysis of recurrent events and a terminating event. Statistics in Medicine 16, 911–924. [DOI] [PubMed] [Google Scholar]
- Fahrmeir L. (1998). Discrete survival-time models. In: Armitage P. and Colton T (editors), Encyclopedia of Biostatistics. Chichester: Wiley, pp. 1163–1168. [Google Scholar]
- Fisher E. S., Bynum J. P. and Skinner J. S. (2009). Slowing the growth of health care costs: lessons from regional variation. NEJM 360, 849–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J. H. (2001). Greedy function approximation: a gradient boosting machine. Annals of Statistics 29, 1189–1232. [Google Scholar]
- Gelfand A. E. and Smith A. F. M. (1990). Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association 85, 398–409. [Google Scholar]
- Ghosh D. and Lin D. Y. (2000). Nonparametric analysis of recurrent events and death. Biometrics 56, 554–562. [DOI] [PubMed] [Google Scholar]
- Ghosh D. and Lin D. Y. (2003). Semiparametric analysis of recurrent events data in the presence of dependent censoring. Biometrics 59, 877–885. [DOI] [PubMed] [Google Scholar]
- Gramacy R. B. and Polson N. G. (2012). Simulation-based regularized logistic regression. Bayesian Analysis 7, 567–590. [Google Scholar]
- Hahn P. R. and Carvalho C. M. (2015). Decoupling shrinkage and selection in Bayesian linear models: a posterior summary perspective. Journal of the American Statistical Association 110, 435–448. [Google Scholar]
- Hill J. L. (2011). Bayesian nonparametric modeling for causal inference. Journal of Computational and Graphical Statistics 20, 217–240. [Google Scholar]
- Holmes C. and Held L. (2006). Bayesian auxiliary variable models for binary and multinomial regression. Bayesian Analysis 1, 145–168. [Google Scholar]
- Hosmer D. W. Jr,, Lemeshow S. and May S (2008). Applied Survival Analysis: Regression Modeling of Time to Event data, 2nd edition Chichester: Wiley. [Google Scholar]
- Ishwaran H., Kogalur U. B., Blackstone E. H. and Lauer M. S. (2008). Random survival forests. Annals of Applied Statistics 2, 841–860. [Google Scholar]
- Jain S. and Kamimoto L. (2009). Hospitalized patients with 2009 H1N1 influenza in the United States, April-June 2009. NEJM 361, 1935–1944. [DOI] [PubMed] [Google Scholar]
- Kalbfleisch J. D. and Prentice R. L. (2002). The Statistical Analysis of Failure Time Data, 7th edition Chichester: Wiley. [Google Scholar]
- Kapelner A. and Bleich J. (2016). bartMachine: machine learning with Bayesian Additive Regression Trees. Journal of Statistical Software 70, 1–40. [Google Scholar]
- Kuhn M. and Johnson K. (2013). Applied Predictive Modeling. New York: Springer. [Google Scholar]
- Linero A. R. (2016). Bayesian regression trees for high dimensional prediction and variable selection. Journal of the American Statistical Association, 1–11. doi: 10.1080/01621459.2016.1264957. [DOI] [Google Scholar]
- McCulloch R. E., Carvalho C. and Hahn R. (2015). A general approach to variable selection using Bayesian nonparametric models. Joint Statistical Meetings, Seattle, 08/09/15–08/13/15. [Google Scholar]
- McCulloch R. E., Sparapani R. A., Gramacy R., Spanbauer C. and Pratola M. (2018). BART: Bayesian Additive Regression Trees. https://cran.r-project.org/package=BART. [Google Scholar]
- Robert C. P. (1995). Simulation of truncated normal variables. Statistics and Computing 5, 121–125. [Google Scholar]
- Singh S., Lin Y., Kuo Y., Nattinger A. B. and Goodwin J. S. (2014). Variation in the risk of readmission among hospitals: the relative contribution of patient, hospital and inpatient provider characteristics. Journal of General Internal Medicine 29, 572–578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith M., Saunders R., Stuckhardt L. and McGinnis J. M. (editors). (2013). Best Care at Lower Cost: The Path to Continuously Learning Health Care in America. Washington, D.C.: The National Academies Press; https://www.nap.edu/read/13444. [PubMed] [Google Scholar]
- Sparapani R. A., Logan B. R., McCulloch R. E. and Laud P. W. (2016). Nonparametric survival analysis using Bayesian Additive Regression Trees (BART). Statistics in Medicine 35, 2741–2753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson W. A., Jr, (1977). On the treatment of grouped observations in life studies. Biometrics 33, 463–470. [PubMed] [Google Scholar]
- Wang M. C., Qin J. and Chiang C. T. (2001). Analyzing recurrent event data with informative censoring. Journal of the American Statistical Association 96, 1057–1065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei L. J., Lin D. Y. and Weissfeld L. (1989). Regression analysis of multivariate incomplete failure time data by modeling marginal distributions. Journal of the American Statistical Association 84, 1065–1073. [Google Scholar]
- World Bank. (2015). http://data.worldbank.org/indicator/SH.XPD.TOTL.ZS.
- Xu D., Daniels M. J. and Winterstein A. G. (2016). Sequential BART for imputation of missing covariates. Biostatistics 17, 589–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuckerman R. B., Sheingold S. H., Orav E. J., Ruhter J. and Epstein A. M. (2016). Readmissions, observation and the Hospital Readmissions Reduction Program. NEJM 374, 1543–1551. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.