Population-Averaged Atlas of the Macroscale Human Structural Connectome and Its Network Topology

Abstract

A comprehensive map of the structural connectome in the human brain has been a coveted resource for understanding macroscopic brain networks. Here we report an expert-vetted, population-averaged atlas of the structural connectome derived from diffusion MRI data (N=842). This was achieved by creating a high-resolution template of diffusion patterns averaged across individual subjects and using tractography to generate 550,000 trajectories of representative white matter fascicles annotated by 80 anatomical labels. The trajectories were subsequently clustered and labeled by a team of experienced neuroanatomists in order to conform to prior neuroanatomical knowledge. A multi-level network topology was then described using whole-brain connectograms, with subdivisions of the association pathways showing small-worldness in intra-hemisphere connections, projection pathways showing hub structures at thalamus, putamen, and brainstem, and commissural pathways showing bridges connecting cerebral hemispheres to provide global efficiency. This atlas of the structural connectome provides representative organization of human brain white matter, complementary to traditional histologically-derived and voxel-based white matter atlases, allowing for better modeling and simulation of brain connectivity for future connectome studies.

Introduction

The organization of the structural connections in the human brain determines how neural networks communicate, thereby serving as a critical constraint on brain functionality and providing potential etiology for clinical pathology (Bota et al., 2015; Sporns, 2014). Characterizing this structural organization has relied on either histological slides or neuroanatomically-validated atlases based on individual subjects (Amunts et al., 2013; Ding et al., 2016); however, a comprehensive population-averaged 3-dimensional (3D) structural connectome at the macroscale level has yet to be constructed. A population-averaged connectome is critical for demonstrating representative topological interconnectivity in the general population, a stated objective of the national investment in the Human Connectome Project (Setsompop et al., 2013; Van Essen et al., 2013). If achieved, such a map of the structural connectome could augment existing histological and single-subject atlases, thus allowing for robust modeling and simulation in both empirical and theoretical studies.

To date, diffusion MRI is the only non-invasive tool for mapping the 3D trajectories of human macroscopic white matter pathways (Fan et al., 2016; McNab et al., 2013), with preliminary success at resolving the normative pattern of several major white matter pathways (Catani et al., 2002; Guevara et al., 2012; Mori et al., 2009; Mori et al., 2008; Peng et al., 2009; Thiebaut de Schotten et al., 2011). This has been realized by resolving local fiber orientations at the voxel level and delineating entire axonal trajectories by implementing a stepwise tracking algorithm (Basser et al., 2000; Mori et al., 1999; Wedeen et al., 2012). Nonetheless, there are several caveats to the success of diffusion MRI fiber tracking, including the identification of false tracts and suboptimal coverage of small pathways or those with complex geometry (Reveley et al., 2015; Thomas et al., 2014). Indeed, the percentage of valid connections can range from 3.75% to 92% due to differences in reconstruction methods and tracking algorithms (Maier-Hein et al., 2016). Improving the quality of resolved fiber pathways using diffusion MRI can be achieved by high-angular-resolution modalities (Glasser et al., 2016), a template averaged across a large number of subjects to facilitate fiber tracking (Yeh and Tseng, 2011b), and neuroanatomical expertise to resolve errors in the automated fiber tracking process (Meola et al., 2015a). Template-based approaches have been shown to reliably capture the morphological characteristics of several major white matter fascicules when validated against cadaver microdissection approaches (Fernandez-Miranda et al., 2015; Meola et al., 2016a; Meola et al., 2015a; Meola et al., 2016b; Wang et al., 2016b; Wang et al., 2013; Yoshino et al., 2016b). Yet building a comprehensive tractography atlas of major and minor white matter pathways is still challenged by the problem of false fiber pathways, even when relying on high angular resolution data.

Here we constructed a population-averaged structural connectome, including both major and minor pathways, using an expert-vetted approach. We employed high-angular-resolution diffusion MRI data (n=842) from healthy subjects in the Human Connectome Project (HCP) database (Van Essen et al., 2012). The data from each subject were spatially registered and simultaneously reconstructed in the standardized ICBM-152 (ICBM: International Consortium for Brain Mapping) template space using q-space diffeomorphic reconstruction (QSDR)(Yeh and Tseng, 2011b). QSDR allows for aggregating diffusion data into an averaged template of voxelwise diffusion distributions while preserving fiber continuity after nonlinear deformation to enable template space fiber tracking. The averaged diffusion pattern of the entire sample is thus representative of non-pathological structural characteristics within healthy subjects. Based on this template, a total of 550,000 tracks were generated using a tracking method that was shown to achieve the highest number of valid connections in an open competition (Maier-Hein et al., 2016). Generated tracks were subsequently clustered and then labeled by a team of clinical neuroanatomists, capitalizing on their previous experience in both cadaveric white-matter and comparative tractography techniques (Fernandez-Miranda et al., 2015; Wang et al., 2016b). Furthermore, the tracks were categorized into the projection, association, and commissural pathways to generate multi-level connectograms illustrating network topology at the macroscopic level. The strategy of this approach allowed us to compile a comprehensive atlas of the structural connectome in the human brain at the population level, allowing for taxonomical identification of pathways that together comprise the full macroscopic structural connectome.

Methods

Diffusion MRI acquisitions

We used the minimally-preprocessed data (Glasser et al., 2013) from Human Connectome Projects (Q1–Q4 release, 2015) acquired by Washington University in Saint Louis and University of Minnesota (Van Essen et al., 2012). A total of 842 subjects (372 males and 470 females, age 22 ~ 36, demographics available at https://db.humanconnectome.org/) had diffusion MRI scanned on a Siemens 3T Skyra scanner using a 2D spin-echo single-shot multiband EPI sequence with a multi-band factor of 3 and monopolar gradient pulse. The spatial resolution was 1.25 mm isotropic. TR=5500 ms, TE=89.50 ms. The b-values were 1000, 2000, and 3000 s/mm². The total number of diffusion sampling directions was 90, 90, and 90 for each of the shells in addition to 6 b0 images. The preprocessed data were corrected for eddy current and susceptibility artifact. The matrices for gradient nonlinearity distortion correction were used in the following diffusion MRI reconstruction.

Q-space diffeomorphic reconstruction

The diffusion data for each subject was registered and reconstructed into the ICBM-152 space simultaneously using the q-space diffeomorphic reconstruction (QSDR)(Yeh and Tseng, 2011b). QSDR combines nonlinear spatial registration and high-angular-resolution reconstruction of diffusion data to conserve the diffusible spins and preserve the continuity of fiber geometry for fiber tracking. QSDR used the deformation field to directly calculate the spin distribution function (SDF) in the standard space. SDF, denoted as $\psi \left(\widehat{\mathbf{u}}\right)$, is the empirical distribution of the density of spins that have diffusion displacement oriented at direction $\widehat{\mathbf{u}}$ during the diffusion time. The SDF of each voxel were discretely sampled at 642 directions (8-fold tessellated icosahedron) using the following formula.

$$\psi \left(\widehat{\mathbf{u}}\right)=\left|J_{\phi }\right|Z_0\sum _i{W}_i\left(\phi \left(\mathbf{r}\right)\right)\text{sinc}\left(\sigma \sqrt{6D{b}_i}<{\widehat{\mathbf{g}}}_i,\frac{J_{\phi }\widehat{\mathbf{u}}}{\Vert J_{\phi }\widehat{\mathbf{u}}\Vert }>\right)$$ (1)

Where i iterates through each diffusion weighted images Wi. φ is a diffeomorphic mapping function that maps ICBM-152 space coordinates r to the subject’s space. J_φ is the Jacobian matrix of the mapping function, whereas |J_φ| is the Jacobian determinant. W_i(φ(r)) are the diffusion signals acquired at φ(r). b_i is the b-value, and ${\widehat{\mathbf{g}}}_i$ is the direction of the diffusion sensitization gradient. σ is the diffusion sampling ratio controlling the detection range of the diffusing spins. D is the diffusivity of water, and Z₀ is the constant estimated by the diffusion signals of free water diffusion in the brain ventricle (Yeh and Tseng, 2011b). The nonlinearity of diffusion gradients was corrected using the nonlinear terms of the magnetic field obtained from gradient coils. The HCP dataset includes a 3-by-3 gradient deviation matrix for each voxel to estimate the effective gradient direction and strength. This matrix was applied to the diffusion sensitization gradient, ${\widehat{\mathbf{g}}}_i$ in Eq. (1) to correct the effect of gradient nonlinearity.

The registration component in QSDR used Fourier basis as the deformation function (Ashburner and Friston, 1999). The original setting used a set of 7-by-9-by-7 Fourier basis at x-y-z directions, and the computation and memory bottleneck was at the inverse of a 1327-by-1327 matrix (not a sparse matrix). We increased the resolution of the Fourier basis by 4-fold (i.e. 28-by-36-by-28 Fourier basis), which required solving an 84676-by-84676 matrix for each optimization iteration. Here instead of solving the large matrix using a standard Gauss-Jordan method (a complexity of O(n³)), which would increase the computation time by a factor of (4×4×4)³=262,144, we used the Jacobi method that allowed for parallel processing and could utilize solutions from the previous iteration to speed up the processing. This greatly reduced the computation complexity to O(n) and only increased the computation time by a factor of 4×4×4=64. The parallel processing further reduced the computation time, allowing us to reconstruct the data using multi-thread resources. The FSL (FMRIB’s Software Library, www.fmrib.ox.ac.uk/fsl) fractional anisotropy (FA) template was used as a template for ICBM-152 space, and the subjects’ anisotropy maps were used to calculate the deformation parameters. The final SDFs were generated at 1-mm resolution.

The registration accuracy was evaluated by the coefficient of determination (i.e., R²) value between each subject and template image. The distribution of the R² values, as shown in Suppl. Figure 1, is skewed with a leftward tail. We therefore looked at subjects with the lowest R² values at this tail for identification of outliers. This allowed us to identify two problematic datasets (#173132 and #103515) that were then reported to the HCP Consortium. It is noteworthy that we did not use the existing HCP alignment or other high accuracy diffeomorphic registration methods in our spatial normalization (Archer et al., 2017; Peng et al., 2009; Varentsova et al., 2014; Zhang et al., 2011). The alignment of those methods has good point-to-point matching; however, QSDR requires sufficient a constraint on the Jacobian matrix in the white matter tissue because a large rotation and distortion will disrupt the continuity of fiber geometry across voxels and cause a fiber tracking algorithm to fail. The fiber architecture in the white matter can be heavily distorted to match gyral foldings. A constraint on the Jacobian matrix will avoid this pitfall and ensure that the local fiber directions will present a coherent geometry. The Fourier basis method (Ashburner and Friston, 1999) used here intrinsically limits the largest possible rotation and allows for fiber tracking in the ICBM-152 space.

Construction of an SDF template

The SDFs of all subjects were then averaged, voxel-by-voxel, to obtain a 1-mm SDF template termed HCP-842. Before averaging, the SDFs of each subject were scaled by a constant value to ensure that the free water SDFs were normalized to one (Yeh and Tseng, 2011b). The computation was conducted using the cluster at Center for the Neural Basis of Cognition, a joint Institute of Carnegie Mellon University and the University of Pittsburgh. The cluster had 24 nodes and 320 CPUs. The total size of SDF data from 842 subjects was around 1.5 terabytes (after compression), and the computation took a month of time to complete.

Whole-brain tractography

We used a deterministic fiber tracking algorithm that leverages information in the SDF (Yeh et al., 2013). Each of the streamlines generated was automatically screened for its termination location. A white matter mask was created by applying DSI Studio’s default anisotropy threshold (0.6 Otsu’s threshold) to the SDF’s anisotropy values. The mask was used to eliminate streamlines with premature termination in the white matter region.

To determine the adequate density for whole-brain seeding, previous work has shown that, on average, there are around 3 fiber populations in a 2.4-mm cubic voxel (Jeurissen et al., 2013). This indicated that at least 3 seeds points are needed for each voxel with a volume of 2.4-by-2.4-by-2.4 mm³, which is 0.2 seeds per mm³. To meet the minimal requirement, we obtained 500,000 whole-brain streamlines in addition to 50,000 streamlines to cover the spinal cord connections eliminated by the white matter mask. The total number of streamlines achieved an average seeding density of 1.0 seed per mm³, which is 5 times of the minimum requirement.

The fiber tracking was conducted using angular thresholds of 40, 50, 60, 70, and 80 degrees to capture fiber pathways with different turning morphology. Each angular threshold generated 100,000 streamlines, and a total of 500,000 streamlines were obtained. Since the white matter mask also removed streamlines connecting to/from the spinal cord, an additional set of whole brain tracking was conducted to allow streamlines to terminate at the lowest section of the brainstem. The fiber tracking was also conducted using angular thresholds of 40, 50, 60, 70, and 80 degrees. Each angular threshold generated 10,000 streamlines, and a total of 50,000 streamlines were obtained. We used different parameter combinations because different fiber trajectories are best resolved by different tractography schemes. For example, a larger angular threshold is needed for tracking fiber pathway with abrupt turning (e.g. Meyer’s loop at the optic radiation), whereas some projection pathways do not have sharp turning (e.g. corticospinal tracts) and thus can rely on lower angular thresholds.

Initial clustering using Hausdorff distance

The tractography was clustered using single-linkage clustering. We measured the Hausdorff distance (Huttenlocher et al., 1993; Pujol et al., 2015) between a pair of streamlines X and Y as

$$d_H\left(\text{X},\text{Y}\right)=\text{ max}\left\{{\text{max}}_{x\in X}{\text{ min}}_{y\in Y}\text{\hspace{0.17em}d}\left(\text{x},\text{y}\right),{\text{max}}_{y\in Y}{\text{ min}}_{x\in X}\text{\hspace{0.17em}d}\left(\text{x},\text{y}\right)\right\}$$ (2)

X is a set of coordinates, i.e. X={x}, whereas Y is another set of coordinates, i.e. Y={y}. d(x,y) calculates the Euclidean distance between two coordinates x and y, and the d_H(X,Y) calculates the Hausdorff distance between set X and Y. Different merging thresholds were tested, and we chose 2-mm as the merging threshold to avoid over-segmentation (shorter distance) and over-merging (longer distance). The 500 largest clusters, in terms of track counts, were selected because the remaining clusters contained less than 0.01% of the total streamlines (i.e. < 50 streamlines). The same cluster selection strategy was applied to our second set of the 50,000 streamlines (i.e. the streamlines connecting to/from spinal cords), and the first 50 largest clusters were collected. Since each cluster may contain streamlines with repeated trajectories, we removed redundant trajectories that are substantially close to the one another using a Hausdorff distance of 1 mm.

Expert labeling and examination

The 550 clusters were manually labeled by our neuroanatomy teams, including four senior neuroanatomists (JFM, AM, MY, FY) and junior neuroanatomists (DF and SP). The labeling was based on evidence from publicly available white matter atlases, existing literature, microdissection evidence, and neuroanatomy books (Table S1). The first examination round was the manual labeling conducted by 3 neuroanatomists (FY, DF, and SP). Each of the neuroanatomists independently inspected the termination locations and connecting routes of each of the 550 clusters based on publications listed in Table S1. The 2009a, nonlinear asymmetric, ICBM-152 T1-weighted image (The McConnell Brain Imaging Centre, Montreal Neurological Institute, McGill University) (Fonov et al., 2011) was used to assist inspection. The anatomical label of each cluster was independently assigned and subsequently compared to identify inter-observer differences, including the naming of the cluster and whether the cluster is a false one. The inter-observer differences were found in 20 clusters (3.6% of the clusters), mostly involving the branches and segments of fiber pathways, and resolved in a joint discussion between two junior (DF, SP) and two senior neuroanatomists (FY, JFM). The clusters with the same neuroanatomy name were grouped together to form major fiber bundles. The merged bundles underwent a second round of inspection by both senior and junior neuroanatomists to identify missing branches and remove false connections. The inspection identified missing branches in anterior commissure (olfactory and occipital connections), corticothalamic tract (temporal connections), corticostriatal tract (occipital connections), corticobulbar tract, corticopontine tract (temporal and occipital connections), and tapetum of the corpus callosum. These branches were specifically tracked by placing regions of interest at the target area. The same angular and anisotropy thresholds were used. The seeding density was increased until a sufficient number of tracks were generated from the tracking algorithm to cover the regions. The final fiber bundles were subsequently categorized into the projection, association, commissural, cerebellar, brainstem, and cranial nerve pathways.

The next examination round further checked for other missing minor pathways that require a dense sampling to form a bundle. This was done by projecting the fiber bundles back to the white matter and looking for areas without track coverage. Using a region-based approach, the senior neuroanatomists (MY, AM, and FY) tracked missing minor pathways including acoustic radiation, posterior commissure, brainstem pathways such as rubrospinal tract (RST), spinothalamic tract (STT), dorsal longitudinal fasciculus (DLF), lateral lemniscus (LL), medial lemniscus (ML), and cranial nerves such as CN VII, CN VIII, and CN X. These pathways were tracked according to previous microdissection studies (Fernandez-Miranda et al., 2015; Wang et al., 2016b). The course of the posterior column sensory pathway, running within the fascicles gracile and cuneatus toward the primary sensory cortex, was manually terminated at the level of the thalamus and labeled as ML. This segment in the brainstem corresponds to the second order neurons running from the nucleus gracile and cuneatus to the thalamus.

Connectivity matrix, connectogram, and network measures

The expert-vetted tractography was used to generate connectivity matrices. A weighted connectivity matrix was quantified using a cortical parcellation based on regions derived from the AAL atlas (Table S2). It is noteworthy that our tractography atlas can be readily applied to any cortical parcellation atlas, and currently there is no consensus on how network nodes should be defined. Here we used only one of the most popular parcellation from the AAL atlas to illustrate the network characteristics.

The average of along-track SDF values was used as the connectivity value. The connectograms of each fiber bundle and whole brain tracks (both expert-vetted) were generated using CIRCOS (http://mkweb.bcgsc.ca/tableviewer/visualize/). The network measures such as network characteristic path length, global efficiency, local efficiency, clustering coefficient were calculated using the definition formulated in Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/). The influence of the projection, association, and commissural pathways was calculated by calculating the change of network measures (quantified by percentage of the original) after removing the tracks.

The University of Pittsburgh Institutional Review Board reviewed and approved the study by the expedited review procedure authorized under 45 CFR 46.110 and 21 CFR 56.11 (IRB#: PRO16080387).

Data and Code Availability

The processing pipeline (DSI Studio), SDF data of all 842 subjects, and HCP-842 template are available at http://dsi-studio.labsolver.org. The SDF template can be reproduced using the HCP data and documentation on the website. The atlas data, including the track trajectories and connectograms, are available at http://brain.labsolver.org.

Results

A high spatial and angular resolution diffusion template of the human brain

Diffusion MRI data from 842 participants were reconstructed in the ICBM-152 space to calculate the SDF(Yeh and Tseng, 2011b; Yeh et al., 2010) within each voxel (Fig. 1a). The goodness of fit between the normalized image and the template was reported as an R² (Fig. S1). These values ranged from 0.73 to 0.86, and the quantiles were 0.81 (25%), 0.82 (50%), and 0.83 (75%), suggesting that the distribution of R² values were mostly centered around 0.82, and more than 75% subjects had R² values greater than 0.80. An SDF is an empirical distribution of the density of diffusing water orientations, calculated for each voxel to reveal the underlying fiber architectures (Fig. 2a). The SDFs of all subjects were averaged to build the HCP-842 SDF template, which represents an average diffusion pattern within a normal population (Fig. 1b and Fig. 2a). Figure 2b shows the peak orientations of fibers in each voxel, resolved from the group-averaged SDFs, near the corpus callosum crossing at central semiovale (red: left-right, green: anterior-posterior, blue: inferior-superior). The SDF peaks reflect the local orientation of underlying fiber bundles, and the magnitudes measured at the peaks provide anisotropy estimates. The peaks and magnitudes offer the necessary information for a fiber-tracking algorithm to delineate long-distance white matter trajectories.

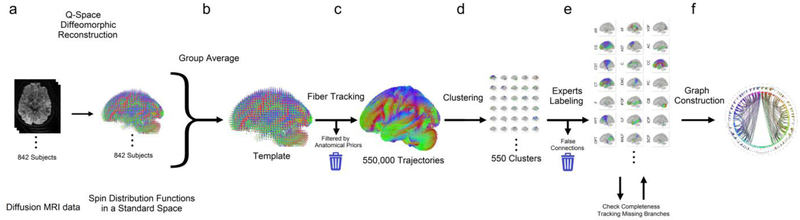
Fig. 1.

Flow chart of the processing steps used to construct a population-averaged structural connectome of the human brain. (a) A total of 842 subjects’ diffusion MRI data were reconstructed in a common standard space to calculate the spin distribution function at each imaging voxel. (b) The spin distribution functions were averaged to build a template of the diffusion characteristics of the normal population. (c) The template was used to guide a fiber tracking algorithm and generate a total of 550,000 trajectories. (d) Automatic track clustering was applied to cluster trajectories into fiber bundles. (e) A team of experienced neuroanatomists manually labeled each cluster and identified false pathways according to the neuroanatomy evidence. The clusters with the same labeled were grouped together as an atlas of structural connectome. An additional quality check was conducted to ensure complete coverage. (f) The atlas was then used to build the connectogram showing the connections between brain regions.

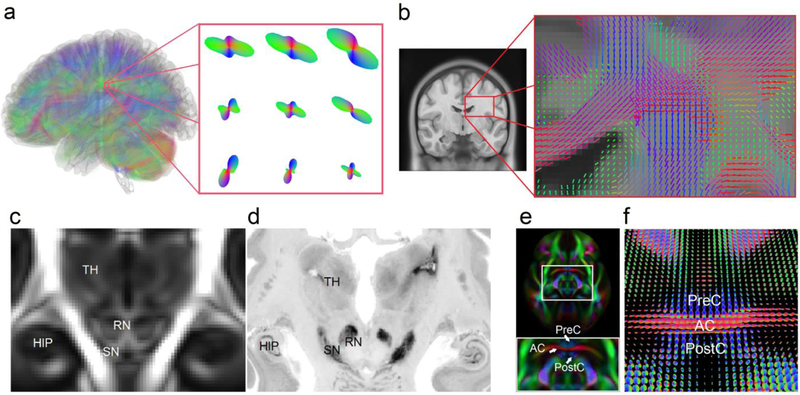
Fig. 2.

(a) Diffusion MRI allows for quantifying, for each imaging voxel, the orientation distribution of the water diffusion (termed spin distribution function, SDF) to reveal the underlying structural characteristics of axonal fiber bundles in a color-coded surface (red-blue-green indicates the orientation at the x-y-z axis, respectively). The protruding points of the SDFs indicate the orientation of fiber bundles. (b) The color sticks represent the peak orientations on SDFs. The coronal view shows that SDF can resolve crossing fibers at central semiovale, a white matter region where the corpus callosum crosses vertical passing fibers. The SDFs averaged from a total 842 subjects provide orientations of the local axonal connections. The information can be used to drive a fiber tracking algorithm to delineate white matter connections. (c) The SDF template of the human brain averaged from 842 diffusion MRI scans (termed the HCP-842 template) shows structural characteristics of the human brain. The magnitude map of the HCP-842 template reveals structures such as hippocampus (HIP), thalamus (TH), red nucleus (RN), and substantia nigra (SN), which are consistent with the histology image from BigBrain slides (d). (e) The orientation map of the HCP-842 template allows for delineating the complicated structures, such as the clamping structure between the anterior commissures (AC) and the pre-commissural (PreC) and post-commissural (PostC) branches of the fornix. The structural characteristics are also illustrated by the SDFs of the HCP-842 template in (f).

Although the group-averaged SDFs appear smoother due to the averaging effect, they are still capable of resolving major crossing architectures. The number and percentage of voxels that contain more than one fiber orientations are listed in Table 1. These results were obtained by re-gridding the template at different resolutions to aggregate information about underlying fiber pathways in each voxel. The table shows that after re-gridding at 2-mm³ and 2.5-mm³ resolution, more than 80% of the white-matter voxels in the HCP-842 template had more than one distinct fiber orientation. These percentage values are consistent with previous estimates of 60~90% of voxels having multiple fiber orientations when sampled and reconstructed at a 2.4mm³ resolution (Jeurissen et al., 2013). It is noteworthy that the percentage of multi-fiber voxels dropped substantially at 1.5-mm³ and 1-mm³ resolutions. This can be explained by Fig. S2 showing how common branching (red fibers, Fig. S2A), turning (green fibers, Fig. S2A), and superimposing (yellow fibers, Fig. S2B) configurations can result in multiple fiber populations in 2-mm spatial resolution but not in the 1-mm resolution. This is because a larger voxel at 2-mm resolution can include a longer segment of tracks (e.g. Fig. S2A) or include a nearby fiber population (e.g. Fig. S2B) that results in multiple fiber populations resolved in the voxel.

Table 1:

Number of voxels with more than on fiber orientations resolved in different resolutions

Resolution	Voxels with more than one fiber orientations*	Total white matter voxels	Percentage (%)*
1 mm	76452	606662	12.60
1.5 mm	114856	195705	58.69
2 mm	74283	89306	83.18
2.5 mm	43551	49050	88.789

^*may include turning, crossing, or branching fibers

Qualitatively, the HCP-842 appears to resolve underlying neuroanatomical architecture with high fidelity in spatial resolution. Comparing a coronal slice of the HCP-842 (1-mm resolution, Fig. 2c) with a similar section from the BigBrain histology image (the 200-micron resolution version, Fig. 2d), we see that HCP-842 clearly delineates subcortical structures such as the hippocampus (HIP), substantia nigra (SN), red nucleus (RN), and thalamus (TH). The high spatial resolution of the orientation map is even more apparent at the anterior commissure (AC) (Fig. 2e), a small left-right connecting pathway clamped by the pre-commissural (PreC) and post-commissural (PostC) branches of fornix that run in the vertical direction (color-coded by blue). The clamping structure formed between AC and fornix is a benchmark for examining the spatial resolution of the template. Figure 2e resolves AC from the PreC and PostC branches, whereas Figure 2f shows the averaged SDFs at the same region depicting the structural characteristics of AC with the PreC and PostC branches of the fornix. The ability to resolve branches of fornix from AC reveals the intricate sensitivity of the HCP-842 to map detailed brain connections.

Supervised labeling and segmentation of major pathways

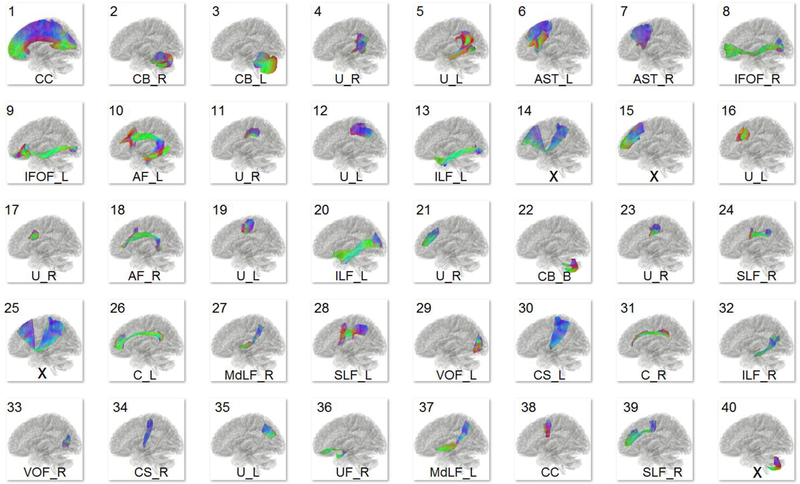
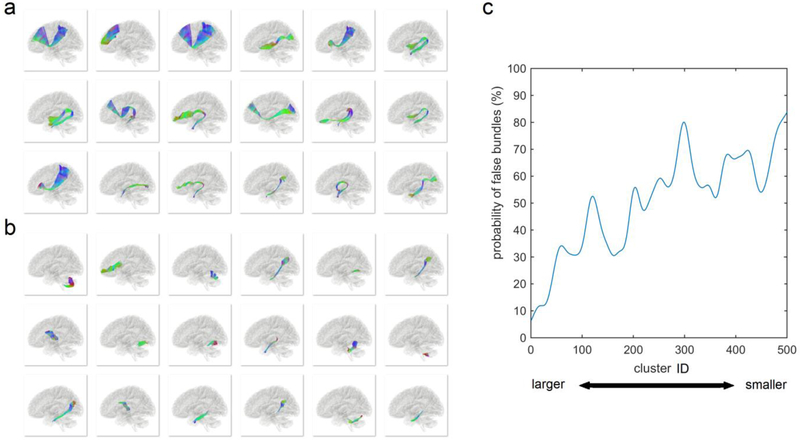
To isolate major and minor white matter fascicles, we applied whole-brain fiber tracking to the HCP-842 group-average template, producing a total of 550,000 fiber trajectories in the ICBM-152 space to achieve an average density of 1 track per voxel (Fig. 1c). A white matter mask was used to remove tracks that have premature terminations in the core white matter. The remaining whole-brain tracks were then automatically clustered by a single-linkage clustering algorithm, generating unique clusters of fiber bundles (Fig. 1d). The trajectories that were proximally close to one another were grouped. Each cluster could subsequently contain a different number of trajectories based on the anatomical proximity of the tracks. Figure 3 shows the largest 40 out of the 550 clusters as an example, where the size of a cluster is determined by the number of its containing tracks. Shorter pathways, such as the uncinate fasciculus, will receive less seeding counts in the tracking process and thus be estimated to have a smaller size. Many track bundles were also represented by more than one cluster component. For example, cluster #1 and #38 are both labeled as the corpus callosum. A team of clinical neuroanatomists then examined and labeled the clusters according to neuroanatomical nomenclature. Table S1 lists all labels used in naming the clusters and the relevant neuroanatomy literature used for examination. Label “X” indicates a false track, which may arise due to false continuations (Fig. 4a) or premature termination (Fig. 4b). Only the 550 largest clusters were used because the false rate (either false continuation or premature termination) increased substantially in clusters with a smaller size (Fig. 4c). The labeled clusters were subsequently merged according to their neuroanatomical label. Missing components of the large fiber bundles were tracked separately and merged to ensure completeness as per the literature (Fig. 1e).

Fig. 3.

The 40 largest clusters (selected from a total of 550 clusters) generated from automatic track clustering and their labels assigned by neuroanatomists. False connections are assigned by “X”, whereas the others assigned by their corresponding neuroanatomy abbreviations.

Fig. 4.

False connections due to (a) false continuation and (b) premature termination identified by the neuroanatomists. A false continuation is a common cause of false trajectories and often found in regions with two fiber population cross on top of each other. Premature termination is often due to a failure in resolving crossing or branching pattern in the white matter. (c) The probability of a cluster labeled as “false” increases substantially with decreased cluster size. This suggests we can discard smaller clusters as there are mostly false connections.

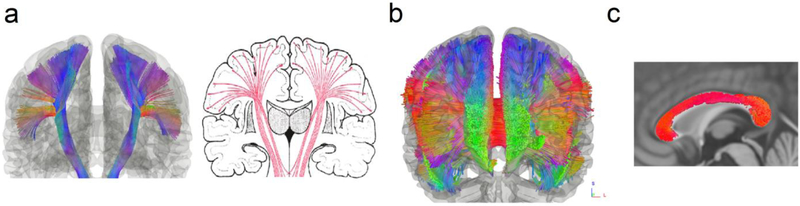
The high-angular-resolution quality of the atlas can be appreciated in the corticospinal and corticobulbar tracts generated from our pipeline (Fig. 5a). These show a fanning projection pathway from the precentral (motor) cortex along the cortical surface that is consistent with the anatomical evidence (right, modified from Gray’s Anatomy). The lateral fanning parts are known to cross with the horizontally-passing corpus callosum and cannot be reliably resolved using the traditional low-angular-resolution approaches due to their limited ability to resolve crossing fibers (Chenot et al., 2018). In addition, the coronal view of the corpus callosum (Fig. 5b) also shows a widespread fanning pattern, not otherwise trackable using the lower-angular-resolution methods. The midline portion of the corpus callosum tracks (Fig. 5c) shows matching volume with the ICBM-152 T1-weighted images, suggesting that the atlas can also provide volumetric measurements. Thus, the atlas appears to capture more complete portions of major pathways that are typically lost using traditional approaches.

Fig. 5.

The angular resolution of the structure connectome atlas illustrated. (a) The corticospinal and corticobulbar tracks (left) in the structural connectome atlas present a fanning pattern consistent with the known neuroanatomy (right). Mapping this fanning pattern requires high-angular-resolution scans to resolve the crossing configuration in the middle the pathway. (b) The coronal view of the corpus callosum mapped by the atlas shows a wide spreading fanning pattern, which cannot be mapped using a low-angular-resolution approach. (c) The mid portion of the corpus callosum matches well with the ICBM-152 T1-weighted images, suggesting that the track bundles in the atlas have volumes matching the standard template.

A population-averaged atlas of macroscopic structural connectome

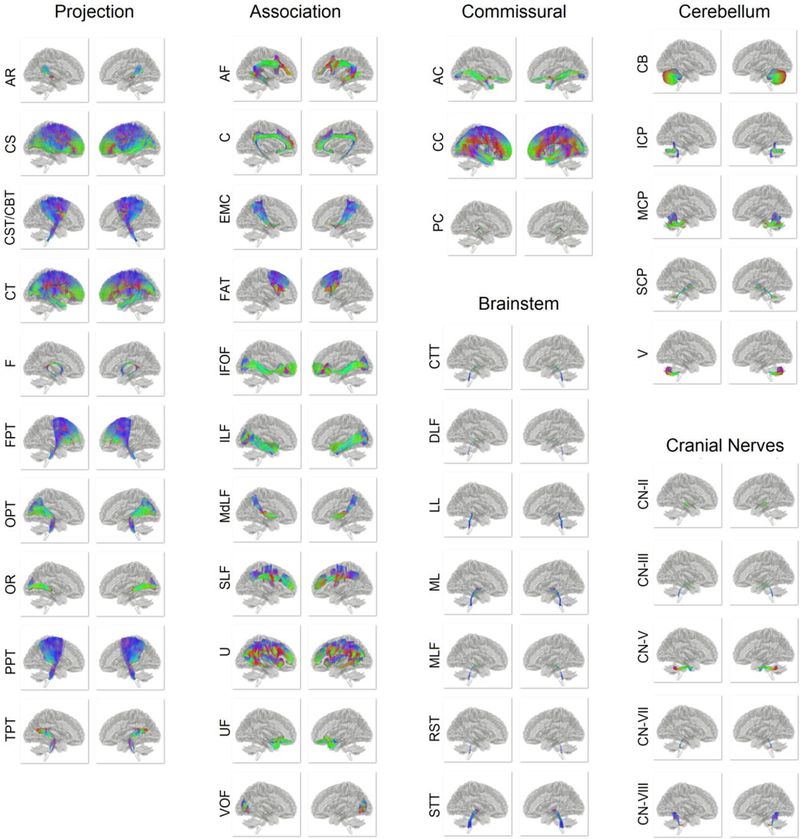
The full atlas of the structural connectome is shown in Fig. 6 (abbreviation listed in Table S1) and includes the most comprehensive map of white matter pathways yet reported. This includes the projection pathways that connect cortical areas with subcortical nuclei and brainstem. Acoustic radiation has not been previously reported in tractography due to the complicated crossing pattern of the pathway. The association pathways connect disparate cortical areas, including a set of U-fibers (U). The commissural pathways connect the two hemispheres and include the corpus callosum, anterior commissure, and posterior commissure. Posterior commissure has not been previously reported in tractography. The cerebellar pathways include the cerebellar tracts (CB) and peduncles (SCP, MCP, ICP), and they provide the major input, output, and internal connectivity of the cerebellum. We were even able to resolve several brainstem pathways, such as central tegmental tract (CTT), dorsal longitudinal fasciculus (DLF), lateral lemniscus (LL). Finally, we discovered a limit of the current spatial resolution, where a set of cranial nerves including CN III, CN VII, and CN VIII were successfully identified, but CN I, IV, VI, and IX could not be identified due to insufficient spatial resolution. The detailed connective routes of the structural connectome atlas are presented in Supporting Information, including projection pathways (Fig. S3), association pathways (Fig. S4), commissural pathways (Fig. S5), cerebellar pathways (Fig. S6), brainstem pathways (Fig. S7), and cranial nerves (Fig. S8). It is worth noting that several cranial nerves cannot be found in the HCP-842 template due to the limitation of its spatial resolution. The full atlas, including the track trajectories and connectograms, is publicly available at http://brain.labsolver.org.

Fig. 6.

Overview of the population-averaged structural connectome atlas categorized into the projection, association, and commissural pathways in addition to cerebellum pathways, brainstem pathways, and cranial nerves. Each pathway contains thousands of trajectories showing the representative connections of the 842 subjects between brain regions in a standard space. The trajectories are color-coded by the local orientation (red: left-right, green: anterior-posterior, blue: inferior-superior). This connectome atlas provides normative connection routes between brain regions that can facilitate network analysis, simulation and modeling.

Neuroanatomical constraints on connective topology

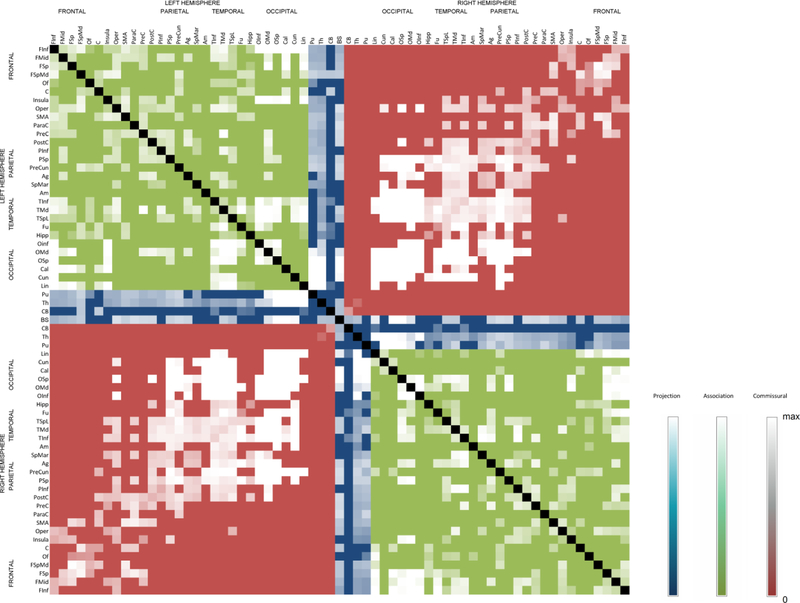
Figure 7 shows region-to-region connectivity matrix weighted by the SDF magnitude along the fiber pathways, segmented into the projection, association, and commissural pathways. The abbreviations for brain region are listed in Table S2. Higher intensity (white) indicates greater SDF magnitude along the pathway.

Fig. 7.

The connectivity matrix constructed from the human connectome atlas. The color division shows the division of three major track systems—projection (blue), association (green), and commissural (red)—in the human brain. The intensity shows the between region connectivity quantified the magnitude of the along-track diffusion properties quantified by spin distribution functions.

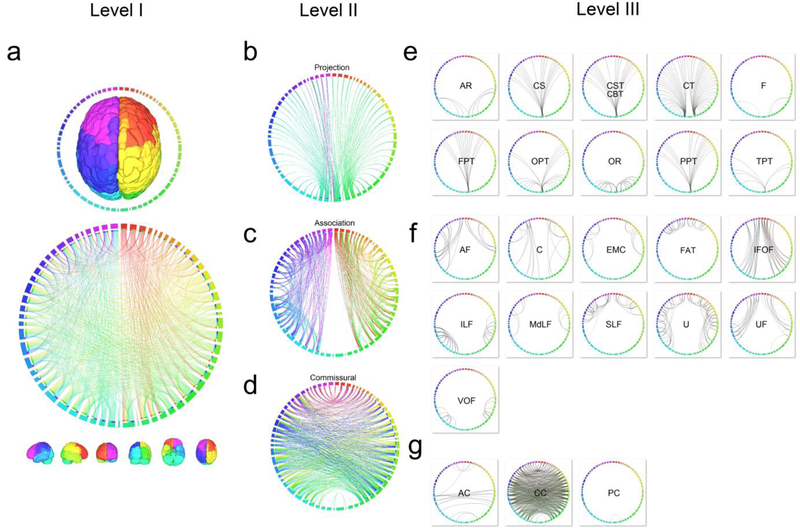
The connectograms of the structural connectome are illustrated in a multi-level approach (Fig. 8). The connectogram of the whole brain pathways illustrates the first level of the gross network topology (Fig. 8a, the high-resolution version shown in Fig. S9). The overall figure shows a dense network topology, and its network characteristics cannot be readily visualized due to the high complexity of the brain network at this level. The connectograms of the projection, association, and commissural pathways in Fig. 8b, 8c, and 8d depict the second level of the network topology (high-resolution details in Fig. S10), and within this level, the connectograms start to reveal important network features. The projection pathway in Fig. 8b indicates hub structures at thalamus, putamen, and brainstem, illustrating the role of these regions in integrative sensorimotor function between the cerebral cortex and corresponding peripheral systems. The association pathway, as shown in Fig. 8c, forms clusters within each hemisphere and contributes a substantial amount of clustering coefficient and local efficiency (Table 2), elucidating its small-worldness that involves multiple relevant gray matter regions. The commissural pathways, as shown in Fig. 8d, serve as a bridge connecting both hemispheres and provide global efficiency (Table 2) to integrate information across cerebral hemispheres. In Fig. 8e, the connectograms of each fiber bundle are further divided to show the third level of the network topology in much more detail, and the illustration reveals a consistent hub formation for different fiber bundles, albeit with an alternative connectivity pattern to the cerebral cortex. Fig. 8f also shows clustering topology within different cortical areas, whereas Fig. 8g shows bridge-like symmetric structures of inter-hemisphere connections. Together, these unique topologies based on the class of fiber pathway highlights the rich taxonomy of structural connectome in the human brain that reflects unique information processing constraints.

Fig. 8.

The multi-level connectograms of the human structural connectome. (a) The first level of the overall structural connectome shows a dense connections pattern in the average structure connectome. (b) The second level of the connectogram shows the network characteristics in each pathway system. The projection pathway forms a hub structure at thalamus, putamen, and brainstem. The association pathway is constituted of numerous clusters in the brain networks. The commissural pathway has long-range connections between hemispheres that provide global efficiency. (c) The third level of the connectogram reveals the network pattern of each fiber pathways under the projection, association, and commissural system. The connection patterns inherit the characteristics of their belonging pathway system shown in the second level connectogram.

Table 2:

Change of network measures with/without projection, association, and commissural pathways

Pathway System	Clustering Coefficient (%)	Network Characteristic Path Length (%)	Global Efficiency (%)	Local Efficiency (%)	Small Worldness (%)
Projection	−0.30	−5.38	3.35	4.60	5.08
Association	62.27	−7.95	6.88	57.90	66.91
Commissural	−18.65	−10.57	8.11	−7.47	−8.24

A positive value indicates an increase of network measures with the pathways added.

Discussion

Here we present the first complete population-level atlas of the human structural connectome and its network topology, delineating fiber pathways within the cerebrum, cerebellum, brainstem, and a subset of cranial nerves. The fiber trajectories were generated from a group-averaged template of 842 subjects using a fiber tracking algorithm that has been shown to minimize tracking errors relative to other methods (Maier-Hein, 2016). Using an automated clustering approach, tracks were grouped into small bundles and subsequently labeled by a team of clinical neuroanatomists and vetted according to their neuroanatomic nomenclature. This combination of optimizing strategies allowed us to construct a high-quality structural connectome atlas of the human brain. This addresses a critical need in connectivity estimates that used to suffer from a high false positive error rate in diffusion MRI fiber tracking. The group average further addresses a common concern in conventional cadaver studies: whether pathways shown in cadaver dissection can be representative enough to the general population. A group-averaged tractography atlas can complement cadaver study by offering an overview picture of common brain pathways derived from a large population. The atlas will thus serve as a stepping stone for future studies to look into individual differences in the structural connectome. To this end, this HCP-842 tractography atlas and its associated data set will be made publicly available (http://brain.labsolver.org) to promote future connectomic studies and assist neuroscientists to gain insight into the structural topology of the human brain.

We should note that several human white matter atlases have been previously released. These include voxel segmentations on individual subjects that label the core of major pathways (Mori et al., 2009; Mori et al., 2008; Peng et al., 2009; Zhang et al., 2011) or tractography atlases based on tracking individual subjects data (Catani et al., 2002; Guevara et al., 2012; Thiebaut de Schotten et al., 2011; Zhang et al., 2008). Our atlas expands on these currently available resources by providing a comprehensive characterization of normative major and minor white matter fascicles constructed from a large sample of 842 individuals who were imaged using high angular and high spatial resolution diffusion acquisitions, allowing for the resolution of multiple fiber populations within a white matter region to delineate the intertwining architecture of human white matter. This novel population-level description of the structural connectome characterizes both the normative 3D trajectories of white matter fascicles and delineates how gray matter regions in the cerebrum, cerebellum, and brainstem are physically connected by nearly all macroscopic white matter pathways. For the first time, this atlas offers structural detail and network topology of both large and small pathways, such as the clamping structure between the fornix and the anterior commissure that cannot be discerned from individual studies due to lower resolution and signal-to-noise ratio of conventional diffusion MRI.

While overcoming many challenges, our current approach still has its limitations. First, our atlas does not address the variability of the fiber pathways across subjects. While it is entirely feasible to repeat the fiber tracking procedures for each of the HCP subjects, the labeling of 550 clusters of all 842 subjects may require a substantial amount of expert efforts. This labor-intensive approach would require several years worth of human labor to complete. Thus an automated approach to replace expert labeling would better assist this future endeavor, but developing such an automated classifier is well beyond the scope of the current study. Another issue we did not address in this study is whether 842 subjects is representative enough or whether it could be feasible to get a normative atlas with fewer or more subjects. We have previously constructed templates using 60 subjects (Beukema et al., 2015), 90 subjects (Yeh and Tseng, 2011a), and 488 subjects (Meola et al., 2015b) and conducted template-space fiber tracking (Wang et al., 2016a; Wang et al., 2012; Yoshino et al., 2016a). There were substantial differences observed between these templates that appeared to be due, in large part, to variability in the averaging. Thus with larger samples, the estimate of the true population mean should become more stable. Therefore we included the most number of subjects from the highest directional resolution data sets that we could at the time we started the project (i.e., the 900 subject HCP sample). In addition to issues related to individual variability, there could be errors in manual labeling of the clusters, and thus there should be better ways to address the inter-observer differences, as we only resolved differences by a group discussion with the goal of reaching a consensus on every track. This would save some time, but not enough to make this feasible and extensible enough to use in applied studies. Of course, there are also controversies in neuroanatomical structures (Meola et al., 2015a) that can be further complicated by individual differences. Thus, we have made all of the clusters data, their labels, and the entire atlas publicly available, thereby allowing for future modifications to improve the atlas as well as the development of better tools for automated segmentation.

Moreover, the fiber tracking algorithm used in this study could still have false positive and false negative results. While expert assistance may address part of this issue, it cannot handle the false negative problem, and there could be missing tracks in our atlas. For example, several cranial nerves that are smaller than 1-mm in width were not detected by our method. These can only be tracked using images acquired at a much higher resolution. Of course, the accuracy of spatial registration can be improved through further algorithmic refinements, and other template construction methods could be explored in future work (Archer et al., 2017; Yang et al., 2017). Also, the spatial registration method used in QSDR only relies on anisotropy information; however, it is possible to include structural images or the entire diffusion data (Park et al., 2003) to boost the accuracy of the registration method. The accuracy of track clustering can also be improved using a more sophisticated method (Siless et al., 2018). We should point out, however, that these refinements would only further to improve the reliability and resolution of the results reported here, rather than point to a critical failing of the approach described here.

In addition, the expert examination may have its own errors, especially for identifying minor pathways and branches. It is also possible that the branching patterns of the white matter pathways differ person-to-person, and the population-averaged SDF template for whole-brain tractography may miss some branches. These missing branches could be obtained by applying the same tractography algorithm to the non-averaged or less-averaged datasets. Finally, the atlas reveals only three levels of the network topology, as more recent studies have focused on detailed subcomponents of the fiber bundles (e.g. SLF I, II, and III)(Fernandez-Miranda et al., 2015; Wang et al., 2016b). Although the spatial resolution of the atlas can be improved, it provides a macroscopic framework for future connectomic studies to explore microscopic connections under its categorical system.

Despite these limitations, a vetted atlas of the population-level structural connectome has many benefits for clinical, scientific, and educational applications. The atlas can be used to derive a representative pattern of network measures to assist graph theoretical analysis of clusters and hubs in the brain connectome. It can be used to confirm or explore potential cortical connections from functional measures (e.g., functional connectivity), augmenting current functional-structural correlative inferences or supplementing prior anatomical connectivity expectations in studies that do not have access to individual dMRI data. This, for example, may enable future investigations into the correlation of white-matter lesions with known gross-white matter structures. Another advantage of the current atlas is that it includes a normative template of diffusion distribution across the brain. This may allow for future efforts comparing normal diffusion patterns with those from the neurological or psychiatric pathologies. Finally, in science education, the atlas is a novel resource superseding conventional 2D slice-based histological atlases. The trajectory information provides panoramic views on the relative location of each white matter bundle, allowing for an in-depth understanding of the white matter structure.