Mass-Balance Models for Scrutinizing Supramolecular (Co)polymerizations in Thermodynamic Equilibrium

Conspectus

Recent years have witnessed increasing attention on supramolecular polymerization, i.e., the formation of one-dimensional aggregates in which the monomeric units bind together via reversible and usually highly directional non-covalent interactions. Because of the presence of these reversible interactions, such as hydrogen bonding, π–π interactions, or metal coordination, supramolecular polymers exhibit numerous desirable properties ranging from high thermoresponsiveness to self-healing and great capacity for processability and recycling. These properties relate to intriguing experimentally observed nonlinear effects such as the monomer-dependent presence of a critical temperature for aggregation and a solvent- and temperature-tunable aggregate morphology. For coassemblies this is complemented with monomer-ratio- and monomer-compatibility-dependent internal order as well as majority-rules-type chiral amplification. However, the dynamic nature of the (co)polymers and the intricate interplay of many interactions make these effects difficult to rationalize without theoretical models.

This Account presents recent advances in the development and use of equilibrium models for supramolecular copolymerization based on mass balances, mainly developed by our group. The basic idea of these models is that we describe a supramolecular (co)polymerization by a set of independent equilibrium reactions, like monomer associations and dissociations, and that in thermodynamic equilibrium the concentrations of the reactants and products in each reaction are coupled via the equilibrium constant of that reaction. Recursion then allows the concentration of each possible aggregate to be written as a function of the free monomer concentrations. Because a monomer should be present either as a free monomer or in one of the aggregates, a set of n equations can be formed with the n free monomer concentrations as the only unknowns. This set of mass-balance equations can then be solved numerically, yielding the free monomer concentrations, from which the complete system can be reconstituted.

By a step-by-step extension of the model for the aggregation of a single monomer type to include the formation of multiple aggregate types and the coassembly of multiple monomer types, we can capture increasingly complex supramolecular (co)polymerizations. In each step we illustrate how the extended model explains in detail another of the experimentally observed nonlinear effects, with the common denominator that small differences in association energies are intricately amplified at the supramolecular level. We finally arrive at our latest and most general approach to modeling (cooperative) supramolecular (co)polymerization, which encompasses all of our earlier models and shows great promise to help rationalize also future systems featuring ever-increasing complexity.

Introduction

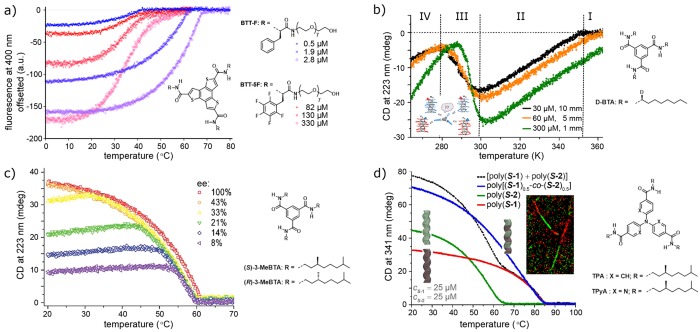
Supramolecular polymers are one-dimensional aggregates in which the monomeric units bind together via reversible and usually highly directional non-covalent interactions. A wide variety of naturally occurring and synthetically made molecules are known to form such aggregates, typically driven by hydrogen bonding, π–π interactions, metal coordination, and/or hydrophobic interactions. The reversible nature of these non-covalent interactions provides supramolecular polymers with a wide array of desirable properties ranging from high thermoresponsiveness to self-healing and a great capacity for processability and recycling.¹⁻³ However, a prerequisite for their wide applicability is a thorough understanding and ensuing control of their behavior. A common way to investigate supramolecular (co)polymers has been to follow quantities such as the absorbance, circular dichroism, or fluorescence in titration and cooling experiments. Figure 1 illustrates a selection of nonlinear phenomena discovered in this way over the past decade, which have been attributed to monomer-dependent high thermoresponsiveness with or without a critical temperature for polymer formation (Figure 1a),⁴ solvent- and temperature-tunable aggregate morphology (Figure 1b),⁵ majority-rules-based copolymerization of enantiomers (Figure 1c),⁶ and monomer-ratio- and monomer-compatibility-dependent internal order within copolymers (Figure 1d).⁷ Because of the dynamic nature of supramolecular (co)polymers and the intricate interplay of many interactions, the use of models has proven indispensable to understand the molecular basis of these effects.

Figure 1.

Examples of nonlinear behavior in supramolecular (co)polymerizations. (a) Cooling curves for C₃-symmetric benzotrithiophenes BTT-F and BTT-5F with and without a sharp elongation temperature, respectively, at various concentrations in water (data obtained from ref (4)). (b) Cooling curves for deuterated benzenetricarboxamides (BTAs) in heptane indicating temperature-dependent aggregate morphologies. Adapted from ref (5). Copyright 2013 American Chemical Society. (c) Cooling curves of majority-rules-based copolymerization of two BTA enantiomers. Adapted from ref (6). Copyright 2010 American Chemical Society. (d) Cooling curves and super-resolution microscopy indicating the formation of supramolecular block copolymers from two triarylaminetriamide-based monomers. Adapted from ref (7). Copyright 2018 American Chemical Society.

Various models have been proposed in the literature to describe supramolecular (co)polymerizations. For the aggregation of a single monomer type, kinetic and thermodynamic models have shown success in distinguishing distinct mechanisms.⁸⁻¹⁷ Models for the coassembly of multiple monomer types are typically restricted to the thermodynamic equilibrium state and are often based on statistical mechanical approaches using partition functions and the transfer matrix method.¹⁸⁻²⁹ Here we advocate a more direct computation of the concentrations of monomers in equilibrium occurring in copolymers via the law of mass action. We provide a concise overview of the resulting mass-balance models that we have derived^5,7,30−33 over the years to explain the experimentally observed effects in Figure 1. Following a didactic approach, we start by introducing the mass-balance approach and subsequently apply that to increasingly complex supramolecular (co)polymerizations. Starting from aggregation of a single type of monomer into a single aggregate type and proceeding through competitive formation of multiple aggregate types and coassembly of two monomer types, we systematically arrive at our recently published³⁴ most general copolymerization model, which encompasses all of those earlier models.

Thermodynamic Equilibrium of Chemical Reactions

The equilibrium states of coupled chemical reactions have been studied extensively in the literature. In the general case, m chemical species (“molecules”) M₁, ..., M_m are built out of n building blocks (“atoms”) B₁, . . ., B_n, where each species consists of a given fixed number of building blocks and there exist r equilibrium reactions with positive equilibrium constants between these species. The reactions leave the number of building blocks invariant, i.e., for each reaction the total number of building blocks occurring in the reactants equals the total number of building blocks occurring in the products. The task is to compute the concentrations of the various species in thermodynamic equilibrium given the total amount of each building block.

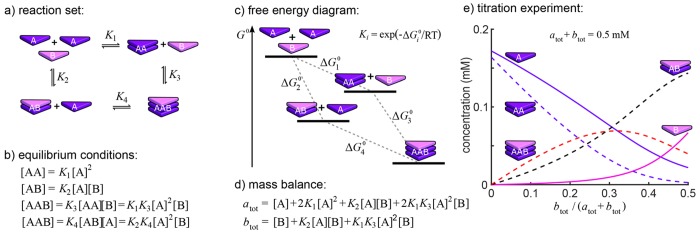
Consider as an example the case with n = 2 building blocks (A and B), m = 5 species (A, B, AB, AA, and AAB), and r = 4 bimolecular equilibrium reactions between these species, as illustrated in Figure 2a. The law of mass action dictates that in equilibrium, for sufficiently dilute well-mixed systems, the concentrations of the species satisfy the equilibrium conditions shown in Figure 2b. Apart from showing that the concentrations of all species can be expressed in terms of the concentrations of the free building blocks ([A] and [B]), these equilibrium conditions imply that the four reactions are not independent. Both routes to construct AAB lead to formulas for the concentration of AAB in terms of the concentrations of A and B, and these relations can only hold both if K₁K₃= K₂K₄. This is the detailed balance condition (see Wegscheider³⁵ and Onsager³⁶), which states in the general form that the product of the equilibrium constants along two different reaction sequences leading to the same final result must be equal. If the equilibrium constants K_i are related to the corresponding standard free energy gains ΔG_i^° by K_i = exp(−ΔG_i/RT), the condition boils down to ΔG₁^° + ΔG₃ = ΔG₂^° + ΔG₄. This means that the total gain in free energy is independent of the route via which species AAB is formed (Figure 2c), which is required for the model to have physical and chemical meaning.³⁷

Figure 2.

Example system of coupled chemical equilibrium reactions illustrating detailed balance and the mass-balance approach. (a) Reaction set for the formation of AAB trimers from A and B monomers via bimolecular equilibrium reactions. (b) The conditions on equilibrium concentrations. (c) Free energy diagram. (d) Mass-balance equations for the two building blocks A and B. (e) Equilibrium concentrations of the five species in a titration experiment as solved from these two mass-balance equations for ΔG₁^° = −21 kJ·mol^–1, ΔG₂ = −28 kJ·mol^–1, and ΔG₃^° = −30 kJ·mol^–1 at T = 293 K and a total concentration of 0.5 mM.

Omitting any one of the four reactions will not change the equilibrium concentrations of the species. As it is impossible to omit more reactions without changing the equilibrium state, this example constitutes three independent reactions. The equilibrium concentrations of AA, AB, and AAB are thus given by the first three relations in Figure 2b. These equations, which relate the concentrations of the various species, are commonly denoted as “mass-action laws”.

The mass-action laws alone are not sufficient to determine the concentrations of all species for given total concentrations of the building blocks A and B, i.e., a_tot and b_tot. To account for the total amounts of building blocks A and B in the system, the notion of equivalent concentration is introduced. The equivalent concentration of a building block in a species is defined as the concentration of that building block that results if that species is broken down into its individual building blocks. For instance, in our example the equivalent concentrations of A and B in AAB are 2[AAB] and [AAB], respectively, since each AAB contains two A building blocks and only one B building block. Using this notion of equivalent concentration, the mass-balance equations can be formulated as follows:

For each building block type, the sum of its equivalent concentrations in all species must be equal to the given total building block concentration.

If there is an independent reaction for each species that is not a building block, these equations have a unique solution.³⁸⁻⁴⁰ The mass-balance equations form a set of nonlinear algebraic equations that can be solved by a suitable numerical method. For the current example, this leads to the mass-balance equations for [A] and [B] provided in Figure 2d. In Figure 2e the concentrations of all five species, found by numerically solving the mass-balance equations, are shown as functions of the fraction of B building blocks in the solution at constant overall concentration of A and B. This illustrates that the mass-balance approach can be used to delineate the concentrations of all individual species, which can be nicely visualized in what we call speciation plots. Some other examples of finite coassembly, fitted to experimental data, are given in refs (41−44).

In the sequel we will use this general scheme, which is thus based on the assumption that the reactions take place in a homogeneous mixture of sufficiently dilute reactants, to derive models to investigate the equilibrium properties of supramolecular (co)polymers, i.e., (co)assemblies of monomers into one-dimensional aggregates that in principle can grow unlimitedly long. These models thus do not describe metastable (kinetically trapped) or other out-of-equilibrium states. We assume that copolymers are directed, e.g., by the direction of intermonomeric hydrogen bonds, from a bottom element to a top element and describe their growth by a minimal independent set of reactions consisting of dimerizations and elongations at the top. Other growth mechanisms like monomer insertion/deletion⁴⁵ and/or fragmentation/coagulation⁴⁶ may occur but will not change the thermodynamic equilibrium state because of the detailed balance conditions.

One-Component Supramolecular Polymerization

We start by considering a single monomer type (A) that can aggregate into a single polymer type. As pioneered by Oosawa and Kasai,⁸ a set of independent reactions describing such a supramolecular polymerization consists of a dimerization step (A + A ⇄ A₂) and elongation steps (A_i + A ⇄ A_i+1), where A_i represents an aggregate consisting of i monomers. Though in principle the equilibrium constants of all these reactions could be distinct, successful models include the isodesmic case, where all of the equilibrium constants are equal, and the cooperative case with two distinct equilibrium constants, one for the first steps up to the formation of a critical nucleus and the other for the subsequent elongation steps.^{8,11,12,47−50}

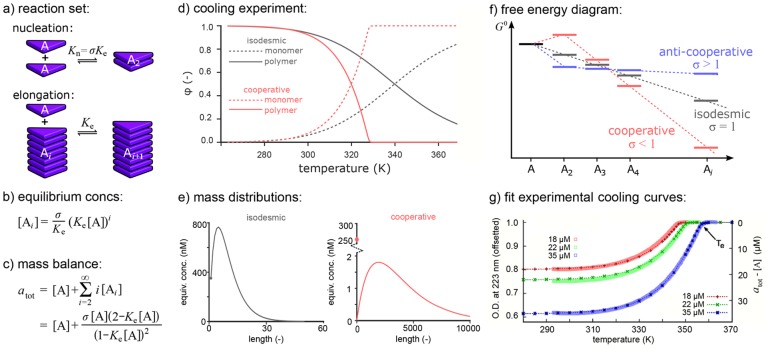
For the case with nucleus size = 2, the reaction scheme is illustrated in Figure 3a. The ratio of the equilibrium constants for the nucleation step (K_n) and the elongation steps (K_e) determines the cooperativity of the system (σ = K_n/K_e). For σ < 1 the system is called cooperative, whereas for σ > 1 it is called anticooperative; for σ = 1 the isodesmic case is reobtained. The difference among cooperative, isodesmic, and anticooperative aggregation is elucidated by considering the total free energy gain (using K_i = exp(−ΔG_i^°/RT)) in the construction of a polymer as a function of the aggregate length (Figure 3f). For the isodesmic case, where all of the equilibrium constants are equal, the aggregate’s free energy decreases linearly with its length. For the cooperative case, the free energy also decreases linearly for aggregate lengths above the nucleus size but decreases slower or even increases up to the nucleus size. Contrastingly, in the anticooperative case the energy gain is largest in the nucleation steps.

Figure 3.

Model for one-component supramolecular polymerization. (a) Reaction set. (b) Polymer equilibrium concentrations. (c) Mass balance equation. (d) Cooling curves for isodemic (ΔH_iso^° = −65 kJ·mol^–1 and ΔS_iso = −100 J·mol^–1·K^–1) and cooperative (ΔH_e^° = −75 kJ·mol^–1, ΔS_e = −133 J·mol^–1·K^–1, and NP = −30 kJ·mol^–1) polymerizations for a_tot = 10 μM. (e) Mass distributions of those polymers at 293 K, i.e., equivalent concentrations of monomers in polymers as a function of the length of those polymers. (f) Schematic free energy diagram for isodemic and (anti)cooperative polymerizations. (g) Fit of the one-component model to experimental cooling curves for BTAs at three different concentrations. Adapted with permission from ref (30). Copyright 2011 Springer Nature.

The concentrations of the A_i aggregates can be computed from the reaction equilibria as [A₂] = K_n[A]² and [A_i+1] = K_e[A][A_i] for all i ≥ 2. Together this allows the concentrations of all possible aggregates to be expressed as functions of the monomer concentration (Figure 3b). The mass-balance implies that the total concentration of A in the system (a_tot) should be equal to the equilibrium monomer concentration ([A]) plus the sum of the equivalent concentrations of A for aggregates of all different lengths. Because the equivalent concentration of A in the aggregate A_i is given by i[A_i] and all of the [A_i] can thus be expressed in terms of the monomer concentration, this yields a single mass balance equation with the monomer concentration [A] as a single unknown (Figure 3c). Using algebra, the summation over all polymer lengths in this formula can be replaced by a single rational fraction (Figure 3c), which can be solved by numerical or analytical methods. For given total concentration of building blocks a_tot, this thus yields the equilibrium monomer concentration [A], from which subsequently the concentrations of all other polymers A_i can be computed, as well as properties such as the degree of polymerization (φ = ∑_i = 2^∞i[A_i]/a_tot) and the distribution of the polymer lengths.

The mass-balance equation for this one-component model has three parameters, viz. the equilibrium constant K_e, the cooperativity σ, and the total monomer concentration a_tot. Varying these parameters and repeatedly solving the mass-balance equation for each parameter combination allows different speciation plots to be computed. For instance, if K_e and σ depend on the temperature T as K_e = exp(−ΔG_e^°/RT) and σ = exp(NP/RT), where NP is the nucleation enthalpy penalty, the behavior of the system as a function of temperature can be shown in a cooling curve plot, such as in Figure 3d. Such cooling curves of the degree of polymerization (Figure 3d) clearly show that an isodesmic polymerization has a sigmoidal dependence on the temperature, while the hallmark of a cooperative polymerization is a sharp transition from only monomers above a so-called elongation temperature (T_e) to a sharp increase in the amount of polymers below this temperature.⁵¹ Both types of curves resemble experimentally obtained cooling curves (e.g., Figure 1a), and in ref (31) we have released a tool to fit such experimental curves with this one-component model (Figure 3g) to quantify the thermodynamic parameters of such supramolecular polymerizations. Similarly, for a fixed temperature the behavior as a function of the total concentration a_tot can be shown in a titration curve. This also shows much sharper transitions for cooperative polymerization, where aggregates primarily form above a critical concentration of 1/K_e, compared with isodesmic polymerization, where significant amounts of monomers and aggregates coexist at all concentrations.⁴⁷ An additional advantage of the model is that it allows one to zoom in on the individual polymers in the system. For example, zooming in on the mass distribution at fixed temperature and concentration shows that polymers that grow via a cooperative mechanism are much longer than aggregates that grow via an isodesmic mechanism (Figure 3e).

Pathway Complexity

A first generalization of the above one-component model is the case where a single monomer type A can form two distinct aggregate types. Though the exact nature of the aggregates is irrelevant here, we will denote these aggregates (with length i) as J_i and H_i, respectively, as the distinct aggregate types may for instance be J-type coupled aggregates and helical aggregates. As an example we consider the case that one polymer type (J) grows isodesmically while the other polymer type (H) grows cooperatively (Figure 4a),⁵² i.e., the two cases considered in the previous section. It should be noted that although there are no direct reactions between aggregates of the two distinct polymer types, these aggregates are linked to each other via the free monomers as they are built from the same monomer type.

Figure 4.

Single monomer type aggregating via competing pathways. (a) Reaction set for the formation of isodesmic and cooperative aggregates from the same monomer. (b) Conditions on the equilibrium concentrations. (c) Cooling curves (parameters as in Figure 3). (d) Monomer concentration, compared with those of the pure isodesmic and pure cooperative systems. (e) Mass-balance equation. (f) Fit to the data in Figure 1b. Adapted from ref (5). Copyright 2013 American Chemical Society.

Analogous to the previous section, the concentrations of all polymers can be expressed in terms of the free monomer concentration [A] (see Figure 4b). Because a monomer should either be a free monomer or be present in one of the J-aggregates or in one of the H-aggregates, the mass-balance equation for this system states that the total concentration of A in the system (a_tot) should be equal to the equilibrium monomer concentration ([A]) plus the sum of the equivalent concentrations of A for J-aggregates of all different lengths and the sum of the equivalent concentrations of A for H-aggregates of all different lengths (Figure 4e). Using algebra, the two summations over all polymer lengths in this formula can be replaced by two single rational fractions, after which the equation can be solved numerically, providing the free monomer concentration [A] for a given a_tot.

As an example, we consider the case where the temperature dependence of K_e is stronger than that of K_iso, leading to a temperature-dependent competition between the J and H polymers. This competition results in a sharp change in the occurring polymers at around T = 287 K (Figure 4c). This sharp transition can be understood by zooming in on the temperature dependence of the concentration of free monomer. Figure 4d shows the free monomer concentration for this competition model along with the free monomer concentrations for a model with only the isodesmic pathway and a model with exclusively the cooperative pathway. Clearly, the monomer concentration in the presence of the competing pathways follows the monomer concentration for the aggregate type with the lowest monomer concentration. Consequently, the dominant aggregate type changes at the temperature where the monomer concentrations corresponding to the individual aggregate types cross, i.e., close to the temperature where the free energies for the two pathways are equal.⁵²

This mass-balance approach can be adapted straightforwardly to competition between two distinctly cooperative aggregate types⁵³ or to competition between cooperative and anticooperative aggregate types⁵⁴ or even pure dimer formation.⁵⁵ The approach can also readily be extended to more polymer types. An intriguing example thereof was provided by Nakano et al.,⁵ who studied the self-assembly of BTAs with deuterium as the stereocenter (Figure 1b). From the fit with a model for the aggregation of chiral BTAs in four different polymer types, i.e., two opposite helicities for two types of helical polymers (denoted as 35 and 45, respectively), the rather concentration-independent transition temperature between regions II and III in Figure 1b appears to be the temperature at which the two polymer types are equally stable (Figure 4f). Fitting these extended one-component models to experimental data thus allows the elucidation of competing aggregate types in supramolecular polymerizations and quantification of (small) differences in stabilities between those aggregate types.

Majority Rules

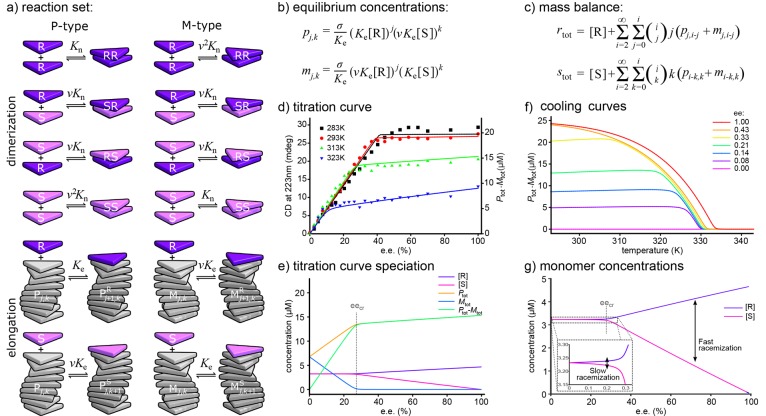
A second generalization of the one-component model is the extension to multiple monomer types. A relatively simple but fascinating example is the copolymerization of two enantiomers (the R and S enantiomers, denoted as R and S, respectively) into helical supramolecular aggregates. If their stereocenter is sufficiently close to the core of the supramolecular polymers, such enantiomers will have a preference for aggregates with either P or M helical sense (denoted as P and M, respectively). If the R enantiomers favor the P-type aggregates, their mirror-image S enantiomers will favor the M-type aggregates. Aggregation of R enantiomers into P-type aggregates and the equivalent aggregation of S enantiomers into M-type aggregates could be described using two independent one-component models with the same equilibrium constants. However, if the stereocenter is sufficiently small, R monomers can also mix into M-type aggregates and, mutatis mutandis, S monomers into P-type helices. Such a copolymerization could be described (Figure 5a) by some additional dimerization reactions to account for all possible dimers and, assuming that the elongation of an aggregate is independent of its composition, just two additional reactions for elongation of aggregates with their respective nonpreferred enantiomers. The equilibrium constants for these elongations with nonpreferred enantiomers can then be assumed to be a factor ν = exp(MMP/RT) smaller than those for the preferred enantiomers, where the mismatch penalty (MMP) is the energetic cost of adding a monomer to an aggregate of its nonpreferred helicity compared with its preferred helicity.

Figure 5.

Majority-rules copolymerization. (a) Reaction set for the supramolecular polymerization of two enantiomers (R and S) into aggregates with two opposite helical senses (P and M). The gray parts represent aggregates of arbitrary length and composition. (b) Equilibrium concentrations of copolymers of both helical senses containing jR monomers and kS monomers. (c) Mass-balance equations. (d) Fitting of the model (lines, ΔH_e^° = −66 kJ·mol^–1, ΔS_e = −101.5 J·mol^–1·K^–1, NP = −35 kJ·mol^–1, and MMP = −2.1 kJ·mol^–1) to experimental CD titration curves (symbols). (e) Speciation plot for the fit at 313 K. (f) Cooling curves corresponding to data in Figure 1c. (g) Zoom in on the monomer concentrations in (e) explaining the experimental observation of two time scales in racemization. Panels (d–f) adapted with permission from ref (30). Copyright 2011 Springer Nature.

The concentration p_j,k (respectively m_j,k) of each aggregate type denoting a P-type (respectively M-type) aggregate consisting of jR enantiomers and kS enantiomers can then be expressed in terms of the free monomer concentrations [R] and [S] (Figure 5b). Because for both enantiomers it again holds that the molecules should be present either as a monomer, in one of the P-type aggregates, or in one of the M-type aggregates, two mass-balance equations can be derived (Figure 5c) with the free monomer concentrations [R] and [S] as the two unknowns, which can be solved numerically for given overall concentrations r_tot and s_tot, as has been illustrated by Markvoort et al.³⁰ and ten Eikelder et al.³¹

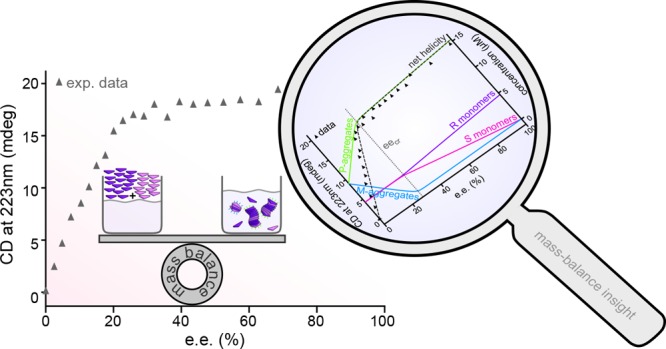
Solving the mass-balance equations for different ratios of r_tot and s_tot and various temperatures thus allows cooling curves of for instance the difference in equivalent concentrations of the P- and M-type aggregates to be drawn (Figure 5f). As circular dichroism (CD) spectroscopy probes such excess helical sense experimentally, those model curves can be directly compared to the CD cooling curves at different enantiomeric excesses (ee = (r_tot – s_tot)/(r_tot + s_tot)) in Figure 1c. Rather than as a function of temperature, the CD could also be followed as a function of ee. Figure 5d clearly shows that a small excess of one enantiomer leads to a strong bias toward copolymers with helicity corresponding to the major enantiomer and that the CD data for such a so-called majority-rules experiment can be excellently fitted over a range of different temperatures using only a single parameter, i.e., the MMP.⁶ The other parameters (i.e., σ and K_e) were fixed at their values determined from fits to cooling curves of enantiomerically pure solutions with the one-component model.

While experimental CD spectra show only the difference in the amounts of material in P- and M-type helices, an advantage of the model is that it once more allows a focus on the composition of the system. Figure 5e shows for 313 K not only model results for P_tot – M_tot but also P_tot and M_tot individually as well as the free monomer concentrations. Such a speciation plot shows that the kink in the CD curves coincides with a critical ee (ee_cr)^30,31 above which only the aggregates corresponding to the majority enantiomer are present, while below this ee_cr both P- and M-type aggregates are present. Moreover, it shows that the slope in the CD spectrum to the left of the kink corresponds to the increase in the amount of P-type aggregates at the expense of M-type aggregates, whereas the slope in the CD spectrum to the right of the kink originates in a stronger decrease in [S] than increase in [R] due to purer aggregates at higher ee. Interestingly, it also shows that below ee_cr the free monomer concentrations of the two enantiomers are almost equal, whereas above ee_cr these rapidly diverge.

These highly nonlinear monomer concentration profiles also explain the intriguing base-catalyzed racemization observed by Cantekin et al.,³² which featured two distinct time scales. Namely, zooming in on the monomer concentrations (Figure 5g) shows that below ee_cr the monomer concentration corresponding to the majority enantiomer is still fractionally higher than that of the minority enantiomer and that only at ee = 0 are the monomer concentrations exactly equal. As a result, a racemization reaction that takes place only in the monomeric phase (i.e., R ⇄ S) will proceed fast above ee_cr and significantly slower once the critical ee is reached. The same work also showed deracemization by the addition of a third chiral monomer type that copolymerizes along with the others but does not racemize. Extension of the model with this third monomer type showed that the final ee of this deracemization process would be close to the above-mentioned ee_cr, predicting optimal deracemization for large MMP and cooperativity.

General Copolymerization

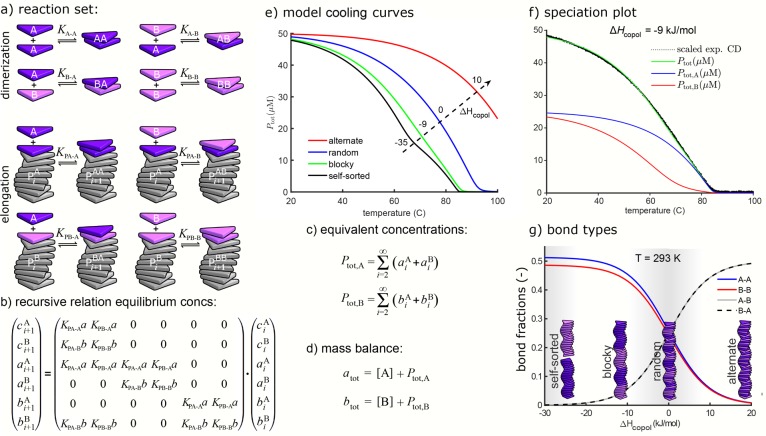
In the majority-rules system considered in the previous section, the equilibrium constants in the elongation phase (i.e., K_e and νK_e) depended on the type of monomer (R or S) and the type of copolymer to which it was added (P or M). To model more general copolymerizations, it is useful to assume that the equilibrium constants may also depend on the top element of the copolymer before addition of the new monomer and thus on both monomers between which a bond is broken or a new bond is formed. The corresponding equilibrium constants can be written as K_PA–B for the elongation of a copolymer P^A (i.e., a copolymer P with arbitrary composition but with an A at the top) with a monomer B, and similarly for the other combinations. The full set of reactions for a single copolymer type is shown in Figure 6a.

Figure 6.

General copolymerization for one copolymer type. (a) Reaction set for copolymerization of two monomer types A and B. (b) Recursive relation for (equivalent) concentrations of copolymers with either an A or B on top, with a = [A] and b = [B]. (c) Total equivalent concentrations of A and B in aggregates. (d) Mass-balance equations. (e) Model-predicted cooling curves for different ΔH_copol values. (f) Speciation plot for ΔH_copol = −9 kJ·mol^–1 and CD data. (g) Bond fractions as functions of ΔH_copol. In (e–g), ΔH_AA = −53 kJ·mol^–1, NP_A = −40 kJ·mol^–1, ΔH_BB = −50 kJ·mol^–1, NP_B = −20 kJ·mol^–1, ΔS_AA = ΔS_BB = ΔS_AB= ΔS_BA = −60 J·mol^–1·K^–1, and a_tot = b_tot = 25 μM. Panels (e) and (f) adapted from ref (7). Copyright 2018 American Chemical Society.

The formulation of the mass-balance equations for this case is somewhat more complicated, as the dependence of the equilibrium constants in the elongation phase on the top of the copolymer necessitates separate treatment of copolymers with top A and top B. Let c_i^A and c_i be the concentrations of copolymers of length i with top A and top B, respectively. Moreover, let a_i^A and a_i represent the equivalent concentrations of A in those copolymers of length i with top A and top B, respectively, and b_i^A and b_i the corresponding equivalent concentrations of B. These six variables can be computed by an iteration process with a 6 × 6 matrix (Figure 6b). The total equivalent concentration of A in copolymers, P_tot,A, i.e., the sum of equivalent concentrations of A in all copolymers of all lengths with top A as well as those with top B (Figure 6c), can now be computed with matrix algebra. In the same way, the total equivalent concentration of B in copolymers, P_tot,B, can be computed. The two resulting mass-balance equations (Figure 6d) formalize again that each monomer is either a free monomer or occurs in some copolymer. These equations, with free monomer concentrations [A] and [B] as unknowns, can be solved numerically.

An interesting example of a copolymerization is the mixture of two triarylaminetriamide-based supramolecular copolymers⁷ (Figure 1d), which individually form supramolecular polymers, with one having higher cooperativity and a higher elongation temperature than the other. The parameters for the A homopolymers (K_PA–A and K_A–A) and for the B homopolymers (K_PB–B and K_B–B) were selected on the basis of experimental homopolymer cooling curves. If it is assumed that the (co)polymers can grow at both ends with the same equilibrium constants, the only free parameter is the equilibrium constant K_PA–B, which is described with an interaction enthalpy ΔH_AB. The relative strength of the homopolymer versus the heteropolymer interaction can be described by ΔH_copol = ΔH_AA + ΔH_BB – ΔH_AB – ΔH_BA. In Figure 6e the resulting equivalent concentration of polymerized material (i.e., P_tot = P_tot,A + P_tot,B) is shown for four different values of ΔH_copol, of which −9 kJ/mol resulted in the best agreement with the experimental CD data (Figure 6f). The advantage of the model is that apart from the overall degree of polymerization, also the temperature-dependent composition of the supramolecular copolymers can be followed (Figure 6f). This shows that at temperatures above the elongation temperature of the weakest homopolymerization, those monomers can already mix into aggregates nucleated from the other monomers, and that the ratio between the two monomer types in the polymers is highly nonlinear with temperature. Moreover, another characteristic of the internal structure of the copolymers that can be extracted from the model is the fractions of the various possible bonds. Figure 6g shows that depending on ΔH_copol the copolymers range from self-sorted via blocky and random to alternating polymers, with ΔH_copol = −9 kJ/mol that gave the best fit to the experimental data corresponding to a blocky structure. These examples clearly show that extensions of the mass-balance model to two components allow the rationalization and quantification of various effects in supramolecular copolymerizations.

Conclusion

We have derived step-by-step a series of mass-balance models describing increasingly complex supramolecular (co)polymerizations and have shown how these models have helped to provide an increased understanding of the molecular basis of supramolecular aggregation. We recently extended the latter of these models to multiple aggregate types, where the binding free energy of each pair of monomer types in each aggregate type can be set independently.³⁴ The resulting model encompasses all mass-balance models for supramolecular (co)polymerizations presented here and gives a general method to model supramolecular (co)polymerization. Though in principle it could be extended further to more than two monomer types or to the case that the equilibrium constants in copolymerization depend on the added monomer and the top k (k = 2, 3, ...) elements of the copolymer, so far we have refrained from doing this given the many new parameters. In ref (34), MATLAB scripts have also been provided to solve the model numerically for any (co)polymerization of one or two types of monomer into an arbitrary number of distinct aggregate types as well as to calculate (co)polymer properties such as the average length, the fractions of bonds between specific monomer types, and the average length of blocks of one monomer type. We most recently applied these scripts to delineate the copolymerization of chiral and achiral analogues of BTA and thio-BTA in modified types of sergeant-and-soldiers and majority-rules experiments⁵⁶ as well as to investigate the effect of competitive sequestration, chain capping, and intercalation on supramolecular polymer lengths.⁵⁷ Moreover, these scripts also allow other interested researchers to apply mass-balance models to rationalize their current and future supramolecular (co)polymerization systems. We envision that this will help to unravel a wealth of other phenomena in supramolecular (co)polymerizations in the future.

Biographies

Huub M. M. ten Eikelder received an M.Sc. in Applied Mathematics and a Ph.D. in Theoretical Physics. He worked as an assistant professor in the Computational Biology Group of the Department of Biomedical Engineering at the Eindhoven University of Technology and as a member of the Institute for Complex Molecular Systems.

Albert J. Markvoort received an M.Sc. in Physics and a Ph.D. in Computer Science and currently works as an assistant professor in the Computational Biology Group of the Department of Biomedical Engineering at the Eindhoven University of Technology and as a member of the Institute for Complex Molecular Systems on the development and application of molecular simulations.

The authors declare no competing financial interest.