Coupling brain-tumor biophysical models and diffeomorphic image registration

Abstract

We present SIBIA (Scalable Integrated Biophysics-based Image Analysis), a framework for joint image registration and biophysical inversion and we apply it to analyze MR images of glioblastomas (primary brain tumors). We have two applications in mind. The first one is normal-to-abnormal image registration in the presence of tumor-induced topology differences. The second one is biophysical inversion based on single-time patient data. The underlying optimization problem is highly non-linear and non-convex and has not been solved before with a gradient-based approach.

Given the segmentation of a normal brain MRI and the segmentation of a cancer patient MRI, we determine tumor growth parameters and a registration map so that if we “grow a tumor” (using our tumor model) in the normal brain and then register it to the patient image, then the registration mismatch is as small as possible. This “coupled problem” two-way couples the biophysical inversion and the registration problem. In the image registration step we solve a large-deformation diffeomorphic registration problem parameterized by an Eulerian velocity field. In the biophysical inversion step we estimate parameters in a reaction–diffusion tumor growth model that is formulated as a partial differential equation (PDE). In SIBIA, we couple these two sub-components in an iterative manner. We first presented the components of SIBIA in “Gholami et al., Framework for Scalable Biophysics-based Image Analysis, IEEE/ACM Proceedings of the SC2017”, in which we derived parallel distributed memory algorithms and software modules for the decoupled registration and biophysical inverse problems. In this paper, our contributions are the introduction of a PDE-constrained optimization formulation of the coupled problem, and the derivation of a Picard iterative solution scheme. We perform extensive tests to experimentally assess the performance of our method on synthetic and clinical datasets. We demonstrate the convergence of the SIBIA optimization solver in different usage scenarios. We demonstrate that using SIBIA, we can accurately solve the coupled problem in three dimensions (256³ resolution) in a few minutes using 11 dual-x86 nodes.

1. Introduction

We present the SIBIA framework that comprises a mathematical formulation, algorithms, and software for joint image registration and biophysical inversion. Given a volumetric segmentation of a magnetic resonance imaging (MRI) dataset of a glioma (primary brain tumor) patient, SIBIA simultaneously registers this image to a segmented MRI dataset of a normal brain (an atlas) and fits a biophysical tumor growth model. Such a joint registration–biophysical inversion approach is motivated by two practical problems: (1) Often, we need to calibrate complex macroscopic biophysical PDE models using a single-time snapshot dataset. Since the biophysical model is typically a dynamical system, it is unclear how to fit model parameters using just a single-time dataset since we do not have the initial state. Replacing the missing second patient snapshot by a healthy atlas and coupling registration between patient and atlas with the tumor growth model attempts to resolve this problem. (2) We want to register normal MR images to MR images with abnormalities. This normal-to-abnormal registration finds applications in surgical planning (e.g., mapping structural and functional information to a patient image), longitudinal studies, followups, or population studies.

We focus on applying SIBIA to the registration of segmented normal images to segmented MR images of glioma patients. Many image analysis workflows for gliomas involve fitting biophysical models for tumor characterization and prognosis [1,2], for image registration [3–5], and for image segmentation [6–8]. In many methods for these image analysis and biophysical modeling problems, an essential step is the solution of an inverse tumor-growth problem, i.e., for instance the calculation of the initial conditions for tumor growth; this process can be combined with registration and segmentation as in [7].

1.1. Statement of the problem and summary of the approach

The specific scenario we are interested in is summarized in Fig. 1. We are given a single snapshot of the multimodal MRI of a glioma patient. Let us assume that we have obtained a segmentation of the MRI in healthy tissue and abnormal tissue, i.e., we have labels for white matter, gray matter, cerebrospinal fluid (CSF), cerebellum, ventricles, and tumor.¹ Since the tumor-growth problem is typically a time dependent problem, we need at least two time snapshots to invert for parameters. Ideally we would like to have both initial and final conditions of the tumor in order to infer parameters. That is, we would like an image of the healthy brain of the patient, the white, gray, and CSF structure right before the tumor appeared, which of course we do not have. One way for partially tackling this problem is to use a pre-segmented normal healthy brain (atlas). This is the step that requires registration. The best way to describe this is to consider the “forward problem”: Assume we are given the (healthy) atlas, a tumor-growth model, and a deformation map (represented as advection with a given velocity field). Then, we first apply the tumor growth model to the healthy image and produce a new segmentation that has both healthy tissue and tumor. In a second step, we warp this image using the given deformation map. This image is the tumor-plus-deformation warped atlas. In the “inverse problem”, we seek to compute the tumor-growth parameters and deformation parameters so that the tumor-plus-deformation warped atlas image matches the patient image.

Fig. 1.

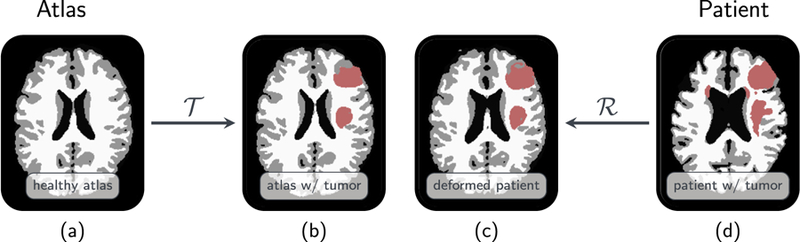
Here we summarize the joint registration and biophysical inversion in SIBIA. (a) shows the segmented healthy brain (the atlas), (b) tumor-bearing atlas brain generated by biophysical simulation, (c) patient tumor registered to atlas (in atlas space), (d) tumor-bearing patient brain. The inputs are the images (a) and (d). The outputs are the tumor growth parameters, the registration parameters, and images (b) and (c). Here is $\tau$ the forward tumor map, which given image (a) grows a tumor and generates image (b). Similarly, $\mathcal{R}$ is the forward registration map, which given image (d) generates image (c). In SIBIA, we compute tumor-growth parameters and registration parameters so that images (b) and (c) are as similar as possible (in the L² norm). In this example, the biophysical tumor growth parameters are the initial conditions for a reaction–diffusion equation. The registration is parameterized using an Eulerian framework and a velocity field that is used to advect image (d) to image (c).

Thus, SIBIA combines the following steps: (i) a forward tumor solver growing a virtual (or synthetic) tumor in the segmented healthy atlas brain, (ii) the inverse tumor solver determining the initial condition for tumor growth given an observation at a later time, (iii) a forward linear advection solver that implicitly computes the warped image given the velocity field, and (iv) a large-deformation diffeomorphic image registration solver. We couple tumor inversion and image registration (both are optimization problems) to an outer, coupled optimization problem. Because both tumor models and registration formulations are always in flux and in varying complexity, tightly coupling them using a Newton method would require continuous significant software engineering effort. Our goal is a scheme that allows leveraging of the underlying optimization solvers and allows more flexibility. Motivated by this need for model flexibility, we consider the viability of a Picard (or fixed point) iteration.

1.2. Contributions

1. First, we formulate the coupled tumor growth and registration optimization problem in Section 3 and derive its first order optimality conditions and a reduced gradient of the objective function with respect to the tumor parameters and the velocity. This reduced gradient is used in our solver scheme as a convergence and correctness check. To our knowledge this is a new result.

2. We propose a Picard iteration including a parameter-continuation scheme for solving the system based on modular tumor and image registration components. This allows great flexibility in both the type of tumor models and registration but also in the underlying solvers for the two subproblems.

3. We conduct a large number of numerical experiments on synthetic and real data that demonstrate the validity and efficiency of our approach, in particular, we show that the Picard iteration efficiently reduces the gradient and converges to a local minimum. We conduct a mesh-dependence analysis in the convergence rate in which we show that our scheme is not sensitive to the mesh size (for both velocity and tumor parameters). We consider six clinical images that include multifocal tumors and we demonstrate the effectiveness of the method.

4. We examine the sensitivity of our solver on the choice of the tumor model variant. We consider three variants of the tumor model: a reaction model, a reaction–diffusion model, and a simple radial basis approximation (no time evolution; the tumor is simply approximated at the observation time). We conclude on the usefulness of each of these variants depending on the goal of the analysis.

1.3. Limitations and open issues

Several limitations and unresolved issues remain. One limitation is that we do not provide a general theoretical proof that the Picard scheme converges. We discuss this further in Section 4.1. A second limitation is the fact that we are not using a Newton method. Indeed, we do not claim that our algorithm is algorithmically optimal. It is quite possible that a Newton method for the coupled problem would perform better. However, we present numerical evidence that our Picard is efficient and converges to acceptable accuracy in a mesh independent way (see Section 5). Another important limitation is that our tumor model does not include mass-effect, instead we use a simple phenomenological reaction–diffusion model [9–11]. Our simple model is quantitatively useful for image analysis and tumor characterization [1,12–14], but has limited predictive capabilities. We are currently working on integrating a mass-effect, which is considered critical for characterizing tumor aggressiveness [3,15,16] as well as more complex reaction–diffusion models. SIBIA can naturally be extended to these more complex models although of course more tests will be necessary to demonstrate convergence of the Picard scheme.

1.4. Literature review

We presented fast algorithms for the individual components of SIBIA in [17] where we introduced the key computational kernels (reaction–diffusion, advection, and inverse solution based on FFT and particle-in-mesh methods) and demonstrated their scalability on very large images and distributed-memory architectures. Our problem formulation results in a mixed-type PDE-constrained optimization problem that poses significant numerical challenges. We refer to [18–21] for a general introduction into PDE-constrained optimization and to [22–24] for reviews on its application to medical image analysis. We will limit ourselves to the work most closely related to ours in the following.

The first component of SIBIA is image registration. We refer to [25,26] for a general overview of medical image registration. Registering the atlas to the patient requires finding correspondences between two topologically different images — one with tumor and one without tumor. The key issue here is the ill-defined correspondence arising from the presence of a tumor in only one of the images to be registered. A simple strategy to deal with this issue is to consider the tumor area as non-informative and mask it from the optimization [27–29] or to relax the registration in the area affected by the tumor [30]. This, however, yields poor registration quality for tumors with severe tissue deformation due to mass effect. Another strategy is to simultaneously invert for the deformation map and a drift in intensity representing the imaging abnormality associated with the tumor [31,32], which can also be applied to other registration problems with topological differences (for instance, pre- and postoperative image registration [4]). While it may produce acceptable results for the purpose of atlas-based segmentation and registration, it cannot be used in the context of model prediction—which is our ultimate goal. Our prior work on diffeomorphic image registration [33–37] forms the basis for the proposed methodology based on the pioneering work in [38–40] (see [33] for additional references).

The second component of SIBIA is the calibration of brain tumor models to medical imaging data [16,17,41–43]. The associated PDE operator is a parabolic, non-linear, reaction–diffusion equation [10,11]. Despite its phenomenological character, this model is capable of generating simulations that are in good agreement with observations of abnormalities in standard MR imaging data and has been used by other groups besides ours [1,12,14,44–51]. Our implementation features inversion operators for the initial tumor concentration, for diffusivity parameters, or for the growth rate [41]. Related optimal control formulations can, e.g., be found in [12,52–59]. Unlike most existing approaches (with the exception of [60]), our parametrization of the problem [41,42] allows us to invert for multifocal tumors. Numerical methods for solving the tumor calibration problem are based either on point estimate or Bayesian inference methods [14,61]. Bayesian inference characterizes the uncertainty in the model parameters. In this paper, we just focus on methods for point estimates using an adjoint formulation. Our approach can be extended to the Bayesian setting [62].

The integration of biophysical brain tumor simulations with deformable image registration is not new [3,5,7,63–65]. In [3,5,64,65], a purely mechanical model for tumor progression was used. The two key limitations of the work in [3,5,64,65] are (i) that the model is oversimplified; it did not provide the capabilities to generate tumors with complex shapes (ii) that these models do not provide information about the progression and infiltration of cancerous cells into surrounding healthy tissue. The proposed formulation does not share these limitations.

The work that is closest to ours is [4,6,7,63]. In those papers the authors presented a framework for joint segmentation, registration, and tumor modeling. What sets our work apart are (i) the solver (we do not iterate on both control variables simultaneously; we perform a block elimination and iterate resulting in an interleaved optimization on the controls using globalized Newton–Krylov solvers as opposed to derivative free-optimization [3,5,7,59,63–65]); (ii) an efficient parallel implementation [17,35]; (iii) the derivation of the optimality systems for the fully coupled problem; (iv) the parametrization for the initial condition of the tumor, which not only allows us to represent multifocal tumors but also to significantly simplify the PDE constraint without losing segmentation accuracy; (v) and finally the integration with a state-of-the-art algorithm for constrained large deformation diffeomorphic image registration [33–35,37].

1.5. Outline

After introducing our notation in Section 2, we present the coupled formulation and the individual subcomponents (tumor growth) and registration and derive the first order optimality conditions in Section 3. In Section 4, we discuss our main contribution besides the formulation of the coupled problem and its decomposition—a modular iterative Picard solver scheme along with further algorithmic details. We summarize the setup for the experiments in Section 5.1 and present numerical results on both synthetic and clinical data in Section 5. We provide additional details on the numerical experiments for the clinical dataset in the Appendix.

2. Notation

Before presenting the models used for tumor growth and image registration, we summarize the notation used throughout the manuscript.

Segmentation labels and probability maps.

For each healthy brain tissue type, i.e., gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF; which includes the ventricles), we use a separate probability map. We represent these probability maps as a space–time vector field

$$\mathit{m}(\mathit{x},t)={(m_i(\mathit{x},t))}_{i=1,\mathrm{...},3}\in {ℝ}^3\hspace{1em}\text{with}\hspace{1em}{m}_1=m_{GM},m_2=m_{WM},m_3=m_{CSF}$$ (1)

with m_i (x, t ) ∈ [0, 1] defined on the space–time interval Ω × [0, 1]³ with boundary ∂Ω. The domain occupied by brain tissue (healthy or unhealthy) is denoted by Ω_B ⊂ Ω. The fourth probability map is c(x, t ) ∈ [0 1], also defined in Ω_B; c is the output of the tumor forward simulation and represents the probability to encounter cancerous cells at a location x at time t . For convenience, we also define the space–time domains U = Ω × (0, 1] and $\overline{U}=\Omega \times [0,1)$.

Labels, i.e., characteristic functions calculated based on given threshold values for tumor and healthy tissue types are used only in the evaluation of our results to compute Dice coefficients.

Patient and atlas data.

Data of the actual patient image are marked with a subscript T (template, m_T , c_T ), data of patient images advected to the atlas domain with a subscript P (m_P , c_P ), and those of the atlas brain with a subscript A (m _A, c_A).

Dependency on time and space.

In most formulations, we do not explicitly include the dependency on the spatial position x, but only the time dependency. For instance, c_A(0) denotes the initial tumor probability map defined in the atlas image, whereas c_A(1) is the tumor at time t = 1 (solution of the tumor forward problem). This is the point in time associated with the patient image. Probability maps in the atlas image evolve in the non-dimensional (tumor growth) time interval [0, 1]. For diffeomorphic image registration, we introduce a pseudo-time variable t ∈ [0, 1] and invert for a stationary velocity field v(x); t does not have a physical meaning; we associate t = 0 with the undeformed patient image (image to be registered; template image) and t = 1 with its deformed representation. We make more explicit definitions below.

Vector notation.

Given a vector field m ∈ ℝ³, we compute ∇m (∂_j m_i )_{i, j=1,2,3}, ∈ ℝ^3,3. That is, given a velocity field v ∈ ℝ³, ∇m v ∈ ℝ³ indicates a matrix–vector multiplication. The standard scalar product in ℝ³ is denoted by “·” and the outer product between two vector fields will be denoted by “⊗”. In addition, we define the following inner products:

$${\langle \mathit{m},\tilde{\mathbf{m}}\rangle }_{L^2{(\Omega )}^3}:=\sum _{i=1}^3{\langle m^i,{\tilde{m}}^i\rangle }_{L^2(\Omega )},\hspace{1em}\hspace{1em}{\Vert \mathit{m}\Vert }_{L^2{(\Omega )}^3}^2:=\sum _{i=1}^3{\Vert m^i\Vert }_{L^2(\Omega )}^2.$$ (2)

3. Formulation

3.1. Formulation of the coupled problem

Our formulation is a coupled PDE-constrained optimization problem. The input data are the (1) tumor-free atlas brain image m_A(x, 0) (which we call “reference” image or “healthy atlas”) and (2) the tumor-bearing patient image (which we term “template image” or “patient with tumor image”). The latter includes the brain geometry m_T (x) and the patient’s tumor c_T (x). These images are vector images, i.e., they are probability maps for every tissue type class (white matter, gray matter, cerebrospinal fluid, and tumor). We invert for a stationary velocity field $\mathit{v}(\mathit{x}):={(v^1(\mathit{x}),v^2(\mathit{x}),v^3(x))}^{\text{⊤}}$ (establishes the spatial correspondence between the patient and atlas image), a parameter vector p (parametrizes the simulated tumor in the tumor-free atlas image), and a mass-source map w(x) (controls the computed deformation pattern) as follows:

$$\underset{\mathit{v},\mathit{p},w}{\text{min}}\hspace{1em}\mathcal{J}\left(v,p,w\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\text{with}\hspace{1em}\mathcal{J}(v,p,w):={\mathcal{D}}_c(c_A,c_p)+{\mathcal{D}}_{\mathit{m}}({\mathit{m}}_A,{\mathit{m}}_p)+{\beta }_{\mathit{p}}{\mathcal{S}}_{\mathit{p}}+{\beta }_{\mathit{v}}{\mathcal{S}}_{\mathit{v}}+{\beta }_w{\mathcal{S}}_w\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}$$ (3a)

subject to

$${\partial }_t{c}_A-\text{div}k\nabla c_A-f(c_A)=0\text{in}\hspace{0.17em}U,$$ (3b)

$$c_A(0)=\Phi \mathit{p}\text{in}\hspace{0.17em}\Omega ,$$ (3c)

$${\mathit{m}}_A(1)={\mathit{m}}_A(0)(1-c_A(1))\text{in}\hspace{0.17em}\Omega ,$$ (3d)

$${\partial }_t{\mathit{m}}_P+\nabla {\mathit{m}}_P\mathit{v}=0\text{in}\hspace{0.17em}U,$$ (3e)

$${\mathit{m}}_P(0)={\mathit{m}}_T\text{in}\hspace{0.17em}\Omega ,$$ (3f)

$${\partial }_t{c}_P+\nabla c_p\cdot \mathit{v}=0\text{in}\hspace{0.17em}U,$$ (3G)

$$c_P(0)=c_T\text{in}\hspace{0.17em}\Omega ,$$ (3h)

$$\text{div}\hspace{1em}\mathit{v}=w\text{in}\hspace{0.17em}U,$$ (3i)

with periodic boundary conditions on ∂Ω.

Here (3b)–(3d) represent the forward tumor model; and (3e)–(3i) represent the forward registration problem. The objective functional $\mathcal{J}$ in (3b) consists of the following building blocks:

1. the two driving L²-distance measures

   $${\mathcal{D}}_c(c_A,c_p):=\frac{1}{2}{\Vert c_A(1)-c_P(1)\Vert }_{L^2(\Omega )}^2,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\text{and}\hspace{1em}\hspace{1em}\hspace{1em}{\mathcal{D}}_{\mathit{m}}({\mathit{m}}_A,{\mathit{m}}_P):=\frac{1}{2}{\Vert {\mathit{m}}_A(1)-{\mathit{m}}_P(1)\Vert }_{L^2{(\Omega )}^3}^2$$

   that measure the discrepancy between the simulated tumor in atlas space c_A(1) (solution of the tumor forward problem (3b) with initial condition (3c) parameterized by p) and the transported probability map c_P (1) of cancerous cells for the patient data (solution of the registration forward problem (3g) with initial condition (3h)) and the discrepancy between the healthy tissue probability maps in atlas space with tumor (calculated according to (3d)) and the transported probability maps of healthy tissue for the patient data (solution of the registration forward problem (3e) with initial condition (3f));
2. three regularization operators balanced against the discrepancy measures ${\mathcal{D}}_c$ and ${\mathcal{D}}_{\mathit{m}}$ based on regularization weights β_j > 0, j ∈ {v, w, p} involving

   1. a regularization operator ${\mathcal{S}}_{\mathit{p}}$ for Φ p (an L²-norm),
   2. a regularization operator ${\mathcal{S}}_{\mathit{v}}$ for v (an H¹ Sobolev norm; defined in (10b)), and
   3. a regularization operator ${\mathcal{S}}_w$ for w (an H¹ Sobolev norm; defined in (10b)).

Next we discuss in detail the two forward problems (tumor growth and image advection).

Forward Tumor Problem.

We model the tumor growth based on the population density c_A(x, t ), which is obtained by solving (3b)–(3c). Two main phenomena are included: proliferation of cancerous cells and the net migration of cancerous cells into surrounding healthy tissue [11].² The proliferation model is a logistic growth function f (c_A) :=ρ c_A(1 – c_A) with reaction coefficient ρ(x) :=ρ _f ρ₀(x). ρ _f denotes the scaling of the spatially variable characteristic growth rate parameters defined by white and gray matter, i.e., ρ₀(x) := ρ_w m_WM (x) ρ_g m_GM (x). The migration model is based on an inhomogeneous (potentially anisotropic) diffusion process with diffusion coefficient k(x) := k _f k₀(x)I + k_a T(x). Here, k _f and k_a are the scaling factors for the isotropic and anisotropic parts of the diffusion tensor, T(x) is a weighted diffusion tensor modeling anisotropy. In our test cases in Section 5, we always use isotropic diffusion, i.e., k_a = 0. The isotropic part is k₀(x) := k_wm_WM (x) k_gm_GM (x). This yields a non-linear parabolic PDE with non-constant coefficients for the tumor concentration c given by (3b)–(3c).

We use a parametrization Φ p for the tumor initial condition c_A(0) as originally in (3c) in an n _p-dimensional space spanned by Gaussian basis functions, i.e., $\mathit{p}\in {ℝ}^{n_{\mathit{p}}},\Phi \mathit{p}:={\sum }_{i=1}^{n_{\mathit{p}}}{\Phi }_i{p}_i$ with Gaussian basis functions Φ_i : Ω_B → ℝ. We set the Gaussians in CSF to zero to prevent a spurious diffusion of cancerous cells into the area associated with CSF. Once the tumor density has been computed we can adjust the probability of the other tissue labels by Eq. (3d).

For notational convenience, we represent the process of solving (3b)–(3d) with the operator

$${\mathcal{T}}^{\text{fwd}}(\mathit{p},{\mathit{m}}_A(0)):=({\mathit{m}}_A(1),c_A(1)),$$ (4)

which maps p in (3c) to the tissue labels of the atlas image at time t = 1. This simple model is by no means predictive on its own, but is the de-facto standard approach when it comes to modeling tumor progression as seen in medical imaging [1,9,44,46,47,63]. Some results available in the literature have suggested that this model can offer (to some extent) predictive capabilities when integrated with medical imaging information [9,66]. Its usefulness is in segmentation and registration algorithms that use normal atlas information and in producing features (e.g., tumor parameters) to augment image-based features for tumor staging and prognosis. Note that usually the stand-alone tumor model is stated in the actual brain domain Ω_B with Neumann boundary conditions, which is the actual biophysical problem. In our numerical implementation, however, we extend k by a small parameter, set ρ = 0 in Ω\Ω_B , discretize in Ω using periodic boundary conditions, and use a penalty approach to approximate the boundary conditions at ∂Ω_B. One can show that this “fictitious domain method” approximates the correct boundary conditions and as we refine the discretization it converges to the correct solution (compare [41,63]).

Advective Image Transformation (Forward Problem).

The image registration velocity v is used to transport both the brain geometry m_T and the tumor concentration c_T from patient to atlas space. The input for our formulation is not image intensities [33,34,36,37] but the probability maps for tissue classes (see (1); WM, GM, CSF, and tumor). The formulation we propose here is suited for general problems that involve the registration of vector fields. The template image (image to be registered) ${\mathit{m}}_T:\overline{\Omega }\to {ℝ}^3$ is given by the probability maps of the patient’s healthy anatomy in all areas except the part hidden by the tumor. We treat the probability map for the tumor, c_T (x), as an individual entity to make the coupled formulation in (3) more accessible. We register the three probability maps for healthy tissue and the tumor concentrations. Given some template image m_T (x), some tumor concentration c_T (x), and a stationary velocity field v(x), the forward problem describes the advective transformation of m_T and c_T in a pseudo-time interval [0, 1) as given in (3e) –(3i).

Solving (3e) –(3i) defines the implicitly given operator

$${\mathcal{R}}^{\text{fwd}}(\mathit{v},{\mathit{m}}_T,c_T):=({\mathit{m}}_P(1),c_P(1)),$$ (5)

which maps the template images m_T and c_T to images m_P and c_P defined at pseudo-time t = 1. For simplicity, we will later slightly abuse our notation and use the operator ${\mathcal{R}}^{\text{fwd}}$ also for the advection of only m, c or one of the components of m, i.e., m_WM , m_GM , or m_CSF .

3.2. Optimality conditions and fully coupled gradient

We use the method of Lagrange multipliers to transform the constrained problem (3) into an unconstrained one.

The Lagrangian of (3) reads

$$\begin{gathered} {\mathcal{L}}_G(c_A,c_P,{\mathit{m}}_P,{\mathit{m}}_A(1),\alpha ,{\lambda }_c,{\mathbf{\lambda }}_{\mathit{m}},v,\mathbf{\xi },\mathit{p},\mathit{v},w)=\mathcal{J}(\mathit{p},\mathit{v},w) \\ +{\langle \alpha (0),(c_A(0)-{\Phi }_{\mathit{p}})\rangle }_{L^2(\Omega )}+{{\int }_0^1\langle \alpha ,{\partial }_t{c}_A-\nabla \cdot (\mathit{k}\nabla c_A)-f(c_A)\rangle }_{L^2(\Omega )}\text{d}t \\ +{\int }_0^1{\langle {\lambda }_{\mathit{m}},{\partial }_t{\mathit{m}}_P+\nabla {\mathit{m}}_P\mathit{v}\rangle }_{L^2{(\Omega )}^3}\text{d}t+{\langle {\lambda }_{\mathit{m}}(0),{\mathit{m}}_P(0)-{\mathit{m}}_T\rangle }_{L^2{(\Omega )}^3} \\ +{\int }_0^1{\langle {\lambda }_c,{\partial }_t{c}_P+\nabla c_P\cdot \mathit{v}\rangle }_{L^2(\Omega )}\text{d}t+{\langle {\lambda }_c(0),c_P(0)-c_T\rangle }_{L^2(\Omega )} \\ +{\int }_0^1{\langle v,\text{div}\hspace{0.17em}\mathit{v}-w\rangle }_{L^2(\Omega )}\text{d}t+{\langle \xi ,{\mathit{m}}_A(1)-(1-c_A(1)){\mathit{m}}_A(0)\rangle }_{L^2{(\Omega )}^3}, \end{gathered}$$ (6)

with the state fields c_A, c_P , m_P , and m _A(1), the adjoint fields α, λ_c, λ_m, ν, and ξ, and the inversion fields p, v, and w. The strong form of the first-order optimality conditions for Eq. (6) is given by the following equations:

$$tumor\hspace{0.17em}forward\hspace{1em}\hspace{1em}\hspace{1em}{\delta }_{\alpha }{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\text{given}\hspace{0.17em}\text{by}\hspace{0.17em}(3\text{b})-(3\text{c})$$ (7a)

$${\delta }_{\xi }{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\text{given}\hspace{0.17em}\text{by}\hspace{0.17em}\left(3\text{d}\right)$$ (7b)

$$tumor\hspace{0.17em}ad\text{joint}\hspace{1em}\hspace{1em}\hspace{1em}{\delta }_{c_A}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\partial }_t\alpha -\nabla \cdot \mathit{k}\nabla \alpha -\alpha \rho +2\alpha \rho c_A=0\hspace{1em}\hspace{1em}\hspace{1em}\text{in}\hspace{0.17em}\overline{U},$$ (7c)

$${\delta }_{c_A(1)}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}{c}_P(1)-c_A(1)-\mathbf{\xi }{\mathit{m}}_A(0)-\alpha (1)=0\hspace{1em}\hspace{1em}\hspace{1em}\text{in}\hspace{0.17em}\Omega .$$ (7d)

$${\delta }_{\mathit{m}A}{}_{(1)}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathit{m}}_P(1)-{\mathit{m}}_A(1)-\mathbf{\xi }=\mathbf{0}\hspace{1em}\hspace{1em}\text{in}\hspace{0.17em}\text{Ω,}$$ (7e)

$$registration\hspace{0.17em}forward\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\delta }_{\mathbf{\lambda }}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\text{given}\hspace{0.17em}\text{by}\hspace{0.17em}(3\text{e})-(3\text{i})$$ (7f)

$$registration\hspace{0.17em}adjoint\hspace{1em}\hspace{1em}{\delta }_{\mathit{m}P}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\partial }_t{\mathbf{\lambda }}_{\mathit{m}}-\text{div(}{\mathbf{\lambda }}_{\mathit{m}}\otimes \mathit{v})=\mathbf{0}\text{in}\hspace{0.17em}\overline{U},$$ (7g)

$${\delta }_{\mathit{m}P(1)}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathit{m}}_A(1)-{\mathit{m}}_P(1)-{\mathbf{\lambda }}_{\mathit{m}}(1)=\mathbf{0}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\text{in}\hspace{0.17em}\Omega ,$$ (7h)

$${\delta }_{c_P}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\partial }_t{\lambda }_c-\text{div(}{\lambda }_{\text{c}}\mathit{v})=0\hspace{1em}\text{in}\hspace{0.17em}\overline{U},$$ (7i)

$${\delta }_{cP(1)}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{c}_A(1)-c_P(1)-{\lambda }_c(1)=0\hspace{1em}\text{in}\hspace{0.17em}\Omega ,$$ (7j)

$$tumor\hspace{0.17em}inversion\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\delta }_{\mathit{p}}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\nabla }_{\mathit{p}}{\mathcal{S}}_{\mathit{P}}(\mathit{P})-{\text{Φ}}^{\text{T}}\alpha (0)=0\hspace{1em}\text{in}\hspace{0.17em}\Omega ,$$ (7k)

$$registration\hspace{0.17em}inversion\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\delta }_{\mathit{v}}{\mathcal{L}}_G=0:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\nabla }_{\mathit{v}}{\mathcal{S}}_{\mathit{v}}(\mathit{v})+\mathcal{K}[{\int }_0^1{(\nabla {\mathit{m}}_P)}^T{\mathbf{\lambda }}_{\mathit{m}}+\nabla c_P{\lambda }_c\text{d}t]=\mathbf{0}.$$ (7l)

Note, that ${(\nabla \mathit{m})}^T\mathbf{\lambda }={\sum }_i^3{\lambda }_i{\left({\partial }_1{m}_i,{\partial }_2{m}_i,{\partial }_3{m}_i\right)}^T$ and that we have not given an equation for w. The operator $\mathcal{K}$ in (7l) is a pseudo-differential operator that is derived by eliminating w in (3i). We discuss more details below.

In summary, the first-order optimality conditions (7) define the gradient of the Lagrangian and comprise a system of non-linear partial differential equations, which is quite formidable since it has 11 fields in addition to the tumor initial condition parameters p. Though we later decompose our fully coupled problem into sub-components, the gradient is required to assess convergence of our modular Picard scheme. Instead of using the full gradient of the Lagrangian given by (7), we use an elimination method (or also called a “reduced-space method” [19]) to solve these equations. That is, we solve forward and adjoint equations exactly and evaluate the gradient of the Lagrangian with respect to the inversion variables v and p³: Given p and v, we wish to compute the gradient of $\mathcal{J}$, i.e., g_p and g_v. This gradient computation involves the following steps:

1. Solve the forward tumor growth and registration equations (3c)–(3d) for the state variables c_A(t), c_P (t), m_P (t),m _A(1).

2. Compute the coupling adjoint variable ξ from Eq. (7e).

3. Solve the adjoint tumor equations (7c) and (7d) for α(t ).

4. Solve the adjoint registration equations (7g)–(7j) for λ_m(t ) and λ_c(t ).

5. Evaluate the gradients using the inversion equations (7k) and (7l) at v and p:

$${\mathit{g}}_{\mathit{v}}={\beta }_{\mathit{v}}{\nabla }_{\mathit{v}}{\mathcal{S}}_{\mathit{v}}(\mathit{v})+\mathcal{K}[{\int }_0^1{(\nabla {\mathit{m}}_P)}^T{\mathbf{\lambda }}_{\mathit{m}}+\nabla c_P{\lambda }_c\text{d}t],\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathit{g}}_{\mathit{p}}={\beta }_{\mathit{p}}{\nabla }_{\mathit{p}}{\mathcal{S}}_{\mathit{p}}(\mathit{p})-{\Phi }^{\text{T}}\alpha (0).$$ (8)

At a stationary point g = (g_v, g _p)^T vanishes.

3.3. Decomposition into subcomponents — inverse tumor and image registration

In the following, we formulate separate inverse problems for tumor growth and image registration that are used as high-level components in our coupling algorithm presented in 4.1. We show that the optimality conditions of the sub-problems together yield the optimality conditions of the coupled problem. This observation is the basis for our Picard iteration using tumor and registration as modular components instead of a gradient descent or Newton method with line search for the coupled problem (3).

Inverse Tumor Problem.

In the inverse tumor problem, we seek an initial condition for the forward tumor problem that recovers c_p(1) and m_p(1) at time t = 1 as well as possible, i.e., we solve the minimization problem

$$\underset{\mathit{p}}{\text{min}}{\mathcal{J}}_T(\mathit{p})\hspace{1em}\text{with}\hspace{1em}{\mathcal{J}}_{\text{T}}(\mathit{p}):={\mathcal{D}}_c(c_A,c_P)+{\mathcal{D}}_m({\mathit{m}}_A,{\mathit{m}}_P)+\frac{{\beta }_p}{2}{\Vert \Phi \mathit{p}\Vert }_2^2$$ (9a)

subject to the constraints (3b)–(3d). Eq. (9) defines a concrete instance for the tumor regularization operator ${\mathcal{S}}_{\mathit{p}}$ in (3).

The Lagrangian of (9) reads

$${\mathcal{L}}_T(c_A,\mathit{p},\alpha )={\mathcal{J}}_T(\mathit{p})+{\langle \alpha (0),c_A(0)-\Phi \mathit{p}\rangle }_{L^2({\Omega }_{\text{B}})}+{{\int }_0^1\langle \alpha ,{\partial }_t{c}_A-\nabla \cdot \mathit{k}\nabla c_A-\rho c_A(1-c_A)\rangle }_{L^2({\Omega }_{\text{B}})}\text{d}t$$

The first-order optimality condition of the tumor problem are given by (3b) –(3d), (7c)–(7e), and (7k).

Image Registration (Inverse Problem).

We seek a velocity v that advects the given template (patient) images to images that are as close as possible to the corresponding images in the atlas brain (denoted with a subscript A). That is, we solve the following minimization problem:

$$\underset{\mathit{v}}{\text{min}}{\mathcal{J}}_R(\mathit{v})\hspace{1em}\text{with}\hspace{1em}{\mathcal{J}}_{\text{R}}(\mathit{v}):={\mathcal{D}}_{\mathit{m}}({\mathit{m}}_A,{\mathit{m}}_P)+{\mathcal{D}}_c(c_A,c_P)+{\beta }_{\mathit{v}}{\mathcal{S}}_{\mathit{v}}(\mathit{v})+{\beta }_w{\mathcal{S}}_w(w)$$ (10a)

subject to (3e)–(3i). The regularization in (10a) is a smoother for v and w and given by an H¹-seminorm for v, and an H¹-norm for w (i.e., for div v according to (3i)), respectively:

$${\mathcal{S}}_{\mathit{v}}(\mathit{v})=\frac{1}{2}{\int }_{\Omega }\sum _{i=1}^3{\left|\nabla v^i(\mathit{x})\right|}^2\text{d}\Omega ,\hspace{1em}\hspace{1em}{\mathcal{S}}_w(w)=\frac{1}{2}{\int }_{\Omega }{\left|\nabla w(\mathit{x})\right|}^2\text{d}\Omega .$$ (10b)

The Lagrangian for the image registration problem reads

$$\begin{gathered} {\mathcal{L}}_R(c_P,{\mathit{m}}_P,\mathit{v},{\mathbf{\lambda }}_{\mathit{m}},{\lambda }_c)={\mathcal{J}}_R(\mathit{v}) \\ +{{\int }_0^1\langle {\mathbf{\lambda }}_{\mathit{m}},{\partial }_t{\mathit{m}}_P+\nabla {\mathit{m}}_P\mathit{v}\rangle }_{L^2{(\text{Ω)}}^{\text{3}}}\text{d}t+{\langle {\mathbf{\lambda }}_{\mathit{m}}(0),{\mathit{m}}_P(0)-{\mathit{m}}_T\rangle }_{L^2{(\Omega \text{)}}^{\text{3}}} \\ +{{\int }_0^1{\langle {\lambda }_c,{\partial }_t{c}_P+\nabla c_P\cdot \mathit{v}\rangle }_{L^2(\Omega \text{)}}\text{d}t+\langle {\lambda }_c(0),c_P(0)-c_T\rangle }_{L^2(\Omega \text{)}} \\ +{\int }_0^1{\langle v,\text{div}\hspace{1em}\mathit{v}-w\rangle }_{L^2(\Omega \text{)}}\text{d}t. \end{gathered}$$

Taking variations, we obtain the first-order optimality conditions [34] for the registration problem as (3e)–(3i), (7g)–(7j), and (7l). As mentioned before, the operator $\mathcal{K}$ in (7l) is a pseudo-differential operator that is derived by eliminating w in (3i). For the case of exact incompressibility (w = 0), it is the Leray projection $\mathcal{K}\left(u\right):=u+\mathrm{\nabla }{\mathrm{\Delta }}^{-1}$ div u; for a non-zero w, the projection operator becomes slightly more involved; we refer to [33,34] for additional details.

Next, we discuss the Picard iteration and the numerical discretization of the forward and adjoint problems.

4. Numerical ingredients — Picard and sub-components

The focus of the present work is on the formulation of the coupled problem and the numerical scheme used to solve the associated optimization problem. The algorithms for the individual subblocks have been published in [17,33–35,37,41,67]. The main ingredients can be described as follows: (i) All PDEs are spatially discretized in Ω = [0, 2π]³. (ii) All spatial derivatives (∇, div , and higher derivatives) are computed using 3D Fourier transforms. (iii) Although in the formulation we present the derivatives in the strong form, in our implementation we use a discretize-then-optimize approach for the tumor equations and an optimize-then-discretize approach for the registration. (iv) The solution of pure advection equations is done using a semi-Lagrangian time-stepping scheme to avoid stability issues and small time-steps.⁴ (v) We use Krylov and matrix-free Newton methods for linear and nonlinear solvers. (vi) We use a Picard iteration scheme for the coupled optimization problem, without line search.⁵

In the following subsections, we give more details on the proposed Picard iteration scheme, and then give a short overview of the numerical methods used to solve the tumor and image registration forward and inverse problems.

4.1. The Picard iteration algorithm

Here we discuss the solution of (3). As we discussed in the introduction, we use a modular approach in which we combine tumor growth inversion and diffeomorphic registration models in an (interleaved) Picard iteration scheme. This scheme iteratively improves both the tumor initial condition’s parametrization p and the registration velocity v. This allows us to establish a coupling of both components in an easy and efficient way; the solver subcomponents can be exchanged as required. Our results presented in Section 5 demonstrate that the Picard iteration is a powerful approach that reduces the gradient of the fully coupled formulation as given in (8).

The outline of our Picard scheme is simple.⁶ It is convenient to restate (3) in terms of the compact notation for the forward operators given by (4) and (5). With this notation the optimization problem is given by

$$\underset{\mathit{v},\mathit{p}}{\text{min}}{\mathcal{D}}_c(c_A(1),c_P(1))+{\mathcal{D}}_{\mathit{m}}({\mathit{m}}_A(1),{\mathit{m}}_P(1))+{\beta }_{\mathit{p}}{\mathcal{S}}_{\mathit{p}}+{\beta }_{\mathit{v}}{\mathcal{S}}_{\mathit{v}}$$

$$\text{s}.\text{t}.:\hspace{0.17em}({\mathit{m}}_A(1),c_A(1))={\mathcal{T}}^{\text{fwd}}(\mathit{p},{\mathit{m}}_A(0)),\hspace{1em}({\mathit{m}}_P,c_P(1))={\mathcal{R}}^{\text{fwd}}(\mathit{v},{\mathit{m}}_T,c_T).$$

One step in our Picard iteration is summarized as follows.

1. Given m_p, c_P , solve the inverse tumor problem for p, m_A, and c_A:

   $$min\hspace{0.17em}{\mathcal{D}}_c\left(c_A\left(1\right),c_P\left(1\right)\right)+{\mathcal{D}}_{\mathit{m}}\left({\mathit{m}}_A\left(1\right),{\mathit{m}}_P\left(1\right)\right)+{\mathcal{S}}_{\mathit{p}},\hspace{1em}s.t.:({\mathit{m}}_A\left(1\right),c_A\left(1\right))={\tau }^{\text{fwd}}\left(\mathit{p},{\mathit{m}}_A\left(0\right)\right).$$
2. Given c_A, m _A, solve the image registration problem for v, m_P and c_P:

   $$min\hspace{0.17em}{\mathcal{D}}_c\left(c_A\left(1\right),c_P\left(1\right)\right)+{\mathcal{D}}_{\mathit{m}}\left({\mathit{m}}_A\left(1\right),{\mathit{m}}_P\left(1\right)\right)+{\mathcal{S}}_{\mathit{v}},\hspace{1em}s.t.:\left({\mathit{m}}_P\left(1\right),c_P\left(1\right)\right)={\mathcal{R}}^{\text{fwd}}(\mathit{v},{\mathit{m}}_T,c_T).$$

This iteration defines new iterates for p and v. Here we just described the two inverse problems for the tumor initial condition and registration velocity in a compact form. The precise details are given in Section 3.3. Since the individual optimization problems are subcomponents of the original optimization and ${\mathcal{S}}_{\mathit{p}}$ and ${\mathcal{S}}_{\mathit{v}}$ are independent from the respective other subsolver’s result, each Picard iteration is guaranteed to reduce the objective function of (3). However, this does not imply convergence since the Picard reductions may stagnate. Our numerical experiments indicate however that this is not the case and the scheme is convergent. Our Picard scheme can be interpreted (and eventually analyzed) as a block Gauss–Seidel type iteration over the optimality system (7) of the coupled problem. The reduced gradient’s norm of (3) can be interpreted as a residual norm after such an iteration over p and v.

Now, let us give more details on the initialization of the Picard iteration. We start with an initial guess for $\mathit{p}\in {ℝ}^n{}^{{}_p}$ and v (both zero), compute the center of mass of the given patient tumor c_T and place the Gaussian basis functions for the tumor initial condition parametrization as a regular grid around the center of mass of the tumor in patient space. In our current algorithm, the grid of Gaussian basis functions is fixed throughout the Picard iterations, i.e., we do not re-compute the center of mass of the tumor or advect the Gaussian basis functions with the velocity v.

Let us also mention some additional implementation details that significantly affect the performance of the method: (i) We use the solution v from the previous Picard iteration as an initial guess for the new registration iteration to reduce the run time (warm start). (ii) We perform a continuation in the regularization parameter β_v (we start with a large value and successively reduce it). We explain this below. (iii) We do not have a proof for the convergence of the proposed Picard scheme to a minimizer of the fully-coupled optimization problem in (3). Such a proof is beyond the scope of the present paper and remains for future work. We provide numerical evidence that shows that our scheme reduces the gradient of the fully-coupled problem.

Let us remark that we have implemented the gradient of the coupled problem in Section 3 in order to verify that our Picard iteration actually reduces the gradient of the global optimization problem. An implementation of a scheme that iterates simultaneously on both control variables (i.e., solves the global problem), requires more work and will be addressed in a follow-up paper. We show experimentally in various settings that our algorithm is effective and generates registration results that are in excellent agreement with the patient data. Next, we give additional details on the numerical methods used in SIBIA.

Parameter continuation.

Eq. (3) is a nonlinear, non-convex, and ill-conditioned optimization problem that involves a system of reaction–diffusion and pure advection vector equations. The joint forward problem alone has eight unknowns per grid point. The joint inversion problem has twenty unknowns in four dimensions. The computational costs can be quite significant. Furthermore, due to the ill-conditioning and non-convexity, the solver can stagnate. To accelerate convergence, we employ a parameter-continuation scheme to convexify the problem and reduce the chance of getting trapped in local minima. Extensive experimental studies showed that it is sufficient to use parameter continuation for the registration regularization parameter β_v. We use a Tikhonov-type regularization (additional details can be found in [33]) and start with ${\beta }_v^0$ in the first Picard iteration. In each iteration k, the candidate ${\beta }_v^k$ is reduced by one order of magnitude until the specified lower bound for the determinant of the deformation gradient is breached for a candidate ${\beta }_v^k$. The registration solver disregards the associated solution, sets the candidate value for ${\beta }_v^k$ to ${\beta }_v^k\leftarrow {\beta }_v^{k-1}-\left({\beta }_v^{k-1}-{\beta }_v^k\right)/2$ and restarts the inversion with the velocity of the former Picard iteration as initial guess. This process is repeated until the lower bound for the determinant of the deformation gradient is no longer violated. If no violation of the determinant of the deformation gradient was detected during the registration solve, we finalize the current Picard iteration and proceed with the next iteration until we reach the specified smallest admissible value for β_v. Besides globalization, this continuation scheme stabilizes the registration problem and automatically identifies an adequate regularization parameter β_v for the H¹-Sobolev norm for v in every Picard iteration.

Stopping conditions.

Since we can compute the reduced gradient and the objective function we could, in principle, use standard optimization stopping criteria [68]. However, for practical reasons we use a simpler scheme. Since we use parameter continuation, we finalize our Picard iteration either when β_v reaches the prescribed minimum or when we reach a user-defined lower bound for the determinant of the deformation gradient. The lower bound for β_v is a safeguard against numerical instabilities that can occur if v becomes highly irregular (see [37] for a discussion). In both cases we execute two additional Picard iterations with the final value for β_v, instead of iterating until convergence. This scheme leads to more predictable behavior in terms of wall-clock time. Note that the reduced gradient in (7) is computed using an optimize-then-discretize approach and is consistent with the objective function only up to discretization errors.

4.2. Numerics for the tumor inversion and registration sub-blocks

The optimality conditions of both (9a) and (10a) are complex, multi-component, non-linear operators for the state, adjoint, and control fields. We employ an inexact, globalized, preconditioned Gauss–Newton–Krylov method for both problems. In reduced space methods, the reduced space Hessian system has a very similar structure as the first order optimality conditions; we can employ the same numerical strategies we use for the solution of the PDE operators in the first order optimality conditions (see below). We refer to [24,33,37,41] for details on the reduced space Hessian system and its discretization.

Numerical solution and discretization of the PDE operators.

To discretize forward and adjoint tumor and registration problems in space and time, we use regular grids consisting of N₀ × N₁ × N₂, × N_i ∈ ℕ grid points. For all spatial differential operators, we use a spectral projection scheme as described in [17,35]. The mapping between the spatial and spectral coefficients is done using FFTs (the implementation of the parallel FFT library is presented in [67]). Corresponding to the spectral collocation scheme, we assume that the functions in our formulation (including images) are periodic and continuously differentiable and apply filtering operations and periodically extensions of the discrete data to meet these requirements.

To solve the forward and adjoint tumor problem, we use an unconditionally stable, second-order Strang-splitting method, where we split the right-hand side of (3b) and (7c) into diffusion and reaction (see [41,63] for details). The diffusion sub-steps are solved using an implicit Crank–Nicolson method. The solver is a preconditioned conjugate gradient method with a fixed tolerance of 1E−6. The reaction sub-steps are solved analytically. We enforce a positivity constraint on the initial tumor concentration before we apply the forward operator to make sure that c(x, t ) is in [0, 1] for all x ∈ Ω and t ∈ [0, 1]. This thresholding operation is necessary since the parametrization allows for negative concentrations for the initial condition c_A(0) (the coefficient vector p can have negative entries) and the logistic growth function would amplify these negative values in time.

In the image registration module, we solve the hyperbolic transport equations in (3g), (7g), and (7i) based on a semi-Lagrangian scheme [35,37]. Semi-Lagrangian schemes are a hybrid between Lagrangian and Eulerian schemes. They are unconditionally stable and, like Lagrangian schemes (see [36] for an example in the context of diffeomorphic registration), require the evaluation of the space–time fields that appear in our optimality conditions at off-grid locations defined by the characteristic associated with v. We compute the values of these space–time fields at the off-grid locations with a cubic Lagrange polynomial interpolation model. The time integration for computing the characteristic and for the solution of ordinary differential equations along it (if necessary) is based on a second order accurate Runge–Kutta scheme. We refer to [35,37] for a precise definition of these computations.

Newton–Krylov solver.

We initialize our solvers for both reduced gradient systems (7k) and (7l) with a zero initial guess and use an inexact, globalized, preconditioned Gauss–Newton–Krylov method. We terminate the tumor inversion if the relative change of the norm of the reduced gradient in (7k) is below a user defined threshold opttol_T > 0. The reference gradient is the gradient obtained for the zero initial guess for p in the first Picard iteration. For the registration problem, we use a combination of the relative change of (i) the norm of the gradient in (7l), (ii) the objective in (10a) and (iii) the control variable v, all controlled by a single parameter opttol_R > 0, as a stopping criterion. We also specify a maximal number of Newton iterations (maxit_N,T and maxit_N,R) and a lower bound of 1E−6 for the absolute norm of the gradient as a safeguard against a prohibitively high number of iterations. Details for the stopping conditions can be found in [33,69]; see [70, 305 ff.] for a discussion.

We invert the inner linear KKT systems using a matrix-free PCG method. We terminate the PCG method when we either reach a predefined tolerance for the relative residual norm of the PCG method or exceed the maximum number of iterations (maxit_K,T and maxit_K,R). We perform inexact solves [71,72] with a tolerance that is proportional to the norm of the reduced gradient of our problem. The key idea here is to not invert the Hessian accurately if we are far from an optimum (large gradient norm). Details about this approach can be found in [68, p. 165ff.].

4.3. Parallel algorithms and computational kernels

Our parallel implementation is described in detail in [17,35]. We use a 2D pencil decomposition for 3D FFTs [73,74] to distribute the data among processors. We denote the number of MPI tasks by P = P₀ P₁. Each MPI task gets a total of N₀/ P₀ × N₁/ P₁ × N₂ values. We use the open source library AccFFT [67], which supports parallel FFT on CPU and GPU for both single and double precision computations. For parallel linear algebra operations, we use PETSC as well as its optimization interface TAO [75,76]. The other computational kernel besides FFTs is the cubic Lagrange polynomial interpolation model used for the semi-Lagrangian time integration of hyperbolic transport equations. We refer to [17,34] for additional details on the parallel implementation of this interpolation kernel. We provide an algorithmic complexity analysis for the registration in [35] and for the FFT in [41].

5. Numerical experiments

We test the performance of our method on synthetically generated and clinical datasets. Note that all experiments carried out are full 3D simulations. Following standard practice, we use 2D cross-sections of 3D data to depict our results.

SIN.

In our first problem, we consider a synthetic problem in which all the data are periodic, band-limited functions. Our goal with this example is to conduct a mesh refinement to investigate the convergence of the Picard solver. To construct the images, first we grow a tumor in the atlas and then, we advect it with a smooth, band-limited velocity to create a patient image. For this smooth data there are no issues with respect discretization errors and we can focus on the performance of the optimization solver. For a Newton method we expect the number of optimization iterations for the outer solver to be mesh independent. We conduct this experiment to test our Picard scheme in a similar scenario.

ATAV.

This first class of real brain synthetic test cases is used as a proof of concept to assess the convergence of our Picard scheme, its robustness with respect to the tumor model, and the sensitivity of tumor reconstruction quality in terms of the tumor model and its parameters. It uses analytic tumor and analytic velocity (fully synthetic; ground truth for tumor parameters and velocity is known); see Section 5.3 for details. It comes in three different flavors: (i) ATAV-REAC with reaction only and diffusion disabled, (ii) ATAV-DIF with reaction–diffusion model, and (i) ATAV-LD with reaction only and diffusion disabled and a small number n _p of Gaussian basis functions for the initial condition.⁷

RTRV.

This second class of real brain test cases uses real clinical images used in the study described in [7]. It uses real patient data, diffusion disabled and enabled; see Section 5.4 for details.

5.1. General setup

Common Parameters.

We list all model and numerical parameters that are common to all test cases in Table 1 and those that are specific for the test cases in Table 2. In the following, we shortly motivate some of the more involved choices:

Table 1.

Common parameters used in all brain data based test cases: opttol_R, opttol_T are the convergence tolerances for registration and tumor inversion ((7l) and (7k)); β_p is the regularization parameter for the tumor inversion (see (9a)); d is the spacing between the Gaussian basis function, σ their standard deviation; ${\beta }_{\mathit{v}}^0$ and ${\beta }_{\mathit{v}}^{\text{min}}$ are the initial and final values for the β-continuation scheme as described in 4.1 applied in image registration, determined based on which values have been shown to yield best results in numerical tests for the RTRV test problem.

opttolR	opttolT	βp	d	${\beta }_v^0$	${\beta }_{\mathit{v}}^{\text{min}}$
1E−3	1E−3	2.50E−4	1.5σ	1	1E−3

Table 2.

Summary of the parameters for the generation of the synthetic test cases and the inversion. We report values for the following parameters: N_i , i = 1, 2, 3 denotes the grid size used for the discretization of the problem; ρ_w and ρ_g are the characteristic reaction factors for white and gray matter, ρ _f is the overall reaction scaling factor; k_w and k_g are the characteristic diffusion parameters for white and gray matter, k _f the overall scaling parameter for the isotropic part of the inhomogeneous diffusion coefficient for net migration of cancerous cells into surrounding tissue; n _p is the number of Gaussian basis functions used for the parametrization of the tumor initial condition, σ is the standard deviation of the associated Gaussian basis functions, and maxit_i = (maxit_i,N , maxit_i,K ) denotes the maximum number of Newton iterations and Krylov iterations (for the KKT system) for the tumor inversion (i = T ) and registration (i = R), respectively,.

	SIN	ATAV-REAC	ATAV-DIF	ATAV-LD	RTRV
Ni	{64, 128, 256}	128	128	128	256
ρw	1	1	1	1	1
ρg	0	0	0	0	0.2
ρ f	15	15	{5, 10, 15}	{5, 10, 15}	{0, 5, 10, 15}
kw	1	1	1	1	1
kg	0	0	0	0	0.1
k f	0	0	{0, 1E−2}	{1E−2, 1E−1}	{0,1E−2}
n p	{8, 64, 512}	125	125	8	{125, 343}
σ	π/10	π/10	π/10	π/15	Auto
maxitT	(100, 100)	(50, 100)	(30, 60)	(30, 60)	(30, 30)
maxitR	(100, 100)	(50, 80)	(50, 80)	(50, 80)	(10, 20)

β_p has been determined experimentally for a purely synthetic test case with image resolution N_i = 128 and n _p = 125 Gaussian basis functions. For variations of N_i and n _p in our test cases, we observed that the inversion is not sensitive with respect to β_p. Accordingly, we fixed it for all test cases. Smaller values did not further reduce the tumor mismatch in our Picard iteration scheme. To initialize the Gaussian basis, the sub-domain for the grid of basis functions is chosen a priori for the synthetic test cases and determined automatically for the real patient data (cases RTRV) to cover the actual tumor volume in an optimal way: We set the center of the grid for the parametrization to the center of mass of the tumor. The support of the domain covered by the basis functions is the ℓ^∞-ball that covers the entire patient’s tumor in ℝ³. We adjust the standard deviation σ of the Gaussian functions and the distance of their centers automatically. The values are chosen such that their quotient remains constant, and equal to the value used in the synthetic cases. This allows us to ensure a similar conditioning for Φ and to use a fixed β _p.

The choice for n _p depends on the appearance of the patient’s tumor (shape and size). We need to be able to parameterize sufficiently complex initial conditions to recover tumors with a complex appearance. Accordingly, we invert for a varying number of parameters n _p on a case-by-case basis (n _p ∈ {8, 125, 343}) (see Table 2). For the class of synthetic test cases (ATAV), we use an image resolution of 128³ to be able to perform more experiments in limited time, for the real patient data, we use 256³ to ensure high accuracy. Two additional parameters that control the subcomponent solvers are opttol_R , opttol_T as described in Section 4.

Data.

For the generation of the synthetic cases, we use normal brain imaging data obtained at the University of Pennsylvania. For the test case on real imaging data, we use the data available after the first iteration of GLISTR [6,7,77]. The data for these results are the patient data used in the study presented in [6,7]. We consider six datasets from this repository (patient IDs: AAMH, AAAN, AAAC, AAMP, AAQD and AAWI). The original datasets have more labels than we use in our Picard iterations. In particular, they contain background (BG), white matter (WM), gray matter (GM), cerebellum (CB), cerebrospinal fluid (CSF), ventricles (VE), edema (ED), enhancing tumor (ENH), and necrotic tumor (NEC). We construct the labels (WM), (GM), (CSF), (BG) and (TU) by integrating (i) (CB) into (BG), (ii) (VE) into (CSF), and (iii) (ENH), (NEC) and (ED) into (TU).

For all brains, we use the labels white matter (WM), gray matter (GM), cerebrospinal fluid (CSF), and background (BG). The motivation for introducing an additional label BG is technical. We have to ensure the partition of unity across all probability maps for each x in Ω, i.e., all labels have to sum up to one. For example, for the atlas data at t = 1 we have

$$\forall \mathit{x}\in \Omega :c_A(\mathit{x},1)+\sum _{i=1}^4{m}_{A,i}(x,1)\stackrel{!}{=}1$$

Note that m _BG is not used as a label in the image registration formulation (10a). Glial matter is integrated in BG.

Performance Measures.

We perform the registration from the patient space to the atlas space. However, we report all performance measures in the patient space, since the patient space is the relevant space from an applications point of view (for atlas based segmentation).⁸ An important point to note here is that velocity based image registration offers an immediate access to the inverse of the deformation applied to an image; we can essentially solve the forward problem with a negative velocity to obtain the action of the inverse deformation map. We use the following measures to assess the performance of our approach: The relative mismatch/residual ${\mu }_{B,L^2}$ between patient anatomy and atlas anatomy after registration (i = 1: GM; i = 2: WM; i = 3: CSF), and the relative mismatch/residual ${\mu }_{T,L^2}$ between patient tumor and atlas tumor after registration:

$${\mu }_{B,L^2}:=\frac{{\sum }_{i=1}^3{\Vert {\mathcal{R}}^{\text{fwd}}(-\mathit{v},m_{A,i}(1))-m_{T,i}\Vert }_2}{{\sum }_{i=1}^3{\Vert m_{A,i}(0)-m_{T,i}\Vert }_2}\hspace{1em}{\mu }_{T,L^2}:=\frac{{\Vert {\mathcal{R}}^{\text{fwd}}(-\mathit{v},c_A(1))-c_T\Vert }_2}{{\Vert c_T(1)\Vert }_2}$$

The Dice coefficient DICE_l,B for the individual label maps (generated by thresholding; see below) associated with the probability maps for l = W M , l = GM , and l = CSF , for the patient and atlas anatomy, as well as the average Dice coefficient DICE_B across all labels:

$${\text{DICE}}_{l,B^c}:=2\frac{\left|H({\mathcal{R}}^{\text{fwd}}(-\mathit{v},m_{A,l}(1)))\cap H(m_{T,l})\right|}{\left|H\left({\mathcal{R}}^{\text{fwd}}(-\mathit{v},m_{A,l}(1))\right)\right|+\left|H(m_{T,l})\right|},\hspace{1em}{\text{DICE}}_B=\sum _{l=1}^3{\text{DICE}}_{\text{l,B}}/3$$

where $\left|\cdot \right|$ is the cardinality of the set and H is a characteristic function of a label with threshold 0.5, i.e.,

$$H(u(x)):=\{\begin{array}{cc}1\hfill & \hfill \text{for u}(x)\ge 0.5,\\ 0\hfill & \hfill \text{else},\end{array}$$

for all x ∈ Ω. We also report values for the Dice coefficient computed for the probability maps of the tumor, denoted by DICE_T. Further, we monitor the relative change of the gradient for the coupled problem (see Section 3) for the final iteration k:

$${\Vert \mathit{g}\Vert }_{\text{rel}}:={\Vert {\mathit{g}}^k\Vert }_2/{\Vert {\mathit{g}}^0\Vert }_2.$$

where g^k is the gradient of the coupled optimization problem (3) after the kth Picard iteration and g⁰ the gradient for the initial guess. Finally, the relative ℓ²-error for the computed velocity and the initial condition (under the assumption that we know the true velocity v^⋆ and the true tumor parameters p^⋆; synthetic test problem) at the final (kth Picard) iteration is calculated according to

$$e_{\mathit{v},L^2}\hspace{0.17em}:={\Vert {\mathit{v}}^{★}-{\mathit{v}}^k\Vert }_2/{\Vert {\mathit{v}}^{★}\Vert }_2\hspace{1em}\hspace{1em}\hspace{1em}{e}_{c0,L^2}:={\Vert c_A^{{}^{★}}(0)-c_A^k(0)\Vert }_2/{\Vert c_A^{{}^{★}}(0)\Vert }_2$$

$$e_{\mathit{v},L^2,rel}\hspace{0.17em}:={\Vert {\mathit{v}}^{k-1}-{\mathit{v}}^k\Vert }_2/{\Vert {\mathit{v}}^{k-1}\Vert }_2\hspace{1em}\hspace{1em}\hspace{1em}{e}_{c0,L^2,rel}:={\Vert c_A^{k-1}(0)-c_A^k(0)\Vert }_2/{\Vert c_A^{k-1}(0)\Vert }_2$$

Hardware.

The runs for all test cases were executed on the Tier-1 supercomputer HazelHen at the High Performance Computing Center HLRS in Stuttgart (www.hlrs.de), a Cray XC40 system with a peak performance of 7.42 Petaflops comprising 7712 nodes with Xeon E5–2680 v3 processors and 24 cores on two sockets per node. The nodes are connected via an Aries interconnect. For data sizes of N_i = 128, i = 0, 1, 2, we use 3 nodes with 64 MPI tasks and for N_i = 256, i = 0, 1, 2, we use 11 nodes and 256 MPI tasks.

5.2. Test case SIN

Purpose.

The purpose of this experiment is to verify the convergence of our scheme and check the dependence of the convergence rate on the mesh size. For smooth problems, Newton’s method is known to converge quadratically near the solution and is expected to have a convergence rate that is mesh independent [21]. What about our Picard scheme? We will use this numerical experiment to informally answer this question.

Results.

We report results in Table 3 and Fig. 2. We report the relative (to the initial value) reduction in the objective function value ${\Vert \mathcal{J}\Vert }_{\text{rel}}$, the relative (to the initial value) norm of the reduced gradient ${\Vert g\Vert }_{\text{rel}}$, as well as the relative norm $e_{c0,L^2,rel}$ and $e_{\mathit{v},L^2,rel}$, respectively of the update for the inversion variables is reported over the first 23 Picard iterations. We report the relative norm of the reduced gradient (8) of the coupled formulation (3) in Fig. 2 for three different mesh resolutions.

Table 3.

Results for the sinusoidal analytic tumor / analytic velocity (SIN) test case; ground truth: (ρ _f = 15, ρ_w = 1, ρ_g = 0, k _f = 0, p = p^⋆, v = −v^⋆). We report convergence of the Picard iteration scheme for the SIN test case for three runs with increasingly refined mesh. For the registration, we increase the number of inversion variables by a factor of eight starting from N_i = 64 points per dimension, to N_i = 128 and N_i = 256; for the tumor parameters, we choose n _p to be 8,64, and 512 respectively. To study the convergence of our scheme, we perform 20 Picard iterations after termination of the parameter-continuation scheme for the regularization parameter of the registration solver. The relative objective function value ${\Vert \mathcal{J}\Vert }_{\text{rel}}$ and the relative gradient norm ${\Vert g\Vert }_{\text{rel}}$ of the coupled problem in (3) are reported for every iteration. Further, for each iteration we report the relative norm of the update $e_c{}_{0,L^2,rel}$ and $e_{\mathit{v}}{}_{,L^2,rel}$ of the inversion variables p and v respectively.

		Ni = 64,np = 8				Ni = 128,np = 64				Ni = 256,np = 512
It	${\beta }_{\upsilon }$	${\Vert \mathcal{J}\Vert }_{\text{rel}}$	${\Vert g\Vert }_{\text{rel}}$	$e_{c0,L^2,rel}$	$e_{\upsilon ,L^2,rel}$	${\Vert \mathcal{J}\Vert }_{\text{rel}}$	${\Vert g\Vert }_{\text{rel}}$	$e_{c0,L^2,rel}$	$e_{\upsilon ,L^2,rel}$	${\Vert \mathcal{J}\Vert }_{\text{rel}}$	${\Vert g\Vert }_{\text{rel}}$	$e_{c0,L^2,rel}$	$e_{\upsilon ,L^2,rel}$
init	-	1.00	1.00	–	–	1.00	1.00	–	–	1.00	1.00	–	–
1	1	6.67E−1	9.42E−3	–	–	6.73E−1	2.48E−3	–	–	6.67E−1	8.76E−4	–	–
2	1E−1	5.84E−1	5.37E−4	–	–	5.88E−1	2.27E−4	–	–	5.84E−1	7.58E−5	–	–
3	1E−2	3.08E−1	2.42E−4	8.08E−3	1.01E+1	3.08E−1	1.88E−4	2.66E−2	6.02	3.08E−1	6.97E−5	2.28E−2	4.97
4	1E−2	3.03E−1	1.77E−4	2.48E−3	1.51	3.04E−1	1.01E−4	2.35E−2	2.48	3.03E−1	4.37E−5	2.55E−2	2.94
5	1E−2	3.02E−1	1.44E−4	1.34E−3	2.60E−2	3.00E−1	6.20E−5	7.16E−3	1.33E−1	3.02E−1	2.62E−5	1.00E−2	1.48E−1
6	1E−2	3.01E−1	1.18E−4	8.72E−4	1.43E−2	3.02E−1	4.66E−5	2.51E−3	7.70E−2	3.01E−1	1.81E−5	3.61E−3	9.79E−2
7	1E−2	3.01E−1	9.64E−5	5.61E−4	7.25E−3	3.02E−1	3.78E−5	1.29E−3	4.61E−2	3.01E−1	1.41E−5	1.63E−3	6.43E−2
8	1E−2	3.00E−1	7.91E−5	3.62E−4	4.37E−3	3.02E−1	3.12E−5	8.04E−4	2.70E−2	3.00E−1	1.15E−5	9.29E−4	3.96E−2
9	1E−2	3.00E−1	6.50E−5	2.38E−4	3.30E−3	3.02E−1	2.59E−5	5.29E−4	1.61E−2	3.00E−1	9.51E−6	5.89E−4	2.48E−2
10	1E−2	3.00E−1	5.35E−5	1.57E−4	2.71E−3	3.02E−1	2.15E−5	3.54E−4	9.98E−3	3.00E−1	7.89E−6	3.89E−4	1.58E−2
11	1E−2	3.00E−1	4.40E−5	1.05E−4	2.31E−3	3.02E−1	1.79E−5	2.39E−4	6.42E−3	3.00E−1	6.56E−6	2.62E−4	1.02E−2
12	1E−2	3.00E−1	3.63E−5	6.99E−5	1.90E−3	3.02E−1	1.49E−5	1.63E−4	4.22E−3	3.00E−1	5.47E−6	1.78E−4	6.75E−3
13	1E−2	3.00E−1	2.99E−5	4.69E−5	1.58E−3	3.02E−1	1.24E−5	1.12E−4	2.09E−3	3.00E−1	4.55E−6	1.21E−4	4.54E−3
14	1E−2	3.00E−1	2.46E−5	3.16E−5	1.30E−3	3.02E−1	1.04E−5	7.63E−5	3.09E−3	3.00E−1	3.50E−6	8.33E−5	3.10E−3
15	1E−2	3.00E−1	2.03E−5	2.13E−5	1.07E−3	3.02E−1	8.64E−6	5.26E−5	1.35E−3	3.00E−1	3.17E−6	5.74E−5	2.19E−3
16	1E−2	3.00E−1	1.67E−5	1.44E−5	8.85E−4	3.02E−1	7.21E−6	3.63E−5	1.71E−3	3.00E−1	2.64E−6	3.96E−5	1.60E−3
17	1E−2	3.00E−1	1.38E−5	9.73E−6	7.29E−4	3.02E−1	6.05E−6	2.51E−5	9.31E−4	3.00E−1	2.21E−6	2.74E−5	1.20E−3
18	1E−2	3.00E−1	1.14E−5	6.59E−6	6.01E−4	3.02E−1	5.08E−6	1.59E−5	7.94E−4	3.00E−1	1.86E−6	1.89E−5	8.04E−4
19	1E−2	3.00E−1	9.37E−6	4.47E−6	4.95E−4	3.02E−1	4.30E−6	1.12E−5	6.62E−4	3.00E−1	1.57E−6	1.16E−5	6.50E−4
20	1E−2	3.00E−1	7.73E−6	3.03E−6	4.08E−4	3.02E−1	3.64E−6	7.61E−6	5.22E−4	3.00E−1	1.34E−6	8.04E−6	5.29E−4
21	1E−2	3.00E−1	6.37E−6	2.06E−6	3.36E−4	3.02E−1	3.09E−6	5.23E−6	4.27E−4	3.00E−1	1.14E−6	5.69E−6	4.42E−4
22	1E−2	3.00E−1	5.26E−6	1.40E−6	2.77E−4	3.02E−1	2.62E−6	3.71E−6	3.59E−4	3.00E−1	9.63E−7	4.08E−6	3.74E−4
23	1E−2	3.00E−1	4.35E−6	6.45E−7	2.29E−4	3.02E−1	2.23E−6	1.91E−6	3.05E−4	3.00E−1	8.17E−7	2.10E−6	3.17E−4

Fig. 2.

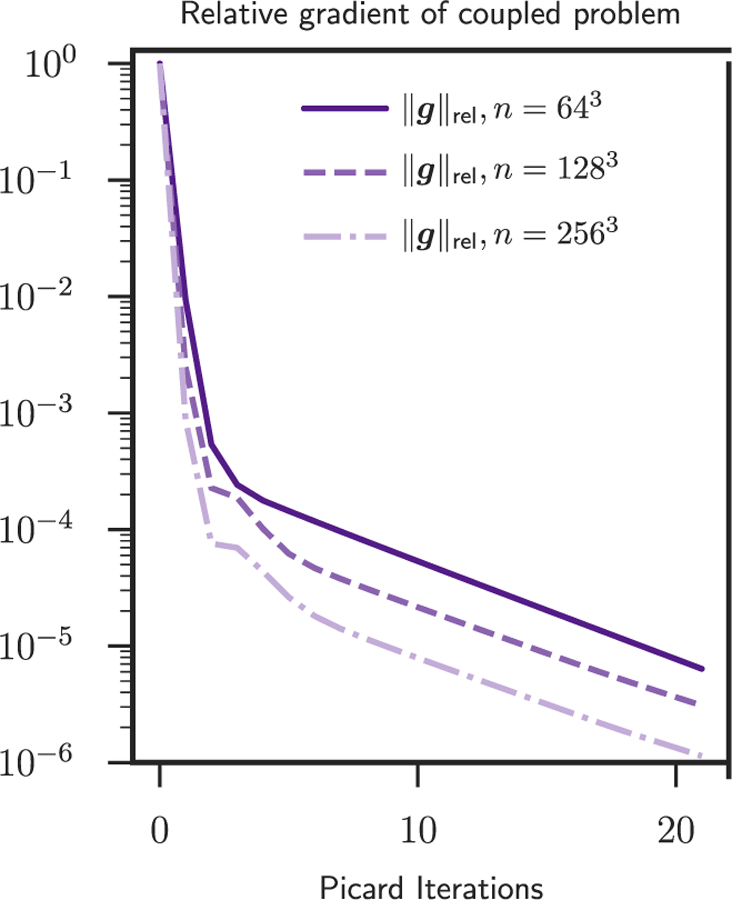
Here we summarize the norm of the reduced gradient of (3) as a function of the Picard iteration number for the sinusoidal analytic tumor / analytic velocity (SIN) test case. The exact numbers are reported in Table 3. The tree different curves correspond to the three different spatial resolutions for the velocity and tumor parameters. We use N_i ∈ {64, 128, 256} points per dimension for the velocity and analogously p ∈ {8, 64, 512}. We perform 20 Picard iterations after termination of the parameter-continuation scheme for the regularization parameter of the registration solver. We have two observations. First, the convergence of our scheme does not deteriorate as we increase the mesh resolution. As we refine the mesh we can reduce the gradient further and the number of iterations does not deteriorate (as it would be the case for a steepest descent method). Second, the convergence of our scheme eventually slows down for all mesh sizes.

Setup.

We consider a fully synthetic, smooth test case using sinusoidal functions for white matter and gray matter, defining the artificial brain. We use white matter for the atlas configuration as $m_W{}_M:=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.cos\left(x_1\right)sin\left(x_2\right)+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and gray matter as m_GM := 1 − m_WM . No CSF is used here (m_{C SF} := 0). Based on a smooth, sinusoidal velocity ${\mathit{v}}^{\star }\left(\mathit{x}\right)={\left(v_1^{\star }\left(\mathit{x}\right),v_2^{\star }\left(\mathit{x}\right),v_3^{\star }\left(\mathit{x}\right)\right)}^T$ with ${\mathit{v}}_1^{★}\left(\mathit{x}\right)=sin\left(x_3\right)cos\left(x_2\right)sin\left(x_2\right),v_2^{★}\left(\mathit{x}\right)=sin\left(x_3\right)cos\left(x_3\right)sin\left(x_3\right),$ and $v_3^{★}\left(\mathit{x}\right)=sin\left(x_2\right)cos\left(x_1\right)sin\left(x_1\right)$, we generate a patient configuration by growing a tumor in the atlas configuration and advecting the resulting abnormal brain with v^⋆ to the patient space. Different from all other test cases and Table 1, we set the tolerance for the relative gradient in the registration and in the tumor inversion solver to opttol_R = opttol_T =1E−7 and allow maxit_R = (100, 100) and maxit_T = (100, 100) Newton and Krylov iterations, respectively. We solve the subcomponent problems accurately to isolate the coupled solver convergence from issues related to early termination in the component solvers. The target value for the regularization parameter β_v in the continuation scheme is set to 1E−2. This also differs from the value chosen for all other test cases and Table 1. The smooth data used in SIN provide less geometric structures to the image registration problem and, thus, requires higher regularization for v. We consider three mesh resolutions in which we increase the resolution for both v and p. In particular we consider grids with 64, 128, and 256 points per dimension and Gaussian grids of size 8, 64, and 512 for the tumor parametrization with a slightly larger spacing of 2σ than in the other test cases.

Observations.

This experiment indicates that our method is mesh-independent. For example, in Table 3 we see that within seven iterations for all resolutions both p and v have essentially converged. We also achieve five orders of magnitude reduction in the relative reduced gradient ${\Vert g\Vert }_{\text{rel}}$, given by (8). Once the reduction in the gradient reaches 1e-5 or so, our method slows down. A Newton method would converge much faster assuming we used a gradient consistent to the objective function. Recall that we use an optimize-then-discretize approach. Due to the semi-Lagrangian time-stepping for the pure advection steps, this gradient is different than the discretize-then-optimize gradient that is needed for the second-order convergence of a Newton method.

Conclusion.

We conclude that although our modular iteration scheme does not perform as well as Newton’s method, it features mesh-independent linear convergence with good convergence rates until we reach gradient values that are significantly lower than what is required and feasible (due to discretization and modeling errors) in real clinical cases. Indeed, as we will see next, the Dice coefficients for the different tissue types converge within a few iterations to their final value for all synthetic and clinical datasets. So the behavior of our scheme appears to be robust and independent of the particular dataset.

5.3. Test case ATAV

Purpose.

This experiment is a proof of concept. We test the numerical accuracy of our scheme, identify the inversion accuracies we can ideally expect (i.e., the errors we get if we use the forward operators to generate the observations for our coupled inversion), and study the convergence of our solver.⁹ With ATAV-REAC and ATAV-DIF, we in addition test the sensitivity of our approach with respect to perturbations in the model and model parameters. In ATAV-LD, we restrict the admissible initial condition parametrization for tumor growth to a very low dimensionality in order to exclude fully grown tumors as initial conditions. We examine, whether this increases the sensitivity of the reconstruction quality for the tumor with respect to correct model parameters.

Setup.

ATAV is based on real brain geometries, but uses a tumor grown with our forward solver in a synthetically generated patient image. We use a resolution of N_i = 128. We choose p = p⋆, which defines $c_A\left(0\right)=c_A^{\star }\left(0\right)$, grow a tumor in the tumor-free atlas, which gives $c_A^{\star }$ (1), choose v = v^⋆, deform the atlas with the grown tumor by advecting the probability maps with the negative velocity v^⋆. This gives us m_T and c_T (patient image with tumor). The velocity v^⋆ is generated by registering two tumor-free images of two different individuals (${\beta }_{\mathit{v}}^{\star }=1E-4$). The center of mass for the synthetic tumor is set to (x¹, x², x³) = 2π · (0.285, 0.36, 0.5). As initial condition for the artificial tumor generation, we enable two of the Gaussians at the center of the grid of Gaussians. See Section 5.1 for further details on the parameters. As a baseline, we also report results for the sole registration of the healthy anatomy (i.e., neglecting the tumor forward solve to generate the data). In addition to that, we quantify the numerical error of our scheme for solving the transport equations (forward registration). This is done by solving the forward problem twice, once with the original and once with the reverted (negative) velocity. The associated error is given by

$$\frac{{\Vert c_A{(1)}^{\star }-{\mathcal{R}}^{\text{fwd}}(-{\mathit{v}}^{\star },{\mathcal{R}}^{\text{fwd}}({\mathit{v}}^{\star },c_A{(1)}^{\star }))\Vert }_2}{{\Vert c_A{(1)}^{\star }\Vert }_2}=9.37\text{E}-2$$ (11)

Whereas we disable diffusion (k _f = 0) in ATAV-REAC, we use the full tumor model including diffusion (k _f 0) for ATAV-DIF. In ATAV-REAC, the same growth rates ρ_w, ρ_g with scaling ρ _f and k_w, k_g with scaling k _f are used for growing the tumor and for the inversion to reconstruct the initial condition. In ATAV-DIF, we use values for the reaction and diffusion coefficients for the inversion in the Picard iterations, that are either the same or differ from those used for the generation of the tumor. In ATAV-LD, we use the full reaction–diffusion tumor model and enforce the initial tumor to be small, i.e., only invert for n _p = 8 parameters, which results in a grid of 2 × 2 × 2 Gaussians that cover the true initial condition of the artificially grown tumor. We expect this to increase the sensitivity of our inversion with respect to the tumor parameters (we cannot fully represent the whole patient tumor purely based on a linear combination of the basis functions). For the inversion, we again consider a variety of models and model parameter combinations, which includes the use of the “correct” (ground truth) tumor parameters. We also consider the case in which we completely neglect the tumor model (i.e., ρ _f = k _f = 0) and just invert for the basis.

Results.

We report results for the registration of anatomy (without tumor) in Table 4. Results for the inversion in ATAV-REAC are presented in Fig. 3 and assess the reconstruction quality (Dice and residuals) and the reduction of the reduced gradient with respect to the iteration index. We also report the error between the ground truth c_A(0)^⋆ = Φ p^⋆ and v^⋆ and the estimated iterates as well as the relative norm of the gradient of the fully coupled problem in (3).

Table 4.

Reference results for geometry registration only between healthy atlas and healthy patient. The table shows values for the relative mismatch for the geometry (${\mu }_{B,L^2}$) and the associated Dice coefficient DICE_B as well as the relative ℓ²-error for the reconstruction of the velocity field $e_{\mathit{v},L^2}$ with respect to the ground truth v^⋆.

maxitR	${\mu }_{B,L^2}$	DICEB	$e_{\mathit{v}}{{}_{,L}}_{{}^2}$
(50, 80)	1.78E−1	9.37E−1	3.59E−1
(10, 20)	1.68E−1	9.36E−1	3.14E−1

Fig. 3.

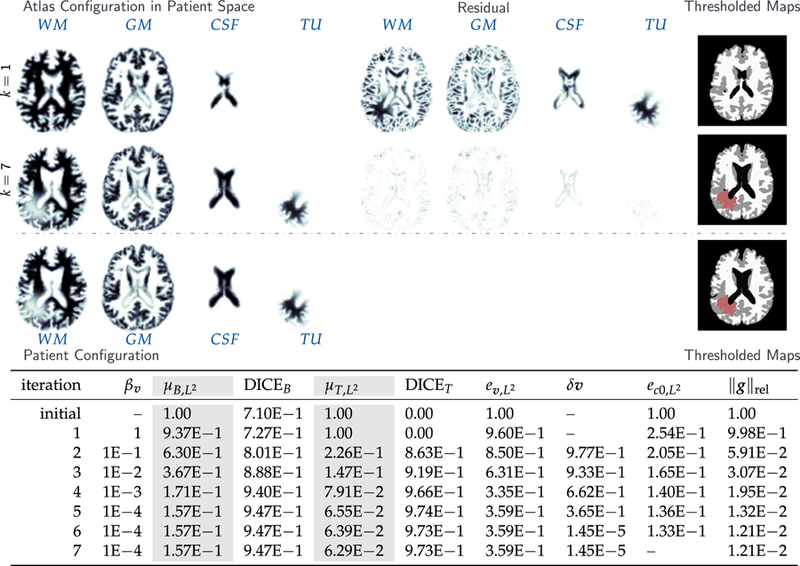
Results for the analytic tumor / analytic velocity reaction-only (ATAV-REAC) test case; ground truth: (ρ _f = 15, ρ_w = 1, ρ_g = 0, k _f = 0, p = p^⋆, v = −v^⋆). The figure shows probability maps for the labels of the healthy atlas brain and the patient brain with tumor generated from a tumor grown in the atlas and known atlas to patient advection velocity (see text for details; axial-slice 64). We show the initial configuration for the problem (top row; iteration k = 1), the final configuration after joint registration and tumor inversion (middle row; iteration k = 7; the atlas image probability maps are transported to the patient space), and the target patient data (reference image; bottom row). Each row contains (from left to right) the probability maps for WM, GM, CSF, and TU, the residual differences (if available) between the probability maps, and a hard segmentation based on the given probabilities for the individual tissue classes. The table on the bottom provides quantitative results for the inversion. We report the average mismatch for the probability maps for the brain tissue labels ${\mu }_{B,L^2}$ and the tumor ${\mu }_{T,L^2}$ , the mean DICE coefficient for brain tissue DICE_B and tumor DICE_T, respectively. The reconstruction quality is given in terms of convergence of v^k and $c_A^k$ (0) towards the ground truth v^⋆ and $c_A^k$ (0), respectively ($e_{\mathit{v},L^2}$ and $e_{c0,L^2}$). We cannot expect this error to go to zero for several reasons. First, we lose information when we construct the test case (zero gradients in the intensity of the image), second our numerical solver introduces errors (in particular, the solver for the transport equations). We in addition to that report the change in update in the velocity v across successive iterations $\delta v=\parallel v^k-v^k{}^{-1}\parallel /\parallel v^k{}^{-1}\parallel$. Finally, we also list the relative norm of the gradient for the coupled problem in (3) $\left({\Vert g\Vert }_{\text{rel}}\right)$.

For ATAV-DIF, quantitative results for the inversion are shown in Table 5, qualitative results can be found in the supplementary material in Fig. A.10. In addition to reconstruction quality and gradient reduction, we list the run time for the Picard scheme per iteration and the percentage spent in each individual solver (tumor and registration), respectively. Note that tumor and registration run times do not add up to 100% as further parts of the code such as the calculation of the reduced gradient and the steering of the Picard iteration are not included in the measurements.

Table 5.

Results for the analytic tumor/analytic velocity with non-zero diffusion (ATAV-DIF) test case; ground truth: (ρ _f = 10, ρ_w = 1, ρ_g = 0, k _f = 1.00E−2, k_w = 1, k_g = 0, p = p^⋆, v = −v^⋆). We report values for the (summed) norm of the residual between the respective probability maps for the different brain tissue classes ${\mu }_{B,L^2}$ and tumor ${\mu }_{T,L^2}$ in patient space, the mean Dice coefficient for brain tissue DICE_B and tumor DICE_T , respectively, as well as the relative norm of the gradient ${\Vert g\Vert }_{\text{rel}}$ for the global coupled problem (3). We report results for different values of ρ _f ∈ {5, 10, 15} used in the inversion (ρ _f = 10 is the ground truth). We report the time spent per iteration (in seconds; top run) or in total (in seconds; bottom runs) for the entire Picard inversion, and the amount of that time spent in the tumor inversion and image registration (in percent (top run); in seconds (bottom runs)), respectively. Note that the latter sums up to less than 100% as we do not explicitly measure time spent in additional coupling functionality and forward solvers. These runs are performed using 64 MPI tasks on three nodes of HazelHen (see Section 5.1 for details). The top block shows the course of the inversion with respect to the Picard iteration index for the correct parameters (ground truth) for ρ _f and k _f . The four rows on the bottom show the final result for our Picard scheme for different parameter and model combinations.

iterations	βv	${\mu }_{B,L^2}$	DICEB	${\mu }_{T,L^2}$	DICET	${\Vert g\Vert }_{\text{rel}}$	$T^{it}[s]$	$T_{inv}^{tu}[\%]$	$T_{inv}^{reg}[\%]$
non-zero diffusion with ground truth parameters ρf = 10,kf = 1E−2
ref	−	1.00	7.14E−1	1.00	0.00	1.00
1	1	9.32E−1	7.32E−1	1.00	0.00	9.94E−1	2.11E+3	99.7	0.2
2	1E−1	6.52E−1	8.01E−1	2.08E−1	8.56E−1	7.45E−2	2.88E+2	96.0	2.1
3	1E−2	3.79E−1	8.88E−1	1.47E−1	9.12E−1	3.87E−2	3.94E+2	91.8	6.9
4	1E−3	1.75E−1	9.39E−1	8.08E−2	9.63E−I	2.45E−2	3.98E+2	72.7	26.1
5	1E−4	1.60E−1	9.48E−1	5.93E−2	9.78E−1	1.77E−2	2.00E+2	35.4	62.1
6	1E−4	1.60E−1	9.48E−1	5.77E−2	9.77E−1	1.72E−2	1.34E+2	46.6	49.6
7	1E−4	1.60E−1	9.47E−1	5.63E−2	9.76E−1	1.73E−2	7.10E+1	0.0	93.0
varying ρ f ∈ {5,10,15},kf = 1E−2, ground truth ρf =10,kf = 1E−2							T otal [s]	$T_{inv}^{tu}[\text{s}]$	$T_{inv}^{reg}[\text{s}]$
ρf = 5	1E−4	1.61E−1	9.46E−1	6.48E−2	9.67E−1	2.21E−2	4.37E+3	3.95E+3	3.97E+2
ρf = 10	1E−4	1.60E−1	9.47E−1	5.63E−2	9.76E−1	1.73E−2	3.60E+3	3.17E+3	4.01E+2
ρf = 15	1E−4	1.61E−1	9.48E−1	6.39E−2	9.72E−1	1.41E−2	3.96E+3	3.53E+3	4.00E+2
ρf = 10, kf = 0, ground truth pf =10,kf =1E−2							Ttotal [s]	$T_{inv}^{tu}[\text{s}]$	$T_{inv}^{reg}[\text{s}]$
ρf = 10	1E−4	1.60E−1	9.48E−1	5.95E−2	9.71E−1	1.74E−2	4.25E+2	2.25E+1	4.01E+2

For ATAV-LD, we show simulation results in Fig. 5 (for sagittal and coronal slices, Fig. A.11) and report quantitative results in Table 6. We plot the trend of the relative tumor mismatch with respect to the regularization parameter β_v for the Sobolev norm for the registration velocity (and by that the Picard iteration index) in Fig. 4.

Fig. 5.

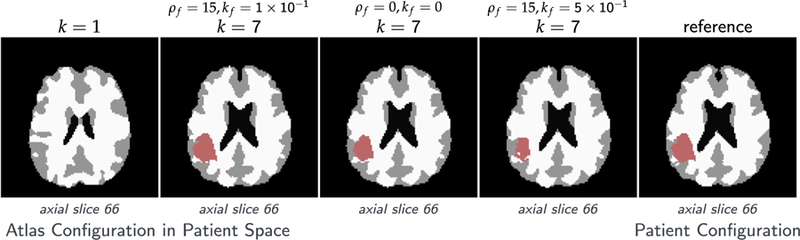
Tumor and brain labels for the analytic tumor with analytic velocity with non-zero diffusion and low-dimensional initial condition (ATAV-LD) test case; ground truth: (ρ _f = 15, ρ_w = 1, ρ_g = 0, k _f = 1.00E−1, k_w = 1, k_g = 0, p = p⋆ (in patient domain), v N/A); for the ‘correct’ tumor parameters ρ _f = 15, k _f = 1.00E−1, and the two different settings ρ _f = 15, k _f = 5.00E−1 and ρ _f = k _f = 0.

Table 6.

Results for the analytic tumor with analytic velocity with diffusion and low-dimensional initial condition (ATAV-LD) test case; ground truth: (ρ _f = 15, ρ_w = 1, ρ_g = 0, k _f = 1.00E−1, k_w = 1, k_g = 0, p = p^⋆ (in patient domain), v N/A). We use a low-dimensional parametrization for the initial condition with n _p = 8 Gaussians (σ = π/15). We report the (summed) mismatch for the probability maps for the brain tissue ${\mu }_{B,L^2}$ and tumor ${\mu }_{T,L^2}$ in patient space, the mean Dice coefficient for hard segmentations of brain tissue (DICE_B ) and tumor (DICE_T ), respectively, and the relative norm of the gradient $\left({\Vert g\Vert }_{\text{rel}}\right)$ for the coupled problem (3). We assess the final state of the reconstruction using different values for ρ _f ∈ {5, 10, 15, 20} and k _f ∈ {0, 1E−1}. Absolute timings are given for the tumor inversion and image registration, respectively using 64 MPI tasks on three nodes of HazelHen. Note that the latter sums up to less than the reported total run time as we do not explicitly measure time spent in additional coupling functionality and forward solvers. We always reach the target value of β_v = 1E−4.

ρ	k	It	${\mu }_{B,L^2}$	DICEB	${\mu }_{T,L^2}$	DICET	${\Vert g\Vert }_{\text{rel}}$	$T^{total}[\text{s}]$	$T_{inv}^{tu}[\text{s}]$	$T_{inv}^{reg}[\text{s}]$
		initial	1.00	7.18E−1	1.00	0.00	1.00	–	–	–
0	0	final	1.96E−1	9.45E−1	2.80E−1	8.48E−1	4.16E−2	3.78E+2	3.33	3.77E+2
15	0		1.87E−1	9.46E−1	2.04E−1	9.16E−1	1.70E−2	3.78E+2	2.19	3.78E+2
15	IE−1		1.69E−1	9.48E−1	4.68E−2	9.65E−1	1.73E−2	4.72E+3	4.17E+3	4.59E+2
15	5E−1		1.90E−1	9.41E−1	3.37E−1	4.71E−2	1.78E−2	6.67E+3	5.54E+3	4.29E+2
15	IE−2		1.79E−1	9.47E−1	1.57E−1	9.31E−1	1.51E−2	2.23E+3	1.50E+3	4.31E+2
5	IE−1		1.71E−1	9.46E−1	6.50E−2	9.57E−1	2.45E−2	1.96E+3	1.50E+3	3.87E+2
10	IE−1		1.70E−1	9.47E−1	4.98E−2	9.62E−1	2.01E−2	3.90E+3	2.90E+3	3.73E+2
10	IE−2		1.79E−1	9.47E−1	1.65E−1	9.26E−1	1.91E−2	2.17E+3	1.63E+3	3.66E+2
20	IE−1		1.70E−1	9.48E−1	5.45E−2	9.56E−1	2.02E−2	3.07E+3	2.62E+3	3.88E+2
20	IE−2		1.80E−1	9.47E−1	1.60E−1	9.18E−1	1.20E−2	2.03E+3	4.51E+2	3.78E+2

Fig. 4.

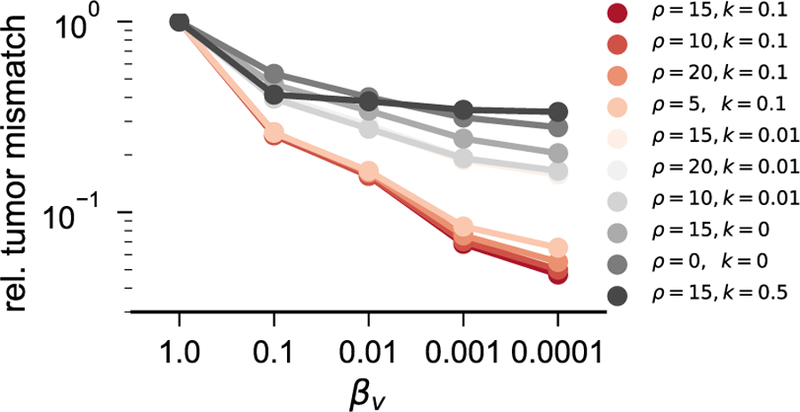
Mismatch reduction as a function of the regularization parameter β_v for the analytic tumor with analytic velocity, diffusion and low-dimensional initial condition (ATAV-LD) test case; ground truth: (ρ _f = 15, ρ_w = 1, ρ_g = 0, k _f = 1.00E−1, k_w = 1, k_g = 0, p = p^⋆ (in patient domain), v N/A). We use an initial condition parameterized with only n _p = 8 Gaussians (σ = π/15) and an analytic tumor with non-zero diffusion. The plot shows the relative mismatch for the tumor probability map ${\mu }_{T,L^2}$ in patient space. Note that we reduce β_v by a factor of ten in each Picard iteration; the plot shows the mismatch reduction over the Picard iterations if read from right to left.

Observations.

The most important observations are (i) that the reconstructed data (tumor and registered anatomy) are in excellent agreement with the patient data, and (ii) we are able to reduce the reduced gradient (8) by two orders of magnitude in seven iterations of our Picard scheme for ATAV-REAC and significantly more than a factor of 50 for all experiments in ATAV-DIF and ATAV-LD.

The numerical error for the advection in (11) is 9.37E−2. The relative mismatch for the anatomy obtained for our iterative Picard scheme is in the order of the advection error for the forward image registration problem. We can also see that the reconstruction of c_A(0)^⋆ and c_A(1)^⋆ seems to be bounded by this error. In fact, due to the advection error that leads to a mismatch in this order in the atlas domain, this is the best we can expect without over-fitting the data. Similar observations can be made if we compare the inversion results with the results obtained for the registration for healthy brains (neglecting the tumor simulations) reported in Table 4. Hence, the quality of tumor reconstruction is comparable to the quality of pure image registration between the healthy geometries. This is an excellent result that clearly demonstrates the potential of our approach. The obtained Dice coefficient for the brain anatomy is in the order of what we see for the sole registration of healthy anatomies.¹⁰ Note that the mismatch between the true velocity v^⋆ and the recovered velocity v^k reported for ATAV-REAC is due to the fact that image registration is an inherently ill-posed problem: the velocity can only be reconstructed exactly in image areas with non-zero gradients and if there are only non-zero intensity differences between the images to be registered in areas that do correspond to one another.¹¹ In addition, we ask for the reconstruction of a vector field from scalar data.

The Dice coefficient for the brain anatomy increases from 7.10E−1 to 9.47E−1 in ATAV-REAC, where we obtain a final Dice coefficient of 9.73E−1 for the tumor. The results for ATAV-DIF and ATAV-LD show that the used model and the dimensionality of the initial conditions do not have a significant impact on the quality of the inversion (Dice and mismatch).

We can furthermore see that we can significantly reduce the norm of the reduced gradient (8) to 1.21E−2. We can also see that once we have reached the target regularization parameter β_v = 1E−4 we do not make any more progress. The update for the velocity tends to zero, the changes in the reduced gradient are small and the error measures (residual and Dice) do no longer change significantly.

For ATAV-DIF, we see that we obtain a slightly better mismatch (5.63E−2) and Dice coefficient (9.76E−1) for the tumor probability map if we use the correct ρ _f . These results suggest that we can identify the correct ρ _f if we run multiple inversions for the initial condition. However, we note that these differences are small (the mismatch is between 5.95E−2 and 5.63E−2 and the Dice is between 9.71E−1 and 9.76E−1, respectively, for the tumor). Overall, we obtain an excellent agreement between patient data and atlas data irrespective of the model choice. These observations are confirmed by careful visual inspection of Fig. A.10 (supplementary material; shows only results for the “correct” tumor parameters). This can be explained by the parametrization of the initial condition. We can reconstruct complex tumor shapes even with a simple model. Overall, this indicates that using a reaction-only model might be sufficient for pure diffeomorphic image registration,¹² where a comparison of the total run time for the last row in Table 5 to the total run times attained when enabling diffusion shows that we can save a factor of 10 in run time by disabling diffusion. Another interesting behavior within our scheme is that, during the first few iterations, most time is spent in the tumor inversion, whereas, as we reduce β_v, the registration does most of the work. This is to be expected, since the run time of our scheme (more precisely, the condition number of the Hessian) for diffeomorphic registration, is not independent of β_v [33,36].

The most important observation for ATAV-LD is that we can identify the correct pair of diffusion and reaction rates that have been used to generate the synthetic test based on slightly more pronounced differences in the overall mismatch and Dice scores than in ATAV-DIF. The sensitivity with respect to changes in the diffusion parameter k _f is larger than with respect to changes in the growth rate ρ _f . We expect this much more pronounced dependence on the diffusion model if we parameterize the initial condition on a grid with a smaller support, since we need the cancerous cells to diffuse to areas more distant to the tumor center in order to be able to reconstruct the whole tumor. The trend of the relative mismatch for the tumor in Fig. 4 highlights this effect. The curves almost cluster in terms of the different choices for the diffusion coefficient; we overall achieve significantly better mismatch if we choose the correct diffusion coefficient. We can also see that the curves plateau much earlier in cases where we use the wrong parameter combinations. The tumor mismatch takes values between 3.37E−1 and 4.68E−2 with a Dice score of 4.71E−2 to 9.65E−1.

Conclusion:

We conclude that our Picard scheme is efficient and converges to a valid (local) minimum in the search space (we reduce the relative global gradient, the distance measure, and significantly increase the Dice coefficient). We attain an excellent agreement between the data (patient tumor and geometry) and the predicted state (transported atlas geometry and predicted tumor) with a final Dice coefficient of 9.47E−1 and 9.73E−1 for the labels of the anatomy and tumor in ATAV-REAC and only slightly worse values in ATAV-DIF and ATAV-LD.

The integration of a diffusion model into our inversion is very costly, at least for our current implementation. Designing a more efficient forward solver for the diffusion operator requires more work. We could demonstrate that our parametrization of the initial condition allows us to generate high-fidelity registration results, especially for the healthy anatomy, irrespective of the model that has been used to generate the data. These are clearly preliminary results, but they provide some evidence that reaction-only models might be sufficient for pure image registration (something that is quite certainly not the case if we target parameter identification and tumor growth prediction) [63].

We can also observe that there are subtle differences in the reconstruction quality of the tumor if we use the “correct” growth rate for the inversion for ATAV-DIF, that are more pronounced in ATAV-LD. Overall, we conclude that we (i) can neglect the diffusion model in the context of diffeomorphic registration and compensate the resulting loss in accuracy by a higher-dimensional Gaussian basis, (ii) might be able to identify appropriate growth rates if we run multiple inversions for different parameters with a low-dimensional Gaussian basis.

5.4. Test case RTRV

Purpose.

We test our approach on real data of patients diagnosed with glioma tumors and study the registration quality for a variety of parameter choices for the tumor growth model.

Setup.

This test scenario consists of real patient brains with real tumors for which we do not know any parameters. The patient datasets are the first proposal for a patient segmentation produced in the first iteration of GLISTR [7]. We provide additional details about this database in Section 5.1. We have to identify the support of the domain spanned by the Gaussian basis functions for the tumor initial condition parametrization as well as their spacing d, and the standard deviation σ for any unseen patient. This is done automatically. As some of the real tumors are multifocal, we use n _p = 343 Gaussians in our first set of experiments on all six brains for the initial condition parametrization. In contrast to the synthetic test cases ATAV-REAC, ATAV-DIF and ATAV-LD, we allow the tumor to grow also in gray matter instead of in white matter only, but with a reaction parameter that is five times smaller than in white matter (see Table 2 for details). We use a variety of models and parameter settings in our Picard scheme for the two patients AAMH and AAAN to not only assess the performance of our method but also study its sensitivity towards parameter changes and model complexity. We vary the reaction parameter ρ _f between 0 and 15 and choose the diffusion coefficient k _f either as 0 or 1.00E−2. See Section 5.1 for additional details on the setup of the test case and the parameters.

Results.

Figs. 6–8 show the healthy atlas (k = 1) in the top row and the corresponding patient image with tumor in the bottom row for axial, saggital, and coronal orientations. The hard segmentations for the results computed with the proposed approach are shown in the middle row using the same orientations. In Table 7, we summarize the results for all patient datasets. We report the initial and final values for the mismatch and Dice coefficients associated with the probability maps for the tumor and the brain anatomy, as well as the relative norm of the gradient of the coupled problem in (3). We also report timings for the entire inversion. Fig. 9 shows more detailed images of the probability maps for the patient AAMH (complex and large tumor). More detailed visual results with information on more iterations of our inversion algorithm for all patients are given in Appendix (Figs. A.12 through A.17). Results for varying reaction and diffusion for AAMH and AAAN are listed in Table 8. Note that all parameter choices refer to the model used for tumor reconstruction in the Picard scheme. The true growth parameters of the tumors are unknown.

Fig. 6.

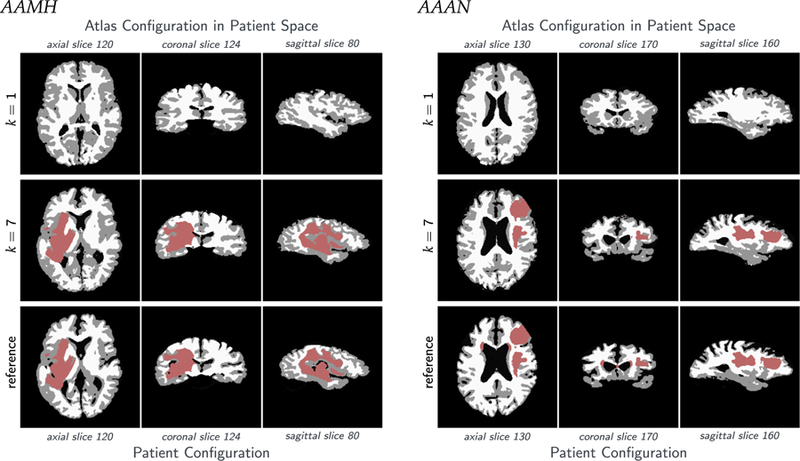
Tumor and brain labels for the real tumor with real velocity (RTRV) test case; ground truth (ρ N/A, k N/A, p N/A, v N/A); patients AAMH, AAAN. We set the parameters for the tumor solver to ρ _f = 15, k _f = 0 (reaction-only). We use n _p = 343 Gaussians for the inversion. The top row shows the original atlas image. The bottom row shows the patient image. The row in the middle shows the solution for our coupled scheme.

Fig. 8.

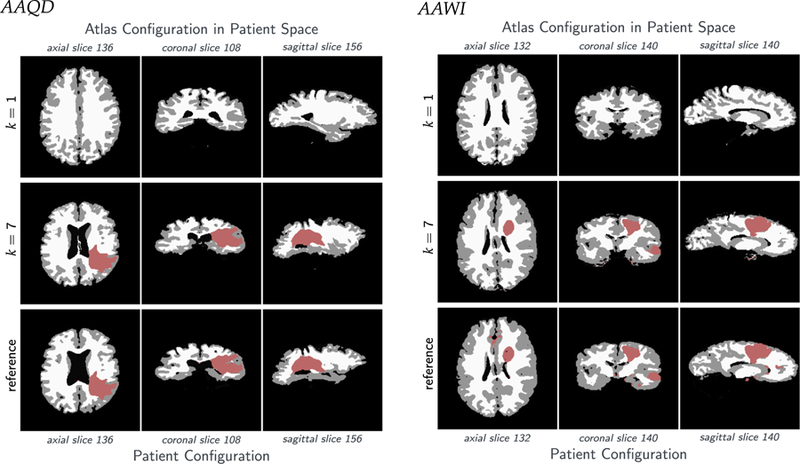
Tumor and brain geometry for the real tumor with real velocity (RTRV) test case; ground truth (ρ N/A, k N/A, p N/A, v N/A); patients AAQD, AAWI. We set the parameters for the tumor solver to ρ _f = 15, k _f = 0 (reaction-only). We use n _p = 343 Gaussians for the inversion. The top row shows the original atlas image. The bottom row shows the patient image. The row in the middle shows the solution for our coupled scheme.

Table 7.

Summary of results for the real tumor with real velocity (RTRV) test case, ground truth (ρ N/A, k N/A, p N/A, v N/A); based on real clinical data (taken from [7]). We set the tumor parameters to ρ _f = 15, k _f = 0 (reaction-only). We use a parametrization of tumor initial conditions with n _p = 343 Gaussians. We report the (summed) mismatch for the brain tissue probability maps (${\mu }_{B,L^2}$) and tumor probability map (${\mu }_{T,L^2}$) in patient space, the mean Dice coefficient for the hard segmentation corresponding to the brain tissue (DICE_B ) and the tumor (DICE_T ), respectively, as well as the relative norm of the gradient for the coupled problem (3) $\left({\Vert g\Vert }_{\text{rel}}\right)$. We also report the total run time in seconds (T _total ), and the run time of the individual components of our Picard scheme, respectively (also in seconds; tumor solver:$T_{inv}^{tu}$; image registration: $T_{inv}^{reg}$). Note that the latter sums up to less than the reported total run time as we do not explicitly measure time spent in additional coupling functionality and forward solvers. We execute our code in parallel on 11 nodes using 256 MPI tasks of HazelHen.

Patient		βv	${\mu }_{B,L^2}$	DICEB	${\mu }_{T,L^2}$	DiceT	${\Vert g\Vert }_{\text{rel}}$	$T^{total}[\text{s}]$	$T_{inv}^{tu}[\text{s}]$	$T_{inv}^{reg}[\text{s}]$
AAMH	Initial	1	1.00	4.36E−1	1.00	0.00	1.00	–	–	–
	final	1E−4	3.45E−1	7.92E−1	1.95E−1	9.57E−1	3.92E−2	6.28E+2	1.95E+2	4.35E+2
AAAN	initial	1	1.00	4.37E−1	1.00	0.00	1.00	–	–	–
	final	1E−4	3.54E−1	8.35E−1	3.77E−1	8.91E−1	1.06E−1	6.34E+2	2.15E+2	4.17E+2
AAAC	initial	1	1.00	4.82E−1	1.00	0.00	1.00	–	–	–
	final	1E−4	3.36E−1	8.44E−1	2.45E−1	9.55E−1	4.38E−2	4.92E+2	1.59E+2	3.32E+2
AAMP	initial	1	1.00	4.74E−1	1.00	0.00	1.00	–		–
	final	1E−4	3.32E−1	8.05E−1	1.34E−1	9.75E−1	3.31E−2	6.48E+2	2.36E+2	4.13E+2
AAQD	initial	1.00	1.00	2.92E−1	1.00	0.00	1.00	–	–	–
	final	1E−4	3.24E−1	8.06E−1	2.55E−1	9.31E−1	9.88E−2	1.10E+3	2.19E+2	8.81E+2
AAWI	initial	1	1.00	4.53E−1	1.00	0.00	1.00	–	–	–
	final	1E−4	3.45E−1	7.87E−1	3.92E−1	8.74E−1	5.26E−2	6.84E+2	2.92E+2	3.90E+2

Fig. 9.

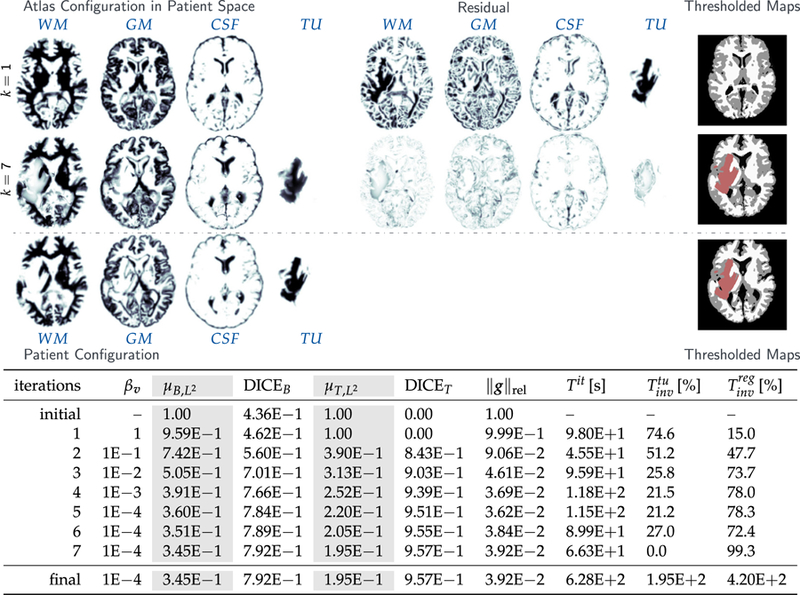
Results for the real tumor/ real velocity (RTRV) test case, ground truth (ρ N/A, k N/A, p N/A, v N/A) and the AAMH patient. The figure shows probability maps for the labels of the healthy atlas brain (k = 1; top row) and the AAMH patient (target) brain probability maps with tumor (bottom row), along with the reconstructed probability maps, i.e., the final result of our inversion algorithm (k = 7; middle row) (axial-slice 120). In the table, we report the (summed) mismatch for the brain tissue probability maps (${\mu }_{B,L^2}$) and tumor probability map (${\mu }_{T,L^2}$) in patient space, the mean Dice coefficient for the hard segmentation corresponding to the brain tissue (DICE_B ) and the tumor DICE_T , respectively, as well as the relative norm of the gradient for the coupled problem (3) $\left({\Vert g\Vert }_{\text{rel}}\right)$. We also report the run time per iteration in seconds (T ^it ), and the percentages ($T_{inv}^{tu}$) and ($T_{inv}^{reg}$) of this run time spent in the tumor solver and the image registration solver, respectively. Note that the latter sums up to less than 100% as we do not explicitly measure time spent in additional coupling functionality and in the forward solvers. The last row shows the final state and summed absolute timings for the respective solvers in seconds.

Table 8.

Results for the AAMH and the AAAN patient real tumor/ real velocity (RTRV) test case, ground truth (ρ N/A, k N/A, p N/A, v N/A) using real clinical input data. The table shows the (summed) mismatch for the brain tissue probability maps (${\mu }_{B,L^2}$) and tumor probability map (${\mu }_{T,L^2}$) in patient space, the mean Dice coefficient for the hard segmentation corresponding to the brain tissue (DICE_B ) and the tumor (DICE_T ), respectively for different values for reaction scaling parameter ρ _f and of the diffusion coefficient scaling parameter k _f ., as well as the relative norm of the gradient for the coupled problem (3) $\left({\Vert g\Vert }_{\text{rel}}\right)$. We also report the total run time in seconds (T _total ), and the run time of the individual components of our Picard scheme, respectively (also in seconds; tumor solver:$T_{inv}^{tu}$; image registration:$T_{inv}^{reg}$). Note that the latter sums up to less than the reported total run time as we do not explicitly measure time spent in additional coupling functionality and forward solvers. We execute our code in parallel on 11 nodes using 256 MPI tasks of HazelHen.

	ρf	kf	np	${\mu }_{B,L^2}$	DICEB	${\mu }_{T,L^2}$	DICET	${\Vert g\Vert }_{\text{rel}}$	$T^{total}\left[\text{s}\right]$	$T_{inv}^{tu}\left[\text{s}\right]$	$T_{inv}^{reg}\left[\text{s}\right]$
ID AAMH	initial canfig			1.00	4.36E−1	1.00	0.00	1.00	–	–	–
	0	0	343	3.40E−1	7.92E−1	l.47E−1	9.69E−1	l.19E−1	6.09E+2	2.13E+2	3.63E+2
	0	0	125	3.38E−1	7.95E−1	1.73E−1	9.62E−1	1.31E−1	5.09E+2	7.86E+l	4.04E+2
	15	0	343	3.45E−1	7.92E−1	1.95E−1	9.57E−1	3.92E−2	6.28E+2	l.95E+2	4.35E+2
	15	0	125	3.50E−1	7.91E−1	2.36E−1	9.53E−1	4.83E−2	4.47E+2	7.20E+l	3.48E+2
	5	lE−2	343	3.44E−1	7.92E−1	l.88E−1	9.64E−1	7.68E−2	l.23E+4	l.18E+4	3.41E+2
	10	lE−2	343	3.46E−1	7.92E−1	2.0 7E−1	9.62E−1	5.16E−2	l.33E+4	l.28E+4	3.44E+2
	15	lE−2	343	3.48E−1	7.93E−1	2.35E−1	9.59E−1	3.47E−2	1.18E+4	l.13E+4	3.63E+2
ID AAMN	initial canfig.			1.00	4.37E− 1	1.00	0.00	1.00	-	-	-
	0	0	343	3.42E−1	8.39E−1	2.56E−1	9.36E−1	2.19E−1	6.58E+2	2.02E+2	4.23E+2
	0	0	125	3.56E−1	8.33E−1	4.40E−1	6.68E−1	2.36E−1	4.54E+2	8.89E+l	3.38E+2
	15	0	343	3.54E−1	8.35E−1	3.77E−1	8.91E−1	l.06E−1	6.34E+2	2.15E+2	4.17E+2
	15	0	125	3.67E−1	8.30E−1	5.71E−1	3.44E− 1	1.28E−1	4.67E+2	8.38E+l	3.57E+2
	5	lE−2	343	3.50E−1	8.35E−1	3.17E−1	9.06E−1	1.79E−1	1.82E+4	1.77E+4	3.33E+2
	10	lE−2	343	3.52E−1	8.35E−1	3.60E−1	8.85E−1	l.41E−1	l.88E+4	l.82E+4	3.41E+2
	15	lE−2	343	3.S5E−1	8.34E−1	3.98E−1	8.62E−1	l.13E−1	1.85E+4	l.80E+4	3.28E+2

Observations.

The most important observation is that we obtain very good registration results – qualitatively and quantitatively – in what is an extremely challenging registration problem. From visual inspection of the data alone (Fig. 6 through Fig. 8) we can immediately see that there are significant anatomical differences between the atlas image and the patient images, and across patients. The tumors vary significantly in shape and size. Overall, this poses considerable challenges to our framework. The results reported in Fig. 6 through Fig. 8 and in Fig. 9 clearly demonstrate that the deformed atlases are in very good agreement with the patient data for all six subjects. We reach Dice coefficients between 7.87E−1 to 8.44E−1 and 8.74E−1 to 9.75E−1 for the probability maps associated with the anatomy and the tumor. These results are slightly worse than those obtained for the artificially grown tumors in the former sections, but still competitive. We also note that the initial Dice coefficients for the anatomy range between 2.92E−1 and 4.74E−1 for these data, which is drastically worse than what we have seen in our synthetic test cases. The run times are comparable to our former experiment. We again achieve a reduction of the relative norm of the gradient for the coupled problem in (3) of about two orders of magnitude (slightly less than what we saw before). The results of our study with varying tumor model parameters presented in Table 8 show that there are slight variances in the results depending on the parameter choices, but the Picard iteration scheme is successful in all cases. Further enhancements of our environment are required to enable the identification of the ‘correct’ tumor growth parametrization.

Conclusions:

We have tested our formulation on real data that pose significant challenges due to large inter-subject anatomical variability and a strong variation in the appearance of the tumor, in shape, size, location and growth behavior. We use a very simple model that only accounts for logistic growth. This, in combination with a flexible, high-dimensional parametrization of the initial condition allows us to overcome these challenges. We achieve extremely promising registration accuracies with a Dice score of up to 8.44E−1 and 9.75E−1 for the label maps associated with the probability maps of the brain anatomy and the tumor in what is an extremely challenging problem. Runs with variation of the growth parameter ρ _f show, on the one hand, that it is important to identify the correct parameters to achieve optimal quality of tumor reconstruction. We, therefore, believe that it will be possible to identify physical tumor growth parameters from our coupled solver if the tumor model is enhanced (anisotropic diffusion, mass effect, . . . ) and we consider ‘correct’ time horizons and/or restrict the initial conditions of tumor to point seeds (see first steps following this idea in ATAV-LD). On the other hand, the results for varying model parameters show the robustness of our Picard scheme with respect to the model and parameter choice. Furthermore, the reconstruction results for the AAAN patient data show that we can reconstruct multifocal tumors with comparable quality and computational costs.

6. Conclusion

We have presented a new method for the registration of images of patients diagnosed with mono- or multifocal brain tumors to a common reference atlas. Application scenarios are biophysical model calibration and image registration. Our method combines stand-alone forward and inverse tumor [41] and diffeomorphic registration [33–35,37] by means of an efficient coupling scheme based on a Picard iteration. It allows us to exploit available, tailored implementations for the solution of the subproblems [17,35], while monitoring convergence using the coupled gradient information. We invert simultaneously for the control variables of both problems—a parametrization of the initial condition for the tumor model, and a smooth velocity field to capture the inter-subject variability of brain anatomy. Here is what we have learned from our experiments on synthetic and real data:

1. Despite the fact that our scheme neglects coupling terms that appear in our coupled optimization problem, we could experimentally show that it efficiently reduces the coupled gradient. A convergence proof of the Picard scheme to a local minimum is beyond the scope of this paper and remains subject to future work.

2. We could demonstrate that our parametrization of the initial condition allows us to generate high-fidelity registrations irrespective of the complexity of the data or the model used for the tumor simulations. If we reduce the number of basis functions used for initial condition parametrization, this is no longer true.

3. In studies with various models from a pure interpolation with the basis functions that parameterize the initial condition (zero reaction and diffusion coefficient) over a reaction-only, to a full reaction–diffusion model, we could show in our synthetic cases, that we get the highest accuracy in tumor reconstruction, if we use the correct model. This implies that our framework could eventually serve as a powerful tool for model selection. A rigorous verification of this claim requires significantly more work and remains for the future.

4. Overall, our numerical study, which includes real brain images with real tumors, shows that we can achieve high-fidelity results with an overall low mismatch and high Dice score in particular for the simulated and observed tumor, with Dice coefficients ranging from 93% for real tumors above a critical size, and up to 97% for artificially grown tumors in a real brain geometry.

5. We are able to solve the joint registration and biophysical inversion problem on hardware and wall-clock time that fits clinical requirements. We used 128 × 86 cores for our simulations. This configuration is not exotic and it is found in many hospitals that already use such clusters for bioinformatics and image analysis. On such a machine, our real data simulations would require about two hours. Considering that standard MRI imaging already takes 30–45 min, the simulation run time is acceptable.

Let us emphasize that our tumor model is currently not sophisticated enough to allow prediction, but the tumor-registration coupling approach that we present in this work and for which we can show good computational performance and high accuracy for various real brain data test cases lays the basis for further developments with improved tumor solvers and, finally, a parameter identification and growth prediction tool. The next steps for SIBIA are to improve the biophysical tumor-growth model by first adding mass-effect and second higher-fidelity tumor growth models.

Fig. 7.

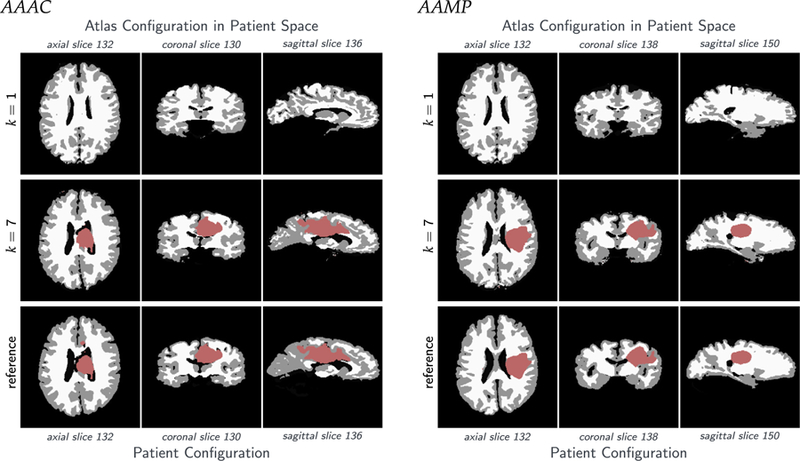
Tumor and brain geometry for the real tumor with real velocity (RTRV) test case; ground truth (ρ N/A, k N/A, p N/A, v N/A); patients AAAC, AAMP. We set the parameters for the tumor solver to ρ _f = 15, k _f = 0 (reaction-only). We use n _p = 343 Gaussians for the inversion. The top row shows the original atlas image. The bottom row shows the patient image. The row in the middle shows the solution for our coupled scheme.

Appendix. Supplementary material

A.1. Supplementary material for the ATAV testcase

We present additional qualitative data for the ATAV-DIF testcase and the ATAV-LD testcase.

A.2. Supplementary material for the RTRV testcase

We show detailed results for the RTRV real data test cases for six patient datasets (AAAC, AAAN, AAMP, AAMH, AAQD, AAWI; first proposal for a patient segmentation produced in the first iteration of GLISTR [7]). Fig. A.12 through Fig. A.17 show axial slices of the evolution of the probability maps of the atlas brain tissue labels (in patient space) and the reconstructed tumor (in patient space) throughout our inversion algorithm. Brain tissue probability maps, tumor probability map, mismatch for all labels as well as the hard segmentation image are given for Picard iterations k = {1, 2, 4, 6}.

Fig. A.10.

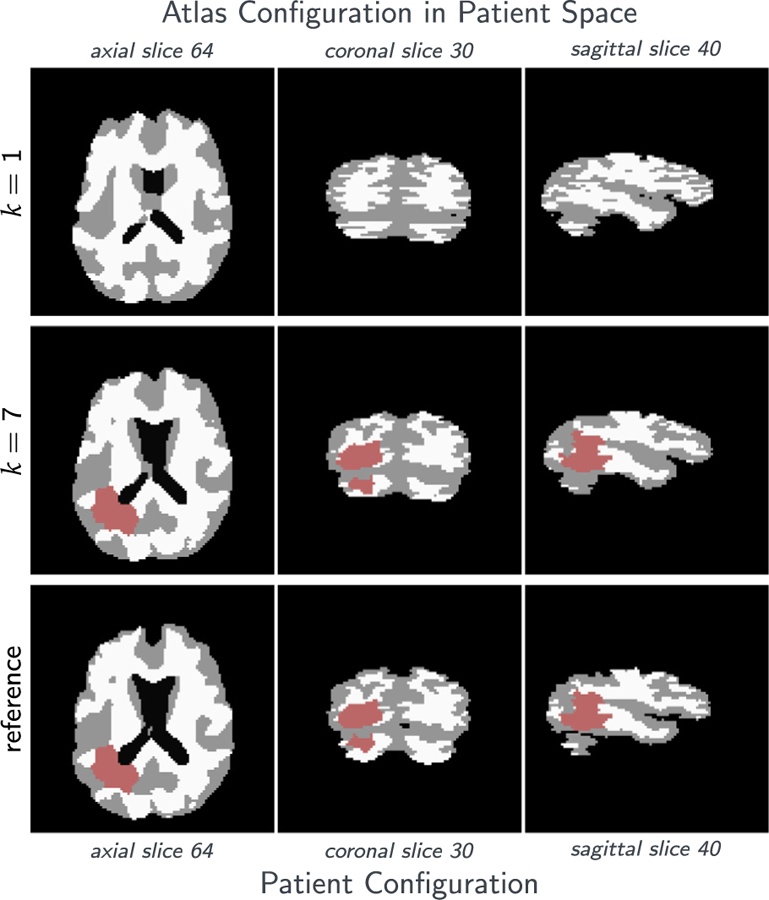
Tumor and brain labels (obtained by thresholding probability maps) for the analytic tumor with analytic velocity with non-zero diffusion (ATAV-DIF) test case; ground truth: (ρ _f = 10, ρ_w = 1, ρ_g = 0, k _f = 1.00E−2, k_w = 1, k_g = 0, p = p^⋆, v = −v^⋆). We show results for the inversion (velocity and initial condition) if we use the true (“correct”) tumor parameters used to generate the test case (i.e., ρ _f = 10 and k _f = 1.00E−2). The top row shows the initial label maps for the atlas image. The middle row shows the label maps for the atlas image after registration (transported to the patient space) and the bottom row shows the label maps for the patient data. We can see that the results are qualitatively in excellent agreement. This is confirmed by the values for the mismatch and Dice coefficients for the labels and probability maps for the individual tissue classes reported in Table 5.

Fig. A.11.

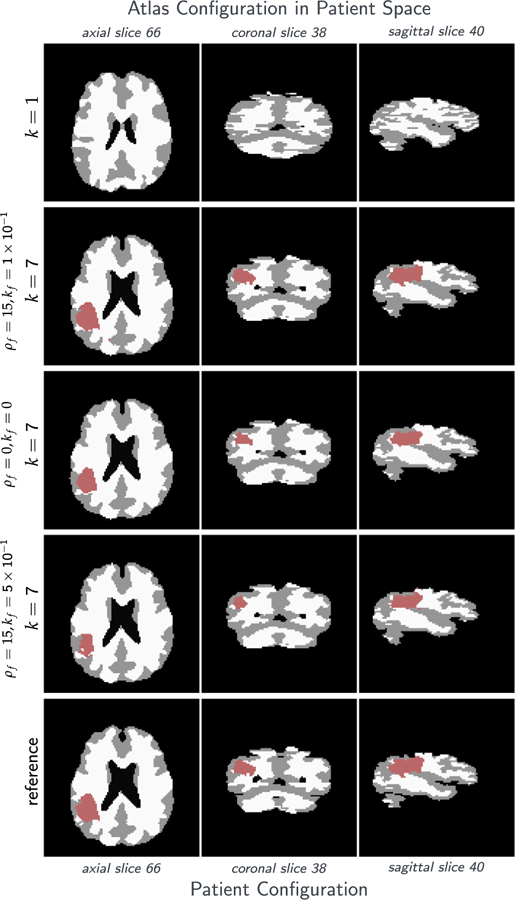
Tumor and brain labels for the analytic tumor with analytic velocity with non-zero diffusion and low-dimensional initial condition (ATAV-LD) test case; ground truth: (ρ _f = 15, ρ_w = 1, ρ_g = 0, k _f = 1.00E−1, k_w = 1, k_g = 0, p = p^⋆ (in patient domain), v N/A); for the ‘correct’ tumor parameters ρ _f = 15, k _f = 1.00E−1, and the two different settings ρ _f = 15, k _f = 5.00E−1 and ρ _f = k _f = 0.

Fig. A.12.

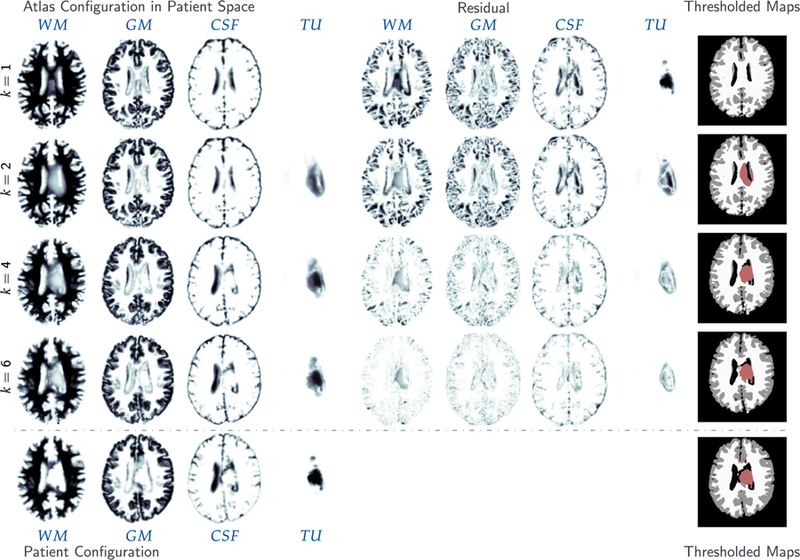
Results for the real tumor/ real velocity (RTRV) test case, ground truth (ρ N/A, k N/A, p N/A, v N/A) and the AAAC patient. The figure shows probability maps for the labels of the healthy atlas brain (k = 1; top row) and the AAAN patient (target) brain probability maps with tumor (bottom row), along with the reconstructed probability maps throughout the Picard iterations (k = 2, 4, 6) (axial-slice 132).

Fig. A.13.

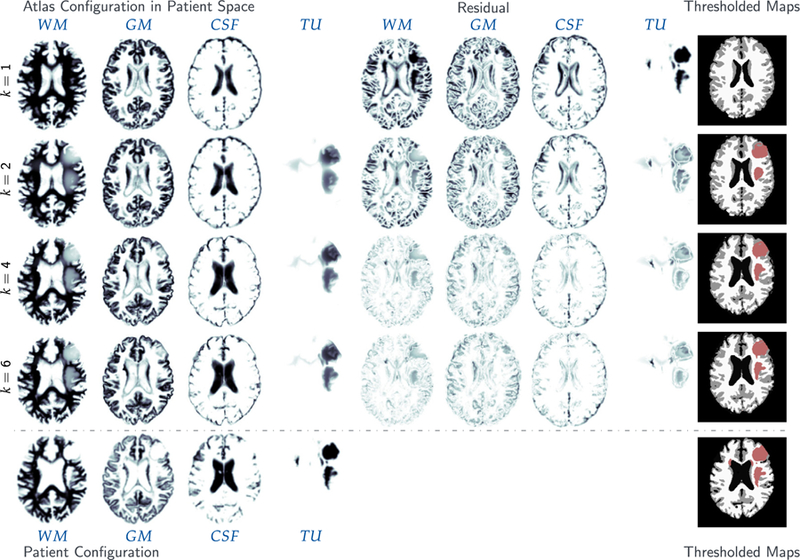
Results for the real tumor/ real velocity (RTRV) test case, ground truth (ρ N/A, k N/A, p N/A, v N/A) and the AAAN patient. The figure shows probability maps for the labels of the healthy atlas brain (k = 1; top row) and the AAAN patient (target) brain probability maps with tumor (bottom row), along with the reconstructed probability maps throughout the Picard iterations (k = 2, 4, 6) (axial-slice 132).

Fig. A.14.

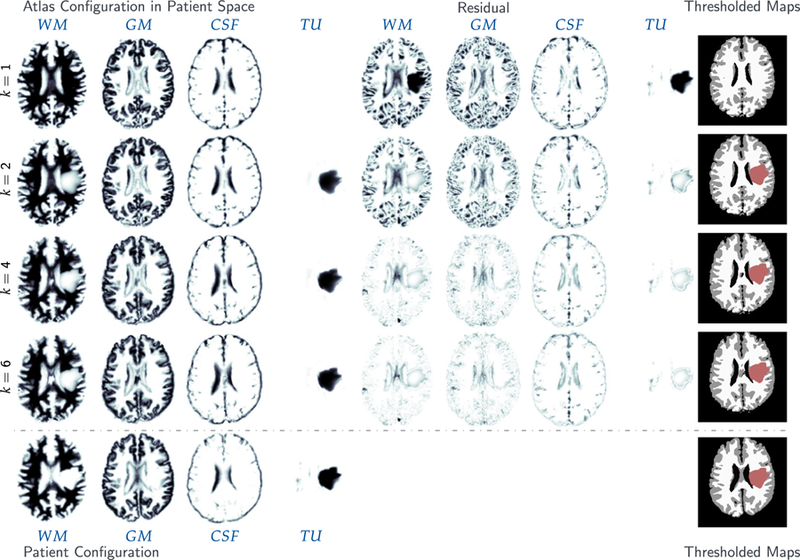
Results for the real tumor/ real velocity (RTRV) test case, ground truth (ρ N/A, k N/A, p N/A, v N/A) and the AAMP patient. The figure shows probability maps for the labels of the healthy atlas brain (k = 1; top row) and the AAAN patient (target) brain probability maps with tumor (bottom row), along with the reconstructed probability maps throughout the Picard iterations (k = 2, 4, 6) (axial-slice 132).

Fig. A.15.

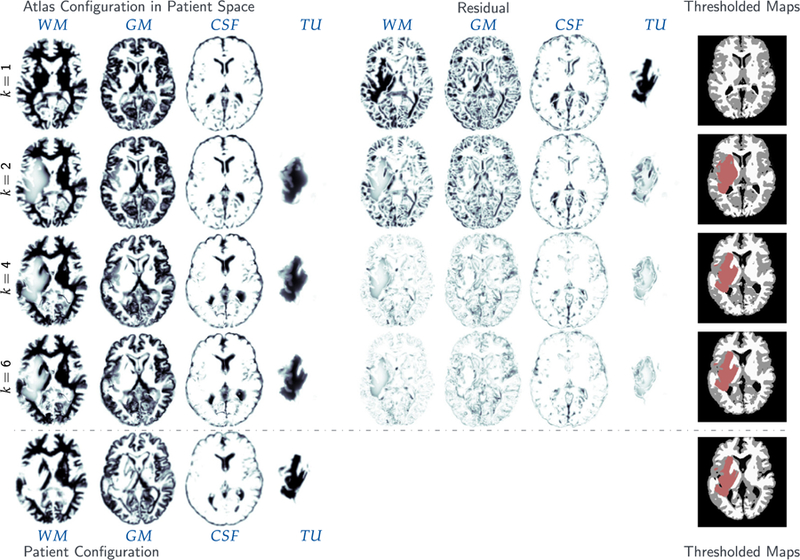
Results for the real tumor/ real velocity (RTRV) test case, ground truth (ρ N/A, k N/A, p N/A, v N/A) and the AAMH patient. The figure shows probability maps for the labels of the healthy atlas brain (k = 1; top row) and the AAAN patient (target) brain probability maps with tumor (bottom row), along with the reconstructed probability maps throughout the Picard iterations (k = 2, 4, 6) (axial-slice 120).

Fig. A.16.

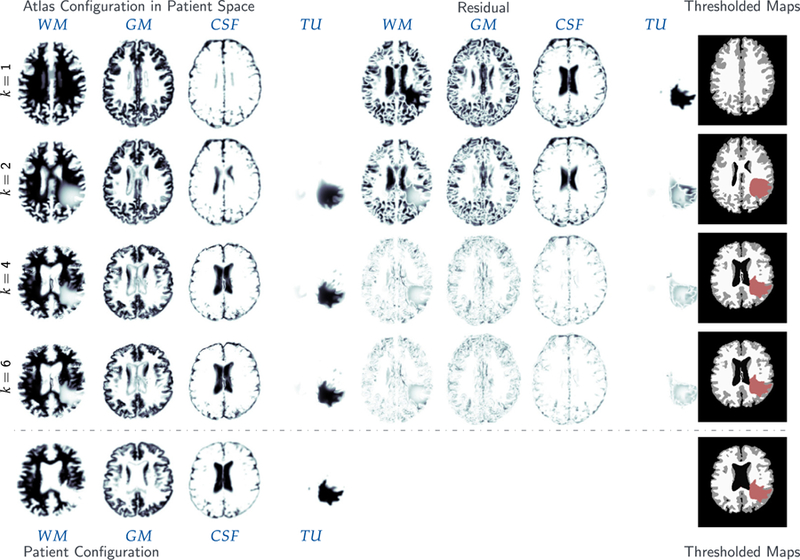
Results for the real tumor/ real velocity (RTRV) test case, ground truth (ρ N/A, k N/A, p N/A, v N/A) and the AAQD patient. The figure shows probability maps for the labels of the healthy atlas brain (k = 1; top row) and the AAAN patient (target) brain probability maps with tumor (bottom row), along with the reconstructed probability maps throughout the Picard iterations (k = 2, 4, 6) (axial-slice 136).

Fig. A.17.

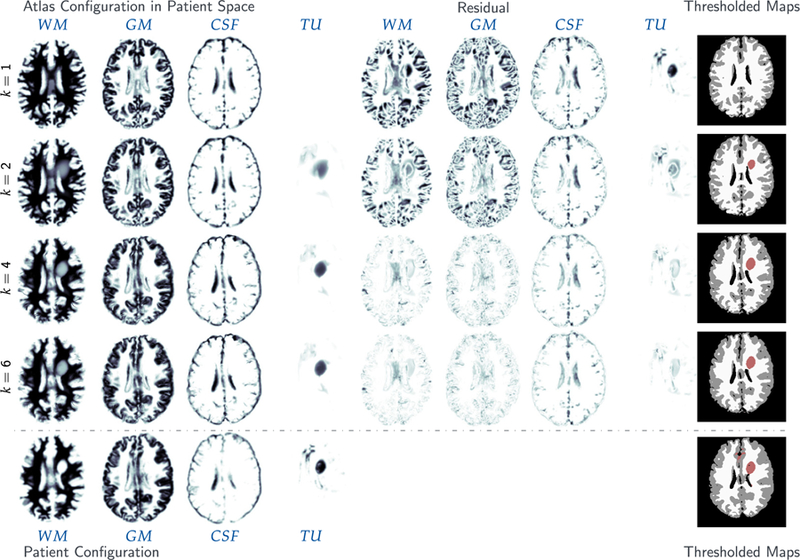
Results for the real tumor/ real velocity (RTRV) test case, ground truth (ρ N/A, k N/A, p N/A, v N/A) and the AAWI patient. The figure shows probability maps for the labels of the healthy atlas brain (k = 1; top row) and the AAAN patient (target) brain probability maps with tumor (bottom row), along with the reconstructed probability maps throughout the Picard iterations (k = 2, 4, 6) (axial-slice 132).