Skip to main content
PMC home page
Science Advances logoLink to Science Advances
. 2019 Dec 20;5(12):eaax6061. doi: 10.1126/sciadv.aax6061

A new metal transfer process for van der Waals contacts to vertical Schottky-junction transition metal dichalcogenide photovoltaics

Cora M Went 1,2, Joeson Wong 3, Phillip R Jahelka 3, Michael Kelzenberg 3, Souvik Biswas 3, Matthew S Hunt 4, Abigail Carbone 5, Harry A Atwater 2,3,6,*
PMCID: PMC6924982  PMID: 31903417

We develop a new technique for transferring metal contacts to create ultrathin solar cells from 2D materials.

Abstract

Two-dimensional transition metal dichalcogenides are promising candidates for ultrathin optoelectronic devices due to their high absorption coefficients and intrinsically passivated surfaces. To maintain these near-perfect surfaces, recent research has focused on fabricating contacts that limit Fermi-level pinning at the metal-semiconductor interface. Here, we develop a new, simple procedure for transferring metal contacts that does not require aligned lithography. Using this technique, we fabricate vertical Schottky-junction WS2 solar cells, with Ag and Au as asymmetric work function contacts. Under laser illumination, we observe rectifying behavior and open-circuit voltage above 500 mV in devices with transferred contacts, in contrast to resistive behavior and open-circuit voltage below 15 mV in devices with evaporated contacts. One-sun measurements and device simulation results indicate that this metal transfer process could enable high specific power vertical Schottky-junction transition metal dichalcogenide photovoltaics, and we anticipate that this technique will lead to advances for two-dimensional devices more broadly.

INTRODUCTION

Two-dimensional (2D) semiconducting transition metal dichalcogenides (TMDs), including MoS2, WS2, MoSe2, and WSe2, are promising for many optoelectronic applications, including high specific power photovoltaics (1–5). With absorption coefficients one to two orders of magnitude higher than conventional semiconductors, monolayer (<1 nm thick) TMDs can absorb as much visible light as about 15 nm of GaAs or 50 nm of Si (6). Both multilayer and monolayer TMDs can achieve near-unity broadband absorption in the visible range (7, 8). Because of their layered structure and out-of-plane van der Waals bonding, TMDs have intrinsically passivated surfaces with no dangling bonds and can form heterostructures without the constraint of lattice matching.

To take advantage of the intrinsically passivated surfaces of TMDs, gentle fabrication techniques are needed to form metal contacts without damaging the underlying semiconductor. A number of new contact techniques have been presented recently, including 1D edge contacts (9), via contacts embedded in hBN (10), slowly deposited In/Au contacts (11), and 2D metals (12). Recently, Liu et al. (13) have shown that transferring rather than evaporating metal contacts onto TMDs can yield interfaces with no Fermi-level pinning, where the Schottky barrier height can be predicted by the ideal Schottky-Mott rule. Their work demonstrates the use of transferring an arbitrary 3D metal onto a 2D material, forming a nondamaging van der Waals contact. However, this technique requires a final aligned lithography step to expose the contact under the polymer used for transfer, which limits its scalability (13).

To date, the above techniques for gentle contact fabrication have been applied to device geometries where carriers are collected laterally rather than vertically. Laterally contacted TMD devices use contact spacing on the order of 5 μm, which would be prohibitively expensive to fabricate for large-area, low-cost photovoltaic devices. Although laterally contacted devices are important for electronic applications, such as field effect transistors, vertically contacted devices are preferable for optoelectronic applications that require scalable photoactive areas, such as solar cells. Van der Waals contacts could have an even greater advantage for these vertical device geometries, where the ratio of contact area to device area is often higher than in lateral device geometries.

Schottky-junction solar cells represent one specific device geometry where van der Waals metal contacts could enable high performance in vertical devices. Although vertical-junction solar cells are more aligned with conventional photovoltaics (14), most Schottky-junction TMD solar cells studied have been lateral-junction devices (13, 15, 16). Vertical Schottky-junction TMD solar cells have been limited by ohmic current-voltage (I-V) behavior, low external quantum efficiencies, and low open-circuit voltages, likely due to Fermi-level pinning induced by contact evaporation (7, 17). New gentle contact fabrication techniques have the potential to eliminate this Fermi-level pinning, enabling high-efficiency vertical TMD solar cells in the Schottky-junction geometry.

Here, we develop a simple technique for transferring metal contacts, where all lithographic patterning is done on a donor substrate rather than on the active device. We apply this technique to vertical Schottky-junction solar cells with multilayer TMD absorber layers. Because of the trade-off between bandgap energy and photoluminescence quantum yield, the theoretical maximum power conversion efficiency achievable for multilayer and monolayer single-junction solar cells is similar (4, 18), and further, tunneling limits transport in monolayer vertical devices (19), so we focus on multilayer devices in this work. Ultrathin (10- to 20-nm) WS2 forms the absorber layer, while Ag and Au form the asymmetric work function contacts. Devices made with transferred metal contacts show diode-like I-V behavior with a near-unity ideality factor and high VOC, while similar devices made with evaporated metal contacts show ohmic I-V behavior and near-zero VOC. We demonstrate peak external quantum efficiency (EQE) of >40% and peak active-layer internal quantum efficiency (IQEactive) of >90% in transferred-contact devices. Using a solar simulator, we measure a photovoltaic power conversion efficiency of 0.46%, comparable to what has been seen in ultrathin vertical TMD photovoltaics with a p-n junction rather than a Schottky junction (20, 21). Device simulations of further-optimized geometries suggest that this new metal transfer process has the potential to enable Schottky-junction TMD solar cells with power conversion efficiencies greater than 8% and specific powers greater than 50 kW/kg.

RESULTS AND DISCUSSION

Fabrication of vertical WS2 Schottky-junction solar cells

We prepare vertical WS2 Schottky-junction solar cells made from 16-nm-thick WS2 absorber layers, with Ag (ϕAg ≈ 4.3 eV) and Au (ϕAu ≈ 5.1 eV) as asymmetric work function contacts (Fig. 1A) (13). Template-stripped Ag, which exhibits a root-mean-square roughness <0.5 nm, forms both the electron-collecting bottom contact and back reflector for all devices (22). We mechanically exfoliate WS2 directly onto the Ag substrate. The subwavelength-thick WS2 achieves broadband, angle-insensitive absorption on top of the highly reflective Ag, giving the WS2 a deep purple color (7, 23). For transferred-contact devices, we transfer thin Au disks from a thermally oxidized Si donor substrate to form the semitransparent hole-collecting top contact, using the process described in the following section. Both the top surface of the template-stripped Ag and the bottom surface of the transferred Au inherit the smoothness of the SiO2/Si donor substrate, leading to near atomically sharp metal-WS2 interfaces (13, 22). Using cross-sectional analysis by transmission electron microscopy (TEM), we examine the interface between the transferred Au and the WS2 (Fig. 1B). We find that in contrast to depositing Au via electron-beam evaporation (13), transferring Au does not damage the intrinsically passivated WS2 layers, as evidenced by the columns of atoms visible in the TEM image. Figure 1C shows an optical image of a completed device. For comparison, we also fabricate devices by direct evaporation of thin Au disks onto the WS2 using standard photolithography techniques.

Fig. 1. Vertical Schottky-junction multilayer WS2 solar cells with transferred contacts.

Fig. 1

Open in a new tab

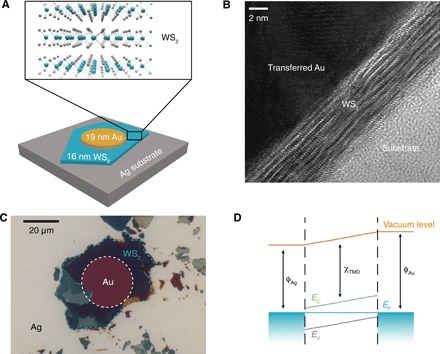
(A) Bottom: Schematic of device structure. Top contact is a transferred gold disk; bottom contact and back reflector is template-stripped silver. Top: 3D representation of multilayer WS2. W, blue spheres; S, gray spheres. (B) Cross-sectional image of metal-semiconductor interface captured by transmission electron microscopy (TEM). (C) Optical image of device. (D) Solar cell band diagram obtained from electrostatic simulations.

The ideal band diagram of this Schottky-junction solar cell is shown in Fig. 1D. We assume a doping concentration of 1014 cm−3 for WS2, as provided by the bulk crystal vendor. Since the length of the depletion region at a Schottky junction between bulk WS2 and either Au or Ag is on the order of 1 μm, the device is fully depleted. We measure the final thicknesses of the WS2 and the Au to be 16 and 19 nm, respectively, using atomic force microscopy.

Metal transfer process

We develop a new, simple process for transferring metal contacts onto TMDs (Fig. 2). This process relies on a self-assembled monolayer (SAM) to reduce the adhesion between the Au and the SiO2/Si donor substrate (24), a thermoplastic polymer to preferentially pick up or drop down the metal (25), and a variable peeling rate to tune the velocity-dependent adhesion between a metal and a viscoelastic stamp (24).

Fig. 2. Metal transfer process.

Fig. 2

Open in a new tab

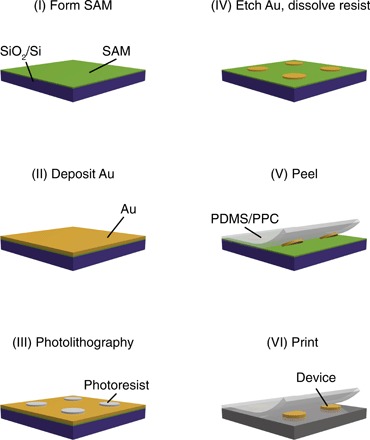
Briefly, a self-assembled monolayer (SAM) is applied to a clean SiO2/Si substrate (I). Au is deposited in an electron beam evaporator (II). Disk contacts are defined using photolithography (III), and the surrounding Au is etched away (IV). To peel the contacts, a polydimethylsiloxane (PDMS)/polypropylene carbonate (PPC) stamp is laminated to the contacts, heated above the glass transition temperature of PPC, and then cooled and removed quickly (V). To print the contacts, the PDMS/PPC stamp is aligned and laminated onto the device and then peeled away slowly above the glass transition temperature of PPC, leaving the contacts behind (VI).

Briefly, we create a SAM on clean thermally oxidized Si chips in a vacuum desiccator (24). We then deposit 20 nm of Au via electron-beam evaporation. Using photolithography, we define the contact areas with positive photoresist and a positive photomask. We etch the Au outside the masked contact areas and then dissolve the remaining photoresist in acetone, leaving Au disks on the SAM-coated SiO2/Si substrates. We prepare a polydimethylsiloxane (PDMS) stamp coated with the thermoplastic polymer polypropylene carbonate (PPC) on a glass slide (25). In a 2D transfer setup, we align and slowly lower the stamp onto a contact at 60°C. We set the temperature to 40°C, and once the stage reaches that temperature, we raise the transfer arm rapidly to peel the stamp and pick up the contact. We align the contact with the target TMD and slowly lower the stamp down at 60°C, and then slowly peel it away immediately after contact at the same temperature. The contact delaminates from the PDMS/PPC stamp and sticks to the TMD. Further details of the procedure are provided in section S1.

This metal transfer technique has worked in 15 of 16 devices fabricated thus far (>90% yield). It works for both 20- and 100-nm-thick Au and can likely be extended to other metals and to larger-scale contacts [i.e., for contacts to chemical vapor deposition (CVD)–grown TMDs]. A substantial advantage of this technique is that, whereas prior metal transfer techniques require a final aligned electron-beam lithography step to expose the contact area (13), this technique only uses unaligned photolithography to define the initial contacts on the SiO2/Si donor substrate. This allows for batch fabrication of an array of contacts that can then be picked up, aligned, and printed to form multiple devices. Further, this metal transfer process could enable van der Waals contacts to air- and moisture-sensitive nanomaterials, such as lead halide perovskites or black phosphorus, to be formed without removing the sample from an inert environment.

Comparison of transferred and evaporated metal contacts

We measure I-V curves under illumination with a 633-nm laser focused to a ~1-μm2 spot in a confocal microscope at room temperature. In devices with transferred metal contacts, we observe rectifying I-V curves and a pronounced photovoltaic effect (Fig. 3A). We measure a VOC of 510 mV under the maximum laser excitation. Short-circuit current follows a power law as a function of incident power, ISC = Pincα, with α close to 1 (Fig. 3C). According to the diode equation, VOC scales linearly with ln(ISC) and can be fit with an ideality factor n = 1.2 (Fig. 3D). This near-unity ideality factor confirms the high interface and material quality in these devices. The ideality factor, diode-like behavior, and high open-circuit voltage suggest that a Schottky junction is successfully formed in devices with transferred contacts.

Fig. 3. Comparison of devices with transferred and directly evaporated top metal contacts.

Fig. 3

Open in a new tab

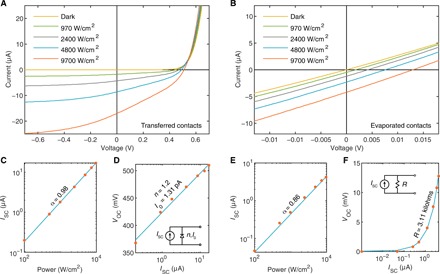
(A and B) Power-dependent I-V characteristics of devices with transferred (A) and evaporated (B) Au top contacts taken under excitation with a 633-nm laser focused to a spot size of ~1 μm2. (C and E) Short-circuit current of devices with transferred (C) and evaporated (E) Au contacts. Symbols, measurements; line, power law fit. (D and F) Open-circuit voltage of devices with transferred (D) and evaporated (F) Au contacts. Symbols, measurements; line, fit. Insets show representative circuit diagrams. n is the ideality factor, and I0 is the dark saturation current extracted from the diode fit in (D). R is the resistance extracted from the linear fit in (F).

In contrast, we observe resistive behavior and a small photovoltaic effect in devices with evaporated top metal contacts (Fig. 3B). ISC versus Pinc follows a power law with α < 1 (Fig. 3E). As shown in Fig. 3F, this device behaves as a resistor with R = 3.1 kilohms. At comparable laser powers, VOC is around 4 mV in evaporated-contact devices and 400 mV in transferred-contact devices, and JSC is three to four times higher for transferred contacts than for evaporated contacts. Previous work demonstrates that because of Fermi-level pinning, evaporated Au and transferred Ag have effectively the same barrier height for electrons and holes (13). Assuming an effective work function difference between Au and Ag of 50 meV, device simulations can predict the purely resistive behavior in an evaporated-contact Schottky-junction device (fig. S1). This evidence points to strong Fermi-level pinning in devices with evaporated contacts due to interface states induced by the Au evaporation.

In devices with transferred contacts, the slope of the I-V curve at short circuit increases linearly with increasing laser power, corresponding to a decreasing shunt resistance (fig. S2A). This photoshunting effect occurs in solar cells without perfectly selective contacts due to increased minority carrier conductivity across the device under illumination (26, 27). Device simulations can replicate this photoshunt pathway without the addition of any external shunt resistance (fig. S2B). In future devices, the introduction of contacts with greater carrier selectivity or the combination of a p-n junction with a Schottky junction could reduce or eliminate the photoshunting observed here.

Quantum efficiency and photocurrent generation

Light beam induced current (or photocurrent) maps, acquired with a 633-nm laser in a confocal microscope, show uniform current generation under the entire Au disk contact, except where shaded by the contact probe (Fig. 4A). The uniformity of the photocurrent demonstrates that the Au is homogeneously semitransparent and in good contact with the TMD. This indicates that the area of the Au disk can be used to accurately define the device active area (fig. S3) and suggests that 1D device simulations are sufficient to describe the behavior in these vertical devices (28). Further, it demonstrates that there are no visible bubbles created during the metal transfer process.

Fig. 4. Photocurrent and quantum efficiency.

Fig. 4

Open in a new tab

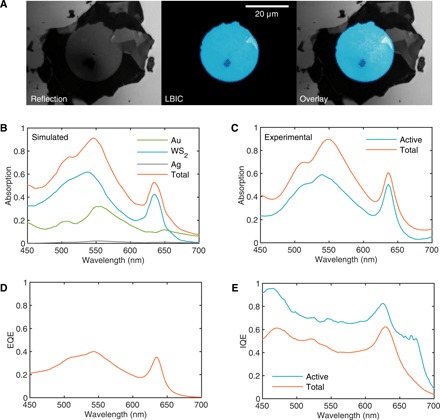
(A) Confocal reflection, photocurrent, and reflection/photocurrent overlay maps for the device shown in Fig. 1. The dark spot in the lower left part of the device active area is a probe tip artifact. (B) Simulated total absorption in the device and absorption in each device layer. (C) Experimental total absorption in the device and active-layer absorption calculated by subtracting the simulated parasitic absorption from the experimentally measured total absorption. (D) Measured EQE. (E) Internal quantum efficiency (IQE) calculated from external quantum efficiency (EQE) and absorption; active-layer IQE calculated from EQE and active-layer absorption.

The measured total absorption (Fig. 4C) matches well with the absorption calculated using the transfer matrix method (Fig. 4B), as has been previously demonstrated in TMD solar cells (7, 17). To calculate the active-layer absorption in the experimental WS2 devices, we subtract the simulated parasitic absorption (the sum of the Au and Ag curves in Fig. 4B) from the experimentally measured total absorption in Fig. 4C. The mean active-layer absorption from 450 to 650 nm is 39%. The reduced absorption in our devices relative to what has been previously demonstrated in WS2 on a metal back reflector (~80% over this wavelength range) (7) is due to parasitic absorption and reflection losses from the 19-nm-thick Au top contact. Using a more transparent top contact could double our photogenerated current, assuming identical work function and conductivity.

The EQE of the device follows the spectral shape of absorption well, averaging 28% from 450 to 650 nm and reaching a peak of above 40% around 550 nm (Fig. 4D). To accurately determine the EQE, we multiply by a shading factor of 1.39 to correct for shading from the probes (see Materials and Methods). The IQE remains relatively flat across all wavelengths above the bandgap, averaging 49% from 450 to 650 nm (Fig. 4E). The IQEactive, calculated by dividing the EQE by the active-layer absorption rather than the total absorption, is greater than 90% at its peak and averages 74% between 450 and 650 nm (Fig. 4F). This high IQEactive suggests efficient collection of photogenerated carriers in transferred-contact devices.

Performance under one-sun illumination

Vertical Schottky-junction WS2 solar cells with transferred top contacts achieve reasonable photovoltaic performance when measured under simulated AM1.5G illumination. Figure 5 shows the AM1.5G I-V behavior of a representative device. We divide the measured current by the device active area to yield current density, and then further divide by a factor of 0.67 to account for spectral mismatch between our solar simulator calibration point and the true AM1.5G spectrum (see Materials and Methods; fig. S4) (29). The spectral mismatch correction leads to a 50% increase in short-circuit current, so the VOC and power conversion efficiency of the device are likely underestimated here. We measure a VOC of 256 mV, a corrected JSC of 4.10 mA/cm2, a fill factor of 0.44, and a power conversion efficiency of 0.46%. This efficiency is in the range of what others have reported for ultrathin TMD photovoltaics (16, 17, 20, 21). Using the densities of Au, WS2, and Ag, we estimate a specific power of 3 kW/kg for this device.

Fig. 5. Photovoltaic performance under one-sun illumination.

Fig. 5

Open in a new tab

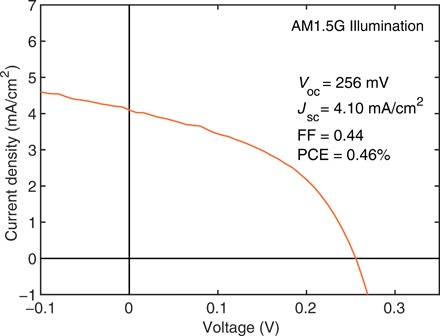
I-V characteristics of a vertical Schottky-junction multilayer WS2 solar cell measured using an AM1.5G solar simulator, corrected for spectral mismatch. FF, fill factor. PCE, power conversion efficiency.

By fitting the one-sun I-V curve using the diode equation with series and shunt resistances, we estimate a shunt resistance (RSH) of 231 ohm cm2 and a negligible series resistance (RS), as shown in fig. S5. The shunt resistance is likely due to the photoshunting behavior discussed above and could be reduced by design and realization of contacts that are more carrier selective.

This photovoltaic performance is consistent among multiple measurements and devices. The JSC of 4.10 mA/cm2 that we measure with the solar simulator is within 10% of the JSC that we calculate by integrating the EQE over the solar spectrum (4.55 mA/cm2). We believe that probe shading, which we correct for in EQE measurements but not in solar simulator measurements, accounts for the 10% discrepancy. Although the JSC varies because of differences in thickness and, therefore, absorption in exfoliated flakes, the VOC is replicable across all devices fabricated for this work. As shown in figs. S6 and S7, VOC is between 220 and 260 mV in all four devices measured under one-sun illumination, and VOC is greater than 220 mV in six different devices measured under illumination with a halogen lamp (~20 suns power density). The I-V curves show no hysteresis when swept in the forward and backward directions (fig. S8).

Simulated performance of optimized devices

To examine and further optimize the performance of these devices, we simulate a variety of device geometries. The assumed material parameters of the WS2 are detailed in table S1. Simulating the same device geometry as our experimental device yields the I-V curve in Fig. 6A. The simulated JSC of 5.7 mA/cm2 is consistent with our measured active-layer IQE of 74% and the JSC of 4.55 mA/cm2 estimated from the EQE. The simulated VOC of 646 mV and RSH of 2240 ohms cm2 are considerably higher than the VOC of 256 mV and RSH of 231 ohms cm2 observed in our one-sun measurements. This demonstrates that with further optimization, our device geometry could achieve higher voltages and less shunting than we currently see (fig. S9). As a first improvement, we suggest replacing Au with a different high work function metal, as Au is known to form thiol bonds with sulfides that could affect the quality of the van der Waals contact (13, 30).

Fig. 6. Simulated performance of optimized devices.

Fig. 6

Open in a new tab

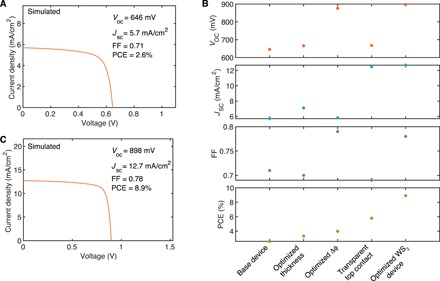
(A) Simulated I-V characteristics of the device geometry used in our experiments, assuming no external series/shunt resistances. (B) Simulated VOC, JSC, fill factor (FF), and power conversion efficiency (PCE) for optimized devices. Apart from the final device geometry (“Optimized WS2 device”), optimizations are independent, not cumulative. (C) Simulated I-V characteristics of the fully optimized WS2 device.

To identify a potential path toward high-efficiency vertical Schottky-junction WS2 solar cells, we simulate a series of optimized devices (Fig. 6B). The use of an optimized thickness of WS2 (26 nm) for maximum absorption under 20 nm of Au increases the JSC to 7.1 mA/cm2. The JSC can be further increased to 12.5 mA/cm2 by replacing Au with a transparent top contact, assuming an identical work function to Au and no parasitic absorption or reflection. By selecting metal work functions that are optimally aligned to the conduction and valence bands of WS2 (ϕ1 = 4.05 and ϕ2 = 5.2 eV; e.g., In and Pd), we predict a VOC increase of 230 mV. Combining transparent top contacts and optimized metal work functions yields the device shown in Fig. 6C, with a VOC of 898 mV, a JSC of 12.7 mA/cm2, a fill factor of 0.78, and a power conversion efficiency of 8.9%. This simulated power conversion efficiency in a device with a thickness <150 nm represents a specific power of 58 kW/kg, demonstrating that this metal transfer process has the potential to enable devices with an unprecedented power-per-unit-weight ratio for transportation and aerospace applications.

CONCLUSIONS

We develop here a process for transferring metal contacts with near-atomically smooth interfaces that has high yield, allows for batch fabrication, and eliminates aligned lithography. We expect that this procedure will be highly relevant and useful to the 2D community and to researchers working on air-sensitive nanomaterials, as it allows all processing to be done on the contacts rather than the device. By applying this new technique to vertical Schottky-junction TMD solar cells, we demonstrate that transferred contacts are particularly advantageous for vertical device geometries, which are important for photovoltaic and other optoelectronic applications due to their scalable active areas. Recent advances in techniques such as growth of wafer-scale 2D TMDs via CVD (31–33) and pickup and stacking of large-area van der Waals materials (34) will enable the scaling of TMD solar cells from the micrometer to the wafer scale.

The rectifying I-V curves shown in transferred-contact devices and resistive I-V curves shown in evaporated-contact devices support the hypothesis that transferring contacts can reduce Fermi-level pinning and allow the work function asymmetry between the contacts to define the maximum achievable VOC. We observe active-layer absorption >55%, EQE >40%, and active-layer IQE >90% in these devices, demonstrating efficient collection of photogenerated carriers. Under one-sun illumination, we measure a VOC of 256 mV, a JSC of 4.10 mA/cm2, a fill factor of 0.44, and a power conversion efficiency of 0.46%. We highlight areas for improvement by simulating the behavior of optimized devices based on this architecture and show 8.9% simulated efficiency and 58-kW/kg simulated specific power in a device with transparent top contacts, optimized thickness, and ideal metal work functions for carrier extraction.

Given the proof-of-concept performance and the clear pathways for improvement presented here for devices less than 150 nm thick, ultrathin vertical Schottky-junction TMD solar cells with transferred contacts are promising candidates for high specific power photovoltaic applications. We anticipate that this new metal transfer process will enable similar advances for 2D TMD devices beyond Schottky-junction solar cells and for nanomaterial-based devices more broadly.

MATERIALS AND METHODS

Device fabrication

Template-stripped silver substrates were prepared, as described previously (17, 22). WS2 was mechanically exfoliated directly onto template-stripped silver from the bulk crystal (HQ Graphene) using Scotch tape. For transferred-contact devices, Au top contacts were prepared and transferred using the metal transfer technique summarized in the main text and described in detail in section S1. The SAM used was trichloro(1H,1H,2H,2H-perfluorooctyl)silane (Sigma Aldrich), the photoresist used was S1813, and the Au etchant used was Transene Gold Etchant TFA. For evaporated-contact devices, Au top contacts were patterned using standard photolithography techniques as described previously (17). Contacts were fabricated on WS2 within 12 hours of exfoliation. Final WS2 and Au thicknesses were confirmed using atomic force microscopy (Asylum Research).

Cross-sectional analysis by TEM

Site-specific, cross-sectional lamella samples were prepared near the middle of metal contacts using a Nova 600 NanoLab (Thermo Fisher) scanning electron microscope with a gallium focused ion beam and an AutoProbe 200 sample lift-out system (Oxford Instruments). TEM imaging was carried out in a Tecnai TF-30 (Thermo Fisher Scientific) operated at 300 kV in high-resolution TEM mode.

Photocurrent and power-dependent I-V

Photocurrent and power-dependent I-V were measured on a scanning confocal microscope (Zeiss Axio Imager 2) using a long working distance objective [50×; numerical aperture (NA), 0.55]. Devices were contacted using piezoelectrically controlled micromanipulators (MiBots, Imina Technologies). I-V curves were measured with a Keithley 236 Source-Measure Unit using custom LabView programs. Laser powers were measured using a USB power meter (ThorLabs). All measurements were performed under ambient temperature and pressure.

Absorption and EQE

Absorption and EQE were measured using a home-built optical setup with a long working distance objective (50×; NA, 0.55). A supercontinuum laser (Fianium) was coupled to a monochromator to produce a tunable, monochromatic light source. A chopper and lock-in detection were used for all measurements. For absorption, the sample reflectance was measured using a National Institute of Standards and Technology (NIST)–calibrated photodetector (Newport 818-ST2-UV/DB) with a beamsplitter. A protected silver mirror (Thorlabs) was used to calibrate the reflectance based on its reported reflectance curve, and a dark background was subtracted from both measurements. For EQE, the current generated by the sample was probed using MiBots and compared with the current collected by the NIST-calibrated photodetector when placed at the sample position, corrected by the photodetector’s responsivity. Absorption and EQE measurements were both corrected by a shading factor of 1.39 that corrects for the shading of the MiBot tips, which was calculated by comparing absorption with and without the tips in place and averaging over the spectral range 450 to 650 nm.

Solar simulator

One-sun I-V curves were measured using a 1-kW Xenon arc lamp (Newport Oriel) with an AM1.5G filter (ABET Technologies). To ensure 100-mW/cm2 incident power, the lamp power was adjusted to generate the correct current on an Si reference cell placed at the same location as the sample. MiBots were used to contact the device, and I-V curves were measured with a Keithley 2425 SourceMeter using custom LabView programs. The current density was divided by a spectral mismatch factor to account for the difference in bandgap between our WS2 sample and our Si reference cell and the difference in spectrum between our solar simulator and AM1.5G (29). As no EQE data were available for our device below 400 nm, linear extrapolation was used, leading to about a 5% error in the spectral mismatch factor and the reported JSC values. The device area was assumed to be that of the Au disk, which has a diameter of 28 μm.

Device simulations

Absorption and generation were calculated using the transfer matrix method, with optical constants for WS2 taken from literature (35). We then used the calculated generation rate as an input into a finite-element device physics simulation software package that solves the semiconductor drift-diffusion equations. All other device simulations were performed using Lumerical CHARGE, a software package that uses the finite-element drift-diffusion method to calculate charge transport in semiconductor devices. The WS2 doping was specified by the bulk crystal vendor (HQ Graphene). Other WS2 parameters, including bandgap (36), work function (37), DC permittivity (38), effective mass (39), out-of-plane mobility (40–42), and photoluminescence quantum yield (43–45) were taken from the literature and are listed in table S1. The radiative recombination coefficient was calculated using the Roosbroeck-Shockley relation (46), and the Shockley-Read-Hall lifetime for minority carriers was then estimated using the photoluminescence quantum yield.

Supplementary Material

http://advances.sciencemag.org/cgi/content/full/5/12/eaax6061/DC1
supp_5_12_eaax6061__index.html (1.5KB, html)
Download PDF
aax6061_SM.pdf (797.2KB, pdf)
A new metal transfer proces for van der Waals contacts to vertical Schottky-junction transition metal dichalcogenide photovoltaics
supp_5_12_eaax6061__index.html (1.5KB, html)

Acknowledgments

We thank S. Nam for the useful discussions. Funding: This work was supported by the DOE “Photonics at Thermodynamic Limits” Energy Frontier Research Center under grant DE-SC0019140. C.M.W. and J.W. acknowledge support from the NSF Graduate Research Fellowship under grants 1745301 and 1144469. C.M.W. acknowledges fellowship support from the Resnick Sustainability Institute. Author contributions: C.M.W. fabricated the devices, performed the measurements, and performed the simulations. C.M.W., J.W., P.R.J., and S.B. developed the metal transfer technique. J.W. and P.R.J. assisted with the simulations. M.K. assisted with the solar simulator, absorption, and EQE measurements. M.S.H. and A.C. assisted with the TEM sample preparation and imaging. H.A.A. supervised all the experiments, calculations, and data collection. All authors contributed to the data interpretation, presentation, and writing of the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/12/eaax6061/DC1

Section S1. Detailed metal transfer procedure

Fig. S1. Simulated I-V curve for evaporated devices.

Fig. S2. Photoshunting.

Fig. S3. Active area.

Fig. S4. Spectral mismatch.

Fig. S5. Fitting for one-sun I-V curve.

Fig. S6. Reproducibility.

Fig. S7. Microscope images of other fabricated devices.

Fig. S8. Forward/backward scans.

Fig. S9. Matching simulations to experimental device.

Table S1. WS2 parameters for device simulations.

REFERENCES AND NOTES

  • 1.Reese M. O., Glynn S., Kempe M. D., McGott D. L., Dabney M. S., Barnes T. M., Booth S., Feldman D., Haegel N. M., Increasing markets and decreasing package weight for high-specific-power photovoltaics. Nat. Energy 3, 1002–1012 (2018). [Google Scholar]
  • 2.Mak K. F., Lee C., Hone J., Shan J., Heinz T. F., Atomically Thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010). [DOI] [PubMed] [Google Scholar]
  • 3.Splendiani A., Sun L., Zhang Y., Li T., Kim J., Chim C.-Y., Galli G., Wang F., Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 10, 1271–1275 (2010). [DOI] [PubMed] [Google Scholar]
  • 4.Jariwala D., Davoyan A. R., Wong J., Atwater H. A., Van der Waals materials for atomically-thin photovoltaics: Promise and outlook. ACS Photonics 4, 2962–2970 (2017). [Google Scholar]
  • 5.Yang Z., Liao L., Gong F., Wang F., Wang Z., Liu X., Xiao X., Hu W., He J., Duan X., WSe2/GeSe heterojunction photodiode with giant gate tunability. Nano Energy 49, 103–108 (2018). [Google Scholar]
  • 6.Bernardi M., Palummo M., Grossman J. C., Extraordinary sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials. Nano Lett. 13, 3664–3670 (2013). [DOI] [PubMed] [Google Scholar]
  • 7.Jariwala D., Davoyan A. R., Tagliabue G., Sherrott M. C., Wong J., Atwater H. A., Near-unity absorption in van der Waals semiconductors for ultrathin optoelectronics. Nano Lett. 16, 5482–5487 (2016). [DOI] [PubMed] [Google Scholar]
  • 8.Huang L., Li G., Gurarslan A., Yu Y., Kirste R., Guo W., Zhao J., Collazo R., Sitar Z., Parsons G. N., Kudenov M., Cao L., Atomically Thin MoS2 Narrowband and Broadband Light Superabsorbers. ACS Nano 10, 7493–7499 (2016). [DOI] [PubMed] [Google Scholar]
  • 9.Wang L., Meric I., Huang P. Y., Gao Q., Gao Y., Tran H., Taniguchi T., Watanabe K., Campos L. M., Muller D. A., Guo J., Kim P., Hone J., Shepard K. L., Dean C. R., One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013). [DOI] [PubMed] [Google Scholar]
  • 10.Telford E. J., Benyamini A., Rhodes D., Wang D., Jung Y., Zangiabadi A., Watanabe K., Taniguchi T., Jia S., Barmak K., Pasupathy A. N., Dean C. R., Hone J., Via method for lithography free contact and preservation of 2D materials. Nano Lett. 18, 1416–1420 (2018). [DOI] [PubMed] [Google Scholar]
  • 11.Wang Y., Kim J. C., Wu R. J., Martinez J., Song X., Yang J., Zhao F., Mkhoyan A., Jeong H. Y., Chhowalla M., Van der Waals contacts between three-dimensional metals and two-dimensional semiconductors. Nature 568, 70–74 (2019). [DOI] [PubMed] [Google Scholar]
  • 12.Liu Y., Stradins P., Wei S.-H., Van der Waals metal-semiconductor junction: Weak Fermi level pinning enables effective tuning of Schottky barrier. Sci. Adv. 2, e1600069 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Liu Y., Guo J., Zhu E., Liao L., Lee S.-J., Ding M., Shakir I., Gambin V., Huang Y., Duan X., Approaching the Schottky–Mott limit in van der Waals metal–semiconductor junctions. Nature 557, 696–700 (2018). [DOI] [PubMed] [Google Scholar]
  • 14.Furchi M. M., Höller F., Dobusch L., Polyushkin D. K., Schuler S., Mueller T., Device physics of van der Waals heterojunction solar cells. NPJ 2D Mater. Appl. 2, 3 (2018). [Google Scholar]
  • 15.Fontana M., Deppe T., Boyd A. K., Rinzan M., Liu A. Y., Paranjape M., Barbara P., Electron-hole transport and photovoltaic effect in gated MoS2 schottky junctions. Sci. Rep. 3, 1634 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Akama T., Okita W., Nagai R., Li C., Kaneko T., Kato T., Schottky solar cell using few-layered transition metal dichalcogenides toward large-scale fabrication of semitransparent and flexible power generator. Sci. Rep. 7, 11967 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Wong J., Jariwala D., Tagliabue G., Tat K., Davoyan A. R., Sherrott M. C., Atwater H. A., High photovoltaic quantum efficiency in ultrathin van der Waals heterostructures. ACS Nano 11, 7230–7240 (2017). [DOI] [PubMed] [Google Scholar]
  • 18.Amani M., Lien D.-H., Kiriya D., Xiao J., Azcatl A., Noh J., Madhvapathy S. R., Addou R., KC S., Dubey M., Cho K., Wallace R. M., Lee S.-C., He J.-H., Ager J. W., Zhang X., Yablonovitch E., Javey A., Near-unity photoluminescence quantum yield in MoS2. Science 350, 1065–1068 (2015). [DOI] [PubMed] [Google Scholar]
  • 19.Lee C.-H., Lee G.-H., van der Zande A. M., Chen W., Li Y., Han M., Cui X., Arefe G., Nuckolls C., Heinz T. F., Guo J., Hone J., Kim P., Atomically thin p–n junctions with van der Waals heterointerfaces. Nat. Nanotechnol. 9, 676–681 (2014). [DOI] [PubMed] [Google Scholar]
  • 20.Li H.-M., Lee D., Qu D., Liu X., Ryu J., Seabaugh A., Yoo W. J., Ultimate thin vertical p–n junction composed of two-dimensional layered molybdenum disulfide. Nat. Commun. 6, 6564 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Furchi M. M., Pospischil A., Libisch F., Burgdörfer J., Mueller T., Photovoltaic effect in an electrically tunable van der Waals heterojunction. Nano Lett. 14, 4785–4791 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.McPeak K. M., Jayanti S. V., Kress S. J. P., Meyer S., Iotti S., Rossinelli A., Norris D. J., Plasmonic Films Can Easily Be Better: Rules and Recipes. ACS Photonics 2, 326–333 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Kats M. A., Blanchard R., Genevet P., Capasso F., Nanometre optical coatings based on strong interference effects in highly absorbing media. Nat. Mater. 12, 20–24 (2013). [DOI] [PubMed] [Google Scholar]
  • 24.Feng X., Meitl M. A., Bowen A. M., Huang Y., Nuzzo R. G., Rogers J. A., Competing fracture in kinetically controlled transfer printing. Langmuir 23, 12555–12560 (2007). [DOI] [PubMed] [Google Scholar]
  • 25.Pizzocchero F., Gammelgaard L., Jessen B. S., Caridad J. M., Wang L., Hone J., Bøggild P., Booth T. J., The hot pick-up technique for batch assembly of van der Waals heterostructures. Nat. Commun. 7, 11894 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Würfel U., Cuevas A., Würfel P., Charge carrier separation in solar cells. IEEE J. Photovolt. 5, 461–469 (2015). [Google Scholar]
  • 27.Waldauf C., Scharber M. C., Schilinsky P., Hauch J. A., Brabec C. J., Physics of organic bulk heterojunction devices for photovoltaic applications. J. Appl. Phys. 99, 104503 (2006). [Google Scholar]
  • 28.Snaith H. J., The perils of solar cell efficiency measurements. Nat. Photonics 6, 337–340 (2012). [Google Scholar]
  • 29.Snaith H. J., How should you measure your excitonic solar cells? Energ. Environ. Sci. 5, 6513–6520 (2012). [Google Scholar]
  • 30.Desai S. B., Madhvapathy S. R., Amani M., Kiriya D., Hettick M., Tosun M., Zhou Y., Dubey M., Ager J. W., Chrzan D., Javey A., Gold-mediated exfoliation of ultralarge optoelectronically-perfect monolayers. Adv. Mater. 28, 4053–4058 (2016). [DOI] [PubMed] [Google Scholar]
  • 31.Zhang X., Choudhury T. H., Chubarov M., Xiang Y., Jariwala B., Zhang F., Alem N., Wang G.-C., Robinson J. A., Redwing J. M., Diffusion-controlled epitaxy of large area coalesced WSe2 monolayers on sapphire. Nano Lett. 18, 1049–1056 (2018). [DOI] [PubMed] [Google Scholar]
  • 32.Zhang X., Zhang F., Wang Y., Schulman D. S., Zhang T., Bansal A., Alem N., Das S., Crespi V. H., Terrones M., Redwing J. M., Defect-controlled nucleation and orientation of WSe2 on hBN: A route to single-crystal epitaxial monolayers. ACS Nano 13, 3341–3352 (2019). [DOI] [PubMed] [Google Scholar]
  • 33.Kang K., Xie S., Huang L., Han Y., Huang P. Y., Mak K. F., Kim C.-J., Muller D., Park J., High-mobility three-atom-thick semiconducting films with wafer-scale homogeneity. Nature 520, 656–660 (2015). [DOI] [PubMed] [Google Scholar]
  • 34.Kang K., Lee K.-H., Han Y., Gao H., Xie S., Muller D. A., Park J., Layer-by-layer assembly of two-dimensional materials into wafer-scale heterostructures. Nature 550, 229–233 (2017). [DOI] [PubMed] [Google Scholar]
  • 35.Li Y., Chernikov A., Zhang X., Rigosi A., Hill H. M., van der Zande A. M., Chenet D. A., Shih E.-M., Hone J., Heinz T. F., Measurement of the optical dielectric function of monolayer transition-metal dichalcogenides: MoS2,MoSe2,WS2, and WSe2. Phys. Rev. B 90, 205422 (2014). [Google Scholar]
  • 36.Kam K. K., Parkinson B. A., Detailed photocurrent spectroscopy of the semiconducting group VIB transition metal dichalcogenides. J. Phys. Chem. 86, 463–467 (1982). [Google Scholar]
  • 37.Keyshar K., Berg M., Zhang X., Vajtai R., Gupta G., Chan C. K., Beechem T. E., Ajayan P. M., Mohite A. D., Ohta T., Experimental determination of the ionization energies of MoSe2, WS2, and MoS2 on SiO2 using photoemission electron microscopy. ACS Nano 11, 8223–8230 (2017). [DOI] [PubMed] [Google Scholar]
  • 38.Laturia A., Van de Put M. L., Vandenberghe W. G., Dielectric properties of hexagonal boron nitride and transition metal dichalcogenides: From monolayer to bulk. NPJ 2D Mater. Appl. 2, 6 (2018). [Google Scholar]
  • 39.Wickramaratne D., Zahid F., Lake R. K., Electronic and thermoelectric properties of few-layer transition metal dichalcogenides. J. Chem. Phys. 140, 124710 (2014). [DOI] [PubMed] [Google Scholar]
  • 40.Massicotte M., Schmidt P., Vialla F., Schädler K. G., Reserbat-Plantey A., Watanabe K., Taniguchi T., Tielrooij K. J., Koppens F. H. L., Picosecond photoresponse in van der Waals heterostructures. Nat. Nanotechnol. 11, 42–46 (2016). [DOI] [PubMed] [Google Scholar]
  • 41.Li D., Cheng R., Zhou H., Wang C., Yin A., Chen Y., Weiss N. O., Huang Y., Duan X., Electric-field-induced strong enhancement of electroluminescence in multilayer molybdenum disulfide. Nat. Commun. 6, 7509 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Cao G., Shang A., Zhang C., Gong Y., Li S., Bao Q., Li X., Optoelectronic investigation of monolayer MoS2/WSe2 vertical heterojunction photoconversion devices. Nano Energy 30, 260–266 (2016). [Google Scholar]
  • 43.Zhao W., Ghorannevis Z., Chu L., Toh M., Kloc C., Tan P.-H., Eda G., Evolution of electronic structure in atomically thin sheets of WS2 and WSe2. ACS Nano 7, 791–797 (2012). [DOI] [PubMed] [Google Scholar]
  • 44.Zeng H., Liu G.-B., Dai J., Yan Y., Zhu B., He R., Xie L., Xu S., Chen X., Yao W., Cui X., Optical signature of symmetry variations and spin-valley coupling in atomically thin tungsten dichalcogenides. Sci. Rep. 3, 1608 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Amani M., Taheri P., Addou R., Ahn G. H., Kiriya D., Lien D.-H., Ager J. W., Wallace R. M., Javey A., Recombination kinetics and effects of superacid treatment in sulfur- and selenium-based transition metal dichalcogenides. Nano Lett. 16, 2786–2791 (2016). [DOI] [PubMed] [Google Scholar]
  • 46.van Roosbroeck W., Shockley W., Photon-radiative recombination of electrons and holes in germanium. Phys. Rev. 94, 1558–1560 (1954). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

http://advances.sciencemag.org/cgi/content/full/5/12/eaax6061/DC1
supp_5_12_eaax6061__index.html (1.5KB, html)
Download PDF
aax6061_SM.pdf (797.2KB, pdf)
A new metal transfer proces for van der Waals contacts to vertical Schottky-junction transition metal dichalcogenide photovoltaics
supp_5_12_eaax6061__index.html (1.5KB, html)

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/12/eaax6061/DC1

Section S1. Detailed metal transfer procedure

Fig. S1. Simulated I-V curve for evaporated devices.

Fig. S2. Photoshunting.

Fig. S3. Active area.

Fig. S4. Spectral mismatch.

Fig. S5. Fitting for one-sun I-V curve.

Fig. S6. Reproducibility.

Fig. S7. Microscope images of other fabricated devices.

Fig. S8. Forward/backward scans.

Fig. S9. Matching simulations to experimental device.

Table S1. WS2 parameters for device simulations.

Articles from Science Advances are provided here courtesy of American Association for the Advancement of Science

RESOURCES