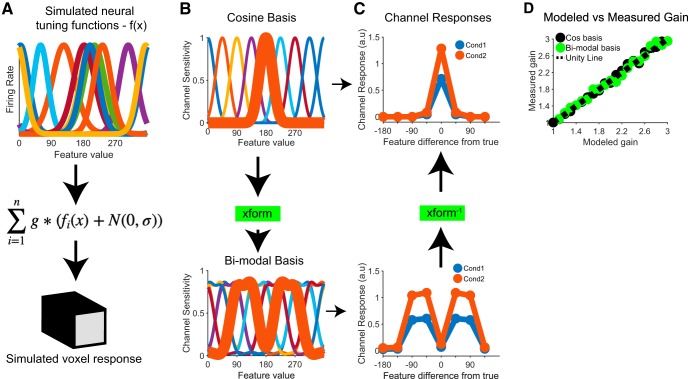
Figure 1.

Differences between conditions can be preserved across invertible linear transforms. A, We simulated voxel-level fMRI data where each voxel’s response was generated based on the sum of simulated responses across a population of simulated neurons with randomly centered tuning preferences and variable bandwidth (here, n = number of neurons, set to 100, although only 10 neural tuning functions are shown for clarity; see code on GitHub for full set of model parameters; https://github.com/tommysprague/iem_sim). Noise was added to the neural responses and then the gain factor (g) was applied to the data from each condition (condition 1: g = 1, condition 2: g = 1.8). For display purposes the noise (N) was set to 0 for panels A–C (following Gardner and Liu, 2019, their Fig. 3) and was set to 10 for panel D. B, We analyzed data using two different formats of channel basis functions, mirroring those used by Gardner and Liu (2019). Importantly, the two bases are related by an invertible linear transform (xform). C, Reconstructed channel response profiles differ in similar ways: condition 2 has a higher amplitude than condition 1, regardless of the basis set used, and the bimodal channel response profiles are related by the inverse of the linear transform that was used to create the bimodal basis in the first place (xform⁻¹). D, Modeled gain compared to measured gain between conditions 2 and 1, computed using both the raised cosine basis set and the transformed bimodal version of the cosine basis set. Because there is not a straightforward way to quantify amplitude for the channel response profiles computed from the bimodal basis, we instead implemented a model-free quantification scheme in which we computed the ratio of the area under each channel response profile (i.e., ratio of area under the curve in condition 2 compared to condition 1).