Significance
Despite its practical importance, the adhesion of soft materials to rough surfaces is not understood. Rough surfaces show adhesion hysteresis: a difference in adhesion behavior between loading and separation. This behavior is typically attributed (often without evidence) to viscoelastic energy dissipation and cannot at present be quantitatively linked to surface topography. This work uses in situ measurements of contact between soft elastomers of varying stiffness against hard substrates, whose topography was characterized down to the atomic scale. Results reveal the direct relationship between Griffith fracture and the detachment of adhesive contacts and suggest a quantitative model that describes both the loading and separation behavior. The findings will guide the development of reversible adhesives for soft robotics, biomaterials, and pick-and-place manufacturing.
Keywords: adhesion, surface topography, multiscale surface roughness, contact mechanics, soft matter
Abstract
A mechanistic understanding of adhesion in soft materials is critical in the fields of transportation (tires, gaskets, and seals), biomaterials, microcontact printing, and soft robotics. Measurements have long demonstrated that the apparent work of adhesion coming into contact is consistently lower than the intrinsic work of adhesion for the materials, and that there is adhesion hysteresis during separation, commonly explained by viscoelastic dissipation. Still lacking is a quantitative experimentally validated link between adhesion and measured topography. Here, we used in situ measurements of contact size to investigate the adhesion behavior of soft elastic polydimethylsiloxane hemispheres (modulus ranging from 0.7 to 10 MPa) on 4 different polycrystalline diamond substrates with topography characterized across 8 orders of magnitude, including down to the angstrom scale. The results show that the reduction in apparent work of adhesion is equal to the energy required to achieve conformal contact. Further, the energy loss during contact and removal is equal to the product of the intrinsic work of adhesion and the true contact area. These findings provide a simple mechanism to quantitatively link the widely observed adhesion hysteresis to roughness rather than viscoelastic dissipation.
Many natural and engineering processes—such as a human picking up an object, a gecko climbing trees, or a tire gripping the road—require enough adhesion and friction to achieve the task, while maintaining the ability to release the surface afterward (1–3). All natural and manmade surfaces contain roughness at some scales, and this roughness strongly affects adhesion (4–6). Therefore, fundamental understanding of the reversible adhesion of a soft material to a rough surface is a grand scientific challenge, with significant technological applications. For instance, pick-and-place techniques in manufacturing are used from large-scale factories (7) all the way down to nanoscale transfer printing (8). Biomedical devices must securely adhere to skin when measuring vital signs or delivering drugs but then must be removed without pain for disposal or reuse (9). Tires, seals, and gaskets are used extensively in vehicles and industrial machinery (3). Finally, there has been significant recent progress in the field of soft robotics, with the goal of creating machines that will be able to manipulate objects like the human hand or climb walls like geckos (10).
Our understanding of adhesive contact between smooth, soft, elastic materials was elegantly resolved in a seminal paper in 1971, where Johnson, Kendall, and Roberts (JKR) showed that the contact area under applied load is larger than predicted by the classic Hertz model (11, 12). However, the presence of surface roughness significantly alters the contact behavior. As a rough contact is loaded, it obeys the trends of the JKR model, but the measured apparent work of adhesion is significantly lower than the intrinsic value ; the latter is a thermodynamic parameter that depends on intermolecular interactions between the materials (13). Upon retraction, adhesion hysteresis is observed on rough surfaces, where the behavior deviates significantly from that of loading and from the JKR predictions. If the JKR formalism is applied, one calculates a work of adhesion (for retraction) that is much larger than and may not have thermodynamic significance (14–18).
Even though all practical surfaces are rough, quantifying the loss of adhesion due to roughness has remained a challenge. One widely used category of models describes rough surfaces as an array of individual contacting bumps (asperities) of a certain size (19–21), where the surface properties are computed from the collective behavior of the individual asperities. However, these models focus only on a single size scale of roughness, whereas most natural and engineering surfaces are rough over many length scales (22, 23). To address the multiscale nature of roughness, Persson developed a set of continuum mechanics models to describe soft-material adhesion at rough contacts as a function of the power spectral density (PSD) (24–26). The PSD, , is a mathematical tool for separating contributions to topography from different length scales λ, and is commonly represented as a function of wavevector . In particular, under the assumption that the soft material fully conforms to the roughness of the hard material, and by assuming that the materials behave linear elastically, one such model (24) predicts how the intrinsic work of adhesion can be replaced by an apparent value that depends on material parameters and surface roughness.
The key remaining challenge for the experimental validation and practical application of these recent contact theories has been the experimental measurement of surface topography across all size scales. Surface roughness exists down to the atomic scale, and these smallest scales have been shown to be critically important for contact and adhesion (3, 6, 27, 28). Yet, the conventional techniques for measuring surface topography—such as stylus or optical profilometry and atomic force microscopy (AFM)—are incapable of measuring roughness down to the nanoscale (29, 30). Furthermore, because surface roughness exists over many length scales, no single technique is capable of characterizing a surface completely (30). The novelty of the present investigation lies in the combination of well-controlled adhesion measurements with complete characterization of topography across all scales, spanning from millimeters to angstroms. This all-scale characterization eliminates the assumptions (30, 31) that are typically required for describing a surface beyond the bounds of measurement (such as self-similarity or self-affinity), thus enabling unprecedented scientific insight into the nature of rough-surface adhesion. Without such comprehensive topography measurements, the assumptions and accuracy of soft-material contact theories remain untested.
While the aforementioned mechanics models describe the behavior of a material under load, they do not predict the adhesion hysteresis, the difference in behavior between loading and separation. Instead, the increase in adhesion energy upon retraction is often attributed (sometimes without evidence) to velocity-dependent dissipation of energy due to bulk viscoelasticity (32–34). However, roughness-induced adhesion hysteresis is still observed even for systems that show no evidence of viscoelasticity on smooth surfaces (35, 36). Furthermore, it may not even be appropriate to apply an equilibrium-based theoretical model (such as JKR for smooth surfaces or Persson’s model for rough surfaces) to the nonequilibrium separation behavior (37, 38). Thus, our current understanding of the adhesion hysteresis is incomplete. Here, we investigate the origins of energy loss in order to demonstrate the fundamental contribution of surface roughness.
Results and Discussion
To understand the dependence of adhesion on roughness, we performed in situ measurements of the load-dependent contact of 16 different combinations of soft spheres and rough substrates. We have chosen polydimethylsiloxane (PDMS) as our elastomer and synthetically grown hydrogen-terminated diamond as the hard rough substrates because both have low surface energies. We wanted to avoid adhesion hysteresis due to interfacial bonding (for example, PDMS in contact with silica surfaces) (39, 40); therefore, low-energy materials were chosen (41) to focus specifically on the adhesion hysteresis that arises due to surface topography.
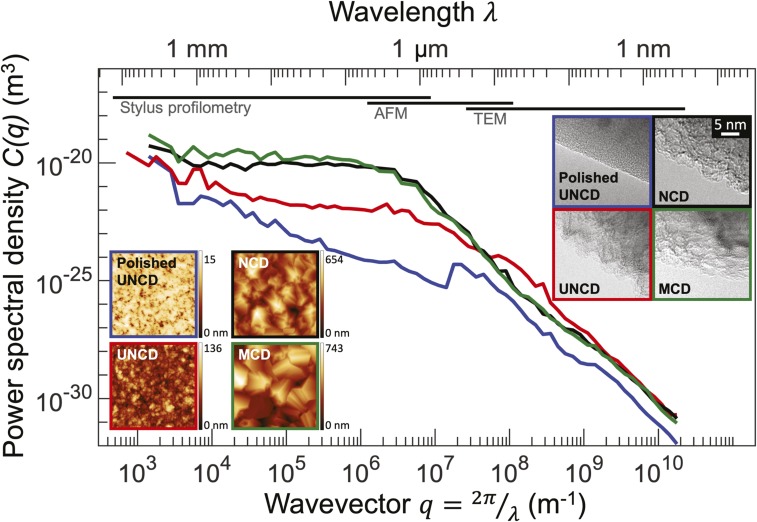
We used a recently developed approach (29) to characterize the surface topography of 4 different nanodiamond substrates across 8 orders of magnitude of size scale, including down to the angstrom scale (Fig. 1). These four substrates are: microcrystalline diamond (MCD); nanocrystalline diamond (NCD); ultrananocrystalline diamond (UNCD); and a polished form of UNCD (polished UNCD). More than 50 individual topography measurements were made for each substrate (Methods and SI Appendix, section 1) using transmission electron microscopy (TEM), AFM, and stylus profilometry. Results were combined to create a single comprehensive PSD describing each surface.
Fig. 1.
Comprehensive topography characterization for four rough nanodiamond surfaces. The surface topography was measured using a multiresolution approach that combines TEM, AFM, and stylus profilometry. Regions of applicability of each technique are indicated with horizontal bars and are delineated more specifically in SI Appendix, Fig. S2. The nanodiamond surfaces are colored as follows: UNCD is shown in red, NCD in black, MCD in green, and polished UNCD in blue. AFM images (of 5-μm lateral size, Left Inset) and TEM images (Right Inset) are shown. More than 50 measurements for each surface are combined using the PSD, which reveals the contribution to overall roughness from different length scales (wavelengths). These comprehensive descriptions of surface topography enable the determination of true surface area and stored mechanical energy due to the topography, which are necessary to understand adhesion.
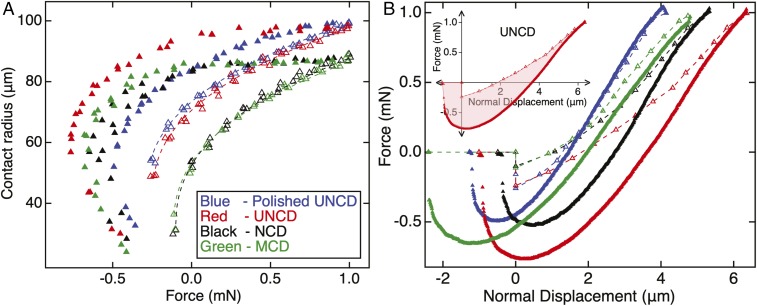
Four types of soft, elastic PDMS hemispheres were synthesized, following the methods from refs. 34, 42, and 43, with elastic moduli ranging from 0.7 to 10 MPa. The PDMS hemispheres were loaded under displacement control to a maximum load of 1 mN before unloading to separation. (The synthesis and testing are described in Methods and SI Appendix, section 2.) Real-time measurements were made of contact radius, load, and displacement, as shown in Fig. 2.
Fig. 2.
Adhesion measurements during approach and retraction. Loading and adhesion tests were performed with ultrasmooth PDMS hemispheres of varying stiffness from 0.7 to 10 MPa. Representative curves from one material (with E = 1.9 MPa) are presented in this figure, and those of other materials are shown in SI Appendix, Fig. S5. The load-dependent contact radius (shown in A) was measured using in situ optical microscopy. The apparent work of adhesion upon approach was extracted by fitting the loading data (hollow points) using the JKR model (dashed lines). The force-displacement curves (B) were used to calculate the energy loss during contact by performing a closed-circuit integral (Inset). Both approach and retraction experiments were conducted at a very low speed, 60 nm/s.
The apparent work of adhesion during approach is extracted by using the JKR model to fit the measured contact radius a as a function of load F (12):
| [1] |
where R is the radius of the hemispherical lens and the effective modulus is defined as , E is Young’s modulus, and ν is the Poisson ratio. This yields a different value of apparent work of adhesion for each of the 16 contacts. The surface chemistry of the PDMS and the nanodiamond is expected to be similar in all cases, and therefore all contacts should have approximately the same value of . Before testing the hemispheres with rough surfaces, they were tested against a smooth silicon wafer coated with a low-surface-energy octadecyltrichlorosilane (OTS) monolayer to verify that there is negligible adhesion hysteresis due to viscoelasticity (SI Appendix, Fig. S6).
To analyze the dependence of on modulus and multiscale surface topography, we use a model of conformal contact, based on Persson and Tosatti (24). Those authors postulated that the product of and (the apparent or projected area) is given by a balance of adhesive energy and stored elastic energy :
| [2] |
with, where and are the surface energies of the soft and hard surfaces, respectively, and is the interfacial energy between them. The term is the true surface area of the rough hard surface. However, Eq. 2 makes 2 important assumptions that must be addressed: It neglects the change in area of the soft elastomer surface from to upon contact, and it assumes that the surface energy of the soft material is independent of strain. These 2 assumptions can be corrected by modifying the energy balance to explicitly include the work done in increasing the surface area of the elastomer.
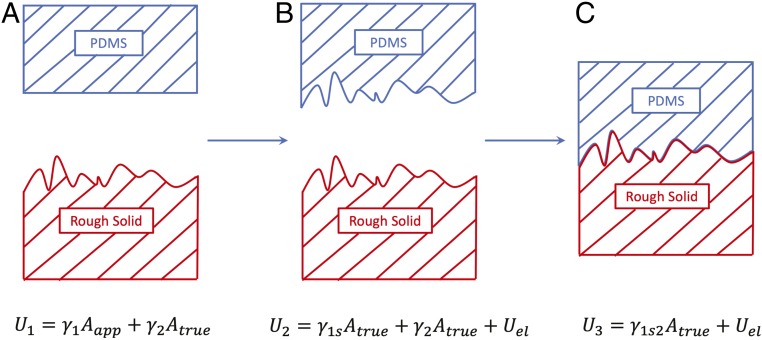
The Persson–Tosatti energy balance implies that the area of the PDMS surface does not change. While this may be valid for small-slope surfaces, in the more general case the area will increase from to , as shown schematically in Fig. 3.
Fig. 3.
During adhesion, the materials go from the initial state (A) to the final state (C). However, to fully account for the energy change, one must consider the change in area of the soft material, which is represented schematically by including the intermediate state (B). The equations give the expression for the total energy of the system in each of the three states.
To go from the initial state (Fig. 3A) to the intermediate state (Fig. 3B), there is an energy change from to . The PDMS is stretched and its surface energy changes depending upon the applied strain, which can be represented as a function of the area:
| [3] |
Then, to go from the intermediate state (Fig. 3B) to the final state (Fig. 3C), there is an energy change of
| [4] |
Thus, the total work to go from the initial state to the final state is equal to + :
| [5] |
This is the total energy change equal to . Finally, we can rewrite the total energy balance as
| [6] |
where , and is the surface energy of the stretched elastomer. If we now make the assumption that the surface energy of the soft elastomer is not a strong function of strain (44), then and we can simplify the energy balance and rearrange it to explicitly show as a function of 2 roughness-dependent terms, and :
| [7] |
The stored elastic strain energy can be calculated from the PSD using the approach of Persson and Tosatti (24):
| [8] |
where is the radial average of the 2-dimensional (2D) power-spectral density. For calculating the PSD, we follow the conventions used in ref. 30. is calculated from the 1-dimensional (1D) PSD (Fig. 1) as described in Methods. Finally, we derived a closed-form expression for the roughness-dependent increase in surface area, which works for arbitrary values of root-mean-square surface slope (SI Appendix, section 3):
| [9] |
with calculated from the PSD as (30). For generality, all integrals were performed over the entire range of size scales over which topography was measured; if the range of wavevectors is instead cut off at the contact size (ca. 100 μm), the extracted results are identical (within 0.1%). Taken together, Eqs. 7–9 demonstrate the predicted dependence of on material properties (, ) and topography .
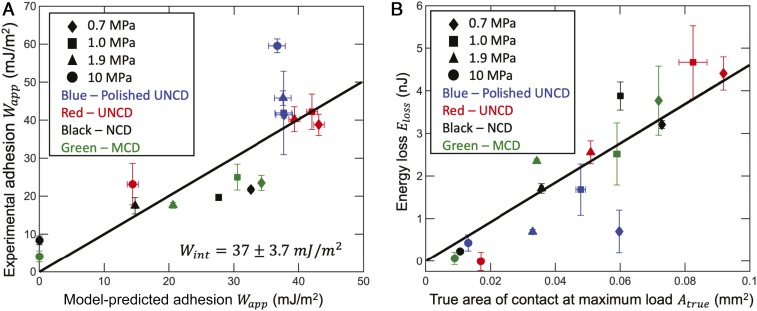
The model for (Eq. 7) is applied to the measured data as shown in Fig. 4A using = 25 ± 5 mJ/m2 for PDMS. This value was chosen based on prior work (41, 45), which also showed that the surface energy of PDMS does not change significantly with molecular weight. Furthermore, in the present investigation, water contact-angle measurements were performed on all PDMS materials and yielded values in the range of 103° to 107°, further supporting that all PDMS materials used in this investigation have similar surface energy. In applying this model, the minimum physically reasonable value of is set to zero; predicted values below zero (for 10-MPa PDMS on NCD and MCD) imply that the surfaces will not perfectly conform. The best correlation between the experimentally measured work of adhesion and the predictions of Eq. 7 was obtained using the intrinsic work of adhesion of 37.0 ± 3.7 mJ/m2 (R2 = 0.67). The reasonable value of R2 (0.67) and the low value of standard error (3.7 mJ/m2) suggest good agreement between the model and the experimental measurements. The scatter in the experimental values as compared to the model is attributed to spot-to-spot variations. The theory outlined above cannot capture these spot-to-spot variations because it assumes a thermodynamic limit, corresponding to contacts of infinite size. The finite size of the experimental contact means that it is subject to finite-size fluctuations, such as a nonnegligible probability for single anomalous asperities to dominate the response at low loads (46). In contrast, the theoretical analysis samples the whole statistical distribution of the surface’s roughness. Overall, the proposed model which explicitly accounts for the change in area of the soft surface (Eq. 7) achieves significantly improved model predictions; if we do not account for this change (calculations shown in SI Appendix, section 4), the best fit to the measured data is significantly poorer (R2 = 0.29).
Fig. 4.
Comparison of work of adhesion and energy loss with the proposed model of conformal contact. In A, experimental measurements of apparent work of adhesion during approach are well-fit using the balance of adhesive and elastic energy described in the main text (Eqs. 7–9); here the solid line shows y = x. In B, the energy loss is plotted as a function of true contact area (Eq. 10). The solid line is a linear fit to the data and has a slope of 46.2 ± 7.7 mJ/m2 (R2 = 0.8).
The retraction portion of contact differs sharply from approach (as shown in Fig. 2), and the JKR model does not provide an adequate fit to the unloading data. Despite the poor fit, the JKR model can be used to extract a value for work of adhesion upon retraction, either by applying it only to the pull-off point, or by applying it to the several (ca. 6) points before pull-off. Doing so (SI Appendix, section 2) yields work of adhesion values in the range of 20 to 160 mJ/m2. However, there is little consistency between these values and there is no connection to the intrinsic value of work of adhesion determined from the approach data.
Instead, we analyze the total energy loss during contact and separation. This quantity is computed as the integral under the loading and unloading curve, as shown in Fig. 2 B, Inset. The in situ measurements of contact size yield the apparent area of contact during testing; to determine the true area of contact, we must multiply by the roughness-induced increase in true surface area (Eq. 9). We now plot the energy loss versus the true area of contact at maximum preload. Fig. 4B shows a linear correlation:
| [10] |
with a best-fit intrinsic work of adhesion of 46.2 ± 7.7 mJ/m2. The prior value of the work of adhesion (37.0 ± 3.7 mJ/m2) was measured during approach from the measured contact radius as a function of applied load. The latter value of work of adhesion (46.2 ± 7.7 mJ/m2) was obtained for the whole contact cycle (approach and separation) using the closed-circuit integral of the force-displacement curve. These values agree within their experimental uncertainties, despite being measured using very different approaches. This agreement suggests that we are indeed measuring an intrinsic work of adhesion for the materials, governed by the fundamental molecular interactions, rather than an effective property that may be governed by experimental parameters or the roughness.
The present description of soft-material contact on rough surfaces assumes fully conformal contact. No method exists at present to directly verify this assumption, neither the in situ optical microscopy used in this investigation nor the fluorescence or other techniques for imaging contact used elsewhere (e.g., ref. 47). However, the present results demonstrate that the experimentally measured behavior of these 16 material pairs, during both loading and separation, is consistent with a model of conformal contact. This provides indirect evidence for the accuracy of this description of contact, and its underlying assumptions.
The results in Fig. 4 provide a simple physical mechanism to explain both the lower work of adhesion during approach and the adhesion hysteresis upon retraction. During approach, the apparent work of adhesion is reduced from by the energy required to deform the soft material to achieve conformal contact. This reduction can be quantitatively calculated using comprehensive, multiscale measurements of topography (Eqs. 7–9). Furthermore, the energy loss during contact and separation matches with the product of and the true contact area at the maximum preload. Surface heterogeneities are known to pin the contact edge such that the retraction process depins the surface in instantaneous jumps over small, localized microscopic regions (48). We show that Griffith’s argument (49) can be applied: These jumps occur once the elastic energy available is equal to the interface energy, and all elastic energy is dissipated in the creation of new surface.
Overall, the results show significant adhesion hysteresis in the absence of viscoelastic dissipation and therefore demonstrate a fundamental origin of irreversible energy loss in soft materials that arises due to the roughness-induced increase in surface area and Griffith-like separation of the contact. This insight can be leveraged in applications involving reversible adhesion to real-world materials that contain roughness, such as the fields of soft robotics, biomaterials, and pick-and-place manufacturing. Eqs. 7–10 quantify the relative contributions to measured adhesion from material properties (intrinsic work of adhesion, elastic modulus, and Poisson ratio) and from surface topography (as characterized by a multiscale PSD including atomic-scale information). This understanding suggests strategies to predict adhesion and to rationally modify it by tailoring the surface composition and surface topography.
Methods
Synthesis of Nanodiamond Substrates.
Nanodiamond films (Advanced Diamond Technologies, Inc.) were deposited using a tungsten hot-filament chemical vapor deposition system with parameters as described in ref. 50. An H-rich gas mixture was used, with the chamber pressure of 5 Torr and a substrate temperature of 750 °C. The ratio of boron to carbon was maintained at 0.3 wt %, to achieve high conductivity in the final film. The CH4-to-H2 ratio was modified (as described in ref. 51) to tune the grain size: achieving micro-, nano-, and ultrananocrystalline diamond. All films were grown to a thickness of 2 μm. Chemical-mechanical planarization was performed on an undoped UNCD film to create the polished UNCD samples. Previous surface analysis of synthetically grown diamond surfaces has shown similar surface composition regardless of grain size (52–54).
Synthesis of PDMS Hemispheres.
The smooth, soft, elastic hemispheres were composed of cross-linked PDMS. To achieve systematic variation in modulus, we have used simple network theory, where changing the cross-linking molecular weight changes the cross-linking density and subsequently elastic modulus (34, 42), , where is the density of the polymer, is the gas constant, is absolute temperature, and is the cross-linked molecular weight. The curing system consisted of materials obtained from Gelest Inc.: vinyl-terminated PDMS of different molecular weights (DMS V-05 [ = 800 g/mol], V-21 [ = 9,000 g/mol], V-31 [ = 28,000 g/mol], and V-41 [ = 62,700 g/mol]); tetrakis-dimethylsiloxysilane (SIT 7278.0) as tetra-functional cross-linker; platinum carbonyl cyclo-vinyl methyl siloxane complex (SIP 6829.2) as catalyst; and 1,3,5,7-tetravinyl-1,3,5,7-tetramethyl cyclo-tetra siloxane (SIT 7900.0) as inhibitor. The vinyl-to-hydride molar ratio of 4.4 was maintained for all of the samples, avoiding excess cross-linker evaporation to minimize adhesion hysteresis from unreacted side chains as reported by Perutz et al. (43). The catalyst was added as 0.1% of the total batch. An additional reaction inhibitor was added to the DMS V-05 batch to avoid early cross-linking (5 times the catalyst amount). Hemispherical lenses were cast on fluorinated glass dishes using a needle and a syringe. Since the PDMS mixture has a higher surface energy than the fluorinated surface, the drops maintain a contact angle on the surface, giving a shape of a hemispherical lens. These lenses were imaged in profile using an optical microscope and could be fit easily with a 3-point circle to extract the necessary radius. They were cured at 60 °C for 3 d in a heating oven and Soxhlet-extracted using toluene at 124 °C for 24 h. After 12 h of drying in open air, the hemispheres were dried under vacuum at 120 °C overnight. The sol fraction for all of the batches was found to be less than 5%.
The fluorinated dishes were prepared by growing a monolayer of heptadecafluoro 1,1,2,2 tetrahydrodecatrichloro silane on clean base-bath–treated borosilicate glass Petri dishes. The OTS monolayer was prepared on silicon wafers (obtained from Silicon Inc.) that had been pretreated with piranha solution (3:7 ratio of 30% hydrogen peroxide: sulfuric acid [concentrated]). Silicon wafers were cleaned with an ample amount of water before use. The wafers were blown dry with nitrogen and plasma-treated before dipping in 1 wt % OTS solution in toluene under nitrogen purge for 8 h. The static water contact angle obtained was 110° ± 2° with negligible contact-angle hysteresis.
Multiscale Characterization of Surface Topography.
Large-scale topography characterization: Stylus profilometry.
The largest scales of topography were measured using 1D line scans with a stylus profilometer (Alpha Step IQ; KLA Tencor) with a 5-μm diamond tip. Data were collected at a scanning speed of 10 , with data points every 100 nm. A total of 8 measurements were taken on each substrate, with 2 measurements each at scan sizes of 0.5, 1, 2, and 5 mm. These measurements were taken at random orientations of the sample and did not show meaningful variations with direction. A parabolic correction was applied to all measurements which removed the tilt of the sample and the bowing artifact from the stylus tool. In 2 sessions (for the UNCD and polished UNCD), the larger scan sizes exhibited consistent nonparabolic trends due to instrument artifacts. In these cases, this was corrected by performing reference scans on polished silicon wafers and subtracting the averaged reference profiles from the sample measurements. Representative scans of stylus profilometry for all 4 materials are shown in SI Appendix, Fig. S1.
Midscale topography characterization: AFM.
The substrates were measured using an atomic force microscope (Dimension V; Bruker) in tapping mode with diamond-like carbon-coated probes (Tap DLC300; Mikromasch). For all substrates, square measurements were taken with the following lateral sizes: 3 scans each at 100 nm, 500 nm, and 5 µm and 1 scan each at 250 nm and 1 µm. The scanning speed was maintained at 1 for all scans. Each scan had 512 lines, with 512 data points per line, corresponding to pixel sizes in the range of 0.2 to 98 nm. The values of free-air amplitude and amplitude ratio were kept in the range of 37 to 49 nm and 0.15 to 0.3, respectively. While AFM provides a 2D map of surface topography, the data were analyzed as a series of line scans, both to facilitate direct comparison with other techniques and to avoid apparent anisotropy due to instrument drift. Representative scans of AFM for all 4 materials are shown in the Fig. 1, Left Inset.
Small-scale topography characterization: TEM.
Topography was measured on scales from microns to angstroms following the approach developed in ref. 55. For the UNCD, NCD, and MCD, the “wedge deposition technique” was used, whereas for polished UNCD, the “surface-preserving cross-section technique” was used (55). Briefly, the wedge deposition technique involves depositing the film of interest, in the same batch, on both flat silicon wafers (used for adhesion testing) and on standardized TEM-transparent silicon wedge samples (for TEM imaging). The surface-preserving cross-section technique is similar to conventional techniques for extraction of a TEM cross-section from a bulk sample (using grinding, polishing, dimple grinding, and ion etching); however, modifications (especially to the ion etching step) ensure that the original surface topography is unmodified from its original state. The samples were imaged using a transmission electron microscope (JEM 2100F; JEOL) operated at 200 keV. The images were taken with a 2,000- × 2,000-pixel camera using magnification levels from 5,000× to 600,000×.
The nanoscale surface contours were extracted from the TEM images using custom MATLAB scripts that create a digitized line profile based on a series of points selected by the user. The TEM images obtained were first rotated to make the surface horizontal and then the material’s boundary was traced. While the vast majority of the measured surfaces were well-behaved functions, that is, there was a single value of height (y axis) for each horizontal position (x axis), there were some cases where 2 adjacent points were captured with identical or decreasing horizontal position. In these cases, the latter point was removed. In just 12 out of the 210 measurements, there were small portions of the profile that were reentrant. This character is not necessarily physically meaningful as it depends on the rotation of the TEM image during image analysis. Because the mathematical analyses (especially the calculation of PSD) require well-behaved functions, these regions were excluded from analysis.
Combination of All Measurements into Complete, Multiscale PSD Curves.
For every topography measurement, the PSD was computed using the conventions described in refs. 29 and 30. The line scans from stylus profilometry, AFM, and TEM all yield descriptions of the height h(x) over lateral position x. The Fourier transform of the surface topography is given by ; the PSD is computed as the square of the amplitude of h̃(q), that is, . Here, L is the length of the line scan. Since all collected data were analyzed as 1D line scans, then the computed PSDs were of the form of , using the nomenclature of ref. 30.
For the tip-based measurement techniques (AFM and stylus), the tip-radius artifacts (30, 56) were eliminated using the criterion described in equation 2 of ref. 29. This calculation was performed based on the tip radius measured using scanning electron microscopy images of the stylus tip and TEM images of the AFM probes after they were used for AFM measurement. Measured PSD data for wavevectors above the cutoff (calculated separately for each combination of tip and surface) were eliminated as unreliable. Finally, all reliable PSDs describing a single surface were combined into a single curve by computing the arithmetic average of the individually measured PSDs.
Calculation of scalar roughness parameters.
The PSD can be integrated (as described in refs. 29 and 30) to compute scalar descriptors of the surface: the root-mean-square (RMS) height , RMS slope , and RMS curvature . The value of these parameters will depend on the scale over which they are measured (29); when all scales of topography are included, the computed values are as shown in SI Appendix, Table S1.
Calculation of the 2D PSD from the 1D PSD.
All topography measurements in the present investigation are analyzed as 1D line scans, and therefore the 1D PSD is presented in Fig. 1. However, the calculations proposed by Persson and Tosatti (24) (and their modifications used in the present paper) employ a 2D isotropic PSD. Under the assumption of isotropic roughness, the 2D PSD can be calculated from the 1D PSD, as described in ref. 30. For this, we use equation A.28 of ref. 30:
| [11] |
where is the short wavelength cutoff, in this case defined by the minimum wavelength at which roughness is measured (4 Å). This form of the 2D PSD is shown in SI Appendix, Fig. S3 and is used in the calculations for stored elastic energy and true surface area (Eqs. 8 and 9).
In Situ Contact Experiments and Analysis.
Contact experiment methodology.
The contact experiment for each hemisphere–substrate combination was carried out using the setup shown in SI Appendix, Fig. S4 where simultaneous force and contact area measurement were taken during loading and unloading (Fig. 2). Optically transparent PDMS hemispheres of 2- to 3-mm diameter were used, with height greater than 700 μm to avoid substrate effects from the hemisphere’s sample mount (57, 58). The maximum load applied for every measurement was 1 mN and the cycle was completed with a constant velocity of 60 nm/s.
Contact experiment analysis: Extracting values of work of adhesion.
To extract the apparent work of adhesion, the loading data are fit to the JKR equation (Eq. 1). These fits are shown as dashed lines in Fig. 2 and SI Appendix, Figs. S5 and S6. Since the contact radius, applied force, and radius of the lens are known, then the apparent work of adhesion and effective elastic modulus can be computed. The elastic moduli of the PDMS are calculated using the Poisson ratio for elastomers of 0.5 and using the modulus and Poisson ratio for diamond of 1,100 GPa and 0.06, respectively (59). (However, because the effective modulus values are dominated by the properties of the elastomer, the precise values of diamond modulus are nearly insignificant.) The extracted values of modulus are those shown in the legend of Fig. 4 and are comparable to ref. 34. The extracted values of are shown in SI Appendix, Table S2.
Testing PDMS for adhesion hysteresis.
Before measuring work of adhesion on the rough nanodiamond substrates, the PDMS hemispheres were tested for inherent hysteresis against a low-surface-energy OTS monolayer, which had been coated on a smooth silicon wafer. Plots of contact radius versus force are shown in SI Appendix, Fig. S6 for PDMS of different elastic moduli in contact with the OTS reference surface. The work of adhesion values obtained for loading and unloading fits are listed in SI Appendix, Table S3 showing comparable values and low hysteresis. This OTS reference testing was repeated before and after the measurements on the nanodiamond substrates to rule out any permanent changes in the cross-linked structure of PDMS due to testing. The hemispheres did not show significant deviation from the original numbers in the after-test measurements. The closed-circuit integral for the force-displacement curve (calculated as shown in the Fig. 2 B, Inset) for PDMS–OTS have values that are at least an order of magnitude smaller than those measured on the rough surfaces (SI Appendix, Table S3).
Data for this publication are available from the University of Pittsburgh’s data repository: D-Scholarship@Pitt (60).
Supplementary Material
Acknowledgments
Dr. K. Vorovolakos, Prof. M. K. Chaudhury, and Prof. C. Cohen provided necessary guidance to make soft materials. We thank Dr. B. N. J. Persson, Daniel Maksuta, Michael C. Wilson, and Antoine Sanner for helpful comments. We thank Prof. K. Beschorner for help with statistical analysis. T.D.B.J. acknowledges support from the NSF under award CMMI-1727378. A.D. acknowledges funding from the NSF (DMR-1610483). Use of the Nanoscale Fabrication and Characterization Facility in the Petersen Institute of NanoScience and Engineering is acknowledged.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: Data for this publication are deposited using the University of Pittsburgh’s data repository: D-Scholarship@Pitt. This includes the data from the surface topography characterization (Fig. 1) and the contact testing (Fig. 2), as well as the computed quantities that are reported in Fig. 4. This is available under repository ID no. 37812 (DOI: 10.18117/c76w-y421).
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1913126116/-/DCSupplemental.
References
- 1.Ayyildiz M., Scaraggi M., Sirin O., Basdogan C., Persson B. N. J., Contact mechanics between the human finger and a touchscreen under electroadhesion. Proc. Natl. Acad. Sci. U.S.A. 115, 12668–12673 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Niewiarowski P. H., Stark A. Y., Dhinojwala A., Sticking to the story: Outstanding challenges in gecko-inspired adhesives. J. Exp. Biol. 219, 912–919 (2016). [DOI] [PubMed] [Google Scholar]
- 3.Persson B. N. J., Albohr O., Tartaglino U., Volokitin A. I., Tosatti E., On the nature of surface roughness with application to contact mechanics, sealing, rubber friction and adhesion. J. Phys. Condens. Matter 17, R1–R62 (2005). [DOI] [PubMed] [Google Scholar]
- 4.Luan B., Robbins M. O., The breakdown of continuum models for mechanical contacts. Nature 435, 929–932 (2005). [DOI] [PubMed] [Google Scholar]
- 5.Jacobs T. D. B., et al. , The effect of atomic-scale roughness on the adhesion of nanoscale asperities: A combined simulation and experimental investigation. Tribol. Lett. 50, 81–93 (2013). [Google Scholar]
- 6.Pastewka L., Robbins M. O., Contact between rough surfaces and a criterion for macroscopic adhesion. Proc. Natl. Acad. Sci. U.S.A. 111, 3298–3303 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Popa D. O., Stephanou H. E., Micro and mesoscale robotic assembly. J. Manuf. Process. 6, 52–71 (2004). [Google Scholar]
- 8.Carlson A., Bowen A. M., Huang Y., Nuzzo R. G., Rogers J. A., Transfer printing techniques for materials assembly and micro/nanodevice fabrication. Adv. Mater. 24, 5284–5318 (2012). [DOI] [PubMed] [Google Scholar]
- 9.Yu Z., Cheng H., Tunable adhesion for bio-integrated devices. Micromachines 9, 529 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tang Y., Zhang Q., Lin G., Yin J., Switchable adhesion actuator for amphibious climbing soft robot. Soft Robot. 5, 592–600 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Hertz H., On the contact of rigid elastic solids. J. Reine Angew. Math. 92, 156–171 (1882). [Google Scholar]
- 12.Johnson K. L., Kendall K., Roberts A. D., Surface energy and the contact of elastic solids. Proc. R. Soc. A 324, 301–313 (1971). [Google Scholar]
- 13.Israelachvili J. N., Intermolecular and Surface Forces (Academic Press, London, ed. 3, 2015). [Google Scholar]
- 14.Briggs G. A. D., Briscoe B. J., The effect of surface topography on the adhesion of elastic solids. J. Phys. D Appl. Phys. 10, 2453–2466 (1977). [Google Scholar]
- 15.Fuller K. N. G., Tabor D., The effect of surface roughness on the adhesion of elastic solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 345, 327–342 (1975). [Google Scholar]
- 16.Maeda N., Chen N., Tirrell M., Israelachvili J. N., Adhesion and friction mechanisms of polymer-on-polymer surfaces. Science 297, 379–382 (2002). [DOI] [PubMed] [Google Scholar]
- 17.Luengo G., Pan J., Heuberger M., Israelachvili J. N., Temperature and time effects on the “Adhesion Dynamics” of poly(butyl methacrylate) (PBMA) surfaces. Langmuir 14, 3873–3881 (1998). [Google Scholar]
- 18.Tiwari A., et al. , The effect of surface roughness and viscoelasticity on rubber adhesion. Soft Matter 13, 3602–3621 (2017). [DOI] [PubMed] [Google Scholar]
- 19.Archard J. F., Elastic deformation and the laws of friction. Proc. R. Soc. A 243, 190–205 (1957). [Google Scholar]
- 20.Greenwood J. A., Williamson J. B. P., Contact of nominally flat surfaces. Proc. R. Soc. A 295, 300–319 (1966). [Google Scholar]
- 21.Jackson R. L., Streator J. L., A multi-scale model for contact between rough surfaces. Wear 261, 1337–1347 (2006). [Google Scholar]
- 22.Thomas T. R., Sayles R. S., Some problems in the tribology of rough surfaces. Tribol. Int. 11, 163–168 (1978). [Google Scholar]
- 23.Mandelbrot B. B., Passoja D. E., Paullay A. J., Fractal character of fracture surfaces of metals. Nature 308, 721–722 (1991). [Google Scholar]
- 24.Persson B. N. J., Tosatti E., The effect of surface roughness on the adhesion of elastic solids. J. Chem. Phys. 115, 5597–5610 (2001). [Google Scholar]
- 25.Yang C., Persson B. N. J., Molecular dynamics study of contact mechanics: Contact area and interfacial separation from small to full contact. Phys. Rev. Lett. 100, 024303 (2008). [DOI] [PubMed] [Google Scholar]
- 26.Persson B. N. J., Scaraggi M., Theory of adhesion: Role of surface roughness. J. Chem. Phys. 141, 124701 (2014). [DOI] [PubMed] [Google Scholar]
- 27.Hyun S., Pei L., Molinari J. F., Robbins M. O., Finite-element analysis of contact between elastic self-affine surfaces. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 70, 026117 (2004). [DOI] [PubMed] [Google Scholar]
- 28.Putignano C., Afferrante L., Carbone G., Demelio G., The influence of the statistical properties of self-affine surfaces in elastic contacts: A numerical investigation. J. Mech. Phys. Solids 60, 973–982 (2012). [Google Scholar]
- 29.Gujrati A., Khanal S. R., Pastewka L., Jacobs T. D. B., Combining TEM, AFM, and profilometry for quantitative topography characterization across all scales. ACS Appl. Mater. Interfaces 10, 29169–29178 (2018). [DOI] [PubMed] [Google Scholar]
- 30.Jacobs T. D. B., Junge T., Pastewka L., Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 5, 013001 (2017). [Google Scholar]
- 31.Zhang X., Xu Y., Jackson R. L., An analysis of generated fractal and measured rough surfaces in regards to their multi-scale structure and fractal dimension. Tribol. Int. 105, 94–101 (2017). [Google Scholar]
- 32.Silberzan P., Perutz S., Kramer E. J., Chaudhury M. K., Study of the self-adhesion hysteresis of a siloxane elastomer using the JKR method. Langmuir 10, 2466–2470 (1994). [Google Scholar]
- 33.Choi G. Y., Kim S., Ulman A., Adhesion hysteresis studies of extracted poly(dimethylsiloxane) using contact mechanics. Langmuir 13, 6333–6338 (1997). [Google Scholar]
- 34.Vorvolakos K., Chaudhury M. K., The effects of molecular weight and temperature on the kinetic friction of silicone rubbers. Langmuir 19, 6778–6787 (2003). [Google Scholar]
- 35.Chen Y. L., Helm C. A., Israelachvili J. N., Molecular mechanisms associated with adhesion and contact angle hysteresis of monolayer surfaces. J. Phys. Chem. 95, 10736–10747 (1991). [Google Scholar]
- 36.Pickering J. P., Van Der Meer D. W., Vancso G. J., Effects of contact time, humidity, and surface roughness on the adhesion hysteresis of polydimethylsiloxane. J. Adhes. Sci. Technol. 15, 1429–1441 (2001). [Google Scholar]
- 37.Kesari H., Doll J. C., Pruitt B. L., Cai W., Lew A. J., Role of surface roughness in hysteresis during adhesive elastic contact. Philos. Mag. Lett. 90, 891–902 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Peressadko A. G., Hosoda N., Persson B. N. J., Influence of surface roughness on adhesion between elastic bodies. Phys. Rev. Lett. 95, 124301 (2005). [DOI] [PubMed] [Google Scholar]
- 39.Yurdumakan B., Harp G. P., Tsige M., Dhinojwala A., Template-induced enhanced ordering under confinement. Langmuir 21, 10316–10319 (2005). [DOI] [PubMed] [Google Scholar]
- 40.She H., Malotky D., Chaudhury M. K., Estimation of adhesion hysteresis at polymer/oxide interfaces using rolling contact mechanics. Langmuir 14, 3090–3100 (1998). [Google Scholar]
- 41.Chaudhury M. K., Interfacial interaction between low-energy surfaces. Mater. Sci. Eng. R Rep. 16, 97–159 (1996). [Google Scholar]
- 42.Vaenkatesan V., Li Z., Vellinga W. P., de Jeu W. H., Adhesion and friction behaviours of polydimethylsiloxane–A fresh perspective on JKR measurements. Polymer 47, 8317–8325 (2006). [Google Scholar]
- 43.Perutz S., Kramer E. J., Baney J., Hui C. Y., Cohen C., Investigation of adhesion hysteresis in poly(dimethylsiloxane) networks using the JKR technique. J. Polym. Sci., B, Polym. Phys. 36, 2129–2139 (1998). [Google Scholar]
- 44.Liang H., Cao Z., Wang Z., Dobrynin A. V., Surface stress and surface tension in polymeric networks. ACS Macro Lett. 7, 116–121 (2018). [DOI] [PubMed] [Google Scholar]
- 45.Chaudhury M. K., Whitesides G. M., Correlation between surface free energy and surface constitution. Science 255, 1230–1232 (1992). [DOI] [PubMed] [Google Scholar]
- 46.Pastewka L., Robbins M. O., Contact area of rough spheres: Large scale simulations and simple scaling laws. Appl. Phys. Lett. 108, 221601 (2016). [Google Scholar]
- 47.Weber B., et al. , Molecular probes reveal deviations from Amontons’ law in multi-asperity frictional contacts. Nat. Commun. 9, 888 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Persson B. N. J., Nanoadhesion. Wear 254, 832–834 (2003). [Google Scholar]
- 49.Griffith A. A., The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. A 221, 582–593 (1921). [Google Scholar]
- 50.Zeng H., et al. , Boron-doped ultrananocrystalline diamond synthesized with an H-rich/Ar-lean gas system. Carbon 84, 103–117 (2015). [Google Scholar]
- 51.Auciello O., et al. , Are diamonds a MEMS’ best friend? IEEE Microw. Mag. 8, 61–75 (2007). [Google Scholar]
- 52.Sumant A. V., et al. , Toward the ultimate tribological interface: Surface chemistry and nanotribology of ultrananocrystalline diamond. Adv. Mater. 17, 1039–1045 (2005). [Google Scholar]
- 53.Härtl A., et al. , Protein-modified nanocrystalline diamond thin films for biosensor applications. Nat. Mater. 3, 736–742 (2004). [DOI] [PubMed] [Google Scholar]
- 54.Fuentes-Fernandez E. M. A., et al. , Synthesis and characterization of microcrystalline diamond to ultrananocrystalline diamond films via Hot Filament Chemical Vapor Deposition for scaling to large area applications. Thin Solid Films 603, 62–68 (2016). [Google Scholar]
- 55.Khanal S. R., et al. , Characterization of small-scale surface topography using transmission electron microscopy. Surf. Topogr. Metrol. Prop. 6, 045004 (2018). [Google Scholar]
- 56.Church E. L., Takacs P. Z., Effects of the nonvanishing tip size in mechanical profile measurements. Opt Test Metrol III Recent Adv Ind Opt Insp 1332, 504–514 (1991). [Google Scholar]
- 57.Deruelle M., Hervet H., Jandeau G., Léger L., Some remarks on JKR experiments. J. Adhes. Sci. Technol. 12, 225–247 (1998). [Google Scholar]
- 58.Wald M. J., Considine J. M., Turner K. T., Determining the elastic modulus of compliant thin films supported on substrates from flat punch indentation measurements. Exp. Mech. 53, 931–941 (2013). [Google Scholar]
- 59.Klein C. A., Cardinale G. F., Young’s modulus and Poisson’s ratio of CVD diamond. Diam. Relat. Mater. 2, 918–923 (1993). [Google Scholar]
- 60.Dalvi S., et al. , Data associated with publication: “Linking energy loss in soft adhesion to surface roughness.” D-Scholarship@Pitt. 10.18117/c76w-y421. Deposited 18 November 2019. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.