Shaping the zebrafish myotome by intertissue friction and active stress

Significance

How do tissues self-organize to generate the complex organ shapes observed in vertebrates? Organ formation requires the integration of chemical and mechanical information, yet how this is achieved is poorly understood for most organs. Muscle compartments in zebrafish display a V shape, which is believed to be required for efficient swimming. We investigate how this structure emerges during zebrafish development, combining live imaging and quantitative analysis of cellular movements. We use theoretical modeling to understand how cell differentiation and mechanical interactions between tissues guide the emergence of a specific tissue morphology. Our work reveals how spatially modulating the mechanical environment around and within tissues can lead to complex organ shape formation.

Abstract

Organ formation is an inherently biophysical process, requiring large-scale tissue deformations. Yet, understanding how complex organ shape emerges during development remains a major challenge. During zebrafish embryogenesis, large muscle segments, called myotomes, acquire a characteristic chevron morphology, which is believed to aid swimming. Myotome shape can be altered by perturbing muscle cell differentiation or the interaction between myotomes and surrounding tissues during morphogenesis. To disentangle the mechanisms contributing to shape formation of the myotome, we combine single-cell resolution live imaging with quantitative image analysis and theoretical modeling. We find that, soon after segmentation from the presomitic mesoderm, the future myotome spreads across the underlying tissues. The mechanical coupling between the future myotome and the surrounding tissues appears to spatially vary, effectively resulting in spatially heterogeneous friction. Using a vertex model combined with experimental validation, we show that the interplay of tissue spreading and friction is sufficient to drive the initial phase of chevron shape formation. However, local anisotropic stresses, generated during muscle cell differentiation, are necessary to reach the acute angle of the chevron in wild-type embryos. Finally, tissue plasticity is required for formation and maintenance of the chevron shape, which is mediated by orientated cellular rearrangements. Our work sheds light on how a spatiotemporal sequence of local cellular events can have a nonlocal and irreversible mechanical impact at the tissue scale, leading to robust organ shaping.

Organ shape formation requires the integration of genetic information (1–4) with mechanical processes such as directed cell division and rearrangements (5–11) and interactions between tissues (12). The highly robust form of organs (7) suggests that forming a precise shape is essential. Yet, it remains an open question how different biophysical and genetic processes dynamically interact during organogenesis (13, 14).

In the zebrafish embryo, most somites emerge from the presomitic mesoderm (PSM) Fig. 1A, with the anterior-most somites generated from the mesoderm during gastrulation (15, 16). Somites emerging from the PSM are specified by periodic segmentation around every $30\hspace{0.17em}\text{min}$ (17, 18). The stage of a somite’s development is denoted by S$N$; $N$ counts the number of following somites, with a newly specified somite being S1 (Fig. 1A). Somites give rise to slow- and fast-twitch muscle fibers and dermomyotome and various progenitor cells, before maturing into the myotome (19–23). The final myotome consists of slow muscle fibers, whose progenitors are initially located near the notochord, and multinucleated fast fibers, whose progenitors are initially located more laterally (Fig. 1B).

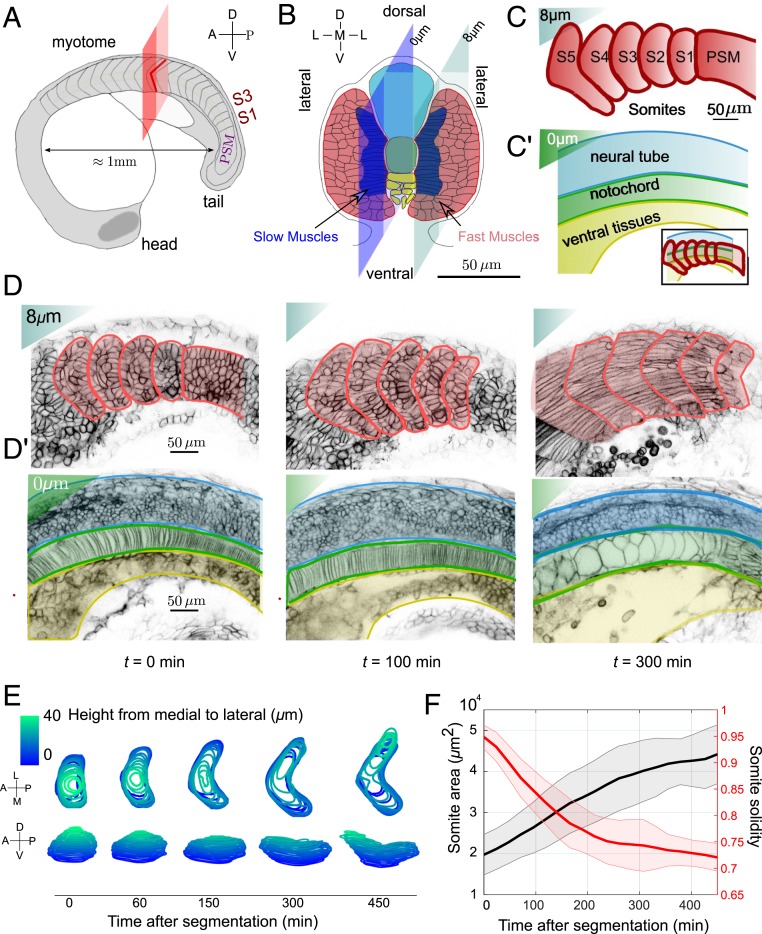
Fig. 1.

The chevron architecture of the future myotome emerges early after segmentation from the presomitic mesoderm (PSM). (A) Sketch of a 21-somite zebrafish embryo. Transverse plane to AP axis is shown in red. Two somites, at stages S1 and S3, are highlighted. (B) Sketch of S3-stage somite ($t\approx 90$ min postsegmentation) in the transverse plane. Dark blue (red) cells are future slow (fast) muscle cells, respectively. The dark and light blue planes represent the cross-sectional views shown in C and D. The notochord is at the center, with the neural tube (light blue) located more dorsally and ventral tissues below (yellow). (C and C′) Cartoon of somite shape after segmentation: (C) plane lying $z=8\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ from notochord and underlying tissues and (C′) plane crossing the notochord, neural tube, and ventral tissues. Inset shows shape of somites superimposed on underlying tissues. (D and D′) Confocal images of embryos expressing Lyn-td-Tomato and superimposed contours of (D) somites and PSM (red lines) and (D′) neural tube, notochord, and ventral tissues (blue, green, and yellow lines, respectively) at $t=\mathrm{0,100,300}$ min postsegmentation from PSM for midbody somites (i.e., around the red plane in Fig. 1A). (E) The 3D evolution of somite shape after segmentation from PSM of a representative wild-type embryo. (F) Cross-sectional area and solidity (ratio of somite area to area of its convex hull) of segmented somites for the most medial layer of future fast muscle fibers (as in D) as a function of time after segmentation. Shaded region represents $\pm 1$ SD. Average is performed over 11 somites from 6 embryos.

The mature myotome has a distinctive V (“chevron”) shape that emerges soon after segmentation (24) (Fig. 1A), which is thought to be important for swimming in fish (25). A number of hypotheses have been proposed to explain chevron formation, including roles for the swimming motion itself (26), older myotome segments acting as templates for younger segments (27, 28), tissue shear flow between the notochord and the developing myotome (29), and the interplay between intrasegmental tension and fixed myotome boundaries (24).

Here, we combine quantitative analysis of in vivo imaging data with modeling to show that a robust chevron shape emerges from the interplay between short-ranged cellular processes (e.g., differentiation and neighbor exchanges) and long-ranged mechanical processes mediated by the coupling between the developing myotome and its surrounding tissues.

Somite Bending Initiates Soon after Its Segmentation

We imaged developing somites at subcellular resolution from within the PSM (earliest S − 2) to the mature myotome stage (S5 onward) (Fig. 1 C and D and Movie S1). We typically imaged from the 18-somite stage to completion of primary myogenesis. Immediately after segmentation, somites are roughly cuboidal (30, 31) (Fig. 1 D and E). Quantifying the somite contours over $8\hspace{0.17em}\mathrm{h}$, we see chevron formation occurs predominantly during S1 to S5 (Fig. 1E and SI Appendix, Fig. S1). Somite volume is approximately constant during the $7\hspace{0.17em}\mathrm{h}$ following segmentation (SI Appendix, Fig. S1G). After segmentation, new somites begin to flatten in the medial–lateral (ML) axis, with spreading in the dorsal–ventral (DV) axis, leading to increased contact area with the medially underlying tissues (notochord, neural tube, and ventral tissues) (Fig. 1 E and F and Movie S2).

Concurrently with spreading, a “U” shape emerges in the medial region of the somite that always points toward the embryo anterior. This U subsequently sharpens into a chevron (Fig. 1E). The DV spreading and subsequent formation of the chevron shape are reduced under Sonic Hedgehog (Shh) signaling inhibition by cyclopamine (SI Appendix, Fig. S2). Chevron formation involves breaking somite symmetry along the anterior–posterior (AP) axis, which is, at least partially, cell fate dependent.

Chevron Angle Is Reduced by Both Internal and External Perturbations to the Myotome

The myotome shape is sensitive to perturbations (32, 33), including to signaling pathways (34, 35), the surrounding extracellular matrix (ECM) (36, 37), and the surrounding tissues (38, 39). Under perturbation, the myotome becomes more U-like or even flat. We are unaware of perturbations that sharpen the chevron, suggesting the shape is tightly controlled and may be evolutionarily optimized. We quantified the chevron angle when slow muscle cell fate is disrupted using genetic (${\mathit{smo}}^{-/-}$, Movie S3) and drug (cyclopamine, Movie S4) perturbations of the Shh pathway. Increasing cyclopamine dosage gradually reduces slow muscle number (SI Appendix, Fig. S2 C and D). We complemented these measurements with data from the literature (SI Appendix, SI Methods and Table S1). The chevron angle increases linearly from $90^{○}$ toward $180^{○}$ with decreasing slow muscle number (Fig. 2A). In contrast, altering the ECM at the somite interfaces—e.g., Col15a1${\mathrm{a}}^{MO}$, ${\mathit{lamc1}}^{-/-}$, and ${\mathrm{F}\mathrm{u}\mathrm{k}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{n}}^{MO}$ [which perturbs laminin expression (37)] (SI Appendix, SI Methods and Table S1)—drastically reduced chevron angle, while slow muscle number remains largely unchanged (Fig. 2A). These results suggest that both muscle cell differentiation (intrinsic to each somite) and ECM interactions (at the interface between somites and surrounding tissues) are critical in forming the chevron.

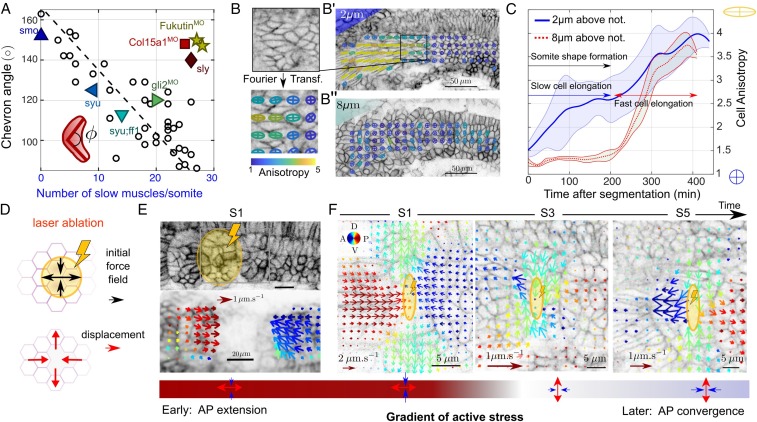
Fig. 2.

Slow muscle elongation leads to anisotropic stresses. (A) Chevron angle (in degrees) in most medial layer of future fast muscle fibers against number of slow muscles per somite at S4. Black circles: cyclopamine-treated embryos at different concentrations. Triangles: morpholinos and mutants affecting cell differentiation [dark blue $△$, smo (61); light blue $⊲$, syu (62); cyan $▿$, syu + ff1 (62); and green $⊳$, gli${\mathrm{2}}^{MO}$ (41)]. Morpholinos or mutants altering tissue integrity [dark yellow $\star$, Fukutin (37); light red $\square$, Col15a1${\mathrm{a}}^{MO}$ (36); dark red $\diamond$, sly (32, 63)]. See SI Appendix, SI Methods and Table S1 for further details ($N=30$ embryos and $n=41$ somites). (B) Fourier transform image analysis method (42) provides cell elongation field, with anisotropy represented by ellipsoids (SI Appendix, SI Methods). Cell elongation is along the major axis of the ellipse. (B′and B$″$) Elongation maps of future slow (B′, $2\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ above notochord) and fast (B$″$, $8\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ above notochord) muscle fibers. (C) Mean cell anisotropy after segmentation within a medial plane containing slow muscle fibers (solid blue line) and a more lateral plane, composed of fast muscle fibers (dashed red line). Shaded regions represent $\pm 1$ SD. Average is performed over 11 somites from 6 embryos. (D) Cartoon of predicted relaxation direction upon ablation of early somitic tissue. (E, Top) Laser ablation (yellow region) of somites expressing lyn-tdTomato at stages S0 and S1. (E, Bottom) Corresponding time-averaged tissue velocity from optic flow analysis in the $10\hspace{0.17em}\mathrm{s}$ after ablation. Arrow color represents direction and length represents speed. (F) DV-orientated laser ablation at the DV midline of the medial layer of future fast fibers (yellow region), at different somite stages, with tissue velocity from optic flow analysis superimposed in the $10\hspace{0.17em}\mathrm{s}$ after ablation. Color coding is as in E. Note the velocity scale is different for S1 compared to S3 and S5. (E and F, Bottom) Schematic of the inferred stress directions imposed by the ablated element on the tissue.

Somite Deformation Occurs Concomitant with Slow Muscle Elongation but prior to Fast Muscle Elongation

Concurrent with the tissue shape changes, cells within the somite begin differentiation into specific muscle fibers to form the myotome (19, 22, 23, 30, 40, 41). The most-medial layer of cells differentiates into slow muscles at the onset of somite segmentation (Fig. 1B) (23). These cells, which are epithelium-like before segmentation, rapidly elongate along the AP axis until they span the somite compartment. We quantified muscle elongation dynamics using a Fourier transform method to analyze the evolution in cellular anisotropy (Fig. 2 B and C) (42). We find signatures of future slow muscle elongation prior to segmentation, and these cells rapidly extend over the next $100\hspace{0.17em}\text{min}$ (Fig. 2C). Fast muscle elongation occurs later, around $250\hspace{0.17em}\text{min}$ after segmentation (Fig. 2C). In Fig. 1E, we see that the chevron is apparent $200\hspace{0.17em}\text{min}$ after segmentation, prior to fast muscle elongation. Despite fast muscles representing $>80\%$ of somitic cells, the future myotome acquires the chevron shape before most muscles have elongated.

What role does slow muscle elongation play in chevron formation? To understand the direction of cellular-scale forces exerted on the tissue during chevron formation we used UV laser ablations (43) (SI Appendix, SI Methods). Ablating the whole somite at stage S1, we observe rapid relaxation of neighboring tissues toward the ablated region. This implies that newly segmented somites are exerting pressure on their neighbors (Fig. 2 D and E and Movie S5). We performed finer laser ablations on S1, S3, and S5 somites using DV-orientated ablations (Fig. 2F; SI Appendix, Fig. S3; and Movie S6). Ablations in S1 somites show AP convergence and DV extension (Fig. 2F). In older somites the response is opposite, although the velocities are smaller (Fig. 2F). The signs of the convergent-extension flows are consistent with anisotropic stresses that are extensile along the AP axis in early somites (correlating with slow muscle elongation) and tensile in older somites.

Spatiotemporal Variation in Somite–Tissue Coupling Correlates with the Chevron Shape

As perturbations to surrounding tissues and ECM alter the future myotome shape, we explored the mechanical coupling between somites and surrounding tissues. We imaged embryos injected with lyn-Kaede (photo-switchable protein; SI Appendix, SI Methods); by switching Kaede at a somite boundary, we can observe the differential movement of the notochord and neural tube with respect to the somite (Fig. 3A). Using 2D optic flow, we quantified the cellular velocity fields inside the somites in different ML planes and in the adjacent notochord, skin, and neural tube (Fig. 3B and SI Appendix, SI Methods). We computed the averaged in-plane 2D velocity fields, as the shear velocities along the ML axis were comparatively small (SI Appendix, Fig. S4 A–C).

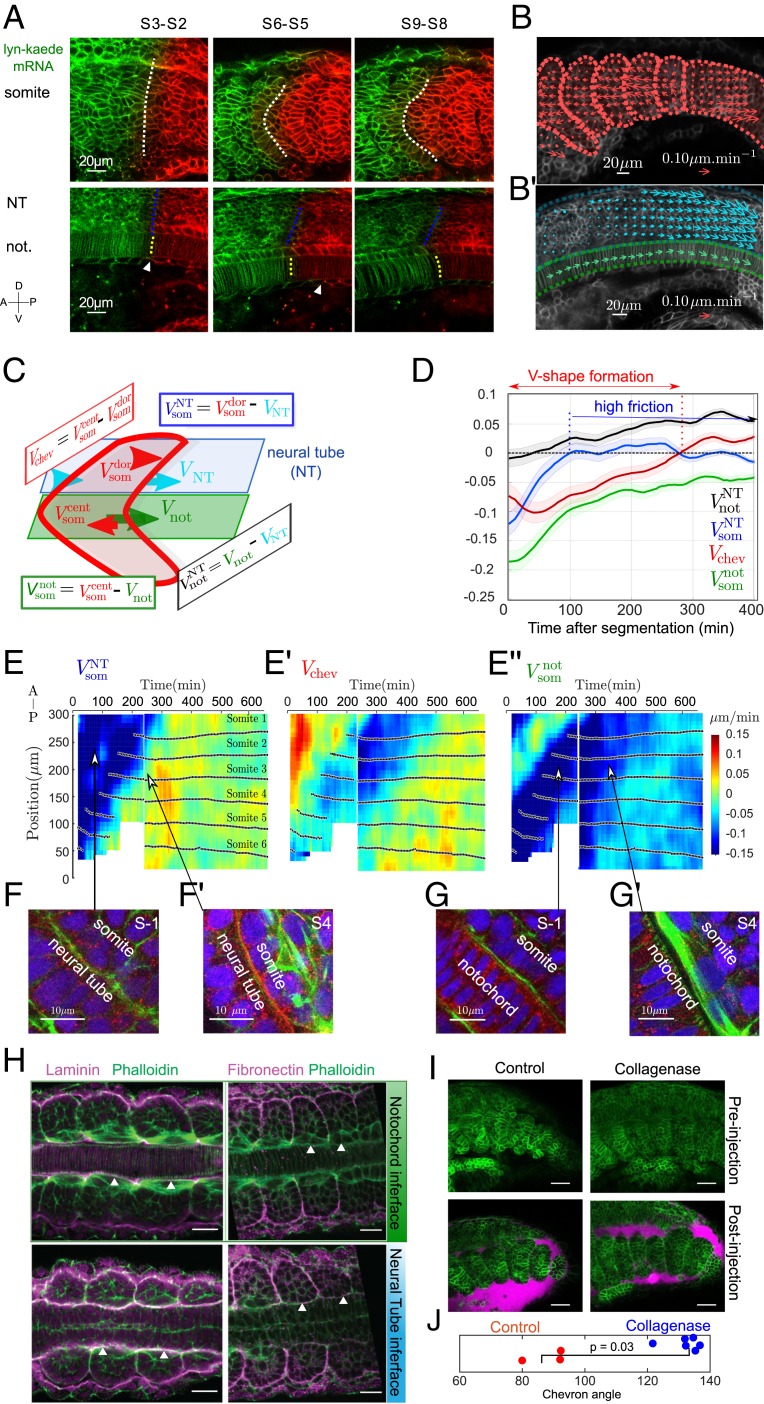
Fig. 3.

Differential tissue flow and tissue contact correlate with chevron emergence. (A) Lyn-Kaede showing relative movement of the somites (Top) with respect to the notochord and neural tube (Bottom) from S2 to S9. Kaede photoswitching was performed at the S2 stage in the more posterior somites (SI Appendix, SI Methods). Dashed lines highlight interfaces between the fluorescent regions. (B and B′) Velocity fields estimated by optic flow in WT embryos (SI Appendix, SI Methods) within the somite (som, red arrows, B), neural tube (NT, cyan arrows, B′) and notochord (not, green arrows, B′). (C) Definition of the mean AP velocities within each tissue. Color scheme is as in B. (D) Average relative tissue AP velocities ($n=11$ somites, $N=5$ embryos) after segmentation from the PSM. Shaded regions represent $\pm 1$ SD. (E, E′, and E$″$) Kymographs of shear velocities $V_{\mathrm{s}\mathrm{o}\mathrm{m}}^{\mathrm{N}\mathrm{T}}$, $V_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{v}}$, and $V_{\mathrm{s}\mathrm{o}\mathrm{m}}^{\mathrm{n}\mathrm{o}\mathrm{t}}$ show somite-to somite reproducibility of the features identified in D. Each panel is from 2 embryos, with stitching at $t=220$ min. Black dots indicate the position of each somite’s center of mass along the AP axis, with somite labeling representing somite number with respect to the start of the movie. In E′, negative shear (blue colored region) indicates region of chevron shape emergence. (F and G) Confocal images of actin (green), laminin (red), and nuclei (blue) in transverse plane to the ML axis for somites S − 1 and S − 4. (Scale bar: $10\hspace{0.17em}\mathrm{\mu }\mathrm{m}$.) (F and F′) Somite–neural tube interface at S − 1 (F) and S4 (F′). (G and G′) Somite–notochord interface at S − 1 (G) and S4 (G′). Arrows highlight correlation between actin localization and relative tissue velocities in E–E$″$. (H) Laminin (Left) and fibronectin (Right) antibody staining (SI Appendix, SI Methods) at the somite–notochord (Top row) and somite–neural tube (Bottom row) interfaces, imaged along the DV axis. Rightmost somite is in stage S1. Arrowheads highlight accumulation (or lack) of ECM components at the somite boundary with other tissues. (Scale bar: 20 $\mathrm{\mu }\mathrm{m}$.) (I) The 18-hpf embryos pre- and postinjection with collagenase or control. Green is Lyn-Td-Tomato and cyan is Dextran Alexa 647 showing the extracellular space. Postinjection images were taken $10$ min after injection. (Scale bar: $25\hspace{0.17em}\mathrm{\mu }\mathrm{m}$.) (J) Quantification of chevron angle $24$ h postcollagenase injection. The 3 most posterior intact somites are quantified, along with the equivalent position in the control (P value from Mann–Whitney test).

To gain insight into the physical coupling between tissues, we focused on relative tissue velocities. We considered the velocity component along the AP axis for each tissue: $V_{\mathrm{n}\mathrm{o}\mathrm{t}}$ (notochord), $V_{\mathrm{s}\mathrm{o}\mathrm{m}}$ (somite), and $V_{\mathrm{N}\mathrm{T}}$ (neural tube) (SI Appendix, SI Methods). We define the shear velocity within the somite $V_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{v}}$ as the relative difference in the velocity of cells at the DV midline and of those in more dorsal positions (Fig. 3C). Similarly, we define shear velocities between somites and neural tube ($V_{\mathrm{s}\mathrm{o}\mathrm{m}}^{\mathrm{N}\mathrm{T}}$), somites and notochord ($V_{\mathrm{s}\mathrm{o}\mathrm{m}}^{\mathrm{n}\mathrm{o}\mathrm{t}}$), and notochord and neural tube ($V_{\mathrm{n}\mathrm{o}\mathrm{t}}^{\mathrm{N}\mathrm{T}}$) (Fig. 3C). Each of these shear velocities has distinct behavior (Fig. 3 D and E and SI Appendix, Fig. S5).

In agreement with the chevron formation timescale identified in Fig. 1F, $V_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{v}}<0$ during the first $5\hspace{0.17em}\mathrm{h}$ after segmentation (Fig. 3E′). During this time, the notochord moves more posteriorly than the neural tube as $V_{\mathrm{n}\mathrm{o}\mathrm{t}}^{\mathrm{N}\mathrm{T}}$ remains positive after segmentation (Fig. 3D). Hence, somites are not passively deformed by an underlying tissue shear, in which case the chevron would point toward the embryo posterior. Soon after segmentation $V_{\mathrm{s}\mathrm{o}\mathrm{m}}^{\mathrm{N}\mathrm{T}}\approx 0$, implying that the somite and neural tube move concomitantly (Fig. 3 D and E). Before segmentation, future somites and notochord move concomitantly, while $V_{\mathrm{s}\mathrm{o}\mathrm{m}}^{\mathrm{n}\mathrm{o}\mathrm{t}}<0$ throughout the $6\hspace{0.17em}\mathrm{h}$ after segmentation (Fig. 3E″), implying that somites move anteriorly relative to the notochord. The ventral tissues are more challenging to image. Using Kdrl:GFP (44), an endothelial marker, we see the posterior movement of ventral tissues correlates with the ventral movement of the somite (SI Appendix, Fig. S6A and Movie S7. The somite is also in contact with the skin (laterally). The skin is moving posteriorly relative to the somite (SI Appendix, Fig. S4D and Movie S8).

From these observations, we hypothesize 1) that somites are strongly coupled after segmentation to the neural tube and ventral tissues, 2) that somites and notochord are mechanically coupled prior to segmentation and uncoupled afterward, and 3) that somites and skin are weakly coupled.

Mechanical Coupling between Tissues Varies in Time

Do the spatial and temporal changes in relative tissue movements correlate with changes in the physical interactions between the tissues? To answer this, we first examined the tissue connectivity. We antibody stained for ECM components laminin and fibronectin (45) (Fig. 3 F–H and SI Appendix, Fig. S6 E and F). Laminin and fibronectin display enrichment between the somite–neural tube and somite–ventral tissue interfaces compared to the somite–notochord interface. These results are qualitatively consistent with the dorsally and ventrally located tissues having greater connectivity with the somite than with the notochord. To observe the intertissue space around somites, we injected fluorescently labeled dextran (SI Appendix, SI Methods). Consistent with that above, we observe a larger gap between the somite and notochord than for the somite–neural tube boundary (SI Appendix, Fig. S6 B–D). Exploring the temporal changes in connectivity, we see that before segmentation future somitic cells are in contact with the notochord (Fig. 3G). After segmentation, a gap emerges between these cells and the notochord (Fig. 3G′) together with the appearance of large actin fibers (Movie S9). This increased separation suggests reduced friction between the notochord and the somite. In contrast, somitic cells appear to maintain contact with the neural tube (Fig. 3 F and F′).

Following refs. 46 and 47, we expect strongly (weakly) adhered tissues to have high (low) effective interfacial friction. Such a framework has proved fruitful in understanding tissue–tissue interactions during early zebrafish morphogenesis (48) and here we hypothesize that such differential interactions are key to forming the chevron. To test the role of friction, we injected collagenase into embryos at the 18-somite stage (SI Appendix, SI Methods). Within 10 min of treatment the chevron shape is lost (Fig. 3I). The myotome shape remains deformed 24 h after treatment with low levels of collagenase (Fig. 3J and SI Appendix, Fig. S6G). This provides evidence that intertissue friction is important in chevron formation. Combined with our above evidence on spatiotemporally varying patterns of ECM component expression, we hypothesize that such friction is spatially inhomogeneous during myotome formation.

Below, we incorporate differential tissue friction, along with somite spreading and anisotropic stresses due to muscle cell differentiation, within a vertex model to test how tissue–tissue coupling drives emergence of the chevron shape.

Vertex Model Simulations of Tissue Shape Formation

The somite chevron shape first emerges in the most medial plane, near the notochord (Fig. 1E and SI Appendix, Fig. S1), before propagating laterally. We see that somitic tissue flows occur mainly within planes orthogonal to the ML axis (SI Appendix, Fig. S4). Therefore, we consider a 2D model of myotome formation focused on the medial region of the developing myotome, as this is where the chevron shape first emerges and dynamics in the AP and DV axes are more rapid than in the ML axis. Our model implicitly incorporates 3D dynamics; somite spreading in the medial layer (Fig. 1E) is related to complex 3D cellular reorganization of the whole somite (SI Appendix, Fig. S9 and ref. 23). This approach enables us to use a 2D representation of the more complex 3D morphology.

Relative tissue movement results in friction forces, which are balanced by internal forces (${\mathbf{F}}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}}$) due to spreading, differentiation, and cell tension forces. Here, we express friction forces in terms of velocities defined with respect to a fixed frame of reference, in which new somites are added at a constant segmentation speed ${\mathrm{v}}_{\mathrm{s}\mathrm{e}\mathrm{g}}$ (Fig. 4A). The local force balance equation at position $\mathbf{x}$ within the somite is given by

$${\eta }_{\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}}\left\{\mathbf{v}\left(\mathbf{x}\right)-{\mathbf{v}}_{\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}}\right\}+{\eta }_{\mathrm{s}\mathrm{k}\mathrm{i}\mathrm{n}}\left\{\mathbf{v}\left(\mathbf{x}\right)-{\mathbf{v}}_{\mathrm{s}\mathrm{k}\mathrm{i}\mathrm{n}}\right\}={\mathbf{F}}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}}\left(\mathbf{x}\right),$$ [1]

where $\mathbf{v}\left(\mathbf{x}\right)$ represents the local 2D somite tissue velocity and ${\mathbf{v}}_{\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}}$ the local 2D velocity of the tissue in contact with the somite. ${\eta }_{\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}}$ denotes the friction coefficient between the somite and the relevant tissue, which depends on the position $\mathbf{x}$: ${\eta }_{\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}}={\eta }_{\mathrm{N}\mathrm{T}}$, ${\eta }_{\mathrm{n}\mathrm{o}\mathrm{t}}$, or ${\eta }_{\mathrm{V}\mathrm{T}}$ for positions overlying the neural tube, notochord, and ventral tissues, respectively. ${\mathbf{v}}_{\mathrm{s}\mathrm{k}\mathrm{i}\mathrm{n}}$ is the skin velocity and ${\eta }_{skin}$ the effective friction representing the lateral interaction between the somite and skin.

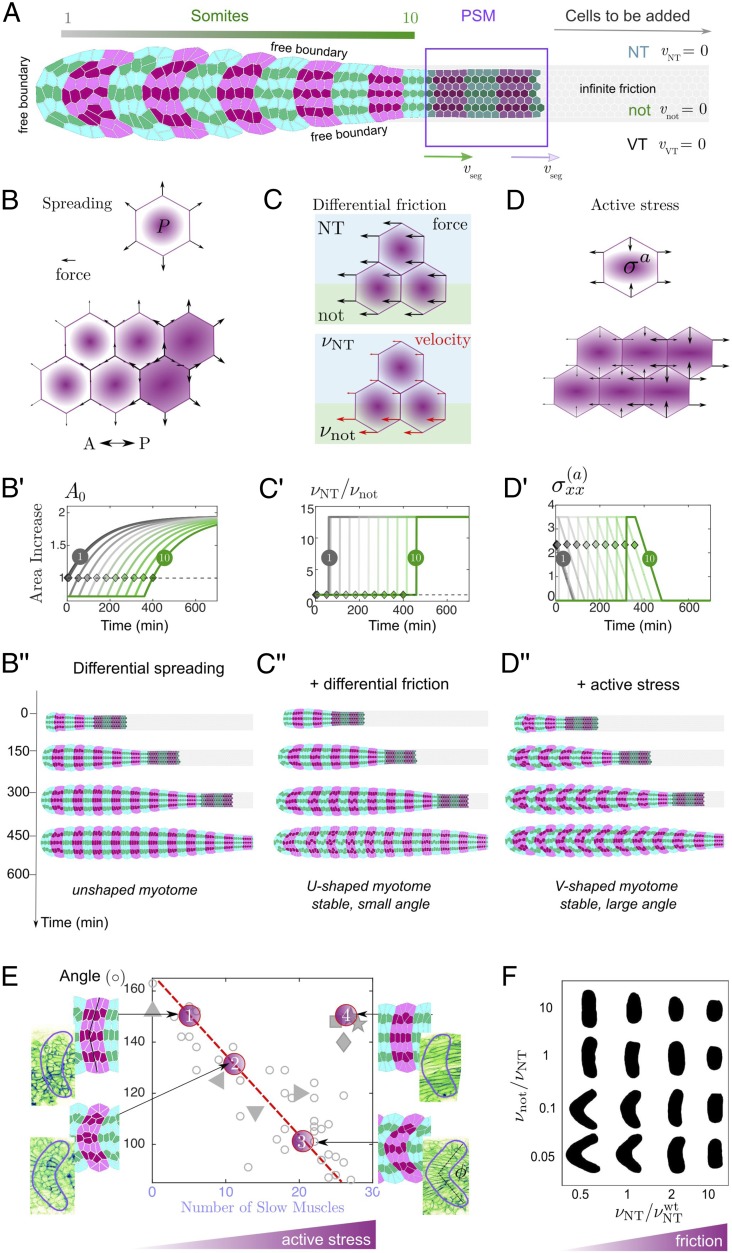
Fig. 4.

Vertex model of chevron formation. (A) Simulated geometry used in the model. Simulated cell number increases with time as new cells are progressively added from the tailbud (purple box); magenta (green) cells belong to somite number $2N$ ($2N+1$), respectively. New somites appear at a velocity $V_{\mathrm{s}\mathrm{e}\mathrm{g}}=1\hspace{0.17em}\mathrm{s}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{e}/\left(30\hspace{0.17em}\text{min}\right)$. Tension is increased along the somite–somite boundaries. (B–D) Principle elements included within the vertex model: (B) Differential spreading is implemented through increased cellular pressure along the AP axis, leading to a spatial modulation along the embryo axis of cellular outward forces (black arrows). (B′) Exponential increase in somite target area as a function of time, based on experimental measurements. Gray curve (dark green) corresponds to first (last) somite formed in simulation (diamonds indicate timing of segmentation of specific somite from PSM, A). (B$″$) Simulations with differential spreading only. (C) Vertex displacement (red arrow) is spatially modulated by an inhomogeneous friction coefficient $\nu$, where $\nu ={\nu }_{\mathrm{N}\mathrm{T}}={\nu }_{\mathrm{V}\mathrm{T}}$ for vertices over the neural tube and ventral tissues and $\nu ={\nu }_{\mathrm{n}\mathrm{o}\mathrm{t}}$ otherwise. (C′) The ratio of ${\nu }_{\mathrm{N}\mathrm{T}}$ to ${\nu }_{\mathrm{n}\mathrm{o}\mathrm{t}}$ is implemented as a step function. (C$″$) Simulations with somite spreading and differential friction. (D) An imposed bulk active stress ${\sigma }^{\left(a\right)}$ leads to elongation forces along the AP axis (black arrows; see SI Appendix for derivation). (D′) Evolution of the extensile stress along the AP axis for different somite stages, with maximal stress 60 min before segmentation, corresponding to the onset of slow muscle fiber elongation. (D$″$) Simulations with active differentiation stresses and differential friction (wild-type case): Somites acquire a stable chevron shape. (E) Comparison of experimentally measured chevron angle (Fig. 1G) with the angle measured for 4 simulation outcomes. Only the active differentiation stress level is varied from points 1 to 3 (all other parameters fixed), describing embryos treated with $50\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}$ (1) and $10\hspace{0.17em}\mathrm{\mu }\mathrm{m}\mathrm{o}\mathrm{l}$ (2) of cyclopamine and wild-type embryos (3). (4) corresponds to the homogeneous friction case with ${\nu }_{\mathrm{n}\mathrm{o}\mathrm{t}}={\nu }_{\mathrm{N}\mathrm{T}}$, describing perturbed tissue–tissue coupling of Col15a1${\mathrm{a}}^{MO}$. (F) Somite shape variations depending on ${\nu }_{\mathrm{N}\mathrm{T}}$ and ${\nu }_{\mathrm{n}\mathrm{o}\mathrm{t}}/{\nu }_{\mathrm{N}\mathrm{T}}$.

From our live imaging we see that some terms in Eq. 1 likely do not play significant roles in shaping the myotome. First, as shown by the presence of interstitial space between the somite and skin (SI Appendix, Fig. S6) and also that the somite and skin move in opposite directions relative to each other during chevron formation (SI Appendix, Fig. S4), we neglect the term ${\eta }_{\mathrm{s}\mathrm{k}\mathrm{i}\mathrm{n}}{\mathbf{v}}_{\mathrm{s}\mathrm{k}\mathrm{i}\mathrm{n}}$. Similarly, movement of the notochord appears to be largely independent of the somite, suggesting that ${\eta }_{\mathrm{n}\mathrm{o}\mathrm{t}}{\mathbf{v}}_{\mathrm{n}\mathrm{o}\mathrm{t}}$ is negligible. The neural tube and ventral tissues move with similar velocity to the somite during chevron formation, implying $\left(\mathbf{v}-{\mathbf{v}}_{\mathrm{N}\mathrm{T}}\right)\approx \left(\mathbf{v}-{\mathbf{v}}_{\mathrm{V}\mathrm{T}}\right)\approx 0$. See SI Appendix for further discussion. We tested these assumptions by running the simulations including the measured velocities, and we saw qualitatively similar results (SI Appendix, Fig. S7 G and H).

To model the internal forces generated within each somite we implemented a 2D vertex model of the medial compartment (Fig. 4A). We do not distinguish specific muscle types. Each cell is described by a polygon whose summits, called vertices, correspond to the edges of cell–cell interfaces. Cellular movements and deformations are described through the dynamics of the cell vertices $\mathbf{v}\left({\mathbf{X}}_i\right)={\dot{\mathbf{X}}}_i$, where ${\mathbf{X}}_i$ is the location of the vertex $i$. Including the above approximations, the force-balance Eq. 1 becomes

$${\nu }_{\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}}{\dot{\mathbf{X}}}_i={\mathbf{F}}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}}\left({\mathbf{X}}_{\mathrm{i}}\right)={\mathbf{F}}_{\mathrm{d}\mathrm{i}\mathrm{ff}}+{\nabla }_{{\mathbf{X}}_{\mathrm{i}}}E,$$

where, generally, ${\nu }_{\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}}={\eta }_{\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}}\left({\mathbf{X}}_i\right)+{\eta }_{\mathrm{s}\mathrm{k}\mathrm{i}\mathrm{n}}$ is a spatially dependent friction coefficient and the internal forces are decomposed in 2 parts: 1) an active contribution, denoted $F_{\mathrm{d}\mathrm{i}\mathrm{ff}}$, which is generated by slow muscle fiber differentiation, and 2) an elastic contribution ${\nabla }_{{\mathbf{X}}_i}E$, representing cell-scale forces regulating cell shape. Following ref. 49, we consider

$$E=\sum _{C,I}\left[\lambda {\left(A_C-A_0\right)}^2+\beta {\left(P_C-P_0\right)}^2+{\gamma }_I{L}_I\right],$$

where $A_0$ ($P_0$) represents the preferred area (perimeter) of a cell $C$, $A_C$ ($P_C$) the actual area (perimeter) of a cell at a given time, and $L_I$ the length of cell–cell interface $I$. $\lambda$ represents the pressure forces involved in cell area regulation, while $\beta$ and ${\gamma }_I$ represent the strength of cell- and interface-dependent tensions, respectively (Fig. 4A). After segmentation, almost no cellular exchanges with neighboring somites are observed. We model this compartmentalization by increasing the tension $\gamma$ along the somite–somite boundaries. Finally, to simulate growth and division within the tailbud and addition of new cells to the PSM, we continuously add new cells at the posterior end of the tissue, at a rate determined by the segmentation clock (18). See SI Appendix, SI Methods for further details.

Somite Spreading and Differential Friction Are Sufficient to Generate a Shallow Chevron Shape

We first tested the effects of spatially varying friction and somite spreading in the model. To simulate spreading we varied each cell’s target area $A_0$ at time $t$ after segmentation: $A_0\left(t\right)=A_0+\left(A_f-A_0\right)\exp \left(-\left(t-{\tau }_{\mathrm{s}\mathrm{e}\mathrm{g}}^N\right)/{\tau }_{\mathrm{s}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{d}}\right)$, with ${\tau }_{\mathrm{s}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{d}}=200\hspace{0.17em}\text{min}$ extracted from experiment (Fig. 4 B and B′), and ${\tau }_{\mathrm{s}\mathrm{e}\mathrm{g}}^N$ is the segmentation time of the $N\text{th}$ somite. During spreading, each cell has increasing target area and hence exerts pushing forces on its neighbors. We first considered somite spreading with uniform friction (Fig. 4B″). Along the DV axis of the somite, all cells have the same target area and spread together. However, along the AP axis the cells are not at the same stage of spreading. Newer (and subsequently smaller) somites have a higher spreading rate than more anterior (older) somites, resulting in a net force along the central part of more anterior somites. Subsequently, a slight bending toward the head occurs, but this is insufficient to irreversibly deform the somites; they relax once spreading is finished (Movie S10).

We next introduced spatially inhomogeneous friction within the model (Fig. 4 C and C′). After segmentation, the friction coefficient is decreased over a central region modeling the notochord interface, while it is increased in the other regions corresponding to the neural tube and ventral tissues interfaces (Fig. 4C′). Combining spreading with nonuniform friction leads to somites deforming into a shallow chevron (Fig. 4C″and Movie S11). As cells lying above the notochord slide faster than those located more dorsally or ventrally, the stress due to somite spreading creates a DV shear that deforms somites into a U shape. Such tissue deformation also alters individual cell shapes. If the tissue is sufficiently plastic, then cell rearrangements relieve the stress induced by the shape changes, resulting in a sharpened somite boundary and the emergence of a stable but shallow chevron in early somites. However, this shape does not propagate to younger somites as the tissue spreading rate is too slow to trigger cell rearrangements in later segments (SI Appendix, Fig. S7C).

An Anterior–Posterior Gradient of Active Differentiation Stress Amplifies the Chevron Angle

Slow muscle elongation (Fig. 2) likely exerts an anisotropic stress on the somitic tissue. To model the effects of this stress, we used active gel theory, a hydrodynamic description of the actomyosin cortex that encompasses contractility and filament polymerization through a local anisotropic stress tensor (50) (SI Appendix, SI Methods). To discriminate its contribution from somite spreading, we considered a traceless active stress field which we call differentiation stress; we first consider the case with positive component along the AP axis (extensile direction) and negative component along the DV axis (contractile direction) (Fig. 4D). We further assume that the extensile stress along the AP axis is maximal at segmentation, with a linear decrease to zero by the end of slow muscle elongation (S6) (Fig. 4D′). Such a stress profile is consistent with the observed timing of slow muscle elongation (Fig. 2C), as well as the anisotropy in the recovery flows postablation from S1 to S3 (Fig. 2F). The inclusion of such an anisotropic stress profile is sufficient to shape the tissue into a stable and sharp chevron shape (Fig. 4D″ and Movie S12). To account for the divergent postablation recovery flows at S5 (Fig. 2F), we tested the case with the same stress gradient, yet with a final nonzero negative AP-axis component (contractile AP-axis stress). We find a slight further increase in the chevron angle (Movie S13). We emphasize that what matters is the gradient in anisotropic stresses; an extensile stress decreasing from posterior to anterior leads to a net force exerted toward the anterior side. In contrast, assuming an increased tensile stress along the AP axis (e.g., by switching the sign of the anisotropic stress) leads to an inverted chevron pattern (SI Appendix, Fig. S7A).

Model Predictions for Myotome Shape under Perturbations

We now test quantitative predictions of our model for chevron shape under perturbations. The chevron angle changes with slow muscle number (Fig. 2A); in our model, this corresponds to changing the active differentiation stress. Without active differentiation stress, the model predicts a transient shape deformation before relaxing. Such dynamics are strikingly similar to $sm{o}^{-/-}$ embryos, where there is no slow muscle specification (Movie S3). Intermediate levels of active differentiation stress in the model result in reduced chevron angle, as observed experimentally (Fig. 4E). Perturbations to the interactions between tissues (e.g., Col15a1${\mathrm{a}}^{MO}$ or collagenase) likely reduce the effective differential friction between tissues. Using homogeneous friction (while leaving the active differentiation stress unchanged) results in a mild but stable bending of the myotome, consistent with experiments (Fig. 4E).

Where possible, we have used realistic parameters motivated from experiments (SI Appendix, SI Methods and Table S2). To test parameter sensitivity, we explored the model predictions for myotome shape across a broad parameter space for the friction, cell tension, and active stress terms. The resultant chevron shape is sensitive to the intertissue friction (Fig. 4F and SI Appendix, Fig. S7C), with the chevron apparent for high (low) neural tube (notochord) friction. We tested the effect of DV asymmetry in the friction profile (our ECM staining shows DV asymmetry in adhesion molecule distribution), by implementing ${\nu }_{\mathrm{N}\mathrm{T}}>{\nu }_{\mathrm{V}\mathrm{T}}>{\nu }_{\mathrm{n}\mathrm{o}\mathrm{t}}$. A chevron still emerges, although it is asymmetric (SI Appendix, Fig. S7F and Movie S14), which is qualitatively consistent with the chevron shape observed in vivo. Varying the magnitude and orientation of the active stress (SI Appendix, Fig. S7A) shows that the chevron shape is robust, although the final angle is dependent on the magnitude of the active stress. Cell tension also plays a role in sharpening the final chevron angle (SI Appendix, Fig. S7B). Finally, we confirmed the simulated chevron shape was robust to fluctuations (SI Appendix, SI Methods and Movie S15).

To summarize, we have developed a predictive 2D model of the initial stages of chevron shape formation in the zebrafish somite. The key ingredients are differential somite spreading (a 3D phenomenon that corresponds to somite area increase in 2D), spatially heterogeneous friction forces, and a gradient of anisotropic stress along the AP axis.

Dynamics of Chevron Formation

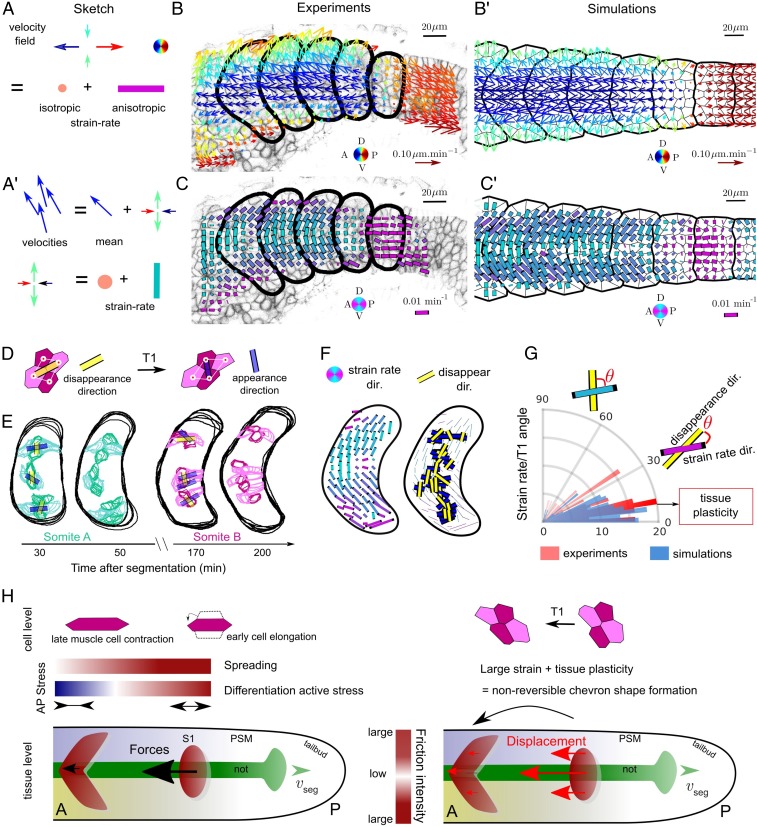
We challenged the model’s capacity to reproduce the tissue dynamics seen during chevron formation. In both experiments and simulations, we quantified the tissue velocity, anisotropic strain rate (ASR) (SI Appendix, SI Methods), and isotropic strain rate (Fig. 5 A–C and SI Appendix, Fig. S8). The ASR provides the local tissue expansion direction (Fig. 5A). The experimental and simulated ASR fields share common features: 1) In S1, somites undergo AP extension (purple bars, Fig. 5C), correlating with the onset of slow muscle elongation (Fig. 2). This pattern is similar to that produced by a single cell actively extending in a passive tissue (SI Appendix, Fig. S8C), yet at the larger tissue level. 2) In S2 somites, the ASR is near zero. 3) From S3 to S6, somites undergo shear between the central and dorsal regions.

Fig. 5.

Model accurately predicts orientation of cellular rearrangements. (A and A′) Definition of velocity field (arrows) and corresponding strain rates. (A′) Decomposition of velocities into isotropic and anisotropic strain-rate components. (B and B′) Comparison of velocity fields measured in experiments (B) (with optic flow; SI Appendix, SI Methods) and simulation (B′). Arrow color represents direction and length represents speed. (C and C′) Comparison of anisotropic component of the strain rates (ASR) in experiments (C) and simulations (C′). Bar color represents orientation (AP [magenta] and DV [cyan]) and length represents magnitude of the ASR (SI Appendix, SI Methods). (D) Scheme of cellular rearrangements, with cells losing contact joined by yellow bar and cells forming new contacts joined by blue bar. (E) Experimental examples of 3D cellular rearrangements for 2 somites at different somite stages. (F) Time- and ensemble-averaged ASR (Left) compared to accumulated cell rearrangement orientations superimposed on the ASR map (Right) ($n=4$ somites). (G) Rose plot alignment of cellular rearrangements with ASR in experiments ($n=44$ from 4 somites) and simulations ($n=60$ from 6 simulated somites). (H) Recapitulative cartoon. Gradients of spreading and active differentiation stresses result in an overall force oriented toward the anterior; reduced friction over the notochord leads to an increased displacement of the somite region over the notochord; large somite deformations are stabilized by cell rearrangements (tissue plasticity).

Plastic-like behavior is required to acquire a stable chevron shape, as an elastic material will eventually relax since the shear stresses generated by cell differentiation and spreading are transient. We observe experimentally that tissue flows do not generate large cell deformations (SI Appendix, Fig. S9) and that cell division is infrequent in the somite ($<10\hspace{0.17em}\%$ of cells divide during S1 to S5). Hence, we focused on the role of cell rearrangements in the tissue plasticity (51, 52). We tracked cellular shapes in 3D within S1, S2, and S3 somites (Fig. 5 D and E; SI Appendix, Fig. S9; and Movie S16) and superimposed these rearrangements with the ASR field map (Fig. 5F and SI Appendix, SI Methods). We implemented passive cell rearrangements within the model. The shear forces emerging in the model orientate the passive cellular rearrangements along the ASR (Fig. 5G), consistent with the bulk somitic tissue having plastic-like behavior (53).

While intrasomite cell rearrangements are needed, intersomite cell exchanges should be limited to preserve somite shape. Our simulations predict roughening of somite–somite interfaces when somite compartmentalization is abolished (SI Appendix, Fig. S10A). To test this, we examined tissue shear in ${\mathit{tbx6}}^{-/-}$ embryos, which lack clear somite boundaries. Slow and fast muscles are still present and appear to rearrange in a similar fashion to that of wild-type embryos (32, 54). We generated artificial boundaries in ${\mathit{tbx6}}^{-/-}$ embryos using lyn-Kaede to demarcate regions that approximate the interface between S1 and PSM in a wild-type embryo (SI Appendix, Fig. S10 B and C). The initially smooth DV-orientated boundary becomes rough and curved, which is in agreement with the model with no surface tension at the somite–somite interface.

Discussion and Conclusion

Putting our above experimental and theoretical results together, we propose the following sequence of events leading to chevron-shaped myotomes (Fig. 5H): 1) Increased line tension between developing somites leads to mechanically segmented cell compartments (Fig. 4A); 2) somite differential spreading (Fig. 4B) leads to a pressure gradient along the AP axis, which, combined with the onset of a differential friction along the DV axis (Fig. 4C), leads to a buckling instability; and 3) muscle fiber elongation further contributes to buckling (Fig. 4D), which triggers cell rearrangements that maintain a stable chevron shape. Our 2D model incorporates features resulting from the 3D dynamics of the somite, yet neglects cell heterogeneities within the somite (SI Appendix, Fig. S9 D–F). Although we cannot discount other possible mechanisms, our model is sufficient to recapitulate the dynamics of myotome shape formation in both wild-type and perturbed embryos, including the orientation of cell rearrangements. Our work has also revealed the importance of tissue plasticity in stabilizing the chevron pattern. Of course, our model loses some 3D information, particularly the dynamics of cell rearrangements along the ML axis. Such dynamics may play important roles in processes such as muscle fusion, but here we are able to explain the chevron shape of the myotome without explicitly including such ML dynamics.

With our quantitative data, we can critically assess models of chevron formation: 1) The chevron shape is induced by a gradient of mechanical stresses along the AP axis in somites derived from the PSM, rather than a constant AP stress as proposed by ref. 24. However, ref. 24 focused on the first 7 somites to form which are generated simultaneously and do not derive from the PSM (15, 16) so our models are not incompatible. 2) Differential friction between tissues is essential for chevron formation, but the tissue shear flow between the notochord and the developing myotome itself does not directly drive chevron formation (29). Instead, newly formed somites appear to slide across the notochord, with dorsal and ventral tissues adhering more strongly to the somite.

Recent works have shown how anisotropic stresses can generate complex flows within in vitro tissues (55–57), how tissue–tissue friction affects tissue flows during early zebrafish embryogenesis (48), and how rheological properties set the shape of the zebrafish PSM and tailbud (58). Here, we integrate these approaches in a vertex model framework to understand the shaping of a functional organ in terms of the interplay between anisotropic stresses generated by muscle cell differentiation, spatially heterogeneous friction, and tissue plasticity. We include the effect of muscle differentiation as a coarse-grained anisotropic stress. However, our vertex model framework could be useful in future work to study the impact of heterogeneous cell-type differentiation on local stress generation at the cellular level and on the evolution of the spatial organization and morphologies of different cell types within the myotome (SI Appendix, Fig. S9).

It is interesting to compare our model with somite formation in other vertebrate systems, such as the chicken and mouse embryos (59), where somites do not acquire a chevron shape. Our model requires the notochord to be centered to generate the chevron shape. In mouse and chicken embryos the notochord is located toward the ventral somite border. Given such tissue arrangement, we do not expect somites to buckle, even in the presence of differential tissue–tissue frictions (60), and this is consistent with our simulations (SI Appendix, Fig. S11 and Movie S17). Our work suggests that both intertissue interactions and tissue positioning play key roles in shaping the myotome.

SI Appendix

Additional technical aspects of the strains, drug treatment, DNA constructs used in the experiments, and simulation details can be found in SI Appendix.

Data Availability Statement

The data and codes that support the plots within this paper and other findings of this study are available from the corresponding authors upon request.