Pressure-induced topological phase transition in noncentrosymmetric elemental tellurium

Significance

Topological Weyl semimetal, which is a gapless semimetallic phase protected by symmetry, generally appears by band gap closing in noncentrosymmetric semiconductors. So far, there have been only a limited number of reports of such a topological phase transition so that many basic aspects have remained unexplored. Here we report potential signatures of the topological phase transition under pressure in elemental tellurium with noncentrosymmetric chiral crystal structure. Our result represents that elemental tellurium can be one of the model systems for the topological phase transition from a semiconductor to a Weyl semimetal, opening the avenue for studying the topological phase transition by the external field and resultant topological properties.

Abstract

Recent progress in understanding the electronic band topology and emergent topological properties encourage us to reconsider the band structure of well-known materials including elemental substances. Controlling such a band topology by external field is of particular interest from both fundamental and technological viewpoints. Here we report possible signatures of the pressure-induced topological phase transition from a semiconductor to a Weyl semimetal in elemental tellurium probed by transport measurements. Pressure variation of the periods of Shubnikov–de Haas oscillations, as well as oscillation phases, shows an anomaly around the pressure theoretically predicted for topological phase transition. This behavior is consistent with the pressure-induced band deformation and resultant band-crossing effect. Moreover, effective cyclotron mass is reduced toward the critical pressure, potentially reflecting the emergence of massless linear dispersion. The present result paves the way for studying the electronic band topology in well-known compounds and topological phase transition by the external field.

Topological phase of matter is a central issue in recent condensed-matter physics. It is characterized by the nontrivial electronic band topology which causes the emergent electrical, magnetic, and optical properties of solids (1, 2). One of the important topics in this field is the search for the phase control between topologically trivial phase and topologically nontrivial phase. Such a topological phase transition is generally realized by changing the chemical composition of compounds (3–7) or by applying the external field such as the magnetic field, electric field (8), or pressure (9–11). Although it can be directly probed by the angle-resolved photoemission spectroscopy in the former case, optical or transport measurements and comparison with the theoretical calculations are necessary for verifying the topological phase transition induced by external fields.

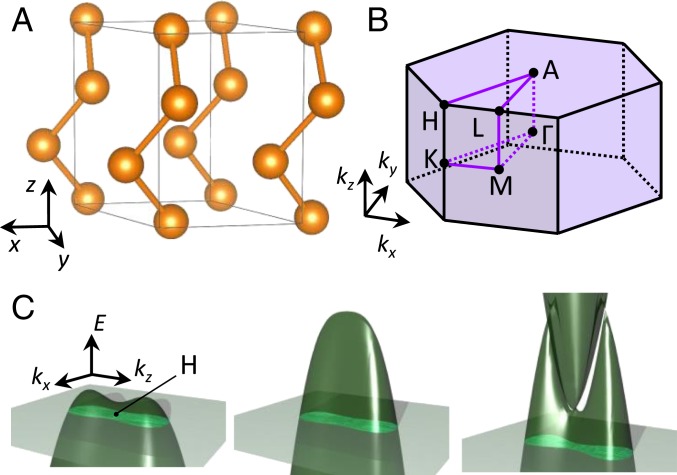
An elemental substance is an ideal platform to study characteristic properties of topological phases and topological phase transition since it has a simple crystal or band structure and we can easily compare it with theoretical calculations (12–17). Since the spin–orbit interaction often plays the key role for the band inversion and the emergence of the topologically nontrivial phase, elemental substance with large spin–orbit interaction can be a potential candidate. For example, topological nature of electronic bands has been discussed in Bi, Sb, and As so far (12–15). Tellurium is also a potential elemental substance with strong spin–orbit interaction. Fig. 1A shows the crystal structure of tellurium. Helical chains along the z axis are arranged via weak van der Waals interaction in a hexagonal array. Depending on the chirality of helical chains, it belongs to the space group P3₁21 or P3₂21. At the ambient pressure, tellurium is a p-type semiconductor in which electronic and optical properties are mainly dominated by the valence and conduction band around the H point in the hexagonal Brillouin zone (Fig. 1B). Previous studies clarified the characteristic camelback-like valence-band dispersion with minimum energy E_c at H point (Fig. 1 C, Left) and that strong spin–orbit interaction should be taken into account to explain the transport and optical properties (18). Observation of the current-induced magnetization due to the chiral structure has been reported (19) and Te is known also as a good thermoelectric material with high figure of merit due to its valley degeneracy and band nesting (20).

Fig. 1.

Pressure-induced band deformation and topological phase transition of elemental tellurium. (A) Crystal structure of Te. Helical chains along the z axis are weakly coupled by van der Waals force. (B) Brillouin zone of Te. Electronic bands around H points are dominant in electronic and optical properties of Te. (C) First-principle calculations of Te band under pressure (P = 0 GPa (Left), P = 1.88 GPa (Middle), and P = 2.62 GPa (Right), respectively) and cross-section of the Fermi surface (shaded region) when the magnetic field is applied perpendicular to the cleavage plane (zx plane). Topological phase transition from a semiconductor to a Weyl semimetal is predicted around P = 2 GPa.

Recently, the topological nature of the Te band has attracted renewed interest due to its noncentrosymmetric crystal structure and strong spin–orbit interaction (21–24). First-principle calculation predicts that elemental tellurium shows the topological phase transition under pressure (24). Under the application of pressure, characteristic camelback-like valence-band dispersion first disappears (Fig. 1 C, Middle), turning into the normal parabolic band dispersion. With increasing the pressure, the band gap continuously shrinks so that the valence band and conduction band finally touch at the points around the H point (Fig. 1 C, Right), leading to the topological transition from a semiconductor to a Weyl semimetal. (In SI Appendix, we show the detailed band evolution under pressure.) In Weyl semimetal phase, band-crossing points (Weyl points) are stable against the perturbation and will not disappear to open the gap (i.e., topologically protected). This argument of topological transition under pressure is consistent with the general discussion for noncentrosymmetric crystals based on the symmetry (25).

In this study, we have probed the pressure variation of the electronic band in elemental tellurium through electric transport, especially focusing on the Shubnikov–de Haas (SdH) oscillations and found the potential signature of the pressure-induced topological phase transition. Periods of SdH oscillations, as well as phases, sensitively change by pressure, reflecting the band deformation under pressure. In a sample with low carrier density, periods of SdH oscillations show an anomalous jump around P = 0.5 GPa, which is consistent with the theoretically predicted pressure-induced Lifshitz transition (SI Appendix). Furthermore, nonmonotonous pressure dependences of SdH oscillation periods and phases have been observed in all samples irrespective of carrier density, which can be well understood by the characteristic Fermi surface deformation and Berry phase change during the topological phase transition. Our result represents that elemental tellurium can be one of the model systems which show the topological phase transition from a semiconductor to a Weyl semimetal. It also implies that oscillations can be a sophisticated probe to detect the band deformation and resultant topological phase transition.

Results and Discussion

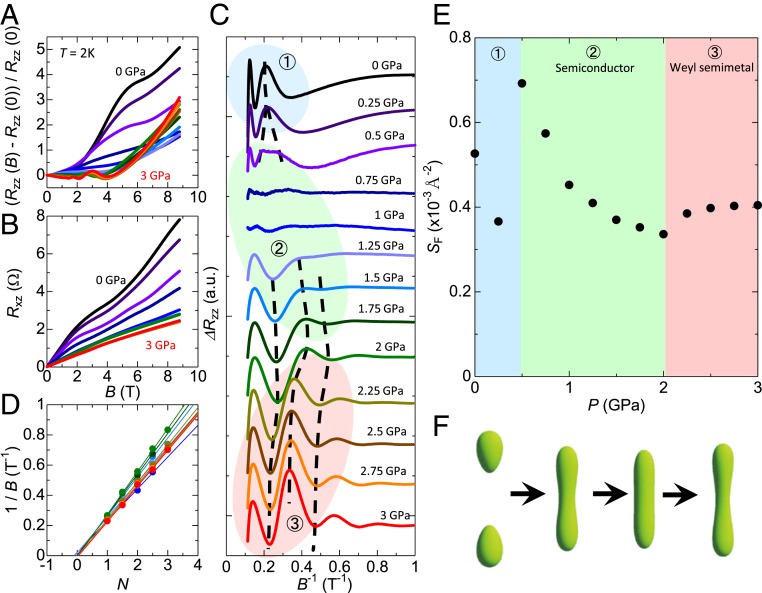
In Fig. 2 A and B, we show the magnetoresistance (R_zz) and Hall effect (R_xz) of sample 1 under various pressures. In this work, we mainly applied the magnetic field perpendicular to the natural growth surface (zx plane) and the current direction is fixed to be the z axis. [We also studied pressure dependence of SdH oscillations in another configuration $\left(B\parallel I\parallel z\right)$ in SI Appendix.] Carrier density $n_{\text{Hall}}$ of sample 1 estimated from the Hall effect is $n_{\text{Hall}}=2.7\times {10}^{16}{\text{cm}}^{-3}$ (Carrier number studied in this work ranges from $n_{\text{Hall}}$ ∼ ${10}^{16}{\text{cm}}^{-3}$ to ${10}^{17}{\text{cm}}^{-3}$.) Clear SdH oscillations have been observed at T = 2K in both R_zz and R_xz, which are apparently dependent on the pressure. Fig. 2C represents the oscillating component of R_zz calculated by subtracting the polynomial function. Maximum and minimum positions are linearly fitted in the index plots (Fig. 2D). In this index plot, we assigned minimum of R_zz as an integer. Cross-sectional areas of the Fermi surface (S_F) are calculated from the periods of the oscillating components (or slopes of index plots) by the following relation and are plotted as a function of the pressure in Fig. 2E:

$$S_{\text{F}}=\frac{2\pi e}{\hslash \mathrm{\Delta }\left(1/B\right)},$$

where $e$, $\hslash$, and $\mathrm{\Delta }\left(1/B\right)$ are electron charge, Planck’s constant, and the period of the oscillation, respectively.

Fig. 2.

SdH oscillations of sample 1 (E_F > E_c). (A and B) Magnetoresistance (A) and Hall effect (B) of sample 1 under various pressures. Clear SdH oscillations have been observed at T = 2K. (C) Oscillating components of the resistance calculated by subtracting the polynomial background from A. (D) Landau index plot of sample 1. We chose the minimum of the resistance as an integer index. (E) Pressure dependence of the cross-sectional area of Fermi surface estimated from the periods of oscillations. S_F shows the anomalous jump around P = 0.5 GPa and upturn at P = 2 GPa. (F) Pressure evolution of the calculated 3D Fermi surface for the sample with E_F = 1 meV at ambient pressure. From the left figure, P = 0 GPa, P = 0.6 GPa, P = 1.22 GPa, and P = 2.16 GPa, respectively.

At the ambient pressure, S_F calculated from the oscillation period is $0.526\times {10}^{-3}\cdot {\mathrm{\AA }}^{-2}$, indicating that Fermi energy of sample 1 locates above the minimum of the camelback-like valence-band dispersion (E_c) (SI Appendix). As we increase the pressure, each peak in oscillations first shows the systematic change (Fig. 2C, region 1) but suddenly splits into 2 peaks around P = 0.5 GPa (Fig. 2C, region 2). At this pressure, S_F estimated from the period of SdH oscillations is almost doubled as shown in Fig. 2E (regions 1 and 2). This split of SdH oscillation and anomalous jump of S_F is considered to be the signature of pressure-induced Lifshitz transition. As predicted by calculations (Fig. 1C), characteristic camelback-like valence-band dispersion disappears under pressure. Fermi level of sample 1, first locating above the minimum of the camelback-like valence-band dispersion (E_c), can pass through the E_c during the systematic pressure-induced band deformation, which causes the Fermi surface topology change and resultant Lifshitz transition. In Fig. 2F, we show the pressure variations of the calculated 3D Fermi surface in which Lifshitz transition is illustrated in the first step.

After this Lifshitz transition, SdH oscillations again show the systematic change with pressure, showing another anomaly around P = 2 GPa (Fig. 2E); when the pressure is below 2 GPa, S_F decreases with pressure (region 2) while it turns upward above P = 2 GPa (region 3). This anomaly is considered to be caused by the band touching predicted by calculations. Before the band touching occurs, Fermi surface is becoming more 3D-like and isotropic by applying the pressure so that the Fermi surface is elongated along the k_x and k_y direction while it shrinks along the k_z direction. Therefore, cross-sectional area of the Fermi surface perpendicular to the magnetic field (k_z-k_x plane) decreases, mainly reflecting the elongation along the k_y direction (second and third schematics in Fig. 2F). On the other hand, once the conduction band and valence band touch, the shape of the Fermi surface becomes anisotropic again since the original conduction-band minimum keeps decreasing under pressure and causes the deformation of the Fermi surface as it gets close to the Fermi energy (second and third schematics in Fig. 1C and third and fourth schematics in Fig. 2F). Thus, the anomaly of S_F around P = 2 GPa represents the band touching and can be the potential signature of the topological phase transition from a semiconductor to a Weyl semimetal.

We note that the Hall coefficient is also affected by the pressure in sample 1 (Fig. 2B), which indicates the carrier increase under pressure. It might be because carriers trapped by the defect levels are released under pressure, causing the increase of the carrier density toward P = 2 GPa (Fig. 2B). However, the increase of the carrier density cannot explain the observed decrease of S_F below P = 2 GPa so that pressure dependence of S_F does not come from the carrier density change but can be mainly attributed to the pressure-induced band deformation. It is also noted that the Hall coefficient is almost unchanged above 2 GPa. In SI Appendix, we discuss the phase of SdH oscillations (or intercept of the index plot), which show the cross-over behavior from P < 2GPa to P > 2GPa, offering the important insight into the change of the band dispersion or Berry phase originating from spin texture (26–32).

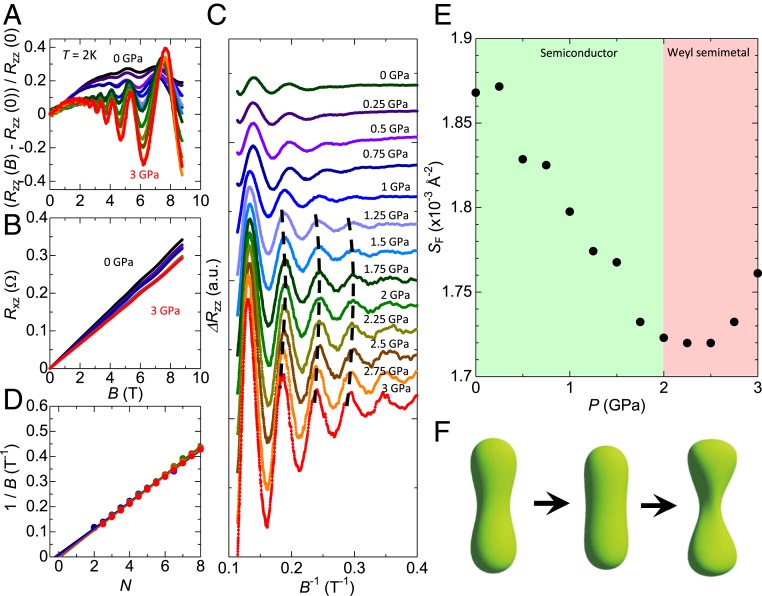
We also studied the samples with different Fermi energies at the ambient pressure. Fig. 3 A–F show R_zz (A), R_xz (B), oscillating components of R_zz (C), index plot (D) under various pressures, and pressure dependence of S_F (E), and calculated 3D Fermi surface (F) for sample 2. Carrier density $n_{\text{Hall}}$ of sample 2 estimated from the Hall effect is $n_{\text{Hall}}=4.1\times {10}^{17}{\text{cm}}^{-3}$. According to the oscillation period, the Fermi level of sample 2 is estimated to locate below E_c at the ambient pressure (SI Appendix). Differently from sample 1, S_F does not show an anomalous jump around P = 0.5 GPa (Fig. 3E). This means there is no pressure-induced Lifshitz transition in sample 2, being consistent with E_F < E_c. Nevertheless, pressure dependence of S_F still shows the upturn around P = 2 GPa (Fig. 3E) similarly to sample 1, indicating that possible signature of the topological phase transition from a semiconductor to a Weyl semimetal (Fig. 3F) is successfully probed also in sample 2. We have confirmed that similar behavior can be observed in the other 2 samples with Fermi energy below E_c at the ambient pressure (sample 3 and sample 4; see SI Appendix). Intercept $\delta$ in the index plot shows cross-over behavior around P = 2 GPa also in sample 2, corroborating the above scenario of possible topological phase transition (SI Appendix).

Fig. 3.

SdH oscillations of sample 2 (E_F < E_c). (A and B) Magnetoresistance (A) and Hall effect (B) of sample 2 at T = 2K under various pressure. (C) Oscillating components of the resistance. (D) Landau index plot of sample 2. (E) Pressure dependence of the cross-sectional area of Fermi surface estimated from the periods of oscillations. S_F shows the anomaly around P = 2 GPa similarly to sample 1 (Fig. 2E). (F) Pressure evolution of the calculated 3D Fermi surface for the sample with E_F = 5 meV at ambient pressure. From the left figure, P = 0 GPa, P = 1.22 GPa, and P = 2.62 GPa, respectively.

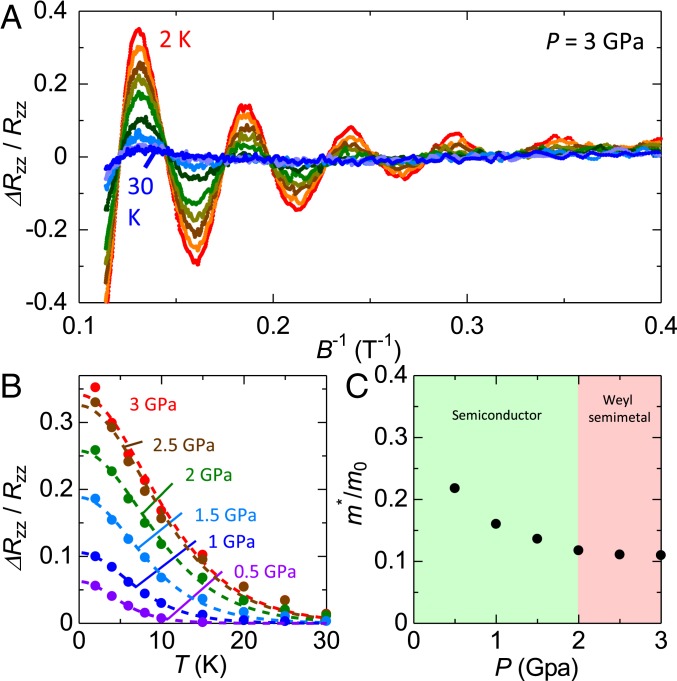
Finally, we discuss the pressure variation of the effective mass of sample 2. In Fig. 4A, oscillating components of sample 2 under P = 3 GPa at various temperatures are displayed. Magnitude of the oscillations decreases with increasing the temperature, which is plotted in Fig. 4B. According to the following Lifshitz–Kosevich formula for a 3D system (33), we can estimate the effective mass $m^{\ast }$ from the temperature dependence of the oscillation amplitude $\mathrm{\Delta }{R}_{zz}/R_{zz}$,

$$\mathrm{\Delta }{R}_{zz}/R_{zz}\propto {\left(\hslash {\omega }_{\text{C}}/2E_{\text{F}}\right)}^{1/2}\text{exp}\left(-2{\pi }^2{k}_{\text{B}}{T}_{\text{D}}/\hslash {\omega }_{\text{C}}\right)\frac{2{\pi }^2{k}_{\text{B}}T/\hslash {\omega }_{\text{C}}}{\sinh \left(2{\pi }^2{k}_{\text{B}}T/\hslash {\omega }_{\text{C}}\right)}.$$

Here, $k_{\text{B}}$, $T_{\text{D}}$, and ${\omega }_{\text{C}}$ are Boltzmann’s constant, Dingle temperature, and cyclotron frequency ${\omega }_{\text{C}}=\frac{eB}{m^{\ast }\hspace{0.17em}}$, respectively. We calculate the effective mass at each pressure from the temperature dependence of $\mathrm{\Delta }{R}_{zz}/R_{zz}$ (Fig. 4B) and plot values normalized by free-electron mass $m_0$ as a function of the pressure in Fig. 4C. Effective cyclotron mass is reduced by applying the pressure, reflecting the transition from massive band dispersion at the ambient pressure to the massless linear band dispersion in Weyl semimetal phase. Pressure variation of $m^{\ast }$ is settled around P = 2 GPa similarly to $\delta$, which almost coincides with the anomaly point of S_F, possibly because that band deformation is suppressed after the topological phase transition. From the fitting of temperature variation of SdH oscillations by the Lifshitz–Kosevich formula, we also obtained the Fermi velocity $v_{\text{F}}=4.0\times {10}^4$ m/s and quantum lifetime ${\tau }_{\text{Q}}=1.4\times {10}^{-13}$ s at P = 3 GPa. Transport lifetime defined by ${\tau }_{\text{transport}}=\mu \hslash k_{\text{F}}/e{v}_{\text{F}}$ is estimated as ${\tau }_{\text{transport}}=8.5\times {10}^{-13}$ s, which is an order of magnitude larger than ${\tau }_{\text{Q}}$. It is noted that ${\tau }_{\text{transport}}$ is generally larger than ${\tau }_{\text{Q}}$, since ${\tau }_{\text{transport}}$ measures the backscattering process that relaxes the current while ${\tau }_{\text{Q}}$ is sensitive to all processes that cause Landau level broadening (31).

Fig. 4.

Pressure variation of the effective mass. (A) Oscillating component of sample 2 under P = 3 GPa at various temperatures. (B) Temperature dependence of amplitude of SdH oscillations under various pressures. Dashed line represents the fitting by the Lifshitz–Kosevich formula. (C) Pressure variation of the effective mass $m^{\ast }$ normalized by free-electron mass $m_0$. $m^{\ast }$ decreases with pressure, showing the convergent behavior toward P = 2 Gpa.

In conclusion, we have successfully probed the potential signature of the pressure-induced topological phase transition from a semiconductor to a Weyl semimetal in elemental tellurium. Present results indicate that electric transport including SdH oscillations is a powerful probe to detect the topological phase transition, especially under external field such as the pressure. In view of rich variety of materials whose topological nature is not fully unveiled, our findings will open the way to rediscover the topologically nontrivial band and topological phase transition in well-known materials.

Materials and Methods

Sample Preparations.

Single crystals of Te were prepared by a physical vapor transport technique. Elemental Te (6N) grains of ∼0.5 g were sealed in an evacuated quartz tube (∼φ11 mm × φ9 mm × 120 mm), and the ampule was put in a 2-heating-zone tube furnace (34). Temperatures at the source (Te grains) and the growth zone were set to 450 and 360 °C, respectively. After ∼70 h, single crystals of Te with ∼3-mm length having a hexagonal prism shape as similar to a quartz crystal were obtained.

Transport Measurements.

Resistivity and Hall effect have been measured with the use of a physical property measurement system (Quantum Design, Inc.). Hydrostatic pressure is applied by using a piston-cylinder pressure cell and Daphne 7474 (pressure-transmitting medium). We applied the magnetic field perpendicular to the natural growth surface (zx plane) and current direction is parallel to the z axis.

First-Principle Calculation.

Our calculations are based on the density-function theory in the local density approximation. We calculate the fully relativistic electronic structure by a first-principles code QMAS (Quantum MAterials Simulator) based on the projector augmented-wave method. The plane-wave energy cutoff is set to 40 Ry, and the 6 × 6 × 6 k mesh is employed. We evaluate the self-energy correction in the GW approximation (GWA) (35, 36) using the full-potential linear muffin-tin orbital code (37, 38). In the GWA, we neglect the spin–orbit interaction. The 6 × 6 × 6 k mesh is sampled and 51 × 2 unoccupied conduction bands are included, where ×2 is the spin degrees of freedom. We construct 9 × 2 maximally localized Wannier functions (MLWFs) originating from the 5p orbitals and diagonalize the fully relativistic Hamiltonian with the GW self-energy correction expressed in the MLWF basis. Experimental structures for the trigonal phase are used in the present study. At pressures between available experimental data, we determine the Hamiltonian in the MLWF basis by linear interpolation.

Data Availability.

The data that support the plots within this paper are available in Datasets S1–S24.