Supraglacial lake drainage at a fast-flowing Greenlandic outlet glacier

Significance

We present in situ records of a rapidly draining supraglacial lake in a fast-flowing sector of the Greenland Ice Sheet. Despite supraglacial lake drainage influencing ice sheet dynamics at a variety of scales, existing in situ studies have been conducted exclusively at the slower, less dynamic land-terminating sector. We describe the scale and extent of dynamic response in a marine-terminating system, and identify 1) spatially distributed behavior not previously observed in in situ studies, and 2) interannual variation unique to fast-flowing glaciers. We propose that many lakes thought to drain slowly are, in fact, draining rapidly via hydrofracture. As such, rapid drainage events, and their net impact on ice sheet dynamics, are being notably underestimated.

Abstract

Supraglacial lake drainage events influence Greenland Ice Sheet dynamics on hourly to interannual timescales. However, direct observations are rare, and, to date, no in situ studies exist from fast-flowing sectors of the ice sheet. Here, we present observations of a rapid lake drainage event at Store Glacier, west Greenland, in 2018. The drainage event transported 4.8 $\times$ 10⁶ m³ of meltwater to the glacier bed in $\sim$5 h, reducing the lake to a third of its original volume. During drainage, the local ice surface rose by 0.55 m, and surface velocity increased from 2.0 m$\cdot$d⁻¹ to 5.3 m$\cdot$d⁻¹. Dynamic responses were greatest $\sim$4 km downstream from the lake, which we interpret as an area of transient water storage constrained by basal topography. Drainage initiated, without any precursory trigger, when the lake expanded and reactivated a preexisting fracture that had been responsible for a drainage event 1 y earlier. Since formation, this fracture had advected $\sim$500 m from the lake’s deepest point, meaning the lake did not fully drain. Partial drainage events have previously been assumed to occur slowly via lake overtopping, with a comparatively small dynamic influence. In contrast, our findings show that partial drainage events can be caused by hydrofracture, producing new hydrological connections that continue to concentrate the supply of surface meltwater to the bed of the ice sheet throughout the melt season. Our findings therefore indicate that the quantity and resultant dynamic influence of rapid lake drainages are likely being underestimated.

Variation in the rate of meltwater input into the subglacial system of the Greenland Ice Sheet forces dynamic responses at a range of scales, from hourly (1–3) to seasonal (4–6) and longer (7, 8). A notable source of meltwater delivery is via rapid supraglacial lake drainages, whereby lakes drain to the bed of a glacier or ice sheet in the space of a few hours. The large volume of water delivered rapidly to the bed during drainage results in hydraulic ice–bed separation, which is expressed at the surface as decimeter-scale ice uplift (2, 9, 10). These evacuations induce short-term ice flow accelerations via a reduction in basal traction (1, 2, 11), modifying the seasonal efficiency of the subglacial system (5, 12, 13), and opening new surface-to-bed connections (14) that can then continue to deliver meltwater to the bed (15). Since the advent of satellite records in the 1970s, supraglacial lakes have formed in greater numbers, at higher elevations, and at larger sizes in response to warmer summers (16–18). However, the net effect of an increasing meltwater supply on the dynamics of the Greenland Ice Sheet is the subject of ongoing debate (7, 8, 19–21).

Satellite observations show that 28 to 45% of all supraglacial lakes in west Greenland drain rapidly (17, 18), although multiyear studies indicate that even lakes that exhibit rapid drainage behavior do so in fewer than half of years (22, 23). Rapid drainage occurs when water opens a surface-to-bed connection via hydraulic fracture (1–3). However, the exact timing of hydrofracture is seemingly stochastic, with studies failing to support the hypothesis that the drainage of lakes can be explained by any critical thresholds relating to lake hydrology (depth, volume, or morphology), glaciological setting (hypsometry, velocity, or strain) or meteorological conditions (17, 24). Lakes often drain in clusters (17) because the transfer of water to the base of the ice sheet when one lake drains increases the tensile stresses near other lakes, triggering further hydrofractures (25). Recent research has hypothesized that most lakes drain in these cascading events (25) and that preexisting weaknesses in the ice may play a role (3, 24). However, field studies capturing rapid drainage are limited and have previously only been conducted on slow-flowing ($\sim$100 m$\cdot$y⁻¹), land-terminating regions of the ice sheet (1–3, 11, 26). It is unclear to what extent knowledge of subglacial hydrology at land-terminating margins may be applied to fast-flowing marine-terminating systems (27) where supraglacial lakes are equally numerous (18, 24).

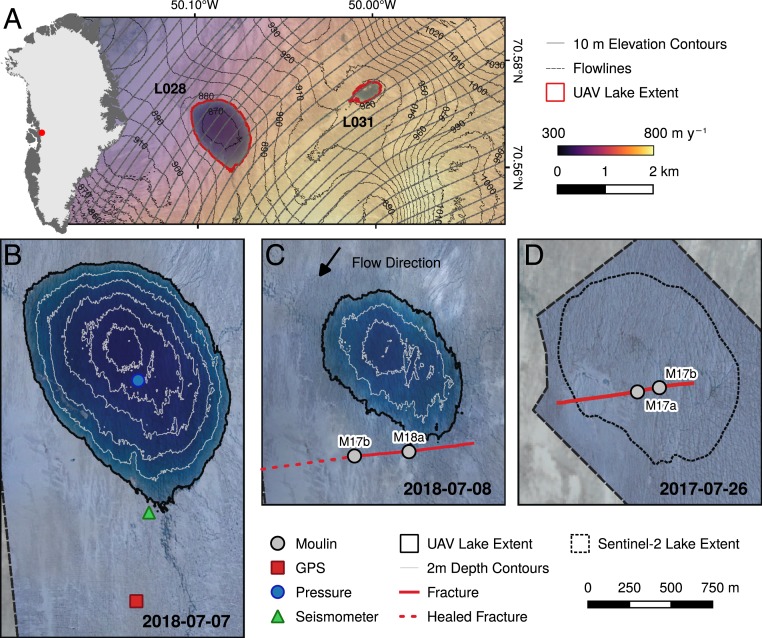
Here, we present field measurements of the rapid drainage of the supraglacial lake “Lake 028” (70.57°N, 50.08°W; Fig. 1) located $\sim$30 km from the marine terminus of Store Glacier (Qarassap Sermia) in west Greenland, at a site where annual ice flow averages $\sim$600 m$\cdot$y⁻¹. We combine data from repeat unmanned aerial vehicle (UAV) photogrammetry with in situ geophysical observations from pressure transducer, dual-frequency GPS, and seismometers. The addition of high-resolution photogrammetry data allows the spatial distribution of dynamic response to be assessed, and aids detailed structural interpretation of the drainage event. We present observations at high spatial and temporal resolutions, describe the lake drainage mechanism, interpret the dynamic effects and structural history of the lake drainage, and discuss the larger-scale significance of the observed mode of lake drainage.

Fig. 1.

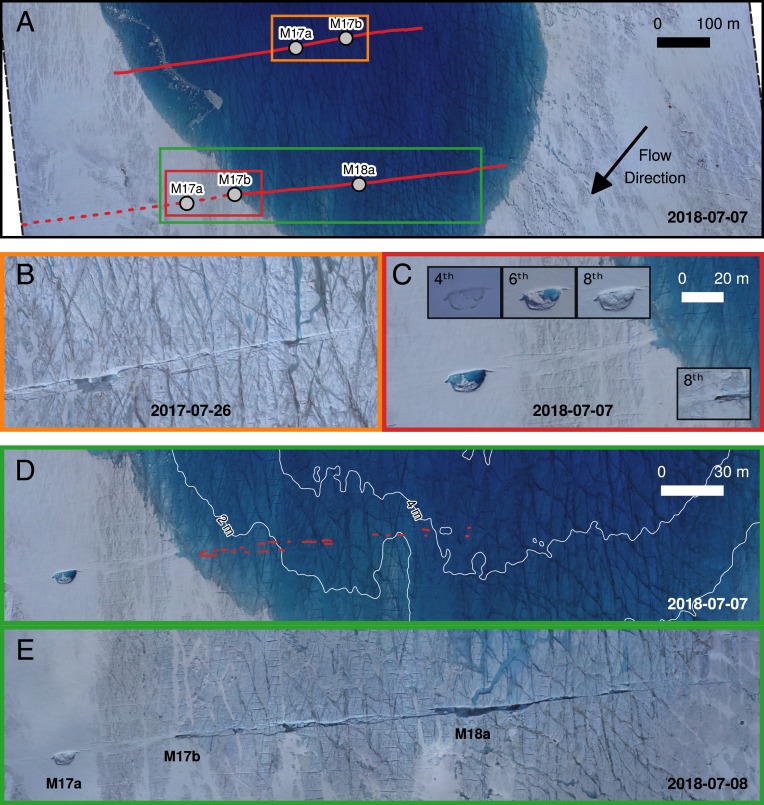
(A) Location of Lake 028 and Lake 031 (red outlines). Sentinel-2 image from 2018-07-07 overlaid with the MEaSUREs 2017 velocity dataset (28) and contour lines from ArcticDEM (29) (Inset is location of Store Glacier in Greenland). (B) Lake 028 on 2018-07-07, $\sim$5 h prior to the onset of drainage, with instrument locations highlighted. (C) Lake 028 on the 2018-07-08 $\sim$4 h after peak drainage, with $\sim$1-km-long fracture marked with solid red line, and moulins marked as gray dots. Dashed red line marks the location of the healed 2017 crevasse in 2018. (D) Bed of fully drained Lake 028 on 2017-07-26, with maximum observed lake margin (from 2017-06-26) outlined with short-dashed black line. Location of the main drainage fracture (red line) is marked, and moulins marked as gray dots.

Results

The 2018 Lake Drainage Event.

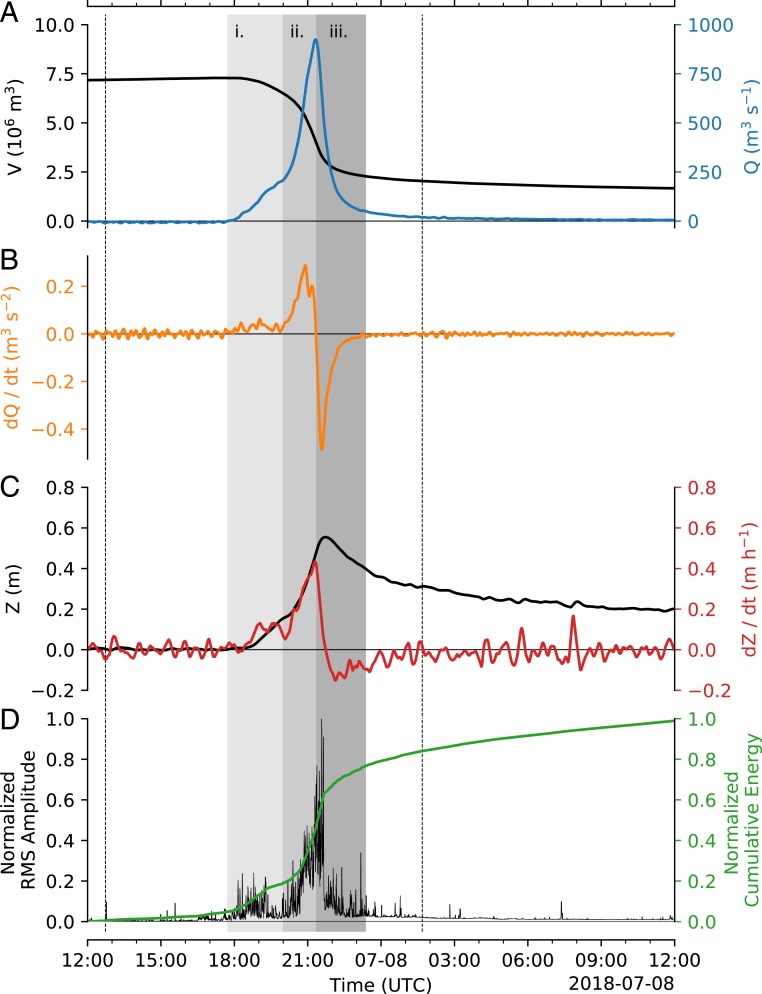
Records from a pressure transducer installed at the bed of Lake 028 on 2018-07-04 were converted into time series of volume and discharge (Fig. 2 A and B) using lake bathymetry derived from UAV photogrammetry (SI Appendix, SI Text). These data indicate that, in the 3 d prior to drainage, the volume of Lake 028 was increasing at a rate between 1 and 10 m³ s⁻¹. At its maximum extent on 2018-07-07, Lake 028 was 1.25 km² in area, 7.3 $\times$ 10⁶ m³ in volume, and fed by 3 supraglacial streams. A single outflow channel emerged at the southern lakeshore (Fig. 1B). The lake reached its maximum size immediately prior to drainage, which began on 2018-07-07 1742 coordinated universal time (UTC) (Fig. 2A). Rapid discharge (defined following ref. 2 as >50 m³ s⁻¹) initiated at 1832 UTC, accelerated notably at ∼1958 UTC (Fig. 2B), and reached its peak (924 m³ s⁻¹) at 2120 UTC. After this, discharge decayed exponentially; 2322 UTC marked the end of rapid (Q > 50 m³ s⁻¹) drainage, which lasted $\sim$5 h in total. Lake volume continued to decline for the remainder of the record as flow into the moulin continued: at 2018-07-08 0000 UTC, the lake volume was 2.2 × 10⁶ m³, but, by 2018-07-24 1800 UTC, it was 3.1 × 10⁵ m³. A small ($\sim$200-m diameter) lake was still present in Sentinel-2 imagery by the end of the ablation season, and had frozen over by November 2018.

Fig. 2.

Time series of (A) lake volume (V) and discharge (Q); (B) rate of change of discharge (dQ/dt); (C) surface uplift (Z) and rate of uplift (dZ/dt); and (D) normalized rms (RMS) seismic amplitude, and normalized cumulative energy at Lake 028. Dashed lines at 1245 UTC and 0140 UTC mark the timing of preflight and postflight drainage UAV surveys shown in Fig. 1 B and C. Shading marks the 3 phases of rapid drainage outlined in the discussion. A version of this figure cropped to the time of rapid discharge is available as part of Movie S1.

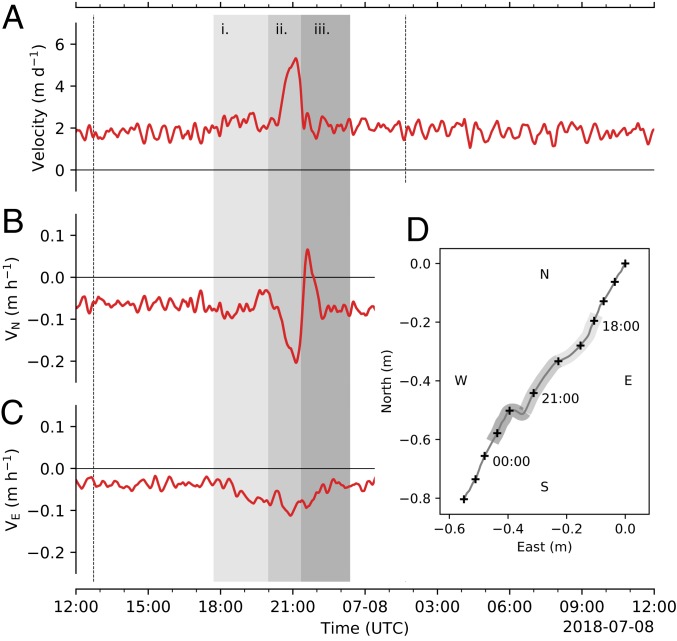
In addition to discharge measurements, we recorded ice uplift (Fig. 2C), seismic activity (Fig. 2D), and horizontal ice velocity (Fig. 3) using a GPS and seismometer located to the south of the lake (Fig. 1B). At ∼1830 UTC, coincident with the start of rapid (Q > 50 m³ s⁻¹) drainage, ice uplift initiated at a rate of $\sim$0.1 m$\cdot$h⁻¹. This rate increased, in tandem with discharge, to a maximum rate of $\sim$0.4 m$\cdot$h⁻¹ at 2117 (contemporaneous with maximum discharge). Peak surface uplift of 0.55 m occurred at 2143 UTC. Subsequently, the ice surface did not return to a predrainage elevation, instead settling $\sim$0.2 m above predrainage levels (Fig. 2C) for the rest of the summer melt season. Trends in seismic data are consistent with those in discharge and surface uplift records. Following low-level (0 to 0.2 normalized rms amplitude) activity in the initial drainage period, activity accelerated rapidly after 1958 UTC, reaching a maximum amplitude at 2134 UTC (coincident with maximum deceleration in discharge), at which point seismic activity returned abruptly to levels of <0.3 for the remainder of the drainage period. Ice velocity was relatively consistent until 2020 UTC, at which point rapid acceleration was observed, from a background velocity of $\sim$2.0 m$\cdot$d⁻¹ to a peak of 5.33 m$\cdot$d⁻¹ at 2107 UTC (Fig. 3A). Termination of the event was equally rapid, and, by 2127 UTC, velocities had returned to normal levels. However, this resultant velocity hides anomalous directional movement (Fig. 3 B–D). In the early stage of drainage (prior to the step accelerations observed in other data at $\sim$2000 UTC), the ice velocity trended in a westward direction (parallel with fracture orientation), unaccompanied by any significant change in magnitude. Coincident with the period of most rapid drainage, an anomalous southward displacement initiated (perpendicularly away from the fracture), peaking at a rate of 0.2 m$\cdot$h⁻¹ at 2107 UTC. Following this, a sharp northward anomaly occurred at 2136 UTC, coincident with maximum negative discharge rate and peak seismic activity.

Fig. 3.

Time series of location data obtained from GPS instrumentation located $\sim$750 m downflow of Lake 028 (Fig. 1B), including (A) resultant horizontal velocity and the (B) northerly (V_N) and (C) easterly (V_E) components of velocity, together with (D) mapped horizontal displacement between 2018-07-07 1500 UTC and 2018-07-08 0200 UTC, with hourly locations marked with crosses. Dashed lines at 1245 UTC and 0140 UTC mark the timing of preflight and postflight drainage UAV surveys shown in Fig. 1 B and C. Shading marks the 3 phases of rapid drainage outlined in the discussion.

Spatially Distributed Uplift and Ice Flow Dynamics.

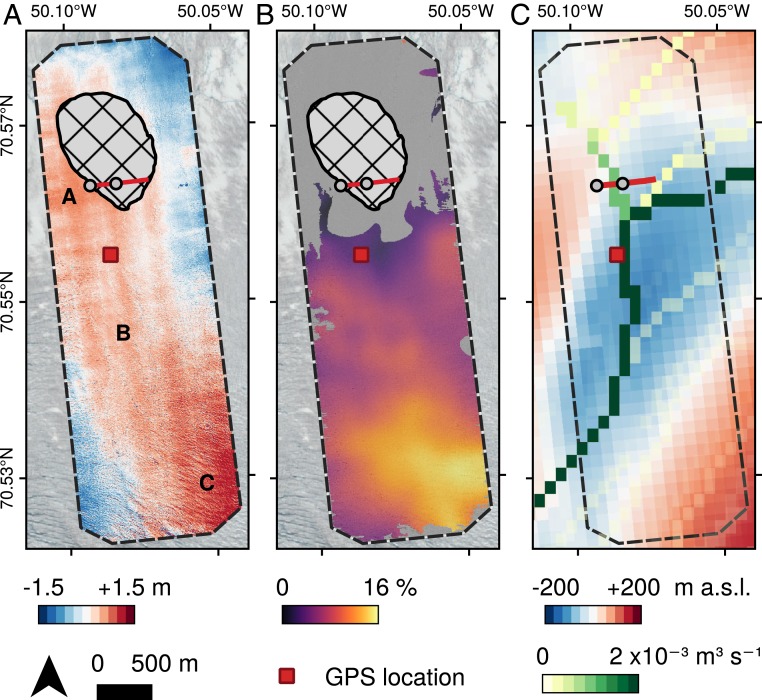
Repeat UAV photogrammetry captured at approximately daily intervals before and after the lake drainage event (SI Appendix, Table S1) provides records of the spatial distribution of the ice sheet’s response to drainage in the region surrounding Lake 028 (SI Appendix, Table S1). An immediate postdrainage survey at 2018-07-08 0145 UTC—$\sim$2 h after the termination of rapid drainage—allows us to map drainage-induced uplift (Fig. 4A). We identify 3 distinct regions of uplift. The first major region of uplift (region A) was located surrounding the fracture, on the southwest side of the lake basin. A second major region of uplift (region C) was located at a distal site 4 km south-southeast of the fracture. They are linked by a region of lower-magnitude uplift (region B).

Fig. 4.

(A) Absolute uplift postdrainage at 2018-07-08 0144 UTC relative to 2018-07-06 1639 UTC control, with regions A, B, and C, referred to in the text, labeled. (B) Relative acceleration over the period 2018-07-06 to 2018-07-09 relative to 2018-07-18 to 2018-07-24 control. The gray region marks area of insignificant change based on estimated uncertainty (see Materials and Methods). (C) Modeled water routing, showing contours of discharge following an input of water to the system; m.a.s.l., meters above sea level.

Velocity fields are derived from repeat UAV surveys. We compare 2 velocity fields, one over the lake drainage period (2018-07-06 to 2018-07-09) and one from a late-season control period (2018-07-18 to 2018-07-24) to highlight regions of anomalous ice velocity during drainage (Fig. 4B). These data show that the short-term (on a scale of hours) acceleration observed in the immediate vicinity of Lake 028 (Fig. 3C) is not visible on a multiday timescale. In contrast, considerable acceleration was observed at the distal site (region C), where ice velocity increased by up to 15% relative to the late-season control period. This suggests that ice velocity here was persistently elevated through the observation period, compared to only short-term acceleration around the lake site itself. This distal region also corresponds to an area of uplift in the elevation difference data.

Inception and Propagation of Fractures.

The 2018 fracture was a direct continuation of a fracture formed during the complete rapid drainage of Lake 028 in 2017 (Fig. 1D). Two notable moulins occurred along the 2017 fracture (Fig. 5B): one larger (M17a in Fig. 5A) and one smaller (M17b in Fig. 5A), the latter of which became the dominant drainage moulin for the rest of the 2017 season. By 2018, this preexisting fracture had advected $\sim$500 m southwest (Fig. 5 A and C), and both moulins, as well as the fracture, had closed. Between 2018-07-04 and 2018-07-06, Lake 028 overtopped and began filling M17a (Fig. 5 C, Top Left Inset). By the 2018 drainage event, the maximum extent of Lake 028 was coincident with the location of M17b (Fig. 5C); postdrainage, this moulin showed evidence of reactivation, as it was no longer water-filled (Fig. 5 C, Bottom Right Inset). M17a must also have been reactivated, as it was empty of water post drainage (Fig. 5 C, Top Left Inset).

Fig. 5.

UAV orthophotos of Lake 028 identifying key geomorphological features. (A) Locations of the main drainage fracture (red lines) in 2017 (top) and 2018 (bottom) are marked, along with associated moulins. Dashed red line marks the location of the healed 2017 crevasse in 2018. Colored boxes indicate locations of B–E. (B) The 2017 crevasse and associated moulins 17a and 17b in 2017. (C) The 2017 crevasse and associated moulins on 2018-07-07 immediately prior to drainage. Insets show moulin 17a on 2018-07-04, 2018-07-06, and 2018-07-08 (top left) and moulin 18a on 2018-07-08 after drainage (bottom right). (D) Region of Lake 028 subsequently fractured on 2018-07-07, prior to drainage; 2-m-depth contours are marked in white, and crevasses exploited during drainage are in red. (E) Fracture of Lake 028 on 2018-07-08.

Extending from M17b, the western extent of the 2018 fracture was dominated by uneven edges and grabens (Fig. 5E). This section of the lake bed is also a region where a number of smaller, preexisting surface crevasses occur (on the order of 10 m long and 0.5 m wide). The edges of the western extent of the 2018 fracture can be matched directly to these preexisting crevasses (red lines in Fig. 5D), suggesting that the crevasses were exploited during drainage to form the larger fracture. The eastern extent of the 2018 fracture was typified by clean, linear fracturing (Fig. 5E), an appearance distinct from the western extent.

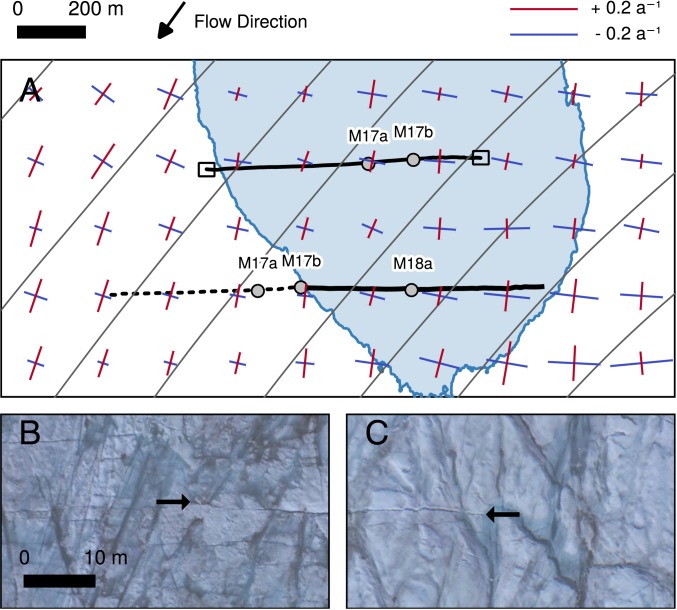
The orientation of the fractures in both years was at $\sim 45^{○}$ to the direction of flow. Comparing this orientation to principal strain rates (Fig. 6A) shows that the fractures occurred perpendicular to the direction of first principal strain, indicating that the drainage fracture is a mode I extensional fracture. In 2017, there were no obvious closed moulins or healed fractures to exploit. Instead, the fracture most likely initiated at its western edge, where numerous small surface crevasses occur, due to the extensional strain regime (Fig. 6B), that could be exploited by hydrofracture. This hydrofracture could then propagate into the compressive lake basin due to inflow of water, first from the supraglacial stream network along the western lake shore and, ultimately, from the lake itself, leading to full column penetration by hydrofracture. The compressional strain regime on the northeastern (i.e., upflow) side of the lake (Fig. 6A), evidenced by a lack of crevasses in the area (Fig. 6C), is likely to have limited the eastern extent of the hydrofracture in both 2017 and 2018.

Fig. 6.

(A) Surface principal strain rates (red and blue lines) derived from 2017 annual MEaSUREs velocity data (28). The 2018-07-08 maximum lake area is marked in blue, and flowlines are marked in gray. Black lines define the drainage fracture in 2017 (top) and 2018 (bottom), with the dotted line showing the location of the healed 2017 crevasse in 2018. Black boxes, from left to right, mark locations of UAV orthophotos in B, showing presence of crevasses surrounding western edge of fracture, and C, showing lack of crevasses around eastern edge of fracture. Black arrows identify the fracture limit.

Discussion

Lake Drainage Mechanism.

Observational evidence suggests that the drainage of Lake 028 in July 2018 initiated via the refilling of a closed moulin formed during the 2017 lake drainage, and subsequent reactivation of the 2017 hydrofracture. Between UAV surveys on 2018-07-05 (0200 UTC) and 2018-07-06 (1640 UTC), Lake 028’s shoreline reached the location of the former moulin M17b. At this point, neither M17a nor M17b was open, as evidenced by the filling of moulin M17a between 2018-07-06 (1640 UTC) and 2018-07-07 (1245 UT) (Fig. 5 C, Top Right and Top Middle Insets). In the hours prior to rapid drainage, minor seismic activity began (Fig. 2D), indicative of the episodic hydromechanical reopening of the moulins. In the postdrainage survey (2018-07-09 1615 UTC), these moulins were empty (Fig. 5 C, Top Right and Bottom Insets), indicating that they had connected hydraulically, most likely to the glacier’s bed, during the drainage event. Lake drainages have previously been proposed to exploit preexisting moulins (2, 3). Evidence suggests that water entering the subglacial system through preexisting moulins can trigger hydrofracture by inducing localized acceleration and hence a transient extensional flow regime in a “precursor” event (3, 30). However, there is no evidence of precursory acceleration or surface-to-bed connection at Lake 028. Furthermore, there is no evidence of any precursory uplift indicating a triggering upstream drainage event (2, 25). We suggest that high background tensile stresses were likely sufficient for a surface-to-bed connection to commence as soon as the lake overtopped the preexisting moulin. Taking the previously studied Lake F (2) as a contrasting example, first principal strains (SI Appendix, Fig. S1) are an order of magnitude lower than at Lake 028 (Fig. 6A), and are not clearly aligned with fracture direction, suggesting that background stresses do not exert a strong control in slow-flowing regions. This observation sheds light on the proposition that supraglacial lakes can drain in a “cascading” chain reaction (25). While this mechanism may explain how hydrofracture in low-stress regimes can occur in response to upstream drainage, there is still no explanation for the triggering of the upstream events themselves. We propose that lakes like Lake 028 can act as “trigger lakes,” that is, situated in stress regimes where the simple intersection of an expanding lake with a preexisting moulin is enough to trigger hydrofracture. In contrast, lakes from previous in situ studies may be considered “response lakes,” that is, lakes which require a precursory event in order to drain.

Following drainage initiation, we interpret geophysical activity as representing 3 clear phases (2): phase i (1742 UT to 1958 UTC), drainage onset; phase ii (1958 UTC to 2122 UTC), fracture opening; and phase iii (2122 UTC to 2322 UTC), fracture closing (these phases are highlighted in Figs. 2 and 3). Phase i began with the initiation of drainage at 1742 UTC. It was characterized by discharge, uplift, acceleration, and seismic activity that was relatively low compared to later drainage. We suggest that, in phase i, water was delivered to the bed exclusively through the reactivated M17b, and discharge rates increased via the mechanical or thermal erosion of the moulin and the remnant 2017 fracture. This mechanism would explain the distinctive morphology of the western extent of the 2018 fracture, characterized by the exploitation of preexisting crevasses to form distinctive graben structures (Fig. 5E).

Phase ii of Lake 028’s drainage began at 1958 UTC with a step increase in discharge (Fig. 2 A and B). A sudden and rapid southward ice displacement is visible in the GPS record at this time (Fig. 3B). Given the GPS location 900 m south of the east–west oriented fracture, we interpret this as strong evidence of mechanical fracture opening (2). We interpret the clean, linear fracturing distinctive of the eastern half of the 2018 fracture (Fig. 5E) as indicating that the fracture propagated via hydrofracture rather than by mechanical or thermal erosion. This hydrofracture mode began once the fracture propagated into depths greater than 4 m (Fig. 5D). As such, this depth likely represents the point at which—in this particular setting—hydrostatic pressure was sufficient to initiate full-column hydrofracture. The westernmost extent of the new hydrofracture was also coincident with the location of M18a, suggesting that hydrofracture initiation allowed M18a to connect to the bed. The formation of M18a at this point would have coincided with, and thus explains, the dramatically increased water discharge from Lake 028 at the beginning of phase ii (Fig. 2A). This inference is supported by a marked increase in the intensity of seismic activity in this period (Fig. 2D), as well as peak horizontal velocity, likely forced by hydraulic jacking. Phase ii terminated at the point of peak discharge (Fig. 2A), which was coincident with the beginning of fracture closure as indicated by the GPS data (Fig. 3B).

Phase iii is defined from the beginning of negative dQ/dt at 2122 UTC. Throughout this period, decreasing discharge was observed: 14 min into the period, at 2134 UTC, maximum deceleration in discharge occurred (Fig. 2B). This timing coincided with a maximum in seismic activity, and, 3 min later (2137 UTC), the northward anomaly in the GPS record reached a maximum (the northward anomaly occurred from 2128 UTC to 2214 UTC). We interpret these closely spaced events as strong evidence of rapid fracture closure occurring in this period. This period of lake drainage was captured with 10-s time-lapse photography from a location to the southeast of the lake (Movie S1). This footage shows that early phase iii, when discharge declined most rapidly ($\sim$2130 UTC to 2215 UTC), occurred simultaneously with the lake level dropping beneath that of the fracture. At this point, a plume of water vapor developed at the fracture mouth as the fracture transitioned from being fully water-filled to a water–air mix. When the fracture was filled to the surface, water pressure exceeded ice overburden pressure and allowed the fracture to remain open. As water content in the fracture reduced, water pressure also lowered and led to fracture closure, lower water inputs, and the subsequent cessation of uplift and acceleration. Therefore, the triggering event for termination of the short-term dynamic response to drainage was the drop in lake water level beneath that of the fracture elevation.

Although we define the end of phase iii at 2320 UTC based on the termination of drainage of >50 m³ s⁻¹, there is a long tail to observed hydrological activity. By the time of the postdrainage UAV survey at 2018-07-08 0145 UTC, the edge of the lake was still proximal to the fracture, and 8 separate channels were flowing into the fracture. By the time of the subsequent UAV survey (2018-07-08 1515 UTC), only 3 channels remained, and, 24 h later (2018-07-09 1615 UTC), one supraglacial channel and associated moulin remained, which dominated for the rest of the melt season.

The elevation time series from the GPS located to the south of the lake shows a persistent postdrainage surface uplift of $\sim$0.2 m above the predrainage level (Fig. 2C). Previous studies have reported a similar phenomenon (1–3, 11), interpreting it as transient water storage at the bed or reverse dip/slip faulting (2). We did not observe any evidence of reverse faulting, so we favor the hypothesis that the persistent uplift is indicative of changes to the subglacial system. Substantial surface lowering (>1 m) was observed in the northeast area of the study site (Fig. 4A). Given that this lowering was spatially confined and observed over only $\sim$33 h, it cannot be explained by surface melt alone. We hypothesize that this excess lowering could relate to a loss of subglacially stored water or sediment in this region following lake drainage. Hence, this pattern of persistent uplift downstream of the lake and surface lowering upstream could be explained by some combination of rerouting of the subglacial hydrological system (31) leading to increased water storage beneath the location of the GPS and/or the redistribution of subglacial sediment during rapid lake drainage (32).

Spatial Distribution of Dynamic Response.

The northwest region of ice uplift (region A in Fig. 4A) was located proximal to the fracture. We interpret this to be a result of hydraulic jacking in the region surrounding the direct injection of water to the bed. In modeling studies, this has been interpreted as a turbulent sheet or water “blister” (10) spreading radially from the moulin injection point. Measured uplift here peaked at $\sim$0.8 m, which is consistent with previous studies (1–3, 11). Uplift was focused to the southwest of the lake center (Fig. 4A), in contrast to previous studies of alpine and ice sheet lake drainages which have speculated that ice uplift is greatest near the center of lakes (1, 2, 9). This likely reflects the location of surface-to-bed hydrological connections: The fracture and moulins reported here were located offset in this direction from the lake center, whereas previous studies of lake drainages have been of lakes that hydrofractured at their center.

The area of lower-magnitude uplift observed in region B (Fig. 4A) correlates with the predicted peak subglacial discharge pathway (Fig. 4C) derived from modeled subglacial hydrological routing (see Materials and Methods). We interpret uplift at region B to have resulted from hydraulic jacking—and subsequent concentration of water—along preferential flow routes as lake water was routed away from the injection site. The >1-km-wide region over which this uplift is distributed leads us to envisage the subglacial hydrology as a turbulent sheet or blister rather than a single efficient channel. Uplift similar to that observed at region B has not been observed previously, but our interpretation agrees with modeling results (10), which found that large and efficient subglacial channels do not form rapidly as a result of rapid lake drainage. Instead, water flows downstream once blister growth is restricted by basal topography.

In contrast, the distal area of high-magnitude uplift located in region C has not been observed or predicted previously. It does not correlate with subglacial flow routes predicted by modeled hydrological routing, which continues along the bedrock trough (Fig. 4C). One option to explain this divergence between the inferred and modeled water routing pathways could be due to errors in BedMachine v3, which has reported uncertainty in excess of 50 m around region C. However, while this would explain a simple divergence between inferred and modeled pathways, it does not explain why the uplift of region C is greater than at regions A or B. We suggest that (assuming the modeled hydrological routing is correct) region C constitutes an area of less efficient subglacial drainage, which resulted in higher water retention and enhanced hydraulic jacking.

The pattern of water routing described above may also explain why ice acceleration over the drainage period (Fig. 4B) was concentrated in region C, while acceleration elsewhere, particularly at the lake site itself, was less pronounced. The velocity field in Fig. 4B represents a 3-d period, and, as such, the significant short-term ($\sim$hours) accelerations observed in the GPS data are likely averaged out. If the northern and central sections of the drainage system became more efficient following lake drainage and moulin formation, then there would be limited dynamic response in these areas throughout most of the velocity observation period. Meanwhile, at region C, an inefficient drainage system may have allowed continuing dynamic response to variations in water input. Dynamic response may have been greater than predrainage, as meltwater from the entire catchment area was then being delivered efficiently to the bed via moulin M18a, increasing discharge rates. Hence, the most sensitive response to a lake drainage event on the timescale of days to weeks was not necessarily at the location where water is injected at the bed, but instead is governed by the subglacial pathway taken by the water as well as by the physical state of the hydrological system at the bed. These observations align with regional-scale remote sensing data (33), which identified that areas of peak acceleration through a melt season coincide with bedrock troughs and intervening ridges, where hydraulic gradients are weak and the rate at which turbulent flow enlarges conduits through melting is low. The study identified these factors as particularly strong in areas where bedrock structures are not well aligned with regional ice flow—as occurs at region C (Fig. 4C). In situ studies of lake drainages frequently locate ground instrumentation close to the lake site (1–3, 26). For better quantification of distributed dynamic impacts of lake drainage, future work may wish to also study potential distant “hotspots” as informed by low hydraulic gradients in the basal environment.

Influence of Structural History on Lake Drainage Mode.

In recent history, Lake 028 has displayed 3 different behaviors. Between 2011 and 2016, the lake did not drain rapidly at all, and froze over at the end of each melt season. In 2017, the lake was able to drain completely through a newly formed hydrofracture located in the lake center. We hereafter call this a “primary” hydrofracture. In 2018, the lake drained by reactivating a fracture formed during the previous year’s drainage event. We hereafter call this a “secondary” hydrofracture. However, as the fracture had advected $\sim$500 m southwest and was oriented 45° to the flow direction, the fracture did not cut across the deepest section of the lake, and, as such, the lake failed to drain completely. Here, we make a further distinction between “complete” and “partial” rapid drainage. By 2019, any 2018 moulins had advected out of the lake basin entirely, and, as such, secondary hydrofracture could not occur again. Instead, in 2019, Lake 028 again underwent complete rapid drainage by primary hydrofracture (SI Appendix, Fig. S2).

The concept of rapid drainage via the reactivation of preexisting crevasses and moulins has been proposed previously in slow-moving ($\sim$100 my⁻¹), land-terminating sectors of the Greenland Ice Sheet at Lake F (2) and North Lake (3). However, Lake 028 exhibits markedly different behavior from previous in situ studies on 2 counts. The first is that of interannual behavior. Manual inspection of 32 y of available Landsat and Sentinel-2 satellite imagery between 1985 and 2018 suggests that Lake 028 rapidly drained 12 times (38% of years), of which 2 (2006 and 2018, 17% of drainages) show clear evidence of “secondary” drainage features (SI Appendix, Fig. S3). Meanwhile, for a parallel analysis of 10 y (2009–2018) of data, Lake F (2) and North Lake (3) fully drained every year, except for 1 y each (2011 at Lake F and 2014 at North Lake) where the lakes did not fill at all. Our interpretation of these years is that moulins from the previous year remained open, preventing the lakes from forming.

The second difference is the extent of drainage. North Lake and Lake F are both described as reactivating previous moulins/fractures (2, 3), and hence would be classified here as draining via secondary hydrofracture. However, they undergo complete rapid drainage, whereas Lake 028 only undergoes partial rapid drainage. We suggest that these differences in behavior can be explained by 2 compounding factors: 1) the lower ice velocity in land-terminating sectors of the ice sheet ($\sim$100 m$\cdot$y⁻¹) means that relict moulins and fractures do not advect out of the lake bed after only 1 y, increasing the chance of drainage via secondary hydrofracture; and 2) fractures at Lake F and North Lake are aligned parallel with flow direction, meaning that, year on year, the reactivated fracture intersects the approximate lake center for consecutive years, allowing for complete rapid drainage. Controls on the orientation of lake drainage fractures in a land-terminating setting have been previously considered in a modeling context (25), where the variable direction of flow routing at the bed was considered to be the primary influence on fracture orientation. Here, we show that background stress regime can have strong control on fracture orientation, and, as such, identify the important role of preexisting fractures (in 2018) and crevasses advected into the lake basin (in 2017) on fracture orientation, and therefore also on the degree to which rapid lake drainage is complete or partial.

As a result of the 2 factors described above, North Lake and Lake F consistently experience complete rapid drainage via secondary hydrofracture (2, 3). In contrast, lakes like Lake 028, which 1) exist in fast-flowing sectors of the ice sheet where structural weaknesses are rapidly advected outside the lake-bed and 2) occur in strain regimes (such as regions of rapidly accelerating ice, or zones of shear) that do not create flow-parallel fractures, make secondary hydrofracture uncommon. Instead, in years without relict moulins or hydrofractures (e.g., 2017), primary hydrofracture must occur by exploiting only surface crevasses, potentially aided by other factors such as the drainage of neighboring lakes that trigger short-term perturbations in the regional stress/strain regime (17, 25). In the absence of these factors, rapid drainage may not occur at all (e.g., 2011–2016). As a result, lake drainages may be less common (on an individual, interannual level) in fast-flowing sectors of the ice sheet. Given that multiyear remote sensing studies have found that most lakes that exhibit rapid drainage behavior do so less than 50% of the time (22, 23), Lake 028 could provide a representative model for these lakes’ interannual behavior.

The above discussion has implications for remote sensing studies designed to identify rapidly draining lakes automatically. The nature of partial rapid drainage appears site-specific, but, if widespread in fast-flowing sectors of the ice sheet, then automated lake identification routines in remote sensing studies are highly likely to be misclassifying rapid lake drainages where, like Lake 028 in 2018, only partial drainage occurs. Many classifications use a threshold of 80 to 90% loss in area (18, 23, 34) or volume (17, 35, 36) within a defined period (often 2 to 6 d) to qualify as a rapid drainage event (i.e., drainage via hydrofracture). In this binary classification, lakes that only drain partially are also assumed to drain slowly (on the scale of $\sim$days) into preexisting moulins via fast incision of a supraglacial outlet channel (11, 37, 38). However, only 41% of area (1.25 to 0.51 km²) and 66% of volume (7.1 to 2.3 × 10⁶ m³) was lost overnight from Lake 028, meaning that this drainage would not be classified as a rapid/hydrofracture-induced drainage by published identification routines, whereas in situ records of the event clearly show that it meets this criterion in terms of flux and hydrological connection to the bed. Identifying the mode of drainage of Lake 028 in medium-resolution optical imagery can be difficult even when manual identification is used. A key identifying feature is that the configuration of surface outlet channel direction and fracture orientation is such that secondary drainage cuts off the outflow channel, which is present for the full season in years with no drainage (SI Appendix, Fig. S4). It is likely, then, that existing remote sensing routines are underestimating the number of actual rapid lake drainage events. This has important consequences when subglacial hydrological models are forced, in part, by these remotely sensed observations (e.g., refs. 21 and 25), as these models are correspondingly underestimating the total water volume rapidly delivered to the bed, as well as, later in the season, the locations at which water is being delivered. The identification of hydrofracture is known to be highly sensitive to the precise criteria applied (18), and these findings further highlight a need for more nuanced remote sensing routines to detect drainages.

If rapid lake drainages are more extensive than previously thought, wider implications exist for Greenland Ice Sheet hydrology and dynamics, as lake hydrofracture is thought to be the primary control on moulin density and extent (14). Moulins are the primary mechanism by which rapid lake drainages can have a longer-term (weeks to years) influence on subglacial hydrology: While supraglacial lakes may contain only $\sim$3% of the total melt season runoff volume, a further $\sim$21% has been estimated to drain through newly opened moulins created by hydrofracture events, and an additional $\sim$15% through preexisting moulins created during previous melt seasons (38), which can remain active for many years in a row (15). Furthermore, moulins act to concentrate meltwater delivery spatially, to a point source, and also temporally, as water transfer via moulin is nearly instantaneous compared to drainage through crevasse systems (39). Our finding that partial lake drainages also occur through hydrofracture indicates that many lakes previously inferred to drain by overtopping or channel incision (11), in fact, are establishing moulins and hydrological connections to the bed (14). Consequently, a larger portion of the subglacial drainage system could be subject to a persistent, yet also highly variable, meltwater supply from the surface. This may mean that, early in the melt season, more of the basal system is subject to pulses in supply (from events such as high-melt days and rainfall) that are capable of overwhelming transmission capacity and therefore enhance basal sliding (39, 40). Later in the season, concentrated meltwater delivery could also accelerate the formation and spatial extent of efficient channels, which have a stabilizing effect on the ice sheet’s flow (5, 14, 40).

Given the relationship between primary and secondary hydrofracture, we argue that consecutive years of rapid lake drainage are more likely in slow-moving sectors of the ice sheet. In fast-flowing sectors, full-depth fractures are rapidly advected out of lake basins, and, therefore, new hydrofractures must exploit shallower surface crevasses, facilitated by a stronger extensional stress regime. Conversely, this implies that, if a lake can hydrofracture just once in a slow-flowing regime, the presence of relict fractures and moulins makes it easier for rapid drainage to reoccur year on year. This is a relevant factor in discussions of interannual dynamic changes in the land-terminating ablation zone (8), but may be especially important in inland sectors of the ice sheet (7), where surface-to-bed connections have been proposed to be less likely (41). However, if decadal-scale dynamic changes to the ice sheet induce even limited extensional crevassing farther inland, one lake drainage via primary hydrofracture may be enough to induce consistent secondary hydrofracture in further years, as relict features are unlikely to advect out of the lake bed within only a few seasons.

Conclusions

Fast-flowing, marine-terminating glacier hydrology represents a key uncertainty in predictions of sea level rise (27), and the long-term response of marine-terminating glaciers to climate change and lake expansion remains unknown. Our results contribute better observational understanding of ice sheet hydrology and dynamics by identifying key differences between supraglacial lakes on fast-flowing and slow-flowing sectors of the ice sheet. As rapid, hydrofracture-induced drainage can occur even at partially draining lakes in fast-flowing sectors, the increased potential density of surface-to-bed connections (14) has implications for subglacial drainage efficiency both in the early melt season (as a positive feedback to ice velocity) and in the long term (as a mitigating effect to increased surface melt). The observation that hydrofracture can occur without any precursory hydrologically induced basal slip (3) identifies a triggering mechanism for cascading lake drainage events (25), which means that the style of drainage observed here could be important in initiating a chain reaction of meltwater delivery to the bed. Furthermore, an increased understanding of the necessary conditions behind year-on-year hydrofracture has significance when considering meltwater delivery to the bed in inland regions, which currently represent a large unknown in predicting future dynamic change of the ice sheet (7, 41). Given the ongoing dominance of mass loss via dynamic losses from the marine-terminating Greenland Ice Sheet (42), improving our understanding of the unique hydrology and dynamics of these sectors is key to constraining mass balance predictions into the 21st century.

Materials and Methods

By the 2018-07-07 drainage event, Lake 028 was instrumented with a GPS receiver, seismometer, and pressure transducer sensor (Fig. 1A). A dual-frequency GPS was installed $\sim$600 m upstream of the lake in July 2017 and, by July 2018, had advected into a position immediately south of the lake. A seismometer was installed in May 2018, and a water-level sensor was installed on 2018-07-04. From this date, regular UAV surveys (SI Appendix, Table S1) were performed over the lake and surrounding environments. Lake 028 drained 3 d later, on 2018-07-07 between ∼1800 UTC and 2300 UTC (Fig. 1B).

Pressure Transducer.

A pressure transducer (Solinst 3001 Levelogger) was installed on 2018-07-04, logging at 2-min intervals. The record was corrected for changes in atmospheric pressure using hourly surface pressure data from ERA-5 reanalysis data (43). A depth–volume relationship was established using a bathymetry map of the lake at 0.2-m resolution produced from depth-corrected UAV-derived digital elevation models (DEMs) (SI Appendix, SI Text). Time series of lake volume ($V$), discharge ($Q$), and rate of change in discharge ($dQ/dt$) were calculated from this depth–volume relationship.

GPS.

We measured ice surface velocity and uplift using a Trimble NetR7 dual-frequency GPS receiver logging continuously at 0.1 Hz using a Trimble Zephyr Geodetic III Antenna. We processed dual-frequency GPS data kinematically (44) using the differential carrier-phase positioning software, Track v. 1.30 (45) (http://geoweb.mit.edu/gg/), and final precise ephemeris from the International Global Navigation Satellite System (GNSS) Service (46). The data were processed against an off-ice reference system, a Trimble NetR9 receiver located on Qarassap Nunata (70.4°N, 50.7°W). We discarded solutions where carrier-phase ambiguities were not fixed to the current integer, where an insufficient number (<4) of double-difference calculations were made, or where position SD exceeded 0.035 m. High-frequency noise was filtered with a 2-pole, low-pass Butterworth filter with a 30-min cutoff period (47). This 30-min window was chosen based on a worst-case horizontal positional uncertainty of 0.035 m and a base ice velocity of $\sim$650 m$\cdot$y⁻¹, following from which assumptions the period over which velocities can be resolved is $\sim$0.5 h. Uncertainty was calculated based on a conservative estimate of the positional uncertainty of $\pm$1 cm propagated through the velocity calculation.

Seismometers.

Seismic monitoring was conducted using a passive HG-7 10 Hz geophone deployed in a shallow (3 m) borehole. Recordings were taken at 400 Hz using a DiGOS DATA-CUBE. Changes in seismic energy were studied using the normalized rms amplitude. Data were decimated to 100 Hz, and a 2-pole, zero-phase band-pass filter (10 to 50 Hz) was applied to eliminate instrument and high-frequency noise. The normalized rms amplitude was then calculated for 60-s time windows. The normalized cumulative amplitude was also calculated to identify rapid changes in seismic energy.

UAV Photogrammetry.

We acquired aerial imagery using a custom 2.1-m fixed-wing UAV (48). The survey plan, designed with the assistance of the 5-m-resolution ArcticDEM mosaic, provided a consistent flight altitude of $\sim$450 m, with a ground-level image footprint of $\sim$660 × 440 m and a ground sampling distance of 11 cm. Digital imagery was acquired by a Sony $\alpha$6000 24 MP camera with a fixed 16-mm lens. Imagery was captured every 90 m along flight lines spaced 240 m apart, in order to achieve a >80% (>60%) overlap along (between) flight lines for photogrammetry purposes. The point cloud was geolocated via GNSS-assisted aerial triangulation, using an on-board Emlid Reach single-frequency carrier-phase GPS receiver (recording at 10 Hz) postprocessed using the Emlid RTKLIB b27 software suite against 10-Hz data from a ground-based NetR9s (48). A total of 11 surveys were performed over the study period between 2018-07-05 and 2018-07-28 (SI Appendix, Table S1).

Photogrammetric outputs were calculated from images and camera positions using AgiSoft Photoscan v.1.4.3 (https://www.agisoft.com), apart from the DEM difference fields displayed in Fig. 4A, which were calculated using the updated Agisoft Metashape 1.5.1. Camera calibration was performed automatically in the bundle adjustment process. From the final dense point clouds, we produced orthophotos at 0.15-m resolution and geoid-corrected DEMs at 0.2-m resolution. Horizontal velocity fields were derived by feature tracking 0.2-m-resolution multidirectional hillshade models (produced using Geospatial Data Abstraction Library (GDAL) 2.2) using open particle image velocimetry (OpenPIV) feature tracking software (49), using an interrogation window size of 320 × 320 pixels and a spacing of 32 pixels (final resolution: 6.4 m). We filtered erroneous values using manually chosen upper and lower thresholds for velocity, signal-to-noise ratio, and divergence from mean annual flow direction. Uncertainties in the velocity field were calculated based on a displacement uncertainty of 0.17 cm, following ref. 48.

When calculating uplift from DEM differencing, we assume the vertical uncertainty to be $\pm$ 0.2 m following ref. 48, which is close to the scale of uplift explored. However, validation against the observed GPS uplift gives some confidence, with a reported GPS uplift of 0.31 cm between the survey periods compared with a mean UAV-derived uplift of 0.34 $\pm$ 0.05 m across a 6-m² sample area around the GPS location. Survey precision estimates (50) were centimetric, so uncertainty was likely dominated by survey-wide systematic biases, giving confidence to this validation measurement.

Hydrological Routing.

As surface water reaches the ice bed, we assume that it flows following gradients in hydraulic potentials. These are calculated using a multiflow direction algorithm, where the flow is diverted to multiple downslope cells in proportion to the slope between them (51, 52). The gradients in hydraulic potential surface are calculated over the catchment of Store Glacier using

$$\nabla \theta ={\rho }_{w}g\nabla Z_b+\alpha {\rho }_{i}g\nabla H,$$ [1]

with $\nabla \theta$ as the gradient of the hydraulic potential surface (in pascals), ${\rho }_w$ and ${\rho }_i$ as the density of water and ice, respectively (in kilograms per cubic meter), and $g$ as the constant of gravitational acceleration (in meters per square second). The glacier geometry is defined with the gradient of bed elevation ($\nabla Z_b$, in meters) and the gradient of ice thickness ($\nabla H$, in meters), taken from BedMachine V3 (53) at 150-m spatial resolution. The coefficient $\alpha$ is a floatation fraction, here set to 1 with the assumption that the subglacial water pressure is equal to the ice overburden pressure. Note that the routing of water in our study region remains similar if we assume that the pressure in the hydrological system is just less than the overburden value ($\alpha$ = 0.9).

In order to derive discharge from mapped hydraulic potential, we use, as input to the subglacial system, gridded total daily runoff from regional climate model RACMO2. A slightly updated model is used relative to that presented in ref. 54: no model physics have been changed, but the spatial resolution of the model has been increased to 5.5 km from 11 km (although output is downscaled to 1 km). Data for the day of drainage were not available at the time of the study. Instead, we use data for 2017-07-26 (a day where a large rainfall event was observed at the study site) as a proxy for a period when high total water input was entering the subglacial system. Discharge was mapped extending $\sim$140 km inland from the calving front, although only a small section of this is presented in Fig. 4C.

Optical Satellite Imagery.

Where optical satellite images were downloaded for red–green–blue visualization, Sentinel-2 imagery was downloaded from the Copernicus Open Access Hub (https://scihub.copernicus.eu) and Landsat 8 OLI imagery from the US Geological Survey Earth Explorer (https://earthexplorer.usgs.gov). Long-term lake drainage history for Lake 028, Lake F, and North Lake were produced using imagery visualized with the Google Earth Engine Digitisation Tool (55).

Ice Surface Strain Rates.

First and second principal strain rates and directions were calculated from MEaSUREs velocity data for 2017 (28). We compute the horizontal part of the strain rate tensor, with derivatives approximated by finite difference of the horizontal velocity field (56, 57). The first principal strain rate was calculated as the highest eigenvalue of the strain rate tensor, and the associated eigenvector is the first principal direction. The second principal strain rate (direction) was the lowest eigenvalue (eigenvector).

Data Deposition.

The geophysical time series, UAV-derived raster, and modeled water routing data reported in this paper are available at UK Polar Data Center, https://doi.org/10.5285/481D4120-1A72-468B-8CD4-84B4E14CDEAB.