Automated characterization of anthropomorphicity of prosthetic feet fitted to bone-anchored transtibial prosthesis

Abstract

Objective:

This study describes differentiating prosthetic feet designs fitted to bone-anchored transtibial prostheses based on an automated characterization of ankle stiffness profile relying on direct loading measurements. The objectives were (A) to present a process characterizing stiffness using innovative macro, meso and micro analyses, (B) to present stiffness profiles for feet with and without anthropomorphic designs, where anthropomorphicity is defined as a similarity of the moment-angle dependency in prosthetic and in the anatomical ankle, (C) to determine sensitivity of characterization.

Methods:

Three participants walked consecutively with two instrumented bone-anchored prostheses including their own prosthetic feet and Free-Flow foot meeting the anthropomorphicity criterion by design. Angle of dorsiflexion was extracted from video footage. Bending moment was recorded using multi-axis transducer attached to osseointegrated fixation. The automated characterization of stiffness involved a 12-step process relying on data-based criterion.

Results:

The meso analyses confirmed bilinear behavior of moment-angle curves with Index of Anthropomorphicity of −2.966±2.369 Nm/Deg and 2.681±1.089 Nm/Deg indicating a convex and concave shape of usual and Free-Flow feet without and with anthropomorphic designs, respectively.

Conclusions:

The proposed straightforward meso analysis of the stiffness was capable to report clinical meaningful differences sensitive to feet’s anthropomorphicity. Results confirmed the benefits for clinicians to rely on direct loading measurement providing individualized complementary insight into impact of components.

Significance:

This work could assist the developments of standards and guidelines for manufacturing and safe fitting of components to growing population requiring transtibial prostheses with socket or direct skeletal attachment worldwide.

I. INTRODUCTION

Combined efforts from prosthetic care providers, including engineers and practitioners, to restore functional outcomes of individuals with lower limb amputation could be supported by in-depth biomechanical understanding of healthy joints.[1, 2] For instance, Drevelle et al (2014) indicated that “The stiffness related to flexion movement has been proposed to characterise the functioning of the healthy ankle and to define realistic targets for prosthesis design”. [3] This pointed out the importance of the ankle stiffness of a prosthetic foot in restoring functions. [4, 5] Consequently, evidencing ankle stiffness is essential to support clinical decision and prescription of a given foot, particularly when fitted to a transtibial prosthesis.[6]

A. Characterization of ankle stiffness

Ankle stiffness of a prosthetic foot is conventionally represented by a curve showing the progression of angle of dorsiflexion in relation to the bending moment at the ankle joint over the flat foot phase of a gait cycle (GC). [3, 7–12] A linear curve indicates a constant stiffness. However, typical moment-angle curve of prosthetic feet have either a convex or concave shape associated with or without anthropomorphic ankle joint design, respectively.[10–13]

Review of literature focusing on able-bodied as well as individuals with transtibial and transfemoral socket prostheses revealed that the ankle moment-angle curve of a prosthetic foot could be gradually characterized at three levels:

• Macro analyses summarized the stiffness as the slope of the regression line of the whole moment-angle curve.[3, 14]

• Meso analyses relied on bilinear behaviour of moment-angle curve and slopes of the regression lines of the curve after and before a point of curvature (PC) change.[3, 14] Quantification of the criterion of anthropomorphicity described elsewhere could differentiate feet generating concave or convex moment-angle curves.[10–13].

• Micro analyses represented stiffness by a series of instantaneous slopes of regression lines of successive sections of the moment-angle curve.[12]

B. Importance of stiffness in transtibial prostheses

By definition, stiffness in a prosthetic ankle expresses itself as resistance to angulation which is transmitted back to the residuum via traditional socket or osseointegrated fixation.

Previous studies have demonstrated that the moment-angle dependency of a prosthetic ankle fitted to socket-suspended transtibial prostheses affects prosthetic limb joints kinematics, loading and metabolic cost.[7, 15, 16] Furthermore, we demonstrated that a prosthetic ankle generating concave moment-angle curve seen in anatomical ankle decreased noticeably pressure in the socket compared to prosthetic feet generating convex moment-angle curve.[8–10, 13, 15, 17]

It is now commonly accepted that the development of osseointegration is, in part or in whole, associated with loading regimen directly translated from the ground to the fixation that strongly depends on ankle stiffness. [18–29] Therefore, better understanding of the impact of ankle stiffness on osseointegrated fixation could possibly contribute to reduce early loosening of fixation, mechanical failure of percutaneous and medullar parts of fixation, periprosthetic issues and infections that are yet to be fully satisfactorily resolved.[23, 24, 30–35]

Altogether, stiffness characterization might also assist in the development of specific guidelines for design and prescription of feet and ankle units for transtibial prostheses, the sole loading elements under the control of prosthetists that is also subjected to cost-benefit analyses by funders. [36, 37]

C. Limits to characterization of ankle stiffness

Currently, systematic and consistent characterization the true ankle stiffness of a given foot fitted to socket-suspended or bone-anchored transtibial prosthesis is currently limited by several shortcomings.

The identification of the shape of the moment-angle curve is done subjectively using eyeballing for manual selection of PC.[3, 14] The reporting of stiffness is inconsistent between studies using several original outcomes for either macro, meso and micro analysis.[38–40] Altogether, the lack of standard quantitative criteria to conduct and report stiffness might increase intra- and inter-rater variability within and between studies, hinder benchmarking of ankle components and limit meta-analyses of published studies.

The concavity of the stiffness curve indicates that the moment of resistance is low at the beginning of dorsiflexion and then rapidly increases as dorsiflexion progresses up to the heel-off. A dependency of this shape is a component of ballistic synergy that allows the calf and thigh extensor muscles to work mostly in the eccentric contraction mode, which is more biomechanical compared to the concentric contraction mode, and protects leg bones from excessive bending moments.[41, 42]

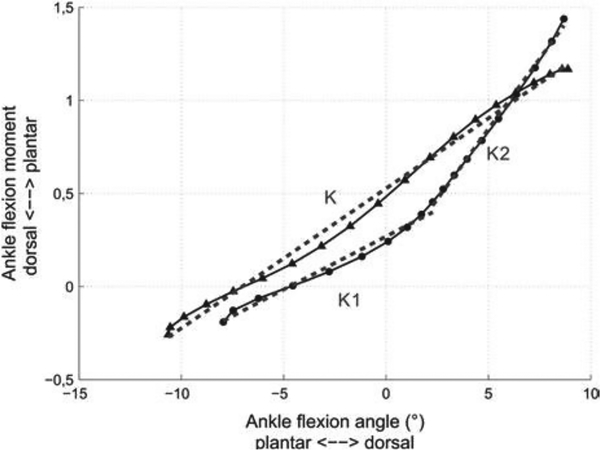
A simple quantification of the moment-angle relationship in healthy patients was suggested in Drevelle et al (2014) and Pillet et al (2014).[3, 14] The concavity of the graph was characterized by two stiffnesses K1 and K2, each stiffness defined as the ratio of the ankle flexion moment to the ankle flexion angle. As shown in Fig 1, K1 and K2 correspond to the slopes of the moment-angle graph in the initial and final states of dorsiflexion. In anatomically healthy gait, K2 is statistically greater than K1.

Fig 1.

The ankle moment as a function of the ankle angle with computed stiffness during level walking for asymptomatic subjects (black disc, K1 and K2) and transfemoral amputees (black triangles, K). Adapted from [3] with permission from the publisher.

Here, we suggest complementing typical meso analyses by introducing an Index of Anthropomorphicity (IA), where IA= K2-K1, corresponding to the difference between the two slopes of the regression lines of the moment-angle curve.

To date, specific algorithm capable of automatically characterizing the stiffness at each level is yet to be developed.

Perhaps less critical is the limitation associated with recording of raw dynamics information required to extract ankle bending moment. Typically, ground reaction forces and moments are collected using floor-mounted force-plates. [43–46] Instrumentation of clinical walkways as well as stairs and ramps is possible but tedious and often costly. More importantly, the sole contact of each foot on a force-plate required for valid dynamic measurements is commonly achieved through personalized arrangement of the starting point and/or force-plate positioning to avoid targeting and/or repetitive recording of invalid trials.[43, 44, 47] Alternatively, a wireless portable kinetic system including a tri-axial transducer embedded in the prosthesis could provide directly bending moment making stiffness assessment possibly somewhat more ecological.[25–27, 45, 46, 48–60]

D. Need for automated characterization of stiffness

Altogether, there is a need for an automated characterisation of ankle stiffness of prosthetic feet relying on direct loading measurement that is relevant to engineers, clinicians and biomechanists for more consistent evidence-based design, fitting and assessments of transtibial socket-suspended prostheses and, perhaps more importantly, BAP.[11, 61]

E. Objectives

The main purpose of this observational case-control series study was to test the hypothesis that an automated characterization of the ankle stiffness relying on direct loading measurement can differentiate feet with and without anthropomorphic designs.

The specific objectives were:

• To present a step-by-step process relying on set data-based criterion for an automated characterization of the shape and magnitude of the stiffness profile of a prosthetic foot featuring macro, meso including IA and micro analyses,

• To present individuals and grouped stiffness profiles for three participants walking with a BAP successively fitted with their own ankle/foot units (i.e., RUSH, Trias, Triton) and Free-Flow foot meeting the anthropomorphicity criterion by design. [8, 15]

• To compare stiffness profiles between feet using minimum clinically important difference to determine sensitivity of levels of analysis to foot design.

II. MATERIALS AND METHODS

A. Participants

This study involved all Queensland-based individuals with unilateral TTA fitted with a BAP using a so-called arm-length recruitment strategy applied by local prosthetists. No exclusion criteria were applied for gender, age, weight and height or level of activity. The specific inclusion criterion included (A) having circa six centimetres clearance between the percutaneous part of the fixation and ankle joint to fit the transducer as well as being (B) fully rehabilitated for at least 18 months, (C) capable to walk 200 m independently with BAP and (D) free of pain and infection at the time of recording. Human research ethical approval was received from the research institution. Written consent was obtained from all participants.

B. Apparatus

Participants walked consecutively with two instrumented prostheses connected to percutaneous part of press-fit osseointegrated fixation that included a connector, a transducer attached with pyramidal adaptors, a pylon, either their own or Free-Flow prosthetic foot (Fig 2). A qualified prosthetist handled all aspects of prosthesis fitting. Each prosthesis was aligned as closely as possible to usual alignment.

Fig 2.

Example of long axes of the leg (LG_l) and foot (LG_f) used to determine ankle angle of dorsiflexion of the instrumented transtibial bone-anchored prosthesis attached to residuum (A) and percutaneous part of osseointegration fixation (B) including connector (C), transducer (D), pylon (E) and multi-axial rolling Free-Flow Foot (Ohio Willow Wood) (f) with anthropomorphic moments of dorsiflexion, inversion/eversion and axial rotation featuring screw for adjustment of initial stiffness (1), tibial surface of rolling contact (2), cushion (3) and base talar surface of rolling (4).

A digital camera (Canon, IXUS, US) with of sampling frequency of 25 Hz captured videos to facilitate extraction of the angle of dorsiflexion at the prosthetic ankle joint. The center of the fixed field of view of the sagittal plane included the whole participant during a full gait cycle of the prosthetic side facing the camera.

A portable kinetic system (iPecsLab, RTC, US) including a tri-axial transducer set of 200 Hz sent wirelessly loading applied on the fixation to a receiver connected to a laptop nearby. The three components of forces and moments were measured with previously established accuracy better than 1 N and 1 Nm, respectively.[48, 51, 54, 62, 63] The prosthetist fitted the transducer as closely as possible to the percutaneous part so that its coordinate system was co-linear with anatomical axes of the fixation (Fig 2). Illustrations of individual position of the transducer in relation to ankle joint will be presented in subsequent Data-In-Brief publication.

C. Recording

First, the prosthetist set up and aligned the instrumented prosthesis with the transducer and selected foot. Then, participants took approximately 15 min to acclimate with prostheses to ensure confidence and comfort before measurement. Next, participants were asked to perform five trials of level walking in straight-line on 5-meter walkway at self-selected comfortable pace, following protocol previously used for individuals with transfemoral BAP. [51, 54, 62] Finally, the prosthesis was removed to allow benchtop calibration and removal of transducer (i.e., zero-offset).

D. Processing

The first primary outcomes were spatio-temporal gait characteristics. Raw video footage and loading data were imported, synchronized and processed in a customized Matlab software program (MathWorks Inc., MA, USA) allowing identification of a common heel contact (HC) and toe off (TO). Manual detection of HC and TO events was achieved using vertical displacements of heel and toe of prosthetic foot as well as force applied the long axis of the fixation, respectively. These events were used to extract typical confounders of ankle stiffness including the cadence, duration of GC as well as duration of support and swing phases expressed in seconds and percentage of GC. [50]

The second primary outcome was the prosthetic ankle angle of dorsiflexion. Raw video footage were imported into a motion analysis software package (Kinovea) allowing manual selection of the angle projected in sagittal plane between the long axes of leg (LG_L) and foot (LG_F) intersecting at the ankle joint for each frame of the support phase with accuracy of approximately 2 Deg (Fig 2). The raw angles were tabulated into Matlab software program that calculated the final angle of dorsiflexion expressed in degree (e.g., raw angle-90 Deg).

The third primary outcome included the raw loading data initially imported in the Matlab program that were offset according to the magnitude of the load yielded during calibration. The bending moment was expressed in Nm without bodyweight normalisation and translation to ankle joint to report the actual range of loading and stiffness characteristics that could potentially be the most responsible for physiological development of osseointegration around the fixation. However, some bending moment information expressed in percentage of bodyweight will be presented in subsequent Data-In-Brief publication.

Both angle dorsiflexion and bending moment datasets were time normalized from 0 to 100 to facilitate averaging of trials and reporting of onset of events and durations in percentage of support (%SUP).

E. Characterization

The series of secondary outcomes characterized the prosthetic ankle stiffness profile over each GC. The automated characterization relied on set data-based criterion in each of the 12-step process as detailed in Table I.

TABLE I.

Overview of 12-step process for an automated characterization of stiffness profile including the shape of the moment-angle curve and magnitude of the stiffness of ankle joint fitted to a transtibial prosthesis

1	Characterize shape
1.1	Select flat foot pbasis (FLT)
1.1.1	Detect toe contact (TC) corresponding the minimum magnitude of angle dorsiflexion during first half of support phasis
1.1.2	Detect heel off (HO) corresponding the maximum magnitude of angle dorsiflexion during second half of support phasis
1.2	Recognize curvature of stiffness curve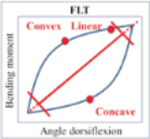
1.2.1	Establish a reference line between the lowest and highest point of the stiffness curve
1.2.2	Count the number of points considered as “linear”, “convex” or “concave” with a magnitude within, above or below 5% of 80% of central section of line, respectively
1.3	Identify the point of curvature (PC)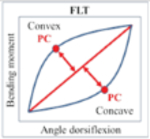
1.3.1	Detect the maximum point above or below the line for convex and concave curve, respectively
1.3.2	Categorize the curve as convex or concave depending on the number of points and PC above or below the line
2	Characterize magnitude
2.1	Perform macro analysis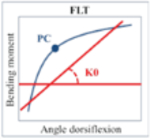
2.1.1	Determine regression line of whole stiffness curve
2.1.2	Extract K0 corresponding to the slope of the line
2.2	Perform meso analysis
2.2.1	Determine regression lines of stiffness curves before and after PC
2.2.2	Extract Kl and K2 corresponding to the slopes of the lines before and after PC and calculate IA=K2–KL respectively
2.3	Perform micro analysis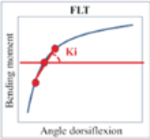
2.3.1	Determine regression lines of stiffness curve for every 4 points with a window of 3 points around
2.3.2	Extract Ki corresponding to the slopes of each line

The first six steps characterized the trochoid curvature of the moment-angle curve involving:

• Duration between relevant events occurring during flat foot phasis of the support corresponding the beginning and end of plantar flexion,

• Recognition of shape of the curve based on categorising each data points as “linear”, “convex” or “concave” depending on their magnitude in relation to a reference line, and identification of the PC where the moment-angle curve changes angulation.

The last six steps extracted outcomes characterizing the magnitude of stiffness relying on:

• A macro analysis represented by K0 corresponding to the slope of the regression line of the whole moment-angle curve as reported in Drevelle et al (2014) and Pillet et al (2014), [3, 14]

• A meso analysis represented by IA equal to the difference between K2 and K1 corresponding the slope of the regression line of moment-angle curve after and before PC, so that an IA positive (K1<K2) or negative (K1>K2) confirmed a concave or convex shape as defined in Pitkin (2010), respectively.[64]

• A micro analysis including a series of Ki corresponding to instantaneous slopes of regression lines of pre-set successive sections of the moment-angle curve (e.g., every 4 points with a window of 3 points) as suggested in Pitkin (1996). [12]

Altogether, the stiffness profile was characterised by eight discrete outcomes (i.e., duration between HC, TC, HO and TO, onset of PC, magnitude of K0, K1, K2 slopes, IA) and four continuous outcomes (i.e., percentage of data points characterised as “linear”, “convex” or “concave”, Ki).

F. Comparative analysis

Individual stiffness outcomes were averaged after collating trials from each participant (N=5 for each participant). Grouped stiffness outcomes were averaged after collating all trials from three participants (N=15 for each prosthesis). Overall stiffness outcomes was achieved by extracting variables using the averaged grouped angle dorsiflexion and bending moment (N=1 for each prosthesis).

Individual or intra-variability and grouped or inter-variability of a discrete stiffness outcomes were determined using the percentage of variation (PV= absolute [[standard deviation / mean] x100]). We considered than a PV inferior to 20% indicated a low variability.

The difference in discrete stiffness outcomes between feet was determined so that a positive difference indicated that Free-Flow foot was algebraically larger than usual foot. We considered that a difference superior to 10% was above a minimum clinically important difference (MCID). This threshold might appear low compared to other studies comparing prosthetic knee components suggesting that an MCID of 20% was relevant. [65] We believe a lower MCID was justified in the particular case of individuals fitted transtibial BAP given their increase proprioception due to osseoperception provided by osseointegrated fixation. [66]

III. RESULTS

The demographic, amputation and prosthetic information for the two males (P1, P2) and one female (P3) who participated in study between May and July 2017 were summarized in Table II. The usual prostheses included a RUSH foot (RUSH, US) and running shoes, Trias 1C30 (Otto Bock, US) and running shoes as well as Triton - Vertical shock 1C6 (Otto Bock, US) for P1, P 2 and P3, respectively. Only P2 used a foot recommended for transfemoral BAP prostheses fitted to screw-type implant.[73] The direct skeletal attachment was achieved thanks to a surgical procedure involving a total knee replacement and implantation of press-fit osseointegrated fixation.[18] All participants were active with an overall fairly high ambulatory capacity.

TABLE II.

Individual and grouped demographics, amputation and prosthetic information including components of prosthesis fitted with usual and Free-Flow feet

		Participant 1	Participant 2	Participant 3	Grouped
Demographics
Gender	(M/F)	M	M	F	-
Age	(yrs)	38	69	67	58±17
Height	(m)	1.92	1.78	1.58	l.76±0.17
Mass	(kg)	109.12	81.74	59.52	83.46±24.84
BMI	(kg/m2)	29.080	25.123	23.293	25.832±2.958
Amputation
Cause		Other	Trauma	Trauma	-
Side	(L/R)	R	R	L	-
Time since amputatior	(yrs)	9	5	32	15±15
Time since OI	(yrs)	2	2	3	2±1
Length of leg	(cm)	46.94	42.67	37.28	42.3±4.84
Length of residuum	(cm)	12.42	9.38	11.52	11.11±1.56
Length of residuum	(%LoL)	26	22	31	26±4
Usual foot
Brand		RUSH	Otto Bock	Otto Bock	-
Model		RUSH foot	Trias	Triton	-
Footwear		Running shoes	Running shoes	Sandals	-
Foot size	(cm)	27	27	22	25±3
Free-Flow foot
Brand			Ohio Willio Wood		-
Model			Free-Flow		-
Footwear		Running shoes	Running shoes	Sandals	-
Foot size	(cm)	27	26	24	26±2

BMI: Body Mass Index, M: Male, F: Female, L: Left, R: Right, OI: osseointegration, %LoL: Percentage of length of sound leg

A total of 28 out of 30 GCs were analysed, including 14 with usual and Free-Flow feet as a trial with each prosthesis was unsuited for analysis due to technical glitch.

A. Spatio-temporal gait characteristics

As detailed in Table III, the individual cadence, duration of GC and support phases ranged from 40±1 to 52±1 strides/min, 1.158±0.02 to 1.488±0.034 s and 61±1 to 68±2 %GC with usual foot as well as 45±1 to 51±1 strides/min, 1.175±0.016 to 1.46±0.029 s and 61±1 to 64±2 %GC with Free-Flow foot, respectively. All individual and grouped spatio-temporal characteristics presented a low intra- and inter-variabilities. The difference was below MCID for all individual and grouped characteristics except for cadence, duration of GC and support phases in seconds for P1 as well as duration of swing for P3.

TABLE III.

Comparison of individual and grouped spatio-temporal gait characteristics with prosthesis fitted with usual and Free-Flow feet

	Participant 1		Participant 2		Participant 3		Grouped
Usual foot	(N=5)		(N=5)		(N=4)		(N=14)
Cadence (Strides/min)	40±1	L	52±1	L	40±2	L	44±6	L
Duration (s)
Gait cycle	1.488±0.034	L	1.158±0.02	L	1.485±0.07	L	1.386±0.163	L
Support	0.944±0.036	L	0.71±0.011	L	1.015±0.056	L	0.893±0.136	L
Swing	0.545±0.009	L	0.449±0.018	L	0.471±0.036	L	0.492±0.049	L
Duration (%GC)
Support	63±1	L	61±1	L	68±2	L	64±3	L
Swing	37±1	L	39±1	L	32±2	L	36±3	L
Free-Flow foot	(N=5)		(N=4)		(N=5)		(N=14)
Cadence (Strides/rain)	45±1	L	51±1	L	41±1	L	46±4	L
Duration (s)
Gait cycle	1.337±0.041	L	1.175±0.016	L	1.46±0.029	L	1.325±0.12	L
Support	0.827±0.051	L	0.718±0.027	L	0.933±0.01	L	0.826±0.094	L
Swing	0.51±0.018	L	0.458±0.012	L	0.527±0.032	L	0.499±0.036	L
Duration (%GC)		L				L		L
Support	62±2	L	61±1	L	64±2	L	62±2	L
Swing	38±2	L	39±1	L	36±2	L	38±2	L
Difference (Free-Flow foot-Usual foot)
Cadence (Strides/min)	5	A	−1	B	1	B	2	B
Duration (s)
Gait cycle	−0.151	A	0.017	B	−0.026	B	−0.061	B
Support	−0.117	A	0.008	B	−0.082	B	−0.067	B
Swing	−0.035	B	0.009	B	0.056	A	0.007	B
Duration (%GC)
Support	−2	B	0	B	−4	B	−2	B
Swing	2	B	0	B	4	A	2	B

GC: Gait cycle, N: Number of gait cycles, H: High PV, L: Low PV, A: Above MCID, B: Below MCID

B. Individual and grouped stiffness profile

The shape and magnitude provided by macro and meso analyses of all individual and grouped stiffness profiles with both prostheses are presented in Table IV.

TABLE IV.

Comparison of individual and grouped characterization of stiffness profile including mean and standard deviation of shape and magnitude of moment-angle curves of usual and Free-Flow feet fitted to transtibial bone-anchored prosthesis

	Participant 1		Participant 2		Participant 3		Grouped
Usual foot	(N=5)		(N=5)		(N=4)		(N=14)
Shape
Duration (%DUR)
HC to TC	13±6	H	15±2	L	25±3	L	17±7	H
TC to HO	71±6	L	63±5	L	57±3	L	64±8	L
HO to TO	16±3	L	22±3	L	19±3	L	19±4	H
PC	47±8	L	34±3	L	59±8	L	46±12	H
Curvature (%FLT)
Linear	5±4		5±5		8±13		6±7
Convex	74±29		80±24		91±13		81±23
Concave	19±25		14±18		0±0		12±19
Magnitude (Nm/Deg)
K0	4.966±0.813	L	3.843±0.947	H	2.901±0.337	L	3.975±1.116	H
K1	5.454±0.723	L	6.441±1.684	H	3.679±1.440	H	5.299±1.682	H
K2	3.475±1.343	H	2.019±0.420	H	1.299±2.118	H	2.333±1.585	H
IA	−1.978±1.477	H	−4.423±1.670	H	−2.380±3.476	H	−2.966±2.369	H
Free-Flow foot	(N=5)		(N=4)		(N=5)		(N=14)
Shape
Duration (%DUR)
HC to TC	12±3	H	12±O	L	13±4	H	12±3	H
TC to HO	76±3	L	44±12	H	61±10	L	61±15	H
HO to TO	12±4	H	44±12	H	26±6	H	26±15	H
PC	38±7	L	31±3	L	37±4	L	36±6	L
Curvature (%FLT)
Linear	5±2		7±8		11±5		8±6
Convex	42±20		10±4		42±8		33±20
Concave	52±20		80±10		44±12		57±21
Magnitude (Nm/Deg)
K0	2.699±0.250	L	2.910±0.403	L	2.315±0.341	L	2.622±0.396	L
K1	0.730±0.232	H	1.489±0.303	H	0.881±0.172	L	1.001±0.392	H
K2	4.049±0.680	L	3.759±1.096	H	3.254±0.967	H	3.682±0.912	H
IA	3.319±0.679	H	2.270±1.385	H	2.373±1.076	H	2.681±1.089	H
Difference (Free-Flow foot-Usual foot)
Shape
Duration (%DUR)
HC to TC	−2	A	−3	A	−12	A	−5	A
TC to HO	5	B	−19	A	4	B	−3	B
HO to TO	−3	A	22	A	8	A	7	A
PC	−9	A	−3	B	−22	A	−10	A
Magnitude (Nm/Deg)
K0	−2.267	A	−0.934	A	−0.586	A	−1.353	A
K1	−4.724	A	−4.952	A	−2.798	A	−4.299	A
K2	0.573	A	1.740	A	1.955	A	1.349	A
IA	5.297	A	6.692	A	4.753	A	5.647	A

N: Number of gait cycles, %SUP: Percentage of support phases, HC: Heel contact, TC: Toe contact, HO: Heel off, TO: Toe off, PC: Point of curvature, %FLT: Percentage of flat foot phases, IA: Index of Anthropomorphicity, H: High PV, L: Low PV, A: Above MCID, B: Below MCID

The individual stiffness profile with usual foot showed an onset of PC, percentage of data identified as convex, K0 and IA ranged from 34±3 to 59±8 %DUR, 74±29 to 91±13 %FLT, 2.901±0.337 to 4.966±0.813 Nm/Deg and −1.978±1.477 to −4.423±1.670 Nm/Deg, respectively. The individual stiffness profile with Free-Flow foot showed an onset of PC, percentage of data identified as concave, K0 and IA ranged from 31±3 to 38±7 %DUR, 44±12 to 80±10 %FLT, 2.315±0.341 to 2.910±0.403 Nm/Deg and 2.270±1.385 to 3.319±0.679 Nm/Deg, respectively.

Altogether, 15 (47%) and 13 (41%) of the individual and grouped discrete stiffness outcomes with usual and Free-Flow feet had low variability, respectively.

All the differences in duration between both prostheses were strongly above MCID except between TC and HO for P1, P3 and grouped. The differences in onset of PC were below MCID only for P2. The differences were strongly above MCID for all individual and grouped stiffness characteristics obtained with macro (e.g., K0) and meso analyses (i.e., K1, K2, IA).

C. Overall stiffness profile

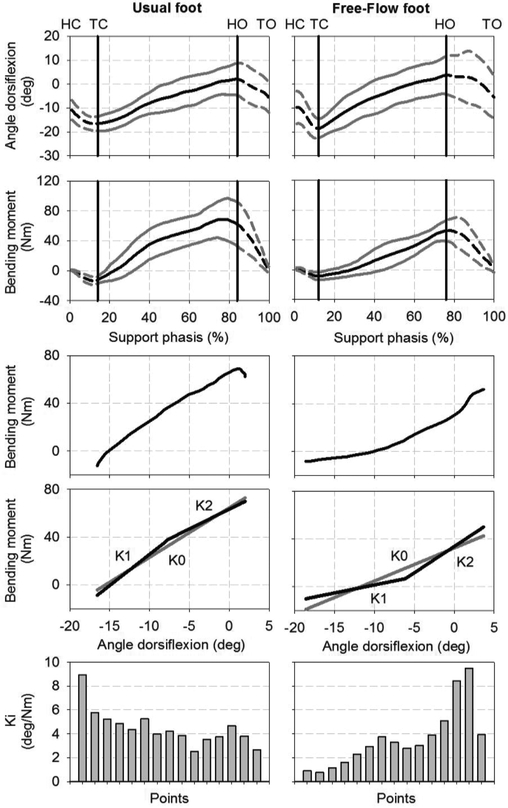
An overview of grouped angle of dorsiflexion and bending moment as well as shape and regression lines deriving from macro, meso and micro analyses of overall moment-angle curves with both prostheses are provided in Fig 3.

Fig 3.

Mean and standard deviation of grouped angle of dorsiflexion and bending moment as well as shape and regression lines deriving from macro (K0), meso (K1, K2) and micro (Ki) analyses of overall moment-angle curves of usual (N=14) and Free-Flow (N=14) feet fitted to transtibial bone-anchored prostheses. HC: Heel contact, TC: Toe contact, HO: Heel off, TO: Toe off

With usual foot, the angle of dorsiflexion progressed by 18.54 Deg from −16.55 Deg to 2.00 Deg while the bending moment progressed by 74.73 Nm from −12.29 Nm to 62.45 Nm between TC and HO, respectively. Overall stiffness profile with usual foot revealed that the durations between HC, TC, HO and TO represented 14%, 70% and 16% of support; the PC occurred at 40%SUP; 100% of the data points was classified as convex; as well as K0, K1, K2 and IA were 4.150 Nm/Deg, 5.220 Nm/Deg, 3.298 Nm/Deg and −1.922 Nm/Deg, respectively.

With Free-Flow foot, the angle of dorsiflexion progressed by 22.27 Deg from −18.60 Deg to 3.67 Deg while the bending moment progressed by 60.21 Nm from −8.28 Nm to 51.94 Nm between TC and HO, respectively. Overall stiffness profile of Free-Flow foot revealed that the durations between HC, TC, HO and TO represented 12%, 64% and 24% of support; the PC occurred at 38%SUP; 3%, 14% and 82% of data points were classified as linear, convex and concave; as well as K0, K1, K2 and IA were 2.758 Nm/Deg, 1.349 Nm/Deg, 4.401 Nm/Deg and 3.052 Nm/Deg, respectively.

Individual angle of dorsiflexion and bending moment as well as moment-angle curves will be presented in subsequent Data-In-Brief publication.

IV. DISCUSSION

A. Outcomes

The results showed that the three usual feet could be classified as non-anthropomorphic accordingly to the proposed criterion (e.g., convex individual moment-angle curves, negative IA). As expected, both grouped onset of the PC (46±12%SUP) and IA (−2.966±2.369 Nm/Deg) had high inter-variability more likely due to the range of usual feet used.

Equally, this study confirmed the anthropomorphic design of Free-Flow foot (e.g., concave individual moment-angle curves, positive IA in agreement with [3, 14]). The onset of PC (36±6%SUP) had low variability. However, IA (2.681±1.089 Nm/Deg) had high inter-variability that might be due to short acclimation time.

Differences of key stiffness outcomes above MCID between both prostheses could only be minimally explained by differences in spatio-temporal characteristics since differences in cadence were mostly below MCID.

Incidentally, the K1, K2 and IA obtained with Free-Flow foot were lower than the ones considered by Major et al (2014) when looking at the effects of prosthetic ankle stiffness on kinematics, dynamics and metabolic cost of individuals fitted with transtibial socket prostheses (K1=[9,420 N-cm/rad=1.644 Nm/Deg, 20,280 N-cm/rad =3.539 Nm/Deg]. K2=[39,430 N-cm/rad=6.882 Nm/Deg, 139,570 N-cm/rad=24.359 Nm/Deg], IA=[5.238 Nm/Deg, 20.820 Nm/Deg]), as well as the ones reported by Drevelle et al (2014) and Pillet et al (2014) for asymptomatic participants ankle stiffness (i.e., K1=0.06±0.02 Nm.kg/Deg =4.26±1.42 Nm/Deg, K2= 0.15±0.05 Nm.kg/Deg = 10.65±3.55Nm/Deg, IA= 6.39±2.13 Nm/Deg).[3, 7, 14]

Nonetheless, this initial benchmarking data tend to confirm the hypothesis that the proposed automated characterization of the ankle stiffness relying on direct loading measurement can differentiate feet with and without anthropomorphic designs fitted to transtibial BAP.

Furthermore, results showed the limitations of some commonly used analyses to determine the magnitude of the stiffness and report anthropomorphicity. The meso analysis provided a positive K0 for both feet. It was partially suitable mainly because all stiffness datapoints progressed around an upward diagonal line as described above. The micro analysis showed differences in Ki between feet. The fine tuning of window size was data processing intensive but this analysis is more likely to assist engineers in the design of components with variable stiffness over the support phase. The meso analysis and particularly the use of IA showed critical differences between feet. This analysis might be preferable in clinical context as it requires extraction of only two basic slopes (K1, K2) while reporting clinical meaningful information that reflect anthropomorphicity.

Finally, the results also highlighted the limitation of basic visual observations combining spatio-temporal and ankle joint angles only that were the least sensitive to difference in foot design. For instance, grouped angle of dorsiflexion progressed by 20.13±5.65 Deg for usual feet and by 24.95±7.46 Deg for Free-Flow feet. The dorsiflexion generated by Flee-Flow foot increased by 20% corresponding to only 4 Deg that is close to angle measurements errors. In contrast, the grouped bending moment progressed by 73.27±29.62 Nm for usual feet and by 54.99±13.37 Nm for Free-Flow feet. The bending moment generated by Flee-Flow foot decreased by 25% corresponding to 18 Nm that is well and truly larger than load measurements errors. It is difficult to ascertain if an expert can visually discriminate differences of angles. Nonetheless, these results confirmed the benefits for clinicians to rely on direct loading measurements providing individualized complementary insight into bespoke impact of components.

B. Limitations

Interpretation of differences in stiffness outcomes between prostheses was limited mainly because of unknown effects of confounders such as individual length of residuum, variation of position of transducer in relation to ankle joint, lack of blinding, short acclimation with Free-Flow foot, effect of foot size and footwear, specific spatial gait characteristics (e.g., speed of walking, walking base, step and stride length), kinematics (e.g., trunk bending, knee flexion, hip range of movement) and kinetics (e.g., knees and hips joint power) information. [65]

By definition, the generalization of stiffness outcomes must be considered carefully giving the typical intrinsic shortcoming of a case-series study and limitations listed above. Nonetheless, this study provided initial benchmark stiffness profile involving 42% of existing population with transtibial amputation fitted with press-fit fixation worldwide.

More generalizable is the methodological contributions for a practical recording, analysis and reporting of ankle stiffness profile. Indeed, this information should be considered and, possibly, educate the design of subsequent studies focusing on characterization of transtibial BAP (e.g., purchase of equipment, recording settings, software development). For example, implementation of meso analysis might reduce noticeably computing time while producing relevant clinical outcomes.

C. Future studies

The proposed meso analysis will facilitate future longitudinal studies comparing prosthetic constructs (e.g., components, alignment) for a larger cohort of individuals fitted with a transtibial prosthesis. [40, 67] This could provide a better understanding of intra- and inter-variability inherent to attachments (fixation vs socket), design of components, participants and daily activities. [68, 69]

Subsequent cross-sectional studies could establish a link between ankle stiffness outcomes and additional 3D biomechanical (e.g., dynamics, kinematics, joint work and power), physiological (e.g., EMG of residuum muscles, metabolic energy consumption, development of osseointegration, skin damages) and participants’ experience (e.g., PEQm, TAPES-M) information.

V. CONCLUSIONS

An attempt to develop a comprehensive automated characterization of ankle stiffness profile for transtibial BAP was shared for the first time. This work was also an initial effort toward laying out characterization principles for stiffness analysis while providing benchmark of stiffness data using feet with and without anthropomorphic designs.

Altogether, this study should be considered as a stepping-stone for manufacturers of components and prosthetic care providers developing international standards and guidelines for fitting safely prosthetic components to growing population of individuals with transtibial amputation fitted socket or osseointegrated fixation worldwide.

Abbreviations

%SUP

Percentage of support phases

BAP

Bone-anchored prosthesis

GC

Gait cycle

HC

Heel contact

HO

Heel-off

IA

Index of Anthropomorphicity

K0

Slope of whole moment-angle curve

K1

First slope of moment-angle curve

K2

Second slope of moment-angle curve

Ki

Instantaneous slopes of the moment-angle curve

LG_F

Long axis of the prosthetic foot

LG_L

Long axis of the prosthetic leg

MCID

Minimum clinically important difference

N

Number of gait cycles

P

Participants (P1, P2, P3)

PC

Point of curvature

PV

Percentage of variation

SUP

Support phases of gait cycle

TC

Toe contact

TO

Toe off