How to Accurately and Privately Identify Anomalies

Abstract

Identifying anomalies in data is central to the advancement of science, national security, and finance. However, privacy concerns restrict our ability to analyze data. Can we lift these restrictions and accurately identify anomalies without hurting the privacy of those who contribute their data? We address this question for the most practically relevant case, where a record is considered anomalous relative to other records.

We make four contributions. First, we introduce the notion of sensitive privacy, which conceptualizes what it means to privately identify anomalies. Sensitive privacy generalizes the important concept of differential privacy and is amenable to analysis. Importantly, sensitive privacy admits algorithmic constructions that provide strong and practically meaningful privacy and utility guarantees. Second, we show that differential privacy is inherently incapable of accurately and privately identifying anomalies; in this sense, our generalization is necessary. Third, we provide a general compiler that takes as input a differentially private mechanism (which has bad utility for anomaly identification) and transforms it into a sensitively private one. This compiler, which is mostly of theoretical importance, is shown to output a mechanism whose utility greatly improves over the utility of the input mechanism. As our fourth contribution we propose mechanisms for a popular definition of anomaly ((β, r)-anomaly) that (i) are guaranteed to be sensitively private, (ii) come with provable utility guarantees, and (iii) are empirically shown to have an overwhelmingly accurate performance over a range of datasets and evaluation criteria.

1. INTRODUCTION

At the forefront of today’s research in medicine and natural sciences is the use of data analytics to discover complex patterns from vast amounts of data [11, 23, 39]. While this approach is incredibly useful, it raises serious privacy-related ethical and legal concerns [5, 7, 20, 21] because inferences can be drawn from the analysis of the person’s data to the person’s identity, causing a privacy breach [19, 24, 26, 27, 37]. In this work, we focus specifically on the problem of identifying anomalous records, which has fundamental applications in many domains and is also crucial for scientific advancements [1, 3, 30, 40, 42]. For example, to treat cancer, we must tell if a tumor is malignant; to stop bank fraud, we must flag the suspicious transactions; and to counter terrorism, we must identify the individuals exhibiting extreme behavior. Note that in such settings, it is imperative to accurately identify the anomalies, e.g., it is critical to identify the fraudulent transactions. However, in all these situations, it is still essential to protect the privacy of the normal (i.e., non-anomalous) records [7, 21] (e.g., customers with a legitimate transaction or patients with a benign tumor) while not sacrificing accuracy (e.g., labeling a malignant tumor as benign).

We solve the problem of accurate, private, and algorithmic anomaly identification (i.e., labeling a record as anomalous or normal by an algorithm) with an emphasis on reducing false negative – labeling an anomaly as normal – rate. The current methods for protecting privacy work well for doing statistics and other aggregate tasks [17, 18], but they are inherently unable to identify anomalous records accurately. Furthermore, the modern methods of anomaly identification label a record as anomalous (or normal) based on its degree of dissimilarity from the other existing records [1, 3, 8, 35]. Consequently, the labeling of a record as anomalous is specific to a dataset, and knowing that a record is anomalous can leak a significant amount of information about the other records. This type of privacy leakage is the core obstacle that any privacy-preserving anomaly identification method must overcome. This work is the first to develop methods (in a general setting where anomalies are data-dependent) to accurately identify if a record is anomalous while simultaneously guaranteeing privacy by making it statistically impossible to infer if a non-anomalous record was included in the dataset.

We formalize a notion of privacy appropriate for anomaly detection and identification and develop general constructions to achieve this. Note that we assume a trusted curator, who performs the anomaly identification. If the data is distributed and the trusted curator is not available, one can employ secure multiparty computation to simulate the trusted curator [9], where now the same methodology as in the previous setting can be used.

Although the privacy definitions and constructions we develop are not tied to any specific anomaly definition, we instantiate them for a specific kind of anomaly: (β, r)-anomaly [35], which is a widely prevalent model for characterizing anomalies and generalizes many other definitions of anomalies [3, 22, 34, 35]. These technical instantiations naturally extend to the other well-known variants of this formalization [1]. Under this anomaly definition, a record (which lives in a metric space) is considered anomalous if there are at most β records similar to it, i.e., within distance r. The parameters β and r are given by domain experts [35] or found through exploratory analysis by possibly using differentially private methods [17, 18] (since these parameters can be obtained by minimizing an aggregate statistic, e.g., risk or average error) to protect privacy in this process.

1.1. Why do we need a new privacy notion?

We consider the trusted curator setting for the privacy. The trusted curator has access to the database, and it answers the anomaly identification queries using a mechanism. The privacy of an individual is protected if the output of an anomaly identification mechanism is unaffected by the presence or the absence of the individual’s record in the database (which is the input to the mechanism). This is the notion of privacy (i.e. protection) of a record that we consider here; it protects the individual against any risk incurred due to the presence of its information and was first formalized in the seminal work of differential privacy [15, 17] (where privacy is quantified by a parameter ε > 0: the smaller the ε, the higher the privacy) and can informally be stated as follows: a randomized mechanism that takes a database as input is ε-differentially private if for any two input databases differing by one record, the probabilities (corresponding to the two databases) of occurrence of any event are within a multiplicative factor e^ε (i.e., are almost the same in all cases). Unfortunately, simply employing differential privacy does not address the need for both privacy and practically meaningful accuracy guarantees in our case. For example, providing privacy equally to everyone severely degrades accuracy in identifying anomalies. For a database, the addition of a record in a region which is sparse in terms of data points creates an anomaly. Conversely, the removal of an anomalous record typically removes the anomaly altogether. Therefore, the accuracy achievable for anomaly identification via differential privacy is limited as explained below.

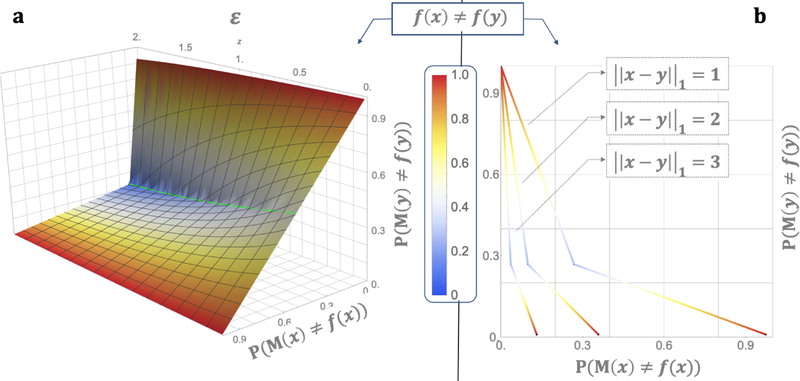
Differential privacy for binary functions $f:\mathcal{D}\to \{0,1\}$, such as the anomaly identification, comes with inherent limitations that can be explained through the graph of Figure 1a. Fix any mechanism M that is supposed to compute f, with the property that this mechanism is differentially private. The mere fact that f is binary and M is differentially private has the following effect. For any two databases x and y that differ in one record say that f (x) = 0 and f (y) = 1. Now, a simple calculation shows that the differential privacy constraints create a tradeoff: whenever M makes a small error in computing f (x) then it is forced to err a lot when computing on its “neighbor” y and vice-versa. Moreover, the higher the privacy requirements are (i.e. for smaller ε) the stricter this tradeoff is, as depicted on Figure 1a. Formally, we state this fact as follows.

Figure 1:

(a) x and y differ by one record, the “ε axis” is for the privacy parameter, the “P (M (x) ≠ f (x)) axis” is for the minimum error over all ε-DP mechanisms M on x for a give error on y on the “P (M (y) ≠ f (y)) axis”. The graph depicts the tradeoff between the errors committed on x and y. (b) this plot is for ε = 1 and otherwise is the same but for different x’s and y’s.

Claim 1. Fix $\epsilon >0,f:\mathcal{D}\to \{0,1\}$, and $\epsilon -DPM:\mathcal{D}\to \{0,1\}$ arbitrarily. For every x and y, if f (x) ≠ f (y) and ‖x − y‖₁ = 1, then P (M (x) ≠ f (x)) ≥ 1/(1 + e^ε) or P (M (y) ≠ f (y)) ≥ 1/(1 + e^ε).

What happens to this inherent tradeoff when x and y differ in more than one record? As shown on Figure 1b this tradeoff is relaxed. We note that for deriving the tradeoff, there was nothing specific to the ℓ₁ metric (used for differential privacy), but instead we could have used any metric over the space of databases; other works that considered general metrics are e.g., [25, 33]. Our work proposes a distance metric which is appropriate for anomaly identification, in conjunction to an appropriate relaxation of differential privacy. This way we will lay out a practically meaningful (but also amenable to analysis) privacy setting.

1.2. What do we want from the new notion?

We want to relax differential privacy since affording protection for everyone severely degrades the accuracy for anomaly identification. One possible relaxation, suitable for the problem at hand, is providing protection only for a subset of the records. We note that such a relaxation is backed by privacy legislation, e.g., GDPR allows for giving up privacy for an illegal activity [21]. Protecting a prefixed set of records, which is decided independent of the database, works when anomalies are defined independent of the other records. However, for a data-dependent anomaly definition, such a notion of privacy fails to protect the normal records. Here the problem arises due to the fixed nature of the set that is database-specific. In the case of a data-dependent definition of anomaly, if we wish to provide privacy guarantee to the normal – call them sensitive – records that are present in the database, then specifying the set of sensitive records itself leaks information and can lead to a privacy breach. Thus, sensitive records must be defined based on a more fundamental premise to reduces such dependencies. This notion of sensitive record plays a pivotal role in defining a notion of privacy, named sensitive privacy, which is appropriate for the problem identifying anomaly.

We remark that although anomaly identification method provide binary labeling, they assign scores to represent how outlying a record is [1, 3]; thus these models (implicitly or explicitly) assign a records a degree of outlyingness with respect to the other records, which the following discussion takes into account.

An appropriate notion of privacy in our setting must allow a privacy mechanism to have the following two important properties. First, the more outlying (or non-outlying) a record is, the higher the accuracy the privacy mechanism can achieve for anomaly identification, which is in contrast to DP (Figure 2c). Second, all the sensitive records should have DP like privacy guarantee for the same value of privacy parameter.

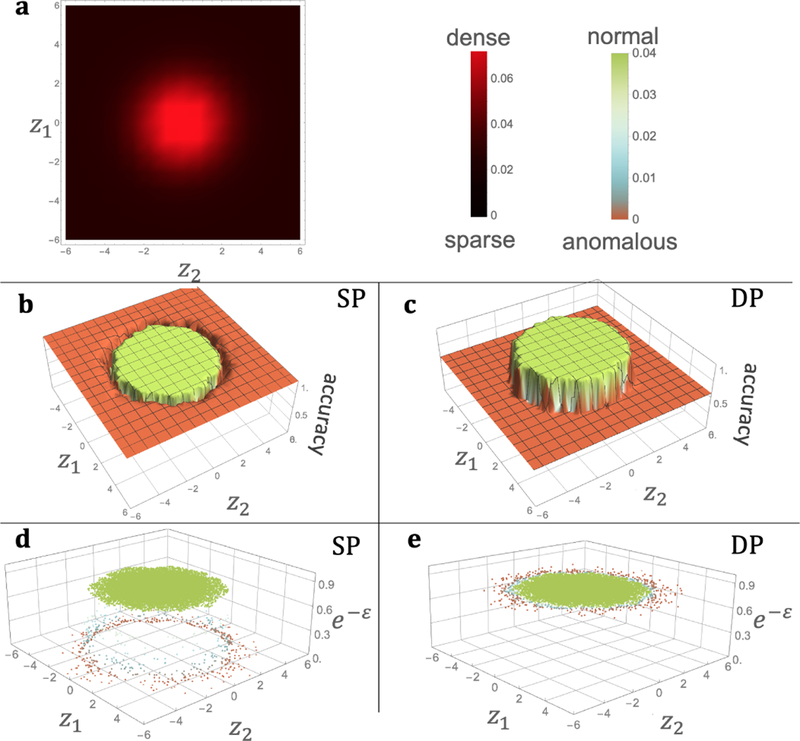
Figure 2:

(b), (c) is for the same data, and (d), (e) is for the same data. (a) gives the density plot of the distribution of the example data. z₁ and z₂ axes give the coordinate of a point (record). (b) and (c) resp. show the accuracy (on vertical axis) for anomaly identification (AId) via sensitively private (SP) and DP mechanisms for the data. The plots give the interpolated results to clarify the relationship of outlyingness and accuracy. (d) and (e) give the privacy (on vertical axis) for each record in the data for private AId. All the green (normal) points in (d) are at the same level as all the points in (e).

The mechanisms that are private under sensitive privacy achieve both the properties (see Figure 2, which gives the indicative experimental results on the example data; see Section A.1 for the details on the experiment and the values of the parameters). Furthermore, it has an additional property: in a typical setting, the anomalies do not lose privacy altogether; instead the more outlying a record is the lesser privacy it has (Figure 2d).

1.3. How do we define the new privacy notion?

To define privacy, we need a metric space over the databases since a private mechanism needs to statistically blur the distinction between databases that are close in the metric space. While differential privacy uses the ‖ · ‖₁ − metric, we utilize a different metric over databases, which can be defined using the notion of sensitive record. Informally, we say a record is sensitive with respect to a database if it is normal or becomes normal under a small change—we formalize this in Section 3. We argue that this notion of sensitive record is quite natural, and it is inspired from the existing anomaly detection literature [1, 3]. Since, by definition, an anomalous record significantly diverges from other records in the database [1, 3], a small change in the database should not affect the label of an anomalous record. Given the definition of sensitive record, a graph over the databases is defined by adding an edge between two databases if and only if they differ in a sensitive record. The metric over the databases is now given by the shortest path length between the databases in this graph. This metric space has the property that databases differing by a sensitive record are closer compared to the databases differing in a non-sensitive record. We use the proposed metric space to define sensitive privacy, which enables us to fine-tune the tradeoff between accuracy and privacy.

2. PRELIMINARIES AND NOTATION

Database:

We consider a database as a multiset of elements from a set $\mathcal{X}$, which is the set of possible values of records. In a database, we assume each record is associated with a distinct individual. We represent a database x as a histogram in $\mathcal{D}=\left\{y\in {\mathbb{N}}^{\mathcal{X}}:\Vert y{\Vert }_1<\infty \right\}$, where $\mathcal{D}$ is the set all possible database, $\mathbb{N}=\{0,1,2,\dots \}$, and x_i is the number of records in x that are identical to i.

Definition 2.1 (differential privacy [15, 17]). For ε > 0, a mechanism M with domain $\mathcal{D}$ is ε-differentially private if for every x, $y\in \mathcal{D}$ such that ‖x − y‖₁ ≤ 1, and every R ⊆ Range (M),

$$P(M(x)\in R)\le e^{\epsilon }P(M(y)\in R).$$

We implicitly assume that the R’s are chosen such that the events “M (x) ∈ R” are measurable.

Anomalies:

For any database x, record $i\in \mathcal{X}$, r ≥ 0, and a distance function $d:\mathcal{X}\times \mathcal{X}\to {ℝ}_{\ge 0}$, $B_x(i,r)=\sum _{j\in \mathcal{X}:d(i,j)\le r}{x}_j$, and define (β, r)-anomaly as follows.

Definition 2.2 ((β, r)-anomaly [35]). For a given database x and record i, we say i is a (β, r)-anomaly in the database x if i is present in x, i.e. x_i > 0, and there are at most β records in x that are within distance r from i, i.e. B_x (i, r) ≤ β.

Whenever we refer to a (β, r)-anomaly, we assume there is an arbitrary distance function d over $\mathcal{X}\times \mathcal{X}$.

Anomaly identification:

Let us now introduce the important and related notion of anomaly identification function, $g:\mathcal{X}\times \mathcal{D}\to \text{{0,1}}$, such that for a given anomaly definition, every record $i\in \mathcal{X}$ and database $x\in \mathcal{D}$, g(i, x) = 1 if and only if i is present in x as an anomalous record (note that no change is made to x). This formulation is extensible to the case where the database over which anomaly identification is performed is considered to include the record for which anomaly identification is desired. Here, the anomaly identification for a record i over a data x can be computed over the database that consists of all the records in x as well as the record i¹.

Private anomaly identification query (AIQ):.

Here, all the private mechanisms we consider have domain $\mathcal{D}$. Thus, we will consider the anomaly identification query to be for a fixed record. We will specify this by the pair (i, g), where i is a record and g an anomaly identification function. Now a private anomaly identification mechanism, $M:\mathcal{D}\to \{0,1\}$, for a fixed AIQ, (i, g), can be represented by its distribution, where for every x, P (M (x) = g(i, x)) is the probability the M output correctly, and P (M (x) ≠ g(i, x)) is the probability that M errs on x.

3. SENSITIVE PRIVACY

Our notion of sensitive privacy requires privacy protection of every record that may be normal under a small change in the database. We use the notion of normality property p to identify the normal records that exist in the database. Formally, for a given definition of anomaly, a normality property, $p:\mathcal{X}\times \mathcal{D}\to \{0,1\}$, is such that for every record i and database x, p (i, x) = 1 if and only if i is present in x as a normal record. Note that the normality property is not the negation of anomaly identification function because for the absent records p = 0 (same as those which do not satisfy the property). We formalize the notion of small change in the database as the addition or removal of k records from the database. We consider this change to be typical and want to protect the privacy of every record that may become normal under this small change in the database.

We now formalize the key notion of sensitive record. For a fixed normality property, all the records whose privacy must be protected are termed as sensitive records.

Definition 3.1 (sensitive record). For k ≥ 1 and a normality property p, we say a record i is k -sensitive with respect to a database x if, for a database y, ‖x − y‖₁ ≤ k and p (i, y) = 1.

Next, we give a couple of definitions of the graphs we consider here. A neighborhood graph, $\mathbb{G}=(\mathcal{D},E)$, is a simple graph such that for every x and y in $\mathcal{D}$, (x, y) ∈ E ⇔ ‖x − y‖₁ = 1. One of the important notions in this work is k-sensitive neighborhood graph, $G_S=\left(\mathcal{D},E^{\prime }\right)$, for k ≥ 1 and a normality property, which is a subgraph of the neighborhood graph, $\mathbb{G}=(\mathcal{D},E)$, such that for every (x, y) ∈ E, (x, y) ∈ E′ ⇔ for some $i\in \mathcal{X}$, |x_i − y_i| = 1 and i is k-sensitive with respect to x or y. Further, the two databases connected by an edge in a (sensitive) neighborhood graph are called neighbors. With this, we can state the notion of sensitive privacy. Note that the k-sensitive neighborhood graph is tied to the normality property, and hence, the anomaly definition.

Definition 3.2 (sensitive privacy). For ε > 0, k ≥ 1, and normality property, a mechanism M with domain $\mathcal{D}$ is (ε, k)-sensitively private if for every two neighboring databases x and y in k-sensitive neighborhood graph, and every R ⊆ Range (M),

$$P(M(x)\in R)\le e^{\epsilon }P(M(y)\in R)$$

We omit k when it is clear from the context. The above condition necessitates that for every two neighbors, any test (i.e., event) one may be concerned about, should occur with “almost the same probability”, that is, the presence or the absence of a sensitive record should not affect the likelihood of occurrence of any event. Here, “almost the same probability” means that the above probabilities are within a multiplicative factor e^ε. The guarantees provided by sensitive privacy are similar to that of differential privacy. Sensitive privacy guarantees that given the output of the private mechanism, an adversary cannot infer the presence or the absence of a sensitive record. Thus for neighboring databases in a sensitive neighborhood graph (G_S), the guarantee is exactly the same as in differential privacy. If x and y differ by one record, which is not sensitive, then they are not neighbors in G_S, and the guarantee provided by sensitive privacy is weaker² than differential privacy, nevertheless, has the same form. So, intuitively, if we only consider the databases, where all the records are sensitive, then differential privacy and sensitive privacy provide exactly the same guarantee. In general, every (ε, k)-SP mechanism M for G_S satisfies $P(M(x)\in R)\le P(M(y)\in R)e^{\epsilon d_{G_S}(x,y)}$ for every x, y and R, where $d_{G_S}$ is the shortest path length metric over G_S.

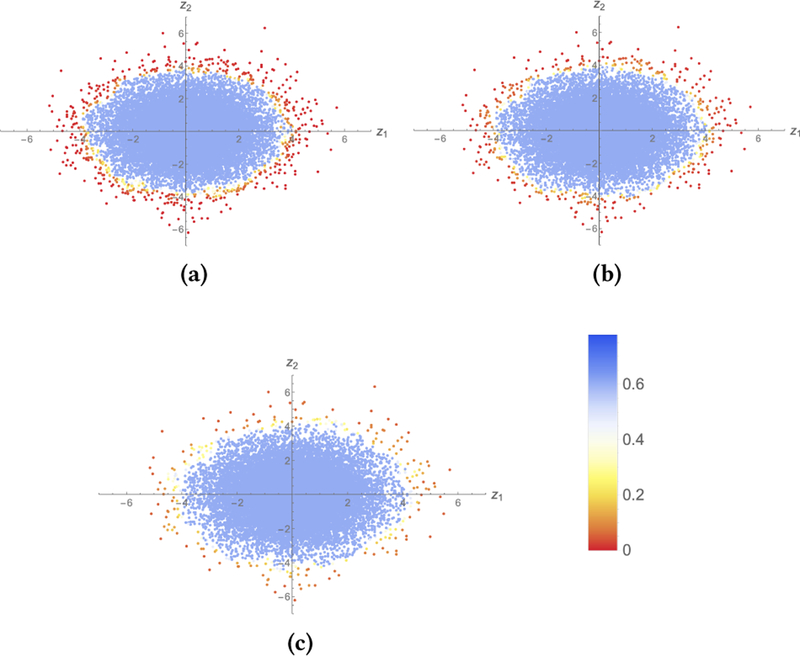
Similar to differential privacy, ε is the privacy parameter: the lower its value, the higher the privacy guarantee. The parameter k, which is associated with the sensitive neighborhood graph, provides a way to quantify what is deemed as a small change in the database, which varies from field to field, but nevertheless in many common cases can be quantified over an appropriate metric space.³. When we increase the value of k, we move the boundary between what is considered sensitive and what is non-sensitive (Figure 3, where the plots are similar to the ones given in Figure 2d for the same parameter values but for varying k): higher the value of k, the more records are considered sensitive, and therefore, must be protected. This is due to the fact that, for any k ≥ 1, if a record is k-sensitive with respect to a database x, it is also (k + 1)-sensitive with respect to x. For example, with respect to a database x, a 2-sensitive record, may not be 1-sensitive, but a 1-sensitive record will also be 2-sensitive.

Figure 3:

(a)-(c), the plot is for the same data. The two axes give the coordinate of a point (record). The color gives the level of privacy, i.e. the value e^−ε, for 0.25-SP AIQ for every record (the data was generated using generated using the distribution given in Figure 2). (a), k = 1. (b), k = 7. (c), k = 14.

3.1. Composition

Our formalization of sensitive privacy enjoys the important properties of composition and post-processing [18], which a good privacy definition should have [32]. Hence, we can quantify how much privacy may be lost (in terms of the value of ε) if one asks multiple queries or post-processes the result of a private mechanism. Here, we recall that sensitive privacy is defined with respect to the k-sensitive neighborhood graph for the privacy parameter ε. Thus, the privacy composes with respect to both, the privacy parameter (i.e. ε) and the sensitive neighborhood graph.

Sequential composition provides the privacy guarantee over multiple queries over the same database, where the same record(s) in the database may be used to answer more than one query. Consider two mechanisms $M_1:\mathcal{D}\to R$, which is ε₁-sensitively private for k₁-sensitive neighborhood graph $G_{S_1}=\left(\mathcal{D},E_1\right)$, and $M_2:\mathcal{D}\times R\to R^{\prime }$, which is ε₂-sensitively private for k₂-sensitive neighborhood graph $G_{S_2}=\left(\mathcal{D},E_2\right)$, with independent sources of randomness. Recall that for a private mechanisms for AIQ, (i, g), is fixed; thus M₁ and M₂ may correspond to different records and anomaly identification function. Now, M₂ (x, M₁(x)) (for every database x) is (ε₁ + ε₂)-sensitively private for $G_S=\left(\mathcal{D},E_1\cap E_2\right)$ (Claim 3). One application of this is that for a fixed G_S, even performing multiple queries interactively will lead to at most a linear loss (in terms of ε) in privacy in the number of queries—in an interactive query over a database x, one firstly gets the answer of M₁, i.e., M₁(x), and based on the answer, one selects M₂ and gets its answer. Furthermore, for a fixed normality property, if k₁ ≤ k₂ then $G_{S_1}$ is a subgraph of $G_{S_2}$, then M₂ is (ε₁ + ε₂)-sensitively private for $G_{S_1}$.

Parallel composition deals with multiple queries, each of which only uses non-overlapping partition of the database. Let $\mathcal{X}=Y_1\cup Y_2$ such that Y₁ ∩ Y₂ = ∅. Now, consider M₁ and M₂, each with domain $\mathcal{D}$, that are respectively ε₁-sensitively private for $G_{S_1}$ and ε_2-sensitively private for $G_{S_2}$, where $G_{S_1}$ is a subgraph of $G_{S_2}$. Further, M₁ and M₂ only depend on their randomness (each with its independent source) and records in Y₁ and Y₂ respectively. In this setting, a mechanism M (x) = (M₁(x), M₂ (x)) is max (ε₁, ε₂)-sensitively private for $G_{S_1}$, or in general case for sensitive neighborhood graph $\left(\mathcal{D},E_1\cap E_2\right)$ (Claim 4), where E₁ and E₂ are the sets of edges for $G_{S_1}$ and $G_{S_2}$ respectively.

We also remark that privacy is maintained under post-processing.

Example:

Consider composition for sensitive privacy for the case of multiple (β, r)-AIQs. Let us say we answer anomaly identification queries for records i₁, i₂, … , i_n respectively for (β₁, r₁), (β₂, r₂), … ,(β_n, r_n) anomalies over the database x, while providing sensitive privacy. Let the mechanism for answering (β_t, r_t)-AIQ for i_t be ε_t-SP for k_t-sensitive neighborhood graph corresponding to (β_t, r_t)-anomaly, and assume it depends on the partition of the database that contains the records within distance r_t of i_t (because it suffices to compute (β_t, r_t)-AIQ) and its independent source of randomness. Let k = min(k₁, … , k_n), β = max(β₁, … , β_n), and r = min(r₁, … , r_n). In this case, the sensitive privacy guarantee for answering all of the queries is m ε for k-sensitive neighborhood graph corresponding to (β, r)-anomaly, where m is the maximum number of i_t’s that are within any ball of radius max(r₁, … , r_n) (Claim 5).

Thus, from the above, it follows that if we fix β, r and k and allow a querier to ask m many (β′, r)-AIQ’s (each may have a different value for β′) such that β′ ≤ β, then we can answer all of the queries with sensitive privacy mε in the worst case for k-sensitive neighbor for to (β, r)-anomaly. The same is true if the queries are for (β, r′) with r′ ≥ r. Furthermore, for fixed β, r and k, answering (β, r)-AIQ for i and i′ such that d (i, i′) > 2r still maintains (ε, k)-SP. One may employ this to query adaptively to carry out the analysis while providing sensitive privacy guarantees over analysis as a whole.

4. PRIVACY MECHANISM CONSTRUCTIONS

In this section we will show how to construct a private mechanisms for (β, r)-anomaly identification. Specifically, (i) we will give an SP mechanism that errs with exponentially small probability on most of the typical inputs (Theorem 4.6), (ii) we will provide a DP mechanism construction for (β, r)-AIQ, which we will prove is optimal (Theorem 4.4), (iii) we will present a compiler construction that can compile a “bad” DP mechanism for AIQ to a “good” SP mechanism (Theorem 4.7) – here good and bad are indicative of utility. We will use these mechanism to evaluate the performance of our method over real world and synthetic datasets.

Recall that a privacy mechanism, $M:\mathcal{D}\to \{0,1\}$, for a fixed AIQ, (i, g), will output the labels of i for the given database, where g is an anomaly identification function and i is a record. The sensitive privacy requires that the shorter the distance between any two databases, x and y, in the sensitive neighborhood graph (G_S), the closer the probabilities of any output (R) of the mechanism M corresponding to the two databases should be, that is, $e^{-\epsilon d_{G_S}(x,y)}\le \text{P}(M(x)=R)/\text{P}(M(y)=R)\le e^{\epsilon d_{G_S}(x,y)}$. Thus, for an x, the greater is the distance to the closest y such that g(i, x), ≠ g(i, y), the higher accuracy a private mechanism can achieve on the input x for answering g(i, x). We capture this metric-based property by the minimum discrepant distance (mdd) function. Fix an anomaly identification function g. For a given sensitive neighborhood graph G_S, ${\text{Δ}}_{G_S}$ is mdd-function, if for every i and x,

$${\text{Δ}}_{G_S}(i,x)=\underset{y\in \mathcal{D}:g(i,y)\ne g(i,x)}{\text{min}}{d}_{G_S}(x,y)$$ (1)

A simple and efficient mechanism for anomaly identification that is both accurate and sensitively private can be given if g and the ${\text{Δ}}_{G_S}$ (the corresponding mdd-function) can be computed efficiently. However, computing the mdd-function efficiently for an arbitrary anomaly definition is a non-trivial task. This is because the metric, $d_{G_S}$, which gives rise to the metric-based property captured by the mdd-function, is induced by (a) the definition of anomaly (e.g. specific values of β and r) and (b) the metric over the records. Thus, making it exceedingly difficult to analyze it in general.

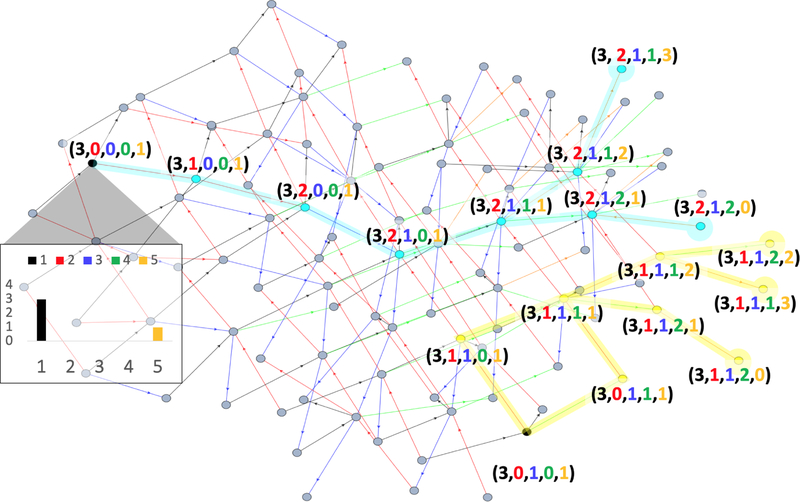
We use the example given in Figure 4 to explain the above mentioned relationships of mdd-function. This figure depicts a subgraph of 1-sensitive neighborhood graph for (β = 3, r = 1)-anomaly. One can appreciate the conceptual difficulty in calculating mdd-function, ${\text{Δ}}_{G_S}$ (for this setting) by for example thinking the value of ${\text{Δ}}_{G_S}(5,(3,0,0,0,1))$ (and recall that this is just a 1-sensitive neighborhood graph). Next, note that for a given database x and a record i, the shorter is the distance of the closest sensitive record from i, the smaller the value of ${\text{Δ}}_{G_S}(i,x)$, e.g. ${\text{Δ}}_{G_S}(5,(3,0,0,0,1))>{\text{Δ}}_{G_S}(5,(3,2,1,0,1))$. Furthermore, the presence of non-sensitive records can also influence the value of the mdd-function, e.g. ${\text{Δ}}_{G_S}(5,(3,0,0,0,1))>{\text{Δ}}_{G_S}(5,(3,0,1,0,1))$ although the closest sensitive record to 5 is the same in both the databases. In addition, the values of β and r also affect the value of mdd-function, and in most realistic settings, the size of $\mathcal{X}$ is large, and the sensitive neighborhood graph is quite complex.

Figure 4:

Sensitive neighborhood graph. A simple example of a 1-sensitive neighborhood graph, G_S, with $\mathcal{X}=\{1,2,3,4,5\}$, ℓ_1-metric over $\mathcal{X}\times \mathcal{X}$, and (β = 3, r = 1)-anomaly. Note that G_S is an undirected graph; arrowheads indicates the record is added at the end node; the color of the edge corresponds (as per the given color code) to the value of the record added. Further, each database x is represented as a 5-tuple with x_i for $i\in \mathcal{X}$ representing the number of records in x that have value i.

Below, we provide our constructions that uses a lower bound on the mdd-function to give sensitively private mechanism, which does not depend upon any particular definition of anomaly. Thus it can be used to give private mechanisms for AIQ’s as long as one is able to compute the lower bound.

4.1. Construction: SP-mechanism for AIQ by lower bounding mdd-function

Here, we show how to construct an SP mechanism for identifying anomalies by using a lower bound, λ, for the mdd-function. Our construction (Construction 1) will be parameterized by λ, which is associated with a sensitive neighborhood graph. Since the sensitive neighborhood graph is tied to an anomaly definition, it will become concrete once we give the definition of anomaly (e.g., see Section 4.1.1 and Section 4.1.2).

For any fixed AIQ, (i, g), and given λ, Construction 1 provably gives an SP mechanism as long as λ fulfills the following two properties: (1) for every i and x, λ(i, x) ≥ 1 and (2) λ is 1-Lipschitz continuous lower bound on the mdd-function (Theorem 4.1).

For a sensitive neighborhood graph, G_S, we say a function $f:\mathcal{X}\times \mathcal{D}\to ℝ$ is α-Lipschitz continuous if for every $i\in \mathcal{X}$ and neighboring databases x and y in G_S, |f (i, x) − f (i, y)| ≤ α.

We remark that although at first it appears that the Lipschitz continuity condition is some side technicality, in fact bounding its value constitute the main part of our argument for privacy of our mechanisms. Thus giving an SP mechanism for (i, g) via Construction 1 reduces to giving a Lipschitz continuous lower bound for the mdd-function corresponding to g.

Construction 1. U_λ

1. Input $x\in \mathcal{D}$.

2. Set t = e^{−ε(λ (i, x)−1)}/(1 + e^ε).

3. Sample b from {0, 1} such that P (b ≠ g(i, x)) = t.

4. Return b.

Note that the above is a family of constructions parameterized by λ (as mentioned above), i.e., one construction, U_λ, for each λ. This construction is very efficiently realizable as long as we can efficiently compute g and λ. Furthermore, the error of the mechanism, yielded by the construction, for any input is exponentially small in λ (Claim 2, which immediately follows from the construction).

Claim 2. For given ε, (i, g), and λ, U_λ (Construction 1) is such that P (U (x) ≠ g(i, x)) = e^{−ε (λ (i, x)−1)}/(1 + e^ε) for every x.

Theorem 4.1 (U_λ is SP). For any given ε, AIQ, and a 1-Lipschitz continuous lower bound λ on the corresponding mdd-function for k-sensitive neighborhood graph, G_S, such that λ ≥ 1, Construction 1 yields an (ε, k)-sensitively private mechanism.

In order to show that the theorem holds, it suffices to verify that for every i and every two neighboring x and y in G_S, the privacy constraints hold. For any AIQ, (i, g), this is immediate when g(i, x) = g(i, y) because λ is 1-Lipschitz continuous. When g(i, x) ≠ g(i, y), λ(i, x) = λ(i, y) = 1 because ${\text{Δ}}_{G_S}(i,x)={\text{Δ}}_{G_S}(i,y)=1$ and λ ≥ 1. Thus, the constraints are satisfied in this case as well. The complete proof for Theorem 4.1 is given in Appendix A.4. Additionally, a simple observation on the proof of Theorem 4.1, shows that if the given λ is α-Lipschitz continuous with α ≥ 1, then Construction 1 yields an (ε · α)-sensitively private mechanism.

In the following two sections, we instantiate Construction 1 to give differentially private and sensitively private mechanisms for performing (β, r)-anomaly identification query. We will use these mechanisms in our empirical evaluation over real world datasets.

4.1.1. Optimal DP-mechanism for (β, r)-AIQ.

Here, we show how to use Construction 1 to give an optimal differentially private mechanism for (β, r)-AIQ. Note that we will use this mechanism in experimental evaluation (Section 5) and compare its performance with our SP mechanism (which we will present shortly). We begin by restating the definition of DP in terms of the neighborhood graph. This restatement will immediately establish that SP generalizes DP, a fact we will use to build DP mechanism.

Definition 4.2 (DP restated with neighborhood graph). For ε > 0, a mechanism, M, with domain $\mathcal{D}$, is ε-differentially private if for every two neighboring databases, x and y, in the neighborhood graph, and every R ⊆ Range (M),

$$P(M(x)\in R)\le e^{\epsilon }P(M(y)\in R).$$

From Definition 3.2 (of sensitive privacy) and Definition 4.2, it is clear that differential privacy is a special case of sensitive privacy, when the k-sensitive neighborhood graphs, G_S, is the same as neighborhood graph, $\mathbb{G}$, i.e., $G_S=\mathbb{G}$. Thus, for $G_S=\mathbb{G}$, a mechanism is ε-differentially private if and only if it is ε-sensitively private. This observation is sufficient to give a differentially private mechanism for AIQ by using Construction 1.

We use $\lambda ={\text{Δ}}_{\mathbb{G}}$ in Construction 1 to give the DP mechanism for (β, r)-AIQ, where ${\text{Δ}}_{\mathbb{G}}$ (mdd-function) for an arbitrary β, r, i and x is given below. This will yield a DP mechanism as long as the given ${\text{Δ}}_{\mathbb{G}}$ for (β, r)-AIQ is 1-Lipschitz continuous, a fact that immediately follows from the above observation and Theorem 4.1. We claim that for any given β and r, ${\text{Δ}}_{\mathbb{G}}$ (given by (2)) is mdd-function for the (β, r)-AIQ and is 1-Lipschitz continuous (Lemma 4.3).

$${\text{Δ}}_{\mathbb{G}}(i,x)=\{\begin{array}{ll}1\hfill & x_i=0\wedge B_x(i,r)<\beta \hfill \\ 2+B_x(i,r)-\beta \hfill & x_i=0\wedge B_x(i,r)\ge \beta \hfill \\ \text{min}\left(x_i,\beta +1-B_x(i,r)\right)\hfill & x_i>0\wedge B_x(i,r)\le \beta \hfill \\ B_x(i,r)-\beta \hfill & x_i>0\wedge B_x(i,r)>\beta \hfill \end{array}$$ (2)

Lemma 4.3. For any fixed (β, r)-AIQ, (i, g), the ${\text{Δ}}_{\mathbb{G}}$ given by (2) is mdd-function for g and is 1-Lipschitz continuous.

The proof of Lemma 4.3 can be found in Appendix A.5.

We claim that for any fixed (β, r)-AIQ, (i, g), $U_{{\text{Δ}}_{\mathbb{G}}}$ (given by our construction) is differentially private and errs minimum for all the inputs (Theorem 4.4), namely, it is pareto optimal. We say $U_{{\text{Δ}}_{\mathbb{G}}}$ is pareto optimal ε-DP mechanism if (a) it is ε-DP and (b) for every ε-DP mechanism $M:\mathcal{D}\to \{0,1\}$ and every database $x\in \mathcal{D}$, $P\left(U_{{\text{Δ}}_{\mathbb{G}}}(x)=g(i,x)\right)\ge P(M(x)=g(i,x))$. Particularly, this implies that of all the DP mechanisms yielded by Construction 1, each corresponding to a different λ, the “best” mechanism is for $\lambda ={\text{Δ}}_{\mathbb{G}}$.

Theorem 4.4 ($U_{{\text{Δ}}_{\mathbb{G}}}$ is optimal and DP). For any fixed (β, r)-AIQ, $U_{{\text{Δ}}_{\mathbb{G}}}$ (Construction 1) is pareto optimal ε-differentially private mechanism, where ${\text{Δ}}_{\mathbb{G}}$ is given by (2).

4.1.2. SP-mechanism for (β, r)-AIQ.

We employ Construction 1 to give a (ε, k)-sensitively private mechanism for (β, r)-AIQ. We provide λ_k below, which is 1-Lipschitz continuous lower bound on the mdd-function for the k-sensitive neighborhood graph for (β, r)-anomaly (Lemma 4.5). For the λ_k, Construction 1 yields $U_{{\lambda }_k}$ that is (ε, k)-SP mechanism, and for non-sensitive records $U_{{\lambda }_k}$ can have exponentially small error in β (Theorem 4.6).

$${\lambda }_k(i,x)=\{\begin{array}{ll}{\text{Δ}}_{\mathbb{G}}(i,x)\hfill & B_x(i,r)\ge \beta +1-k\hfill \\ \beta +1-B_x(i,r)+\text{min}\left(0,x_i-k\right)\hfill & B_x(i,r)<\beta +1-k\hfill \end{array}$$ (3)

Lemma 4.5. Arbitrarily fix k, β ≥ 1 and r ≥ 0. Let g be (β, r)-anomaly identification function and ${\text{Δ}}_{G_S}$ be the mdd-function for g, where G_S is the k-sensitive neighborhood graph for (β, r)-anomaly. The λ_k given by (3) is 1-Lipschitz continuous lower bound on ${\text{Δ}}_{G_S}$.

The proof of Lemma 4.5 is given in Appendix A.7.

It is clear form the definition of λ_k (given by 3) that when a record, i, is k-sensitive with respect to x, ${\lambda }_k(i,x)={\text{Δ}}_{\mathbb{G}}(i,x)$, which implies that there is no gain in utility (i.e. accuracy) compared to the optimal DP mechanism (in Section 4.1.1). However, when a record is not sensitive, $\lambda (i,x)>{\text{Δ}}_{\mathbb{G}}(i,x)$, our SP mechanism achieves much higher utility compared to the optimal DP mechanism, which is especially true for strong (β, r)-anomalies (i.e. the records that lie in a very sparse region).

Theorem 4.6 (accuracy and privacy of $U_{{\lambda }_k}$). Fix any (β, r)-AIQ, (i, g). The mechanism, $U_{{\lambda }_k}$ (Construction 1 for λ_k above) is (ε, k)-SP such that for every i and x, if i not sensitive for x, then

$$P\left(U_{{\lambda }_k}(x)\ne g(i,x)\right)\le e^{-\epsilon |\beta +1-k-B_x(i,r)|}.$$

The privacy claim follows from Lemma 4.5 and Theorem 4.1, while the accuracy claim is an immediate implication from Construction 1 based on the definitions of ${\text{Δ}}_{\mathbb{G}}$ and λ_k – note that B_x (i, r) < β + 1 − k implies i is not sensitive for x (Lemma A.2).

We give an example to show that $U_{{\lambda }_k}$ achieves high accuracy in typical settings. Fix k ≤ β/10. Now for any record i in a database x, satisfying B_x (i, r) ≤ β/2 is an outlier for which $U_{{\lambda }_k}$ will err with probability less that e^{−2ε β/5}.

4.2. Compiler for SP-mechanism for AIQ

In this section, we present a construction compiler, which compiles a differentially private mechanism for an anomaly identification query into a sensitively private one. This SP mechanism can outperform the differentially private mechanism. Furthermore, our compiler is not specific to any particular definition of anomaly or any specific DP mechanism. The differentially private mechanism, which the compiler takes, is given in terms of its distribution over the outputs for every input. The compiled SP mechanism comparatively has much better accuracy for the non-sensitive records; however, for the sensitive records, the SP and the input DP mechanism err by the same amount.

It is noteworthy that for many problems, we already know the distributions given by differentially private mechanisms [15, 17, 18]. Thus, our construction can be employed using these mechanism as long as the distributions given by the differentially private mechanism are not too “wild”, for example, the probability of the wrong answer for any input is not too high (we formalize this below), which is typically true.

The compiler construction is parameterized by δ. This δ must be a non-negative lower bound on ${\text{Δ}}_{G_S}-{\text{Δ}}_G$ that is also 2-Lipschitz continuous (${\text{Δ}}_{G_S}$ and ${\text{Δ}}_{\mathbb{G}}$ are the mdd-functions for an arbitrarily fixed g, and G_S is the k-sensitive neighborhood graph for anomaly definition for g). The non-negativity constraint is a side technicality; however, bounded divergence (i.e., the Lipschitz continuity constraint) and the lower bound constraint play a pivotal role in arguing bout the privacy of the compiled mechanism. Given below is our construction, and it will be useful when obtaining δ is easier than λ, and we already know the distributions of a DP mechanism for the problem.

Construction 2. U_δ

1. Input $x\in \mathcal{D}$.

2. Set $t=\text{P\hspace{0.17em}}(M(x)\ne g(i,x))/e^{\frac{\epsilon }{4}\delta (i,x)}$.

3. Sample b from {0, 1} such that P (b ≠ g(i, x)) = t.

4. Return b.

The differentially private mechanism (in terms of its distributions) that can be transformed (with provable guarantees) through our compiler is termed as a valid mechanism. For ε > 0 and any fixed AIQ, (i, g), we say an ε-DP mechanism, $M:\mathcal{D}\to \{0,1\}$, is valid if for every two neighbors x and y in the neighborhood graph with g(i, x) = g(i, y) = b for some b ∈ {0, 1}, the following holds

$$1-\text{P}(M(x)\ne b)e^{-\epsilon }\le e^{2\epsilon }(1-\text{P}(M(y)\ne b)).$$

Note that any ε-differentially private mechanism, M, for a fixed AIQ, (i, g), that satisfies P (M (x) ≠ g(i, x)) ≤ e^2ε/(1 + e^2ε) for every x is valid – this is shown below for ε > 0 and two arbitrary neighbors x and y such that b = g(i, x) = g(i, y); hence the notion of valid differentially private mechanism is well defined.

$$\text{P}(M(y)\ne b)\le \frac{e^{2\epsilon }}{e^{2\epsilon }+1}\Rightarrow \text{P}(M(y)\ne b)e^{4\epsilon }-\text{P}(M(y)\ne b)\le e^{2\epsilon }\left(e^{2\epsilon }-1\right)$$

since M is ε-DP, it follows from the above

$$\text{P}(M(y)\ne b)e^{4\epsilon }-\text{P}(M(x)\ne b)e^{\epsilon }\le e^{2\epsilon }\left(e^{2\epsilon }-1\right)\Rightarrow 1-\text{P}(M(x)\ne b)e^{-\epsilon }\le e^{2\epsilon }(1-\text{P}(M(y)\ne b))$$

We claim that for a given valid differentially private mechanism, M, for a fixed AIQ, (i, g), and non-negative 2-Lipschitz continuous lower bound δ on ${\text{Δ}}_{G_S}-{\text{Δ}}_{\mathbb{G}}$, Construction 2 complies M into a sensitively private mechanism, U_δ (Theorem 4.7). We stress that for the compiled SP mechanism, the probability of error can be exponentially smaller compared to the input DP mechanism. which is especially true for the non-sensitive records. This leads to an improvement in accuracy. Clearly, as the input mechanism, M, to the compiler becomes better (i.e., has lower error) so does the compiled sensitively private mechanism, U_δ, since the error of U_δ, is never more than that of M.

Theorem 4.7. For k ≥ 1 and a given valid ε/2-DP mechanism, M, for any AIQ, (i, g), and non-negative 2-Lipschitz continuous lower bound, δ, on ${\text{Δ}}_{G_S}-{\text{Δ}}_G$, Construction 2 yields an ε-SP mechanism, U_δ, for k-sensitive neighborhood graph corresponding to the anomaly definition for g such that

$$P\left(U_{\delta }(x)\ne g(i,x)\right)=P(M(x)\ne g(i,x))e^{-\frac{\epsilon }{4}\delta (i,x)}.$$

To confirm the above claim, we show that the mechanism, U_δ, given by the construction above indeed satisfies the privacy constraints imposed by the sensitive privacy definition for every two neighboring databases in k-sensitive neighborhood graph. We can accomplish this by showing that the privacy constraints are satisfied by any two arbitrarily picked neighbors, x and y, for an arbitrarily picked valid ε/2-differentially private mechanism, M, for an anomaly identification query, (i, g) and a δ as specified above. We can divide the argument into two cases, and confirm in each case that the privacy constraints are satisfied. Case 1: δ (i, x) = δ (i, y) = 0, which follows due to M being differentially private; because if M is ε/2-differentially private then it is also ε-differentially private. Case 2: δ (i, x) > δ (i, y) ≥ 0 — this is without loss of generality since x and y are picked arbitrarily. This case holds because of the following: M is valid ε/2-differentially private, δ is non-negative and 2-Lipschitz continuous, g(i, x) = g(i, y) (because for neighboring x and y, ${\text{Δ}}_{G_S}(i,x)-{\text{Δ}}_{\mathbb{G}}(i,x)\ge \delta (i,x)>0$ implies ${\text{Δ}}_{G_S}(i,x)\ge 2)$. We give the complete proof of Theorem 4.7 in Appendix A.8.

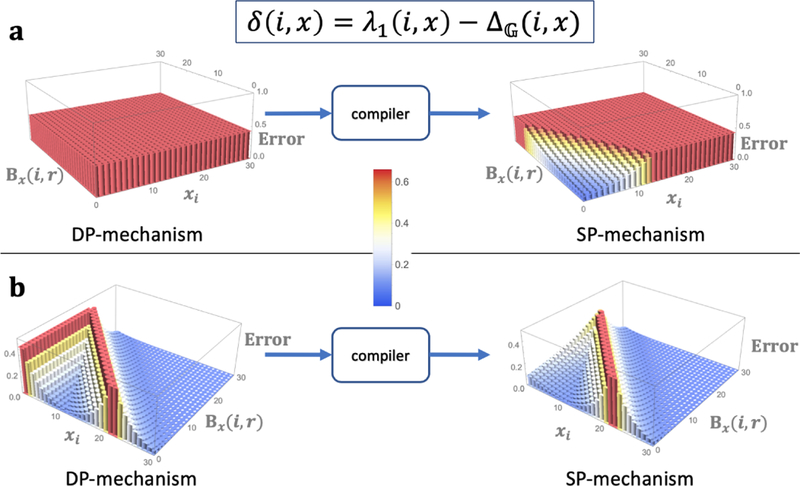
We highlight the effectiveness of the compiler by instantiating it for $\delta (i,x)={\lambda }_1(i,x)-{\text{Δ}}_{\mathbb{G}}(i,x)$ for every i and x for (β, r)-anomaly. Figure 5 shows the compilation of two DP mechanisms for (β, r)-AIQ, which widely differ in their performance. As expected, the compiled SP-mechanism outperforms the input DP-mechanism.

Figure 5:

compilation of DP-mechanism for (β, r)-AIQ into SP-mechanism. In both (a) and (b), the input mechanism is 0.25-DP for a fixed record i and δ (given in the figure). Each database x is given by (x_i, B_x (i, r)) since (β, r)-anomaly identification function only depends upon x_i and B_x (i, r)). Each mechanism is depicted by its error over databases i.e. P (M (x) ≠ g(i, x)). (a), DP-mechanism has constant error ≈ 0.44. (b), DP-mechanism has error $\approx 0.56/e^{0.25{\text{Δ}}_{\mathbb{G}}(i,x)}$.

In Figure 5a, the input DP mechanism, M, has a constant error for every input database, that is, 1/(1 + e^ε) for fixed ε = 0.25. Clearly, this mechanism has extremely bad accuracy. This is a difficult case even for the compiled mechanism, which nevertheless, attains exponential gain in accuracy for non-sensitive records. However, when we input the DP-mechanism given in Section 4.1.1, which is much better than the one in Figure 5a, the compiled mechanism is clearly superior compared to the one in Figure 5a (Figure 5b).

Note that the δ in Figure 5 is a non-negative 2-Lipschitz continuous lower bound on ${\text{Δ}}_{G_S}-{\text{Δ}}_G$ (as required by Theorem 4.7), where λ₁ is given by (3) for k = 1 and ${\text{Δ}}_{\mathbb{G}}$ is given by (2). $\delta ={\lambda }_1-{\text{Δ}}_{\mathbb{G}}\ge 0$ follows because ${\text{Δ}}_{G_S}\ge {\lambda }_1\ge {\text{Δ}}_{\mathbb{G}}$. The first inequality follows from Lemma 4.5. The second one trivially holds true for all the cases except for x_i ≥ 1 and B_x (i, r) < β, where λ₁(i, x) = β + 1 − B_x (i, r) and ${\text{Δ}}_{\mathbb{G}}(i,x)=\text{min}\left(x_i,\beta +1-B_x(i,r)\right)$; thus, even in this case, we get δ (i, x) = max(β + 1 B_x(i, r) − x_i, 0) ≥ 0. The 2-Lipschitz continuity of δ follows from the λ₁ and ${\text{Δ}}_{\mathbb{G}}$ being 1-Lipschitz continuous (Lemma 4.5 and Lemma 4.3). Thus, for any i and two neighbors x and y in G_S (1-sensitive neighborhood graph),

$$|\delta (i,x)-\delta (i,y)|\le |{\lambda }_1(i,x)-{\lambda }_1(i,y)|+|{\text{Δ}}_{\mathbb{G}}(i,x)-{\text{Δ}}_{\mathbb{G}}(i,y)|\le 2.$$

Remark:

We emphasize that both of our constructions are not tied to any specific definition of anomaly, and even the requirement of Lipschitz continuity is due to privacy constraints.

5. EMPIRICAL EVALUATION

To evaluate the performance of the SP-mechanism for (β, r)-anomaly identification, we carry out several experiments on synthetic dataset and real-world datasets from diverse domains: Credit Fraud [10] (available at Kaggle [23]), Mammography and Thyroid (available at Outlier Detection DataSets Library [41]), and APS Trucks (APS Failure at Scania Trucks, available at UCI machine learning repository [14]). Table 1 provides the datasets specifications.

Table 1:

dataset specifications and parameter values.

Dataset	size	dim	(β, r)	true (β, r) - anomalies
Credit Fraud	284,807	28	(1022, 6.7)	103
APS Trucks	60,000	170	(282,16.2)	677
Synthetic	20,000	200	(97,3.8)	201
Mammography	11,183	6	(55,1.7)	75
Thyroid	3, 772	6	(18,0.1)	61

To generate the synthetic data, we followed the strategy of Dong et al. [12], which is standard in the literature. The synthetic data was generated from a mixed Gaussian distribution, given below, where I is the identity matrix of dimension d × d, σ << 1, and e_it is a standard base. In our experiments, we used ρ = .01 and a = 5, and chose a standard bases uniformly at random.

$$(1-\rho )\mathcal{N}(0,I)+\sum _{t=1}^a(\rho /a)\left[\frac{1}{2}\mathcal{N}\left({\sqrt{d/\rho }\mathbf{\text{e}}}_{i_t},{\sigma }^{2}I\right)+\frac{1}{2}\mathcal{N}\left(-\sqrt{d/\rho }{\mathbf{\text{e}}}_{i_t},{\sigma }^{2}I\right)\right]$$

The aim of this work is to study the effect of privacy in identifying anomalies. So we keep the focus on evaluating the proposed approach for achieving privacy for this problem, and how it compares to differential privacy in real world settings. Our experiments make use of (popular) (β, r) notion of anomaly.

Following the standard practice for identifying outliers in the data with higher dimension [1, 28], we carried out the principal component analysis (PCA) to reduce the dimension of the three datasets with higher dimension. We chose, top 6, 9, and 12 features for the Credit Fraud, Synthetic, and APS Trucks datasets respectively. Next, we obtain the values of β and r, which typically are provided by the domain experts [35]. Here, we employed the protocol outlined in Appendix A.2 to find β and r; this protocol follows the basic idea of parameter selection presented in the work [35] that proposed the notion of (β, r)-anomaly. Table 1 gives the values of β and r, which we found through the protocol, along with the number of true (β, r)-anomalies (true anomalies identifiable by (β, r)-anomaly method for the given parameter values).

Error:

We measure the error of a private mechanism (which is a randomized algorithm) as its probability of outputting the wrong answer—recall that in the case of AIQ, there are only two possible answers, i.e. 0 or 1. For each AIQ for a fixed record, we estimate the error by the average number of mistakes over m trials. So for our experiments we choose m to be 10000.

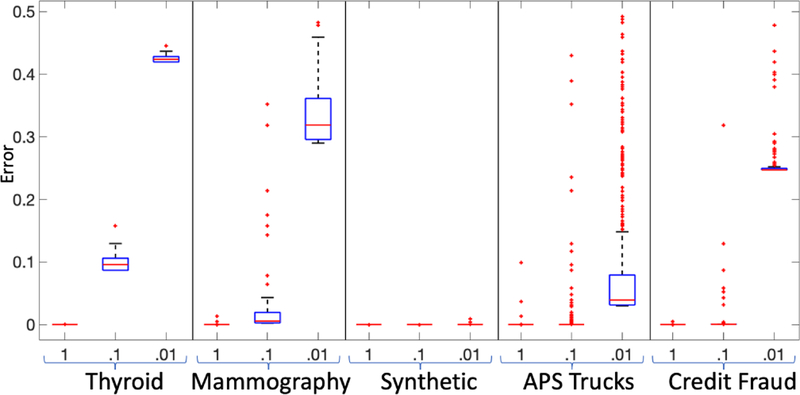
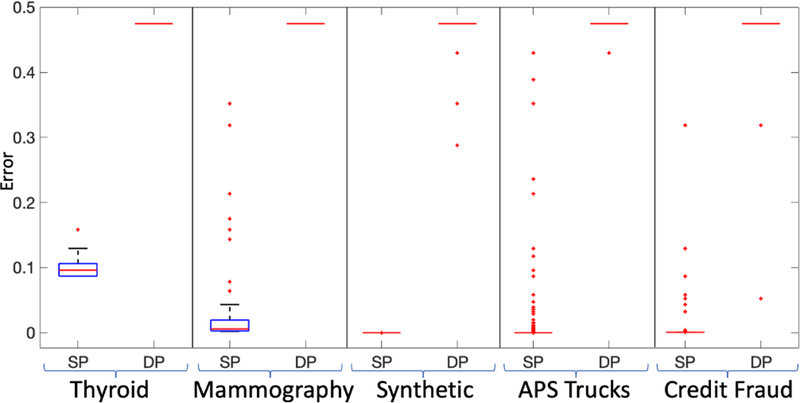
For each dataset, we find all the true (β, r)-anomalies and for each of them perform private anomaly identification query using SP-mechanism (given in Section 4.1.2) and DP-mechanism (given in Section 4.1.1) for ε = 0.01, 0.1, and 1 and compute the error, which we give by the box plot in Figure 6. The reason we only considered our DP mechanism for this part is that it is the best among the baselines (see Table 3) and it also has strong accuracy guarantees (Theorem 4.4). The error of SP-mechanism, in many cases, is so small (e.g. of the order 10⁻¹⁵ or even smaller for larger values of ε) that it can be considered zero for all practical purposes. Furthermore, as the data size increases (and correspondingly the value of β), the error of SP-mechanism reduces. However, in the case of anomalies, the error of DP-mechanism is consistently close to that of random coin flip (i.e. selecting 0 or 1 with probability 1/2) except for a few anomalous records in some cases – we will shortly explain the reason for this. The error of the SP-mechanism was overwhelmingly concentrated about zero (Figure 6), which is also true for the smaller values of ε. Thus, we can have higher privacy guarantee for sensitive records, while still being able to accurately identify anomalies. Also, note that as the size of the dataset increases, not only does the error of SP-mechanism reduces (for anomalies), but also its divergence. Thus, it indicates that our methodology is even more appropriate for big data settings. On the other hand, for anomalies, the errors of DP-mechanism are concentrated about 1/(1 + e^ε) (Figure 7). This is in accordance with our theoretical results and the assumption that the databases are typically sparse.

Figure 6:

box plots of the errors of the SP mechanism for (β, r)-AIQ over the true (β, r)-anomalies for ε = {.01, .1, 1}.

Table 3:

B₁ and B₂ are the best mechanisms from two families of mechanism. DP and SP are the mechanisms from Section 4.1.1 and Section 4.1.2 respectively. Going from red to blue the value decreases. ε = 0.1

Dataset	Precision				Recall				F1-score
	B1	B2	DP	SP	B1	B2	DP	SP	B1	B2	DP	SP
Credit Fraud	0.0101	0.0230	0.9930	0.9963	1.0000	0.0498	0.5250	0.9968	0.0199	0.0315	0.6868	0.9966
APS Trucks	0.0115	0.0165	0.9870	0.9931	1.0000	0.0753	0.5263	0.9954	0.0227	0.0271	0.6865	0.9943
Synthetic	0.0101	0.0114	0.9930	0.9963	1.0000	0.1189	0.5250	0.9968	0.0199	0.0208	0.6868	0.9966
Mammography	0.0070	0.0081	0.0211	0.2004	0.8244	0.1000	0.5250	0.9977	0.0138	0.0149	0.0435	0.3337
Thyroid	0.0174	0.0191	0.1427	0.3100	0.6656	0.2918	0.5250	0.8993	0.0339	0.0358	0.2244	0.4610

Figure 7:

box plots of the error of the SP and the DP mechanisms for (β, r)-AIQ over the true (β, r)-anomalies for ε = 0.1.

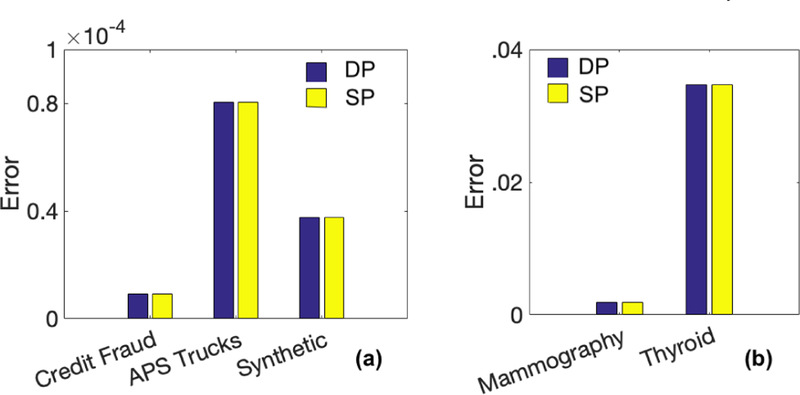
Next, we evaluated the performance over the normal records. Here, both the SP and the DP mechanisms performed equally (Figure 8). For the same value of ε, every sensitive record in the database has the same level of privacy under sensitive privacy as all the records under differential privacy; thus the same level of accuracy should be achievable under both the privacy notions. Here we see again that datasets with larger sizes exhibit very small error.

Figure 8: evaluation over normal records.

(a),(b), give the average error of SP and DP mechanism for AIQ over all the normal records from each data set; ε = 0.1.

To evaluate the performance over future queries, we picked n records uniformly at random from the space of possible (values of) records for each dataset – n was set to be 20% of the size of the dataset. Here too the SP-mechanism outperforms the DP-mechanism significantly (Table 2). This is because most of the randomly picked records are anomalous as per the (β, r)-anomaly, which is due to the sparsity of the databases. This fact becomes very clear when we compare the mean error over the random records to the mean error over the anomalous records in the randomly picked records (see the second and the last column of Table 2). Since the probability of observing a mistake is extremely small (e.g., 1 in 10¹⁰ trials), in Table 2, the mean is computed over the actual probability of error of the mechanism instead of the estimated error.

Table 2:

effect of sparsity of databases. “mean error” is over the randomly picked n records from the possible values of the records for each dataset for SP and DP mechanisms for (β, r)-AIQ. “mean error (anomalies)” is only over the anomalous records in the n picked records. Here, n is 20% of the size of the dataset and ε = 0.1.

Dataset	mean error		mean error (anomalies)
	SP	DP	SP
Credit Fraud	1.1127E–21	0.4750	1.1127E–21
APS Trucks	2.9719E–13	0.4750	2.9719E–13
Synthetic	3.2173E–5	0.4750	3.2173E–5
Mammography	0.0022	0.4749	0.0021
Thyroid	0.0870	0.4750	0.0867

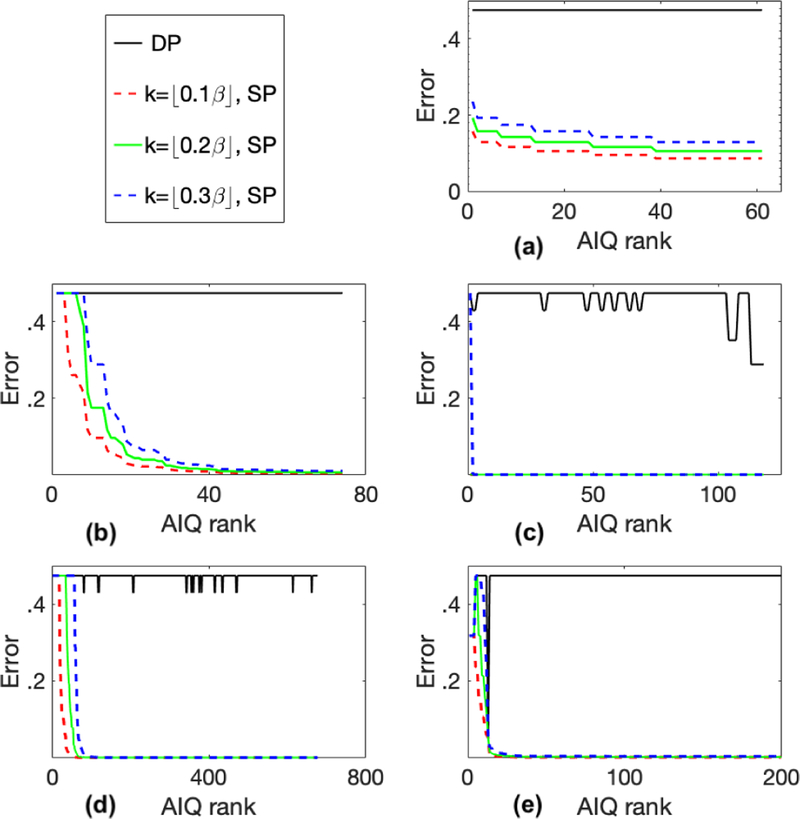
We already saw that by increasing k we move the boundary between sensitive and non-sensitive records (Figure 3). So to observe the effect of varying values of k on real world datasets, we carried out experiments on the datasets with k = ⌊0.1β⌋, ⌊0.2β⌋, and ⌊0.3β⌋ – recall that a record is considered k-sensitive with respect to a database if the record is normal or becomes normal under the addition and (or) deletion of at most k records from the database. Note that if k ≥ β + 1 then every record will be sensitive regardless of the database. The results are provided in Figure 9. Here we conclude that even for the higher values of k SP-mechanism performs reasonably well. Further, if the size of dataset is large enough, then the loss in accuracy for most of the records is negligible.

Figure 9: evaluation over true (β, r)-anomalies for varying k.

(a)-(e), give the errors of SP and DP mechanisms. AIQ rank is given by the error of SP-mechanism for each anomaly: the higher the rank, the lower the error. Mechanisms are as given in Section 4 and ε = 1. (a), Thyroid, (b), Mammography,(c), Credit Fraud, (d), APS Trucks, (e), Synthetic data.

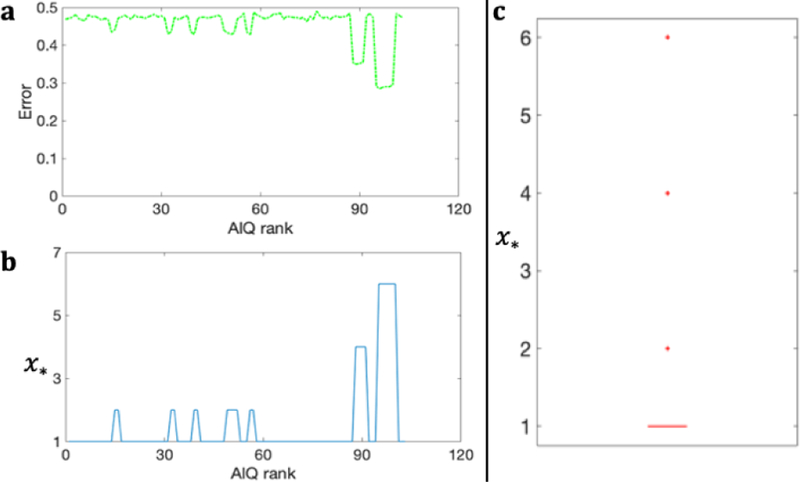
We see that for Credit Fraud and APS Trucks datasets, differentially private AIQ for some of the anomalous records give smaller error. We explain this deviation using the Credit Fraud dataset as an example. The above mentioned deviation in the error occurs whenever the anomalous record is not unique (Figure 10a–b), which is typically rare (Figure 10c). The reason DP-mechanism’s error remains constant in most cases is that the anomalies lie in a very sparse region of space and mostly do not have any duplicates (i.e., other records with the same value – x_i ≈ 1).

Figure 10:

deviation in the DP-mechanism error for the Credit Fraud dataset. In (a), the plot is the same as given in Figure 9c for the DP-mechanism. In (b) and (c), x_* for each record is the number of records in the database x that have the same value. (c), shows the box plot for the data.

Finally, to evaluate the overall performance of our SP-mechanism, we computed precision, recall, and F₁-score [1]. We also provide a comparison with two different baseline mechanisms, B₁, B₂ in addition to pareto optimal DP mechanism (see Table 3).

B₁ and B₂ are the best performing mechanisms (i.e., with the highest F₁-score) from two families of mechanisms. Each mechanism in each of the family is identified by a threshold t, where 0 ≤ t ≤ 1. Below, we describe the mechanisms from both the families for fixed ε, threshold t, record $i\in \mathcal{X}$, and database $x\in \mathcal{D}$. The mechanism in the first family is given as B_1,t (x) = 1 if and only if $\mathcal{O}(x)+\text{Lap}(1/\epsilon )>t\times \left(\Vert x{\Vert }_1+\text{Lap}(1/\epsilon )\right)$; here $\mathcal{O}(x)$ gives the number of anomalies in x and Lap(1/ε) is independent noise from Laplace distribution of mean zero and scale 1/ε. The mechanism in the second family is given as B_2,t (x) = 1 if and only if $\mathcal{O}(x)+\text{Lap}(\beta /\epsilon )>t\times \left(\Vert x{\Vert }_1+\text{Lap}(1/\epsilon )\right)$. Note that, the mechanism from the first family are ε₁-DP, where ε₁ ≥ βε. This is due to the fact that ${\text{max}}_{x,{y\in \mathcal{D}:||x-y||}_1=1}|\mathcal{O}(x)-\mathcal{O}(y)|=\beta$ [15]. However the mechanism from the second family are ε₂-DP,| where ε₂ ≥ ε.

Our mechanism outperforms all the baselines. Furthermore, DP-mechanism largely outperforms the rest of the baselines.

6. RELATED WORK

To our knowledge, there has been no work that formally explores the privacy-utility trade-off in privately identifying anomalies, where sensitive records (which include the normal records defined in a data-dependent fashion) are protected against inference attacks about their presence or absence in the database used.

Differential privacy [15, 17] has shaped the field of private data analysis. This notion aims to protect everyone, and in a sense, many of the DP mechanisms (e.g. Laplace mechanism) achieve privacy by protecting anomalies; and in doing so perturb the information regarding anomalies greatly. This adversely affects the accuracy of anomaly detection and identification. Furthermore, differential privacy is a special case of sensitive privacy (Section 4.1.1).

Variants of the notion of differential privacy address important practical challenges. In particular, personalized differential privacy [29], protected differential privacy [31], relaxed differential privacy [6], and one-sided differential privacy [13] have a reversed order of quantification compared to sensitive privacy. Sensitive privacy, quantifies sensitive records and their privacy after quantifying the database, which is in contrast to the previous work. Thus, under sensitive privacy, it is possible for a record of some value to be sensitive in one database and not in the other, while this cannot be the case in the above mentioned definitions. On the other hand, by labeling records independent to the database (as in the previous work) one can solve a range of privacy problems such as counting queries and releasing histograms. Hence, this work solves the open problem (in [31]). Next, we present an individual comparison with each of the above mentioned previous work along with some other relevant ones from the literature.

Protected differential privacy [31] proposes an algorithm for social networks to search for anomalies that are fixed and are defined independent of the database. This is not extensible to the case, where anomalies are defined relative to the other records [31]. Similarly, the proposed relaxed DP mechanism [6] is only applicable to anomalies defined in data-independent manner.

One-sided differential privacy (OSDP) [13] is a general framework, and is useful for the applications, where one can define the records to be protected independent of the database. Note that the notion of sensitive record in OSDP is different from the one considered here. Further, due to its asymmetric nature of the privacy constrains, OSDP fails to protect against the inference about the presence/absence of a sensitive record (in general), which is not the case with sensitive privacy (see Appendix A.10.1).

Tailored differential privacy (TDP) [36] provides varying levels of privacy for a record, which is given by a function, α, of the record’s value and the database. However, the work is restricted to releasing histograms, where outliers are provided more privacy. Whereas our focus is identifying anomalies, where anomalies may have lesser privacy. Further, the notion of anomaly used in the work [36] is the simple (β, 0)-anomaly. Extending it to the case of r > 0 is a non-trivial task since, here, changing a record in the database may affect the label (outlyingness) of another record with a different value. We also note that sensitive privacy is a specialized case of tailored differential privacy (see Appendix A.10.2.)

Blowfish privacy (BP) [25] and Pufferfish privacy (PP) [33] are general frameworks, and provide no concrete methodology or direction to deal with anomaly detection or identification, where anomalies are defined in a data-dependent fashion. Sensitive privacy is a specialized class of definitions under these frameworks.

Thus, in term of definition, our contribution in comparison with OSDP [13], TDP [36], BP [25], and PP [33], is defining the the notion of sensitive record and the sensitive neighborhood graph that is appropriate and meaningful for anomalies (when defined relative to the other records) and giving constructions and mechanisms for identifying anomalies.

Finally, [4] proposed a method for searching outliers, which can depend on data, but this is done in a rather restricted setting, which has theoretical value (in [4] the input databases are guaranteed to have only one outlier, a structure not present in the typical available datasets; this is in addition to other input database restrictions required by [4]).

Other relaxations of differential privacy such as [2] is specifically for location privacy and [16] is to achieve fairness in classification to prevent discrimination against individuals based on their membership in some group and as such are not applicable to the problem we consider here.

7. KEY TAKEAWAYS AND CONCLUSION

This work is the first to lay out the foundations of the privacy-preserving study of data dependent anomalies and develop general constructions to achieve this. It is important to reiterate that the formalization and conceptual development is independent of any particular definition of anomaly. Indeed, the definition of sensitive privacy (Definitions 3.1 and 3.2), and the constructions to achieve it (Construction 1 and Construction 2) are general and work for an arbitrary definition of anomaly (Theorem 4.1 and Theorem 4.7).

We noted earlier that sensitive privacy generalizes differential privacy. Thus, the guarantees provided by sensitive privacy are similar to that of differential privacy, and in fact, Construction 1 can be employed to give differentially private mechanisms for computing anomaly identification query or any binary function. However, in general, the guarantee provided by sensitive privacy to any two databases differing by one record could be correspondingly weaker than that offered by differential privacy depending on the distance between the databases in the sensitive neighborhood graph. There is also a divergence in guarantees in terms of composition. In differential privacy, composition is only in terms of the privacy parameter, ε. However, for sensitive privacy, composition needs to take into account not only the privacy parameter ε, but also the sensitive neighborhood graphs corresponding to the queries being composed. Nevertheless, the composition and post-processing properties (Section 3.1) hold regardless of the notion of the anomaly.

An extensive empirical study carried out over data from diverse domains overwhelmingly supports the usefulness of our method. The sensitively private mechanism consistently outperforms differentially private mechanism with exponential gain in accuracy in almost all cases. Although it is easy to come up with example datasets where a differentially private mechanism also performs well (e.g., (β, r)-AIQ for i and x when x_i = B_x (i, r) = β/2), the experiments with real data show that such cases are unlikely to occur in practice. Indeed, the experiments show that most of the anomalies occur in the setting, where an ε-DP mechanism performs the worst, that is, its error is close to 1/(1 + e^ε) (a lower bound on the error of any ε-DP mechanism and follows from Claim 1).

To conclude, in this paper, we develop methods for anomaly identification that provide a provable privacy guarantee to all records, which is calibrated to their degree of being anomalous (in a data-dependent sense), while enabling the accurate identification of anomalies. We stress that the currently available methodologies for protecting privacy in data analysis are fundamentally unsuitable for the task at hand: they either fail to stop identity inference from the data, or lack the ability to deal with the data-dependent definition of anomaly. Note that anomaly identification is only the first step to tackling the problem of anomaly detection (finding all the anomalous records in a dataset). In the future, we plan to tackle this and instantiate our framework for other anomaly detection models.

CCS CONCEPTS.

• Security and privacy → Privacy-preserving protocols; • Computing methodologies → Anomaly detection.

A. APPENDIX

A.1. Empirical evaluation protocols

Evaluation over normally distributed data: If the data is from one dimensional normal distribution with mean μ and standard deviation σ then a record i is anomalous (or equivalently an outlier) if |i − μ| ≥ 3σ, and is statistically equivalent to (β = 1.2×10⁻³n, r = 0.13σ)-anomaly [35], where n is the size of the database.

To adapt this result for 2D normal distribution in Figure 2, set $r=0.13\sqrt{{\sigma }_1^2+{\sigma }_2^2}$ and compute β in a similar fashion as above. Next, take 30 samples of size 20K, i.e. n = 20, 000, from the 2D normal distribution, N (μ, Σ), where μ = (0, 0) and $\sum =\left[\begin{array}{ll}2\hfill & 0\hfill \\ 0\hfill & 2\hfill \end{array}\right]$, and run SP-mechanism (given in Section 4.1.2) and DP-mechanism (given in Section 4.1.1) for (β, r)-anomaly identification query to compute accuracy, which is measured by the probability of outputting the correct answer by the private mechanism, and average the results over the samples for each query. We then plot the average accuracy and interpolate the results using one-degree polynomial in the two coordinates (Figure 2b–c). We used the “ListPlot3D” function of Mathematica with the argument “InterpolationOrder” set to 1.

In Figure 2d–e and Figure 3, we plot the level of privacy (in term of ε) that each record (point) has under private anomaly identification query. Here, the level of privacy for a record in a given database is measured by the maximum divergence divergence in the probability of outputting a label when we add or remove the record from the database. For ε-SP-mechanism, U, to compute the value of the privacy parameter, ε, for a record i in a given database x, consider databases y and z. y and z are same as x except for y has one more record of value i and z has one less record of value i—if there is no record of value i in x then z will be the same as x. Now we can calculate e^ε for record i be by (4).

$$e^{\epsilon }=\underset{w\in \{y,z\}}{\text{max}}\underset{b\in \{0,1\}}{\text{max}}\left(\frac{P(U(x)=b)}{P(U(w)=b)},\frac{P(U(w)=b)}{P(U(x)=b)}\right)$$ (4)

A.2. Protocol for (β, r) selection

The main idea is to fix a value of β, for a dataset of size n, as (1 − p) ×n, where p is close to 1, and then search for an appropriate value of r. It is recommended [35] that for the datasets of sizes 10³ and 10⁶, β be (1 − 0.995) ×10³ and (1−0.99995) ×10⁶. By assuming that p is linearly related to n, one can use the provided values to find the value of β for any given dataset. For a fixed value of β, a search is performed to find r that maximize the F₁-score (also known as balanced F-measure), which is a popular performance metric for imbalanced datasets [38], and it is the harmonic mean of precision and recall. We used the following protocol to select the value of r. Initialize r_min = .001, r_max = 40 (or the value that is not smaller than the maximum distance between any two points in the given dataset), r = 0, and S = 0. Next, set r₁ = r_min + (r_max − r_min)/4, r₂ = r_min + 3(r_max − r_min)/4, pick α from [0, 1] uniformly at random and set r₃ = α r₁ + (1 − α) r₂. Compute F₁-score for each of the r′s, i.e. $S_{r_1}$, $S_{r_2}$, and $S_{r_3}$. Let $S_{r_t}$ be the maximum of the computed scores. If $S_{r_t}$ is greater than S then set $S=S_{r_t}$ and r = r_t; further, if $S_{r_2}<S$ and r₂ > r then set r_max = r₂ but if it is not the case and $S_{r_1}<S$ and r₁ < r then set r_min = r₁, otherwise do nothing. Repeat this process, except for the initialization step, until the improvement in S becomes insignificant. In our experiments, repeating the process for ten iterations generally sufficed.

A.3. Proof of Claim 1

Proof. Arbitrarily fix ε > 0, $f:\mathcal{D}\to \{0,1\}$, ε-differentially private mechanism $M:\mathcal{D}\to \{0,1\}$, and x, $y\in \mathcal{D}$ such that f (x) ≠ f (y) and ‖x – y‖₁ = 1; and let b = f (x).

If P (M (y) = b) ≤ 1/(1 + e^ε) then, by differential privacy constraints, we get that P (M (x) = b) ≤ e^ε/(1+e^ε); thus P (M (x) = 1 − b) ≥ 1/(1+e^ε). Similarly, P (M (x) = 1 − b) ≤ 1/(1+e^ε) implies P (M (y) = b) ≥ 1/(1 + e^ε). Hence, from the above, it follows that

$$\text{max\hspace{0.17em}}(\text{P}(M(x)\ne f(x)),\text{P}(M(y)\ne f(y)))\ge 1/\left(1+e^{\epsilon }\right).$$

Since M, x and y were fixed arbitrarily, the claim follows, and this completes the proof. □

A.4. Proof of Theorem 4.1

Proof. Fix arbitrary ε > 0 and a definition of anomaly. Let g be the anomaly identification function and G_S be the k-sensitive neighborhood graph corresponding to it for an arbitrary value of k ≥ 1. Fix λ to be 1-Lipschitz continuous lower bound on the mdd-function, ${\text{Δ}}_{G_S}$, for g such that λ ≥ 1. Let U_λ be as given by Construction 1. Next, fix an anomaly identification query, (i, g), and x, $y\in \mathcal{D}$ that are neighbors (i.e. connected by a direct edge) in G_S.

If g(i, x) = g(i, y) = b from some b ∈ {0, 1} then

$$\begin{gathered} \frac{\text{P}\left(U_{\lambda }(x)\ne b\right)}{\text{P}\left(U_{\lambda }(y)\ne b\right)}=e^{\epsilon (-\lambda (i,x)+\lambda (i,y))} \\ \le e^{\epsilon }|-\lambda (i,x)+\lambda (i,y)| \\ \le e^{\epsilon }(\text{since }\lambda \text{ is }1\text{ -Lipschitz continuous)} \end{gathered}$$

and

$$\begin{gathered} \frac{\text{P}\left(U_{\lambda }(x)=b\right)}{\text{P}\left(U_{\lambda }(y)=b\right)}=\frac{1-\text{P}\left(U_{\lambda }(x)\ne b\right)}{1-\text{P}\left(U_{\lambda }(y)\ne b\right)} \\ =\frac{1+e^{\epsilon }-e^{-\epsilon (\lambda (i,x)-1)}}{1+e^{\epsilon }-e^{-\epsilon (\lambda (i,y)-1)}} \\ =\frac{e^{\epsilon \lambda (i,y)}\left(1+e^{\epsilon }\right)-e^{\epsilon (\lambda (i,y)-\lambda (i,x)+1)}}{e^{\mathcal{E}\lambda (i,y)}\left(1+e^{\epsilon }\right)-e^{\epsilon }} \end{gathered}$$

since λ is 1-Lipschitz continuous, it follows that

$$\frac{\text{P}\left(U_{\lambda }(x)=b\right)}{\text{P}\left(U_{\lambda }(y)=b\right)}=\frac{e^{\epsilon \lambda \left(i,y\right)}\left(1+e^{\epsilon }\right)-1}{e^{\epsilon \lambda \left(i,y\right)}\left(1+e^{\epsilon }\right)-e^{\epsilon }}\le \frac{\left(1+e^{\epsilon }\right)-1}{\left(1+e^{\epsilon }\right)-e^{\epsilon }}=e^{\epsilon }$$

The first inequality holds because λ is 1-Lipschitz continuous, and the second one holds since λ ≥ 1.

On the other hand, if g(i, x) ≠ g(i, y), then λ(i, x) = λ(i, y) = 1. This holds because x and y are neighbors, i.e. $d_{G_S}\left(x,y\right)=1$, and hence, ${\text{Δ}}_{G_S}(i,x)={\text{Δ}}_{G_S}(i,y)=1$ and λ is such that ${\text{Δ}}_{G_S}(j,z)\ge \lambda (j,z)\ge 1$ for every $j\in \mathcal{X}$ and $z\in \mathcal{D}$. Thus, in this case, the privacy constraints trivially hold. This concludes the formal argument. □

A.5. Proof of Lemma 4.3

Proof. Let $\mathbb{G}$ be the neighborhood graph over $\mathcal{D}$, d be the distance metric over $\mathcal{X}\times \mathcal{X}$, $d_{\mathbb{G}}$ be the shortest path length metric over $\mathbb{G}$, and g be the anomaly identification function for (β, r)-anomaly for arbitrarily fixed values of β ≥ 1 and r ≥ 0.

Firstly, we prove the correctness of the ${\text{Δ}}_{\mathbb{G}}$-function given by (2) for (β, r)-AIQ. Arbitrarily fix $i\in \mathcal{X}$ and any database $x\in \mathcal{D}$. We know that the value of g(i, x) only depends upon x_i and B_x (i, r)—recall that g(i, x) = 1 ⇔ x_i ≥ 1 and B_x (i, r) β. Further, $d_{\mathbb{G}}(x,y)=\Vert x-y{\Vert }_1$ since every two databases that differ by exactly one record are directly connected by an edge. Hence, it follows that for $C_i=\{j\in \mathcal{X}:d(i,j)\le r\}$,

$${\text{Δ}}_{\mathbb{G}}(i,x)=\underset{y:g(i,y)\ne g(i,x)}{\text{min}}\Vert x-y{\Vert }_1=\underset{y:g(i,y)\ne g(i,x)}{\text{min}}\sum _{j\in C_i}|x_j-y_j|.$$ (5)

We will consider four cases based on the condition (given in the ${\text{Δ}}_{\mathbb{G}}$-function) that x satisfies. From (5), we know that ${\text{Δ}}_{\mathbb{G}}(i,x)$ is the same as the minimum number of records by which a database y differs such that g(i, x) ≠ g(i, y). Thus in the proof we will modify the database x by adding or (and) removing records from x, and show that minimum number of changes required in x to change the output of g is given by ${\text{Δ}}_{\mathbb{G}}$-function.

Case 1: When x satisfies the first condition, g(i, x) = 0. For any database y such that g(i, y) = 1, it must hold that y_i ≥ 1 and B_y (i, r) ≤ β. So we obtain a y by adding one record of value i to x. Thus ${\text{Δ}}_{\mathbb{G}}(i,x)=1$.

Case 2: When x satisfies the second condition, here again similar to the case above, g(i, x) = 0, and for any database y such that g(i, y) = 1, it must hold that y_i ≥ 1 and B_y (i, r) β. So we will have to add one record of value i to x to obtain a database y′, but now B_y′ (i, r) ≥ β + 1. Thus, to obtain a y, we will have to remove B_y′ (i, r) − β = B_x (i, r) + 1 – β records of values C_i\ {i} from y′ (or x). Thus, ${\text{Δ}}_{\mathbb{G}}(i,x)=1+B_x(i,r)+1-\beta$.

Case 3: Here we assume that x satisfies the third condition; hence g(i, x) = 1. For a y such that g(i, y) = 0, either y_i = 0 or B_y (i, r) ≥ β + 1. Thus ${\text{Δ}}_{\mathbb{G}}(i,x)$ will be the minimum of x_i (which corresponds to the number of records of value i present in x that we will have to remove) and β + 1 − B_x (i, r) (which corresponds to the number of records of values in C_i that we will have to add to x).

Case 4: In this case, g(i, x) = 0 because B_x (i, r) > β. Thus, we will have to remove B_x (i, r) − β records of values in C_i from x such that there is at least on record of value i in the modified x. Hence, ${\text{Δ}}_{\mathbb{G}}(i,x)=B_x(i,r)-\beta$.

Further, in all the cases, ${\text{Δ}}_{\mathbb{G}}(i,x)\ge 1$. Therefore, we conclude the ${\text{Δ}}_{\mathbb{G}}$-function is correct.

Next, we prove that the ${\text{Δ}}_{\mathbb{G}}$-function is 1-Lipschitz continuous. Arbitrary fix i and any two neighboring databases, x and y in $\mathbb{G}$. Let the (k, l) represent that x and y respectively satisfy the k^th and l^th conditions in the ${\text{Δ}}_{\mathbb{G}}$-function, where k, l ∈ [4] such that k ≤ l. We will prove that for each (k, l), the ${\text{Δ}}_{\mathbb{G}}$-function satisfies the 1-Lipschitz continuity condition. Here, note that if the ${\text{Δ}}_{\mathbb{G}}$-function satisfies the 1-Lipschitz continuity condition under (k, l) then it also satisfies the condition under (l, k) because $|{\text{Δ}}_{\mathbb{G}}(i,x)-{\text{Δ}}_{\mathbb{G}}(i,y)|=|{\text{Δ}}_{\mathbb{G}}(i,y)-{\text{Δ}}_{\mathbb{G}}(i,x)|$.

For (1, 1), $|{\text{Δ}}_{\mathbb{G}}(i,x)-{\text{Δ}}_{\mathbb{G}}(i,y)|=0$, and for (2, 2) and (4, 4), $|{\text{Δ}}_{\mathbb{G}}(i,x)-{\text{Δ}}_{\mathbb{G}}(i,y)|\le 1$ since $|B_x(i,r)-B_y(i,r)|\le 1$. Below, we consider rest of the cases.

(3, 3): The case, when B_x (i, r) = B_y (i, r), is trivial. So, let B_x (i, r) = 1 + B_y (i, r)—this is without loss of generality since ‖x − y‖₁ = 1 and $|{\text{Δ}}_{\mathbb{G}}(i,x)-{\text{Δ}}_{\mathbb{G}}(i,y)|=|{\text{Δ}}_{\mathbb{G}}(i,y)-{\text{Δ}}_{\mathbb{G}}(i,x)|$. Thus, ${\text{Δ}}_{\mathbb{G}}(i,x)=\text{min}\left(x_i,\beta -B_y(i,r)\right)$ and ${\text{Δ}}_{\mathbb{G}}(i,y)=\text{min}(y_i,\beta +1-B_y(i,r))$. All the subcases, except for the following, trivially follow from ‖x − y‖₁ = 1.

1. ${\text{Δ}}_{\mathbb{G}}(i,x)=x_i$ and ${\text{Δ}}_{\mathbb{G}}(i,y)=\beta +1-B_y(i,r)$

2. ${\text{Δ}}_{\mathbb{G}}(i,x)=\beta -B_y(i,r)$ and ${\text{Δ}}_{\mathbb{G}}(i,y)=y_i$

(a) is not possible as it requires x_i < y_i; this cannot happen because ‖x − y‖₁ = 1 and B_x (i, r) = 1 + B_y (i, r). As for (b), the following holds for $t={\text{Δ}}_{\mathbb{G}}(i,x)-{\text{Δ}}_{\mathbb{G}}(i,y)$:

$$-1\le \beta -B_y(i,r)-\left(\beta +1-B_y(i,r)\right)\le t\le x_i-y_i\le 1$$

Thus, it follows that 1-Lipschitz continuity condition is satisfied in this case.

(1, 2): This happens when B_x (i, r) = β − 1 and B_y (i, r) = β, which is sufficient for the condition to be satisfied.

(1, 3): It is possible when y_i = 1 and 1 ≤ B_y (i, r) ≤ β; hence ${\text{Δ}}_{\mathbb{G}}(i,y)=y_i$ and the case holds.

(1, 4): This case is not possible since ‖x − y‖₁ = 1, and the case requires B_x (i, r) < β and B_y (i, r) > β.

(2, 3): This case too is not possible since it requires B_x (i, r) ≥ B_y (i, r) and x_i < y_i, when ‖x − y‖₁ = 1.

(2, 4): Here, B_x (i, r) − B_y (i, r) = −1 (since x_i = 0 and y_i ≥ 1); hence the case follows.

(3, 4): Here, it must hold that B_x (i, r) = β and B_y (i, r) = β + 1. Hence, ${\text{Δ}}_{\mathbb{G}}(i,x)=1$ (since x_i ≥ 1) and ${\text{Δ}}_{\mathbb{G}}(i,y)=1$, and the case follows.

Since the ${\text{Δ}}_{\mathbb{G}}$-function satisfies 1-Lipschitz continuity condition under all the cases for arbitrary i and arbitrary neighbors, x and y, in the neighborhood graph, it holds for every i and every two neighbors. Thus the claim follows. This completes the proof. □

A.6. Proof of Theorem 4.4

Proof. Arbitrarily fix ε and a (β, r)-AIQ, (i, g). Let ${\text{Δ}}_{\mathbb{G}}$ be as given by (2) and $U_{{\text{Δ}}_{\mathbb{G}}}$ be as given by Construction 1.

Firstly, note that $U_{{\text{Δ}}_{\mathbb{G}}}$ is ε-DP. It follows from the facts that ${\text{Δ}}_{\mathbb{G}}\ge 1$, is 1-Lipschitz continuous (Lemma 4.3), and SP generalizes DP.

Next, we prove the optimality claim. We prove the claim using its contrapositive, that is, if there is a mechanism that is “better” than $U_{{\text{Δ}}_{\mathbb{G}}}$, then it must not be ε-DP.

Assume there exits a DP mechanism M such that for every x, $P\left(M(x)=g_i(x)\right)\ge P\left(U_{{\text{Δ}}_{\mathbb{G}}}(x)=g_i(x)\right)$ and for a database y, $P\left(M(y)=g_i(y)\right)>P\left(U_{{\text{Δ}}_{\mathbb{G}}}(y)=g_i(y)\right)$ (i.e. $U_{{\text{Δ}}_{\mathbb{G}}}$ is not pareto optimal); fix this y. Note that g_i (·) = g(i, ·). We will prove that M cannot be ε-DP.

Let z be such that $d_{\mathbb{G}}(y,z)={\text{Δ}}_{\mathbb{G}}(i,y)$ and g_i (z) ≠ g_i (y). Let w be a neighbor of z such that $d_{\mathbb{G}}(y,w)={\text{Δ}}_{\mathbb{G}}(i,y)-1$ and b = g_i (w) = g_i (y). Now, assume that M ε-DP. It follows that

$$P(M(w)\ne b)\le e^{\epsilon d_{\mathbb{G}(y,w)}}P(M(y)\ne b)=e^{\epsilon \left({\text{Δ}}_{\mathbb{G}}(i,y)-1\right)}P(M(y)\ne b)<1/\left(1+e^{\epsilon }\right)$$ (6)

The First inequality is due to the DP constrains on M. The second inequality is due to the fact that M is strictly better than $U_{{\text{Δ}}_{\mathbb{G}}}$ on y and the fact that $P\left(U_{{\text{Δ}}_{\mathbb{G}}}(y)\ne g_i(y)\right)=e^{-\epsilon \left({\text{Δ}}_{\mathbb{G}}(i,y)-1\right)}/\left(1+e^{\epsilon }\right)$. Now if M is ε-DP, then P (M (z) ≠ 1 − b) ≥ e^−ε P (M (w) ≠ 1 − b), which together with (6) gives us P (M (z) ≠ g_i (z)) > 1/(1 + e^ε); alternatively, P (M (z) = g_i (z)) < e^ε/ (1 + e^ε). Since we know that M is “better” than $U_{{\text{Δ}}_{\mathbb{G}}}$, and in particular, $P\left(M(z)=g_i(z)\right)\ge P\left(U_{{\text{Δ}}_{\mathbb{G}}}(z)=g_i(z)\right)=e^{\epsilon }/\left(1+e^{\epsilon }\right)$, the above implies that M is not ε-DP. Thus, we conclude the $U_{{\text{Δ}}_{\mathbb{G}}}$ is pareto optimal. □

A.7. Proof of Lemma 4.5

Lemma A.1. Arbitrarily fix a graph, G, that contains all the nodes and a subset of edges of the neighborhood graph, $\mathbb{G}$, and an $X\subseteq \mathcal{X}$. If d_G is the shortest path length metric over G, then for every x, $y\in \mathcal{D}$,

$$d_G(x,y)\ge \Vert x-y{\Vert }_1\ge \sum _{j\in X}|x_j-y_j|\ge \left|\sum _{j\in X}\left(x_j-y_j\right)\right|.$$

Proof. Let $\mathbb{G}$ be the neighborhood graph over $\mathcal{D}$. Arbitrarily fix G, d_G, and X as specified above (in the lemma). Since G contains all the nodes and a subset of edges of $\mathbb{G}$, $d_G(x,y)\ge d_{\mathbb{G}}(x,y)$, where $d_{\mathbb{G}}$ is the shortest path length metric over $\mathbb{G}$ and it is same as ℓ₁-metric over the databases. Hence, it follows that d_G (x, y) ≥ ‖x – y‖_1. The second inequality holds since $X\subseteq \mathcal{X}$ and $\Vert x-y{\Vert }_1={\sum }_{j\in X}|x_j-y_j|$. The Third inequality follows from the reverse triangle inequality. This completes the proof. □

Proof of Lemma 4.5. Arbitrarily fix β, k ≥ 1, r ≥ 0. Let λ_k be as given by (3), the ${\text{Δ}}_{\mathbb{G}}$-function be corresponding to the neighborhood graph, $\mathbb{G}$, the ${\text{Δ}}_{G_S}$-functions be corresponding to the k-sensitive neighborhood graph, G_S, for (β, r)-anomaly, and g be the (β, r)-anomaly identification function. Next, arbitrarily fix a record i and a node (database) x in G_S.

We first show that ${\text{Δ}}_{G_S}$. Below, we show that ${\text{Δ}}_{G_S}(i,x)\ge {\text{Δ}}_{\mathbb{G}}(i,x)$.

$${\text{Δ}}_{G_S}(i,x)=\underset{y\in \mathcal{D}:g(i,x)\ne g(i,y)}{\text{min}}{d}_{G_S}(x,y)\ge \underset{y\in \mathcal{D}:g(i,x)\ne g(i,y)}{\text{min}}{d}_{\mathbb{G}}(x,y)={\text{Δ}}_{\mathbb{G}}(i,x)$$

The first inequality follows from the fact that G_S contains all the nodes and a subset of edges of $\mathbb{G}$. Hence, from Lemma 4.3, we conclude that if B_x (i, r) ≥ β + 1 − k then ${\text{Δ}}_{G_S}(i,x)\ge {\lambda }_k(i,x)\ge 1$.

We now let B_x (i, r) < β + 1 − k and b = g(i, x). Here, it is clear that λ_k (i, x) ≥ 1. Fix any y in G_S such that g(i, y) ≠ b and ${\text{Δ}}_{G_S}(i,x)=d_{G_S}(x,y)$.

Consider the case of x_i = 0. Here, it must hold that y_i ≥ 1 and B_y (i, r) ≤ β. Now, on any of the shortest path from x to y, we will first reach a database z, where i is k-sensitive, and hence, B_z (i, r) ≥ β + 1 − k (from Lemma A.2). Thus, for this z, we get

$$\begin{gathered} {\text{Δ}}_{G_S}(i,x)=d_{G_S}(x,z)+d_{G_S}(z,y) \\ \ge d_{G_S}(x,z) \\ \ge \left(B_z(i,r)-B_x(i,r)\right) \\ \ge \beta +1-k-B_x(i,r)={\lambda }_k(i,x). \end{gathered}$$

The second inequality follows from Lemma A.1, and the third one follows because B_z (i, r) ≥ β + 1 − k.

In the case, when x_i ≥ 1, it must hold that either y_i = 0 or B_y (i, r) ≥ β + 1. If y_i = 0, or B_y (i, r) ≥ β + 1. If y_i = 0, then on any of the shortest path from x to y, we will first reach a database z, where i becomes k-sensitive, i.e., B_z (i, r) ≥ β + 1 − k (from Lemma A.2). If z is the first such database, then z_i ≥ x_i. Thus, we get the following.

$$d_{G_S}\left(x,y\right)=d_{G_S}\left(x,y\right)+d_{G_S}\left(z,y\right)\ge \left(B_z(i,r)-B_x(i,r)\right)+|z_i-y_i|\ge 1+\beta -k-B_x(i,r)+x_i.$$ (7)

The first inequality follows from Lemma A.1, and the second one follows from the fact that B_z (i, r) ≥ β + 1 – k and x_i ≤ z_i. But if B_y (i, r) ≥ β + 1, then

$$d_{G_S}(x,y)=d_{G_S}(x,y)\ge |B_y(i,r)-B_x(i,r)|\ge 1+\beta -B_x(i,r)$$ (8)

From (7) and (8), we get the following, which is sufficient to establish that λ_k is a lower bound on the ${\text{Δ}}_{G_S}$-function.

$${\text{Δ}}_{G_S}(i,x)\ge 1+\beta -B_x(i,r)+\text{min}\left(0,x_i-k\right)={\lambda }_k(i,x)$$

Next, we show that λ_k is 1-Lipschitz continuous. Fix an arbitrary neighbor, y, of x such that λ_k (i, x) ≠ λ_k (i, y), otherwise, the continuity condition is trivially satisfied. If both x and y satisfy the first condition of λ_k, then the continuity condition is satisfied by Lemma 4.3. So assume that x and y satisfy the second condition of λ_k. Here, all the cases except for the following, trivially follow from the fact that ‖x − y‖₁ = 1.

1. λ_k (i, x) = β + 1 − B_x (i, r) and λ_k (i, y) = β + 1 − B_y (i, r) + y_i − k

2. λ_k (i, x) = β + 1 − B_x (i, r) + x_i − k and λ_k (i, y) = β + 1 − B_y (i, r)

If (a) holds then (b) also does by symmetry (i.e., |λ_k (i, x) λ_k (i, y)| = λ_k (i, y) – λ_k (i, x)|) as x and y are picked arbitrarily. (a) holds if x_i − k ≥ 0 and y_i − k ≤ 0; further, ‖x − y‖₁ = 1 implies that x_i − k = 0 and −1 ≤ y_i − k ≤ 0. When y_i − k = 0, the continuity condition is satisfied as |B_x (i, r) − B_y (i, r)| ≤ 1. However, y_i − k = −1 is not possible since ‖x − y‖₁ = x_i − y_i = 1 implies that i is k-sensitive with respect to x or y, which implies that either B_x (i, r) or B_y (i, r) is at least β + 1 − k (from Lemma A.2); this contradicts the assumption for this case. Hence, it follows that here the continuity condition is satisfied as well.

Lastly, consider the case, where y and x respectively satisfy the first and the second condition of λ_k—this is without loss of generality due to symmetry. This will be possible if B_x (i, r) = β − k and B_y (i, r) = β − k + 1. Thus, in all the subcases below, x_i ≤ y_i ≤ x_i + 1.

Consider the subcase of x_i = 0. Here, λ_k (i, x) = 1 and y_i is either 0 or 1. If y_i = 0, then we have:

$${\lambda }_k(i,y)={\text{Δ}}_{\mathbb{G}}(i,y)=2\text{ for }k=1,\text{ and }{\lambda }_k(i,y)={\text{Δ}}_{\mathbb{G}}(i,y)=1\text{ for }k>1$$

But if y_i = 1, ${\lambda }_k(i,y)={\text{Δ}}_{\mathbb{G}}(i,y)=\text{min}\left(y_i,k\right)=1$ as k ≥ 1. Hence, the continuity condition is satisfied for this subcase, when x_i = 0.

Next, let x_i ≥ 1; thus under this subcase it follows that

$${\lambda }_k(i,x)=1+k+\text{min}\left(0,x_i-k\right)=1+\text{min}\left(x_i,k\right)$$

$${\lambda }_k(i,y)={\text{Δ}}_{\mathbb{G}}(i,y)=\text{min}\left(y_i,k\right)\left(\text{ since }{x}_i\le y_i\right)$$

Clearly, if x_i < k, then λ_k (i, x) = 1 + x_i and x_i ≤ λ_k (i, y) ≤ x_i + 1; but if x_i ≥ k, then λ_k (i, x) = 1 + k and λ_k (i, y) = k since x_i ≤ y_i ≤ x_i + 1; hence the continuity condition is fulfilled in this subcase as well.

In all of the above case, |λ_k (i, x) − λ_k (i, y)| ≤ 1. Since β, k, r, i, x, and y (neighbor of x) were picker arbitrarily, we conclude that λ_k is 1-Lipschitz continuous lower bond on the ${\text{Δ}}_{G_S}$-function. This completes the proof. □

A.8. Proof of Theorem 4.7

Proof. Fix any k ≥ 1, ε > 0, a valid ε/2-differentially private mechanism, M, an anomaly identification query, (i, g), and a non-negative 2-Lipschitz continuous lower bound, δ, on ${\text{Δ}}_{G_S}-{\text{Δ}}_{\mathbb{G}}$, where ${\text{Δ}}_{G_S}$ and ${\text{Δ}}_{\mathbb{G}}$ respectively correspond to the k-sensitive neighborhood graph for the anomaly definition corresponding to g, and the neighborhood graph. Let U_δ be the mechanism that Construction 2 yields. Next, fix arbitrary databases x and y that are neighbors in G_S.

When δ (i, x) = δ (i, y) = 0, P (U_δ (z) = b) = P (M (z) = b) for every database z and b in {0, 1}. The privacy constraints in this case, are trivially satisfied.

Next, consider the case, where δ (i, x) > δ (i, y) 0 — this is without loss of generality as x and y are picked arbitrarily. Since M is valid ε/2-differentially private, we get the following for g(i, x) = b for some b ∈ {0, 1},

$$1-\text{P}(M(x)\ne b)e^{-\epsilon /2}\le e^{\epsilon }(1-\text{P}(M(y)\ne b))$$ (9)

Recall that G_S is a subgraph of $\mathbb{G}$ and contains a subset of edges of $\mathbb{G}$, and ${\text{Δ}}_{\mathbb{G}}(i,z)\ge 1$ for every database z. Hence, it follows that ${\text{Δ}}_{G_S}(i,z)\ge {\text{Δ}}_{\mathbb{G}}(i,z)\ge 1$, and ${\text{Δ}}_{G_S}(i,x)=1$ implies ${\text{Δ}}_{\mathbb{G}}(i,x)=1$. Thus, from the above it follows that when ${\text{Δ}}_{G_S}(i,x)-{\text{Δ}}_{\mathbb{G}}(i,x)\ge \delta (i,x)>0$, it must hold that ${\text{Δ}}_{G_S}(i,x)\ge 2$. Since $d_{G_S}\left(x,y\right)=1$ and ${\text{Δ}}_{G_S}(i,x)\ge 2$, we have g(i, x) = g(i, y). So, let b = g(i, x). From (9), we get the following.

$$1-\text{P}(M(x)\ne b)e^{-\epsilon /2}\le e^{\epsilon }(1-\text{P}(M(y)\ne b))\Rightarrow 1-e^{\epsilon }\le \text{P}(M(x)\ne b)e^{-\epsilon /2}-\text{P}(M(y)\ne b)e^{\epsilon }$$

since δ is 2-Lipschitz continuous, we get

$$1-e^{\epsilon }\le \frac{\text{P}(M(x)\ne b)}{e^{\frac{\epsilon }{4}(\delta (i,x)-\delta (i,y))}}-\text{P}(M(y)\ne b)e^{\epsilon }$$

since LHS is negative, and δ ≥ 0, the following holds

$$1-e^{\epsilon }\le e^{-\frac{\epsilon }{4}\delta (i,y)}\left(\frac{\text{P}(M(x)\ne b)}{e^{\frac{\epsilon }{4}(\delta (i,x)-\delta (i,y))}}-\text{P}(M(y)\ne b)e^{\epsilon }\right)\Rightarrow 1-\frac{\text{P}\left(M\left(x\right)\ne b\right)}{e^{\frac{\epsilon }{4}\delta \left(i,x\right)}}\le e^{\epsilon }\left(1-\frac{\text{P}\left(M\left(x\right)\ne b\right)}{e^{\frac{\epsilon }{4}\delta \left(i,y\right)}}\right)\Rightarrow \text{P}\left(U_{\delta }\left(x\right)=b\right)\le e^{\epsilon }\text{P}\left(U_{\delta }\left(y\right)=b\right)$$

In a similar fashion, by swapping x and y in (9), one can show that the privacy constraint P (U_δ (y) = b) ≤ e^ε P (U_δ (x) = b) also holds. Below we show that the other constraints are also satisfied.

$$\frac{\text{P}\left(U_{\delta }(x)\ne b\right)}{\text{P}\left(U_{\delta }(y)\ne b\right)}=\frac{\text{P}(M(x)\ne b)e^{-\frac{\epsilon }{4}\delta (i,x)}}{\text{P}(M(y)\ne b)e^{-\frac{\epsilon }{4}\delta (i,y)}}\le e^{\epsilon }$$

The above inequality holds because M is ε/2-DP and δ is 2-Lipschitz continuous.

Since all the privacy constraints hold for arbitrarily picked neighbors and δ (which satisfies the conditions specified in the claim), and a valid ε/2-differentially private M for an anomaly identification query, the claim holds in general.

As for the claim of accuracy, it is a direct implication from the Construction 2. This completes the proof. □

A.9. Composition

Here, we assume that every mechanism has its independent source of randomness and has the domain $\mathcal{D}$. Further, E(G) for a graph G denotes the set of edges in G. We make the following very simple observation.

Observation 1. For any simple graphs G and G′ over $\mathcal{D}$, two databases are neighbors in the graph $H=\left(\mathcal{D},E(G)\cap E\left(G^{\prime }\right)\right)$ if and only if they are neighbors in G and G′.

Claim 3. If mechanisms M₁ and M₂ are respectively ε₁-SP for $G_{S_1}$ and ε₂-SP for $G_{S_2}$, then M (x) ≔ (M₁(x), M₂(x)) for every x is (ε₁ + ε₂)-SP for $G_S=\left(\mathcal{D},E\left(G_{S_1}\right)\cap E\left(G_{S_2}\right)\right)$.

Proof sketch. The claim follows from M₁ and M₂ being SP for ε₁ and ε₂, and Observation 1, which ensures that the privacy constraints will be met for neighbors in G_S. □

We say, for $Y\subseteq \mathcal{X}$, a mechanism M is Y-dependent if and only if for every r ∈ Rnage (M) and x and y such that x_i = y_i for every i ∈ Y, P (M (x) = r) = P (M (y) = r).

Claim 4. For any partition of $X=Y_1\bigsqcup Y_2$, if mechanisms M₁ and M₂ are respectively Y₁-dependent ε₁-SP for $G_{S_1}$ and Y₂-dependent ε_2-SP for $G_{S_2}$, then M (x) ≔ (M₁ (x), M₂ (x)) for every x is max(ε₁, ε₂)-SP for $G_S=\left(\mathcal{D},E\left(G_{S_1}\right)\cap E\left(G_{S_2}\right)\right)$.

Proof sketch. Firstly, note that M₁ and M₂ being SP for ε₁ and ε₂ along with Observation 1, ensure that the privacy constraints will be met for neighbors in G_S for some value of ε. Further, since every neighbor in G_S differ by one record and mechanisms M₁ and M₂ are respectively Y₁ and Y₂ dependent (for an arbitrarily fixed partition), every privacy constraint will hold for either ε₁ or ε₂. From here the claim follows. □

A.9.1. Proof of Claim 5.

Lemma A.2. Fix arbitrary values for k ≥ 1, β ≥ 1 and r ≥ 0 For (β, r)-anomaly, for every record $i\in \mathcal{X}$ and every database $x\in \mathcal{D}$, i is k-sensitive with respect to x ⇔ B_x (i, r) ≥ β + 1 – k.

Proof. Arbitrarily fix k, β ≥ 1, r ≥ 0, $i\in \mathcal{X}$, and $x\in \mathcal{D}$. Further, fix p to be the normality property corresponding to (β, r)-anomaly.

Firstly, we prove the “if” direction through its contrapositive. So assume B_x (i, r) < β + 1 − k. Now, for every database y such that ‖x − y‖₁ ≤ k, B_y (i, r) ≤ β as we can only add up to k records in x. Thus for each of the above y, p (i, y) = 0, which follows from the definition of (β, r)-anomaly, and i is not k-sensitive with respect to x. This completes the proof for “if” direction.

Next, we prove the “only if” direction. Let B_x (i, r) ≥ β + 1 − k. Now, obtain a database y by adding k records that are the same as i to x. For this y, it holds that ‖x − y‖₁ = k and p (i, y) = 0 because y_i ≥ 1 and B_y (i, r) ≥ β + 1 (since k ≥ 1). Hence, we conclude that i is k-sensitive with respect to x. And this completes the proof as k, β, r, i, and x were chosen arbitrarily. □

For any $i\in \mathcal{X}$ and r ≥ 0, we write Y (i, r) to denote the set $\{j\in \mathcal{X}:d(i,j)\le r\}$.

Claim 5. For any given $n\in \mathbb{N}$ and every t = 1, … , n, arbitrarily fix ε_t, r_t > 0, k_t, β_t ≥ 1, and a mechanism, $M_{i_t}:\mathcal{D}\to \{0,1\}$, that is ε_t-SP for k_t-sensitive neighborhood graph corresponding to (β_t, r_t)-anomaly and is also Y (i_t, r_t)-dependent. Further, let m be the maximum number of i_t’s that are within any ball of radius max(r₁, … , r_n), ε = max(ε₁, … , ε_n), k = min(k₁, … , k_n), β = max(β₁, … , β_n), and r = min(r₁, … , r_n).

If $M(x)≔\left(M_{i_1}(x),\dots ,M_{i_n}(x)\right)$ for every x, then M is mε-sensitively private for k-sensitive neighborhood graph corresponding to (β, r)-anomaly.

Proof. Arbitrarily fix the values for all the symbols used in the claim above as per the specification.

Firstly, we consider the guarantee with respect to the sensitive neighborhood graph. Here it is sufficient to show that the k-sensitive neighborhood graph, G_S, corresponding to (β, r)-anomaly, is a subgraph of the k_t-sensitive neighborhood graph, $G_S^t$, corresponding to (β_t, r_t)-anomaly for every t. Thus we show that, for any t and two databases x and y, if x and y are neighbors in G_S, then they are neighbors in $G_S^t$. So arbitrarily fix x and y that are neighbors in G_S and t ∈ [n]. Since x and y are neighbors in G_S, there exists a record i that k-sensitive with respect to x or y. Let i be k-sensitive with respect to x—this is without loss of generality since x and y are picked arbitrarily. Now, from Lemma A.2, we get that B_x (i, r) ≥ β −k + 1. Since β ≥ β_t and k ≤ k_t, B_x (i, r) ≥ β_t − k_t + 1; this implies that i is k_t-sensitive with respect to x (Lemma A.2), and thus, x and y are neighbors in $G_S^t$. Hence, we conclude that G_S is a subgraph of every $G_S^t$.

Next, we prove the bound on the divergence of probabilities to show that the loss in privacy is at max mε. For any $i\in \mathcal{X}$, let A_i be such that for every t ∈ [n], t ∈ A_i ⇔ d (i, i_t) ≤ r′, where r′ = max(r₁, … , r_n). And let $m={\text{max}}_{i\in \mathcal{X}}|A_i|$. Arbitrarily fix, the neighboring databases x and y in G_S and w ∈ {0, 1}ⁿ. Let i be the record in which x and y differ. Now it follows that

$$\begin{gathered} \frac{\text{P}(M(x)=w)}{\text{P}(M(y)=w)}=\prod _{t\in A_i}\frac{\text{P}\left(M_{i_r}(x)=w_r\right)}{\text{P}\left(M_{i_r}(y)=w_r\right)}\times \prod _{l\in [n]\backslash A_i}\frac{\text{P}\left(M_{i_l}(x)=w_l\right)}{\text{P}\left(M_{i_l}(y)=w_l\right)} \\ =\prod _{t\in A_i}\frac{\text{P}\left(M_{i_t}(x)=w_t\right)}{\text{P}\left(M_{i_t}(y)=w_t\right)}\le \text{exp}\left(\sum _{t\in A_i}{\epsilon }_t\right)\le \text{exp}(m\epsilon ) \end{gathered}$$

Above, the first equality holds because each of the $M_{i_t}$ has its independent source of randomness. The second equality holds because each $M_{i_t}$ is Y (i_t, r_t)-dependent in addition to its randomness and r_t ≤ r′. The first inequality follows from $M_{i_t}$ being ε_t-SP for G_S, which is a subgraph of $G_S^t$. The last inequality follows from the fact that ε ≥ ε_t and m ≥ |A_i|.

Lastly, note that for any W ⊆ {0, 1}ⁿ, it follows that

$$\frac{\text{P}(M(x)\in W)}{\text{P}(M(y)\in W)}\le \frac{\sum _{w\in W}\text{P}(M(x)=w)}{\sum _{w\in W}\text{P}(M(y)=w)}\le \text{exp}(m\epsilon )$$

Thus, we conclude that the claim holds. □

A.10. Relation of SP to other definitions

A.10.1. One-sided differential privacy (OSDP) [13].

It allows for mechanisms to be private that can reveal the presence or absence of a sensitive record in the database. We explain this below. Consider two neighboring databases x and y (i.e., they differ by one record) such that x has exactly one sensitive record and y has no sensitive record, and an ε-OSDP mechanism $M:\mathcal{D}\to \{0,1\}$ with P (M (x) = 0) = 0 and P (M (y) = 0) = 1 – note this is possible as M only needs to satisfy P (M (x) ∈ b) ≤ e^ε P (M (y) ∈ b) for b ∈ {0,1}. Now, if we pick x or y randomly and reveal the output of M, the output will reveal which database was used, and hence if the sensitive record was present or not.

A.10.2. Tailored differential privacy (TDP) [36].

SP is a special case of TDP. Which becomes clearer once we restate TDP for the unbounded case, which we deal with. For $\alpha :\mathcal{X}\times \mathcal{D}\to {ℝ}_{\ge 0}$, a mechanism is α (·)-TDP if for every two databases, x and y differing in a record i, and every R ⊆ Range (M), P (M (x) ∈ R) ≤ e^{α(i, x)} P (M (y) ∈ R). Let for every i and x, $\alpha (i,x)=\epsilon d_{G_S}\left(x,x^{\prime }\right)$ ($x_j^{\prime }=x_j$ for every j ≠ i and $x_i-x_i^{\prime }=1$). Now, it is immediate that a mechanism is α (·)-TDP if and only if it is ε-SP for G_S. A similar statement holds true for Blowfish privacy [25], which follows by considering the sensitive neighborhood graph to be the policy graph.