Abstract
With few exceptions, polydispersity or molecular heterogeneity in matter tends to impede self-assembly and state transformation1–3. Here we report shape transition studies of nematic liquid crystal oligomer (NLCO) drops, which reveal, surprisingly, that molecular heterogeneity in the drops promotes reversible transitions to a rich variety of non-spherical morphologies with unique internal structure. Previously, shape transitions of homogeneous liquid drops with monodisperse ingredients have been reported in equilibrium4–7 and non-equilibrium studies8, 9, with the latter producing filaments at active interfaces, albeit randomly without control. Our experiments employ equilibrium suspensions of drops composed of polydisperse NLCOs. Variation of oligomer chain length distribution, temperature, and surfactant concentration alters the balance between NLCO elastic energy and interfacial energy and drives formation of visually striking nematic structures ranging from roughened spheres to flowers to branched filamentous networks with controllable diameters. The branched structures with confined LC director fields can be produced reversibly over centimeter areas and converted into LC elastomers by UV curing. Remarkably, observations and modeling reveal that chain length polydispersity plays a crucial role in driving these morphogenic phenomena, via spatial segregation. This insight suggests new routes for encoding network structure and function in soft materials.
We study NLCO drops, tens of microns in diameter, dispersed in water containing sodium dodecyl sulfate (SDS) surfactant. SDS creates a strong preference for homeotropic anchoring, wherein the nematic director (molecular orientation) is perpendicular to the drop surface (Fig. 1a). Each surfactant-stabilized NLCO emulsion drop contains a mixture of RM82 monomer and oligomers of RM82 (1,4-bis-[4-(6-acryloyloxyhexyloxy)benzoyloxy]-2-methylbenzene)10 with variable chain lengths (Fig. 1a, details in Extended Data Fig. 1a). Importantly, compared to small molecule LCs, chain length polydispersity of the NLCOs offers new degrees of freedom which can profoundly affect drop morphology, and the NLCOs are readily crosslinked to lock-in nematic order and morphology.
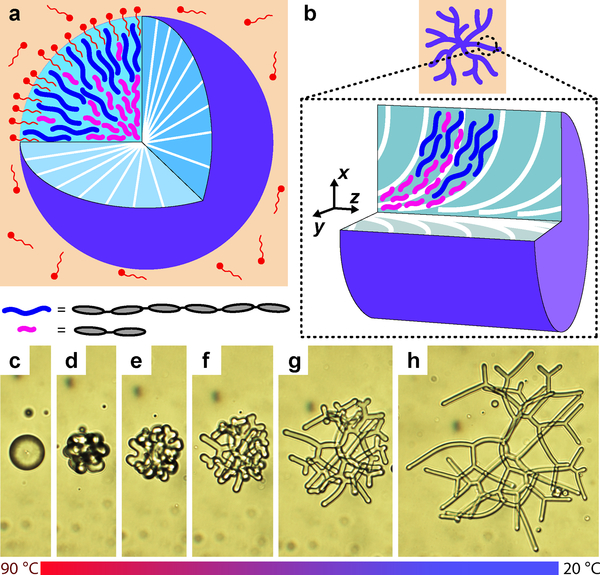
Fig. 1 |. Spontaneous shape transition of NLCO drops.
a-b, The schematics depict a surfactant-stabilized NLCO sphere and filament (purple) in a background aqueous phase (orange). White lines represent the nematic director. The concept of spatial segregation by oligomer chain length is illustrated. Inset: For simplicity, long-chain/short-chain species (blue/pink solid-curves) represent hexamers and dimers, respectively (grey ellipses represent monomers). The z-axis in (b) is parallel (and coincident) to the central filament axis. c-h, An NLCO drop spontaneously (and reversibly) evolves from sphere to an extended and branched filamentous drop as temperature is reduced. Scale bar is 20 μm.
Essential features of the shape transitions are shown in Fig. 1. At a high temperature (~90 °C), while in the nematic phase, the drop is spherical (Fig. 1a, 1c). Here, interfacial energy is large compared to bulk director elastic energy. Upon cooling, the surface tension and bulk elasticity vary, and excess interface is created. This interplay destabilizes the drop, facilitating spontaneous polymorphic transitions to non-spherical equilibrium structures (see exemplar images in Fig. 1c–h; director configurations in Fig. 1a–b; Supplementary Video 1). These polymorphic shape transitions are reversible and repeatable via temperature cycling (see Extended Data Fig. 2, Supplementary Video 2).
Arguably, the major factor driving these shape transitions is the interfacial tension, γ, which decreases with decreasing temperature. This trend was confirmed in pendant drop experiments using large, millimeter-size NLCO drops (Extended Data Fig. 3); it has been reported in other systems7, 11. The decrease in γ is believed to arise from greater molecular ordering at the interface7, 11, 12. In our case, surfactant-induced anchoring and the stronger alignment of NLCOs at lower temperatures enhance interfacial ordering. Additionally, NLCO elastic constants increase with decreasing temperature13. Thus, with reduction of γ, anisotropic bulk elasticity becomes more significant for determining drop shape, increasing potential for spontaneous shape transitions4.
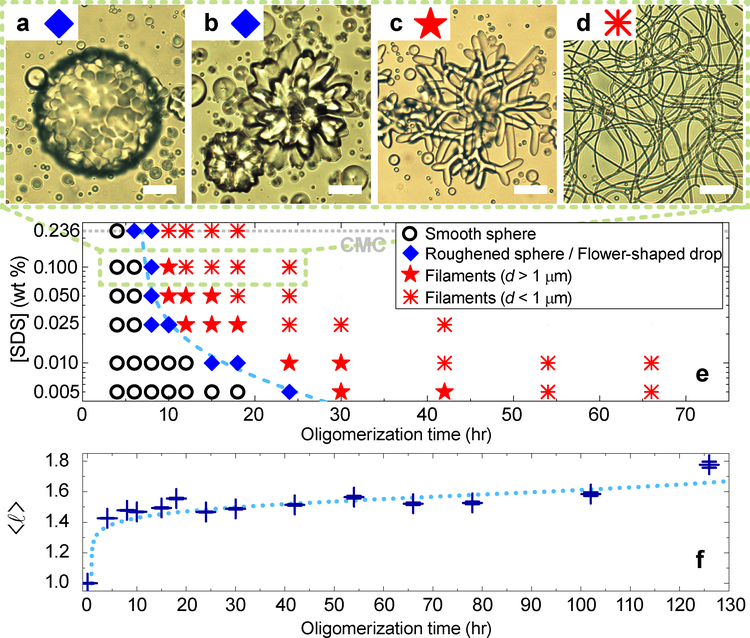
To elucidate the consequences of these effects, we constructed a morphology “state” diagram from samples that experienced the same heating-cooling cycles. Fig. 2a–d exhibit the repeatable drop morphologies: smooth/roughened spheres, flowers, large and small diameter (d) filament networks. The state diagram (Fig. 2e) is shown as a function of surfactant concentration and mean oligomer length, 〈ℓ〉, which increases with total oligomerization time.
Fig. 2 |. Equilibrium NLCO drop morphologies as function of mean oligomer chain length and surfactant concentration.
a-d, Optical images of common NLCO drop morphologies at room temperature in a 0.1 wt% SDS solution. With increasing 〈ℓ〉, the morphologies shown are (a) roughened spheres (see also Fig. 4a), (b) flower-shaped drops, and (c-d) filamentous structures with decreasing filament diameter. e, A state diagram, constructed from data, exhibits the equilibrium morphology (examples in (a-d)) versus 〈ℓ〉 and surfactant concentration. Increasing either parameter facilitates filament formation better. The dashed curve separates spherical and non-spherical drop regimes. f, Size exclusion chromatography shows that 〈ℓ〉 (in units of monomer length) increases with oligomerization processing time (horizontal axis of plots in (e), (f)). Errors in 〈ℓ〉 mainly arise from the measurement uncertainty of long-chain components. Dotted curve is to guide the eye. Scale bar is 20 μm.
Consider the effects of NLCO average chain length. Though all samples are polydisperse, samples prepared with longer oligomerization processing times contain a larger ratio of long-chain to short-chain oligomers and have longer 〈ℓ〉 (Fig. 2f, Methods, Extended Data Fig. 4). Larger NLCO elastic constants are expected for longer 〈ℓ〉14. Additionally, interfacial oligomer assembly with longer 〈ℓ〉 ends to reduce γ (see Extended Data Fig. 3); longer NLCOs increase oligomer chain hydrophobicity which induces more interfacial ordering15, 16. As temperature is lowered, these trends favor drop morphologies with large surface area. More quantitatively, our measurements indicate a crossover transition to non-sphericity when 〈ℓ〉 ≈ 1.5 times the monomer length in 0.1 wt% SDS solutions.
Other factors modify surface tension and affect the state diagram. In contrast to work on non-equilibrium LC filament formation8, 9, our experiments were largely carried out below the critical micelle concentration (CMC) of SDS wherein increasing SDS concentration lowers γ and helps facilitate interfacial roughening and filament formation (Fig. 2e). Additional experiments confirmed that primary phenomena are not unique to SDS surfactant, nor limited to concentrations below CMC (Extended Data Fig. 5, 6).
Given this emerging qualitative picture, we sought more quantitative understanding. To this end, we determined NLCO director configurations using polarization optical microscopy (POM) with full-wave retardation plate. We then applied simple models to determine their free energies. Here we focus on the two limiting morphologies: spherical versus filamentous drops. Spheres exhibit the classic POM texture corresponding to radial hedgehog director configuration with central topological charge +1 (point defect) (Fig. 3a). Filaments exhibit an escaped-radial director configuration (Fig. 3b–c). For all geometries, the single point defect always remains at drop center (Fig. 3a, 3d–e).
Fig. 3 |. Director configurations within NLCO structures.
a, Bright-field image of spherical NLCO drop with a single, central radial hedgehog defect. b-c, POM coupled with full-wave retardation plate enables identification of nematic director configurations within a section of a y-branched NLCO filamentous structure. Yellow indicates northwest-southeast alignment; cyan indicates northeast-southwest alignment. Inset: 2D projected director field schematic. d-e, The hedgehog always remains at the center of drop, even for complex structures, e.g., after evolving to a flower-shape (bright-field (d); POM image and director field schematic (inset)) or a filamentous structure (hedgehog appears as the cross-pattern in POM (e)). Note, structures in (d-e) were weakly confined in a quasi-2D chamber so that filaments tended to grow perpendicular to optical axis, providing easy observation of the point defect. Scale bar is 10 μm.
To predict shape transition phenomena, modeling must account for energetics associated with both interfacial tension and elastic bulk free energy of the confined NLCOs. The calculations require knowledge about the splay (K11), twist (K22), bend (K33), and saddle-splay (K24) NLCO elastic constants, as well as interface anchoring strength. We utilize well known models for the sphere with radial hedgehog director configuration17 and for cylinders with escaped-radial director configuration18. Importantly, all models assume a homogeneous, monodisperse chain length distribution for the NLCOs. The models employ γ from pendant drop experiments, measured drop dimensions, and estimates of elastic constants and interfacial anchoring strength based on small molecule LCs19. Calculations (see Methods, Extended Data Table 1) yield conditions for the sphere-filament free energy instability.
Surprisingly, we found that free energy instabilities only occur if our system has either an unphysically large saddle-splay elastic constant (K24 > 30×K11), or a value of γ that is much smaller (~10x) than those obtained in the pendant drop experiments. Given this discrepancy, we were compelled to consider other effects. In the process we uncovered the importance of NLCO chain length polydispersity (molecular heterogeneity), which can profoundly impact interface and core energetics.
First, consider elastic free energy gradients in small (~10–30 micron) drops versus the large (mm-size) drops used to obtain γ. In small drops, the nematic adopts a single-domain configuration in which the director field experiences large splay distortion near drop center for spheres, or large splay and bend distortion near the central axis for filaments (see Methods). The mm-size drops, by contrast, are composed of many nematic domains, each with different director orientation, and they are filled with many disclination lines. Although director fields in the large drops can be locally non-uniform, most micro-domains remain uniformly aligned, and splay/bend elasticity gradients are not large. Thus, the overall elastic gradient effects in mm-size drops are small.
In the micron-size drops and cylinders, however, oligomers experience significant chain-length dependent driving forces. These forces are induced by elastic energy gradients of the director within the drop, i.e., higher elastic energy density near the core. To reduce system elastic energy, short-chains, which have smaller associated splay elastic constants, will migrate towards the core, and long-chains, which have larger associated elastic constants, will migrate towards the drop surface (Fig. 1a–b). A simple two-component macromer-monomer demixing model with mean oligomer chain length of 〈ℓ〉 ≈ 1.7 for the outer shell and mean oligomer chain length in the core of 〈ℓ〉 ≈ 1.39, for example, predicts an ~10% decrease in elastic free energy due to reduced average rod-length in the core.
As a result of these elastic free energy gradients, interfacial tension in the small drops is lowered dramatically and will differ from large drops. Stronger nematic ordering at the interface driven by the greater numbers of long-chain oligomers will decrease γ by a factor of 10 or more compared to drops with homogeneous oligomer distributions (see Extended Data Fig. 3). Thus, spatial redistribution of polydisperse oligomers in the small drops resolves the issues raised by the original homogeneous model. A conservative reduction of γ by 10x to ~0.1 mN/m yields sphere-filament instabilities with reasonable saddle-splay moduli. Importantly, our experiments with bidisperse distributions of monomers and macromers, made by a different chemical procedure10 support this central new insight about the effects of NLCO polydispersity. See Methods for these latter experiments. Previously, shape transitions were observed in molecularly heterogeneous systems20, and the phenomenon of segregation by size, broadly defined, has been reported in lipid membrane systems21, near topological defects in LC simulations22, and in LC polymer systems mediated by size-dependent nematic/isotropic-transition temperatures23. It is perhaps useful to reconsider these phenomena in light of our experiments.
By contrast, as noted above, spatial redistribution of oligomers is not anticipated in mm-size drops. Segregation is driven largely by director distortion near uniformly distributed disclinations and domain walls and will not induce overall migration to the surface. Thus, the surface of the mm-size drop likely remains a uniform mixture of oligomers with mean chain length set by initial NLCO distribution. The pendant mm-drop γ therefore reflects “average behavior” of the mixture; it should be significantly larger than γ of micron-size drops. Possible curvature-induced forces driving segregation will also be less in large versus small drops.
To harvest these self-assembled morphologies for new functional materials, the NLCOs were UV-crosslinked into nematic liquid crystal elastomers (NLCEs). Representative scanning electron microscopy (SEM) images of the NLCEs are in Fig. 4a–d. By comparing POM images of corresponding NLCE and NLCO structures, we confirmed that director configurations are well-maintained.
Fig. 4 |. SEM images of self-assembled NLCEs.
a-d, Crosslinked NLCEs: (a) roughened sphere, (b) flower, and (c-d) filamentous structures with decreasing diameter. See Fig. 2a–d for corresponding NLCO morphologies observed in bright-field microscopy. The objects shown in (a-c) evolved from a single drop and are depicted in inset schematics; thin filamentous structures grown from several drops are shown (intertwined) in (d) (Inset: filaments with different colors grow from different drops). e-f, Partial view of a centimeter-wide free-standing NLCE fibrous mat and its cross section (cut by a focused-Ga-ion-beam). See Extended Data Fig. 7 for macroscopic image of the mat. g-h, Oriented NLCE fiber yarn. The scale bar in (g) is 100 μm; all other scale bars are 5 μm.
Lastly, we show that these NLCE fibers can be densely packed into centimeter-wide and few-micron-thick, non-woven, free-standing NLCE mats (Fig. 4e–f) by sedimentation. These structures could find applications in responsive filtration and smart fabrics. A NLCE yarn consisting of well-aligned fibers (Fig. 4g–h) was made by directly pulling fibers out of aqueous solution; these yarn-like objects could find use in artificial muscles24, 25 or tunable waveguides. Actuation with the current fibers is not yet apparent in our preliminary studies, probably because of high crosslinking density due to insufficient oligomerization. Variation of LCO chemistry26 should address this issue; work is underway along these lines. Compared to electrospinning27, extrusion24, and wet-spinning25, this new approach for making fibrous structures is simple and scalable without need for sophisticated tools.
To conclude, while polydispersity and molecular heterogeneity are often avoided in synthetic systems, here they facilitate equilibrium transitions among dramatically different morphological structures. This feature can be exploited to create soft materials such as highly branched networks with uniform filament size, i.e., simply by tuning chain length distribution, temperature, and surfactant concentration. Future studies of branching behaviors may provide new insights about drop assembly and stabilization, and, possibly, could reveal connections to molecular heterogeneity driven segregation and phase separation for function in biological matter28–30. Moreover, the self-assembly processes are reversible, and the network structures can be permanently locked by UV crosslinking. The simple rules revealed by the experiments offer new concepts for creation of programmed spatio-temporal networks.
Methods
Synthesis of NLCO drops
The NLCO emulsions were made in three-steps: (1) Preparation of emulsion drops containing monomer/chain-extender mixtures and suspended in an aqueous phase; (2) Oligomerization within individual drops to link LC monomers together into LCOs; (3) Creation of final NLCO drop suspensions in water, which are observed by video microscopy as a function of temperature.
Preparation of emulsions containing precursors (Step 1)
A 1:1 mixture of 1,4-bis-[4-(6-acryloyloxyhexyloxy)benzoyloxy]-2-methylbenzene (monomer RM82, Wilshire Technologies) and n-butylamine (chain-extender, Sigma-Aldrich) was dissolved in chloroform (Fisher Scientific); chloroform is 3x the weight of RM82. A 0.2 wt% (by RM82 concentration) antioxidant, butylated hydroxytoluene (BHT, Sigma-Aldrich), was also added.
The resulting organic phase mixture was then made into a micro-droplet emulsion in an aqueous solution. This was achieved by adding surfactant to the mixture of water and organic-phase and then shaking to create polydisperse drops with diameters ranging from 10 to 100 microns. Three different surfactants were employed: negatively charged sodium dodecyl sulfate (anionic surfactant SDS, Sigma-Aldrich), positively charged hexadecyltrimethylammonium bromide (cationic surfactant C16TAB, Sigma-Aldrich), and neutral polyoxyethylene (20) sorbitan monolaurate (Tween 20, Fisher Scientific). Although phenomena with SDS surfactant is reported in the main text, experiments using the other two surfactants exhibited similar behavior; spontaneous shape transitions are not restricted to a certain type of surfactant. However, in considering surfactants, it is important that homeotropic anchoring of NLCOs is favored. All chemicals were used as received, without further purification/modification. At this stage, the suspended drops contain unchained monomers.
Oligomerization within drops (Step 2)
The RM82/butylamine (chain-extender)/chloroform - SDS/water droplet suspension is next placed in a water bath at 90 °C for oligomerization. During this process, the organic solvent (chloroform) evaporates completely from each emulsion drop, and then the butylamine begins to link the diacrylate RM82s in chains via a self-catalyzed “aza-Michael addition” reaction. Afterward, emulsion drops are composed of main-chain liquid crystal oligomers (LCOs). The degree of oligomerization (i.e., the mean oligomer chain length (〈ℓ〉) is controlled by reaction time.
Note, the NLCO chain length distribution is broad and has a shorter mean oligomer length, 〈ℓ〉, compared to previous LCE work10.
Cooling of the NLCO drops (Step 3)
After the reaction, a small volume of the suspension (i.e., the NLCO emulsion) is pipetted into a pre-heated glass well, sealed with coverslip and glue, and then cooled to 20 °C on a hotplate at a rate of −1 °C/min. The suspension is then annealed (i.e., quickly re-heated to 90 °C and then slowly cooled to 20 °C again) before the drop morphology experiments are carried out.
Note, compared to pure RM82 monomer, which forms a nematic only above 86 °C (nematic in the 86–116 °C temperature range), the present LCOs exhibit a wide nematic window that extends below room temperature (i.e., at least between 20–90 °C).
Drop morphology characterization
Sample cells containing NLCO drops were observed with a Leica DMIR13 inverted optical microscope in bright-field and polarization modes. Leica N Plan 10x, Leica PL Fluotar L 63x, and Leica PL APO 100x objectives were used. Crossed-polarizers and full-wave retardation plates were deployed in the microscope to characterize director configurations within the drops.
Molecular weight measurements of NLCOs
To further characterize the LCO samples, most of the remaining emulsion solution was centrifuged (2000 RCF) at 15 °C and washed with DI water several times to remove surfactant. It was then vacuum dried to remove water.
Part of the resultant bulk sample was then dissolved in tetrahydrofuran (THF stabilize with 250ppm BHT, Alfa Aesar) at a concentration of 1.5 mg/mL for molecular weight analyses. The molecular weight analyses were performed using standard size exclusion chromatography (SEC, Tosoh Bioscience EcoSEC) with flow rate of 1.0 mL/min and with three analytical columns in series: TSKgel G2000HXL, TSKgel G2500HXL, and TSKgel G3000HXL. A standard polystyrene sample (MW = 48,100 Da, Sigma-Aldrich) was also added during the SEC measurements for calibration purposes.
Macroscopic interfacial tension measurement of large NLCO drops
The interfacial tension arising between NLCO drop surfaces and background aqueous phase were measured macroscopically using the pendant drop method31, 32. The pendant drop technique works by analyzing the shape of a large (millimeter-size) liquid drop hanging from a capillary tube (i.e., the flat tip syringe needle), when it is about to detach from the capillary tube. The shape of the hanging drop depends on gravity, on cohesive forces of the drop within the background medium, and on the interfacial tension.
Our pendant drop tensiometry employs a homemade temperature-regulated chamber, which enabled us to measure the system interfacial tension as a function of temperature. Each NLCO bulk sample was injected into a syringe coupled with a flat tip needle. The pendant NLCO drop was made in a 0.1 wt% SDS water solution in the temperature-regulated chamber. High contrast images of the drop contour were obtained while temperature was slowly decreased. The densities of the bulk NLCO were also measured at the different temperatures. Finally, using the methods and software created by Daerr et al.32, we fit the drop contour for each sample at each temperature using the density of bulk NLCO and of the surrounding medium. With this information, the interfacial tension can be deduced (see measured interfacial tensions in Extended Data Fig. 3).
Macromer-monomer mixing experiments
These experiments were designed to confirm the influence of oligomer polydispersity in the shape transition phenomenology of NLCO drops. Specifically, we investigated how the average chain length of the oligomers in the NLCO mixture affects the shape transitions. For this study, however, we employed a synthetic approach to make the NLCO drop mixtures that was different from the methods in the main text.
We first synthesized a main-chain liquid crystal macromer with a number-average molecular weight of approximately 6,900 Da; following the work by Ware et al.10, this macromer had a mean chain length, 〈ℓ〉 ≈ 9, i.e., a mean chain length roughly 9 times the monomer length. This sample had a polydispersity index (PDI) ≈ 1.3 (for comparison with NLCOs in the main text, see Extended Data Fig. 1). Note, PDI is defined as the ratio between weight-average molecular weight () and number-average molecular weight (). PDI = 1 implies uniform polymer chain length.
The macromers thus obtained were then mixed with pure RM82 monomer at different weight ratios in chloroform (chloroform: LC mixture = 3:1 wt/wt). The mixture was then emulsified in 0.1 wt% SDS aqueous solution, and then the chloroform was evaporated in a 90 °C water bath. No further chain growth occurred during this process (confirmed by 1H-NMR) because the chain-extender, n-butylamine, was not added into the mixture. When all chloroform was removed, temperature cycling was carried out following the same protocol described in Methods section. The resulting drop shapes and micro-structures were observed in bright-field and polarization optical microscopy (POM).
Upon cooling, the macromer-monomer NLCO drops transitioned from smooth spheres to roughened spheres, flower-like structures, and filamentous structures (see Extended Data Fig. 4). These effects were dependent on the monomer : macromer weight ratio. Specifically, with increased mean oligomer chain length, 〈ℓ〉, droplet structures with large surface area are preferred (e.g., longer, thinner filaments). The observed phenomenology agrees very well with observations in the main text. Recall, we argued that the increased bulk elasticity and decreased interfacial tension accompanying increased 〈ℓ〉 promotes shape transitions. Quantitatively, as shown in Extended Data Fig. 4b, the droplet’s tendency towards non-sphericity commences when 〈ℓ〉 ≈ 1.4. This supplementary macromer-monomer mixing experiment thus exhibits the same tendency as the experiments that employed the synthesis-in-emulsion scheme. In the latter case, the droplet’s tendency towards non-sphericity commenced when 〈ℓ〉 ≈ 1.5. Note, the 〈ℓ〉 at which non-sphericity commences can vary slightly with drop size.
We also carried out experiments with monomers only. Pure RM82 monomer (〈ℓ〉 = 1) crystalizes during cooling; it is nematic only above 86 °C. Thus, shape transitions are not seen with drops containing only monomer. Furthermore, experiments with drops containing only macromers (〈ℓ〉 ≈ 9, see Extended Data Fig. 1) did not exhibit shape transitions. Evidently, the surface tension in drops with pure macromer is too large to permit shape transitions, presumably due to poor anchoring at the surface33. Moreover, the macromer-only system viscosity is much larger23 than the drops with smaller average chain length, making texture formation/reformation kinetics very slow.
By contrast, the NLCO mixtures we studied maintain good packing at the drop interface, probably because of different formation processes. The NLCOs were synthesized within each SDS stabilized drop. Thus, we expect that homeotropic director “pre-alignment” could already exist at early stages of the oligomerization process in these drops, i.e., when most of the oligomer chains are short and the surfactants can induce good anchoring. Thus, importantly, the monomers are approximately locked into their interfacial structure at the outset. Then as the chains grow longer throughout the drop, the longer oligomers spatially segregate to an already partially ordered surface at high coverage and can help increase order at the interface in a perturbative manner. This segregation and greater molecular packing/order reduces interfacial tension and ultimately induces shape transitions when interfacial tension becomes sufficiently small. In principle, the shape transformation process could still happen for a monodisperse system with very small surface tension. Our polydisperse NLCO mixtures, however, provide an easy segregation-driven route to lowering interfacial tension and elastic energy.
Quantitative calculation of system free energy
Here, we provide details of our model free energy calculations (see also included custom computer codes). We employ equilibrium models because the effects were reversible with slow temperature cycling, and the structures were stable. Note, for rapid quenching (non-equilibrium) it is possible to generate a transient negative surface tension which could also drive the effect.
The Frank free energy for a nematic liquid crystal is given below; it accounts for the elastic energy associated with spatial distortions of the director in the liquid crystal (LC)34, i.e.,
| (1) |
Here K11, K22, and K33 are elastic constants for splay, twist, and bend deformations, respectively. The final term, with the elastic constant K24, is called the saddle-splay; it is absent from the corresponding Euler-Lagrange equation but contributes to the total free energy. Note, for simple solutions, the so-called splay-bend K13 elastic deformation and other second derivatives (or higher order terms) of the director field35, 36 are usually not included, e.g., inclusion of K13 without higher order terms can lead to paradoxes37, 38; nevertheless, interested readers can find free energy models which include K13 and discuss these issues39. To simplify calculations even further, a one-constant limit of the Frank free energy17 is often applied, i.e., K11, K22, K33 are set equal and expressed as a single value, K.
In addition to LC elastic free energy, our modeling includes interfacial free energy,
| (2) |
and LC interface anchoring energy40,
| (3) |
where γ is the interfacial tension, Wa is the anchoring energy coefficient at the interface, and Φ is the angle between the LC director at the interface and the interface normal. Both terms are integrated over the surface.
Starting with these elastic energy expressions, and utilizing well-established elastic models for a sphere (with radial director configuration)17 and for a cylindrical filament (with escaped-radial director configuration)18, 39, 41–43, one can derive expressions for total system free energy.
| (4) |
| (5) |
| (6) |
| (7) |
Here K is the composite elastic constant (i.e., in the one-constant-approximation) of the NLCO mixture. R is the radius of spherical NLCO drop, and r and L are the radius and length of the NLCO cylindrical filament, respectively. The twist elasticity, K22, makes no contribution to the free energy of either the sphere or cylinder, and the anchoring energy term (Eqn. (3)) arises for cylinders with an escaped-radial director configuration, but not for spheres with radial director configurations. Note, in Eqn. (1), (4), and (6), the saddle-splay (K24) term is sometimes ignored, but for our system K24 is essential. Ignoring saddle-splay would require a negative interfacial tension (γ) for the spontaneous shape transitions, which is inconsistent with our measurements of γ and with the reversible, equilibrium shape transition phenomenology observed.
Since we observed a spontaneous transition from spherical to filamentous drops during cooling, we anticipate that an energetically-favorable spontaneous process must have Ff < Fs. We next examine the parameter values needed to favor this spontaneous process.
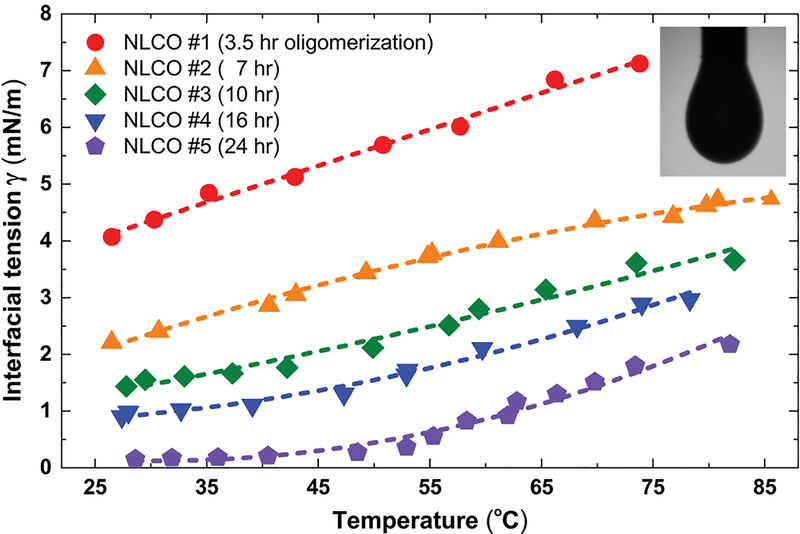
Among these parameters, γ was measured by the pendant drop technique using large (mm-size) drops. For example, the measured γ is 4.64 mN/m at 80 °C and 2.36 mN/m at 30 °C for the sample NLCO#2 which had 7 hours of oligomerization time (see Methods and Extended Data Fig. 3; consult references7,11,12,44,45 about this unusual temperature-dependent trend). In one (typical) sample, R and r were measured by bright-field optical microscopy to be 13.0 μm and 0.65 μm, respectively. Because it is difficult to directly measure the elastic constants and anchoring energy coefficients of our NLCOs, we estimate their values at room temperature: K ≈ 10−10 N and Wa ≈ 10−4 J/m2. These numbers are chosen based on the values, and the relationships between parameters, in drops of monodisperse small molecule LCs. When interfacial free energy is dominant (e.g., at high temperature or with short 〈ℓ〉), we expect the NLCO droplets to remain spherical. Then, knowing the interfacial tension, we can compute an estimate for K. Similarly, since the droplet adopts a radial configuration with a hedgehog defect at its center19, Wa is estimated by assuming that the extrapolation length, ξs ≡ K/Wa ≈ 1 μm, for the spherical drop is much smaller than the drop diameter. Note, Wa typically ranges from 10−6 to 10−3 J/m2 for weak to strong anchoring. (For reader reference, we list experimental values for important parameters. For thermotropic LCs: (1) 5CB has K11 ≈ 6.2×10−12 N and K33 ≈ 8.25×10−12 N (~25 °C); (2) 8CB has K11 ≈ 6.0×10−12 N and K33 ≈ 6.4×10−12 N (~35 °C)46. For lyotropic LCs: (1) DSCG has K11 ≈ 10.2×10−12 N and K33 ≈ 24.9×10−12 N (16 wt%, within ~4 °C of TNI); (2) SSY has K11 ≈ 4.3×10−12 N and K33 ≈ 6.1×10−12 N (29 wt%, within ~2 °C of TNI)47. For liquid crystal monomers that are molecularly similar to RM82: K ≈ 2.6×10−12 N (~97 °C)48. For anchoring energy: (1) 5CB/SiO interfaces have Wa ≈ 4.0×10−5 J/m2 (~35 °C)49; LC mixture (Merck-BDH, MLC 6608)/lecithin interfaces have Wa ≈ 4.6×10−4 J/m2 (23.1 °C)50; 8OCB/DMOAP-treated-glass interfaces have Wa ≈ 1.0×10−4 J/m2 (~75 °C)51.)
The models and criteria above, along with the experimental and estimated parameters, lead to well-defined constraints. A spontaneous shape transition is only possible, for example, when K24 ≳ 32×K11, which is far too large for most LC materials. Note, abandoning the one-constant approximation does not affect this conclusion. In addition, varying K and Wa over a reasonable range, e.g., from 5×10−11 to 10−10 N and 5×10−5 to 5×10−4 J/m2, respectively, does not affect the conclusion (see details in Extended Data Table 1). Revisiting the initial comparison between Eqn. (4) and (6) suggests that a smaller “true” γ is needed to significantly increase the probability of a shape transition. We next consider how this situation can be realized through oligomer polydispersity and spatial segregation.
In applying Eqn. (4) and (6), our models treated the bulk NLCO as a homogeneous material with monodisperse chain length. However, the NLCO mixture is polydisperse; it is composed of oligomers with a broad distribution of chain lengths. This new degree of freedom offers the possibility for spatial rearrangement of the oligomers within the drops, wherein the long-chain-length oligomers move preferentially to the interface and the short-chain-length oligomers move to be closer to the drop center. For micron-size NLCO emulsion drops, molecules can easily diffuse and segregate within the confining structure on experimental time scales.
Based on simple energy considerations, spontaneous segregation to produce a long-chain-rich shell (near the surface/interface) and a short-chain-rich core (e.g., near the sphere-center, or filament/cylinder central-axis) will lower the system free energy. Consider a quantitative example. For spherical drops of radius R, one can compute the elastic free energy density in the shell and core regions using the relation: Felastic = 8πK11R. If we define the core as the central region with radius ranging from 0 to R/2, and the shell as the remainder of the sphere, then the splay elastic energy density in the core is ~7x greater than that in the shell. In our experiments, the bulk elastic energy is lowered because short-chain NLCOs, which have smaller elastic constants, preferentially occupy the core regions which have very substantial director distortions (i.e., large splay or splay/bend elastic distortions). This phenomenon can be understood as a chain-length dependent “driving force” due to the elastic energy density gradient within the drop. This energy gradient between core and shell regions leads to spatial rearrangement of oligomers with different chain lengths.
Moreover, the segregation of long-chain oligomers to the drop surface will reduce the interfacial energy of the drop (compared to a drop containing a homogeneous mixture, as is the case for the mm-size drops). We thus expect, γtrue;micro-emulsion to be less than the corresponding mm-size droplet interfacial tension, γmeasured;mm-drop, measured in the pendant drop experiments: γtrue;micro-emulsion < γmeasured;mm-drop. NLCO polydispersity, and its consequences for chain-length dependent spatial segregation of oligomers within the drop, generates a critical new feature in the micro-emulsion that influences shape transitions and self-assembly. The resultant reduction of interfacial tension reduces the unphysically large K24 requirement (computed above) and thus resolves concerns raised by the simple shape instability model calculations for homogeneous, monodisperse LCs. For example, using the same parameters for K and Wa, but with a reduction of γ by 10x, we obtain the requirement K24 ≳ 5.5×K11, which is in an acceptable range for saddle-splay modulus. Of course, further reduction of γ (as long as interfacial energy still dominates at high temperature) decreases the required K24 value even more and renders shape transitions to be even more likely. (Note also, the segregation-induced decrease in bulk elastic energy will further reduce the requirements for γ reduction, because the decrease in elastic free energy in filaments is greater than in spherical drops.)
We can estimate the reduction of γ induced by oligomer segregation using a simple bidisperse demixing model (alluded to elsewhere in Methods). In the model, one component of the mixture is a monomer (〈ℓ〉 = 1), and the other component is a macromer with 〈ℓ〉 ≈ 9. As shown in Extended Data Fig. 4c, for a monomer:macromer mixture weight ratio of 1:0.7, the overall mean chain length is 〈ℓ〉whole ≈ 1.53. This condition gives rise to filamentous drop structures. Taking this condition to be exemplary for filament formation, we next show how the macromers and monomers segregate into core and shell regions with uneven chain length distributions in order to lower overall system elastic energy.
Since the total amount of monomer and macromer is conserved during segregation, we readily generate an equation relating the monomer:macromer weight ratio and 〈ℓ〉whole of the initial homogeneously distributed mixture to the final, segregated long-chain-rich shell with 〈ℓ〉shell, and short-chain-rich core with 〈ℓ〉core. The resulting relation is:
| (8) |
Here n is the number fraction of macromer in the core region, and Vshell and Vcore are volume of shell and core regions, respectively. Vshell + Vcore = Vtotal. The mean chain length of the core can also be written in a simple form:
| (9) |
For simplicity, we assume that segregation leads to equal volumes of core and shell, and we set 〈ℓ〉shell = 1.70. Eqn. (8) and (9) then give n ≈ 4.9% and 〈ℓ〉core ≈ 1.39. Note, it is straightforward to use this model with other assumptions about the volume segregation ratio and the mean oligomer chain length in the shell; the general qualitative conclusions about system free energy reduction (compared to the homogeneous drop) will be the same for sensible parameters.
To quantify how the chain length redistribution within the structure affects the system’s overall bulk elastic energy, we take 〈ℓ〉core ≈ 1.39 and 〈ℓ〉shell = 1.70, and we compute the elastic free energy volume integrals over the target geometry (e.g., radial/sphere and escaped-radial/filament) using the Frank free energy equation (Eqn. (1)). We then compare the Frank free energy of the segregated system to that of the homogeneously distributed system with 〈ℓ〉whole ≈ 1.53. For this calculation, we assume that the elastic constant is proportional to oligomer mean chain length14,52. The comparison reveals that this reduction in 〈ℓ〉core will decrease bulk elastic energy by ~5% for the sphere and >8% for the filament (i.e., compared to the homogeneously distributed systems).
Most importantly, as a result of oligomer segregation (e.g., an increase of local mean chain length near interface from 1.53 to 1.70, by ~0.17), the interfacial tension is lowered dramatically. To better appreciate this assertion, consider the homogeneous mixtures NLCO#2 (7 hours oligomerization) and NLCO#5 (24 hours oligomerization) in Extended Data Fig. 3. For these samples, the interfacial tension (e.g., at 30 °C) of the drops made with NLCO#5 (0.12 mN/m) is significantly smaller, by a factor of ~20x, compared to that of NLCO#2 (2.36 mN/m), whereas the average chain length changed by only ~0.10. Indeed, from the pendant drop experiments, one would expect that a long-chain-rich interface (with local increase of mean chain length of ~0.17) would reduce γ substantially, i.e., γ would be reduced by at least a factor of 20x. Hence, our earlier statement (in the main text) that “a reduction of γ by 10x to ∼0.1 mN/m yields sphere-filament instabilities with reasonable saddle-splay moduli” is a conservative estimate of the expected change of interfacial tension.
Lastly, we reiterate that in the millimeter-size drops measured by the pendant technique, we expect the chain-length-dependent segregation to be insignificant. Macroscopically, the drop is approximately homogeneous because the millimeter-size drops have many nematic micro-domains (each with a director oriented uniformly along a different direction) and many randomly situated disclination lines. The larger drops have lower curvatures too, and therefore director distortion is reduced near their surfaces. The largest distortions that could drive segregation should occur locally near disclinations and at domain walls distributed roughly uniformly throughout the drop; thus, they will not promote net migration to the surface. Moreover, the required molecular diffusion over long distances will be small because of extremely long diffusion times (domain walls would also act as barriers to oligomer diffusion, etc.). Thus, interfacial tension derived from the pendant drop experiments is set by the macroscopic “average” of the whole droplet, i.e., 〈ℓ〉 of the initial (source) NLCO distributions.
Crosslink NLCO structures into NLCEs
To crosslink structural NLCOs into solid NLCE structures, 2 wt% (by RM82 concentration) 2,2-Dimethoxy-2-phenylacetophenone (radical photoinitiator, Sigma-Aldrich) was added into the initial RM82/butylamine/chloroform mixture. Then the same oligmerization-cooling method described above was performed. After the NLCO emulsions reached their final (desired) equilibrium morphologies, the NLCOs were radically crosslinked into elastomers by UV radiation (365 nm) for a few minutes. We then evaporated the background solution, sputter-coated thin metallic films (gold or iridium) onto the structures, and observed the resulting NLCEs via SEM (dual-beam FEI Strata DB235 Focused Ion Beam/SEM) using a 5.00 kV electron beam.
Data Availability
The authors declare that the data supporting the findings of this study are available within the paper, the Methods section, and Extended Data files. Raw data are available from the corresponding author upon reasonable request.
Code Availability
Custom computer codes associated with modeling in this study are available on GitHub (https://github.com/wei-shao-wei/Molecular-heterogeneity-induces-reconfigurable-nematic-liquid-crystal-drops).
Extended Data
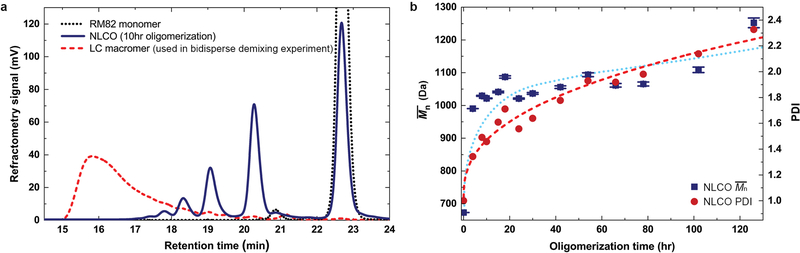
Extended Data Fig. 1 |. Molecular weight (chain length) distribution of NLCO samples measured by size exclusion chromatography (SEC).
a, The NLCO source samples are shown to be a mixture of monomers, dimers, trimers, tetramers, and other oligomers (blue solid line, peak appearing at longer retention time represents shorter chain length). In step-polymerization processes, when the extent-of-reaction is less than 0.9, then monomers dominate the overall molar fraction. For comparison, LC macromers (used in the supporting experiment in Methods) synthesized following the schemes of Ware et al.10 are also included in the plot; the latter show longer mean chain length and very few (if any) short-chain components (red dashed line). Furthermore, since our system is made in an aqueous solution, the polymerization rate is expected to be slower. For reference, the black dotted line shows the peak for pure RM82 monomer. b, Calculated from SEC data (example in (a)), the number-average molecular weight (, blue solid square) and polydispersity index (PDI, red solid circle) of the NLCOs are shown as function of oligomerization time. Both and PDI increase with oligomerization time. The dotted (for ) and dashed (for PDI) curves are to guide the eye. (For comparison, the LC macromer synthesized following the schemes of Ware et al.10 and used in Methods section, “Macromer-monomer mixing experiments”, has ≈ 6,900 Da and PDI ≈ 1.3.)
Extended Data Fig. 2 |. Bright-field optical microscopy images showing reversible shape transitions of NLCO drops during temperature cycling.
a-c, When temperature increases from room temperature (20 °C) to higher temperature (e.g., 90 °C), the NLCO filamentous structures reversibly evolve back into spherical micro-droplets. c-e, Then, during re-cooling, the spherical micro-droplets evolve back into filamentous structures. The drop morphology can be transformed repeatedly, remaining quantitatively similar. Here, multiple small drops evolve in the field-of-view; data in the main text showed only one large evolving drop in Fig. 1c–h. Scale bar: 20 μm.
Extended Data Fig. 3 |. Macroscopic interfacial tension of NLCO pendant drops as function of temperature and NLCO oligomerization time.
The NLCO drop has homeotropic anchoring at the interface in an aqueous solution consisting of 0.1 wt% SDS. The interfacial tension γ decreases with decreasing temperature and increasing NLCO mean oligomer chain length 〈ℓ〉 (consult Fig. 2f in the main text for relation between oligomerization processing time and 〈ℓ〉). Inset: Optical image of a NLCO pendant drop hanging from a flat tip syringe needle (1.26 mm OD) in a 0.1 wt% SDS aqueous solution.
Extended Data Fig. 4 |. Bright-field optical microscopy images of drop morphologies obtained from mixtures of macromers (〈ℓ〉 ≈ 9) and monomers (RM82) at different weight ratios in a 0.1 wt% SDS aqueous solution after cooling.
With a fixed amount of RM82, increasing the concentration of macromers in the drop leads to longer 〈ℓ〉, larger bulk elasticity, and lower interfacial tension. The latter two factors favor interfacial roughening and filament formation. Images are taken at the room temperature after cooling. Scale bar: 50 μm.
Extended Data Fig. 5 |. Bright-field optical microscopy images of NLCO structures in aqueous solutions of different surfactants as a function of the mean oligomer chain length, 〈ℓ〉.
NLCO drops in aqueous solutions with different surfactants, i.e., with either cationic (hexadecyltrimethylammonium bromide, C16TAB) or nonionic (Polysorbate 20, Tween 20) surfactants. These systems exhibit a drop morphology evolution similar to that from SDS, i.e., with respect to cooling and an increase of 〈ℓ〉. After cooling from 90 °C to 20 °C, a representative NLCO drop in a 0.5 mM C16TAB aqueous solution (below CMC, a-c) and a representative NLCO drop in a 0.03 mM Tween 20 aqueous solution (below CMC, d-f). Both evolve with increasing 〈ℓ〉 (consult Fig. 2f in the main text for relation between the oligomerization time and 〈ℓ〉). In all cases, it is important that NLCOs should favor homeotropic anchoring at the drop interface. Images are taken at the room temperature. Scale bars: 20 μm.
Extended Data Fig. 6 |. Bright-field optical microscopy image of aggregated NLCO filamentous structures for SDS concentrations above CMC.
In a 1 wt% SDS aqueous solution, the NLCO drops exhibit similar but more complicated shape transition behaviors than those below CMC (critical micelle concentration), i.e., after cooling from 90 °C to 20 °C. For example, aggregated filamentous structures form and sometimes stick to the substrate due, in part, to micelle-induced depletion. (For comparison, expanded filamentous structures form in aqueous solutions below CMC, see example in Fig. 1h in the main text.) The scale bar is 20 μm.
Extended Data Fig. 7 |. Self-assembled NLCE fibrous mat.
NLCE fibers can be densely packed into centimeter-wide and few-micron-thick, non-woven, free-standing mats by sedimentation. An image of the fibrous mat (mounted on hollowed holder) with diameter greater than 1 cm is shown. Please consult Fig. 4e–f in the main text for corresponding microscopic SEM images of this fibrous mat.
Extended Data Table 1 |. Range of required interfacial tension reduction needed for spontaneous shape transitions of NLCO drops with “physical” saddle-splay modulus.
This table summarizes parameter values that permit shape transitions (with reasonable saddle-splay elastic constants) based on our model free energy calculations. The calculations fix the interfacial tension (γmeasured;mm-drop) at 30 °C measured by the pendant drop technique. A fairly wide range of estimated elastic constants (K) and anchoring energy coefficients (Wa) are employed in the calculations too. Per criteria for a spontaneous shape transition, we demand that the required saddle-splay elastic constant (K24) be of order ∼6 times the splay modulus (or less). The calculations show that a smaller “true” interfacial tension, γtrue;micro-emulsion (expressed as reduction factor of γmeasured;mm-drop in the Table), will significantly relax the saddle-splay requirement. This reduction of γ can be realized through oligomer polydispersity and resultant oligomer spatial segregation in the elastic stress field. Note, a reasonable range for K is 5×10−11 N to 10−10 N; a value of K =10−11 N is probably too small, since it is the same order of magnitude as small molecule LCs such as 5CB.
| γmeasured; mm-drop (mN/m) | K (N) | Wa (J/m2) | Required K24 for shape transition | Reduction factor of γmeasured; mm-drop gives γtrue; micro-emulsion | Required K24 for shape transition with reduced γ |
|---|---|---|---|---|---|
| 2.36 | 5 × 10−11 | 5 × 10−5 ∼5 × 10−4 | 60.2 × K11 | 20x | 5.7 × K11 |
| 2.36 | 10−10 | 5 × 10−5 ∼5 × 10−4 | 31.6 × K11 | 10x | 5.7 × K11 |
| 2.36 | 5 × 10−10 | 5 × 10−4 | 8.6 × K11 | 2x | 5.7 × K11 |
Supplementary Material
Acknowledgements
We thank Kevin B. Aptowicz, Chia-Chih Chang, Peter J. Collings, Alexis de La Cotte, Zoey S. Davidson, Remi Dreyfus, Piotr Habdas, Analisa Hill, Yi-Yun Ho, Randall D. Kamien, Joonwoo Jeong, Tom C. Lubensky, Xiaoguang Ma, Angel Martinez, Chandan K. Mishra, and Peter Palffy-Muhoray for helpful discussions. Ali Soleymannezhad and Justin Timmons from Tosoh Bioscience assisted with SEC operation and analysis. We gratefully acknowledge financial support from the National Science Foundation through DMR16-07378, PENN MRSEC DMR-1720530 including its Optical Microscopy and Electron Microscopy SEFs, and NASA Grants 80NSSC19K0348 and NNX13AL27G.
Footnotes
Competing interests The authors declare no competing financial interests.
Supplementary Information is linked to the online version of the paper at www.nature.com/nature.
References
- 1.Fasolo M & Sollich P Equilibrium phase behavior of polydisperse hard spheres. Phys. Rev. Lett 91, 068301 (2003). [DOI] [PubMed] [Google Scholar]
- 2.Zaccarelli E et al. Crystallization of hard-sphere glasses. Phys. Rev. Lett 103, 135704 (2009). [DOI] [PubMed] [Google Scholar]
- 3.Liddle SM, Narayanan T & Poon WCK Polydispersity effects in colloid-polymer mixtures. J. Phys. Condens. Matter 23, 194116 (2011). [DOI] [PubMed] [Google Scholar]
- 4.Lavrentovich OD et al. Helical smectic A. Europhys. Lett 13, 313–318 (1990). [Google Scholar]
- 5.Gibaud T et al. Reconfigurable self-assembly through chiral control of interfacial tension. Nature 481, 348–351 (2012). [DOI] [PubMed] [Google Scholar]
- 6.Denkov N, Tcholakova S, Lesov I, Cholakova D & Smoukov SK Self-shaping of oil droplets via the formation of intermediate rotator phases upon cooling. Nature 528, 392–395 (2015). [DOI] [PubMed] [Google Scholar]
- 7.Guttman S et al. How faceted liquid droplets grow tails. Proc. Natl. Acad. Sci. USA 113, 493–496 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Toquer G et al. Colloidal shape controlled by molecular adsorption at liquid crystal interfaces. J. Phys. Chem. B 112, 4157–4160 (2008). [DOI] [PubMed] [Google Scholar]
- 9.Peddireddy K, Kumar P, Thutupalli S, Herminghaus S & Bahr C Myelin structures formed by thermotropic smectic liquid crystals. Langmuir 29, 15682–15688 (2013). [DOI] [PubMed] [Google Scholar]
- 10.Ware TH, McConney ME, Wie JJ, Tondiglia VP & White TJ Voxelated liquid crystal elastomers. Science 347, 982–984 (2015). [DOI] [PubMed] [Google Scholar]
- 11.Gannon MGJ & Faber TE The surface tension of nematic liquid crystals. Philos. Mag. A 37, 117–135 (1978). [Google Scholar]
- 12.Butt HJ, Graf K, & Kappl M Physics and Chemistry of Interfaces Ch. 3 (John Wiley & Sons, Weinheim: 2006). [Google Scholar]
- 13.Schiele K & Trimper S On the elastic constants of a nematic liquid crystal. Phys. Stat. Sol. (b) 118, 267–274 (1983). [Google Scholar]
- 14.Kamien RD & Toner J Anomalous elasticity of polymer cholesterics. Phys. Rev. Lett 74, 3181–3184 (1995). [DOI] [PubMed] [Google Scholar]
- 15.Kasten H & Strobl G Nematic wetting at the free surface of 4-cyano-4’-n-alkyl-biphenyls. J. Chem. Phys 103, 6768–6774 (1995). [Google Scholar]
- 16.Tintaru M, Moldovan R, Beica T & Frunza S Surface tension of some liquid crystals in the cyanobiphenyl series. Liquid Crystals 28, 793–797 (2001). [Google Scholar]
- 17.Lubensky TC, Pettey D, Currier N & Stark H Topological defects and interactions in nematic emulsions. Phys. Rev. E 57, 610–625 (1998). [Google Scholar]
- 18.Allender DW, Crawford GP & Doane JW Determination of the liquid-crystal surface elastic constant K24. Phys. Rev. Lett 67, 1442–1445 (1991). [DOI] [PubMed] [Google Scholar]
- 19.Muševič I Liquid Crystal Colloids Ch. 7 (Springer, Switzerland: 2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cholakova D, Valkova Z, Tcholakova S, Denkov N & Smoukov SK “Self-shaping” of multicomponent drops. Langmuir 33, 5696–5706 (2017). [DOI] [PubMed] [Google Scholar]
- 21.Shimshick EJ & McConnell HM Lateral phase separation in phospholipid membranes. Biochemistry 12, 2351–2360 (1973). [DOI] [PubMed] [Google Scholar]
- 22.Sidky H & Whitmer JK Elastic response and phase behavior in binary liquid crystal mixtures. Soft Matter 12, 4489–4498 (2016). [DOI] [PubMed] [Google Scholar]
- 23.Elias F, Clarke SM, Peck R & Terentjev EM Nematic order drives phase separation in polydisperse liquid crystalline polymers. Macromolecules 33, 2060–2068 (2000). [Google Scholar]
- 24.Ahir SV, Tajbakhsh AR & Terentjev EM Self-assembled shape-memory fibers of triblock liquid-crystal polymers. Adv. Funct. Mater 16, 556–560 (2006). [Google Scholar]
- 25.Ohm C et al. Preparation of actuating fibres of oriented main-chain liquid crystalline elastomers by a wetspinning process. Soft Matter 7, 3730–3734 (2011). [Google Scholar]
- 26.Xia Y, Zhang X & Yang S Instant locking of molecular ordering in liquid crystal elastomers by oxygen-mediated thiol-acrylate click reactions. Angew. Chem 130, 5767–5770 (2018). [DOI] [PubMed] [Google Scholar]
- 27.Krause S, Dersch R, Wendorff JH & Finkelmann H Photocrosslinkable liquid crystal main-chain polymers: Thin films and electrospinning. Macromol. Rapid Commun 28, 2062–2068 (2007). [Google Scholar]
- 28.Dufresne ER et al. Self-assembly of amorphous biophotonic nanostructures by phase separation. Soft Matter 5, 1792–1795 (2009). [Google Scholar]
- 29.Saranathan V et al. Structure, function, and self-assembly of single network gyroid (I4132) photonic crystals in butterfly wing scales. Proc. Natl. Acad. Sci. USA 107, 11676–11681 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Radja A, Horsley EM, Lavrentovich MO & Sweeney AM Pollen cell wall patterns form from modulated phases. Cell 176, 856–868 (2019). [DOI] [PubMed] [Google Scholar]
References
- 31.Adamson AW & Gast AP Physical Chemistry of Surfaces Ch. 2 (John Wiley & Sons, New York: 6th ed. 1997). [Google Scholar]
- 32.Daerr A & Mogne A Pendent_drop: An imagej plugin to measure the surface tension from an image of a pendent drop. Journal of Open Research Software 4 (2016). [Google Scholar]
- 33.Terentjev EM Density functional model of anchoring energy at a liquid crystalline polymer-solid interface. J. Phys. II France 5, 159–170 (1995). [Google Scholar]
- 34.Frank FCI Liquid crystals. On the theory of liquid crystals. Discuss. Faraday Soc 25, 19–28 (1958). [Google Scholar]
- 35.Oseen CW The theory of liquid crystals. Trans. Faraday Soc 29, 883–899 (1933). [Google Scholar]
- 36.Nehring J & Saupe A On the elastic theory of uniaxial liquid crystals. J. Chem. Phys 54, 337–343 (1971). [Google Scholar]
- 37.Barbero G & Oldano C Derivative-dependent surface-energy terms in nematic liquid crystals. Nuovo Cim. D 6, 479–493 (1985). [Google Scholar]
- 38.Sparavigna A, Komitov L & Strigazzi A Hybrid aligned nematics and second order elasticity. Phys. Scr 43, 210 (1991). [Google Scholar]
- 39.Crawford GP, Allender DW & Doane JW Surface elastic and molecular-anchoring properties of nematic liquid crystals confined to cylindrical cavities. Phys. Rev. A 45, 8693–8708 (1992). [DOI] [PubMed] [Google Scholar]
- 40.Rapini A & Papoular M Distorsion d’une lamelle nématique sous champ magnétique conditions d’ancrage aux parois. J. Phys. Colloques 30, C4-54–56 (1969). [Google Scholar]
- 41.Cladis PE & Kléman M Non-singular disclinations of strength S = +1 in nematics. J. Phys. France 33, 591–598 (1972). [Google Scholar]
- 42.Meyer RB On the existence of even indexed disclinations in nematic liquid crystals. Philos. Mag. (Abingdon) 27, 405–424 (1973). [Google Scholar]
- 43.Burylov SV Equilibrium configuration of a nematic liquid crystal confined to a cylindrical cavity. J. Exp. Theor. Phys 85, 873–886 (1997). [Google Scholar]
- 44.Li X & Denn MM Interface between a liquid crystalline polymer and a flexible polymer. Macromolecules 35, 6446–6454 (2002). [Google Scholar]
- 45.Wu J & Mather PT Interfacial tension of a liquid crystalline polymer in an isotropic polymer matrix. Macromolecules 38, 7343–7351 (2005). [Google Scholar]
- 46.Bradshaw MJ, Raynes EP, Bunning JD & Faber TE The Frank constants of some nematic liquid crystals. J. Phys. France 46, 1513–1520 (1985). [Google Scholar]
- 47.Zhou S, et al. Elasticity, viscosity, and orientational fluctuations of a lyotropic chromonic nematic liquid crystal disodium cromoglycate. Soft Matter 10, 6571–6581 (2014). [DOI] [PubMed] [Google Scholar]
- 48.Xia Y, Serra F, Kamien RD, Stebe KJ & Yang S Direct mapping of local director field of nematic liquid crystals at the nanoscale. Proc. Natl. Acad. Sci. USA 112, 15291–15296 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yokoyama H, & van Sprang HA A novel method for determining the anchoring energy function at a nematic liquid crystal-wall interface from director distortions at high fields. J. Appl. Phys 57, 4520–4526 (1985). [Google Scholar]
- 50.Yang F, Ruan L & Sambles JR Homeotropic polar anchoring energy of a nematic liquid crystal using the fully leaky waveguide technique. J. Appl. Phys 88, 6175–6182 (2000). [Google Scholar]
- 51.Škarabot M, Osmanagič E & Muševič I Surface anchoring of nematic liquid crystal 8OCB on a DMOAP-silanated glass surface. Liquid Crystals 33, 581–585 (2006). [Google Scholar]
- 52.Ciferri A, Krigbaum WR & Meyer RB Polymer Liquid Crystals Ch. 6 (Academic, New York, 1982). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The authors declare that the data supporting the findings of this study are available within the paper, the Methods section, and Extended Data files. Raw data are available from the corresponding author upon reasonable request.