An efficient approach for physical actions classification using surface EMG signals

Abstract

Physical actions classification of surface electromyography (sEMG) signal is required in applications like prosthesis, and robotic control etc. In this paper, tunable-Q factor wavelet transform (TQWT) based algorithm is proposed for the classification of physical actions such as clapping, hugging, bowing, handshaking, standing, running, jumping, waving, seating, and walking. sEMG signal is decomposed into sub-bands by TQWT. Various features are extracted from each different band and statistical analysis is performed. These features are fed into multi-class least squares support vector machine classifier using two non-linear kernel functions, morlet wavelet function, and radial basis function. The proposed method is an attempt for classifying physical actions using TQWT and its performance and results are promising and have high classification accuracy of 97.74% for sub-band eight with morlet kernel function.

Introduction

The accidental injuries and neurological diseases are responsible for losing the limb functions in human being [1]. With the advancement in recent technology, many bionic rehabilitation hands can be developed to help patients in restoring some or all of the lost motor functionality [1]. The physical actions require assistance between skeletal and muscular systems [2]. For every physical action, skeletal muscles generate currents that can be measured in terms of electromyography (EMG) signal. EMG signals can be recorded in two ways either by inserting needles directly into the muscles called needle electromyography (nEMG) or by placing skin surface electrodes above the muscle called surface electromyography (sEMG) [3]. The sEMG shows better performance for controlling the limb movement and it can be used as a signal source for prosthesis control [1]. sEMG signals are useful in biomedical engineering and man-machine interfaces for various applications like prosthesis and robotic devices control, diagnosis of neuromuscular diseases [4], wheelchairs, virtual mouse and world etc.

Features extracted from the mode of variational mode decomposition and used as input to multi-class least squares support vector machine (MC-LSSVM) classifier with radial basis function (RBF) kernel which classifies physical actions [5]. Sixteen features like integrated EMG, root mean square value, mean absolute value have been reduced using principal component analysis and classified by adaptive neuro-fuzzy inference system [6]. sEMG signals are windowed and features like fourth order autoregressive (AR) coefficients, zero crossing, slope sign changes, power spectrum ratio, detrended fluctuation analysis, and Higuchis fractal dimension are extracted and classified by the artificial neural network (ANN) [7]. Average threshold crossing (ATC) algorithm has used to predict four different hand movements using SVM classifier [8]. The AR model coefficients fusion with wavelet coefficients based model has been explored optimized back propagation (BP) network for classification of EMG signals [9]. Features extracted from the EMG signals have been used with k-nearest neighbor (KNN) classifier For hand gesture recognition [10]. Time-domain and frequency-domain features have been explored with classifiers ANN and Gaussian mixture model for classification of motions EMG signal [11]. Features have been used as input to linear discriminant analysis (LDA), SVM, ANN, and fuzzy logic classifier for control of arm prosthesis using EMG signals [12]. Different upper limb movements have been classified by online and offline methods by using EMG signals [13].

Based on electromechanical delay, EMG signals have been divided into pattern vectors and classified by two cascaded ANN classifiers for recognition of action intention [14]. Flexible analytic wavelet transform (FAWT) explored for physical action classification using EMG signals [15]. Improved empirical mode decomposition has been explored for classification of EMG signals [16]. The wavelet based coefficients used as features for classifying normal and aggressive actions [17]. Time domain based features extracted by PCA used as input to SVM with radial basis kernel function for sketching recognition [18]. Features have been extracted based on top and slope algorithm with LDA for gait subphase detection [19]. Modified mean absolute value type (MAV2) feature has been used with probabilistic neural network (PNN) classifier [20].

Power spectral densities of FFT have been used into ANN for classification of seventeen voluntary actions [21]. Cascade classification and clustering have been used for classification of grasp movements [22]. Dynamic time warping has been used for classification of five lower limbs motions using linear discriminant analysis [23]. Time domain features have been extracted from EMG signals, for gesture recognition and reduced by VLDA feature projection technique and classified by LDA [24]. Time-frequency, frequency, time domain features have been extracted for classification of gait recognition EMG signals [25]. For prediction of Brunn storm stage of the patients by EMG signals, the SVM, KNN, ANN classifiers are used [26]. A combination of time-domain features and coefficients of AR model have been extracted and LDA classifier for hand grasps and finger motions [27].

The nonlinear SEMG-handgrip force relationship was built using wavelet transform [28]. A review was done by comparing sEMG amplitudes of different muscles for different exercises and loads [29]. A control system was developed which controls the robotic arm and adjusts the force exerted according to the correlation analysis between sEMG signal and the force exerted by the subjects during different grasp movements [30]. EMG indices are calculated for muscle fatigue during cycling and are compared based on power output, grey rational grade of indices, and cadence [31]. The reliability of the mechanical and EMG measures performance during bench press exercise vary according to the variable used [32]. A controller was designed to predict different hand grasp movements by sEMG signals using two cascaded ANN [14]. The method combining sEMG and inertial measurements improved classification accuracy in both real time performance and offline classification [33]. sEMG signals and accelerometer signals are fused to recognize the motion patterns to achieve high accuracy [23]. A brief study of muscle activity during different tasks in water has been done and observed that it is lower compared to land-based ones [34].

Recently, the tunable Q-factor wavelet transform (TQWT) has shown the utility for the analysis of different kind of oscillatory signals. TQWT has so far been useful in applications like automated seizure detection by EEG signals [35–37], Emotion classification [38], face recognition [39], automatic power quality disturbances detection [40], classification of power transformer mechanical deformations [41], emotion recognition in left-brain damaged stroke patients [42], motor imagery tasks classification from EEG signals [43], and bearing defects diagnosis [44]. In this paper, TQWT decomposes sEMG signals into sub-bands physical actions classification. Further, time-domain features are used from different sub-band and their statistical analysis is performed. The statistically significant features classify the ten different physical actions using MC-LSSVM classifier. The proposed method is an attempt to classify physical actions using TQWT and its performance and results are promising with good classification accuracy. The rest of the paper is as follows: “Methodology” section describe methodology, dataset, tunable-Q wavelet transform, feature extraction, and MC-LSSVM classifier. “Results and discussion” section explains the results and discussions obtained from simulations and the conclusion has been explained in Sect. “Conclusion”.

Methodology

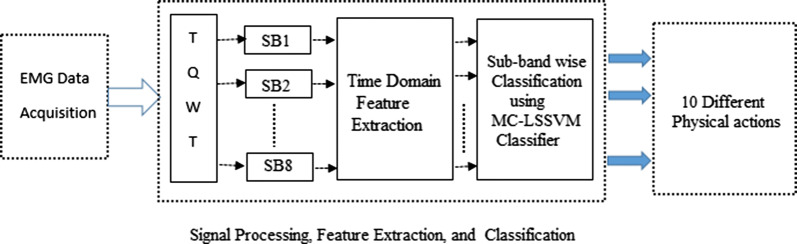
A basic outline of the proposed method is shown in Fig. 1.

Fig. 1.

TQWT based proposed method

Dataset

The dataset is available online in UCI machine learning repository database. The dataset physical action includes ten normal physical actions of one female and three male subjects with age from 25 to 30. Data acquired from eight skin-surface electrodes: triceps, biceps, hamstrings, and thighs. Each signal consists of 10,000 samples and ten normal actions are performed by each subject in an experimental session [45]. Normal actions consist of ten different classes bowing (C1), clapping (C2), handshaking (C3), hugging (C4), jumping (C5), running (C6), seating (C7), standing (C8), walking (C9), and waving (C10). sEMG signals were recorded by Delsys EMG wireless apparatus.

Tunable-Q factor Wavelet Transform

TQWT is a decomposition method generally used in the analysis of oscillatory signals The input signal is divided into several stages of the low pass (LP) and high-pass (HP) sub-bands. The quality factor (Q) and redundancy factor (r) control frequency response of filter bands for which they are called tunable parameters [43]. The N stage of two-channel filter banks, we get N + 1 sub-bands as shown in Fig. 2. For the first level filter bank, sEMG signal y[n] with sampling frequency $F_s$ will be given as input which will give LP $y_0[n]$ and HP $y_1[n]$ as output with sampling frequencies $\alpha F_s$ and $\beta F_s$ where $\alpha$ is LP scaling parameter and $\beta$ is HP scaling parameter (shown in Fig. 3). This LP $y_0[n]$ will be the input for the second stage and output of the second stage LP filter will be input for the third stage and it continues till N stages. The frequency response of $S_1^N(\omega )$ and low pass $S_0^N(\omega )$ after N stages is given by, [46]

$$\begin{array}{cc}& S_0^N(\omega )=\left\{\begin{array}{cc}{\displaystyle \prod _{n=0}^{N-1}{S}_0\left(\frac{\omega }{{\alpha }^n}\right),}\hfill & |\omega |\le {\alpha }^N\pi \hfill \\ 0,\hfill & {\alpha }^N\pi <|\omega |\le \pi \hfill \end{array}\right)\hfill \end{array},$$ 1

$$\begin{array}{cc}& S_1^N(\omega )=\left\{\begin{array}{cc}{\displaystyle S_1\left(\frac{\omega }{{\alpha }^{N-1}}\right)\prod _{n=0}^{N-2}{S}_0\left(\frac{\omega }{{\alpha }^n}\right),}\hfill & (1-\beta ){\alpha }^{N-1}\pi \le |\omega |\le {\alpha }^{N-1}\pi \hfill \\ 0,\hfill & \omega \in [-\pi ,\pi ]\hfill \end{array}\right)\hfill \end{array},$$ 2

where

$$\begin{array}{cc}\hfill S_0(\omega )=& \theta \left(\frac{\omega +(\beta -1)\pi }{\alpha +\beta -1}\right)\hfill \end{array},$$ 3

$$\begin{array}{cc}\hfill S_1(\omega )=& \theta \left(\frac{\alpha \pi -\omega }{\alpha +\beta -1}\right)\hfill \end{array},$$ 4

where $\theta (\omega )$indicates Daubechies filter’s frequency response. The scaling parameters $\alpha$ and $\beta$ are calculated from Q, r and N and they are defined as below [43].

$$\begin{array}{cc}\hfill \alpha =& 1-\frac{\beta }{r}\hfill \\ \hfill \beta =& \frac{2}{Q+1}\hfill \end{array}$$

Q is a dimensionless term and independent on the number of levels which is the ratio of resonator bandwidth and center frequency. Wavelet oscillation is controlled by Q For oscillatory signals high Q value is selected and for transient signals low Q value is selected [35]. r defines the frequency content of sub-bands.

Fig. 2.

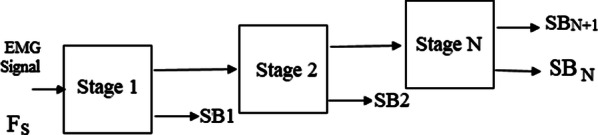
Representation of N stage TQWT

Fig. 3.

Output of first stage of TQWT

There are many advantages of TQWT for which it has been used in the proposed method. It ensures temporal localization and by varying the value of Q-factor it can vary the shape of the wavelet which yields localization in frequency [46]. TQWT gives localization in both time and frequency and will be ideal for analyzing EMG signals for physical actions classification as it is already been applied for other bio-medical signals like EEG.

Feature extraction

For each sub-band, we extract seven-time domain features namely mean ($\mu$), average amplitude change (AAC), maximum value, entropy (H), negentropy (J), first quartile and third quartile. For N sampled sEMG signals with data points $y1,y2,\dots y_N$ these features can be formulated as below.

1. Mean ($\mu$) It is the measure of central tendency. The mean for above data be given by,

   $$\begin{array}{c}\hfill \mu =\frac{1}{N}\sum _{i=1}^N{Y}_i\end{array}$$ 5
2. Entropy (H) It is the measure of randomness or uncertainty. It gives information about the randomness of the signal. It can be mathematically calculated for the above data by, [4]

   $$\begin{array}{cc}\hfill H(Y)=& -\sum _{i=1}^{N}p(y_i)log(p(y_i)\hfill \\ \hfill p(y_i)=& [p(y_1),p(y_2)......],\hfill \end{array}$$ 6

   where $p(y_i)$ denotes probability of ith sample.
3. Negentropy (J) It is the measure of distance to normality. It is the difference between Gaussian entropy and non-Gaussian entropy. It is defined as [4],

   $$\begin{array}{c}\hfill J(Y)=H(Y_{\mathit{gauss}})-H(Y)\end{array}$$ 7
4. Maximum Value It gives the maximum value among the data points in the data set. It is given as [47],

   $$\begin{array}{c}\hfill MAX=max(y_k)\end{array}$$ 8
5. First Quartile It is the median for the first half of the sample set and denoted by Q1. It is given as [47],

   $$\begin{array}{c}\hfill Q1=25\%(y_k)\end{array}$$ 9
6. Third Quartile It is the median of the second half of the data set and denoted by Q3. 75% of the data lies below it and 25% of data lie above it. It is given as [47],

   $$\begin{array}{c}\hfill Q3=75\%(y_k)\end{array}$$ 10
7. Average Amplitude Change (AAC): It is an average of the wavelength which is a measure of complexity and is given by [48],

   $$\begin{array}{c}\hfill AAC=\frac{1}{N}\sum _{i=1}^{N-1}|y_{i+1}-y_i|\end{array}$$ 11

Multi-class least squares support vector machine

The extracted time domain features are fed into MC-LSSVM classifier for classification. Consider ${(x_i,y_i^k)}_{i=1,k=1}^{i=N,k=n}$ as training data, n be classifications number, N be number of training input and output pairs, $x_i$ be input training set of pattern i, and $y_i^k$ denotes the kth output unit of pattern i, MC-LSSVM derivation depends on minimization of below formulation [49].

$$\begin{array}{c}\hfill J_{\mathit{LS}}^n\left(w_k,,,b_k,,,e_{i,k}\right)=\frac{1}{2}\sum _{k=1}^n{w}_k^T{w}_k+\frac{\gamma }{2}\sum _{i=1}^N\sum _{k=1}^n{e}_{i,k}^2\end{array}$$ 12

Let ${\mathrm{\Psi }}_k\left(x_i,,,x_l\right)={\phi }_k^T(x_i){\phi }_k(x_l))$ be the kernel function then the decision function for MC-LSSVM can be given as [50]

$$\begin{array}{c}\hfill f(x)=\text{sign}\left[\sum _{i=1}^N,{\alpha }_{\mathit{ik}},y_i^k,{\mathrm{\Psi }}_k,\left(x_i,,,x_l\right),+,b_k\right]\end{array},$$ 13

where ${\alpha }_i$ represent Lagrangian multipliers, N indicate the number of training data set pairs and b denotes bias. We use RBF and morlet wavelet kernels as they are more efficient. They are defined as below,

$$\begin{array}{cc}& {\mathrm{\Psi }}_k({\mathbf{x}}_i,{\mathbf{x}}_l)=e^{\frac{-\Vert {\mathbf{x}}_i-{\mathbf{x}}_l{\Vert }^2}{2{\sigma }^2}}\hfill \end{array}$$ 14

$$\begin{array}{c}\hfill {\mathrm{\Psi }}_k({\mathbf{x}}_i,{\mathbf{x}}_l)=\prod _{k=1}^{d}cos\left[,{\omega }_0,\frac{({\mathbf{x}}^k-{\mathbf{x}}_i^k)}{a}\right]e^{\frac{-\Vert {\mathbf{x}}_i-{\mathbf{x}}_l{\Vert }^2}{2{\sigma }^2}}\end{array},$$ 15

where $\sigma$ is RBF optimized kernel width and a denotes dilation parameter.

Results and discussion

sEMG signals decompose into band-limited sub-bands by selecting following TQWT parameters, $\text{Q}=1,\text{r}=3$, and $\text{N}=7$ stages, which provide eight sub-bands. Seven-time domain features namely mean, average amplitude change, maximum value, entropy, negentropy, first quartile, and third quartile are extracted for each sub-band. All these extracted features are fed into MC-LSSVM classifier sub-band wise. The decision function of MC-LSSVM classifier depends on the type of kernel function. Selection of optimal kernel plays a major role in the accuracy and performance of the classifier. In this paper, two non-linear kernel functions morlet wavelet and RBF is used for computation of performance parameters. Accuracy denotes the percentage of correct classifications i.e. identification of both positive and negative classes and error (ERR) denotes the percentage of wrong classifications. The sensitivity indicates how well the method identifies the positive class and Specificity indicates how well the method indicates the negative classes. k-fold cross-validation approach with k value as 10 is used to find the above parameters and classify the EMG signal actions. K-fold validation divides the data set into k folds or groups and treats one fold as validation set or testing set and fit the model on remaining k − 1 folds or training set.

Table 1 shows the performance parameters ACC, SEN, SPEC of all sub-bands using RBF and morlet wavelet kernels. For all sub-bands, morlet wavelet has high accuracy than RBF. Among all sub-bands, SB8 with morlet wavelet kernel has provided the highest accuracy of 97.74%. The performance parameters with morlet wavelet kernel are precision (PRE), F1-score, Cohen’s kappa, and ERR 97.74, 0.9774, 0.9749, and 2.26, respectively. The confusion matrix for SB8 is as shown in Table 2. From Table 2, it can be observed that the identification of all the physical actions is more than 95% by proposed method. Table 3 shows the comparison of the proposed method with other previous papers in the same database. The proposed method has high accuracy and good classification performance. It can notice that extracted statistical features and MC-LS-SVM provide better performance for classification of surface-EMG signals.

Table 1.

Performance parameters of all sub-bands using RBF and morlet wavelet kernels

SB	RBF			MORLET
	ACC	SPEC	SEN	ACC	SPEC	SEN
SB1	96.9	99.66	96.9	97.66	99.74	97.66
SB2	96.42	99.6	96.42	97.38	99.71	97.38
SB3	96.54	99.62	96.54	97.54	99.73	97.54
SB4	96.24	99.58	96.24	97.16	99.68	97.16
SB5	96.17	99.57	96.17	97.07	99.67	97.07
SB6	96.28	99.59	96.28	96.9	99.66	96.9
SB7	96.19	99.58	96.19	96.86	99.65	96.86
SB8	97.1	99.68	97.1	97.74	99.75	97.74

Table 2.

SB8 confusion matrix using morlet wavelet

Morlet	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10
C1	95.87	0.91	0.40	0.63	0.79	0.75	0.08	0.08	0.32	0.16
C2	0.28	96.90	1.27	1.11	0.08	0.04	0.04	0.04	0.20	0.04
C3	0.16	1.43	96.63	1.59	0.04	0.00	0.04	0.00	0.08	0.04
C4	0.36	1.15	1.79	95.99	0.04	0.00	0.12	0.04	0.16	0.36
C5	0.32	0.00	0.00	0.00	95.91	2.18	0.40	0.00	0.63	0.56
C6	0.00	0.00	0.00	0.00	1.79	98.17	0.00	0.00	0.04	0.00
C7	0.00	0.00	0.00	0.00	0.00	0.00	99.40	0.00	0.00	0.60
C8	0.04	0.04	0.00	0.04	0.00	0.00	0.00	99.88	0.00	0.00
C9	0.00	0.04	0.04	0.08	0.00	0.00	0.00	0.00	99.76	0.08
C10	0.04	0.08	0.00	0.04	0.04	0.00	0.60	0.04	0.28	98.89

Table 3.

Comparison of proposed method with previous method

Authors	Methods and classifiers	Year	Accuracy (%)
Abdullah et al. [51]	WPD, ensemble tree classifiers	2017	92.1
Proposed method	TQWT based statistical methods, MC-LSSVM	2018	97.74

Conclusion

In this paper, the physical actions of sEMG signals are classified using TQWT based time-domain features. TQWT decomposes EMG signals into sub-bands, features extract namely entropy, mean, negentropy, AAC, maximum value, first and third quartile features individually. The features extracted are fed into MC-LS-SVM classifier for classifying surface EMG signals. The classification results indicate MC-LS-SVM classifier with morlet wavelet kernel for sub-band eight has provided 97.74% accuracy in classifying sEMG signals. The classification results of the proposed method show promising accuracy. In the future, this method can be applied for different applications. The exact identification of physical actions by the proposed method can be used in practical man-machine interface system to help patients for restoring the lost motor functionality.