Quantitative comparison of frequency-domain and delay-and-sum optoacoustic image reconstruction including the effect of coherence factor weighting

Abstract

Image reconstruction in optoacoustic imaging is often based on a delay-and-sum (DAS) or a frequency domain (FD) algorithm. In this study, we performed a comprehensive comparison of these two algorithms together with coherence factor (CF) weighting using phantom and in-vivo mouse data obtained with optoacoustic microscopy. For this purpose we developed an FD based definition of the CF. Our results reveal the equivalence of DAS and FD, with and without CF weighting, in terms of spatial resolution and contrast-to-noise ratio (CNR) but highlight the clear advantage of FD in terms of computational cost, making it preferable for 3D reconstruction or real-time applications. An important additional result of this research is that, contradictory to previous studies, CF weighting does not lead to any improvement in lateral resolution.

1. Introduction

Optoacoustic imaging generates spatially resolved images with contrast given by variations in the optical absorption coefficient of tissue structures. Optoacoustic imaging has the distinct characteristic of producing signals which are time-resolved and thus retain depth information. The two modalities of optoacoustic imaging, tomography and microscopy, acquire optoacoustic pressure signals either through an ultrasound transducer array (tomography) [1], [2] or through mechanical scanning of a focused single-element transducer (microscopy) [3], [4]. In both cases, the raw data must be processed in order to yield high quality images. In the raw data, signals appear spread over a range of detection positions depending on the distance between absorbing structure and array elements (tomography) or absorbing structure and focus position (microscopy).

In optoacoustic tomography raw data, a signal point source appears to be curved away from the transducer array, which is due to the increasing time a pressure wave needs to propagate to detector elements farther from the source. Images are reconstructed from the time-resolved signals acquired by the multi-channel unfocused transducer array using the so called synthetic aperture focusing technique (SAFT) [5], [6]. The attainable resolution is limited laterally by the numerical aperture and center frequency of the array probe and axially by the frequency bandwidth of the transducer [7]. While SAFT can be realized in both time-domain and frequency-domain [8], the term SAFT is often used implying an implementation in time-domain. To avoid confusion, we refer to time-domain SAFT as DAS.

In optoacoustic microscopy, the raw data exhibits a high-resolution focal plane with low-resolution areas above and below the focal plane, akin to an optical microscope. In out-of-focus areas, a signal point source appears to curve away from the focus, with the curvature decreasing with increasing distance from the focal plane. The image resolution in these out-of-focus areas can be recovered from the time-resolved signals using the same reconstruction method by employing the virtual detector concept introduced by Li et al. [9]. The resolution limit is given laterally by the numerical aperture of the acoustic lens and the transducer's center frequency and axially, as in tomography, by the transducer's bandwidth.

In both tomography and microscopy, the reconstruction is typically implemented using a time-domain algorithm, whereby the detected signals are time-shifted to compensate for the delay introduced during image acquisition and then summed up (delay-and-sum, DAS). While the result of the reconstruction provides increased lateral resolution and contrast compared to the raw signal, several groups have reported that lateral resolution and contrast can be further improved by applying the so called coherence factor, which is proposed to increase lateral resolution and signal-to-noise ratio and suppress side-lobes [6], [10], [11], [12].

In spite of its popularity, the use of the DAS algorithm is not without disadvantages. While easy to implement, it is computationally expensive and thus unsuitable for very large pixel counts, applications where fast image reconstruction is required, or for 3D reconstruction (where summing is performed over a 2D area). To increase speed, 3D-DAS can be simplified to perform summing only in two orthogonal grid directions [13] (as opposed to over a 2D area) in order to additionally improve the spatial resolution in the direction perpendicular to the B-scans. This, however, does not result in true 3D resolution as it does not utilize the full extend of available information.

An alternative to time-domain reconstructions are frequency-domain (FD) algorithms, which offer the advantage of lower computational complexity when implemented using an FFT algorithm [14], [15]. This leads to significantly faster processing of large numbers of pixels. While delay-and-sum and frequency-domain algorithms are in principle mathematically equivalent solutions to the same problem, interpolation errors in time-domain and frequency-domain lead to numeric deviations that may result in method-specific noise and artifacts in the reconstructed images.

The speed advantage of FD algorithms stems from their lower computational complexity: For a 2D data set of size n × n the computational complexity is O(n² log₂(n)) for the FD algorithm but O(n³) for the DAS algorithm. For a 3D reconstruction of size n × n × n, the complexity of the FD algorithm is O(n³ log₂(n)), while for the DAS algorithm it is O(n⁵). The relative slowdown of the DAS algorithm in the 3D case comes from the fact that for every voxel, the signal sum is generated over a plane instead of a line. The difference in computational complexity means that the larger the number of pixels, the faster the FD algorithm becomes in comparison. This is especially important when reconstructing in 3D, as the difference in computational complexity is more pronounced when comparing 3D-FFT with 3D-DAS.

Frequency-domain algorithms have been reported to cause more reconstruction artifacts than time-domain algorithms [15], [16]. These artifacts can be reduced to the level of time-domain algorithms by zero-padding, at the expense of an increased calculation time. Alternatively, regularized inverse k-space interpolation [17] improves image quality for a comparatively minor increase in calculation time. This interpolation law uses only a small number of frequency components to calculate an interpolant and is therefore much more efficient than the equivalent summation over a large number of values performed in the DAS algorithm.

Recently, model-based reconstructions started to be employed in optoacoustic imaging for their ability to take into account specific properties such as detector geometry or -aperture [18], [19], [20], spectral attenuation and even local variations in speed of sound. Model-based reconstruction is based on minimizing the difference between the measured signals and the theoretical signals predicted by a forward model using an iterative inversion approach [21], [22], resulting in a reduction of reconstruction artifacts [23], [24] and an increased image quality. These improvements however are obtained at the expense of a higher computational complexity, which often makes model-based reconstruction slow, in particular for large numbers of pixels required for 3D reconstruction.

The object of this study is to experimentally demonstrate that FD with truncated inverse k-space interpolation is equal to DAS in terms of spatial resolution and contrast. We further aim to show that the commonly used coherence factor can equivalently be adapted for the FD algorithm, using an alternative definition. In order to make the comparison objective, the FD algorithm is adapted to match the point spread function of the DAS implementation by equalizing their response to simulated signal data. The two algorithms are thoroughly compared using experimental phantom and in-vivo data obtained with an optoacoustic microscopy setup. The influence of the coherence factor is evaluated for both algorithms.

2. Materials and methods

Reconstruction algorithms

The basis of FD reconstruction is the transformation of the forward model into the frequency-domain [17].

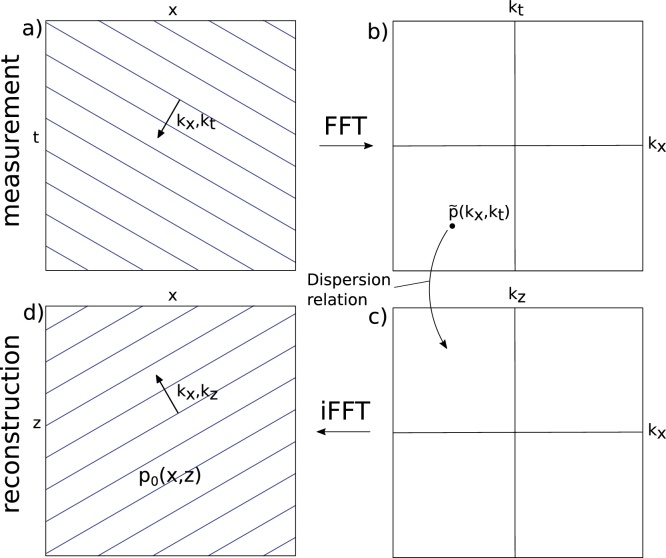
FD reconstruction consists of three steps, which are explained here for the 2D case: first, the raw data is 2D-Fourier-transformed (Fig. 1). Second, frequency components are mapped from the signal temporal frequency domain (k_x, k_t) to the image spatial frequency domain (k_x, k_z) according to the dispersion relation:

$$k_t=-c_s\sqrt{{k_x}^2+{k_z}^2}$$ (1)

Fig. 1.

Schematic representation of FD algorithm acting on single plane wave component. a) measured signal, b) signal frequency-domain, c) image frequency domain and d) reconstructed image.

Where c_s is the speed of sound and k_t, k_x and k_z are the wave vectors of the signal and image, respectively.

Third, the image is obtained by inverse-Fourier-transforming the result of the mapping.

The discrete Fourier transform yields a discrete set of frequencies due to the finite extent of the space-time domain of the experiment. Therefore, employing equation (1) for the mapping of frequency components necessitates the use of an interpolation scheme, as the discrete wave vectors do not match one-to-one. The choice of interpolation law affects magnitude and distribution of image artifacts and influences reconstruction efficiency.

To minimize artifacts, the truncated regularized inverse k-space interpolation law as defined in [17] is used in this study.

Whereas the FD algorithm reconstructs the entire dataset at once, the DAS algorithm uses a pixel-wise operation in time-space-domain, where the signal source is reconstructed through shifting signal channels by the position-dependent time-delay introduced during acquisition and subsequent summing of the channels at the reconstructed pixel position.

The sum is calculated per pixel as [9]:

$$S_{\mathrm{DAS}}(t)=\sum _{i=0}^{N-1}s(i,t-\mathrm{\Delta }{t}_i)$$ (2)

where s(i, t) denotes the detector signal at position i (channel i for an array probe) and time t, Δt_i denotes the time delay for the corresponding position i and N the number of signal channels included in the sum.

The parameter Δt_i in eq. (2) is calculated differently for microscopy and tomography. In microscopy, it is calculated from the pixel position relative to the focal spot as:

$$\mathrm{\Delta }{t}_i=\mathrm{sign}(z-z_f)·\frac{(r^{\prime }-r)}{c_s}$$ (3)

where r′ is the distance of the reconstructed pixel to the focal spot and r = z − z_f the distance of the reconstructed pixel to the focal plane, and sign(z − z_f) changes sign based on whether the reconstructed pixel is located above or below the focal plane. In tomography, the case is simpler as sign(z − z_f) can be omitted since the focal plane is identical with the receiver array.

Since Δt_i can assume any fractional value between the discrete time samples of the signal matrix, the signal s(i, t − Δt_i) in eq. (2) must be interpolated. In this study we used sinc interpolation for this purpose.

All reconstructed images shown in this manuscript correspond to the envelope of the reconstructed signal amplitudes. For raw images, the image corresponds to the envelope of the unprocessed signal amplitudes.

Coherence factor

The coherence factor was previously defined as [11], [10], [12]:

$$\mathrm{CF}(t)=\frac{|{\sum }_{i=0}^{N-1}s(i,t-\mathrm{\Delta }{t}_i){|}^2}{N·{\sum }_{i=0}^{N-1}|s(i,t-\mathrm{\Delta }{t}_i){|}^2}$$ (4)

it is regarded as the per-pixel ratio of the coherent energy to total energy included in the sum. The resulting value ranging from 0 to 1 describes the degree of coherence in the sum of the respective pixel. It is applied to the reconstructed image by pixel-wise multiplication, where it supposedly suppresses the intensity of any pixel for which the summed signals exhibit little coherence. It is worth noting that the multiplication with the coherence factor is a nonlinear operation and as such, will alter the result of linear measures such as CNR in a non-trivial way. It has also been reported that the coherence factor is sensitive to noisy data [25].

To make the coherence factor amenable to the FD approach, we rewrite the definition eq. (4) as:

$$\text{CF}=\frac{|\mathrm{REC}(\text{s}){|}^2}{\text{N}·\mathrm{REC}(|\text{s}{|}^2)}$$ (5)

where s is the signal matrix, N is a normalization matrix corresponding to the shape of the acoustic receiving beam and REC is a linear operator describing the reconstruction. The division and multiplication are done element-wise.

A prerequisite for the definition of the CF according to eq. (5) is that REC(|s|² ) is positive everywhere. While this is the case for the DAS algorithm according to eq. (2) (a sum over positive values is automatically positive), it does not automatically hold for any implementation of the FD algorithm; a superposition of the bipolar plane waves does normally take positive and negative values. The FD implementation used in this study was adapted to closely match the point-spread-function of the DAS implementation, and thus fulfills this prerequisite to a great extent. To compensate for remaining negative values, a small offset larger than the largest negative value is applied to ensure positive, non-zero values. The matching of the two algorithms was achieved by applying frequency-dependent phase and amplitude scaling factors $w(k_t,k_z)$ to the FD signal frequency spectrum. The factors were empirically determined to match FD and DAS reconstructions of simulated plane wave signals:

$$w(k_t,k_z)={(0.1+|k_t|)}^{-0.55}·e^{0.7·\mathrm{sign}(k_z)i}$$ (6)

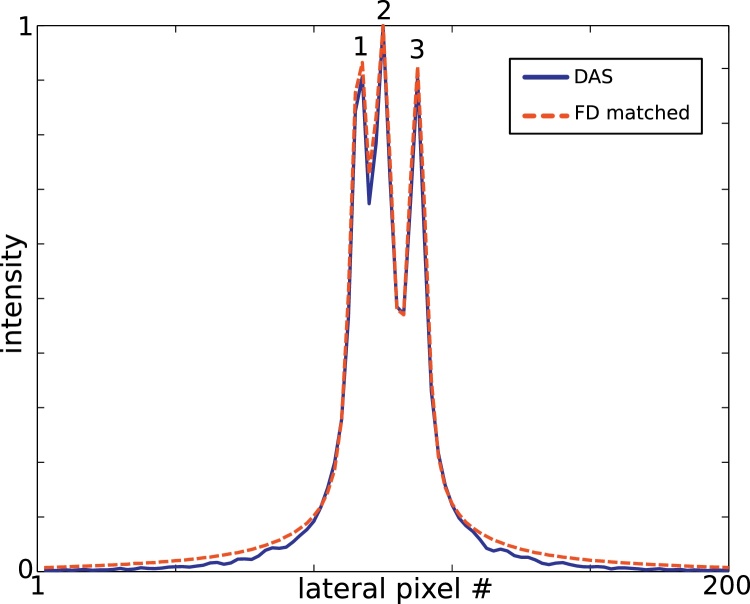
In addition, angular apodization conforming to the receiving angular aperture of the acoustic lens was matched in both algorithms. Fig. 2 demonstrates the quality of the matching by comparing the simulated lateral intensity profile of three signal sources.

Fig. 2.

Lateral intensity profiles of three simulated signal point sources (1,2,3) reconstructed with DAS and matched FD algorithms.

Wire experiment setup

In order to compare the DAS and FD algorithms quantitatively, an experiment was designed that allows determining the achievable acoustic resolution in a statistically meaningful way.

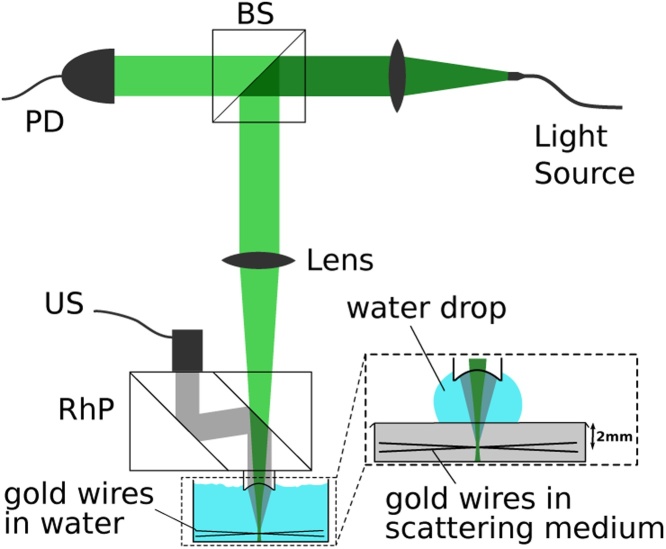
Two 20 μm gold wires were fixed under tension such that they cross at a shallow angle (∼ 3^∘). A 3D optoacoustic image (C-scan) was then recorded of the crossing wires with the two wires oriented orthogonally to the plane of B-scans. The closest distance at which the two wires could be resolved was determined using Sparrow's limit, that is, just before the disappearance of the dip in-between the two signal peaks. Defining the resolution in this way ensures that the result is invariant to non-linear transformations of the signal, such as CF weighting. The experiment was conducted with the wires submerged at a depth of 2 mm from the surface in both water as well as a scattering medium consisting of a 0.5% SMOFlipid solution in water (Fig. 3). Performing the experiment in a highly scattering medium allows the algorithms to be investigated in a situation where artifacts are outweighed by image noise. In such a situation, DAS and FD algorithms may show different noise statistics, which in turn may affect the CF differently.

Fig. 3.

Schematic of the optoacoustic microscope setup used for the wire experiment showing beam splitter (BS), photodiode (PD), ultrasonic transducer (US) and rhomboid prism (RhP). Insert shows adapted phantom for measurements in scattering medium. Setup adapted from [26].

The setup (Fig. 3) used for the quantitative comparison of the algorithms consisted of an 8 ns pulsed laser (Innolas SpitLight DPSS) at 532 nm with a pulse energy of around 85 μJ weakly focused to a beam waist of 600 μm, resulting in a radiant exposure of ∼30 mJ/cm². Focused acoustic detection was achieved via a plano-concave lens (Linos, glass N-BK7) with a surface curvature of R=4.71 mm, which was mechanically attached to the rhomboid prism (Edmund optics, N-BK7) using optical contact bonding so as to avoid reflections from the lens-prism interface. The microscope was run in acoustic-resolution mode, meaning acoustically focused more tightly than optically [7]. Signals were detected using a 50 MHz (70% bandwidth, -6 dB) transducer (Olympus V215-BB-RM, Precision Acoustics submersible preamplifier). The signal was subsequently further amplified (Miteq AU1442-R) and digitized at 16 bit resolution (Spectrum M4i.4420-x8). Mechanical scanning was performed using a computerized 2D stage (Prior H101) with step sizes dx=dy=15 μ m and a maximum scan area of 25x25 mm.

The algorithms were evaluated with respect to lateral resolution and contrast-to-noise level at various depths from the focal plane. CNR was calculated as $\mathrm{CNR}=\frac{|S_{\mathrm{wire}}-m_{\mathrm{bg}}|}{{\sigma }_{\mathrm{bg}}}$; where S_wire is the wire signal envelope amplitude averaged over a defined ROI, while m_bg and σ_bg are the mean and standard deviation of the background.

In-vivo experimental setup

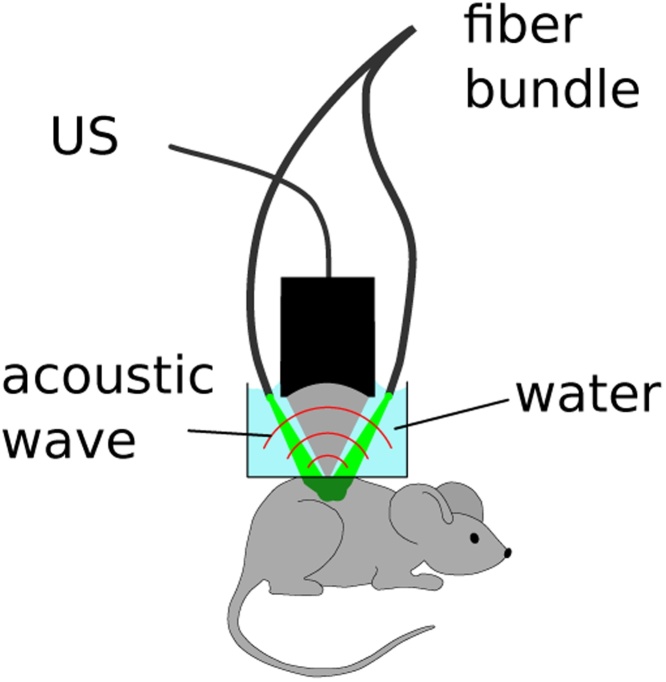
The in-vivo datasets were acquired using an acoustic-resolution optoacoustic microscope based on spherically-focused polyvinylidene fluoride (PVDF) detector with 5–35 MHz bandwidth, focal distance of 6.8 mm and numerical aperture of 0.6 (OOO BARI-NN, Russia)[27]. Sample illumination was conducted via a fiber bundle with distal ends distributed circularly around the active transducer surface, producing a dark-field illumination pattern with a total radiant exposure of 5 mJ/cm² at the sample surface (Fig. 4).

Fig. 4.

Schematic of the optoacoustic microscope setup used for in-vivo imaging showing curved ultrasonic PVDF transducer (US) and fiber bundle (2 ends shown) dark-field illumination.

A 532 nm diode laser (HB Wedge, BrightSolutions, Italy) with a pulse length of 1.4 ns and a pulse energy of 1 mJ was used as the light source. Mechanical scanning was performed using two linear stages (M-664, PI GmbH, Germany) with step sizes dx = dy = 25 μm. OA A-scans corresponding to discrete XY positions of the scanning head were recorded at 200 MHz sampling frequency by a 16 bit digitizer (CSE1622, GaGe, USA). The raw data was bandpass filtered prior to reconstructing in order to increase SNR.

The in vivo experiment was conducted using eight week old balb/c-nude mouse bearing human breast carcinoma SKBR3 (5 · 10⁶ cells injected subcutaneously to the outer side of the thigh 25 days prior to the study). Before the investigation the mouse was anesthetized with an intramuscular injection of the mixture of Zoletil 100 (40 mg/kg) with Rometar (10 mg/kg). The animal was then immobilized in a side position; the center of the tumor was placed into the center of the scanning area. The experiments were conducted in accordance with the requirements of codes and enactments ruling research works to the safety and efficiency of pharmaceuticals (Regulation by Ministry of Health and Social Development of Russian Federation No. 708-n from 23.08.2010), and international legal and ethical codes of experimental use of animals (NIH Publications No. 8023, revised,1978).

3. Results

Wire phantom comparison

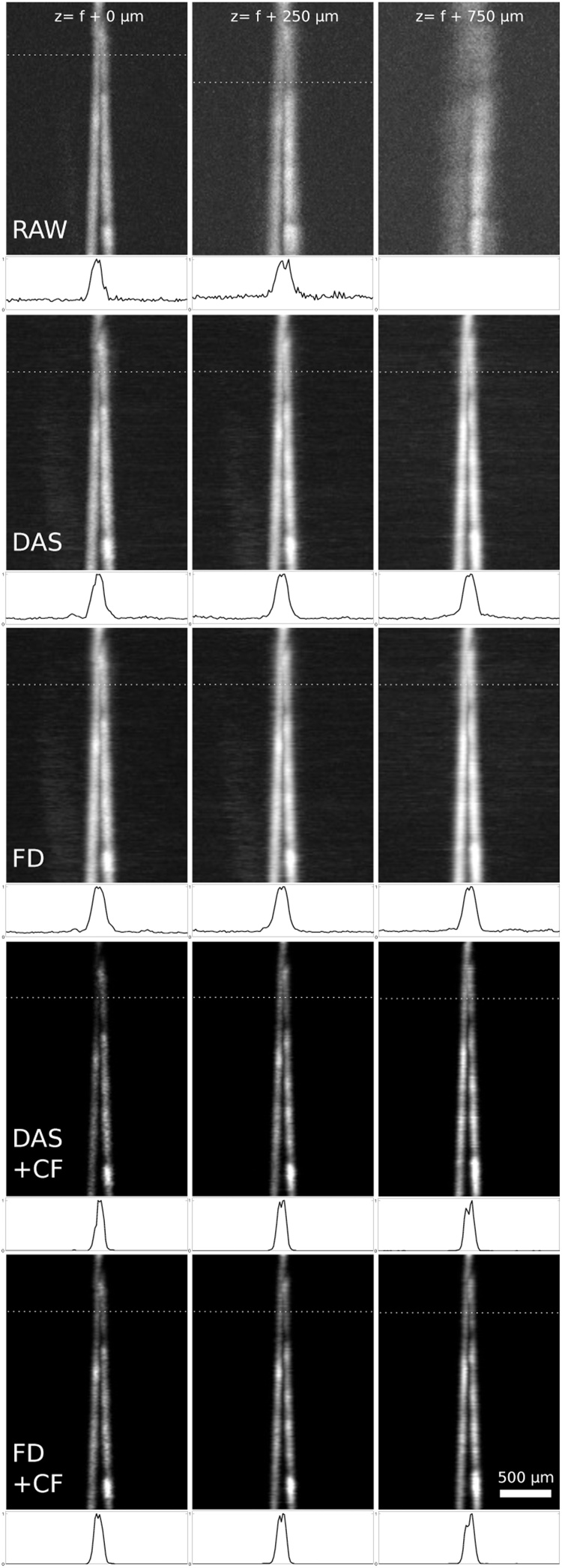
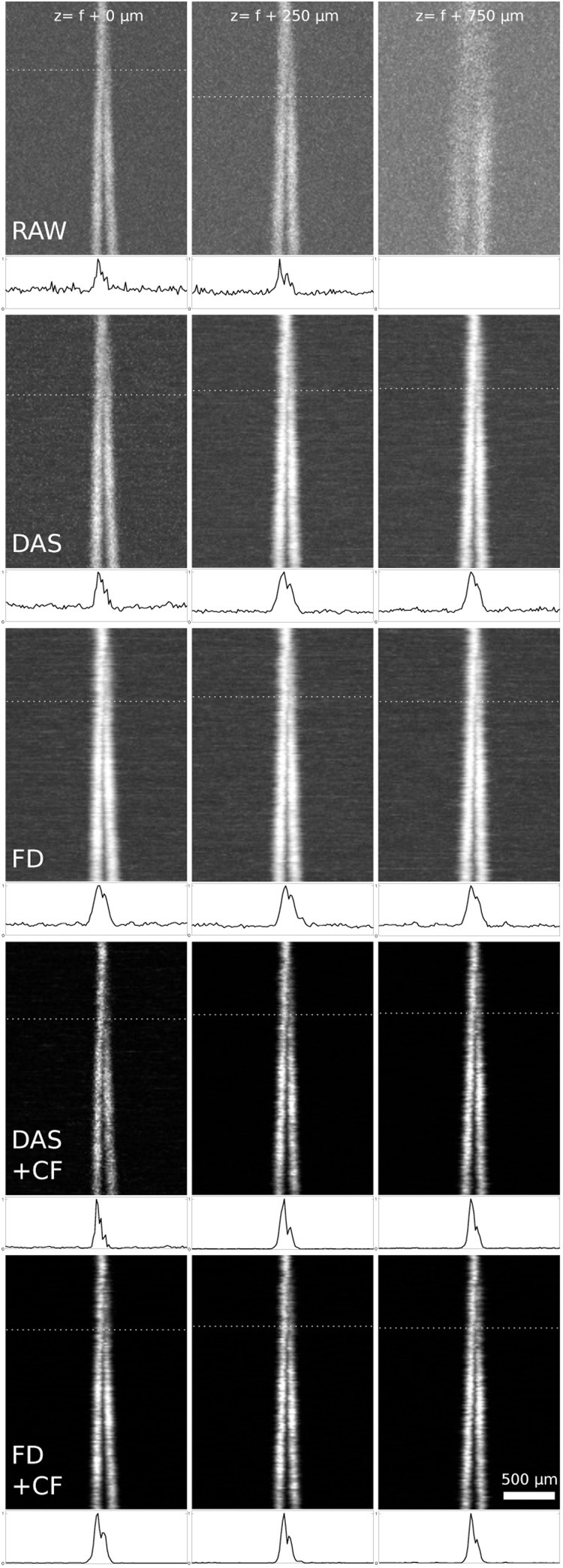
Fig. 5 illustrates how the spatial resolution without reconstruction decreases with increasing distance from the focal plane (top row) and how the resolution is recovered by applying the reconstruction algorithms (second to bottom row). Raw images correspond to the envelope of the unprocessed signal amplitude. The resolution was determined from these images by finding the minimum distance between the wires that would still allow them to be resolved. To increase robustness of the distance measurement, a straight line was fitted to each wire and the distance between the wires at every B-scan was calculated from the line parameters. The resolution limit was then determined by finding the critical B-scan (i.e. at the limit of resolution as defined by the Sparrow criterion). Fig. 6 shows the output of the two algorithms, with and without CF, in optically scattering / low CNR conditions, where the effects of background noise are significant.

Fig. 5.

Maximum amplitude projections of the OA signal of gold wires in water. Raw images (top row), DAS and FD reconstructions (second and third rows) and DAS and FD with coherence factor (fourth and bottom rows) at various z-positions: at the focal plane (left column), at 250 μm and at 750 μm below the acoustic focal plane. The dotted line indicates the critical B-scan with the corresponding intensity profile below. The uneven intensity of the wires is likely attributed to uneven dust adhered to on the gold wire surface.

Fig. 6.

Maximum amplitude projections of the OA signal of gold wires in a scattering medium. Raw images (top row), DAS and FD reconstructions (second and third rows) and DAS and FD with coherence factor (fourth and bottom rows) at various z-positions: at the focal plane (left column), at 250 μm and at 750 μm below the acoustic focal plane. The dotted line indicates the critical B-scan with the corresponding intensity profile below.

The performances of the FD and DAS algorithms were identical in terms of resolution, independent of whether CF weighting was applied or not. For both algorithms, the influence of the CF on the resolution in both low- and high-noise conditions was not significant (Table 1). The error of the distance measurement was estimated at ± 3 μm from the repeatability of measurements; depending on the signal shape the identification of the critical B-scan can be subjective.

Table 1.

Distance between gold wires [±3 μm] at the resolution limit in water/scattering medium. Missing values indicate that the critical B-scan could not be determined due to poor CNR.

	Position from focal plane
Algorithm	f+0 μm	f+250 μm	f+500 μm	f+750 μm
Raw image	61/61 μm	71/79 μm	101/– μm	–/– μm
DAS	64/67 μm	63/64 μm	63/62 μm	62/62 μm
FD	63/62 μm	62/61 μm	62/61 μm	63/62 μm
DAS + CF	64/66 μm	62/63 μm	64/63 μm	65/62 μm
FD + CF	63/63 μm	63/62 μm	63/62 μm	66/62 μm

Both algorithms show a slight resolution degradation close to the focal plane, an effect that has been observed before [25] and appears slightly less pronounced for the FD algorithm.

The CNR appears to be affected by the CF differently for the two algorithms (see Table 2). While application of the CF increased the CNR for both algorithms, a significantly larger increase was observed in the case of the FD algorithm.

Table 2.

CNR [dB] of optoacoustic images of gold wires in water (top) and scattering medium (bottom). CNR was computed with the avg wire signal. The error was calculated from the standard error of the averaged wire signal.

	Position from focal plane
Algorithm	f+0 μm	f+250 μm	f+500 μm	f+750 μm
Raw image	31.1±0.08	27.6±0.12	23.9±0.17	21.9±0.20
	21.3±0.11	19.7±0.11	14.6±0.17	11.9± 0.21
DAS	34.5±0.08	36.0±0.06	35.1±0.06	34.4±0.06
	22.8±0.09	28.0±0.09	28.8±0.07	28.8±0.07
FD	36.6±0.06	36.3±0.06	35.0±0.06	34.5±0.06
	30.0±0.06	29.7±0.06	29.2±0.07	30.2±0.05
DAS+CF	70.9±0.21	71.2±0.14	63.5±0.13	59.2±0.11
	33.9±0.15	45.8±0.12	46.4±0.11	46.6±0.11
FD+CF	81.3±0.14	76.3±0.13	71.2±0.12	64.6±0.11
	48.7±0.12	48.6±0.11	47.9±0.10	48.5±0.11

In water, both algorithms were able to recover the image over the range of focal positions to a CNR of 34–36 dB. With the CF applied, the CNR increased to 60–71 dB for the DAS algorithm (an avg increase of 31.2 dB over the reconstruction without CF) and to 64–81 dB for the FD algorithm (avg increase of 37.8 dB). In the scattering medium, the DAS algorithm resulted in a CNR of 23–29 dB, while the FD algorithm produced a CNR of 29–30 dB. With CF weighting, CNR increased to 34–47 dB (avg increase of 16 dB) for the DAS algorithm, and to 48–49 dB (avg increase of 18.7 dB) for the FD algorithm.

On our reference machine (Intel Core i7-3770, both algorithms running parallelized on all 4 cores in MATLAB), the DAS algorithm performed the wire image reconstruction in 0.23 s per B-scan (200 × 495 pixels) on average. The FD algorithm was faster at 0.05 s/B-scan, almost a factor 5 speedup. With CF weighting, computation times increased to 0.41 s per B-scan for DAS+CF and to 0.10 s for FD+CF, a factor 4 speedup.

In-vivo comparison

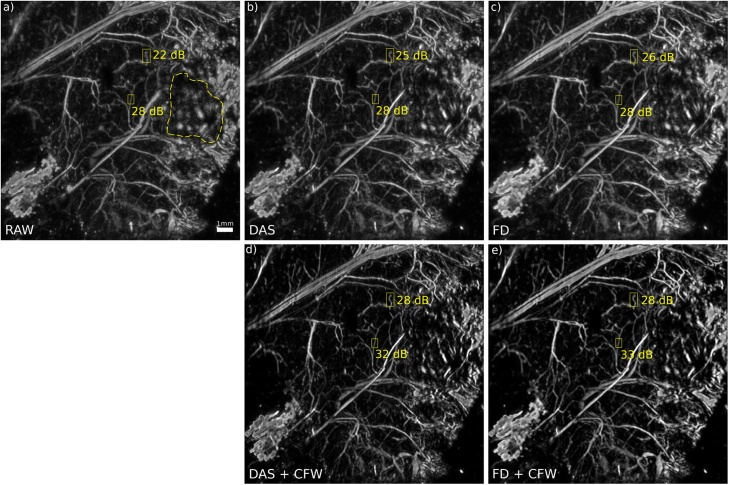
To put the results obtained in the wire experiment in context with a real situation, an optoacoustic image of a mouse subcutaneously implanted tumor was used. DAS and FD reconstructions (Fig. 7b and 7 c) show some improvement over the raw image (Fig. 7a) and an increased CNR. The latter was measured within two small ROI's containing capillaries, with one located near the focal plane (center of the image) and one out-of-focus (upper part of the image). As expected, no change in CNR could be observed near the focal-plane, while in the out-of-focus part the CNR was increased by 3-4 dB. CF weighting yields another 3 dB increase in CNR for the DAS algorithm (Fig. 7d) and a 2 dB increase for the FD algorithm (Fig. 7e) within the same ROI. CF weighting also increased the CNR in the near-focal-plane ROI by 4-5 dB, as was previously observed in the phantom experiment.

Fig. 7.

Maximum amplitude projection of subcutaneously implanted tumor (dashed area in fig. a) in mouse obtained as depicted in Fig. 4. a) raw image b) DAS reconstruction c) FD reconstruction d) DAS+CF weighting e) FD+CF weighting. CNR was measured for indicated ROI.

On our reference machine, average computation time was 7.10 s per B-scan (600x751 pixels) for the DAS algorithm and 0.25 s for the FD algorithm, a factor 28 speedup. With CF weighting, computation times increased to 12 s (DAS+CF) and 0.5 s (FD+CF).

4. Discussion

Our results indicate that DAS and FD image reconstruction algorithms perform equally under both low- and high-CNR conditions. Phantom experiments showed no significant difference in terms of resolution and CNR, with the exception of minor differences appearing in the near-focal-plane region, where a slightly higher resolution and CNR were measured for the FD algorithm. Both algorithms recovered the resolution in the measured out-of-focus areas to closely match the resolution achieved in the focal plane in both high- and low-CNR conditions, in accordance with previously reported findings [9], [25]. However, the two algorithms differed greatly in terms of speed. The observed computation times show a factor 28 speedup for the FD algorithm in the reconstruction of the in-vivo data set.

Contrary to previous reports [11], [25], this study clearly reveals that the coherence factor does not yield any improvement to resolution for either algorithm in both high- and low-CNR cases. The reason for this discrepancy is that previous studies defined the resolution either by the FWHM of a thin wire or by an adaptation of the Rayleigh criterion. Both of these definitions, however, are sensitive to the nonlinear amplitude transformations performed by CF weighting and thus not suitable for assessing its effects on the spatial resolution. Using the Sparrow criterion for determining the resolution avoids these complications and proves that CF weighting does not improve the resolution of optoacoustic imaging. In contrast, using the FWHM of a single wire from Fig. 5 to assess the effect of CF weighting on the delay-and-sum reconstruction yields a misleading result: for both wires, the FWHM criterion shows an apparent improvement in resolution from 76 μm to 42 μm and from 66 μm to 21 μm, respectively.

Our measurements confirmed an increase in CNR when the CF was applied, in accordance with previous findings [11], [9]. However, this improvement in CNR due to CF weighting must be viewed critically. Since CNR, like SNR, is defined as a ratio of energies, applying any non-linear operation to the image means that intensity no longer corresponds linearly to energy and thus the calculated CNR no longer corresponds to energies. Much like the FWHM of a thin absorber is a potentially misleading reference point for image resolution, CNR may be a misleading reference point for assessing the detectability (as opposed to image contrast) of a signal.

Similar conclusions to the phantom experiments can be drawn from the more noisy in-vivo images: DAS and FD reconstruction algorithms perform virtually identically, while CF weighting significantly increased the CNR in both cases. This confirms that the FD algorithm is a perfectly viable (yet substantially faster) alternative to DAS even for the complex, noisy datasets that typically result from in-vivo experiments.

5. Conclusion

We have successfully demonstrated the practical equality of frequency-domain to delay-and-sum reconstruction. While this equality has limitations, such as slight differences in noise homogeneity and focal plane resolution, in a practical scenario any disparities in the output images are negligible. Our results demonstrate that the increased image artifacts often attributed to frequency-domain reconstruction can be mitigated to a neglectable level using truncated regularized inverse k-space interpolation and zero padding the data. The comparison confirmed that the FD algorithm is particularly well-suited for the reconstruction of large data sets due to its lower computational complexity, an advantage especially important for potential real-time applications.

Contrary to previous publications, we have shown that coherence factor weighting does not influence the lateral resolution in any way. In order to properly assess the influence of the coherence factor on the contrast, we suggest calculating the statistical significance level of the signal given the background noise statistics, and to then compare reconstructions with and without CF based on this significance level. Such a comparison, however, is only feasible when the CNR is very low, as many statistical tests, such as Chi-squared or Cramér-von-Mises, are unreliable when the signal is easily differentiated from the background noise.

Biographies

Florentin Spadin received his PhD in physics from the University of Bern, Switzerland, in 2019. He is currently working as a postdoctoral researcher at the Instute of Applied Physics of the University of Bern. His current research focuses on optoacoustic microscopy and image reconstruction.

Michael Jaeger received the Dipl Phil Nat degree in physics from the University of Bern, Switzerland, in 2002, and the PhD in physics from the same university in 2007. In 2010/ 2011 he joined the Institute of Cancer Research at the Royal Marsden Hospital, Sutton, UK. In 2012 he won a career development project under the “Ambizione” scheme from the Swiss National Science Foundation, and is now group leader of the Optoacoustic Imaging Team at the Institute of Applied Physics, University of Bern. His research includes optoacoustic imaging with focus on handheld clinical imaging, as well as novel diagnostic ultrasound modalities such as speed-of-sound imaging.

Robert Nuster received his Ph.D. in experimental physics from the Karl-Franzens-University Graz, Austria, in 2007 with a thesis on development and application of optical sensors for laser induced ultrasound detection. From 2008-2011 he was a postdoctoral research fellow at the Karl-Franzens-University Graz. Since 2011 he has been a senior postdoctoral research fellow. His current research interests include photoacoustic imaging, characterization of materials by laser ultrasound and ultrasound sensor development.

Pavel Subochev (Ph.D.) is the optoacoustic group leader at the Laboratory of Biophotonics (Institute of Applied Physics RAS). He graduated from Lobachevsky State University of Nizhni Novgorod in 2006 and received his PhD in passive acoustic radiometry from the Institute of Applied Physics RAS. Since 2012 Pavel Subochev is focused on the development of new instrumentation for optoacousutic imaging of biological tissues and visited Institute of Applied Physics (University of Bern) in 2014 and 2016.

Martin Frenz received his Master degree in physics from the Albert-Ludwig University of Freiburg, Germany, and his PhD in physics from the University of Bern, Switzerland. In 1995 he joined the University of Texas at Austin, USA. Currently, he is professor and head of the biomedical photonics department and director of the Institute of Applied Physics at the University of Bern, Switzerland. Prof. Martin Frenz is a fellow of SPIE (Society of Photo-Optical Instrumentation Engineers) and serves in the editorial board of several scientific journals. His most recent work has explored new imaging modalities in biomedicine, including quantitative optoacoustic imaging and sensing, speed of sound imaging in reflection mode, in-vivo microscopy, optoacoustic contrast agents for imaging and therapy, light propagation in tissue as well as biomedical laser applications for medical diagnostics and therapy.