Baseline Cocaine Demand Predicts Contingency Management Treatment Outcomes for Cocaine-Use Disorder

Abstract

Cocaine use disorder (CUD) is a significant public health issue. Behavioral interventions such as contingency management (CM) have been demonstrated to be highly effective in promoting cocaine abstinence. However, identifying individual characteristics associated with cocaine relapse may help improve treatment outcomes. Cocaine demand is a behavioral economic measure that shares a scientific foundation with CM. In the current study, we assessed baseline cocaine demand using a hypothetical cocaine purchasing task. Participants (N = 58) consisted of treatment-seeking individuals with CUD. All participants received one month of CM treatment for cocaine abstinence, and treatment responders were defined as presenting six consecutive cocaine negative urine samples from thrice weekly clinic visits. Demand data were well described by the exponentiated demand model. Indices of demand (intensity of demand − Q₀, elasticity - α) were significantly associated with recent (last 30 days) cocaine use. Importantly, linear regression revealed that CM treatment non-responders presented significantly higher Q₀ (p = 0.025). Subsequent quantile regression analyses examining the relationship between CM treatment response and Q₀ revealed statistically reliable effects of being a non-responder across three of the lower percentiles (i.e., 15, 25, and 30). Overall, these findings provide further support for the utility of exponentiated demand model. To our knowledge, this is the first study to demonstrate an association between baseline demand and contingency management response and systematically extend the findings of prior demand research to a novel drug class, cocaine.

Introduction

Cocaine use disorder (CUD) is a significant public health issue. The number of cocaine-related overdose deaths in the U.S. was 13,942 in 2017, representing more than two-fold increase compared to a decade ago (NIDA, 2019). Cocaine increases the risk of morbidity and mortality and is associated with a host of problems negatively affecting not only users, but society at large. Such consequences include but are not limited to crime, incarceration, violence, homelessness, drug-exposed neonates, and increased risk of infectious disease (Barr, Antes, Ottenberg, & Rosen, 1984; Cherubin & Sapira, 1993; Karch, 2005; Kruszon-Moran & McQuillan, 2005; Lucas, 2005; Nnadi, Mimiko, McCurtis, & Cadet, 2005; Schiller & Allen, 2003). Furthermore, CUD is associated with a number of compromised cognitive and behavioral processes associated with reward, motivation, learning, and inhibitory control (Goldstein & Volkow, 2002, 2011; Volkow, Fowler, & Wang, 2003).

Currently, there are no FDA-approved pharmacotherapies for CUD, and current clinical treatment guidelines recommend the use of psychosocial interventions for CUD (De Crescenzo et al., 2018; Kleber et al., 2006). One such intervention is contingency management (CM), an evidence-based treatment that promotes clinically-relevant targets (e.g., cocaine abstinence) by providing contingent consequences, such as vouchers exchangeable for a variety of non-drug rewards (Higgins, Heil, Rogers, & Chivers, 2009). The roots of CM are based on an extensive behavioral literature showing that drug use, like other behavior, is sensitive to environmental consequences. For example, a relatively early meta-analysis observed that CM efficacy was positively related to the magnitude and immediacy of monetary reward (Lussier, Heil, Mongeon, Badger, & Higgins, 2006). A more recent meta-analysis including 50 randomized controlled trials (N = 6,942) evaluated the efficacy and acceptability of twelve psychosocial interventions for CUD and amphetamine use disorder (AUD) compared to treatment as usual (De Crescenzo et al., 2018). CM delivered in the context of a community reinforcement approach (a behavioral-based skills training intervention) was the only treatment to increase cocaine abstinence at the end of treatment, 12 weeks, and at longest follow-up (range 16 to 96 weeks). CM in conjunction with a community reinforcement approach was also found to be superior to other psychosocial interventions with regard to patient dropout. Despite strengths noted above, not all participants respond to CM treatment and identifying individual factors influencing CM response remains an important research goal.

One individual factor that may be informative to CM treatment outcomes is drug demand. Drug demand is a behavioral economic measure that characterizes the relationship between the price (e.g., monetary cost or effort expended) of a drug and the amount of drug consumed. Assessing these choices under conditions of constraint (e.g., finite funds, time to use drugs, etc.) has helped elucidate the decision making processes characterizing motivation to use drug among individuals with SUDs (Bickel, Johnson, Koffarnus, MacKillop, & Murphy, 2014; Hursh & Roma, 2013; Koffarnus & Kaplan, 2018; Mackillop, 2016). Hypothetical drug purchasing tasks are commonly used to assess drug demand and are useful in clinical settings where providing access to drug would be either unethical or impractical given limitations on time and setting (Roma, Reed, DiGennaro Reed, & Hursh, 2017). Drug purchasing tasks have been utilized to assess drug demand for a variety of substances including alcohol, nicotine, marijuana, and opioids (Acker & MacKillop, 2013; Amlung, Acker, Stojek, Murphy, & MacKillop, 2012; Amlung & MacKillop, 2014; Amlung & MacKillop, 2015; Aston, Metrik, & MacKillop, 2014; Jacobs & Bickel, 1999; MacKillop, Amlung, & Acker, 2010; MacKillop et al., 2008; MacKillop & Tidey, 2011; Pickover, Messina, Correia, Garza, & Murphy, 2016). Relatively few purchasing task studies have assessed cocaine demand (Bruner & Johnson, 2014; Petry, 2000, 2001; Petry & Bickel, 1998; Strickland, Lile, Rush, & Stoops, 2016), but results from available studies have consistently demonstrated significant relations between cocaine demand and clinically relevant measures of cocaine use (i.e., positive cocaine urines, self-reported cocaine use). To our knowledge, no studies have assessed whether cocaine demand is related to CM outcomes. However, a relationship is plausible given the shared focus on the reinforcing effects of drug and non-drug rewards.

Drug demand is often characterized by a demand curve, which graphically depicts consumption of a drug, which presumably represents the putative value of a drug, across a range of drug prices. Drug demand curves can be generated by fitting consumption at different drug costs to Equation 1 below (Koffarnus, Franck, Stein, & Bickel, 2015; Yu, Liu, Collins, Vincent, & Epstein, 2014), which is an exponentiated version of the widely used equation proposed by Hursh and Silberberg (Hursh & Silberberg, 2008).

$$Q=Q_0\ast {10}^{k(e^{-\alpha Q_{0}C}-1)}$$ (1)

In both Equation 1 and the Hursh and Silberberg (2008) exponential equation, Q represents consumption of a given drug at price C. The derived values Q₀ and α represent consumption when price approaches zero and demand elasticity, respectively. Elasticity describes the degree to which consumption changes with changes in price, with greater elasticity indicative of relatively quicker decreased consumption with increased price. The parameter k represents the range of consumption values log₁₀ units. Several other values can be derived from the equation that help fully characterize the demand function. Omax is the maximal response output (e.g., amount of money spent) at a given price of drug. This also reflects where responding for drug changes from relatively inelastic to elastic. Pmax is the price point at which Omax is observed. The breakpoint represents the price at which no more drug is consumed. Benefits of the exponentiated equation include being able to include 0 consumption values, overall better fits of the data, as well as better fits of consumption values including Q₀ (Koffarnus et al., 2015; Strickland, Lile, et al., 2016).

The purpose of the current study was to examine the relationship between baseline cocaine demand and response to a four-week abstinence-induction CUD treatment phase involving CM with high-magnitude incentives. Cocaine demand was assessed using a hypothetical cocaine purchasing task. CM response was defined as achieving abstinence, verified by six consecutive cocaine negative urine drug screens from thrice weekly clinic visits. To our knowledge, this is the first study to assess the relationship between cocaine demand and CM treatment outcomes. Given the reinforcement-based conceptual framework shared by both drug demand assessment and CM treatment, we expected to observe meaningful relationships between these measures.

Methods

Participants

The current study was conducted in the context of an ongoing parent study investigating sequential, multiple assignment, randomized trial (SMART) design involving two distinct treatment phases (NCT02896712). Phase 1 involved 4 weeks of high-magnitude reinforcement CM targeting abstinence, defined as cocaine-negative urine drug screens. In addition to CM, participants were randomized to receive one of two evidence-based therapies (i.e., drug counseling, acceptance and commitment therapy (ACT)). No significant differences were noted between the two therapy groups in the current study sample, and results from the two groups were therefore combined. Phase 2 involved 8 weeks of continued treatment that was augmented with pharmacotherapy (modafinil or placebo) for CM non-responders (Schmitz et al., 2018). The current study focuses on Phase 1 only.

Participants were treatment-seeking individuals, 18 to 60 years old, who met current DSM-5 criteria for CUD of at least moderate severity (≥4 symptoms). Eligible participants submitted at least one positive urine toxicology screen for the cocaine metabolite, benzoylecgonine (BE ≥ 150 ng/ml) during intake to ensure enrollment of individuals actively using cocaine. Participants meeting moderate or severe diagnostic criteria for SUDs other than cocaine, marijuana, or nicotine were excluded. Severe alcohol use disorder was exclusionary. Other exclusion criteria included being pregnant, breast-feeding, or having a significant and unstable medical/psychiatric disorder or taking medications contraindicated for modafinil pharmacotherapy. The current study was approved by the University of Texas Health Science Center at Houston Committee for the Protection of Human Subjects (IRB) and conducted in accord with the Declaration of Helsinki (HSC-MS-15-0595 “Developing Adaptive Interventions for Cocaine Cessation and Relapse Prevention”). All participants provided written informed consent.

Materials and Procedure

Cocaine Purchasing Task.

Participants were asked how many rocks of cocaine they would purchase for the day at various prices (i.e., 0, 1, 2, 3, 4, 5, 10, 15, 20, 25, 30, 40, 50, 100, 200, 500, 1000, 2000, 5000, and 10000 dollars). Participants were instructed to assume the following: that their income and savings were what they usually are; the quality of cocaine is the type they usually purchased; there are no other sources of cocaine; any cocaine purchase had to be used within that day; and their craving and desire for cocaine was how they currently felt. The instructions and range of prices for cocaine are similar to that previously reported in the literature (Bruner & Johnson, 2014; Strickland, Bolin, Lile, Rush, & Stoops, 2016; Strickland, Lile, et al., 2016).

Addiction Severity Index-Life (ASI-Lite).

The ASI-Lite (Cacciola, Alterman, McLellan, Lin, & Lynch, 2007), an abbreviated version of the original ASI (McLellan, Luborsky, Woody, & O’Brien, 1980), is a well-established, multi-dimensional, interview-based measure for substance use. The ASI-Lite assesses the respondent’s lifetime and past-month use of several substance classes. The ASI-Lite can be used as a descriptive measure or to determine composite severity scores for drug and alcohol severity. The ASI-Lite also assesses several domains commonly affected by substance use (e.g., employment, legal, psychiatric). In the current study, the ASI-Lite was used to obtain descriptive data about substance use, including number of days (past-month) and years (lifetime) of cocaine use.

Kreek-McHugh-Schluger-Kellogg Scale (KMSK).

The KMSK Scale is a brief screening instrument designed to quantify substance use, as each section assesses frequency amount, and duration of use of a particular substance during the respondent’s most severe use period. Current and past use is assessed as well as mode of use and substance of choice (Kellogg et al., 2003). While administration time of the KMSK is approximately 5 minutes, it is effective in providing rapid dimensional analyses for various substance use exposure (Butelman et al., 2018) The psychometric properties are very good, including concurrent validity as well as sensitivity and specificity for cocaine, opioids, and alcohol use across various populations (e.g., Kellogg et al., 2003; Tang et al., 2011). In the current study, the KSMK was used to derive quantitative data about substance use, including number of years (lifetime) and days (past-month) of cocaine use as well as the “most” money spent on cocaine (lifetime) and the average amount spent on cocaine use in the last 30 days.

Urinalysis.

The integrated E-Z split key cup II (Innovacon Company, San Diego, CA) was used to test for urine cocaine (benzoylecgonine). Per the parent study, the primary outcome for Phase 1 was defined as CM response/non-response. Participants that submitted 6 consecutive (2 weeks) cocaine negative urine samples by week 4 were classified as responders. The two week criteria was chosen as the parent trial required a binary outcome (i.e., treatment responder, non-responder) as part of the adaptive design (Schmitz et al., 2014). Similar definitions have been used in other cocaine trials involving achievement of abstinence early in treatment (Bisaga et al., 2010, 2005, 2006). Those not meeting response criteria were classified as non-responders.

Data Analytic Strategy

All demand curves were fit in GraphPad Prism 6.0f (GraphPad Software Inc.; La Jolla, CA). All statistical analyses were performed using the R statistical computing environment (R Core Team, 2018). Individual participant cocaine demand data were initially assessed for systematicity (Bruner & Johnson, 2014). Demand functions were identified as nonsystematic if 1) units of drug purchases at a given price were at least 20% greater than at the preceding price, or 2) units of drug purchased at the final price were not less than the first price by at least 10%. Note that an exception to the second rule was made in the case of data in which participants reported 0 consumption at all prices of cocaine, even when cocaine was free (n = 5). While it is customary to exclude these data in studies assessing goodness of fit (e.g., Koffarnus et al., 2015; Strickland, Lile, et al., 2016), inclusion of these data is appropriate and potentially informative in the current case as data are being analyzed in relation to clinical outcomes. Of 60 complete observations to date, 2 participants demonstrated non-systematic responding for demand characteristics, leaving a primary sample size of N = 58. Demand data were fit to Equation 1 including zero values as replacing zeros in the exponentiated model is not necessary. The value of k was set to 4 based on the observed range of consumption values. A consistent k value was used for all analyses to allow direct comparisons of Q₀ and α values. The present analysis explored two demand curve parameters: demand intensity (Q₀), and elasticity (α). For the 5 participants presenting 0 consumption across all prices of cocaine, these values were retained for the analysis of Q₀ (rationale described below), but excluded in analyses of α.

Potential confounding variables were considered using established criteria (Assmann, Pocock, Enos, & Kasten, 2000; Pocock, Assmann, Enos, & Kasten, 2002). Any potential confounding variable (i.e., baseline demographic and drug use characteristics) that demonstrated a relationship with both the predictor and the outcome under consideration was included as a covariate where possible (i.e., parametric models).

Fully exploring the relationship between CM treatment response and demand curve parameters presented two noteworthy analytic challenges. First, there were 6 relatively extreme responses: as noted above, 5 participants (ostensibly treatment-seeking) provided a true zero response for free consumption and 1 participant provided an extreme positive true response ($1000). In the present analysis, these values were considered real values, as they were properly systematic (part of a monotonically increasing response), measured and recorded without error, and represented theoretically relevant levels of responding (i.e., even unrealistic or hyperbolic responding provides information about a participant’s drug demand). Second, both parameters exhibited strong positive skew.

To address these challenges, demand curve parameters were each modeled as a function of CM treatment outcomes (responder vs. non-responder) using a series of statistical modeling techniques. First, the non-parametric exact Wilcoxon-Mann-Whitney test (WMW; from the R package coin version 1.2-2; Hothorn, Hornik, Van De Wiel, & Zeileis, 2006) was used to examine differences in demand curve parameters between CM responders and non-responders, even in the presence of tied values. The WMW is agnostic of distribution assumptions but does not allow the inclusion of co-variables.

Demand curve parameter differences were then examined via parametric tests to improve precision in estimation via inclusion of information regarding outcome distributions and to statistically control for potential confounding variables (described in the Results). Multiple linear regression was used to model demand curve parameters as a function of CM response with covariates. Modeling these parameters as outcomes in their raw, skewed metric violated the normality of residuals assumption; therefore, a log transformation (ln(x)) was applied to α while a log + constant transformation (ln(x + c)) was applied to Q₀ to countenance zeroes. Each transformed demand curve parameter was then modeled as a function of CM group while allowing for covariate adjustment. The value C = 1 was chosen as the most defensible option for the constant in this transformation due to its optimal theoretical properties (the transformation of zeroes in the original metric, ln(0 + 1) = 0, are placed in an equally interpretable metric after transformation). This theory-driven choice for C was essential here, as alternative constant choices demonstrated volatility in resulting inferences (smaller/larger values of C provided different standard errors). Notably, this approach is similar to previous efforts in the field, including Strickland et al. (2017), whereby the choice of C was made to establish a minimum positive value equal to 1 (thus also establishing log(x + C) = 0). Another example of a transformation approach was used by Bruner and Johnson (2014), who applied the square root transformation. While this transformation did not yield normality in the present data, it is another excellent choice in that it can handle positive data and zeroes. Each of these transformations follows from the Box-Cox and Yeo-Johnson general power transformation equations (for more detail, see Kuhn & Johnson, 2013).

Quantile regression was then used as an alternate option for modeling a range of percentiles along the distribution of Q₀ as a function of CM treatment response without the volatility of the choice of constant in log transformation (while also allowing covariates and requiring no distributional assumptions). This analysis provided an additional level of inference regarding the relationship between the variables of interest: it allows the inspection of parameter effects across specific locations of an outcome while also resolving the problems of the linear regression with only a minimal increase to interpretation complexity (i.e., evaluation of a range of percentiles of each outcome measure). Previous work has demonstrated the utility of this technique for exploration (particularly in skewed data): examples include investigations of the relationship between mindfulness and depression (Radford et al., 2014), predictors of duration of untreated psychosis (Guloksuz et al., 2016), disability and mental disorders (Cheng et al., 2012), and predictors of third-hand smoke in a neonatal intensive care unit (Northrup et al., In Press). Quantile regression was implemented via the R package quantreg version 5.38 (Koenker, 2018).

The three statistical techniques described above provide slightly different yet complementary levels of information regarding the relationship between demand curve parameters and CM treatment response. Although these parametric versions of these models establish baseline demand as a criterion and CM response as a predictor, it is essential to note that the mathematics of these models are agnostic to the causal direction, and flipping the direction of effects in this manner can lead to difficulty in interpretation. To circumvent this issue, alternative statistical modeling techniques were considered; however, these were ultimately deemed inappropriate or suboptimal for the present research, included the following: Student’s or Welch’s t-test (inappropriate due to non-normally distributed data; cannot include covariates), logistic regression (suboptimal due to problematic separation among responders and non-responders – responders were largely clustered around low demand values, and non-responders clustered around high demand values), gamma regression (no zeroes permitted), and hurdle lognormal or gamma generalized linear modeling (GLM; too few zeroes to appropriately model the initial 0 vs 1+ binomial model).

Sensitivity analyses examined each of the three statistical techniques with regard to the one extreme baseline demand value (z-score > 3.0). Removing this extreme value from analyses resulted in an identical pattern of inferences, and as such the value was included in all analyses given its inherent theoretical value as described above.

Results

Sample Characteristics

Participants in the present sample (N = 58) were mostly male (83%), non-Hispanic (88%), and African-American (71%) with mean age of 50.4 and 12.7 years of education. Table 1 provides an overview of descriptive statistics by CM treatment response groups (responder vs. non-responders) for all socio-demographic characteristics, demand curve parameters, cocaine use characteristics, and other drug use, including significance tests for differences across groups (chi-square or exact Wilcoxon-Mann-Whitney tests where appropriate). Compared to non-responders, responders had more days abstinent during CM treatment, were more likely to have a cocaine-negative sample at intake, and reported less severe scores on lifetime metrics of cocaine use. Subsequent testing revealed no relationships between these variables and Q₀ or α, and therefore did not meet criteria for inclusion as confounding variables as described in the data analytic strategy (Assmann et al., 2000; Pocock et al., 2002); in essence, including such non-confounding variables in the parametric models below would obfuscate the relationships of interest between demand measures and CM response.

Table 1.

Summary of participant socio-demographic and drug-use characteristics by CM treatment response group.

Variable	Responders (n = 15) N (%) or M (SD)	Non-Responders (n = 43) N (%) or M (SD)	Group Difference
Socio-Demographic Characteristics
Sex			χ2 < 0.00, p > 0.999
Female	3 (20%)	7 (16.3%)
Male	12 (80%)	36 (83.7%)
Race			χ2 = 3.16, p = 0.367
African American	13 (86.7%)	28 (65.1%)
Asian	0 (0.0%)	1 (2.3%)
White	2 (13.3%)	9 (20.9%)
Unknown/Other	0 (0.0%)	5 (11.6%)
Ethnicity			χ2 = 0.08, p = 0.775
Hispanic	1 (6.7%)	6 (14.0%)
Non-Hispanic	14 (93.3%)	37 (86.0%)
# Days Abstinent in Study	10.13 (1.8)	1.3 (1.8)	Z = 5.8, p < 0.001
Age	48.47 (9.2)	51 (7.6)	Z = −0.9, p = 0.404
Education	12.93 (1.8)	12.55 (1.4)	Z = 1.1, p = 0.304
Demand Curve Parameters
Q0	13.62 (16)	47.19 (152.8)	Z = −1.9, p = 0.065
α	0.003 (0.01)	0.0017 (0.01)	Z = −0.3, p = 0.804
Cocaine Use Characteristics
SCID - Number of Symptoms	7.4 (2.2)	6.86 (2)	Z = 0.8, p = 0.376
SCID Rating			χ2 < 0.00, p > 0.999
Moderate	4 (26.7%)	12 (27.9%)
Severe	11 (73.3%)	31 (72.1%)
ASI - Years Used (Lifetime)	11.07 (6.6)	17.16 (9.1)	Z = −2.3, p = 0.020
AS I - Days Used (Past 30)	14.27 (9.5)	17.28 (9.6)	Z = −1.2, p = 0.243
KMSK
Lifetime Score	13.13 (2.2)	14.55 (1.8)	Z = −2.4, p = 0.016
Last 30 Day Score	9.13 (1.9)	9.48 (2.1)	Z = −0.9, p = 0.384
Most Spent Lifetime	101.6 (58.7)	236.05 (278.6)	Z = −2.3, p = 0.020
Average Spent Last 30 Days	59.67 (48.8)	76.84 (65.3)	Z = −0.8, p = 0.424
Cocaine Route of Administration			χ2 = 0.14, p = 0.708
Nasal	3 (20%)	5 (11.6%)
Smoking	12 (80%)	38 (88.4%)
Day 1 Status			χ2 = 12.7, p < 0.001
Negative	8 (53.3%)	3 (7.0%)
Positive	7 (46.7%)	40 (93.0%)
Other Drug Use
# Cigarettes/Day	9.88 (8.7)	12.26 (9.6)	Z = −0.7, p = 0.471
# Drinks/Week	2.53 (2.4)	1.81 (2.1)	Z = 1.0, p = 0.325
Cigarette Smoker			χ2 = 0.01, p = 0.933
No	3 (20%)	11 (25.6%)
Yes	12 (80%)	32 (74.4%)
Alcohol Drinker			χ2 = 0.54, p = 0.462
No	4 (26.7%)	18 (41.9%)
Yes	11 (73.3%)	25 (58.1%)

Demand Characteristics, Demographics, & Drug Use

Equation 1 provided an excellent fit to individual demand data (mean R² [range] = 0.94 [0.71 − 1.00], not including data from 5 participants with 0 consumption at all prices in which Equation 1 cannot conform to this response pattern. A Pearson product-moment correlation coefficient was computed to assess the relationship between the observed (directly calculated from observed data points) and derived (Equation 1) values for Q₀ and Omax. Strong positive correlations were observed for both Q₀(r = 1.00, n = 53, p < 0.0001) and Omax (r = 0,94, n = 53, p < 0.0001), providing further support that Equation 1 provided an excellent fit to the demand data.

Collapsing across all participants regardless of group, Spearman’s rho rank-order correlation was used to examine relationships between drug demand characteristics (Q₀ and α) and self-reported measures of cocaine use (Table 2). Q₀ was negatively related to α (−0.530, p < 0.001). Higher Q₀ and lower α values were both significantly associated with measures of recent (last 30 days) cocaine use as measured by the KMSK and a single item assessing average amount of money spent on cocaine, although not self-reported last 30 days of cocaine use on the ASI-Lite. Neither Q₀ nor α values were significantly associated with lifetime measures of cocaine use.

Table 2.

Associations among drug demand characteristics (Q₀ and α) and self-reported measures of cocaine use. Self-report measures include ASI-Lite measures of lifetimes years use and use in last 30 days; KMSK lifetime cocaine use total score; KMSK single item measure of most money spent on cocaine in lifetime; KMSK last 30 day cocaine use total score; and KMSK single item measure average spent on cocaine in past 30 days. Computed correlations used Spearman-method with pairwise-deletion.

	Q0	α	Years Use	Last 30	KMSK Life	Most Spent Life	KMSK 30
α	0.530***
Years Use	−0.06	−0.118
Last 30	−0.086	−0.091	0.141
KMSK Life	0.093	−0.105	0.379**	0.158
Most Spent Life	0.193	0.026	0.235	0.03	0.752***
KMSK 30	0.280*	−0.383**	0.075	0.251	0.308*	0.258
Average Spent 30	0.296*	−0.347*	0.01	−0.096	0.289*	0.407**	0.734***

Significant correlations are in bold. Note that asterisks indicate the following:

^*= p < 0.05;

^**= p < 0.01;

^***= p < 0.001.

Demand Intensity and CM Response – Non-Parametric Testing

The non-parametric exact WMW test, which is agnostic of distributional assumptions, did not find evidence for group differences between CM treatment responders and non-responders on Q₀ (Z = −1.9, p = 0.065).

Demand Intensity and CM Response – Linear Regression

Linear regression on log-transformed values, however, supported the effect of CM treatment response group such that non-responders demonstrated 88.5% higher Q0 (p = 0.025). In other words, higher demand for cocaine was related to worse response to CM treatment as measure by cocaine positive urine samples.

Demand Intensity and CM Response – Quantile Regression

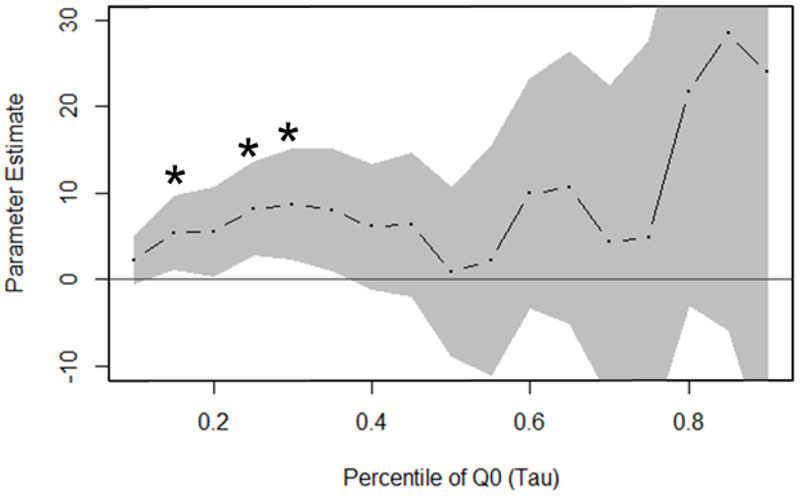
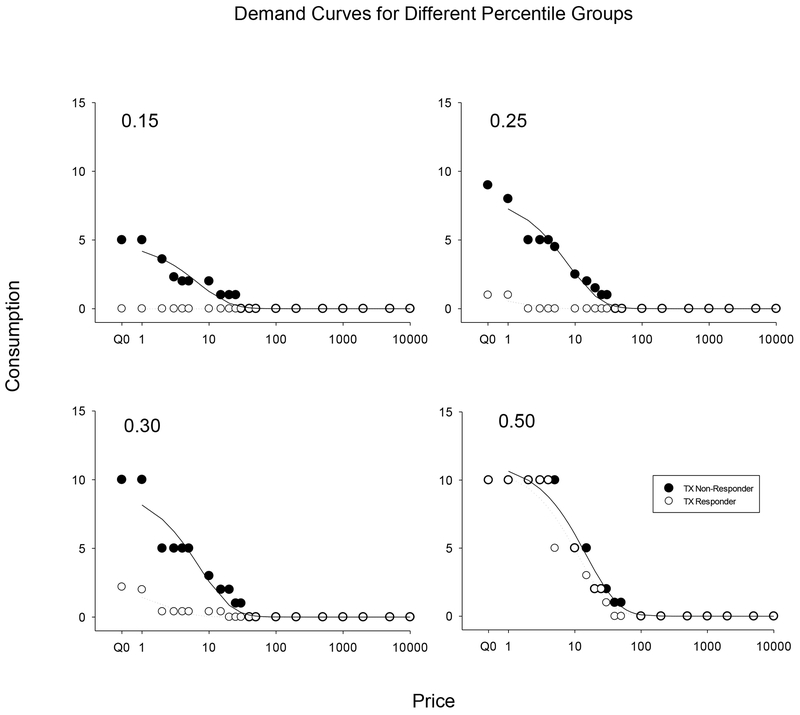
Quantile regression examined the relationship between CM treatment response and demand intensity across a range of Q₀ percentiles (Figure 1) for the entire distribution from the 10th to 90th (by 5), finding statistically reliable effects of being a CM treatment non-responder (relative to responder) at three of the lower tested percentiles (b = 5.38, p = 0.039 @ tau = 0.15; b = 8.17, p = 0.015 @ tau = 0.25; b = 8.66, p = 0.029 @ tau = 0.30), which are readily discernable where the confidence bands do not cross the x-axis at y = 0. Quantile regression also suggested a potential effect of CM response at higher percentiles; however, these analyses demonstrated unreliable estimates and higher standard errors where data was increasingly sparse as graphically illustrated by wider confidence bands (tau > 0.4). These results suggest that the difference between the responder and non-responder groups are driven by lower Q₀ values. Parameter estimates across the range of quantile regression models, provided in Table 2, are measured in units of the raw metric of Q₀ and may be interpreted in the same manner as simple regression coefficients (e.g., at the first quartile [tau = 0.25], CM non-responders demonstrated a 8.17 higher demand intensity in the raw units of Q₀ relative to CM responders). Figure 2 illustrates demand curves for responders (open symbols) and non-responders (closed symbols) at the 15^th percentile (top left), 25^th percentile (top right), 30^th percentile (bottom right), and 50^th percentiles. The 50^th percentile is provided as an illustration of how demand data would be presented traditionally and potentially miss significant differences revealed at lower percentiles.

Figure 1.

Graph of CM treatment response group effect (non-responder relative to responder) at measured percentiles of Q₀ with 95% confidence bands. Asterisks highlight percentile values where statistically reliable effects of being a CM treatment non-responder (relative to responder) were found.

Figure 2.

Demand curves fit to various percentiles (i.e., 0.15. 0.25, 0.30, and 0.50) from the cocaine purchasing task for CM treatment responders (open) and non-responders (closed). Note that the x-axis is on a log scale with a break for Q₀, which represents consumption at near 0 price.

Elasticity and CM Response – All Models

None of our three statistical analyses (i.e., non-parametric exact WMW test, linear regression, and quantile regression) found a significant relationship between α and CM treatment response. Note that unlike Q₀ assessments, α assessments did not include data from participants with 0 consumption at all prices as a demand curve could not be fit to those values.

Discussion

The present analysis explored the relationship between behavioral economic measures of demand and CM treatment response. Overall, the main findings of the study are as follows as measured by the Cocaine Purchasing Task: 1) the exponentiated demand curve provided an excellent fit to individual demand data; 2) demand measures (Q₀ and α) were significantly correlated with measures of recent cocaine use (past 30 day); 3) low Q₀ for cocaine at baseline was associated with group differences in CM treatment response; and 4) the behavioral economic measures of Q₀ were related to CM treatment response among individuals with CUD. We discuss these findings in greater depth below.

While a non-parametric test did not find a significant relationship (p = 0.06), a linear parametric model suggested that on average, higher Q₀ was more strongly associated with non-responders than responders. A closer inspection of the effect of CM response group membership along different levels of the demand intensity distribution (via quantile regression) concurred with the linear model that overall, higher Q₀ was found in non-responders. The relationship between Q₀ and CM treatment non-response was most reliable at lower levels of Q₀ and stronger (but unreliable) at higher levels of Q₀. Overall, these findings suggest that the relationship between Q₀ and CM treatment response was driven by lower levels of baseline Q₀, whereby ostensibly treatment-seeking participants reporting zero values for Q₀ were able to achieve abstinence (responder) while those with Q₀ above a certain threshold invariably did not (non-responder). These findings are consistent with previous studies showing baseline measures of demand predicted treatment-related outcomes for alcohol (MacKillop & Murphy, 2007; Murphy et al., 2015) and tobacco (Mackillop et al., 2016). Interestingly, in the tobacco study, baseline indices of demand predicted treatment outcomes only for individuals for whom smoking abstinence was not a target of CM. Note that in the current study, all participants received CM for cocaine abstinence. To our knowledge, this is the first study to demonstrate that baseline demand is associated with cocaine-treatment response and systematically extend the findings of prior demand research to a novel drug class, cocaine.

The current results also complement findings from studies examining the role of another behavioral economic measure, delay discounting, on treatment outcomes. Delay discounting describes how the value of a reward decreases with increasing delay and provides a model of the myopic decision making characteristic of drug use (Bickel, Jarmolowicz, Mueller, Koffarnus, & Gatchalian, 2012). In a seminal study, baseline delay discounting predicted smoking relapse among pregnant women that had quit smoking once they discovered they were pregnant (Yoon et al., 2007). Subsequently, delay discounting was found to predict CM treatment response for CUD when the magnitude of CM was relatively small, but not when CM magnitude was higher (Washio et al., 2011). One interpretation of these findings is that when treatment is relatively weak (e.g., low magnitude CM), individual differences (e.g., delay discounting) are more likely to predict treatment outcomes, whereas more intensive treatments may overshadow individual characteristics. In the current study, Q₀ was significantly associated with a relatively high magnitude CM treatment (J.M. Schmitz et al., 2018). Taken together, these findings highlight the potential utility of behavioral economic measures such as drug demand and delay discounting, particularly in the context of CM treatment. Populations with SUDs exhibit impaired decision making processes exhibiting persistently high valuation and excessive preference for drug rewards, despite long-term negative consequences (Bickel, Jarmolowicz, Mueller, & Gatchalian, 2011; Bickel et al., 2014; Madden & Johson, 2010). Behavioral economic measures have the potential to inform CM treatment in potentially three ways: 1) identify individuals that are at greater risk of relapse and in need of greater support as in the current study, 2) provide guidance on how to adjust CM parameters (e.g., reward magnitude, frequency of reward) as individuals respond to treatment and their behavioral economic measures potentially change; and 3) potentially provide guidance when developing a new CM intervention based on the demand and discounting characteristics of the target population.

These findings also highlight the utility and importance of multiple statistical analytic techniques for exploring demand data. Here, where a routine non-parametric test failed to demonstrate a relationship between predictor and outcome, a linear model that systematically tested incorporated information about the distribution of the response (Q₀) was able to find evidence for a relationship. Quantile regression was able to take the level of inference even further by examining the relationship across the entire range of the response without the need to complicate the interpretation via data transformation. Our preliminary findings suggest that these types of analyses may be particularly useful in contexts where parameter distributions may be highly influenced by relatively extreme responding, as in the case of treatment-seeking participants reporting zero consumption across all prices of drug. While such responding is often excluded when testing fits of different models of demand, these data are clearly relevant and expected in the context of treatment studies. On the other hand, we also observed participants reporting relatively high levels of cocaine consumption, particularly among CM treatment non-responders. Although these data were orderly and clearly reflect the high valence of cocaine, they likely did not mirror true patterns of cocaine consumptions. In order to obtain more representative data, it may be useful to begin the task with a question such as “What is the most cocaine you have used in a 24 hour period?” in order to provide a concrete reference point.

The current study also supports the utility of the relatively new exponentiated hyperbolic model illustrated in Equation 1 (Koffarnus et al., 2015; Strickland, Lile, et al., 2016; Yu et al., 2014). Although the present study did not compare the exponentiated model with Hursh and Silberbergs’ (2008) model, the exponentiated demand model provide and excellent fit with R² values comparable to that presented previously (Strickland, Lile, et al., 2016) and strong correlations between observed and derived values of Q₀ and Omax. Additionally derived values of Q₀ and α were significantly correlated with relatively recent self-report measures of cocaine use as measured by the KMSK (Kellogg et al., 2003). These results are congruent with previous studies that have observed significant associations between cocaine demand and clinically relevant measures of cocaine use such as positive cocaine urines and self-reported cocaine use (Bruner & Johnson, 2014; Petry, 2000, 2001; Petry & Bickel, 1998; Strickland, Lile, et al., 2016).

As this is an ongoing study, a potential limitation is the relatively small sample size. For example, a larger sample size may have revealed significant differences at higher percentile values (Figure 1). Related to the sample size, the relative number of treatment responders was low in the current study (15 of 58, 26%). The current parent study was based on a previous trial by our group that also utilized a 4-week abstinence-induction phase with high magnitude CM (Schmitz et al., 2014) and reported a slightly higher response rate (33%). We expect the differences are due largely to the smallness of the current sample size. Nevertheless, the low response rate reflects the challenge of achieving initial cessation of cocaine use in severe users, as has been noted in the literature (c.f., Moran et al., 2017). Therefore, although the number of treatment responders may be low in the current study, it is comparable to what we have observed previously and may reflect the severity of cocaine use in our population. A second potential limitation inherent in hypothetical purchasing tasks is that participants’ reports may not mirror real word drug consumption, and this is likely true in the current study where individuals reported they would consume fairly high amounts of cocaine. However, a growing body of research has support the utility of hypothetical purchasing tasks with purchasing tasks predicting drug use, cue reactivity, convergence with established clinical assessments, and reliability over time (for a review see Roma et al., 2017). Additionally, the imbalance in CM response group sizes may have affected the precision in the estimation of effects for the smaller group. Finally, we did not assess longitudinal changes in demand measures. However, assessment of changes in cocaine demand over time in relation to treatment status is a future target of interest once the parent study is completed.

In summary, behavioral economic measures such as drug demand obtained from hypothetical purchasing tasks continue to increase the field’s understanding of important mechanisms associated with SUDs. Results from the current study revealed an association between Q₀ and CM treatment response, which may help inform interventions for CUD in the future.

Table 3.

Model estimates of CM treatment response group effect (non-responder relative to responder) on Q_o by percentile.

Tau (Percentile)	Sample Below N (%)	Sample Above N (%)	Parameter Estimate	Standard Error	t	p
0.10	6 (10.3%)	52 (89.7%)	2.24	1.66	1.35	0.183
0.15	9 (15.5%)	49 (84.5%)	5.38	2.55	2.11	0.039
0.20	12 (20.7%)	46 (79.3%)	5.53	3.09	1.79	0.079
0.25	15 (25.9%)	43 (74.1%)	8.17	3.25	2.51	0.015
0.30	18 (31.0%)	40 (69.0%)	8.66	3.86	2.24	0.029
0.35	20 (34.5%)	38 (65.5%)	8.01	4.24	1.89	0.064
0.40	23 (39.7%)	35 (60.3%)	6.08	4.39	1.38	0.172
0.45	26 (44.8%)	32 (55.2%)	6.38	5.02	1.27	0.209
0.50	29 (50.0%)	29 (50.0%)	0.89	5.91	0.15	0.881
0.55	32 (55.2%)	26 (44.8%)	2.19	8.05	0.27	0.787
0.60	35 (60.3%)	23 (39.7%)	9.96	8.00	1.25	0.218
0.65	38 (65.5%)	20 (34.5%)	10.61	9.53	1.11	0.270
0.70	40 (69.0%)	18 (31.0%)	4.30	10.94	0.39	0.696
0.75	43 (74.1%)	15 (25.9%)	4.88	13.77	0.35	0.724
0.80	46 (79.3%)	12 (20.7%)	21.64	14.90	1.45	0.152
0.85	49 (84.5%)	9 (15.5%)	28.41	20.90	1.36	0.180
0.90	52 (89.7%)	6 (10.3%)	23.94	26.86	0.89	0.377