RAPID AUTOMATED LIVER QUANTITATIVE SUSCEPTIBILITY MAPPING

Abstract

Background:

Accurate measurement of the liver iron concentration (LIC) is needed to guide iron-chelating therapy for patients with transfusional iron overload. In this work, we investigate the feasibility of automated quantitative susceptibility mapping (QSM) to measure the LIC.

Purpose:

To develop a rapid, robust and automated liver QSM for clinical practice.

Study Type:

Prospective

Population:

13 healthy subjects and 22 patients.

Field strength/Sequences

1.5T and 3T / 3D multi-echo gradient-recalled echo (GRE) sequence.

Assessment:

Data were acquired using a 3D GRE sequence with an out-of-phase echo spacing with respect to each other. All odd echoes that were in-phase (IP) were used to initialize the fat-water separation and field estimation (T2*-IDEAL) before performing QSM. Liver QSM was generated through an automated pipeline without manual intervention. This IP echo-based initialization method was compared with an existing graph cuts initialization method (SPURS) in healthy subjects (n=5). Reproducibility was assessed over 4 scanners at 2 field strengths from 2 manufacturers using healthy subjects (n=8). Clinical feasibility was evaluated in patients (n=22).

Statistical Tests:

IP and SPURS initialization methods in both healthy subjects and patients were compared using paired t-test and linear regression analysis to assess processing time and ROI measurements. Reproducibility of QSM, R2*, and proton density fat fraction (PDFF) among the four different scanners was assessed using linear regression, Bland-Altman analysis, and the intraclass correlation coefficient (ICC).

Results:

Liver QSM using the IP method was found to be approximately 5.5 times faster than SPURS (P< 0.05) in initializing T2*-IDEAL with similar outputs. Liver QSM using the IP method were reproducibly generated in all four scanners (average coefficient of determination 0.95, average slope 0.90, average bias 0.002 ppm, 95% limits of agreement between −0.06 to 0.07 ppm, ICC 0.97).

Conclusion:

Use of IP echo-based initialization, enables robust water/fat separation and field estimation for automated, rapid and reproducible liver QSM for clinical applications.

INTRODUCTION

Quantitative Susceptibility Mapping (QSM) (1) is an emerging noninvasive MRI method to quantify iron, calcium and other susceptibility sources for clinical purposes (2). In the liver, QSM promises to minimize the effects of fibrosis and other cellular pathology that interfere with R2* based quantification of liver iron concentration (3), therefore enabling accurate noninvasive monitoring of liver iron to guide iron-chelating therapy for patients with transfusional iron overload (4).

A major challenge in liver QSM is to solve the water-fat separation problem by T2* iterative decomposition of water and fat with echo asymmetry and least squares estimation (IDEAL) (5), a nonconvex problem with solutions that are highly dependent on initialization. The graph cuts exact solution of the simultaneous phase unwrapping and removal of chemical shift (SPURS) problem under the assumption of no water-fat overlap has been found to provide a good initialization for robust liver QSM (6). Nonetheless, the graph cuts procedure is computationally expensive and leads to a processing time on the order of an hour, which is not feasible for routine clinical practice. We propose to use in-phase echoes for rapid initialization of the T2*-IDEAL problem (7,8), and assess the reproducibility and clinical feasibility of liver QSM. The objectives of this study are (i) to implement automated QSM in the liver, (ii) to assess reproducibility of liver QSM at different field strengths, with different manufacturers and models of scanners and (iii) to evaluate the feasibility of performing QSM within the work flow of routine clinical practice.

THEORY

In-phase (IP) echo-based initialization for T2*-IDEAL

The T2*-IDEAL problem of water-fat separation and field estimation is a nonconvex optimization problem of modeling the complex gradient-recalled echo (GRE) signal (S) in terms of fat content (F), water content (W), susceptibility induced field (f) and $R_2^{*}$ decay per voxel (5):

$$E\left(W,F,f,R_2^{*}\right)={\mathit{\text{argmin}}}_{W,F,f,R_2^{*}}{{\sum }_{j=1}^N\Vert S\left(t_j\right)-e^{-R_2^{*}{t}_j}{e}^{-i2\pi f{t}_j}\left(W+F{e}^{-i2\pi {\nu }_F{t}_j}\right)\Vert }_2^2,$$ [1]

where N refers to the number of echoes, t_j is the jth echo time, and v_F is the fat chemical shift in a single-peak model. Proper initialization of the unknowns in Eq.1 is critical for convergence to a biophysically meaningful solution (9). The field f can be initialized using a graph cuts solution to the simultaneous phase unwrapping with removal of chemical shift (SPURS) under the simplified condition of no fat-water overlap to reduce errors of fat/water swaps (6).

Following this approach of obtaining initialization values from simplified conditions, we propose to acquire data using an echo spacing for which water and fat are 180 degrees out of phase (ΔTE= 2.3 msec at 1.5T and 1.15 msec at 3T). Consequently, the odd echoes that have water and fat in phase (IP) with respect to the first echo are used to estimate an initial guess for the field f_IP (10):

$$E\left(f_{IP}\right)={\text{argmin}}_{f_{IP}}{\sum }_{j odd}{\Vert S\left(t_j\right)-\left|S\left(t_j\right)\right|e^{-i2\pi f_{IP}{t}_j}\Vert }_2^2.$$ [2]

Note that this minimization requires both temporal and spatial unwrapping of signal phase for field estimation as commonly practiced in QSM (10). Then the magnitudes of these IP echoes are used to initialize $R_2^{*}$:

$$E\left(a,R_{2IP}^{*}\right)={\text{argmin}}_{a,R_{2IP}^{*}}{\sum }_{j odd}{\Vert \left|S\left(t_j\right)\right|-a\cdot e^{-R_{2IP}^{*}{t}_j}\Vert }_2^2$$ [3]

Here Eq.3 is a standard exponential decay fitting that can be solved using the Marquardt-Levenberg procedure or a rapid robust auto-regression linear operation (11). Finally, the results from Eqs.2&3 are used to reduce Eq.1 into a linear problem (f = f_IP, $R_2^{*}=R_{2IP}^{*}$) over all echoes to calculate initial values for fat and water contents F₀, W₀.

Using a quasi-Newton approach initialized by these values F₀, W₀, f_IP, $R_{2IP}^{*}$, the T2*-IDEAL problem Eq.1 is solved iteratively with input of the complex data of all echoes (12), resulting in maps for fat content F, water content W, field f and R2*. The proton density fat fraction (PDFF) is calculated as: PDFF = |F|/(|F| + |W|).

Quantitative susceptibility mapping (QSM)

QSM is reconstructed from the field following the Bayesian inference (1). The noise is modeled as Gaussian (13). For generating absolute susceptibility value needed in cross-scanner studies, a zero reference is needed and blood in abdominal aorta is chosen for liver QSM (14):

$$\chi ={\mathit{\text{argmin}}}_{\chi }\frac{1}{2}{\Vert w\left(e^{-if}-e^{-i(d*\chi )}\right)\Vert }_2^2+{\lambda }_1{\Vert M_G\nabla \chi \Vert }_1+{\lambda }_2{\Vert M_{\mathit{\text{aorta}}}\left(\chi -{\overline{\chi }}_{\mathit{\text{aorta}}}\right)\Vert }_2^2$$ [4]

where χ denotes susceptibility, w the noise weighting, f the local field after background field removal, d the dipole kernel, M_G the binary edge mask derived from the magnitude image, λ₁,λ₂ regularization parameters, and M_aorta the binary mask of abdominal aorta. The background field is removed using the projection onto dipole fields technique (15).

M_aorta is generated automatically from the magnitude images. In each slice, the initial mask is generated by calculating the center and radius of the aorta through Hough transform using edge information along with the geometry and location of the aorta. The output is used as seed points to a region growing algorithm to generate the final mask. Then Eq.4 is solved iteratively using the quasi-Newton approach (12).

MATERIALS AND METHODS

Data Acquisition

Liver QSM data were acquired within a breath-hold using a multi-echo gradient echo sequence. The acquisition and reconstruction were initially developed and tested on healthy volunteers (n=5). The reproducibility of liver QSM was then evaluated across multiple scanners from 2 manufacturers at 2 field strengths using healthy volunteers (n=8). To assess clinical feasibility, the liver QSM was performed on patients (n=22), including thalassemia major (n=14), polycystic kidney disease (n=7), and suspected iron overload (n=1). Some of the thalassemia patients were undergoing iron-chelation therapy and were expected to have low to moderate liver iron content. While no iron overload was expected in polycystic kidney disease patients, they were recruited to serve as controls in patient study. The study was approved by the Institutional Review Board and written informed consent was obtained from each participant.

The liver QSM acquisition protocol development was performed on a 3T scanner (Magnetom Skyra, Siemens Healthcare, Erlangen, Germany) with an 18-channel body coil. A multi-echo 3D GRE sequence was used with the following imaging parameters: number of echoes = 6, bipolar readout gradients, flip angle = 3°, TE₁ = 1.67 msec, ΔTE = 1.15 msec, TR = 9.5 msec, acquired voxel size = 2.2×1.56×5 mm³, reconstructed voxel size = 0.78×0.78×2.5 mm³, BW = 1500 Hz/pixel, acquisition matrix = 256×179×(28–36), slice and phase Fourier encoding = 7/8, GRAPPA acceleration factor = 2, and acquisition time of 14–19 sec.

The reproducibility test was performed using the following 4 scanners: i) two 1.5T GE scanners (Signa HDxt, GE Healthcare, Waukesha, WI) with 8-channel cardiac coils (S1 and S2), and ii) a 1.5T Siemens scanner (Magnetom Aera, Siemens Healthcare, Erlangen, Germany) with an 18-channel body coil (S3) and iii) the 3T Siemens scanner (S4) described above. The GRE imaging parameters on S4 were the same as those described earlier. The GRE imaging parameters on the S1 and S2 were: number of echoes = 6, unipolar readout gradients, flip angle = 5°, TE₁ = 1.2 msec, ΔTE = 2.3 msec, TR = 14.6 msec, acquired voxel size = 1.56×1.56×5 mm³, BW = 488 Hz/pixel, acquisition matrix = 150×150×(32–36), ASSET acceleration factor = 1.25, and acquisition time of 20–27 sec. The GRE imaging parameters on S3 were: number of echoes = 6, unipolar readout gradients, flip angle = 5°, TE₁ = 1.7 msec, ΔTE = 2.3 msec, TR = 15 msec, acquired voxel size = 2.2×1.56×8 mm³, BW = 1500 Hz/pixel, acquisition matrix = 256×192×(28–36), slice and phase Fourier encoding = 7/8, GRAPPA acceleration factor = 2, and acquisition time of 22 sec.

The patient study was performed on S1 and S2 scanners with imaging parameters as described above. The proposed sequence was added to clinical routine sequences run on patients at these two scanners.

Data Reconstruction

For QSM reconstruction in Eq.4, regularization parameters λ₁ = 0.001 and λ₂ = 0.01 were chosen using a L-curve method (15) and fixed for all cases. For the bipolar data acquired with a 3T scanner, a separate intercept between even and odd echoes due to alternating readout gradients was obtained during the fitting of the field from all echoes (16). Macroscopic field inhomogeneities were corrected (17) in all scans to address the signal dephasing. With the low flip angles prescribed in all acquisitions, T1 weighting was minimized in this study and no correction was performed on water and fat maps (3). The same dataset was used as input to both IP and SPURS algorithms. The susceptibility of aortic blood with an assumed 97% oxygenation level was used for zero referencing, leading to a −0.085 ppm susceptibility relative to water (18). All QSM reconstructions were performed with zero padding before inversion (19) with an output voxel size of 0.78×0.78×2.5 mm³.

A comparison of IP initialization with SPURS initialization was made in 5 healthy subjects in terms of initialization execution time and quantitative values. On output of PDFF, R2* and QSM maps, ROIs on a homogenous region of liver avoiding vessels were drawn for measurements. Paired t-tests and the corresponding p-value and regression analysis and the corresponding coefficient of determination (r²) and slope (k) were calculated in each scanner compare IP and SPURS initialization method.

For reproducibility tests in 8 healthy subjects, an axial slice depicting approximately the same part of the liver was used for ROI analysis, using a large hepatic vein on R2* map as a landmark. ROIs were drawn on the liver avoiding vessels and inhomogeneous regions. ROIs in subcutaneous fat regions were drawn for evaluating water-fat separation performance. PDFF, R2*, and susceptibility values in the liver were calculated across four scanners. To assess reproducibility of the proposed IP initialization method, the intra-class correlation coefficient (ICC) was computed (20). In addition, linear regression and Bland-Altman analysis (obtaing bias b and 95% limits of agreement LoA) were performed each scanner pair using the IP method. To compare IP and SPURS methods, regression and Bland-Altman analysis were performed between the two methods in all subjects across four scanners.

In patients, measurements of initialization execution time, PDFF, R2*, and susceptibility on ROI of a homogenous region of liver avoiding vessels are reported for both IP and SPURS methods. For statistical analysis, paired t-test and linear regression were performed. P-values below 0.05 were considered to indicate statistical significance.

RESULTS

Susceptibility maps were reconstructed successfully in all healthy subjects and in all but 3 patients: one with severe motion artifacts and two others with poor SNR due to a very high liver iron content.

For the method development experiment (healthy subjects, n=5, Table 1 and Fig.S1), ROI analysis of liver indicated good quantitative agreement between both initialization methods, but the IP initialization time is about 6 times shorter than the SPURS initialization time. Corresponding maps (Fig.S1) illustrates similar water, fat, field, and $R_2^{*}$ maps between the IP (Fig.S1a) and SPURS (Fig.S1b) methods of initialization.

Table 1.

Comparison of IP and SPURS initialization methods on a single scanner over 5 healthy subjects. Initialization time and ROI values for liver proton density fat fraction (PDFF), R2* and susceptibility are tabulated. p-value for the paired t-test and coefficient of determination (r²), and slope (k) for linear regression are tabulated for ROI data.

Healthy subject #	Initialization (min)		PDFF (%)		R2* (Hz)		QSM (ppm)
	IP	SPURS	IP	SPURS	IP	SPURS	IP	SPURS
1	7	76	2.5	2.5	31	31	−0.11	−0.14
2	8	26	2.1	2.1	37	37	0.004	0.01
3	7	31	2	2	30	30	0.06	0.09
4	9	60	4.4	4.4	31	31	−0.005	−.005
5	10	54	2.3	2.3	44	44	0.12	0.11
p-value			1		1		0.98
r2			1		1		0.96
K			1		1		1.14

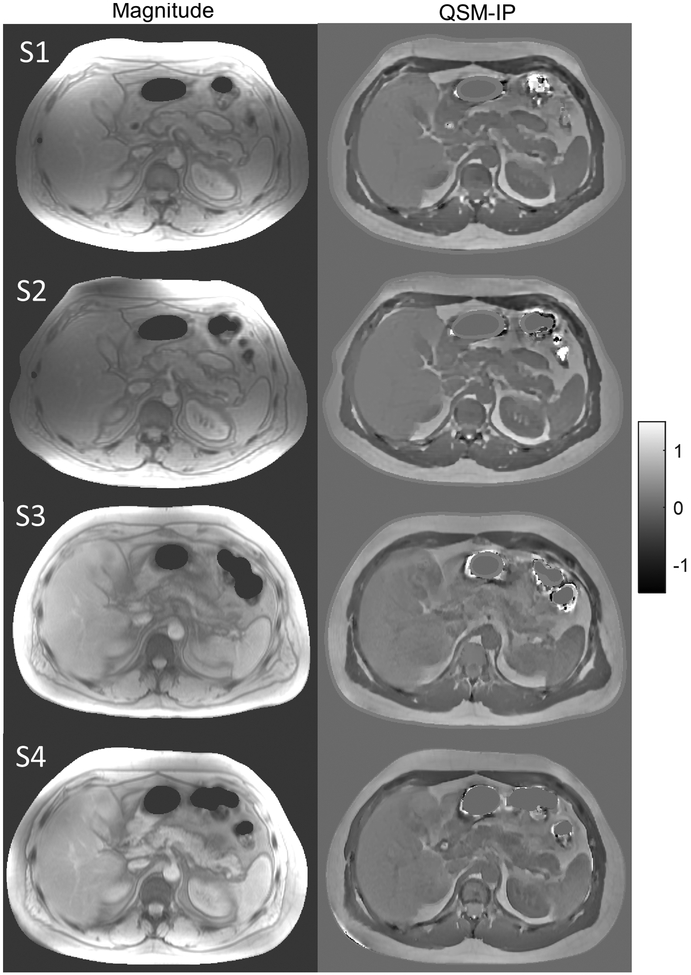
For the reproducibility experiment (healthy subject, n=8, Table 2, Fig.1, Table S1, Figs. S2 and S3), example magnitude and susceptibility maps of the same liver structure using the IP method are illustrated in Figure 1 in a healthy subject scanned at four scanners. QSM images show similar contrast and variation across the 4 scanners. The IP method PDFF maps (Fig.S2) show similar contrast across 4 scanners in Fig.S2. $R_2^{*}$ maps are similar in 1.5T scanners (S1, S2, S3) but $R_2^{*}$ values were higher at 3T (S4), as expected. In Table 2, good agreement was found among PDFF and QSM maps from all 4 scanners with 2 field strengths using the IP method. R2* agreement between scanners of the same field strength was found to agree as well. Note that the lower ICC in liver PDFF compared to subcutaneous region is due to much lower PDFF in the liver (Figs. S3c & S3d). The R2* ICC in pairs involving the 3T scanner are lower due to dependence of R2* on the field strength. Similar agreement was observed using linear regression and Bland-Altman analysis (Table S1). There is very good agreement between both IP and SPURS methods (Fig.S3) and all scanners. Note that SPURS initialization and corresponding susceptibility reconstruction failed over a liver region even after manual intervention in one scan, and required manual intervention for successful field map generation and water/fat separation in 3 more subjects, while the IP method automatically generated all the maps successfully in all subjects.

Table 2:

IP initialization reproducibility among 4 scanners: S1, S2, and S3 at1.5T and S4 at 3T. For ROI measurements of liver proton density fat fraction (PDFF), subcutaneous PDFF, R2*, and susceptibility, intraclass correlation coefficient (ICC) shows that QSM has the best agreement between scanner pairs and among all scanners in 8 healthy subjects.

Scanner pairs#	ICC
	PDFF (Liver)	PDFF (Subcutaneous)	R2*	QSM
S1 and S2	0.93	0.87	0.98	0.99
S1 and S3	0.80	0.84	0.96	0.97
S1 and S4	0.6	0.76	0.55	0.98
S2 and S3	0.79	0.90	0.97	0.95
S2 and S4	0.59	0.93	0.48	0.96
S3 and S4	0.40	0.79	0.54	0.96
All Scanners	0.7	0.85	0.66	0.97

Figure 1.

Magnitude and susceptibility maps using IP method in a healthy subject across 4 scanners including S1, S2, S3, S4.

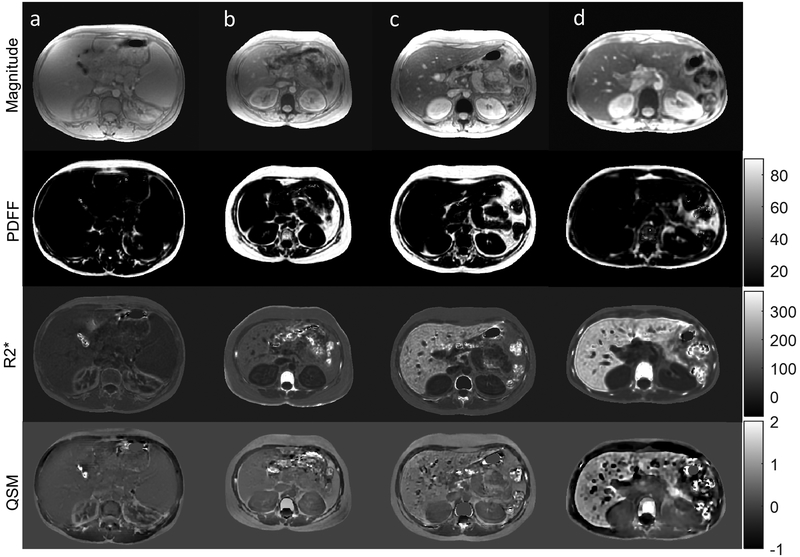
For the clinical feasibility experiment (patients, n=19, Table 3, Fig. 2), Figure 2 shows the magnitude image, PDFF map, $R_2^{*}$ map, and QSM in 4 thalassemia major patients using the IP method. Subjects had iron levels from low (Fig.2a) to high (Fig.2d). Water-fat separation was successful with low fat for these livers (PDFF in the second row). The R2* (third row) and QSM (fourth row) in liver ranged between 34 Hz to 240 Hz and 0.03 ppm to 0.43 ppm respectively, suggesting normal or low to moderate iron overload in these patients. The ROI analysis in all 19 patients is shown in Table 3. For the IP method, PDFF ranged from 1% to 8.6%, R2* ranged from 25 Hz to 388 Hz, and susceptibility from 0.04 ppm to 0.57 ppm. Good agreement between both IP and SPURS methods with a significant reduction (5.3 times) in computation time in the former. Note that SPURS initialization required manual intervention for successful field map generation and water/fat separation in 2 patients, while the IP method automatically generated all the maps successfully in all subjects.

Table 3.

Comparison of IP and SPURS initialization methods on a single scanner over 19 patients. Initialization time and ROI values for liver proton density fat fraction (PDFF), R2* and susceptibility are tabulated. p-value for the paired t-test and coefficient of determination (r²), and slope (k) for linear regression are tabulated for ROI data.

Patient subject #	Initialization (min)		PDFF (%)		R2* (Hz)		QSM (ppm)
	IP	SPURS	IP	SPURS	IP	SPURS	IP	SPURS
1	7	60	2.8	2.8	171	171	0.37	0.39
2	7	23	2.3	2.3	245	245	0.44	0.44
3	7	19	2.4	2.4	80	80	0.25	0.25
4	7	25	1.5	1.5	45	45	0.09	0.09
5	7	24	1.9	1.9	33	33	0.10	0.10
6	8	25	2.5	2.5	37	37	0.10	0.10
7	8	35	8.6	8.4	388	401	0.57	0.59
8	7	31	1.7	1.7	28	28	0.07	0.07
9	7	43	1.6	1.6	140	140	0.32	0.35
10	6	32	1.6	1.6	38	38	0.14	0.14
11	11	76	5.8	5.8	23	23	0.09	0.08
12	7	58	2	2	31	31	0.04	0.04
13	7	72	1.5	1.5	25	25	0.04	0.03
14	8	43	3.2	3.2	27	27	0.04	0.04
15	9	38	1	1	29	29	0.08	0.08
16	7	46	5.8	5.8	225	225	0.39	0.39
17	8	50	1.2	1.2	30	30	0.05	0.05
18	8	31	4.9	4.9	241	241	0.44	0.44
19	7	27	1.9	1.9	66	66	0.16	0.16
p-value			0.99		0.98		0.96
r2			1.00		1.00		1.00
k			0.98		1.02		1.03

Figure 2.

Magnitude, PDFF (%), R2* (Hz), and QSM (ppm) in 4 thalassemia major patients (columns a-d). Liver iron increase (from left to right) is observable in both R2* (Hz) and susceptibility (ppm) maps.

DISCUSSION

Our data demonstrate that automated liver quantitative susceptibility mapping (QSM) is feasible and reproducible across different manufacturers and models of scanners at both 1.5T and 3T. The IP echo-based initialization of the water-fat separation (T2*-IDEAL) problem provides approximately a 5.5-fold improvement in speed compared to the current SPURS initialization over all subjects with no loss of quality. Data acquisition can be performed within a breath-hold using a 3D multi-echo gradient echo (GRE) sequence. We show the proposed method is feasible in patients with low to moderate iron overload in clinical practice.

In general, QSM removes imaging-parameter-dependent blooming artifacts in phase and R2* (qualitative T2* weighted or susceptibility-weighted imaging) for quantitative studies of tissue magnetic susceptibility (21). As expected, QSM has been shown to be superior to R2* in regions near air-tissue interface, such as the midbrain (22,23). For measurement of the liver iron concentration (LIC), a fundamental limitation of the R2* method is that that intravoxel contents other than iron, including fibrosis, steatosis and necroinflammation, also alter relaxation (3). Hepatic fibrosis, highly prevalent in thalassemia major patients (25,26), increases R2* and interferes with accurate measurement of LIC which is challenging for commonly-encountered moderate overload patients (24). Like fibrosis, intravoxel contents including fat also contribute to R2* in a complex nonlinear manner, making it difficult to correct for these interference effects on R2* for accurate LIC estimation from the GRE signal. Using QSM, these intravoxel contents can be compensated according to the linear chemical composition. Moreover, fibrosis commonly encountered in livers of thalassemia major patients may contribute little to magnetic susceptibility (3). For these patients, liver QSM with fat correction promises to substantially improve LIC accuracy (3). Additionally in clinical practice, unlike R2*, susceptibility values can be compared regardless of the field strength (25).

In the absence of cirrhosis, liver tends to have a uniform structure on the mm-imaging scale. This allows volumetric imaging with coarse voxel size (~12mm³) of the whole liver within a breath-hold (~20–30 sec) which fits well in the clinical workflow routine. Use of a zero-reference can help QSM reconstruction accuracy for cross center studies (1,15,26). For zero-reference in this study, we used the prior information that the blood in the aorta is uniform and does not accumulate iron. With similar assumptions, variations within the fat in the abdominal region can be minimized and susceptibility value of 0.7 ppm can be used as a reference (3,26). This requires a fat mask which may be automatically generated from PDFF.

IP initialization improves the initialization speed for T2*-IDEAL by a factor of about 5.5 over all subjects compared to SPURS initiation in MATLAB codes, which may be further reduced to seconds using C code and GPU. This substantial improvement in speed is because Eqs.2&3 in IP avoid the computationally expensive graph cuts in SPURS (6). Another assumption in SPURS is that the fat fraction in a voxel is close to either 0 or 1. This seems to be the situation in the patients studied here. However, when the fat fraction is close to ½, SPURS may not perform well. The IP initialization avoids the SPURS assumption; therefore, IP may be more robust than SPURS in fatty livers and other imaging situations where voxels contain well mixed fat and water.

This study has a number of limitations. The proposed in-phase/out-of-phase acquisition with fixed echo spacing enables a robust method to generate QSM maps. This does introduce constraints on the obtainable readout resolution and/or field of view, which can be addressed by using higher acquisition bandwidth and bipolar readout gradients. Fast signal decay in liver with very high iron content caused severe signal loss at the first echo in 2 cases. This problem may be addressed using a UTE acquisition to allow a significantly shorter first TE (26). The breath-hold acquisition failed in one patient, and navigator gating may be used for free-breathing acquisition (27). No true reference such as biopsy, was available for these subjects to compare the results against a ground truth and a larger cohort of patients is required to further assess feasibility of water/fat separation and successful generation of QSM maps. Adding more scanners including different manufacturers and field strengths will allow a more conclusive, balanced assessment of reproducibility. A single-fat-peak model for water/fat separation was used, and an extension to multi-peak models is straightforward.

In summary, the proposed in-phase echo-based initialization method for water-fat separation is fast and robust. Automated liver QSM is feasible for routine clinical use and reproducible over scanners at various field strengths and for different manufacturers.