The Effect of Phase Cancellation on Estimates of Broadband Ultrasound Attenuation and Backscatter Coefficient in Human Calcaneus In Vitro

Abstract

Broadband Ultrasound Attenuation (BUA) is a clinically-proven indicator of osteoporotic fracture risk. BUA measurements are typically performed in through-transmission with single-element phase sensitive (PS) receivers and therefore can be compromised by phase cancellation artifact. Phase-insensitive (PI) receivers suppress phase cancellation artifact. In order to study the effect of phase cancellation on BUA measurements, through-transmission measurements were performed on 16 human calcaneus samples in vitro using a two-dimensional receiver array that enabled PS and PI BUA estimation. The means ± standard deviations for BUA measurements were 22.1 ± 15.8 dB/MHz (PS) and 17.6 ± 7.2 dB/MHz (PI), suggesting that, on the average, approximately 20% of PS BUA values in vitro can be attributed to phase cancellation artifact. Therefore, although cortical plates are often regarded as the primary source of phase cancellation artifact, the heterogeneity of cancellous bone in the calcaneal interior may also be a significant source. Backscatter coefficient estimates in human calcaneus that are based on PS attenuation compensation overestimate 1) average magnitude of backscatter coefficient at 500 kHz by a factor of about 1.6 ± 0.3 and 2) average exponent (n) of frequency dependence by about 0.34 ± 0.12 (where backscatter coefficient is fit to a power law form proportional to frequency to the nth power).

Introduction

Quantitative Ultrasound (QUS) is a clinically-accepted modality for osteoporotic fracture risk assessment [1, 2]. Broadband Ultrasound Attenuation (BUA) reflects bone mineral density (BMD) [3–15] and mechanical properties [8, 9, 12, 16], both of which are related to fracture risk. Calcaneal BUA has been demonstrated to have a strong connection with osteoporotic fractures in prospective [17–24] and retrospective [25–32] studies. Anisotropy studies suggest that BUA, unlike BMD, is sensitive not only to the quantity of bone intercepting the ultrasound beam but also to the physical arrangement of the bone [33–35]. QUS is cheaper, faster, simpler, and more portable than its x-ray counterparts: dual-energy x-ray absorptiometry (DEXA) and quantitative computed tomography (QCT). Unlike x-ray methods, QUS produces no ionizing radiation. A recently-developed handheld through-transmission calcaneal QUS device appears to represent a significant advance in portability compared with current commercial QUS devices [36]. Despite recent progress in QUS, improvements are needed in order to foster greater clinical acceptance [37].

BUA is usually measured in the calcaneus using two single-element phase-sensitive (PS) broadband transducers in through-transmission geometry. Most studies listed above report that attenuation coefficient exhibits an approximately linear dependence on frequency in the diagnostic frequency range (about 300 – 700 kHz). Two studies have confirmed quasi-linearity up to about 2 MHz [38, 39].

Ultrasonic attenuation measurements can be compromised by phase cancellation [40–45]. Phase cancellation reduces the amplitude of the measured attenuated signal and therefore leads to overestimation of attenuation. Moreover, phase cancellation usually increases with frequency and therefore also tends to lead to overestimation of the slope of attenuation coefficient vs. frequency measurements (which is equivalent to “normalized” BUA or nBUA). Phase cancellation can be suppressed using so-called phase-insensitive (PI) processing [40–43]. PI processing is impossible with single-element PS receivers but possible with arrays (see Methods section).

The first goal of this paper was to investigate the effects of phase cancellation on estimates BUA and nBUA in human calcaneus. Petley et al. reported an average difference between PS BUA and PI BUA of 31.2 dB/MHz (10 human calcanea in vivo) [44]. Strelitzki et al. reported an average difference of 4.4 dB/MHz (10 human calcanea in vitro) [45]. Wear reported an average difference of 14.2 dB/MHz (73 female calcanea in vivo) [46]. The present paper describes another in vitro study on the effect of phase cancellation on BUA measurements in cancellous bone, but with some improvements over the previous study by Strelitzki et al. [45]: First, the array element size was 2 mm instead of 5 mm, resulting in better spatial resolution. Second, the number of receiver elements was 52 instead of 9, resulting in finer sampling.

The second goal of this paper was to investigate the effects of phase cancellation on estimates of backscatter coefficient in human calcaneus. Many studies report estimates of backscatter coefficients that depend on PS estimates of attenuation coefficient for compensation of backscatter measurements [47–55]. Overestimation of attenuation (e.g. due to phase cancellation artifact) leads to overcompensation for the effects of attenuation throughout the scattering volume, and therefore overestimation of backscatter coefficient. The magnitude of this effect is explored in the present paper.

Methods

Bone Samples

16 human calcaneus samples (both genders, ages unknown) were defatted using a trichloro-ethylene solution. All internal and external soft tissues were removed. The lateral cortical layers were sliced off leaving two parallel surfaces with direct access to trabecular bone. The thicknesses of the samples averaged 18 mm. Samples were vacuum degassed underwater in a desiccator. After vacuum, samples were allowed to thermally equilibrate to room temperature prior to ultrasonic interrogation. Ultrasonic measurements were performed in distilled water at room temperature. The relative orientation between the ultrasound beam and the calcanea was the same as with in vivo measurements performed with commercial bone sonometers, in which ultrasound propagates in the mediolateral direction.

Ultrasonic Data Acquisition and Analysis

An Achilles Insight ® (General Electric Lunar Corporation, Madison, WI) clinical bone sonometer was used. This system uses a circular (25.4 mm diameter) broadband piston transducer (center frequency = 500 kHz) for transmission of ultrasound. Radiofrequency (RF) data were acquired using 52 central elements of the Insight’s 590-element 2D receiver array. The central 52 elements were bounded by a 25.4 mm diameter circle that was co-axial with the transmitter. The element spacing was 3.175 mm. The element size was about 2 mm. The beam propagation distance was approximately 10 cm. Data were digitized at 10 MHz. The Achilles Insight displays a real-time attenuation image in order to facilitate accurate positioning of the sample prior to data acquisition.

PS power spectra were obtained by 1) summing 52 time domain RF signals from the central elements of the 2D receiver array, and 2) taking the squared modulus of the Fast Fourier Transform (FFT). PI power spectra were obtained by 1) computing the magnitude of the FFT for each of the 52 time domain RF signals, 2) summing the 52 FFT magnitudes, and 3) squaring.

A calibration spectrum was obtained by performing a measurement with only a water path between the transmitter and receiver. BUA was computed from the slope of a least-squares regression to the logarithm of the frequency-dependent signal loss (difference between calibration and data spectra). The analysis bandwidth was from 400 kHz to 700 kHz (which corresponded to the frequency band of maximum signal-to-noise ratio). Often in biomedical ultrasound, this slope is normalized to the thickness of the sample to yield “attenuation slope” or nBUA (normalized BUA). This is usually not done in clinical bone sonometry, however, since the bone thickness is usually unknown in vivo. (However, recent systems that perform two-sided pulse-echo interrogation have the capability to measure calcaneal thickness in vivo [56, 57]). Thicker bones tend to have less fracture risk so it can be useful for a diagnostic measurement to convey bone thickness information in addition to bone material properties. (Similarly, BMD is an areal rather than a volumetric measurement, measured in g/cm² rather than g/cm³.) Therefore, BUA is generally reported in units of dB/MHz rather than dB/cmMHz. In the present study, both nBUA and BUA were computed. Since the calcaneal thicknesses were fairly constant (18 ± 2 mm), 1) BUA values in dB/MHz were approximately 1.8 times nBUA values in dB/cmMHz, and therefore 2) BUA and nBUA exhibited similar trends.

In order to estimate backscatter coefficient, backscatter measurements must be compensated for the effects of attenuation throughout the scattering volume. Most previous reports of backscatter coefficient measurements in cancellous bone [47–55] use a frequency-dependent attenuation compensation factor presented by O’Donnell and Miller [58].

$$F[\alpha (f),x_0,z]=e^{4\alpha (f)x_0}\frac{4\alpha (f)z}{e^{2\alpha (f)z}-e^{-2\alpha (f)z}}$$

where f is frequency, α is the attenuation coefficient, x₀ is the distance from the transducer to the center of the scattering volume, and z is the length of the scattering volume. (Oelze and O’Brien reported a comprehensive comparison of various frequency-dependent attenuation-compensation functions [59].) The effect of using a PS estimate of α(f) rather than a PI estimate of α(f) to compensate for attenuation has the effect of multiplying the backscatter coefficient estimate by a frequency-dependent attenuation compensation factor ratio,

$$R(f,x_0,z)=\frac{F[{\alpha }_{PS}(f),x_0,z]}{F[{\alpha }_{PI}(f),x_0,z]}.$$

Over the usable bandwidth of a typical transducer, backscatter coefficient measurements from cancellous bone approximately obey a power law [47–55]. If the PS-attenuation-compensation-based and PI-attenuation-compensation-based estimates of backscatter coefficient obey power laws, i.e. η_PS(f) ≈ Af ⁿ and η_PI(f) ≈ Bf ^m, and if R(f, x₀, z) ≈ Cf ^p (over a sufficiently narrow analysis bandwidth), then A = BC and n = m + p. Therefore, the effect of using a PS estimate of α(f) rather than a PI estimate of α(f) to compensate for attenuation is 1) to multiply the midband backscatter coefficient estimate by Cf₀ ^p (where f₀ is the midband frequency), and 2) to elevate the exponent of frequency dependence by p. In order to characterize the effects of using PS attenuation estimates on backscatter coefficient estimates, frequency-dependent attenuation compensation factor ratios were computed for each pair (PS and PI) of attenuation measurements for each bone assuming typical parameters (f₀ = 500 or 800 kHz, x₀ = 8 mm, z = 1 cm). The frequency-dependent functions were averaged (over all 16 bones) and fit to a power law R(f, x₀, z) ≈ Cf ^p.

Results

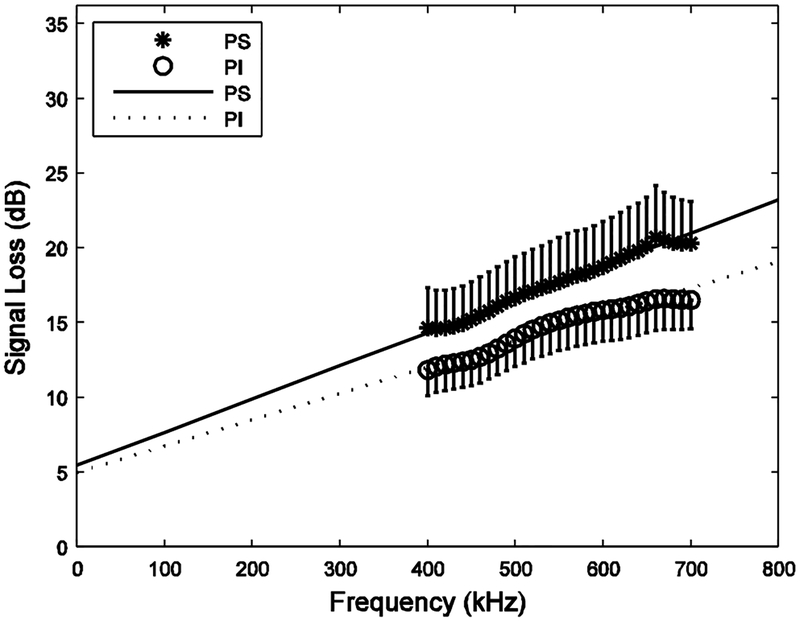
Figure 1 shows PS and PI measurements of signal loss (including reflection losses and attenuation) vs. frequency from the 16 human calcaneus samples. As expected, the PS measurements were higher, due to phase cancellation artifacts. The linear extrapolations to zero frequency for the two processing methods were comparable: 5.4 dB (PS) and 5.0 dB (PI).

1.

Signal loss (including reflection losses and attenuation) versus frequency for the 16 human calcaneus samples for both phase sensitive (PS) and phase insensitive (PI) processing. Least squares linear regression fits are also shown. Error bars denote standard errors.

Figure 2 shows nBUA_PI vs. nBUA_PS for the 16 human calcaneus samples. For low values of attenuation, the two were nearly equal. At higher values of attenuation, PS values tended to be higher. The same trend was reported previously for measurements in vivo [46]. Table I shows means and standard deviations for PS and PI values for nBUA and BUA. The correlation coefficient between nBUA_PI and nBUA_PS was 0.94 (95% confidence interval: 0.83 – 0.98). The least-squares linear fit was nBUA_PI = 0.32 dB/cmMHz + 0.77 * nBUA_PS. BUA exhibited similar trends (see Methods section).

2.

PI nBUA vs. PS nBUA for the 16 human calcaneus samples. (Two pairs of points coincide, giving the appearance of only 14 data points.) A linear fit (solid line) and the 45 degree line of equality (dotted line) are shown.

Table I.

Means and standard deviations for phase sensitive and phase insensitive values for nBUA and BUA.

	nBUA (dB/cmMHz) (attenuation slope)	BUA (dB/MHz)
Phase Sensitive (PS)	12.3 ± 8.8	22.1 ± 15.8
Phase Insensitive (PI)	9.8 ± 7.2	17.6 ± 7.2
Difference	2.5 ± 3.3	4.5 ± 5.9

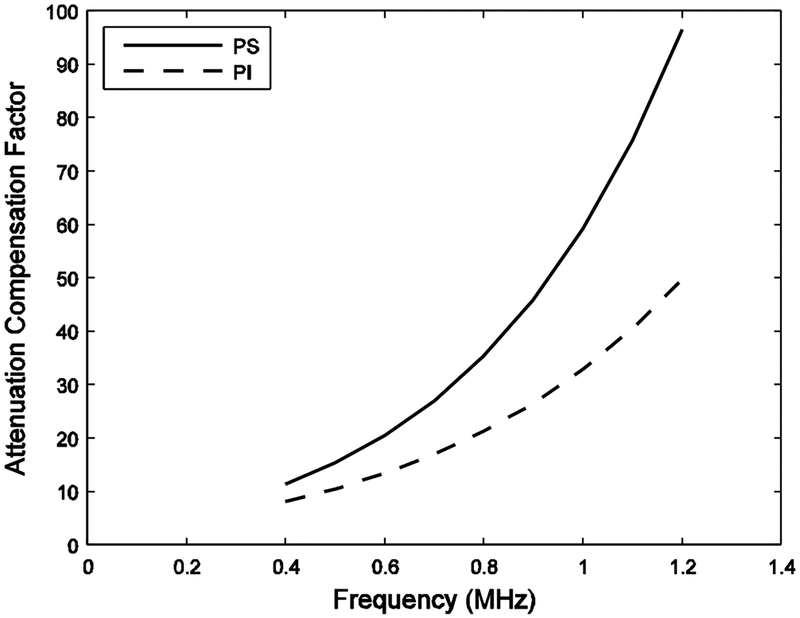
Figure 3 shows PS and PI attenuation compensation factors, F[α(f), x₀, z], for a bone sample. The PS attenuation compensation factor is higher over all frequencies and has a steeper rate of increase with frequency.

3.

PS and PI Attenuation compensation factors for a bone sample.

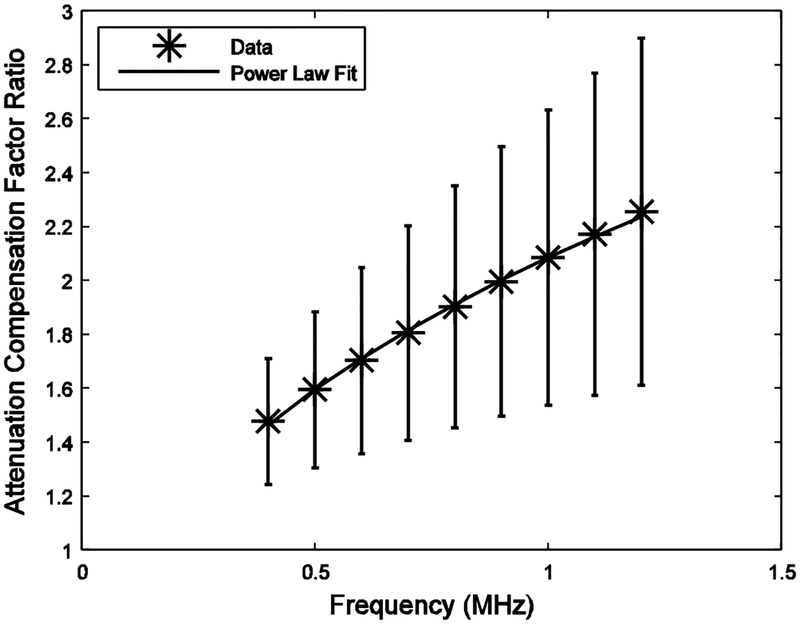
Figure 4 shows the ratio of attenuation compensation factors, R(f, x₀, z), averaged over all 16 bones, which was closely modeled by a power law from 0.4 to 1.2 MHz, a frequency band used in many reports of backscatter coefficient measurements from human calcaneus [49, 50, 52–55]. A power law fit over this frequency range yielded R(f, x₀, z) ≈ (2.1±0.5) f ^0.39±0.15. (It is reasonable to linearly extrapolate measurements of attenuation obtained in the range from 400 kHz to 700 kHz to frequencies up to 1.2 MHz because attenuation in cancellous bone is quasi-linear up to about 2 MHz [38, 39].) A power law fit from 0.3 – 0.7 MHz, another commonly used frequency band [47, 48, 51], yielded a similar result, R(f, x₀, z) ≈ (2.0±0.5) f ^0.34±0.12.

4.

Average ratio of attenuation compensation factors versus frequency (*). Error bars denote standard errors. A power law fit is also shown (solid curve).

Discussion

Strelitzki et al. published a pioneering report comparing PS and PI BUA measurements in human calcaneus samples in vitro [45]. In order to build upon that work, the present study performed PS and PI BUA measurements on human calcaneus samples in vitro using superior measurement hardware. This study suggests that the phase cancellation effects account on the average for about 20% of PS BUA in vitro.

Table 2 gives a summary of four experimental studies, including the present one, that compare PS and PI measurements of BUA. Differences in results may be explained in terms of differences in study populations and measurement methodology:

Table II.

Summary of four experimental studies comparing phase sensitive and phase insensitive measurements of BUA.

Study	Bone State	#	subjects	Marrow present	Receiver array elements		Mean BUA (dB/MHz)		Change
					#	size (mm)	PS	PI	Difference (dB/MHz)	%
Strelitzki45	in vitro	10	cadaver	Yes	9	5	47.9	43.5	4.4	9
present		16	cadaver	No	52	2	22.1	17.6	4.5	20
Petley44	in vivo	10	men and women	Yes	1*	5	~83	~52	31.2	39
Wear46		73	women aged 47 ± 13 yr.	Yes	52	2	81.4	67.2	14.2	17

^*Petley et al. used a single receiver of 5 mm diameter to scan a 25 mm diameter area in steps of 1 mm.

The two in vivo studies exhibited larger levels of BUA than the two in vitro studies. Primary factors responsible for this probably include 1) presence of cortical plates, and 2) generally younger study population (and in Petley’s study, the inclusion of males) with thicker calcaneus and higher BMD. (In order to help resolve the relative importance of these factors, an interesting future study could compare PS and PI BUA for calcaneus samples in vitro before and after cortical plate removal.) Other factors may include 1) presence of surrounding soft tissue and 2) temperature differences. (For further discussion of possible explanations for the differences between these two in vivo studies, see Reference 46).

The values for BUA in the present in vitro study were approximately 50% lower than those in the study by Strelitzki et al. [45]. One likely primary explanation is the absence of marrow in the present study. Note that Nicholson and Bouxsein found nBUA to be 30% lower in water-filled (compared with marrow-filled) human calcaneus samples (12.8 vs. 18.4 dB/cmMHz) [60].

Langton et al. argued (based on computer simulation and experiments on Perspex plates) that increases in BUA measurements due to the presence of cortical plates are likely primarily due to phase cancellation artifacts produced by curved cortical surfaces rather than absorption effects [61]. Xia et al. also argued (based on a theoretical model and experiments on 18 cadaver calcanea) that cortical plates have a significant effect on BUA [62].

Many investigators summarize the frequency dependence of backscattering from cancellous bone by performing power law fits (η(f)=Af ⁿ) to frequency-dependent backscatter coefficient measurements and reporting the exponent n of the fit. Wear reported an average value of n = 3.26 ± 0.20 (standard error) in human calcaneus (300–700 kHz), which is a little higher than the value of approximately 3 predicted by the Faran Cylinder model [47]. Subsequently, Chaffai et al. measured 3.38 ± 0.31 (standard error) in human calcaneus (0.4–1.2 MHz), which is close to the value of 3.48 predicted by the Weak Scattering model [49]. Padilla et al. measured 3.1 ± 1.09 (standard deviation) in human femur (0.4–1.2 MHz) [54]. Since all these backscatter measurements were compensated by PS attenuation functions, it is likely phase cancellation artifact inflated estimated exponents (n) by about 0.3 to 0.4, suggesting that the experimental exponents should be reduced to the 2.9 – 3.0 range for calcaneus and around 2.7 for femur. Even after adjustment for phase cancellation artifacts, frequency-dependence measurements are still in rough agreement with theoretical models, given the accuracy and precision of backscatter measurements, which are limited by many factors including small scattering volumes, sample heterogeneity, multiple scattering, and coherent scattering effects.

Conclusion

Phase cancellation artifacts are significant and can account, on the average, for approximately 20% of measurements of BUA in human calcaneus in vitro. Previously reported measurements of magnitude and frequency dependence of backscatter coefficients from cancellous bone in vitro should be adjusted downward in order to correct for phase cancellation artifacts.

Biography

Keith A. Wear graduated from the University of California at San Diego with a B.A. in Applied Physics in 1980. He received his M.S. and Ph.D. in Applied Physics with a Ph.D. minor in Electrical Engineering from Stanford University in 1982 and 1987.

He was a post-doctoral research fellow with the Physics department at Washington University, St. Louis from 1987–1989. He has been a research physicist at the FDA Center for Devices and Radiological Health since 1989. He has performed research in biomedical applications of ultrasound and magnetic resonance spectroscopy for 15 years. His research has included measurements of ultrasonic scattering properties from tissues, high-resolution spectral estimation, magnetic resonance spectroscopic image reconstruction methods, and analysis of statistical properties of ultrasonic echoes from tissues.

He is an adjunct professor of Radiology at Georgetown University. He is a Fellow of the American Institute for Medical and Biological Engineering and the American Institute of Ultrasound in Medicine (AIUM). He is a senior member of IEEE. He is a member of the Acoustical Society of America, IEEE Ultrasonics Society, the National Osteoporosis Foundation and the AIUM Technical Standards Committee. He is an associate editor of IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control.