Abstract
Background
Design, conduct, and analysis of randomized clinical trials (RCTs) with time to event end points rely on a variety of assumptions regarding event rates (hazard rates), proportionality of treatment effects (proportional hazards), and differences in intensity and type of events over time and between subgroups.
Design and methods
In this article, we use the experience of the recently reported Adjuvant Lapatinib and/or Trastuzumab Treatment Optimization (ALTTO) RCT, which enrolled 8381 patients with human epidermal growth factor 2-positive early breast cancer between June 2007 and July 2011, to highlight how routinely applied statistical assumptions can impact RCT result reporting.
Results and conclusions
We conclude that (i) futility stopping rules are important to protect patient safety, but stopping early for efficacy can be misleading as short-term results may not imply long-term efficacy, (ii) biologically important differences between subgroups may drive clinically different treatment effects and should be taken into account, e.g. by pre-specifying primary subgroup analyses and restricting end points to events which are known to be affected by the targeted therapies, (iii) the usual focus on the Cox model may be misleading if we do not carefully consider non-proportionality of the hazards. The results of the accelerated failure time model illustrate that giving more weight to later events (as in the log rank test) can affect conclusions, (iv) the assumption that accruing additional events will always ensure gain in power needs to be challenged. Changes in hazard rates and hazard ratios over time should be considered, and (v) required family-wise control of type 1 error ≤ 5% in clinical trials with multiple experimental arms discourages investigations designed to answer more than one question.
Trial Registration
clinicaltrials.gov Identifier NCT00490139.
Keywords: proportional hazards, stopping boundaries, accelerated failure time models, power, family-wise type 1 error, early breast cancer
Key Message
While many aspects of the design, conduct, and analysis of randomized clinical trials have become standard, we use the Adjuvant Lapatinib and/or Trastuzumab Treatment Optimization (ALTTO) trial to illustrate that some of our common statistical assumptions must be carefully considered and potentially challenged in future trials.
Introduction
Principles of clinical trials have been developed and standardized during the past 70 years. A brief summary of key principles is presented in supplementary Material, available at Annals of Oncology online. In particular, the design, conduct, and analysis of randomized clinical trials (RCTs) with time-to-event end points rely on standard techniques. The hazard ratio is used to measure the difference in an efficacy outcome between two treatments and is often assumed to be constant over time; that is the hazard functions for the two treatments differ proportionally by the same amount during both early and later follow-up intervals [so-called proportional hazards (PH) assumption] [1]. For time-to-event end points, such as disease-free survival (DFS), the statistical power to detect a given treatment effect depends not on the number of patients enrolled in the trial but on the number of DFS events that have occurred by the time of the analysis. Therefore, the timing of scheduled analyses is based on the number of primary end point events rather than on the amount of follow-up time accrued (so-called event-driven versus time-driven analyses). All of the above features have become de facto standards, but their performance in practice depends upon the extent to which the underlying assumptions hold.
In June 2014, based on the results of the ALTTO (Adjuvant Lapatinib and/or Trastuzumab Treatment Optimisation Trial; BIG 2-06) study, it was announced at the annual meeting of the American Society of Clinical Oncology (ASCO) that the combination of adjuvant lapatinib and trastuzumab did not significantly reduce the risk of DFS events compared with trastuzumab alone in patients with human epidermal growth factor 2 (HER2)-positive early breast cancer [2]. Unbeknownst to the investigators and sponsor at the time, the interim analysis had shown a strong advantage favoring the combination arm that did not cross the efficacy boundaries for early stopping. Could the statisticians determine retrospectively why the results from the primary analysis differed from those of the interim analysis? More importantly, what lessons could be learned from a statistical perspective to improve the design, conduct and analysis of future trials?
Methods
The ALTTO study
Between June 2007 and July 2011, the ALTTO study randomized 8381 patients to 1 year of adjuvant therapy with trastuzumab (T), lapatinib (L), their sequence (T → L), or their combination (L + T). The primary analysis was conducted when 555 DFS events had been observed in the L + T and T arms, triggered by a median follow-up of 4.5 years as specified in the ALTTO protocol. In this article, we use the ALTTO trial as a case study to highlight statistical issues and assumptions that impact the design and analysis of RCTs.
Results
Primary analysis of ALTTO
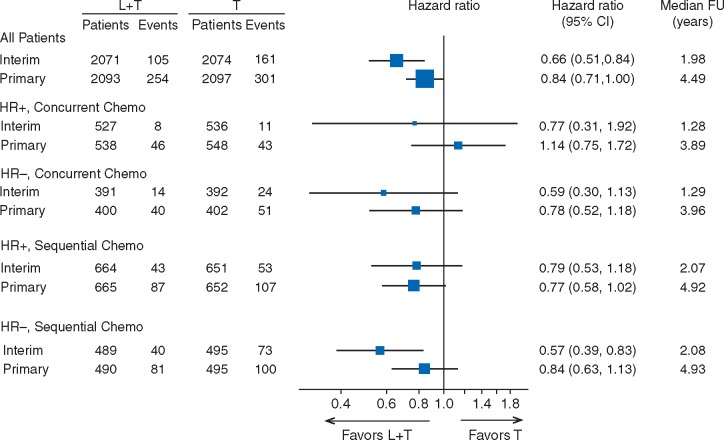
For the primary analysis (clinical cut-off date 6 December 2013), the hazard ratio required to observe a clinically relevant treatment difference was 0.80 and the P-value required for statistical significance was ≤0.025. The observed hazard ratio was 0.84 [95% confidence interval (CI) 0.71–1.00] with a P value of 0.048 (Figure 1). Members of the Independent Data Monitoring Committee (IDMC) might have been surprised by this non-significant P-value, because the interim analysis results based on an August 2011 data cut-off suggested that the dual inhibition therapy (L + T) did have a superior effect compared with trastuzumab alone (T) with hazard ratio of 0.66 (95% CI 0.51–0.84, P = 0.0008, Z-value = −3.35), although this effect did not meet the pre-defined stopping criteria (Z-value < −5.1).
Figure 1.
Forest plot of interim and primary analyses for all patients (top) and for subgroups defined by hormone receptor status (positive [HR+] and negative [HR-]) and by chemotherapy timing (concurrent, sequential). L + T, lapatinib + trastuzumab treatment arm; T, trastuzumab-alone treatment arm; CI, confidence interval; median FU, median follow-up.
Other observations from the primary analysis were as follows:
The treatment effect of the combination L + T versus T appeared to be greatest in patients treated with chemotherapy completed before initiation of any anti-HER2 therapy (sequential administration) as opposed to concurrent administration of chemotherapy and anti-HER2 therapy [hazard ratios of 0.80 (95% CI 0.65–0.98) and 0.94 (95% CI 0.70 to 1.26), respectively).
In recent years, concurrent administration of chemotherapy and anti-HER therapy has become more widely accepted as the standard of care based on the trastuzumab pivotal trials results.
The combination L + T therapy was associated with an unfavorable toxicity profile compared with T alone and patients were less likely to complete L treatment compared with T.
Comparison of treatment effects in subgroups over study duration
The patient population in a clinical trial should be defined carefully and most studies will include stratification factors to balance the treatment allocation across particular patient characteristics of interest. Having carried out a stratified analysis, there is often interest in the treatment effects within the strata, though some caution must be applied on testing across many different subgroups [3].
In ALTTO, analyses by chemotherapy timing were pre-specified in the Statistical Analysis Plan. Having observed the differences in treatment effect between concurrent and sequential treatment, we considered the four subgroups from the combinations of hormone receptor status and chemotherapy timing as well as the overall result for the intent-to-treat (ITT) population at the interim analysis. Figure 1 shows the forest plots of the DFS comparison of L + T versus T from the interim analysis and from the primary analysis databases [2]. Sequential administration dominated enrolment during early years of accrual and was eventually terminated in favor of concurrent administration during later years. The different median follow-up times for the subgroups in Figure 1 reflects this; there was short follow up for patients on the concurrent chemotherapy regimen at the time of the interim analysis and still less follow up than for patients in the sequential administration regimen at the primary analysis.
The Z-value in the interim efficacy stopping rule for ALTTO was very stringent, lower than that stipulated by many other studies. But here this caution seems to have been warranted as the positive hormone receptor status and sequential administration cohort was the only one that did not experience an attenuation of the treatment effect between the interim and primary analyses, that is the hazard ratios for the three other cohorts shifted toward the null.
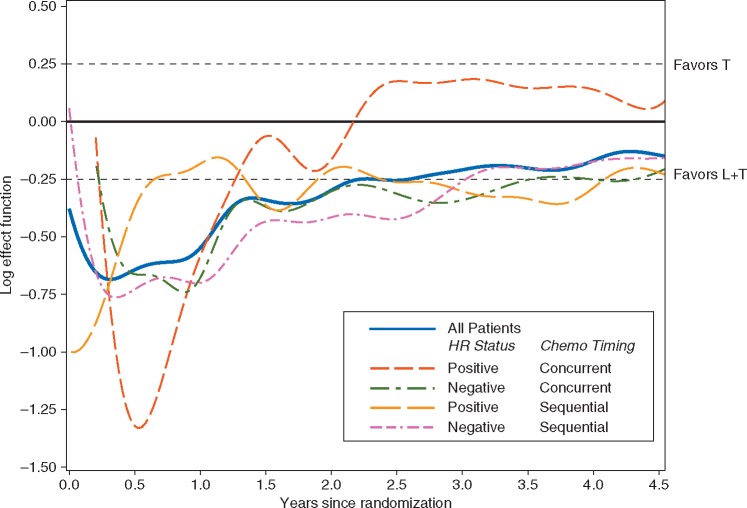
In order to consider changes in the treatment effect during the study, Figure 2 shows a plot of the log-rank process over time, both for the overall population and for each subgroup, with nonparametric smoothing [4]. Here, we are not trying to determine whether there is a specific time point when the L + T arm would have been declared efficacious but to provide a graphical description of any interesting patterns in the treatment effects between subgroups.
Figure 2.
Log effect function plot illustrating the estimated treatment effect of L + T versus T as a function of the years since randomization, for all patients (solid blue line) and for separate patient cohorts defined by hormone receptor status and chemotherapy timing. [Note: hazard ratio = exp (log effect function); that is y-axis values for the log effect function = 0.25, 0.00, −0.25, −0.50, and −0.75 correspond to hazard ratios = 1.28, 1.00, 0.78, 0.61, and 0.47, respectively]. L + T, lapatinib + trastuzumab treatment arm; T, trastuzumab-alone treatment arm; HR, hormone receptor; Chemo Timing, chemotherapy timing.
Probably the most striking feature of the graph in Figure 2 is that the treatment effect in the subgroup with hormone receptor positive and concurrent chemotherapy appears to be quite different from the other subgroups. There is a growing body of evidence that evaluations of the magnitude of treatment effects for targeted therapies require consideration of hormone receptor status. This seems to be less important when patients are treated with sequential administration, an observation that has little current clinical relevance as concurrent administration of non-anthracycline chemotherapy and anti-HER2 treatment has become the standard of care.
It is worth noting that, even though the treatment effects illustrated in Figure 2 clearly vary over time, the usual test for non-proportionality does not give a result that is formally significant at the 5% level.
The analyses presented here are post hoc but should serve as a warning where new evidence about treatments and disease-modifying effects is emerging and could have implications for an ongoing study. We therefore recommend the inclusion of more hypothesis-generating subgroup analyses in phase II studies to inform the design of phase III trials.
Type of event in the primary end point
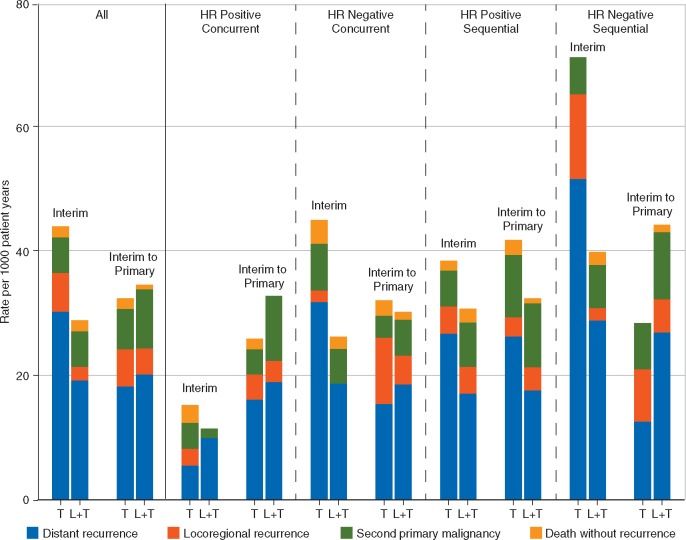
The primary end point, DFS, is defined as the time to the first event, which is either a distant recurrence, locoregional recurrence, secondary primary cancers or deaths without recurrence. Each of these has a different implication for the patient and for any subsequent treatment choice. Figure 3 displays the DFS event rate for time intervals up to the interim analysis and from the interim to the primary analysis for all patients and for subgroups defined by chemotherapy timing and hormone receptor status. Table 1 summarizes the overall DFS event incidence rates without considering the type of event. While the different treatment effects of the hormone receptor status/chemotherapy timing subgroups are again notable, the event rate of distant recurrences for patients with hormone receptor negative disease was lower after the interim analysis. Since regulatory authorities favor including ‘unavoidable events’, such as deaths without recurrence, in the end point definitions, the timing of the analyses may be critical to determine clinically relevant treatment differences. If late events are primarily deaths without recurrence or second primary non-breast cancers, their incidence may not be reduced by the experimental treatment compared with the control.
Figure 3.
Disease-free survival (DFS) event rates (number of DFS events per 1000 patient-years of follow-up) for all patients (on the left) and for separate patient cohorts defined by hormone receptor (HR) status and chemotherapy timing showing overall results and by type of DFS event for the time period from start of study to interim analysis (interim) and for the time period from interim analysis to primary analysis (interim to primary). Each bar shows the contributions to the overall DFS event rate from each of the four types of DFS event (distant recurrence, locoregional recurrence, second primary malignancy, and death without recurrence).
Table 1.
Disease-free survival (DFS) events per 1000 patient-years of follow-up, for the time from start of study to the interim analysis and the time between the interim and primary analyses comparing lapatinib + trastuzumab (L + T) versus trastuzumab (T) overall and for cohorts defined by timing of anti-human epidermal growth factor 2 therapy relative to chemotherapy (concurrent CT or sequential CT) and hormone receptor status (HR+ or HR-)
| Interim analysis (1.98 y MFU) |
Primary analysis (4.49 y MFU) |
||||||
|---|---|---|---|---|---|---|---|
| DFS event ratea (95% CI) |
Hazard ratiob (95% CI) | DFS event ratec (95% CI) |
Hazard ratiob (95% CI) | ||||
| Cohort | N | T | L+T | T | L+T | ||
| All patients | 4190 | 44 (38–51) | 29 (24–35) | 0.66 (0.51–0.84) | 32 (27–38) | 35 (29–41) | 0.84 (0.71–1.00) |
| Concurrent CT; HR+ | 1086 | 15 (8–27) | 11 (6–23) | 0.77 (0.31–1.92) | 26 (18–37) | 33 (24–45) | 1.14 (0.75–1.72) |
| Concurrent CT; HR− | 802 | 45 (30–67) | 26 (16–44) | 0.59 (0.30–1.13) | 32 (22–47) | 30 (21–44) | 0.78 (0.52–1.18) |
| Sequential CT; HR+ | 1317 | 38 (29–50) | 31 (23–41) | 0.79 (0.53–1.18) | 42 (32–55) | 32 (24–43) | 0.77 (0.58–1.02) |
| Sequential CT; HR− | 985 | 71 (57–89) | 40 (29–54) | 0.57 (0.39–0.83) | 28 (19–41) | 44 (33–60) | 0.84 (0.63–1.13) |
MFU, median follow-up; CI, confidence interval; N, number of patients; T, traztuzumab; L + T, lapatinib + trastuzumab; CT, chemotherapy; HR, hormone receptor.
DFS event rate (events per 1000 patient-years of follow-up) for the period of time from start of study to interim analysis.
Hazard ratio (L + T versus T): numbers <1.00 favor L + T.
DFS event rate (events per 1000 patient-years of follow-up) for the period of time between interim and primary analyses.
Validity of the proportional hazards assumption and an alternative to Cox models
The proportional hazards (PH) model of Cox [1] is a widely accepted method for analyzing time-to-event data. However, the assumption of PH holding for the entire length of the follow-up period until the time of the primary analysis may not always be biologically plausible. It may be reasonable to assume that the hazard rates may converge (i.e. hazards ratio approaches 1.0) as follow up continues beyond the adjuvant treatment period.
As an alternative to the Cox model, we fitted accelerated failure time (AFT) models, using either maximum likelihood under the assumption of log-normality or the semi-parametric Buckley and James estimator [5]. AFT models are based on the assumption that the effect of a treatment is to decelerate the course of a disease (‘to stretch the time axis’) by a constant amount. In the special case that the hazard rate is constant (the exponential distribution), the AFT and PH models are identical, but generally the models differ. In particular, the AFT model may be a more accurate description of a disease in which the effect of treatment on the hazard diminishes over time, but the survival curves remain separated [6, 7].
The Cox model and AFT model gave very similar results, suggesting a deceleration factor of about 1.2 in the combination L + T arm relative to the T arm, with a P < 0.02. Since this was not a pre-specified analysis, we clearly cannot claim ‘significance’. However, the difference between these results and those from the PH model is interesting, and may reinforce the view that one might reasonably match the test procedures used to the expected effect type, rather than simply defaulting to the PH Cox model on every occasion. Proportional odds models, fractional polynomials, partitioned survival models, and using Wilcoxon over log-rank testing are other techniques to deal with non-PH [8].
Waiting to accrue more events does not necessarily increase power
It is often assumed that additional follow-up means additional events, which means additional power. However, this is not necessarily true. If the hazard ratio moves toward 1.0 as follow-up increases (as will frequently be the case), the attained power may actually be reduced. Note that this remains true even if the survival curves remain separated, and even if the accrued events are ‘true events of interest’. The decrease in power is less dramatic if the Wilcoxon test is used in place of the log-rank test, and the decrease occurs later, but still occurs.
As an example, we assume an exponential failure model for the control arm, with a constant hazard rate of 0.025 per year, and a piecewise exponential model for the treatment arm (i.e. constant hazards during intervals of follow-up time), with hazard ratio of 0.7 in years 1 and 2 after the start of treatment and a hazard ratio of 1.0 thereafter. The minimum sample size per group required for 80% power in this setting and uniform recruitment over 3 years is 4090. Table 2 shows the effect of changing follow-up period on the power with this number of patients. The power declines after year 2 even as the number of events increases. If we make the slightly more optimistic assumption that the hazard ratio is 0.95 in years 3 onward, the power again declines after year 2, but the degree of power loss is less (Table 2).
Table 2.
Power at 4090 patients per arm in the setting of Figure 1 and a 3-year uniform recruitment assuming hazard ratio of 0.70 in years 1 and 2, and hazard ratio of either 1.00 or 0.95 thereafter
| Hazard ratio after year 2 |
||||
|---|---|---|---|---|
| Hazard ratio = 1.00 |
Hazard ratio = 0.95 |
|||
| Median follow-up Time (year) | Computed power | Expected number of events | Computed power | Expected number of events |
| 2.0 | 0.771 | 340 | 0.777 | 340 |
| 2.5 | 0.800 | 629 | 0.818 | 622 |
| 3.5 | 0.724 | 907 | 0.789 | 893 |
| 4.5 | 0.612 | 1174 | 0.731 | 1154 |
| 5.5 | 0.533 | 1432 | 0.695 | 1407 |
Family-wise error rate control discourages answering more than one question
The FDA guidance on multiple end points [9] is specifically for trials designed and conducted with the intent to submit for regulatory approval. Trials not intended for regulatory submission may require less strict family-wise error rate (FWER) control though in theory the same rules apply.
The ALTTO study was originally designed to compare each of three experimental arms (L + T; T → L; and L alone) versus a T-alone control group. The comparison of L + T versus T was planned to test for superiority, with an 80% power to detect an improvement in DFS with the combination having a hazard ratio of 0.80 (assuming availability of 850 events for the L + T versus T comparison within a median follow-up of 4.5 years). This was prospectively revised to conduct the primary analysis either when 850 DFS events had been observed, or when a median follow-up for DFS of 4.5 years had been completed, whichever occurred first. This would allow the study to be reported within a timeframe when its results would still be relevant to clinical practice and when DFS events were more likely to be breast cancer related.
Because the oral route of administration of L was considered to be more convenient for patients than 18 i.v. injections of T, both of the other comparisons (T → L versus T and L versus T) were planned to test for non-inferiority based on analyses of the per-protocol populations and a non-inferiority margin to rule out an increase in DFS hazard of more than 16% for the experimental arm (i.e. hazard ratio of 1.16 had to be rejected by a one-sided statistical test with the appropriate alpha spend). In the original protocol, to compensate for the conservative nature of the Bonferroni adjustment, the alpha-spending algorithm to control the family-wise type I error rate was based on the ordered P-value approach suggested by Hochberg [10]. This procedure involves ordering the three pairwise P-values from largest to smallest. If the largest were ≤0.05, then all three pairwise null hypotheses would be rejected. If the largest were >0.05, but the second largest were ≤0.025, then the two remaining null hypotheses would be rejected. Finally, if the smallest P-value were ≤0.0166 (the Bonferroni threshold for three pairwise comparisons), then the final null hypothesis would be rejected.
The original statistical plan was revised when the ALTTO IDMC used the protocol-specified futility boundary to recommend closing the L-alone arm due to inferiority of DFS observed at the first interim analysis in 2011. Because lapatinib was associated with an increased risk of diarrhea leading to non-compliance in the T → L arm, the sponsor assumed that regulatory authorities would not accept statistical testing results for the remaining two pairwise comparisons unless ‘strong control of alpha’ could be guaranteed. Thus, using the Hochberg procedure to control FWER was abandoned, and the statistical plan was changed to implement a Bonferroni adjustment of the P-value required to declare statistical significance, that is P ≤ 0.025 would be required to reject each of the remaining null hypotheses.
When the primary analysis of the ALTTO study was carried out in 2015, the P-value testing superiority of L + T versus T was P = 0.048 and the P-value testing non-inferiority of T → L versus T was P = 0.044 (HR 0.93; 97.5% CI 0.76–1.13) [2]. Because the Bonferroni criterion for statistical significance had been incorporated into the revised protocol, P ≤ 0.025 was required for statistical significance. Thus, neither superiority of L + T nor non-inferiority of T → L as compared with T was statistically significant, and ALTTO is considered a negative study. If, however, the original Hochberg procedure had been retained, both pairwise comparisons would have been declared statistically significant because both P-values were ≤ 0.05.
In 2017, the primary analysis of the APHINITY trial, a study of adjuvant pertuzumab and trastuzumab in early HER2-positive breast cancer, was released [11]. APHINITY included only two arms yielding only one pairwise comparison of adjuvant anti-HER2 therapies given concurrently with chemotherapy for a similar population of patients as enrolled in ALTTO. The study was designed to register use of pertuzumab in a new indication and answer only one question. Statistical significance would be achieved if P ≤ 0.05. The P-value testing superiority of pertuzumab + trastuzmab versus placebo + trastuzumab was P = 0.045 (HR 0.81; 95% CI 0.66–1.00) [11]. Despite the fact that HRs and P-values for ALTTO and APHINITY are very similar, the former was a negative study seeking to answer more than one question, while the latter was a positive study because it tested only one treatment comparison.
Discussion
We conclude that:
futility stopping rules are important to protect patient safety, but stopping early for efficacy can be misleading as short-term results may not imply long-term efficacy;
biologically important differences between subgroups may drive clinically different treatment effects and should be taken into account, for example by pre-specifying primary subgroup analyses and restricting end points to events which are known to be affected by the targeted therapies. We recommend the inclusion of more hypothesis-generating subgroup analyses in phase II studies to inform the design of phase III trials;
the usual focus on the Cox model may be misleading if we do not carefully consider non-proportionality of the hazards. The results of the AFT model illustrate that giving more weight to later events (as in the log rank test) can affect conclusions;
the assumption that accruing additional events will always ensure gain in power needs to be challenged. Changes in hazard rates in the treatment arms over time and consequent changes in the hazard ratio over time should be considered;
required family-wise control of type 1 error ≤5% in clinical trials for regulatory submission with multiple experimental arms discourages investigations designed to answer more than one question.
Supplementary Material
Acknowledgements
We thank the patients who participated in the Adjuvant Lapatinib and/or Trastuzumab Treatment Optimization (ALTTO) study; the Breast European Adjuvant Study Team (BrEAST) Data Center; the Frontier Science team; the Breast International Group (BIG) headquarters; the US National Cancer Institute (NCI); the North Central Cancer Treatment Group (NCCTG; Alliance); the ALTTO Executive and Steering Committee members; the Independent Data Monitoring Committee (IDMC) members; the Cardiac Advisory Board members; the three central pathology laboratories; GlaxoSmithKline; Novartis; and the physicians, nurses, trial coordinators, and pathologists involved in this trial. We also thank Karen N. Price for work on the figures. For a listing of the ALTTO investigators and Participating Groups and Institutions, see Appendix Table A1 in Piccart-Gebhart M, Holmes E, Baselga J, et al: Adjuvant Lapatinib and Trastuzumab for Early Human Epidermal Growth Factor Receptor 2–Positive Breast Cancer: Results From the Randomized Phase III Adjuvant Lapatinib and/or Trastuzumab Treatment Optimization Trial. J Clin Oncol. 34: 1034–1042, 2016.
Funding
The ALTTO study was funded by GlaxoSmithKline (GSK) from its inception until 30 November 2015 and by Novartis since then. No specific funding was received by any of the authors for preparation of this article (no grant number applies).
Disclosure
EMH reports institutional grants from GlaxoSmithKline (GSK), Novartis, and Roche during conduct of study. LW reports employment by GSK and Novartis during conduct of the study. ED reports institutional grants from Novartis, GSK, and Roche during conduct of study. ED reports institutional grants and advisory board and honoraria from Roche; and travel grants from Roche and GSK/Novartis outside submitted work. DF reports institutional grants from GSK and Novartis during conduct of study. DF reports institutional grants from AstraZeneca, Roche/Genentech, Servier, Tesaro, Pfizer, and Guardant outside submitted work. JB reports reasonable reimbursement for travel and advisory board/consulting fees from Roche/Genentech during conduct of study. JB reports personal fees as Board of Directors member from Aura Biosciences, Infinity Pharmaceuticals, Grail, Varian Medical Systems, Bristol Myers Squibbs; stock as Board of Directors member from Aura Biosciences, Infinity Pharmaceuticals, Grail, Varian Medical Systems, Bristol Myers Squibbs, Foghorn Therapeutics; reasonable reimbursement for travel, advisory board/consulting fees from Novartis and Eli Lilly; personal fees as Scientific Advisory Board member from Northern Biologics (f/k/a Mosaic Biomedicals) (co-founder and co-chair), PMV Pharma, Juno Therapeutics (acquired by Celgene), Tango(f/k/a Synthetic Lethal), Grail (chair), and Seragon (acquired by Roche); stock as Scientific Advisory Board member from Mosaic (founder), ApoGen Biotechnologies, Juno Therapeutics, and Seragon (acquired by Roche); stock as co-founder of Tango(f/k/a Synthetic Lethal); personal fees from co-founding Venthera; outside submitted work. JB is currently a full time employee of AstraZeneca. ACD reports grants from National Cancer Institute, GSK, and Novartis during conduct of study. RDG reports institutional grants from GSK, Novartis, and Roche during conduct of study. RDG reports institutional grants from Pfizer, Celgene, Merck, Ferring, and Ipsen outside submitted work. All remaining authors have declared no conflicts of interest.
References
- 1. Cox DR. Regression models and life-tables. J R Stat Soc B 1972; 34: 187–220. [Google Scholar]
- 2. Piccart-Gebhart M, Holmes E, Baselga J. et al. Adjuvant lapatinib and trastuzumab for early human epidermal growth factor receptor 2–positive breast cancer: results from the randomized phase III Adjuvant Lapatinib and/or Trastuzumab Treatment Optimization Trial. J Clin Oncol 2016; 34(10): 1034–1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Fletcher J. Subgroup analyses: how to avoid being misled. BMJ 2007; 335(7610): 96.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Schumacher M. Two-sample tests of Cramér-von Mises- and Kolmogorov-Smirnov-type for randomly censored data. Int Stat Rev 1984; 52: 263–281. [Google Scholar]
- 5. Buckley J, James I.. Linear regression with censored data. Biometrika 1979; 66(3): 429–436. [Google Scholar]
- 6. Wei LJ. The accelerated failure time model: a useful alternative to the Cox regression model in survival analysis. Stat Med 1992; 11(14-15): 1871–1879. [DOI] [PubMed] [Google Scholar]
- 7. Coppini DV, Bowtell PA, Weng C. et al. Showing neuropathy is related to increased mortality in diabetic patients—a survival analysis using an accelerated failure time model. J Clin Epidemiol 2000; 53(5): 519–523. [DOI] [PubMed] [Google Scholar]
- 8. David C. Modelling Survival Data in Medical Research, 3rd edition. Chapman & Hall/CRC; Texts in Statistical Science Book 115 2014. [Google Scholar]
- 9.FDA (U.S. Food and Drug Administration). Multiple endpoints in clinical trials: guidance for industry, 2017.
- 10. Hochberg Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika 1988; 69: 493–502. [Google Scholar]
- 11. von Minckwitz G, Procter M, de Azambuja E. et al. Adjuvant pertuzumab and trastuzumab in early HER2-positive breast cancer. N Engl J Med 2017; 377(2): 122–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.