Improved Measurement of Acoustic Output Using Complex Deconvolution of Hydrophone Sensitivity

Abstract

The traditional method for calculating acoustic pressure amplitude is to divide a hydrophone output voltage measurement by the hydrophone sensitivity at the “acoustic working frequency,” but this approach neglects frequency dependence of hydrophone sensitivity. Another method is to perform a complex deconvolution between the hydrophone output waveform and the hydrophone impulse response (the inverse Fourier transform of the sensitivity). In this paper, the effects of deconvolution on measurements of peak compressional pressure (p₊), peak rarefactional pressure (p₋), and pulse intensity integral (PII) are studied. Time delay spectrometry (TDS) was used to measure complex sensitivities from 1 to 40 MHz for 8 hydrophones used in medical ultrasound exposimetry. These included polyvinylidene fluoride (PVDF) spot-poled membrane, needle, capsule, and fiber-optic designs. Subsequently, the 8 hydrophones were used to measure a 4-cycle, 3 MHz pressure waveform mimicking a pulsed Doppler waveform. Acoustic parameters were measured for the 8 hydrophones using the traditional approach and deconvolution. Average measurements (across all 8 hydrophones) of acoustic parameters from deconvolved waveforms were 4.8 MPa (p₊), 2.4 MPa (p₋), and 0.21 mJ/cm² (PII). Compared with the traditional method, deconvolution reduced coefficient of variation (ratio of standard deviation to mean across all 8 hydrophones) from 29% to 8% (p₊), 39% to 13% (p₋), and 58% to 10% (PII).

INTRODUCTION

Hydrophones are used in medical ultrasound exposimetry to measure acoustic pressure waveforms from diagnostic ultrasound transducers [1]. A common approach for estimation of acoustic pressure amplitude is to take the ratio of the hydrophone output voltage to the value of the hydrophone sensitivity at the “acoustic working frequency” [2, 3]. However, this approach neglects frequency dependence of hydrophone sensitivity over the usable bandwidth of the source transducer. This approach may become problematic, for example, for acoustic waveforms that have significant energy in harmonic frequencies, which arise from nonlinear propagation effects. An improved measurement of the acoustic pressure waveform may be obtained by deconvolving the measured hydrophone waveform with the hydrophone impulse response (the inverse Fourier transform of the sensitivity).

The need for deconvolution is increasing in medical ultrasound as source transducers move toward higher frequencies (e.g., 15 MHz and above) [4, 5]. An International Electrotechnical Commission (IEC) standard states that in the presence of short pulses or significant nonlinear distortion, the ± 3 dB bandwidth of the hydrophone should be at least 8 times the acoustic working frequency in order to keep measurement errors below about 5% [2]. When such a bandwidth is not achievable, the standard recommends that deconvolution be performed if “the uncertainty in the measurement becomes unacceptably large due to limited bandwidth of the hydrophone” [2, 3]. In order to perform a complete complex deconvolution of the hydrophone impulse response from measurements of acoustic fields, both the phase and magnitude of the hydrophone transfer function must be known. Unfortunately, hydrophones are often characterized only by the magnitude of their transfer function.

Various methods for measuring phase have been proposed, including methods based on an optical multilayer reference hydrophone [6], an optical-fiber-based probe [5], nonlinear acoustic wave propagation in water [7–9], and TDS [5, 10, 11]. This laboratory previously reported a TDS-based method for measurement of hydrophone complex sensitivity. It was validated over the range from 5–18 MHz for several hydrophone types, including PVDF spot-poled membrane, needle, capsule designs, and a piezoelectric ceramic design [11]. This method was used to show that many hydrophone measurement systems in common use in medical ultrasound exposimetry may be modeled as approximately minimum phase systems [11, 12], which implies that their phase responses can be inferred from measurements of their magnitude responses [13]. The minimum-phase model has previously been applied to an interferometric fiber-optic system [14].

One potentially important application of deconvolution is for improving measurements performed with fiber-optic hydrophones [15–16]. One recent fiber-optic design features an extremely small sensitive element size (10 μm) for high spatial resolution, the ability to withstand high intensity therapeutic fields, and the ability to measure temperature as well as pressure [15]. However, as the authors acknowledge, this design does not result in a high degree of uniformity of frequency response (see Ref. [15], Figure 7). Another fiber-optic design, also capable of withstanding high intensity therapeutic fields, exhibits non-uniform frequency response (see Ref. [16], Figure 2). The inventors of this design therefore recommend deconvolution in conjunction with this device [16]. Another fiber-optic design, however, shows relatively uniform response [5].

The objective of the present work was to investigate the benefits of deconvolution for estimating acoustic output parameters for a typical pulsed Doppler pressure waveform measured with typical hydrophones used in medical ultrasound exposimetry. Due to the broad bandwidth of such waveforms (resulting from nonlinear propagation in water), this objective required modifying the hardware components of a previously reported TDS system [11] to increase the measurement bandwidth, which was expanded for the present study from 5–18 MHz [11] to 1–40 MHz. The acoustic output parameters considered were the peak compressional pressure (p₊), peak rarefactional pressure (p₋), and the pulse intensity integral (PII). The likelihood for mechanical bioeffects is thought to be related to p₋ while the likelihood for thermal bioeffects is thought to be related to PII [17]. In histotripsy applications, p₊ is important for distinguishing regimes of cavitation histotripsy and boiling histotripsy [18].

METHODS

A. TDS-Based Measurement of Magnitude and Phase Response

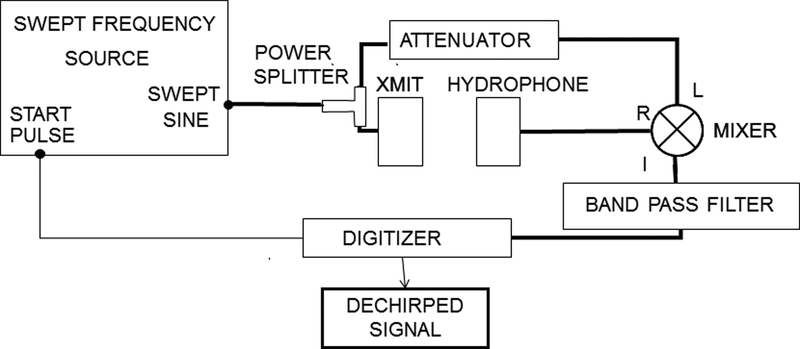
TDS has been used by several authors to measure the magnitude of hydrophone response [19–23]. In the present study, TDS was used to measure both magnitude and phase. The method for measuring magnitude and phase response was similar to that reported previously [11] and will be briefly summarized here. Figure 1 shows a block diagram of the TDS data acquisition system. The source signal is assumed to be a linear, swept-frequency cosine wave denoted by cos(ωt), where ω = 2πf = 2πSt, f = frequency, S = sweep rate, and t = time. The measurement system includes a source transducer, ultrasound propagation from source to receiver, a receiving transducer (e.g., hydrophone), receiving electronics, and any other electronics that are present (e.g., attenuators, filters, hydrophone pre-amplifier, …). The output of the measurement system is given by

$$Y\left(\omega \right)=\left|A\left(\omega \right)\right|\text{ cos}\left[\left(\omega -\Delta \omega \right)\text{t }+{\phi }_{\text{A}}\left(\omega \right)\right],$$ (1)

where A(ω) is the system response with magnitude |A(ω)| and phase Arg [A(ω)] = φ_A(ω), Δω = 2πΔf = 2πSt_D is the TDS offset frequency, t_D = z/c is the system delay time, c is the speed of sound, and z is the distance between the transmitting and receiving transducers. The offset frequency Δω is negative in Equation (1) to signify that the received frequency lags the source signal frequency by this offset.

1.

Block diagram of experimental setup.

The system output (the “R” input to the mixer in Figure 1) is mixed with (i.e., multiplied by) the source signal, cos(ωt) (the “L” input to the mixer in Figure 1). The output of the mixer contains components at the sum and difference frequencies [11],

$$Y\left(\omega \right)\text{ cos}\left(\omega t\right)=\left(1/2\right)\left|\text{A}\left(\omega \right)\right|\left\{\text{cos}\left[\left(2\omega -\Delta \omega \right)t+{\phi }_A\left(\omega \right)\right]+\text{ cos}\left[\Delta \omega t-{\phi }_A\left(\omega \right)\right]\right\},$$ (2)

The mixed signal is then low-pass filtered to remove the sum-frequency component and retain the difference-frequency component, producing the so-called “dechirped” signal,

$$D\left(\omega \right)=\left(1/2\right)\left|A\left(\omega \right)\right|\text{ cos}\left[\Delta \omega t–{\phi }_A\left(\omega \right)\right].$$ (3)

The analytic signal of representation of D(ω) may be denoted by D_R(ω) + iD_I(ω), where D_R(ω) = D(ω), D_I(ω) = H { D(ω) }, H { } denotes a Hilbert transform and the integration variable is t (recall that ω = 2πSt). The Hilbert transform of D(ω) is given by D_I(ω) = (1/2) |A(ω)| sin[Δωt - φ_A(ω)] [11]. The magnitude and phase of the analytic signal representation of D(ω) are given by [D_R²(ω) + D_I²(ω)]^1/2 and arctan [D_I(ω) / D_R(ω)] respectively. Therefore, the magnitude and phase of the system response are given by

$$\left|A\left(\omega \right)\right|=2{\left[{D_R}^2\left(\omega \right)+{D_I}^2\left(\omega \right)\right]}^{1/2},$$ (4)

$${\phi }_A\left(\omega \right)=-\text{ arctan }\left[D_I\left(\omega \right)/D_R\left(\omega \right)\right]+\Delta \omega t$$ (5)

Equivalent expressions for magnitude and phase may also be derived using an I/Q demodulation approach [11].

B. Data Acquisition

Table I shows the 8 tested hydrophones, which were chosen to be representative of types in common use in medical ultrasound exposimetry. System magnitude and phase responses were measured for the 8 hydrophones. The magnitude and phase of the sensitivities of two membrane hydrophones (M1 and M3) were also evaluated by an independent laboratory, the Physikalisch-Technische Bundesanstalt (PTB, Braunschweig, Germany), so that they could be used as references. M1 was used as a reference for measurements on M3, and M3 was used as a reference for all the other hydrophones. A previously-reported substitution method [11] was used to estimate magnitude and phase responses of the remaining hydrophones.

Table I.

Hydrophones

Name	Design	Nominal Sensitive Element Diameter (mm)	Integral Pre-amplifier?
EP	PVDF ellipsoid (capsule)	0.2	yes
NP	PVDF needle	0.6	no
NC	Piezoelectric ceramic needle	0.4	no
M1	Single-layer PVDF membrane with rubber backing	0.5	yes
M2	Bilaminar PVDF membrane	0.4	no
M3	Bilaminar PVDF membrane	0.5	yes
M4	Single layer PVDF membrane	1.0	yes
FO	Fiber Optic	0.01	yes

TDS measurements were performed using four different broadband unfocussed source transducers (approximate center frequencies: 2 MHz, 5 MHz, 30 MHz, and 50 MHz) in order to obtain hydrophone magnitude and phase response over the band from 1 to 40 MHz. Measurements were performed twice for each source transducer and each hydrophone (with repositioning of both) so that 1) sensitivity measurement variability could be estimated and 2) precision could be improved by averaging pairs of measurements. (IEC 62127–1 [2], following common practice, refers to uncertainties evaluated by statistical means as Type A uncertainties). Table II shows transducer properties and TDS parameters for the four sets of measurements. The receiving hydrophone was co-axially positioned a distance z from the source, resulting in a time delay, t_D = z / c, where c is the speed of sound in water. The function generator was a Tektronix (Beaverton, OR, USA) model AFG 3102 function generator. The hydrophone signal was amplified by a 40 dB amplifier (Model 5676, Olympus-NDT, Waltham, MA). For all measurements, this amplifier’s input was terminated with 50 ohms, as specified for the hydrophones that contained an integral preamplifier. For measurements using hydrophones without an integral preamplifier, a buffer amplifier having unity voltage gain was placed between the hydrophone output and the amplifier input to prevent signal loss due to this low impedance 50 ohm load [25]. A frequency mixer (model ZAD-3, Mini-Circuits, Brooklyn, NY, USA) was used to mix the received signal with the swept frequency input signal. The mixed signal was bandpass filtered via an 8-pole Butterworth filter having a roll-off of 48 dB/octave and corner frequencies of Δf ± BW/2 kHz (model 3384, Krohn-Hite, Brocton, MA, USA) to remove the undesired chirp signal and retain the desired “dechirped” TDS signal [11]. The dechirped TDS signal (Eq. 3) was digitized and stored (sampling rate = 100 kHz, vertical resolution = 11 bits) using a digital oscilloscope (model DPO 3054 Tektronix, Beaverton, OR, USA). As may be seen in Table II, the TDS parameters were set in order to maintain constant time resolution and frequency resolution for the four sets of measurements.

Table II.

Transducer properties and TDS parameters. The source frequency was swept linearly from 0 to the maximum sweep frequency. See [11] for relationships among TDS parameters.

Transducer	Biconcave 1–3 piezoelectric composite [24]	Valpey Fisher IS0504HR	Panametrics ZF3001	Olympus P150-2-R2.00
Diameter (cm)	4	1.27	0.635	0.635
Center Frequency (MHz)	2	5	30	50
Maximum Sweep Frequency (MHz)	20	20	40	40
Sweep Time (s)	0.2	0.334	0.334	0.267
Sweep Rate S (MHz/s)	100	60	120	150
Hydrophone Depth (z) (cm)	15	30	15	10
Delay Time tD=z/c (μs)	101	203	101	68
TDS Frequency Δf = StD (kHz)	10.1	12.1	12.1	10.1
Filter Bandwidth (BW) (kHz)	0.67	0.4	0.8	1
Frequency Resolution = S/BW (MHz)	0.15	0.15	0.15	0.15
Time Resolution = BW / S (μs)	6.7	6.7	6.7	6.7

The eight hydrophones were used to receive a pressure waveform that was designed to mimic a pulsed Doppler waveform in a water tank. A Tektronix AFG 3102 function generator produced a signal of approximately 4 cycles at 3 MHz, which was fed into a Gammell Applied Technologies 02–06B pulser [26] that drove a KB-Aerotech (Stratford, CT) MLB 35EL 117245HR transducer (center frequency: 3.5 MHz, diameter: 19 mm, and focal range 6–13 cm). The hydrophones were placed 8.2 cm from the source transducer, which roughly corresponded to the location of maximum peak-to-peak pressure amplitude. At this depth, the −6 dB beam diameter was approximately 1.4λz/d = 3 mm, where λ is the wavelength and d is the transducer diameter. These measurements were digitized and stored (sampling rate = 2.5 GHz, vertical resolution = 11 bits) using a Tektronix (Beaverton, OR, USA) DPO 3054 digital oscilloscope.

C. Data Analysis

Data analysis was performed using Matlab (Natick, MA, USA). Magnitudes of system responses were computed using Equation 4. Phase of system responses were computed two ways: 1) using Equation 5 (direct method), and 2) applying the minimum phase assumption, i. e., taking the inverse Hilbert transform of the natural logarithm of the magnitude of A(ω) [11] (indirect method). An inverse Hilbert transform entails an integral over all frequencies. In practice, data are only available over a finite frequency band. A numerical inverse Hilbert transform over data within a finite frequency band will be valid only if the integrand is negligible outside that frequency band. In this study, the minimum phase model was applied to the transfer function of the entire measurement system, which included source electronics, source transducer, diffraction, hydrophone, and receiving electronics. Because of the limited frequency band of the source transducer, it was possible to satisfy the requirement that the integrand (i.e., measurement system transfer function) was negligible outside the experimental frequency band. It would have been more difficult to apply the minimum phase model specifically to the hydrophone sensitivity, which in this study was typically not negligible outside the experimental frequency band. A substitution method was used to obtain hydrophone sensitivities from system responses [11].

Frequency-dependent phase vectors were unwrapped and smoothed with a rectangular filter of width 50 kHz. An integer multiple of 2π radians was subtracted from the frequency-dependent phase vector difference (between test and reference) so that the mean phase difference over the analysis bandwidth fell between ±2π radians.

The substitution calibration experiment assumes that the test and reference hydrophones are placed at exactly the same depth from the source transducer. A discrepancy in these two depths will introduce an additive phase difference that is a linear function of frequency. Even a slight difference, on the order of four microns (approximately λ/10 at 40 MHz), can produce a substantial effect. Therefore, in order to compensate for this discrepancy, 1) the difference between the direct phase difference vs. frequency measurement (Equation 5) and the indirect phase difference vs. frequency estimate (minimum-phase approach) was least-squares fit to a linear function of frequency, and 2) this linear function of frequency (Δφ = bf) was subtracted from the direct phase difference vs. frequency measurement. Note that the addition or subtraction of a linear phase function in frequency domain corresponds only to a shift in the time domain but not a change in shape of the time domain signal. Koch performed a similar linear adjustment to TDS data by analyzing a low-frequency portion of the spectrum over which the hydrophone phase response was assumed on theoretical grounds to be constant [10]. (Previously, a linear function of the form Δφ = a + bf was used [11]. The inclusion of the constant term, a, was inappropriate. However, it was inconsequential because, as may be seen in Figures 5–7 from [11], the constant terms from linear fits were approximately zero.)

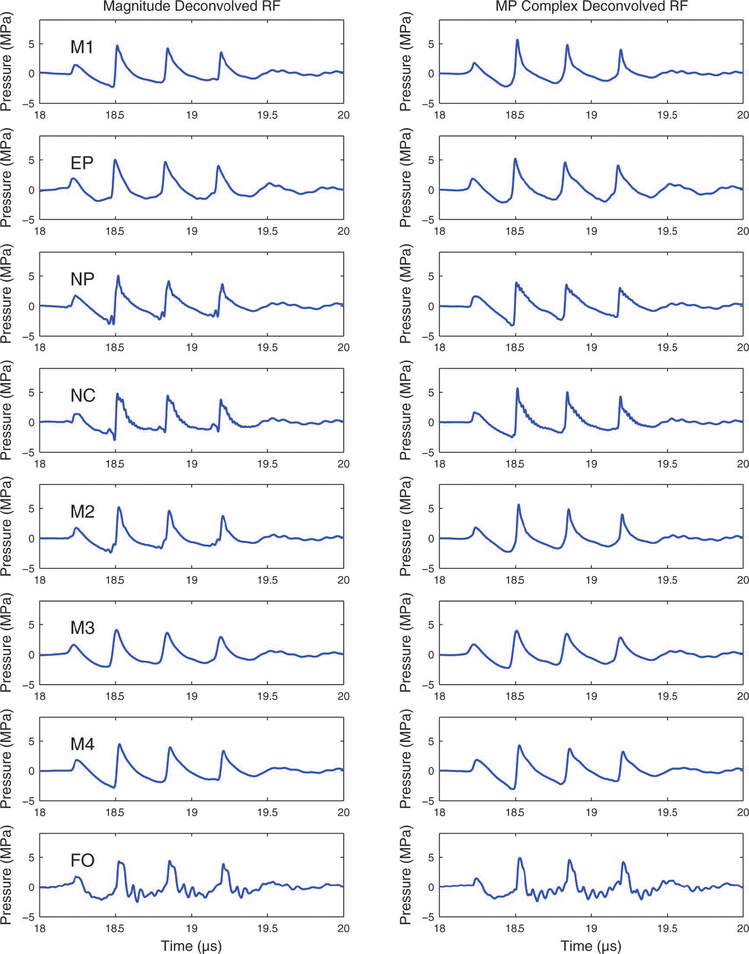
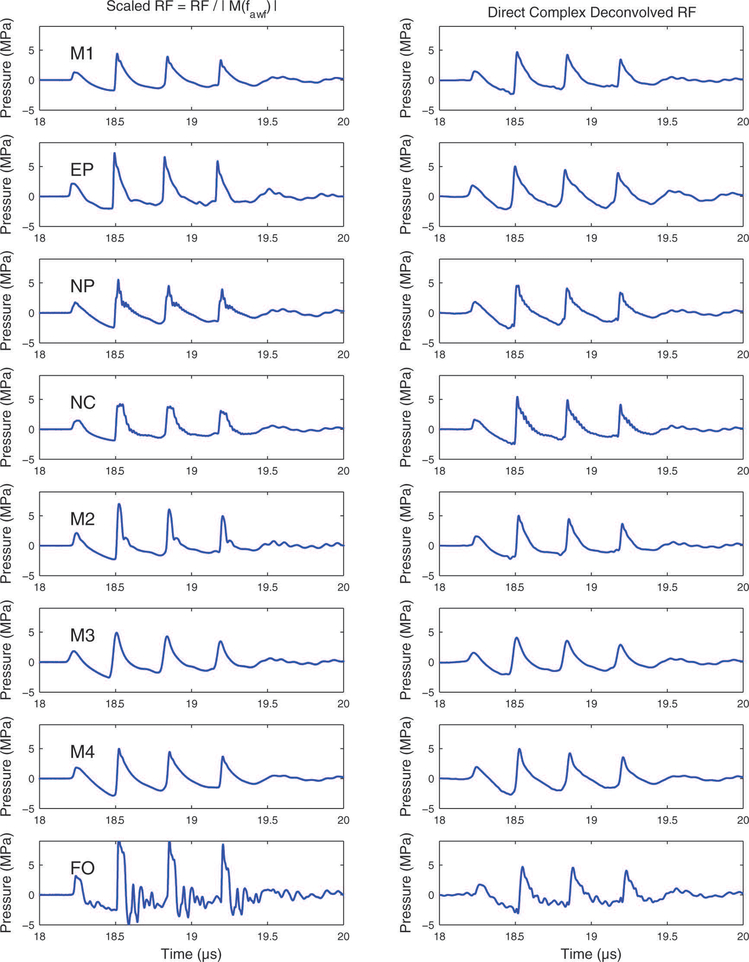
5.

Raw hydrophone output deconvolved with the magnitude of the hydrophone sensitivity (left column) and the complex sensitivity based on the minimum phase assumption.

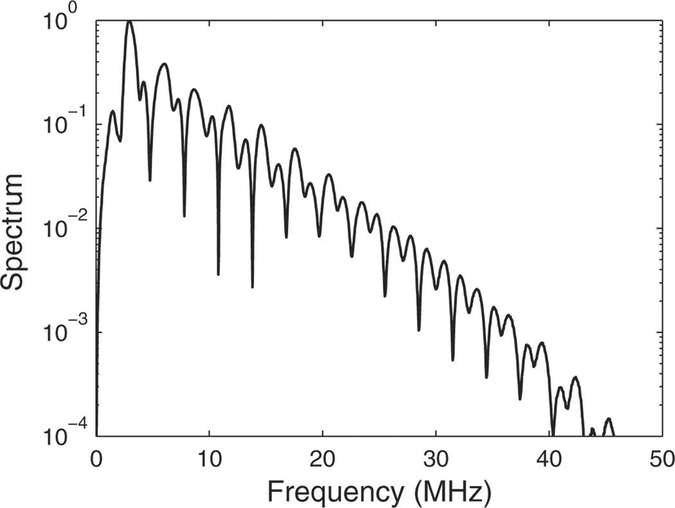
7.

Magnitude of spectrum of test pulse measured with the M4 hydrophone, which had a relatively uniform frequency response.

Broadband sensitivity functions were constructed by concatenating the data acquired with the four broadband source transducers. (See Appendix for details.) Sensitivities at negative frequencies (which were required for the deconvolution) were obtained by assuming that the sensitivity magnitude was an even function of frequency and the sensitivity phase was an odd function of frequency. This Hermitian form for the frequency response follows from assuming that the hydrophone impulse response is a real function. Sensitivities at frequencies below the minimum measurement frequency (near 1 MHz) were estimated as follows. The magnitude of the sensitivity at the minimum measurement frequency was used for all frequencies below the minimum measurement frequency even though the low frequency response is dependent on the hydrophone geometry [22]. The phase at zero frequency was assumed to be zero (as is required for an odd function). The phase at frequencies below the minimum measurement frequency was found by linearly interpolating between zero at zero frequency and the phase measured at the minimum measurement frequency. Prior to deconvolution, signals were low-pass filtered with a zero-mean Gaussian filter of the form exp(−f²/2σ²) MHz in order to suppress amplification of high-frequency noise (resulting from deconvolution), which can be problematic at high frequencies in cases in which the hydrophone sensitivity diminishes to small levels. The value for σ was 35 MHz for all hydrophones except for NP for which σ was reduced to 25 MHz because of particularly low sensitivity for frequencies above 25 MHz.

Pressure waveforms were estimated using 4 methods:

1. Traditional method (ratio of the hydrophone output voltage to the magnitude of the hydrophone sensitivity at the acoustic working frequency) (“Scale”)

2. Deconvolution based on the direct measurement of the complex sensitivity (“Direct”)

3. Deconvolution based only on the magnitude of the sensitivity (“Mag”)

4. Deconvolution based on the estimate of the complex sensitivity assuming that the hydrophone measurement system is minimum phase (“MP”)

The third method, deconvolution based on the magnitude of the sensitivity, was previously proposed by Hurrell [4] as a potential improvement over the traditional method when phase information is unavailable. Similarly, Annex D from Reference [2] implies a magnitude-only deconvolution. The acoustic output parameters (p₊, p₋, PII) were computed using each of the 4 methods for each of the 8 hydrophones.

RESULTS

Figure 2 shows the magnitude and phase of the M1 membrane hydrophone measured by the FDA and the Physikalisch-Technische Bundesanstalt (PTB, Braunschweig, Germany). The FDA measurements used the M3 membrane hydrophone (also calibrated by PTB) as a reference for the measurements in Figure 2. Over the range from 1 MHz to 38 MHz, the RMS difference between the two magnitudes was 8% and the RMS difference between the two phases was 5.2 degrees. Both FDA and PTB measurements capture the rapid oscillations in magnitude and phase at low frequencies. One possible source of disparity is that there was a two-year time lag between the PTB and FDA calibrations. PTB specifies a calibration uncertainty of approximately 10%.

2.

Magnitude and phase of M1 membrane hydrophone measured by the FDA and the Physikalisch-Technische Bundesanstalt (PTB, Braunschweig, Germany).

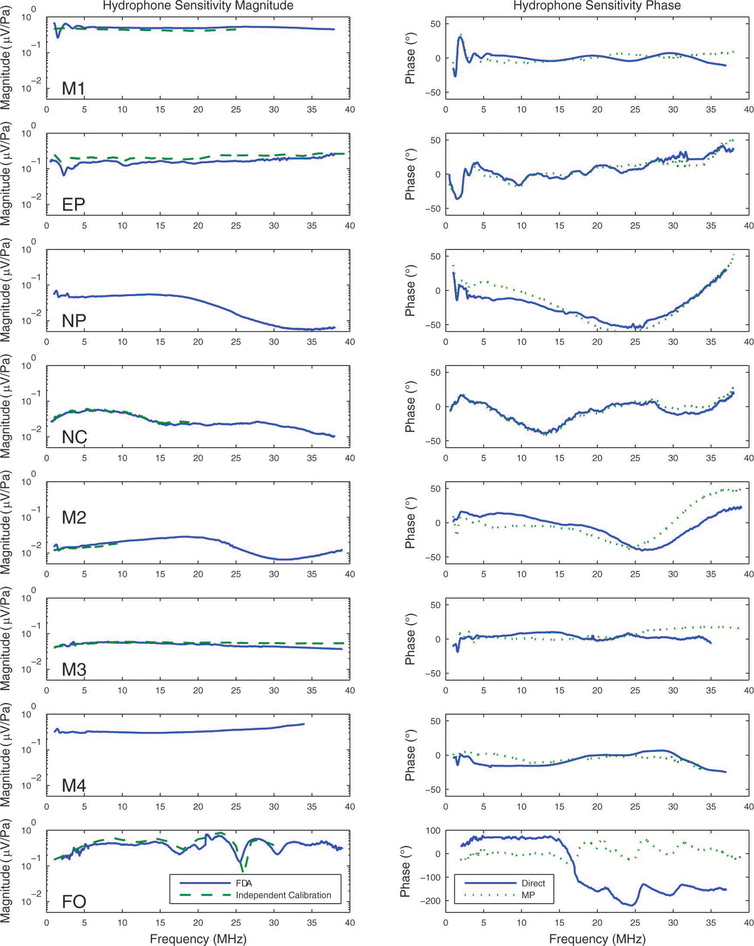
Figure 3 shows the magnitude (left column) and phase (right column) of measurements of sensitivities for the 8 hydrophones. The left column of Figure 3 also shows independent magnitude specifications from a manufacturer or a national measurements laboratory (dashed lines) when available. Generally, the measured magnitudes (solid lines) were in good agreement with independent specifications (dashed lines). The main exception was for the EP hydrophone, for which the discrepancy may be due to temporal drift in sensitivity during the time between the FDA calibration measurements (2011 and 2012) and the independent calibration measurements (2006). (M4 was fabricated at our institution and therefore did not have an independent specification.) From comparison of repeated sensitivity measurements (with repositioning), it was found that precision (standard deviation) of sensitivity magnitude averaged 8.0% at 3 MHz and 7.4% at 20 MHz and that precision of sensitivity phase averaged 3.3 degrees at 3 MHz and 3.1 degrees at 20 MHz. Averaging two sensitivity measurements prior to deconvolution improved measurement precision by a factor of $\sqrt{2}$. The measured phases (solid lines) were in good agreement with the minimum phase computations (dotted lines) for all hydrophones except for the fiber optic hydrophone. The root-mean-square differences between the measured phases and the minimum phase computations were 7 (M1), 6 (EP), 11 (NP), 6 (NC), 20 (M2), 9 (M3), 8 (M4), and 142 (FO) degrees.

3.

Magnitude (left column) and phase (right column) of hydrophone sensitivity. Independent calibrations for magnitude are shown in the left column as dashed lines when available. Minimum phase estimates of phase are shown in the right column as dotted lines.

Figure 4 shows reconstructed pressure waveforms obtained by dividing the hydrophone output voltage by the magnitude of the sensitivity at the acoustic working frequency (left column) and by deconvolving the hydrophone output voltage by the complex hydrophone sensitivity (right column). It can be seen in Figure 3 that the M2 and FO hydrophones had high-pass filter characteristics up to about 15 MHz. This high-pass filtering, which boosted harmonics relative to the fundamental frequency (i.e., the acoustic working frequency), resulted in higher, sharper compressional peaks as shown in Figure 4 (left column). By comparing the left and right columns for Figure 4, it can be seen that deconvolution improved the consistency of the pressure waveforms. The biggest improvement occurred for the fiber-optic (FO) hydrophone.

4.

Raw hydrophone output divided by the magnitude of the sensitivity at the acoustic working frequency (left column) and hydrophone output deconvolved with the complex hydrophone sensitivity (right column).

Figure 5 shows reconstructed pressure waveforms obtained by deconvolving the hydrophone output voltage with the magnitude of the hydrophone sensitivity (left column) and the complex sensitivity based on the minimum phase assumption (right column). In most cases, these methods produced reconstructed pressure waveforms that resembled those produced by deconvolving the hydrophone output voltage with the directly-measured complex hydrophone sensitivity (Figure 4, right column). However, one exception is the waveform acquired with the fiber-optic (FO) hydrophone. In this case, deconvolution with the directly-measured complex hydrophone sensitivity produced a reconstructed pressure waveform that was more consistent in appearance with deconvolved waveforms acquired with the other hydrophones.

Measurements of acoustic parameters obtained from complex deconvolved waveforms were (means ± standard deviations, across all 8 hydrophones) 4.8 ± 0.4 MPa (p₊), 2.4 ± 0.3 MPa (p₋), and 0.21 ± 0.02 mJ/cm² (PII).

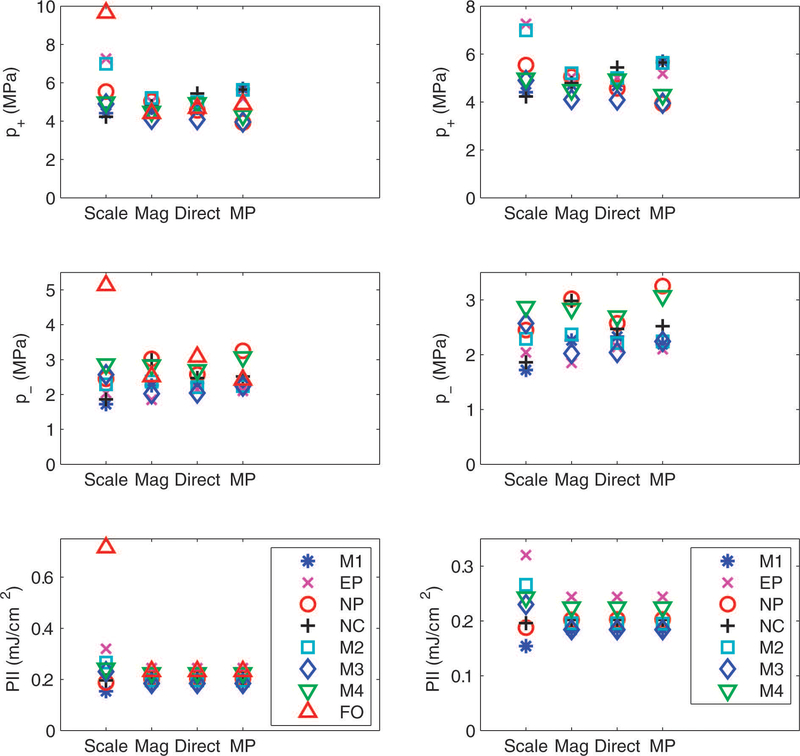
Figure 6 shows peak compressional pressure (p₊), peak rarefactional pressure (p₋), and pulse intensity integral (PII) obtained using the traditional scaling method (“Scale”) and using deconvolution based on the magnitude of the sensitivity (“Mag”), the direct measurement of the complex sensitivity (“Direct”), and the minimum phase estimate of the complex sensitivity (“MP”). Direct deconvolution resulted in a substantial reduction in variance of measurements of p₊, p₋, and PII, regardless of whether the fiber-optic hydrophone was included in the analysis (left panel of Figure 6) or not (right panel of Figure 6). As noted previously [6], PII (unlike p₊ and p₋) does not depend on phase. (This is a consequence of Parseval’s theorem.) Therefore, the three methods of deconvolution yielded identical results for PII for each hydrophone.

6.

Peak compressional pressure (p₊), peak rarefactional pressure (p₋), and pulse intensity integral (PII) obtained using the traditional scaling method (“Scale”) and using deconvolution based on the magnitude of the sensitivity (“Mag”), the direct measurement of the complex sensitivity (“Direct”), and the minimum phase estimate of the complex sensitivity (“MP”). The left column is based on all 8 hydrophones. The right column excludes the fiber-optic hydrophone.

Table III gives means and coefficients of variations (COVs) for the acoustic pulse parameters using “Scale,” “Mag,” “Direct,” and “MP” methods. In addition, Table III gives results obtained by using the “Scale” method with the low-pass filter used for the deconvolution methods. Table III shows that the reduction in COV was primarily due to deconvolution rather than the low-pass filter. The reduction in COV was greater in magnitude when the fiber-optic hydrophone was included in the analysis (top half of Table III), but was still substantial when the fiber-optic hydrophone was excluded (bottom half of Table III). Variability for p₋ in the table could be due in part to low frequencies [27]. In the present study, sensitivities were measured down to approximately f_awf / 3 (approximately 1 MHz) where f_awf is the acoustic working frequency (approximately 3 MHz). Therefore, inadequate deconvolution at very low frequencies (|f|< f_awf / 3) could have contributed error. (IEC Standard 62127–1 [2] recommends that the hydrophone measurement system response should vary by no less than ± 3 dB for frequencies down to f_awf / 2 and up to min { 8 f_awf, 40 MHz }. However, the standard adds that, if possible, the lower limit should be reduced down as far as f_awf / 16.)

Table III.

Means ± standard deviations and coefficients of variation (COV = standard deviation / mean, in parentheses expressed as a percentage) for acoustic pulse parameters for hydrophones obtained using the traditional scaling method (“Scale”), the traditional scaling method plus low-pass filtering (“Scale+LPF”), and using deconvolution based on the magnitude of the sensitivity (“Mag”), the direct measurement of the complex sensitivity (“Direct”), and the minimum phase estimate of the complex sensitivity (“MP”).

	Method	p+ (MPa)	p− (MPa)	PII (mJ/cm2)
All hydrophones	Scale	6.0 ± 1.7 (29%)	2.6 ± 1.0 (39%)	0.29 ± 0.17 (58%)
	Scale+LPF	5.5 ± 1.6 (30%)	2.5 ± 0.9 (35%)	0.27 ± 0.15 (55%)
	Mag	4.7 ± 0.3 (7%)	2.5 ± 0.4 (16%)	0.21 ± 0.02 (10%)
	Direct	4.8 ± 0.4 (8%)	2.4 ± 0.3 (13%)	0.21 ± 0.02 (10%)
	MP	4.9 ± 0.7 (14%)	2.5 ± 0.4 (16%)	0.21 ± 0.02 (10%)
All hydrophones except fiber-optic hydrophone	Scale	5.5 ± 1.1 (20%)	2.3 ± 0.4 (17%)	0.23 ± 0.05 (22%)
	Scale+LPF	5.0 ± 1.0 (20%)	2.2 ± 0.4 (17%)	0.22 ± 0.05 (22%)
	Mag	4.8 ± 0.3 (7%)	2.5 ± 0.4 (18%)	0.21 ± 0.02 (10%)
	Direct	4.8 ± 0.4 (8%)	2.4 ± 0.2 (9%)	0.21 ± 0.02 (10%)
	MP	4.9 ± 0.8 (15%)	2.5 ± 0.4 (17%)	0.21 ± 0.02 (10%)

DISCUSSION

The effects of nonuniform hydrophone sensitivity on measurements of acoustic parameters for a diagnostic ultrasound waveform have been investigated for membrane, needle, capsule, and fiber-optic hydrophones. Deconvolution of hydrophone sensitivity can improve accuracy and precision of measurements of peak compressional pressure (p₊), peak rarefactional pressure (p₋), and pulse intensity integral (PII) from diagnostic ultrasound pulses.

Comparison of the left and right columns of Figure 4 illustrates that deconvolution greatly improved the consistency of reconstructed RF traces. Explanations for remaining discrepancies among deconvolved signals include spatial averaging effects (see sensitive element sizes in Table I), imperfect hydrophone positioning, and calibration uncertainties. The effects of spatial averaging and imperfect hydrophone positioning, which increase with ultrasonic frequency, presumably had a greater impact on estimates of p₊ than estimates of p₋ since p₊ exhibits greater influence from high frequencies than p₋.

As can be seen in Figure 6, deconvolution affected measurements of p₊, p₋, and PII differently. One possible explanation for these differences is related to the waveform shape. The test waveform, which mimicked a pulsed Doppler waveform, exhibited effects of nonlinear propagation. This can be seen in Figure 7, which shows the magnitude of the spectrum of the signal measured using the M4 hydrophone (which had a relatively uniform frequency response). (Note that this signal was measured directly with an oscilloscope without using TDS, so it was not limited to the 40 MHz TDS measurement band.) The effects of nonlinear propagation can also be seen in the time domain (Figure 4, left column), where compressional segments tended to have sharper peaks while rarefactional segments tended to be more rounded. This kind of asymmetry between compressional and rarefactional segments is common for many diagnostic ultrasound signals [28]. It means that higher harmonics of the spectrum manifested themselves more on compressional segments than rarefactional segments. Therefore, compressional features of the nonlinear waveform would be expected to be dominated by higher frequencies while rarefactional features would be expected to be dominated by lower frequencies. Differences in the effectiveness of the deconvolution process for p₊ and p₋ arise as they are dependent on different spectral characteristics of the acoustic field. If hydrophone sensitivities were more uniform throughout the fundamental spectral lobe (e.g., approximately 2 – 4 MHz for the signal studied here) than throughout the entire fundamental plus significant harmonic range (say 2 – 40 MHz), then deconvolution might be expected to have a smaller effect on the fundamental spectral lobe than the harmonic spectral lobes and therefore a smaller effect on rarefactional segments than compressional segments. In addition, errors in assumptions regarding the frequency dependence of complex sensitivity at frequencies below the minimum measurement frequency near 1 MHz (see Methods Section, part C), in combination with some appreciable signal energy below 1 MHz (see Figure 7), may have diminished the effectiveness of the deconvolution process on p₋.

It is useful to consider approaches to deconvolution that do not require knowledge of the phase of the hydrophone sensitivity because hydrophone suppliers often do not provide phase information [4]. As noted previously [6], PII (unlike p₊ and p₋) does not depend on phase. Therefore, as shown in Figure 6 and Table III, estimates of PII were identical for deconvolutions performed with the magnitude of sensitivity and complex sensitivity. Figure 6 and Table III also suggest that for the test signal and hydrophones considered in this investigation, estimates of p₊ (and to a lesser extent, p₋) were similar for deconvolutions performed with the magnitude of sensitivity and complex sensitivity. Although the present dataset is too small to provide definitive conclusions, Figure 6 and Table III suggest that the MP deconvolution may not offer a substantial benefit over the magnitude deconvolution for either p₊ or p₋. This may be partially due to uncertainties in the magnitude of sensitivity feeding through to the calculation of phase from the MP method.

Previously, Hurrell investigated the effect of deconvolution on measurements performed with a membrane hydrophone and a needle hydrophone [4]. Hurrell did not measure phase data but in one case (membrane hydrophone) used a theoretical model to predict phase and in the other case (needle hydrophone) performed deconvolution based on the magnitude of the sensitivity. The membrane hydrophone was used without a matching amplifier and therefore had a monotonically increasing sensitivity for frequencies up to the thickness resonance frequency near 30 MHz. This case is analogous to the hydrophones considered in the present investigation that also exhibited high-pass filter behavior over the main band of frequencies in the test signal (EP, M2, FO). In both investigations, deconvolution noticeably mitigated the excessive sharpness of compressional peaks that had been caused by hydrophone overemphasis of higher frequencies. In comparing nondeconvolved with deconvolved estimates of acoustic waveform parameters for a 2-cycle, 1 MHz pulse measured using the two hydrophones, Hurrell found a reduction in the variation in p₊ from 30% to 18% and a reduction in the variation of p₋ from 12% to 5%.

Wilkens and Koch also investigated the effect of deconvolution on measurements performed with a membrane hydrophone and a needle hydrophone [6]. They measured complex sensitivity using an optical multilayer reference hydrophone. As in Hurrell’s investigation, the membrane hydrophone had a monotonically increasing sensitivity for frequencies up to the thickness resonance frequency near 30 MHz. Wilkens and Koch found that for pulses with center frequencies ranging from 5 – 7 MHz measured with the membrane hydrophone, deconvolution reduced measurements of p₊ by 35%−50% (presumably for the same reasons as explained in the previous paragraph), increased measurements of p₋ by 4%−11%, and decreased measurements of PII by 11%−28%. The substantial reductions of p₊ and PII accompanied by the smaller effect on p₋ are similar to what was found in the present investigation for high-pass-filter hydrophones (EP, M2, FO). In comparing nondeconvolved with deconvolved estimates of acoustic waveform parameters for pulses with center frequencies ranging from 5 – 7 MHz measured using the two hydrophones, Wilkens and Koch found a reduction in the variation in p₊ from 48%−150% to −5%−22% and a reduction in the variation of p₋ from 35%−274% to 5%−30%. The reductions in variations were much greater than those observed by Hurrell and in the present investigation because the needle hydrophone used by Wilkens and Koch had a very nonuniform sensitivity, including a sharp drop of approximately 20 dB between 4 and 5 MHz.

Deconvolution has been applied to high intensity focused ultrasound (HIFU) field measurements. HIFU field measurements can benefit from deconvolution because their spectra exhibit pronounced effects of nonlinear propagation and therefore contain substantial high harmonic content. As in the present study and the two studies mentioned above, Canney et al. found that deconvolution resulted in reduced values for p₊ [29]. For their measurements, obtained with a fiber-optic hydrophone, the reduction of p₊ was on the order of 50% (see Ref. [29], Figure 11). Again, this reduction may be attributable to the high-pass filter characteristic of the hydrophone over a range of frequencies including the fundamental and many low-order harmonics (See Ref. [29], Figure 12b).

Haller et al. compared three hydrophones (fiber-optic, needle, coated membrane) for measurements of HIFU fields [30]. They performed field measurements for two source transducers operated at two power levels each, resulting in a total of four scenarios. Because of challenges associated with HIFU field measurements, they never achieved successful measurements with all three hydrophones for any of the four scenarios. Nevertheless, they found that after deconvolution, discrepancies for p₊ and p₋ were smaller than typical calibration uncertainties of 15%. However, discrepancies for the spatial-peak temporal-average intensity (which is proportional to the pulse intensity integral) were as high as 50%. The authors suggested that different active diameters and different usable frequency ranges of the hydrophones might have contributed to the discrepancies.

A previous investigation by this laboratory indicated that over the range from 5 – 18 MHz, the minimum phase principle could be used to estimate the phase of the hydrophone sensitivity with root-mean-square differences from direct phase measurements less than 4 degrees for several hydrophone types (membrane, capsule, needle) [11]. The minimum phase principle allows phase to be estimated from magnitude measurements, which can be easier to perform than phase measurements. The current investigation extends this finding to a larger set of membrane, capsule, and needle hydrophones over a greater frequency range (1 – 40 MHz). However, in this investigation, when the measurement system included the fiber-optic hydrophone, it did not seem to conform to the minimum phase model. This might be related to resonance behavior of the Fabry-Perot interferometer. Alternatively, it might be due to inaccuracy in the minimum phase estimate arising from the complicated frequency dependence of sensitivity of the fiber-optic hydrophone.

CONCLUSION

The frequency range of a previously-reported TDS-based system for measuring magnitude and phase of hydrophone sensitivity has been extended to 1 – 40 MHz. Complex deconvolution of hydrophone sensitivity has been applied to the task of measuring pressure waveform parameters. For hydrophones with nonuniform sensitivity and acoustic signals with high harmonic content arising from nonlinear propagation, complex deconvolution reduces variability of estimates of p₊, p₋, and PII. When phase information is not available, deconvolution based on magnitude alone offers substantial improvement for p₊, p₋, and PII in many cases.

APPENDIX

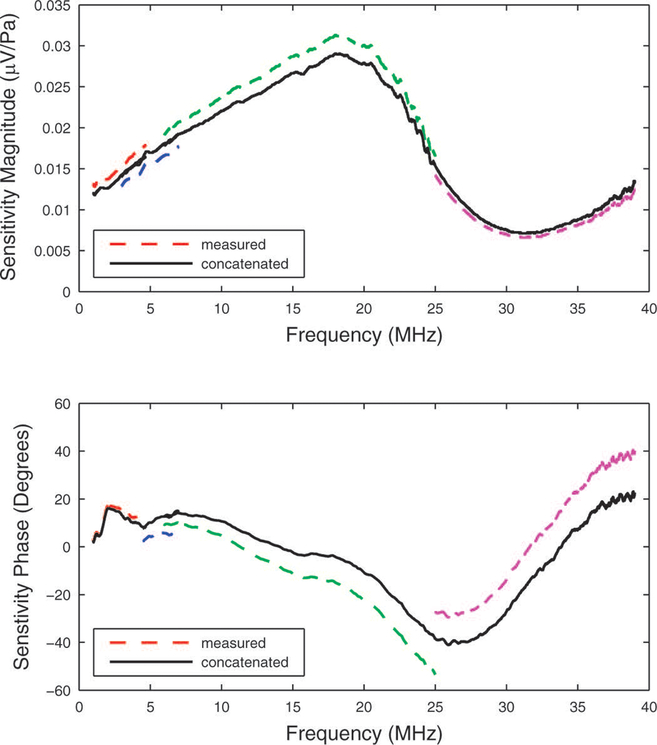
Broadband sensitivity functions were constructed by concatenating the data acquired with the four broadband source transducers with nominal center frequencies of 2, 5, 30, and 50 MHz. The four source transducers produced sensitivity data over frequency ranges that were typically approximately 1–3 MHz, 3–6 MHz, 6–25 MHz, and 25–39 MHz respectively. Figure 8 shows that measurements did not always exhibit perfect agreement at the transition frequencies—3 MHz, 6 MHz, and 25 MHz. This appendix describes how data were adjusted in order to compensate for these disparities, which were likely due to imperfect hydrophone positioning.

8.

Measurements (dashed lines) of sensitivity magnitude (top) and phase (bottom) for the M2 hydrophone. The concatenated functions are shown by the solid lines. See appendix.

A. Adjustment of Sensitivity Magnitude

Let the sensitivity magnitudes measured over each of the four frequency bands be denoted by M₁(f), M₂(f), M₃(f), and M₄(f). Let the transition frequencies between adjacent bands be denoted by f₁₂, f₂₃, and f₃₄ (which in this case would be approximately 3, 6, and 25 MHz respectively). Let the magnitude disparities at the transition frequencies be denoted by

$${\Delta }_{12}=M_2\left(f_{12}\right)–M_1\left(f_{12}\right)$$

$${\Delta }_{23}=M_3\left(f_{23}\right)–M_2\left(f_{23}\right)$$

$${\Delta }_{34}=M_4\left(f_{34}\right)–M_3\left(f_{34}\right)$$

When there was overlap between two adjacent frequency bands, Δ_{i i+1} was computed by taking the average difference between M_i+1 and M_i over the overlapping frequency range. An adjustment term was added to each sensitivity magnitude measurement.

$$M_1\left(f\right)\to M_1\left(f\right)+C_1$$

$$M_2\left(f\right)\to M_2\left(f\right)+C_2$$

$$M_3\left(f\right)\to M_3\left(f\right)+C_3$$

$$M_4\left(f\right)\to M_4\left(f\right)+C_4$$

Three equations may be obtained by imposing continuity at the transition frequencies.

$$C_1–C_2={\Delta }_{12}$$

$$C_2–C_3={\Delta }_{23}$$

$$C_3–C_4={\Delta }_{34}$$

A fourth equation may be obtained by requiring that the average adjustment is zero,

$$C_1+C_2+C_3+C_4=0.$$

With four equations for four unknowns, the adjustment terms C₁, C₂, C₃, and C₄ may be found. The top panel of Figure 8 shows the result obtained for the M2 hydrophone.

B. Adjustment of Sensitivity Phase

According to the Fourier Shift Theorem, a shift in time domain (resulting, for example, from a shift in distance between source and hydrophone) would result in a phase shift in frequency domain that is a linear function of frequency. Therefore, if source-to-hydrophone distances are not exactly equal for all measurements, the measured sensitivity phases could differ by linear functions of frequency. Let the sensitivity phase measured over each of the four frequency bands be denoted by φ₁(f), φ₂(f), φ₃(f), and φ₄(f). Let the phase disparities at the transition frequencies be denoted by

$${\delta }_{12}={\phi }_2\left(f_{12}\right)–{\phi }_1\left(f_{12}\right)$$

$${\delta }_{23}={\phi }_3\left(f_{23}\right)–{\phi }_2\left(f_{23}\right)$$

$${\delta }_{34}={\phi }_4\left(f_{34}\right)–{\phi }_3\left(f_{34}\right)$$

When there was overlap between two adjacent frequency bands, δ_{i i+1} was computed by taking the average difference between φ_i+1 and φ_i over the overlapping frequency range. A linear phase function was added to each sensitivity phase measurement to account for imperfect positioning.

$${\phi }_1\left(f\right)\to {\phi }_1\left(f\right)+D_{1}f$$

$${\phi }_2\left(f\right)\to {\phi }_2\left(f\right)+D_{2}f$$

$${\phi }_3\left(f\right)\to {\phi }_3\left(f\right)+D_{3}f$$

$${\phi }_4\left(f\right)\to {\phi }_4\left(f\right)+D_{4}f$$

As with magnitude, three equations may be obtained by imposing continuity at the transition frequencies.

$$D_1{f}_{12}–D_2{f}_{12}={\delta }_{12}$$

$$D_2{f}_{23}–D_3{f}_{23}={\delta }_{23}$$

$$D_3{f}_{23}–D_4{f}_{23}={\delta }_{34}$$

A fourth equation may be obtained by requiring that the average adjustment is zero,

$$D_1<f_1>+D_2<f_2>+D_3<f_3>+D_4<f_4>=0$$

where <f₁>, <f₂>, <f₃>, and <f₄> are the mean frequencies of the four frequency bands (in this example, 2 MHz, 4.5 MHz, 15.5 MHz, and 32 MHz).

With four equations for four unknowns, the adjustment coefficients D₁, D₂, D₃, and D₄ may be found. The bottom panel of Figure 8 shows the result obtained for the M2 hydrophone.

Concatenating magnitude and phase data in the way described in this appendix is analogous to taking a weighted average of independent measurements, which can result in improved precision.