Challenges Facing Validation of Noninvasive Electrical Imaging of the Heart

Abstract

Noninvasive imaging of regional cardiac electrophysiology remains an elusive target. Such imaging is still in its infancy, particularly in comparison to structural imaging modalities such as magnetic resonance imaging (MRI), x‐ray computed tomography (CT), and ultrasound. We present an overview of noninvasive ECG imaging, and the challenges and successes of the various techniques across a range of applications. Unlike MRI and CT, reconstructing cardiac electrophysiology from remote body surface measurements is a highly ill‐posed problem. We therefore first review the theoretical considerations and associated algorithms that are used to address this issue. We then focus on the important issue of validation, and review and contrast recent advances in this area. Efforts to validate ECG inverse procedures using a modeling‐based approach are addressed first. We then discuss various experimental studies that have been conducted to provide appropriate data for robust validations. We present new data that are simultaneously recorded from dense arrays of electrodes on the epicardium and body surface of anesthetized pigs during sinus rhythm, ventricular pacing, and regional ischemia. These data have been obtained specifically to help validate inverse ECG procedures, and form a useful supplement to recent clinical validation studies. Finally, clinical applications and outstanding issues regarding noninvasive imaging of regional cardiac electrophysiology are addressed.

A major source of cardiac morbidity is electrical rhythm disturbance due to altered electrophysiological substrate. The 12‐lead ECG is the primary clinical tool for noninvasive assessment of cardiac electrical function, but electrocardiographic imaging has seen little development over the last century. The quantitative interpretation of a 12‐lead ECG is based on a high degree of pattern recognition and it lacks the ability to provide detailed quantitative information about regional electrical function. This is due in part to the limited number of recording sites used to sample the electrical field generated by the cardiac source and also its primitive theoretical basis. These limitations have been recognized for many years ¹ and calls for clinical improvement have recently been made. ² , ³

The diagnostic capability of an ECG can be improved by increasing the number of leads used to sample the cardiac electric field, thus increasing the amount of information available about the electrical source. Work in this direction began in the 1960s ⁴ , ⁵ and a variety of electrode configurations have been used to increase the spatial sampling density. ⁶ The increased data produced by the electrode configurations require new methods of visualization and analysis. Interpretation has often been done by building up a database of body surface potential maps from patients with known cardiac conditions and using the database in a pattern‐matching procedure. ⁷ While this approach has been shown to be useful, ⁸ one drawback is that no standard lead set has yet been defined. This has resulted in a variety of databases being developed with little communication between them. The success of this procedure is therefore reliant on the quality of the databases, and can result in spatially inadequate or even incorrect diagnoses.

An alternative to the above pattern‐matching approaches are techniques based on the physical laws governing electrostatics. Quantitative interpretation of densely sampled ECG data in terms of the underlying cardiac electrical activity is an inverse problem. Over the past few decades, various mathematical algorithms have been developed in an attempt to solve the ECG inverse problem. ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ Typically, the ECG inverse problem is not uniquely determined, since there exist multiple versions of the source (cardiac) electric fields that can give rise to the remote (body surface) field measurements.

Early approaches overcame this nonuniqueness issue by modeling the heart as a combination of a small number of fixed or moving dipoles. ¹⁴ It was later recognized that the problem was uniquely determined if it was formulated in terms of reconstructing epicardial potentials from the body surface potential recordings. ¹⁰ However, the reconstruction of epicardial potentials from body surface recordings is an ill‐posed problem. This means that in the presence of noise (which always exists in practice), a solution to the ECG inverse problem may produce a result that bears no resemblance to the true electrical source. The emergence of a general theory for such ill‐posed problems ¹⁵ and the introduction of constraints on the mathematical solutions have resulted in a variety of algorithms for the ECG inverse problem. However, since they are based on a generic approach, most of the modern algorithms fail to incorporate the underlying physiological processes governing the generation of body surface potentials.

An alternative to the epicardial potential approach is to pose the problem in terms of the myocardial activation sequence. ¹⁶ , ¹⁷ , ¹⁸ This has potential advantages over the epicardial potential problem formulation, not least in that it deals directly with the underlying physiological process responsible for generating the body surface potentials (namely, an evolving wave of depolarization). However, it introduces additional complexities in the modeling process, such as the need to accurately model the entire heart instead of just modeling the epicardial surface. Techniques based on this activation imaging approach have been described in several studies. ¹⁹ , ²⁰ , ²¹ , ²²

Given the sound theoretical basis for the above ECG inverse methods, one question that naturally arises is: why have these techniques not superceded the 12‐lead ECG for routine use by clinical cardiologists? Possible reasons are: (1) mathematical methodologies and computational modeling techniques have not been sufficiently powerful nor efficient to be of practical use; (2) there is a lack of invivo experimental and clinical studies that demonstrate the accuracy of these ECG inverse methods on living subjects; and (3) the increased detail obtained via various inverse procedures is not sufficient to justify the extra effort needed to obtain it.

Mathematical solutions to the first issue have been formulated, ¹⁹ , ²⁰ making possible a tractable computational implementation, which will continue to improve with faster CPUs and increasing memory resources. On the other hand, the “ideal” ECG inverse validation study may still be some way off. The essential measures of such a study include: accurate anatomical geometry and tissue architecture (including anisotropic, heterogeneous structure); concurrent electrical measures from the torso (model inputs) and heart (to check ECG inverse predictions); heart and body surface electrode locations; regional distributions of electrical properties (such as conductivities) and associated anisotropy; and all of these measures for a variety of cardiac conditions (normal versus pathological). Furthermore, to complete the ideal validation study, all of these measures would be achieved noninvasively in the same subject, preferably human.

It is only when the issues (1) and (2) above are appropriately addressed that the question of effort versus reward (3) can be addressed. What is clear is that accurate geometrical information is required to make a reasonable attempt at the inverse solution. ²³ , ²⁴ In a clinical setting, obtaining this geometrical information necessitates obtaining an appropriate structural image of the patient using a modality such as MRI or CT. This adds significant extra time and expense to that required for a standard ECG assessment. Technology has a role to play in decreasing this time and expense (e.g., ultra‐fast CT, automatic image segmentation algorithms), but the onus is clearly on those working in the field of inverse electrocardiology to make the case that performing a quantitative inverse procedure justifies the additional costs.

This review first presents a brief summary of the common ECG inverse techniques. We then focus on the variety of experimental, clinical, and modeling studies that have attempted to validate the computational methods.

ECG FORWARD MODELING

ECG inverse procedures all begin with a description of the forward problem, i.e., the problem of relating the electrical source (be it the activation sequence or epicardial or pericardial potentials) to densely sampled body surface ECG signals. The standard forward problem can be expressed as:

(1)

where φ_bx, t) is a vector of body surface electropotential signals at location x and time t, is the so‐called transfer matrix, which contains all the information regarding geometry and tissue conductivities, and φ_h (y, t) is the electrical source on or in the heart at location y (either epicardial or transmembrane time‐varying potentials).

This simple description disguises a number of important issues. First, the quasistatic approximation is universally adopted in this field. Thus, at each time instant, the body surface potential distribution is assumed to be entirely determined by the simultaneous electrical state of the heart source (thus inductive and capacitive effects are assumed to be negligible). Hence, the forward problem can be thought of as a series of independent problems — one for each time instant. Another widely applied assumption is that the cardiac motion can be ignored, at least for restricted time intervals (e.g., during depolarization). Thus, the transfer matrix is assumed to be constant over these restricted time intervals. Third, φ_b (x, t) and are corrupted in practice by a variety of noise sources, each of which may vary with time.

The transfer matrix is constructed by solving the physical equations that relate cardiac activity to the body surface ECG signals. For the epicardial potential formulation, the potential in the volume exterior to the heart is governed by

(2)

where φ_e is the extracellular potential and σ_e is the extracellular conductivity tensor, which is spatially heterogeneous due to various tissues of the body. For the activation formulation, Equation (2) is combined with the governing equation within the heart:

(3)

where σ_i is the intracellular conductivity tensor and φ_m is the transmembrane potential. Equation (1) is obtained from (2) or (3) through the use of an appropriate numerical technique.

Theoretically, the transfer matrix is straightforward to compute. For the epicardial potential imaging problem, the transfer matrix computation is dependent on the geometry and conductivities of the tissues exterior to the heart. For the transmembrane potential/activation time formulation, the transfer matrix is also dependent on the geometry and conductivities of the heart. The issues surrounding the computation of the transfer matrix are mostly practical. For example, the amount and quality of information required to describe the geometric solution domain is debatable, and this necessarily affects the information that may ultimately be required in a clinical setting.

ECG INVERSE MODELING

Starting from the above forward problem, the inverse problem can be relatively simply stated: invert the transfer matrix and apply it to the measured φ_b (x, t) to compute the unknown heart sources φ_h (y, t). For either of the source formulations outlined above, the ill‐posed nature of the discretized inverse problem manifests itself in the severe ill‐conditioning of the transfer matrix, which means that the calculation of its inverse is generally not feasible, even in a noise‐free situation.

Epicardial Potentials Inverse Methods

To produce a useful solution, a pseudoinverse of the transfer matrix can be constructed, using techniques involving a truncated singular value decomposition (SVD) of , or by imposing other numerical procedures such as Tikhonov regularization. ¹⁵ In practice, these two families of methods are the most widely used.

The Tikhonov solution is obtained by minimizing the objective function:

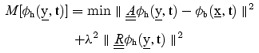(4)

where 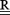is a constraint matrix, ∥∥ is the Euclidean norm, and λ is the regularization parameter, which may be time varying.

There are three common Tikhonov regularization methods—zero, first, and second order, for which 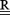is taken to be the identity matrix (zero‐order), a discrete approximation of the surface gradient (first order), or the Laplacian (second‐order). The regularization parameter controls the weight given to the residual and solution norm, and controls the degree of smoothing. The many variants of Tikhonov regularization generally use zero‐order regularization and mainly differ by the manner in which λ is determined. ²⁵

Another method of treating the ill‐conditioned nature of the transfer matrix is to obtain a well‐conditioned rank‐deficient variant of to use in its place. This is easily achieved by truncating an SVD expansion of . The major question that arises with this approach is how to determine the appropriate place to truncate the singular values. The performance of truncated SVD regularization is often indistinguishable from that of zero‐order Tikhonov regularization.

Regularization constraints are often applied independently to the individual members of the ECG time‐series data under the quasistatic approximation. ¹⁰ , ²⁶ , ²⁷ Such approaches neglect the fact that the time‐series components are not independent, since they arise from a propagating wave of excitation. In principle, an approach that simultaneously operates on the entire time series, incorporating physiological temporal constraints, could overcome these shortcomings. ²⁸ , ²⁹ , ³⁰ , ³¹ However, it remains to be established whether such approaches can provide more accurate predictions of cardiac electrical activity in the experimental or clinical settings.

Activation Sequence Inverse Techniques

Activation inverse algorithms revolve around obtaining an initial estimate of the depolarization sequence from the body surface potentials, then refining this estimate through an optimization process designed to minimize the difference between the known torso signals and those predicted using the transfer matrix. The accuracy of the results obtained from this process is strongly dependent on the initial estimate used in the optimization process.

The activation inverse approach has been around for several decades. ¹⁶ , ¹⁸ However, obtaining an appropriate initial estimate of the solution proved to be challenging, until a significant advancement ³² provided greatly improved activation inverse predictions. ¹⁹ The key difference of this work was that instead of trying to obtain an initial estimate of the entire activation sequence (a problem with infinitely many degrees of freedom), one first attempts to locate some key features of the activation sequence, namely, the critical points (which are essentially the activation breakthrough points). With an accurate localization of the critical points, the computation of the entire activation sequence is theoretically well‐posed. This so‐called Critical Point Theorem has paved the way for the practical use of activation inverse algorithms. ¹⁹ Other groups have since adopted the activation inverse approach, ²² , ³³ and modifications to improve the performance of the algorithm have been proposed. ³⁴

ECG INVERSE VALIDATION

Although the theoretical developments of various ECG inverse techniques have been based on mathematically sound formulations, it remains to be established whether these methods can offer useful insight into the electrical function of the heart in the laboratory or clinical setting. Quantitative experimental validation studies are required in order to convince researchers and cardiologists that ECG imaging can aid in the clinical assessment of cardiac function. However, such experimental studies are by no means trivial. In order to assess the accuracy with which ECG inverse methods can reconstruct electrical images of the heart, an “ideal” set of in vivo experimental data would contain the following:

• 1Concurrent sets of densely sampled electropotential signals from the body surface and heart.
• 23D locations of each of the electrical sampling points (electrodes).
• 3Patient‐ or animal‐ specific quantitative descriptions of the anatomical geometry of the torso and all of its constituent organs and tissues.
• 4Spatial descriptions of the electrical properties (e.g., conductivities) of the various tissues, including heterogeneities and anisotropic material descriptions for the appropriate tissues (e.g., heart and skeletal muscle).

The complexity of such an experiment has meant that no attempt has been made to record all of these data for a single patient or animal. It is even questionable as to whether this may even be technically possible. Instead, a variety of experimental studies have reported subsets of these measures, both in vivo and in vitro, with varying quality and accuracy. In an attempt to validate ECG inverse methods, these subsets of recordings have been amalgamated with data from the literature (estimates from other preparations), and/or synthesized data generated using computer models.

Modeling Studies

Since the early theoretical work in developing ECG inverse algorithms, there have been a wide variety of modeling studies that have attempted to assess the accuracy of the methods and highlight the relative importance of various sources of data required to solve the ECG inverse problem. In the absence of the ideal clinical data set, the majority of studies have combined a limited set of experimental recordings with synthetic ECGs. Some of the most detailed studies of this kind ³⁵ , ³⁶ have incorporated dense arrays of epicardial electrograms from dog hearts under a variety of conditions into forward simulations using an anatomically realistic torso geometry to generate body surface signals. These synthetic torso signals were then fed into the inverse algorithm to reconstruct epicardial potentials. There are a number of similar studies of note. ²⁴ , ³⁷ , ³⁸ , ³⁹

While such studies have reported some interesting conclusions, their limitations should not be overlooked. The signals and transfer matrix of these model simulations were noise free. Although attempts were made to “corrupt” the synthetic data by imposing noise, this was often limited to adding noise to the signals, or a small amount of uncertainty to electrode locations. By far the most damaging to any inverse algorithm is the effect of geometric noise, ⁴⁰ particularly that associated with uncertainty in the position of the heart within the torso. ²³ Most of the ECG inverse modeling studies have failed to address this.

Modeling studies have been repeatedly used to determine the importance of various factors, such as the relative conductivities of different tissue types to the accuracy of the ECG inverse predictions. ²⁴ , ³⁶ Typical simulations involved the use of recorded heart data to generate synthetic torso signals via a transfer matrix constructed from one combination of tissues and conductivities. The synthetic signals were then inverted using a transfer matrix constructed from a different (typically reduced) combination of these factors. The original and reconstructed heart signals were then compared to assess the importance of the changes in tissue properties. The major limitation with these studies is that epicardial potentials are extremely sensitive to the surrounding impedances, i.e., changing external tissue properties markedly affects the epicardial potentials. Thus, it is questionable whether the effect of tissue impedances can be determined using such modeling studies.

These limitations all strengthen the need for in vivo data for validation of ECG inverse techniques.

Experimental Studies

The earliest attempts to simultaneously record dense arrays of torso and heart electropotentials were reported by Spach et al. ⁴¹ in the chimpanzee, and Barr and Spach ¹⁰ in the dog. The lack of spatiotemporal resolution and the fact that these studies were published prior to the major theoretical developments in ECG inverse techniques have resulted in limited interpretation of the results in the context of validation of ECG imaging methods. Neither of these data sets is currently available, rendering more a more modern inverse assessment impossible.

A decade later, a carefully controlled series of in vitro experiments involving isolated dog hearts submerged in a torso tank ⁴² provided a good source of data for ECG inverse validation studies. ³⁹ , ⁴³ Using this approach, a range of pathological maneuvres, such as changes in pacing rate and temperature, ⁴⁴ reduced coronary flow, ⁴⁵ and variations in heart location, ²³ were performed to investigate their effects on surface ECG activity. This experimental model provided quantitative information regarding the size, shape, and orientations of the hearts in the known torso geometry, together with locations of the concurrent epicardial and torso surface electropotential recordings, and has been used to examine the effects of varying conductivities and heart position on torso surface recordings. ²³ , ³⁶ While the setup was anatomically realistic, the ECG data arises from a fundamentally in vitro setup, and the conclusions from these studies remain to be demonstrated using in vivo or in situ heart preparations.

To address this, we have developed methods to simultaneously record dense arrays of in situ epicardial and body surface ECGs from anesthetized pigs using a UnEmap recording system (UniServices Ltd, New Zealand). ⁴⁶ Detailed measurements of thorax and cardiac geometry were taken together with individual electrode locations for the torso and heart arrays. Simultaneous electrical activity was reported for a range of epicardial pacing sites, ⁴⁷ and during/following acute regional ventricular ischemia. ⁴⁸ Full details of the ECG mapping techniques, computational model construction and customization, and signal visualization methods have been published previously. ⁴⁶ , ⁴⁹

Figure 1 illustrates concurrent porcine heart and body surface electropotential measures from five experiments under control conditions (sinus rhythm), and during epicardial pacing at two different sites. In all three cases, spatial maps of the mean epicardial activation times and the mean torso QRS integrals illustrate the small variability of the torso ECG recordings for a given epicardial activation sequence. These technically difficult experiments not only provide suitable in vivo data to quantitatively assess the accuracy of ECG imaging techniques, but the repeatability of the torso recordings (i.e., the close proximity of the body surface integral extrema) for similar conditions between experiments suggests that some features may be robustly obtainable using computational ECG inverse methods. Similar repeatability of torso characteristics has been demonstrated in human studies that compared endocardial pace‐mapping results with a database of body surface potential images. ⁵⁰ , ⁵¹

Figure 1.

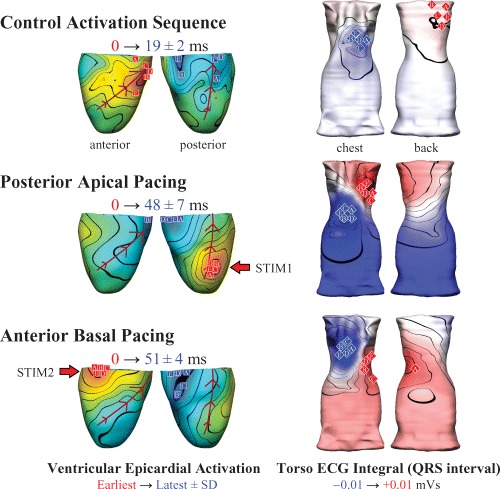
Simultaneous epicardial (left) and body surface ECG (right) imaging in the anesthetized pig (n = 5) during sinus rhythm (control heart rate 156 ± 28 bpm; mean arterial blood pressure [ABP] 122/80 mm/Hg), and epicardial pacing (approximately 25 ppm above the intrinsic rate). Posterior apical pacing (STIM1) significantly increased the dispersion of epicardial activation from 19 ± 2 ms (control) to 48 ± 7 ms (p<0.01) and decreased the ABP by approximately 45/25 mmHg. Activation dispersion for antero‐basal epicardial pacing (STIM2) was 51 ± 4 ms (p<0.01 compared to control) and the ABP dropped by approximately 45/20 mmHg. Epicardial activation and torso ECG integral maps show averaged data, with individual observations indicated for earliest (red squares) and latest (blue squares) epicardial activation, and positive (red diamonds) and negative (blue diamonds) extrema of the torso ECG QRS integral maps. The minor nature of the variations in body surface activity suggests that some electrical features may be robustly obtainable using in vivo inverse ECG imaging.

Figure 2 illustrates changes in epicardial activation and repolarization sequences, together with the concurrent QRST integral maps due to acute ischemia induced by 4 minutes of total LAD occlusion in the anesthetized pig. Epicardial changes were clearly reflected in the body surface recordings, with the marked electrical changes (delayed activation, early repolarization, and elevated ST segments) on the anterior surfaces of the ventricles and torso. An inverse ECG technique applied to human body surface ECGs obtained during acute ischemia ⁵² provided reasonable qualitative agreement with regions of reduced perfusion estimated from fluoroscopic examination of the coronary anatomy. These results and the experimental data illustrated in Figures 1 and 2 suggest that the combination of ECG inverse methods with dense body surface ECG mapping may well serve as a useful non invasive tool to investigate electrocardiac abnormalities in the in vivo experimental or clinical setting.

Figure 2.

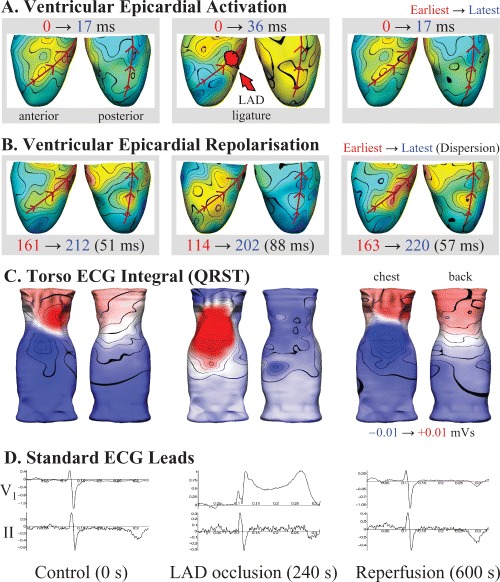
Concurrent epicardial and torso ECG activity before (left), following 4 minutes of total left anterior coronary artery (LAD) occlusion (middle), and after 6 minutes of reperfusion (right) in an anesthetized pig. (A) Epicardial activation sequence mapping highlights the region of slowed conduction (blue) distal to the LAD snare during occlusion, while repolarization (B) was earliest (red) in the same region, consistent with the known effects of ischemia on the cardiac action potential. (C) Body surface QRST integral mapping highlighted a marked region of abnormal positivity adjacent to the ischemic portion of the heart, consistent with the ST segment elevation seen on the standard precordial lead‐V1 (D), while lead‐II showed relatively little change during the entire protocol.

While the animal studies have posed some interesting hypotheses and elucidated potentially useful techniques, validation of the methods, and confirmation of the results in humans remains extremely challenging. The ability to record the ideal set of ECG and geometric data to validate inverse ECG algorithms in the clinical setting is practically infeasible. However, recent attempts have been made in this direction.

A recent study ⁵³ described efforts to validate inverse ECG imaging in humans. Studies were conducted in which CT images of patients were used to create the geometric torso models needed for the transfer matrix computation. Densely sampled (224) body surface ECGs were acquired from several patients, for which epicardial potential inverses were computed. Results were obtained for activation and repolarization in a normal heart, a heart with a conduction defect, pace activation, and atrial flutter. These results were compared to the known disorders and were shown to be in qualitative agreement. However, a quantitative validation was lacking since no in vivo heart recordings were available. Further qualitative validations have been performed previously. ⁵⁴ , ⁵⁵

To date, arguably the most quantitative clinical ECG inverse validation studies ⁵⁶ , ⁵⁷ have assessed the accuracy of methods that reconstruct myocardial activation (depolarization) times. These validation data were based on the fusion of endocardial catheter mapping protocols with MRI, to determine the patient‐specific cardiac and torso geometry. Localization of initial activation sites showed good agreement with data measured using the catheter based CARTO system for paced hearts, for patients with Wolff‐Parkinson‐White syndrome, and in patients with atrial arrhythmias. These are some of the first clinical ECG imaging studies to validate the ECG inverse techniques using concurrent in vivo cardiac and body surface ECGs.

CLINICAL APPLICATIONS AND ISSUES

There are many questions and issues that need to be addressed, and many validation experiments that need to be performed before one can be confident that quantitative noninvasive electrical imaging of the heart can provide efficient and accurate diagnoses in the clinical setting. Such issues include the cost and logistics behind obtaining patient specific anatomical information (via MRI/CT/ultrasound) and whether these can be alleviated to some degree using techniques that can customize models to patients in the absence of detailed information. It is debatable as to whether an inversely computed electrical image of the heart is worth the extra expense, given the historical success of the 12‐lead ECG. Moreover, even if it was worth it, clinical use of such an approach would likely face great inertia from the medical profession due to the dominance of the 12‐lead ECG and the mind set that surrounds it.

However, it is clear that there are many advantages that can be offered by more detailed noninvasive imaging of the electrical activity of the heart, although it should be expected that the prospective imaging modality will be an adjunct rather than a replacement for the 12‐lead ECG. At a minimum, one would expect to provide much greater precision in ECG‐type diagnosis by filtering out the contamination that noncardiac geometric factors have on the ECG. This would improve the sensitivity and specificity of a diagnosis. From the patient perspective, an increased confidence associated with a diagnosis may be worth paying a premium for, helping to alleviate the issue of the increased cost to obtain such a diagnosis.

There is also potential benefit to be obtained from inverse ECG imaging in the guidance and evaluation of antiarrhythmic interventions, for example, in the case of catheter ablation or drug therapy. ⁵⁸ , ⁵⁹ In ablation procedures, a priori determination of the arrhythmogenic focus would certainly be advantageous, but this may be very challenging in many situations, such as for ectopic foci originating from the ventricular septum. Quantitative information regarding the location of ectopic activity or accessory pathways could help guide catheter placement and reduce operating times in the catheter clinic.

It is also worth noting that inverse ECG imaging is a functional imaging technique. It would be interesting to follow, for instance, electrophysiological changes during cardiac stress tests with more precision than is currently available with the 12‐lead ECG. In addition, the study of aging and disease on cardiac electrophysiology would be greatly aided by quantitative electrical imaging of the heart. Although there are still several hurdles to jump before quantitative noninvasive electrical imaging of the heart becomes a routine tool in cardiovascular research or clinical practice, the benefits of the technology are extremely promising.