Skip to main content
PMC home page
Annals of Noninvasive Electrocardiology logoLink to Annals of Noninvasive Electrocardiology
. 2004 Apr 13;9(2):127–135. doi: 10.1111/j.1542-474X.2004.92531.x

Effects and Significance of Premature Beats on Fractal Correlation Properties of R‐R Interval Dynamics

Mirja A Peltola 1, Tapio Seppänen 1, Timo H Mäkikallio 1, Heikki V Huikuri 1
PMCID: PMC6932140  PMID: 15084209

Abstract

Background: Premature beats (PBs) have been considered as artifacts producing a bias in the traditional analysis of heart rate (HR) variability. We assessed the effects and significance of PBs on fractal scaling exponents in healthy subjects and patients with a recent myocardial infarction (AMI).

Methods: Artificial PBs were first generated into a time series of pure sinus beats in 20 healthy subjects and 20 post‐AMI patients. Thereafter, a case‐control approach was used to compare the prognostic significance of edited and nonedited fractal scaling exponents in a random elderly population and in a post‐AMI population. Detrended fluctuation analysis (DFA) was used to measure the short‐term (α1) and long‐term (α2) fractal scaling exponents.

Results: Artificial PBs caused a more pronounced reduction of α1 value among the post‐AMI patients than the healthy subjects, for example, if >0.25% of the beats were premature a >25% decrease in the α1 was observed in post‐AMI patients, but 4% of the premature beats were needed to cause a 25% reduction in α1 in healthy subjects. Both edited (1.01 ± 0.31 vs 1.19 ± 0.27, P < 0.01) and unedited α1 (0.71 ± 0.33 vs 0.89 ± 0.36, P < 0.05) differed between the patients who died (n = 42) and those who survived (n = 42) after an AMI. In the general population, only unedited α1 differed significantly between survivors and those who died (0.96 ± 0.19 vs 0.83 ± 0.27, P < 0.05).

Conclusions: Unedited premature beats result in an increase in the randomness of short‐term R‐R interval dynamics, particularly in post‐AMI patients. Premature beats must not necessarily be edited when fractal analysis is used for risk stratification.

Keywords: heart rate, fractal correlation, premature beats

Spectral and statistical measures of heart rate variability (HRV) provide prognostic information on patients after an acute myocardial infarction. 1 , 2 , 3 However, these conventional methods may not provide adequate information on the complexity that lies inside beat‐to‐beat variability. Several new methods based on chaos and fractal theory have been developed to obtain approaches in quantifying the dynamic properties of R‐R interval time series. 4 , 5 , 6 , 7 , 8 , 9 It has been suggested that nonlinear HRV methods can provide important information on the dynamics of the heart rate variability in various clinical settings. 10 , 11 , 12 , 13 , 14 In particular, detrended fluctuation analysis (DFA) of R‐R interval data has been of increasing interest. Analysis of the short‐term fractal scaling exponent (α1) has provided prognostic information in many patient populations. 11 , 13 , 14

Most ECG recordings include technical or biological artifacts that cause a bias in the reliable measurement of HRV. Premature beats have been commonly considered as one source of error in the HRV analysis and several methods of handling and editing the artifacts and premature beats in the HRV data have been developed and tested. 15 , 16 , 17 , 18 , 19 , 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 It has been recently suggested that premature beats may have an important role in the new dynamic analysis of R‐R interval behavior, and should perhaps be included in the analyses, because they represent the real beat‐to‐beat R‐R interval time series. 13 , 14 However, the true effects of the premature beats on the nonlinear HR variability measures are largely unknown.

The purpose of the present study was to provide more information on the effects of the premature beats on the fractal scaling exponent α1 and α2 in two different populations, that is, among subjects without evidence of structural heart disease and among patients with a recent myocardial infarction (AMI). We tested the hypothesis that the same amount of premature beats may have quantitatively different effects on nonlinear indices of HRV among the healthy subjects and patients with a recent myocardial infarction. We also tested, which of the many editing methods of premature beats is most suitable for fractal analysis of HRV. Finally, we assessed whether the short‐term and long‐term fractal scaling exponents α1 and α2 measured either from original R‐R interval time series including the premature beats or from the R‐R interval data after editing the premature beats separates the patients or subjects who remain alive from those who experienced a cardiac death during the follow‐up.

STUDY POPULATION AND METHODS

The effects of the artificial premature R‐R intervals on nonlinear HRV measures were studied from data sets of 8000 R‐R intervals with pure sinus beats. Twenty R‐R interval time series from 15 healthy subjects with no history of heart disease were selected from a previously described population of 114 healthy subjects 32 and 20 R‐R interval time series of 15 patients who had survived an AMI. The details of the post‐AMI population have been described elsewhere. 33 Mean age of the healthy subjects was 45 ± 11 years and that of post‐AMI patients 54 ± 5 years. General R‐R interval variation was measured by the standard deviation of all normal R‐R intervals (SDNN) and it was significantly lower (P < 0.001) among the post‐AMI patients (85 ± 35 ms) than among the healthy subjects (175 ± 50 ms).

The effects of the real premature beats on the nonlinear HRV measures were studied from 24‐hour R‐R interval data of post‐AMI patients and from 24‐hour R‐R interval data of a random elderly population. Forty‐two post‐AMI patients, who died during the follow‐up of 14 ± 8 months, and 42 post‐AMI patients matched with age, sex, functional class, and ejection fraction, who were alive after the follow‐up, were selected from a previously described post‐AMI population. 33 Beta‐blocker drugs were given to 80 patients (95.2%), digoxin treatment was given to 8 patients (9.5%), and a calcium antagonist to 10 patients (11.9%). Forty‐two healthy elderly subjects, who died during the follow‐up of 120 months and 42 controls, who were alive, matched with age, sex, and functional class were selected from a large survey of the health status of the elderly in the city of Turku, Finland. The details concerning enrollment, diagnosis, and follow‐up of this random sample of 480 people aged 65 or more, who were living in the community from the register of the Social Insurance Institution have been described elsewhere. 34 , 35 , 36 None of the 42 healthy elderly subjects that were included in this study were taking medication. Mean age of the selected elderly healthy subjects was 72 ± 4 years and that of post‐AMI patients 69 ± 8 years. All deaths in both study populations were classified as cardiac deaths. General R‐R interval variation was measured by SDNN and it was significantly lower (P < 0.001) also in this post‐AMI group (81 ± 29 ms) compared to that of the elderly subjects (139 ± 35 ms).

The measurements of the all the 8000 R‐R interval data were done with a RR recorder, a real‐time microprocessor QRS detector system 37 (Polar Electro Oy, Kempele, Finland). The 24‐hour electrocardiographic recordings were performed with a portable two‐channel tape recorder (Oxford Medilog, Oxford, UK) with a sampling frequency of 256 Hz. Measured R‐R intervals were saved in a computer disk for additional processing.

Artificial ectopic beats were generated into the tachograms of 8000 R‐R intervals that included only pure sinus beats. Single premature beats followed by a compensatory pause were uniformly distributed over the whole R‐R interval tachograms in random places. Ectopic beats with compensatory pauses replaced the original sinus beats so that the number of the R‐R intervals remained the same and the tachograms were not shifted. Between two generated ectopic beats there always existed at least three pure sinus beats. Several levels of ectopy were used: amount of ectopy varied from 0.125% to an ectopy level where 35% of the R‐R intervals were qualified as ectopic beats with compensatory pauses. Three different types of prematurity indexes were used so that the premature beats and the compensatory pauses differed by 30%, 20%, or 10% compared to previous normal R‐R interval. Only one type of prematurity was used at a time. Insertion of the artificial premature beats in random places was done three times to obtain an average effect of the ectopy insertion on the nonlinear HRV parameters. The analyses of the fractal scaling exponents were performed for original data with pure sinus beats and for data with different amount of artificial premature beats.

The performance of four different editing methods in the fractal analysis of HRV was studied by editing the generated artificial premature beats with four different methods: deletion, interpolation of degree zero, interpolation of degree one, and cubic spline interpolation. Deletion removes the non‐normal R‐R intervals, interpolation of degree zero replaces the edited R‐R intervals with a local average of the previous accepted normal R‐R intervals. The local nonectopic neighborhood for the interpolation of degree 0 was three R‐R intervals in this study. Interpolation of degree 1 replaces the R‐R intervals with the points obtained from a fitted straight line over the edited R‐R intervals. The basic idea of the cubic spline interpolation is to obtain smooth curves through a number of points. The coefficients of the cubic polynomials are fitted so that the curve passes through the data points without discontinuities. Cubic spline interpolation was computed over the ectopic beats from the local nonectopic neighborhood. The analyses of the fractal scaling exponent α1 and α2 were performed for original data with no premature beats or editing and for data with different amount of edited premature beats.

For all 24‐hour data the preedition of artifacts was done with the interpolation of degree 0. First, premature beats were left unedited and secondly, premature beats were edited with the interpolation of degree 0. The analyses of the fractal scaling exponent α1 and α2 were performed for preedited data including premature beats and for data with edited premature beats.

Fractal Analysis of Heart Rate Variability

Detrended fluctuation analysis was performed and the scaling exponents α1 and α2 were computed to quantify the fractal scaling properties of short‐term and intermediate‐term R‐R intervals time series. Detrended fluctuation analysis is a modified root mean square analysis of random walk and it quantifies the absence or presence of the fractal correlation properties of the heart rate. The details of this method have been described elsewhere. 38 The HR correlation properties were estimated for both short‐term (≤11R‐R intervals, α1) and for long‐term (>11R‐R intervals, α2) R‐R interval data.

For the data of 8000 R‐R intervals the analyses of the fractal scaling exponents were computed over the whole segment and for the 24‐hour data the analysis were done in 8000 R‐R interval segments to achieve an average value for the entire recording period.

Power Spectrum of HRV

The power spectrum of the HRV was computed for the data of 8000 R‐R intervals with premature beats to observe the effects of the premature beats on power spectra in post‐AMI and healthy subject population. Fast Fourier spectrum computation was used.

Statistical Methods

Independent samples t test was used to analyze the differences of the fractal scaling exponent values in patients who died and those who remained alive during the follow‐up. Differences were analyzed in both post‐AMI and general population. A value of P < 0.05 was considered statistically significant.

RESULTS

Performance of Editing Methods

Figure 1 shows the performance of different editing methods in the analysis of the fractal scaling exponents α1 and α2. In the α1 analysis, the interpolation of degree 0 performed best in editing the artificial ectopic beats in both AMI patients and in healthy subjects. In α2 analysis, the cubic spline interpolation produced the smallest error for the healthy subjects, but for the AMI patients the best performance of editing in the α2 analysis was achieved with the interpolation of degree one.

Figure 1.

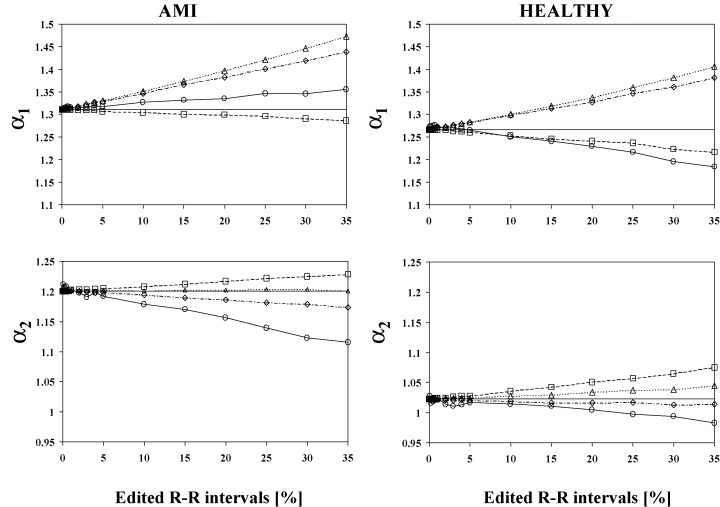
Figure 1

Open in a new tab

Effects of four different editing methods on the values of the fractal scaling analyses for the R‐R interval data of post‐AMI patients and healthy subjects. Mean values of the α1 and α2 analyses are in function of the amount of the edited R‐R intervals. α1 and α2 indicate the scaling exponents analyzed by detrended fluctuation analysis from short and intermediate time windows respectively. The symbols indicate following editing methods: ——= original values, ––= deletion, ‐ ‐ ‐‐ ‐ ‐ = interpolation of degree 0, ‐ ‐ ‐‐ ‐ ‐ = interpolation of degree 1, and ‐ ‐ ‐⋄‐ ‐ ‐ = cubic spline interpolation.

Effects of the Generated Artificial Premature Beats

Figure 2 shows the effects of the artificial premature beats on the analysis of the fractal scaling exponents α1 and α2. The analysis of the α1 was more sensitive to the insertion of the premature beats in the AMI patients compared to healthy subjects. Even a small amount of ectopy insertion produced a large decrement in α1 values with all the three types of the artificial premature beats. Only 0.25% of artificial premature beats of 20% prematurity produced over 25% decrease in the α1 values in the post‐AMI data, but in the healthy subjects more than 4% of artificial premature beats of 20% prematurity were needed to produced over 25% decrease in the α1 values. In the post‐AMI patients, only 1% of artificial premature beats of 20% prematurity decreased the α1 values under 0.75, while in the healthy patients the amount of 10% premature beats were needed to reduce the α1 values under 0.75. Also, in the α2 analysis the effects of the ectopy addition were more remarkable in the AMI patients compared to the healthy subjects. Figure 3 shows effects of the artificial premature beats on the HRV power spectrum of (1) a post‐AMI and (2) a healthy subject. Already with a small inclusion of premature beats the power spectrum of a post‐AMI patient included a larger degree of false frequency components especially in the higher frequency areas compared to the power spectrum of a healthy subject.

Figure 2.

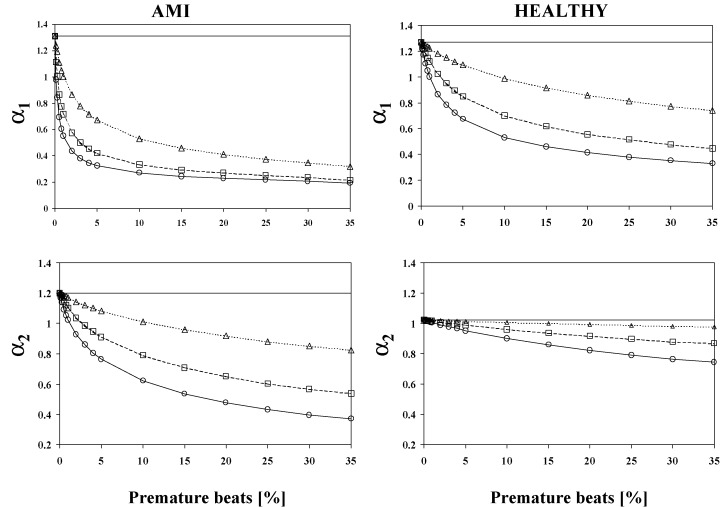
Figure 2

Open in a new tab

Effects of the artificial premature beats on fractal scaling analysis in post‐AMI patients and healthy subjects. Mean values of the α1 and α2 analyses are in function of the amount of the premature beats. α1 and α2 indicate the scaling exponents analyzed by detrended fluctuation analysis from short and intermediate time windows respectively. The symbols indicate following prematurity: ——= original (0% premature beats), ––= 30% prematurity, ‐ ‐ ‐‐ ‐ ‐ = 20% prematurity, and ‐ ‐ ‐‐ ‐ ‐ = 10% prematurity.

Figure 3.

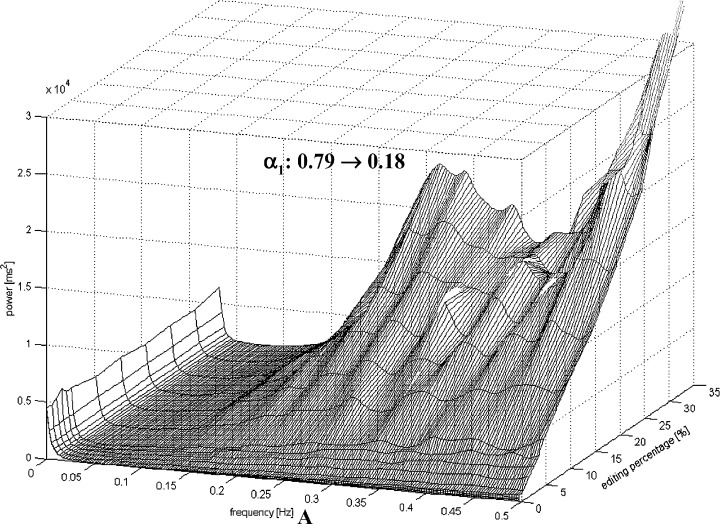
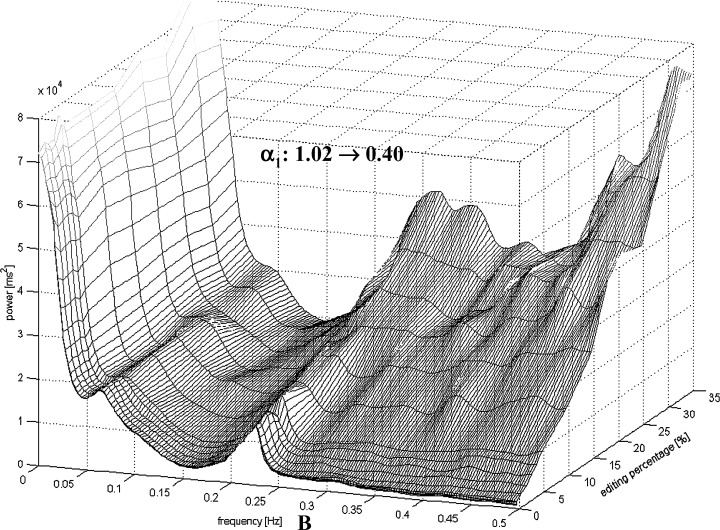
Figure 3

Figure 3

Open in a new tab

HRV power spectrum of (A) a post‐AMI patient and (B) a healthy subject in function of the percentage of the artificial premature beats. Notice a different scaling in (A) and (B) due a different intensity of the spectral components.

Effects of the Real Premature Beats on Fractal Scaling Analysis of 24‐Hour Data

Comparisons of the α1 and α2 analysis in the post‐AMI patients and in the elderly population between those who died and those who survived during the follow‐up are shown in Tables 1 and 2. In post‐AMI, both edited and unedited α1 values differed between survivors and nonsurvivors (P < 0.01 for edited, and P < 0.05 for unedited). In the general population, there were no significant differences between those who died and the survivors in the edited α1 value. However, α1 analyzed from the unedited data differed significantly between the elderly subjects who survived or experienced cardiac death (P < 0.05). In the analysis of α2, there was no significant difference between the survivors and those who died either in post‐AMI or general population.

Table 1.

Measures of HR Dynamics Among the Post‐Infarct Patients Who Died Due to Cardiac Causes During the Follow‐up and Among the Matched Survivors

Clinical 
Variables Dead 
(n = 42) Alive 
(n = 42) P 
Value
Age 69 ± 8  68 ± 8  NS
Men/women 26/16 26/16 NS
EF (%) 39 ± 12 42 ± 10 NS
NYHA‐class II‐III 67% 67% NS
Number of premature beats/hour 26 ± 42 32 ± 68 NS
Measures of HR dynamics
 SDNN 76 ± 25 87 ± 32 NS
 α1‐unedited 0.71 ± 0.33 0.89 ± 0.36 0.05
 α1‐edited 1.01 ± 0.31 1.19 ± 0.27 0.01
 α2‐unedited 1.08 ± 0.20 1.09 ± 0.16 NS
 α2‐edited 1.21 ± 0.11 1.17 ± 0.12 NS
Open in a new tab

Values are expressed as mean ± standard deviation unless otherwise indicated.

EF = ejection fraction; NYHA = New York Heart Association Classification; SDNN = standard deviation of all R‐R intervals; α1= short‐term scaling exponent; α2= long‐term scaling exponent; unedited = analysis of fractal measures of R‐R interval variability including the premature beats; edited = analysis of fractal measures of R‐R interval variability after editing of the premature beats.

DISCUSSION

Time and frequency domain analysis of HRV is typically based on the assumption that various indices of HRV can describe the input of the autonomic nervous system on the sinus node. Therefore, the ectopic beats are traditionally deleted and replaced or edited by artificial R‐R intervals. Similar assumption may not deal with the analysis of dynamic behavior of R‐R intervals by methods based on nonlinear dynamics, however. Unlike the traditional measures of HRV from Holter recordings containing ectopic beats, nonlinear analysis methods may describe true R‐R interval dynamics without deletion and replacement of real R‐R intervals caused by ectopic beats. The present study was designed to assess the effects of premature beats on fractal scaling exponents analyzed by the DFA methods. We chose this particular analysis method because the short‐term fractal scaling exponent has provided important prognostic information in various patient populations.

The following main observations were made in this study. First, premature beats cause quantitatively different effects on short‐term scaling exponent among the healthy subjects and post‐AMI patients. Second, various editing methods may have divergent effects on fractal scaling exponents. Interpolation of degree 0 appeared to be the most suitable for editing of premature beats and artifacts when short‐term scaling exponent is analyzed by the DFA method. Finally, the nonedited short‐term scaling exponent provided prognostic information both in the post‐AMI population and in the random general population.

Effects of Premature Beats on Fractal Scaling Exponents

Analysis of fractal‐like HR behavior by the DFA methods has shown that healthy subjects show only little inter‐individual variation in the short‐term scaling exponent, its values being between 1.0 and 1.3. The present study showed that a relatively large amount of premature beats is needed before this normal fractal‐like HR behavior is broken down toward more random dynamics in the subjects without an evidence of structural heart disease. On the contrary, in post‐AMI patients even a small amount of premature beats resulted in random R‐R interval dynamics.

There is an obvious explanation why a smaller amount of premature beats is needed in post‐AMI patients to break down the normal fractal‐like R‐R interval dynamics. The post‐AMI patients showed a smaller overall HRV, measured by SDNN, as well as smaller beat‐to‐beat R‐R interval oscillations, measured by the high‐frequency spectral component. Figure 3 shows how a HRV power spectrum of (1) a post‐AMI and a (2) healthy subject changes by the inclusion of the artificial premature beats. It can be seen that in a post‐AMI patient already a small amount of premature beats causes an extensive increase in the high frequencies of the power spectrum. In a healthy subject a larger amount of premature beats is required to cause a similar effect in the power spectrum. The scaling exponent α1 is obtained from the slope of the logarithmic fluctuation function versus logarithmic R‐R intervals. Therefore, α1 describes the “roughness” of the R‐R interval time series in the pre‐defined time window. A larger value of the α1 means a smoother signal.

Methods of Editing

In the α1 analysis of the short‐term data, the best performance of editing was achieved with the interpolation of degree 0 in both the post‐AMI and the healthy population. If a large number of R‐R intervals are edited with the interpolation of degree one or spline interpolation the α1 value increases because of a smoothening effect of the spline interpolation on the R‐R interval time series. The deletion method conversely decreases the α1 value by increasing the “roughness” of the signal. This may happen with the R‐R time series with high beat‐to‐beat variability (healthy subjects). But for the time series with a low R‐R variability (AMI patients) the effects of the deletion method can even be opposite: the deletion method may produce an increase in the α1 value by removing only few high frequency fluctuations (smoothening effect) that may appear. The effects of different editing methods on the HRV power spectrum analysis have been reported earlier by Salo et al. 15 Deletion was found to be the most unsuitable editing method for the HRV power spectrum analysis. Interpolation methods were found to perform better in editing process compared to deletion, however, interpolation methods did cause a low‐pass filtering effect by smoothening the tachograms. 15 Overall, the editing methods seem to have a larger magnitude on power spectral components than on fractal scaling exponents studied here.

Edited and Unedited α1 and Mortality

The subjects of the general population who subsequently died due to cardiac problems had a lower short‐term scaling exponent than those who survived when the analysis was done from the real R‐R interval data including the premature beats. The edited short‐term scaling exponent or the number of ectopic beats itself could not separate the survivors from those who died. Thus, reduced overall HRV together with frequent ectopy in the subjects without a known structural heart disease seems to result in altered R‐R interval dynamics toward more random behavior. This change in the dynamic pattern of fractal‐like HR behavior seems to be associated with an increased risk for cardiac death, independent of the study population.

CONCLUSIONS

The type of editing and the amount of ectopic beats have quantitatively different effects on the dynamic measures of fractal‐like R‐R interval behavior among the healthy subjects and post‐AMI patients. This is mainly due to basic differences in the magnitude of overall and beat‐to‐beat HRV between these groups. The present analysis also showed that it is not necessary to delete or edit the ectopic beats when fractal analysis of HRV is used for prognostic purposes among healthy subjects or post‐AMI patients. In fact, unedited short‐term fractal scaling exponent seems to provide more powerful prognostic information that the other HRV indices in general population.

Acknowledgments

Acknowledgments:  The authors wish to thank M.D. Jari Tapanainen, RN Pirkko Huikuri, RN Päivi Karjalainen Ms Anne Lehtinen, and M.S.E.E. Johannes Peltola for technical assistance.

REFERENCES

  • 1. Kleiger RE, Miller JP, Bigger JT, et al Decreased heart rate variability and its association with increased mortality after myocardial infarction. Am J Cardiol 1987;59: 256–262. [DOI] [PubMed] [Google Scholar]
  • 2. Bigger JT Jr, Fliess GL, Steinmann RC, et al Frequency measures of heart rate period variability and mortality after myocardial infarction. Circulation 1992;85: 164–171. [DOI] [PubMed] [Google Scholar]
  • 3. La Rovere MT, Bigger JT, Marcus FI, et al Baroreflex sensitivity and heart‐rate variability in prediction of total cardiac mortality after myocardial infarction. Lancet 1998;351: 478–484. [DOI] [PubMed] [Google Scholar]
  • 4. Skinner JE, Carpeggiani C, Lndisman CE, et al Correlation dimension of heartbeat intervals is reduced in conscious pigs by myocardial ischemia. Circ Res 1991;68: 966–976. [DOI] [PubMed] [Google Scholar]
  • 5. Skinner CE, Pratt CM, Vybiral T. A reduction in the correlation dimension of heartbeat intervals precedes imminent ventricular fibrillation in human subjects. Am Heart J 1993;125: 731–743. [DOI] [PubMed] [Google Scholar]
  • 6. Yamamoto Y, Hughson RL. Coarse‐graining spectral analysis: New method for studying heart rate variability. J Appl Physiol 1991;71: 1143–1150. [DOI] [PubMed] [Google Scholar]
  • 7. Saul JP, Albrecht P, Berger RD, et al Analysis of long‐term heart rate variability: Methods, i/f scaling and implications. Computers in Cardiology 1988;14: 419–422. [PubMed] [Google Scholar]
  • 8. Grassberger P, Procaccia I. Measuring the strangeness of strange attractors. Physica D. 1983;9: 189–208. [Google Scholar]
  • 9. Glenny RW, Robertson HT, Yamashiro S, et al Applications of fractal analysis to physiology. J Appl Physiol 1991;70: 2351–2367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10. Ho KKL, Moody GB, Peng C‐K, et al Predicting survival in heart failure cases and controls using fully automated methods for deriving nonlinear and conventional indices of heart rate dynamics. Circulation 1997;96: 842–848. [DOI] [PubMed] [Google Scholar]
  • 11. Mäkikallio TH, Høiber S, Køber L, et al Fractal analysis of heart rate dynamics as a predictor of mortality in patients with depressed left ventricular function after acute myocardial infarction. Am J Cardiol 1999;83: 836–839. [DOI] [PubMed] [Google Scholar]
  • 12. Lombardi F, Sandrone G, Mortara A, et al Linear and nonlinear dynamics of heart rate variability after acute myocardial infarction with normal and reduced left ventricular ejection fraction. Am J Cardiol 1996;77: 1283–1288. [DOI] [PubMed] [Google Scholar]
  • 13. Huikuri HV, Mäkikallio TH, Peng C‐K, et al Fractal correlation properties of R‐R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infarction. Circulation 2000;101: 47–53. [DOI] [PubMed] [Google Scholar]
  • 14. Vikman S, Mäkikallio TH, Yli‐Mäyry S, et al Altered complexity and correlation properties of R‐R interval dynamics before the spontaneous onset of paroxysmal atrial fibrillation. Circulation 1999;100: 2079–2084. [DOI] [PubMed] [Google Scholar]
  • 15. Salo MA, Huikuri HV, Seppänen T. Ectopic beats in heart rate variability analysis: Effects of editing on time and frequency domain measures. Ann Noninvas Electrocardiol 2001;6(1):5–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16. Lippman N, Stein KM, Lerman BB. Comparison of methods for removal of ectopy in measurement of heart rate variability. Am J Physiol 1994;267: H411–H418. [DOI] [PubMed] [Google Scholar]
  • 17. Vybiral T, Bryg RJ, Maddens MA. Impact of arrhythmias on heart rate variability‐strategies to deal with imperfect clinical data In: Computers in Cardiology. Los Alamitos , CA , IEEE Computer Society Press, 1991, pp. 251–254. [Google Scholar]
  • 18. Xia R, Odemuyiwa O, Murgatroyd F, et al Influence of the artefact of computerised analysis of 24‐hour electrocardiograms on the measurement of spectral components of heart rate variability In: Computers in Cardiology. Los Alamitos , CA , IEEE Computer Society Press, 1991, pp. 269–272. [Google Scholar]
  • 19. Malik M, Xia R, Poloniecki J, et al Influence of the noise and artefact in automatically analysed long term electrocardiograms on different methods for time‐domain measurement of heart rate variability In: Computers in Cardiology. Los Alamitos , CA , IEEE Computer Society Press, 1991, pp. 269–272. [Google Scholar]
  • 20. Birkett CL, Kienzle MG, Myers GA. Mechanisms underlying alterations in power spectra of heart rate variability associated with ectopy In: Computers in Cardiology. Los Alamitos , CA , IEEE Computer Society Press, 1992, pp. 391–394. [Google Scholar]
  • 21. Brüggeman T, Andresen D, Weiss D, et al Heart rate variability: How to exclude extra systoles from the analysis In: Computers in Cardiology. Los Alamitos , CA , IEEE Computer Society Press, 1993, pp. 467–470. [Google Scholar]
  • 22. Malik M, Xia R, Odemuyiwa O, et al Influence of the recognition artefact in automatic analysis of long‐term electrocardiograms on time‐domain measurement of heart rate variability. Med Biol Eng Comput 1993;31: 539–544. [DOI] [PubMed] [Google Scholar]
  • 23. Chungath JJ, Ramanathan A, Kienzle MG, et al Improving the quality of heart rate variability spectra by imposing a constraint on the amount of ectopy in each data segment In: Computers in Cardiology. Los Alamitos , CA , IEEE Computer Society Press, 1993, pp. 727–729. [Google Scholar]
  • 24. Birkett CL, Kienzle MG, Myers GA. Interpolation over ectopic beats increases low frequency power in Heart rate variability spectra In: Computers in Cardiology. Los Alamitos , CA , IEEE Computer Society Press, 1991, pp. 257–259. [Google Scholar]
  • 25. Albrecht P, Cohen RJ. Estimation of heart rate power spectrum bands from real‐world data: Dealing with ectopic beats and noisy data In: Computers in Cardiology. Los Alamitos , CA , IEEE Computer Society Press, 1989, pp. 311–314. [Google Scholar]
  • 26. Sapoznikov D, Luria MH, Mahler Y, et al Computer processing of artifact and arrhythmias in heart rate variability analysis. Comput Method Programs Biomed 1992;39: 75–84. [DOI] [PubMed] [Google Scholar]
  • 27. Malik M, Farrell T, Cripps T, et al Heart rate variability in relation to prognosis after myocardial infarction: Selection of optimal processing techniques. Eur Heart J 1989;10: 1060–1074. [DOI] [PubMed] [Google Scholar]
  • 28. Cripps TR, Malik M, Farrell TG, et al Prognostic value of reduced heart rate variability after myocardial infarction: Clinical evaluation of a new analysis method. Br Heart J 1991;65: 14–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29. Cheung MN. Detection of and Recovery from Errors in Cardiac Interbeat Intervals. Psychophysiology 1981;18(3):341–346. [DOI] [PubMed] [Google Scholar]
  • 30. Berntson GG, Quigley KS, Jang JF, et al An Approach to Artifact Identification: Application to Heart Period Data. Psychophysiology 1990;27(5):586–598. [DOI] [PubMed] [Google Scholar]
  • 31. Zhang X, Yisheng Z. Detection of irregularity index series for QRS complex of ECG 3rd International Conference on Signal Processing, Volume 1, Oct. 1418, 1996, pp. 363–366. [Google Scholar]
  • 32. Pikkujämsä SM, Mäkikallio TH, Sourander LB, et al Cardiac interbeat interval dynamics from childhood to senescence: Comparison of conventional and new measures based on fractals and chaos theory. Circulation 1999;100: 393–399. [DOI] [PubMed] [Google Scholar]
  • 33. Tapanainen JM, Still A‐M, Airaksinen KEJ, et al Prognostic significance of risk stratifiers of mortality, including T wave alternans, after acute myocardial infarction: Results of a prospective follow‐up study. J Cardiovasc Electrophysiol 2001;12: 645–652. [DOI] [PubMed] [Google Scholar]
  • 34. Mäkikallio TH, Huikuri HV, Mäkikallio A, et al Prediction of sudden cardiac death by fractal analysis of heart rate variability in elderly subjects. J Am Coll Cardiol 2001;37: 1395–1402. [DOI] [PubMed] [Google Scholar]
  • 35. Sourander LB, Saraste M, Konu V, et al Continuous ambulatory ECG recordings in a random sample of the aged in Turku. J Clin Exp Gerontol 1986;4: 315–336. [Google Scholar]
  • 36. Räihä IJ, Piha SJ, Seppänen A, et al Predictive value of continuous ambulatory electrocardiographic monitoring in elderly people. Br Med J 1994;309: 1263–1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37. Ruha A, Sallinen S, Nissilä S. A real‐time microprocessor QRS detector system with a 1‐ms timing accuracy for the measurement of ambulatory HRV. IEEE Trans Biomed Eng 1997;44: 159–167. [DOI] [PubMed] [Google Scholar]
  • 38. Peng C‐K, Havlin S, Stanley HE, et al Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995;5(1):82–87. [DOI] [PubMed] [Google Scholar]

Articles from Annals of Noninvasive Electrocardiology : The Official Journal of the International Society for Holter and Noninvasive Electrocardiology, Inc are provided here courtesy of International Society for Holter and Noninvasive Electrocardiology, Inc. and Wiley Periodicals, Inc.

RESOURCES