Assessment of the Stability of the Individual‐Based Correction of QT Interval for Heart Rate

Abstract

Background: Modeling the relationship between QT intervals and previous R‐R values remains a challenge of modern quantitative electrocardiography. The technique based on an individual regression model computed from a set of QT–R‐R measurements is presented as a promising alternative. However, a large set of QT–R‐R measurements is not always available in clinical trials and there is no study that has investigated the minimum number of QT–R‐R measurements needed to obtain a reliable individual QT–R‐R model. In this study, we propose guidelines to ensure appropriate use of the regression technique for heart rate correction of QT intervals.

Method: Holter recordings from 205 healthy subjects were included in the study. QT–R‐R relationships were modeled using both linear and parabolic regression techniques. Using a bootstrapping technique, we computed the stability of the individual correction models as a function of the number of measurements, the range of heart rate, and the variance of R‐R values.

Results: The results show that the stability of QT–R‐R individual models was dependent on three factors: the number of measurements included in its design, the heart‐rate range used to design the model, and the T‐wave amplitude. Practically our results showed that a set of 400 QT–R‐R measurements with R‐R values ranging from 600 to 1000 ms ensure a stable and reliable individual correction model if the amplitude of the T wave is at least 0.3 mV. Reducing the range of heart rate or the number of measurements may significantly impact the correction model.

Conclusion: We demonstrated that a large number of QT–R‐R measurements (∼400) is required to ensure reliable individual correction of QT intervals for heart rate.

An accurate measurement of the QT interval duration from the surface ECG is a challenging task requiring careful consideration of several technical and physiological factors. Among these factors, the recording technique and the measurement methods, ¹ the lead choice, ² and the subjects age and gender ³ are easy to control. Other factors, such as the autonomic balance, ⁴ the repolarization adaptation, ⁵ the effect of QT hysteresis, ⁶ and the QT heart‐rate dependency are more difficult to assess mainly because their levels are likely to be different between individuals. Our study relates to the heart‐rate dependency of QT interval duration. Correcting QT intervals for heart rate allows for comparing repolarization measurements obtained at different heart rates, either between subjects or within the same subject. The most popular correction is Bazett's formula; it is implemented in all commercial ECG systems, but its validity has been highly criticized. ⁷ , ⁸ It underestimates the QT interval at slow heart rate and overestimates it at fast ones. The need for a better correction method is even more important for the safety evaluation process of new drugs where the drug‐induced QT interval prolongation is used as a surrogate marker for the occurrence of torsades de pointes (TdP). A prolongation of 10–20 ms may raise some concerns and a prolongation above 20 ms may jeopardize the future commercial release of a new drug. In this case, the Bazett's correction may lead to both false‐positive and false‐negative observations, and thus it should not be used. ⁸

Among a large set of published correction formulae, Fridericia's is one that seems better than Bazett's. ⁹ , ¹⁰ Nevertheless, the use of a mathematical function characterizing the QT–R‐R relationship and generalized to any patient is a questionable approach because the QT–R‐R relationship was reported to be subject dependent. ¹⁰ Today, there are three alternatives to a general predefined mathematical formula. The first one compares the QT interval for matched heart rate; the so‐called “bin approach” does not use any correction model. ¹¹ The second alternative is a population‐based formulae (or pool formula) based on a QT–R‐R model designed on measurements from all subjects of the study population. ⁹ This alternative may be the best one when a limited number of short ECGs is available for each subject. The third option is an individual‐based formula. This method relies on the computation of a QT–R‐R correction model in each subject. ¹⁰ The resulting model is used to correct the QT measurements for this subject.

The stability of the individual‐based correction model between individuals and between recordings within the same individual has been investigated. ¹⁰ However, there is no study investigating the variation of the individual‐based correction model within the same recording as a function of (1) the number of measurements (N) used to design this model, (2) the heart‐rate range (and variance), and (3) the T‐wave amplitude, which is known to affect the quality of the QT measurements. ¹² In this study, we will use the term “stability” for characterizing this variation of the fitting models.

The first two components are the most relevant ones in the assessment of the quality of a fitting technique under the assumption that the data are homoscedastic. Investigating the limits of stability of individualized formula may help to better understand the limits of the utility of this concept in drug safety investigations.

METHOD

The study population consists of 205 healthy subjects from the Intercity Digital Electrocardiogram Alliance (IDEAL) database. Table 1 reports clinical characteristics of this study population. Twenty‐four‐hour Holter recordings were acquired using the SpaceLab‐Burdick digital Holter recorder (SpaceLab‐Burdick, Inc., Deerfield, WI). This equipment provides 200 Hz sampling frequency signals (5‐ms time resolution) with 16‐bit amplitude resolution (2.5 μV amplitude resolution). Electrocardiograms were acquired using three pseudoorthogonal lead configuration (X, Y, and Z). The QRS detection and beat annotations were obtained using Vision Premier™ (SpaceLab‐Burdick). The QT measurements were automatically measured using the software for COMPrehensive Analysis of the repolarization Signal (COMPAS) developed at the University of Rochester, Heart Research Follow‐up Program (ECG Core Lab, Rochester, NY). The measurements of repolarization in Holter recordings require the use of an averaging technique as well as a filtering process based on preceding heart rate values as reported by Maison‐Blanche et al. ¹³ Median cardiac beats were computed based on 11 consecutive beats in which abnormal beats were removed and heart‐rate stability was assessed (less than 10% variation in heart rate was required). Then, QT measurements from a set of six median cardiac beats were averaged providing one measurement for a set of 66 continuous beats (close to a 1‐minute period). This averaging procedure allows for stabilizing QT measurements when measured from Holter recordings. The issue of QT adaptation to heart rate changes was addressed using a detection threshold on rapid heart rate changes (ΔR‐R > 250 ms), all the cardiac beats in the following 1‐minute segment were excluded from further analysis.

Table 1.

Clinical Characteristics of the Study Population.

	All	Males	Females	P value
N	205	104	101
Age (years)	38.9 ± 15.9	37.3 ± 14.5	40.6 ± 17.1	NS
HR (bpm)	68.4 ± 11.5	66.9 ± 11.8	70.0 ± 11.0*	0.06
BMI (cm/kg2)	24.4 ± 4.5	24.9 ± 3.3	23.8 ± 5.5**	0.0002
QTc (second)	0.43 ± 0.04	0.42 ± 0.04	0.44 ± 0.04	0.016

*P = 0.06; **P = 0.0002 (Wilcoxon two‐sample test).

QTc values are average values from the first 10‐minute ECG in lead Z. Bazett's formula was used for the heart rate correction.

The validation of QT measurements using this software has been done in a previous study. ⁹ Identification of the end of the T wave was done using the maximum slope method where the end of the T wave is located at the crossing point between the maximum slope and the isoelectric line. ¹⁴ The QT–R‐R relationships were analyzed using Matlab software (MathWorks, Inc., Natick, MA). Two models were used: (1) a linear model: (QT =αR‐R +β) and (2) an exponential models (QT =βR‐R^α), referenced as a parabolic model in previous works. ¹⁰

For both linear and parabolic models, we studied: (1) the values of α for the population, considering the entire 24‐hour ECG recording, (2) the stability of α (standard deviation of α: STDα) as a function of N, and (3) the changes in STDα according to the HR range on which the correction model was designed.

Study of the Entire 24‐Hour ECG Recordings

Let N be the number of QT–R‐R measurements included in the design of an individual correction model. We computed QT–R‐R relationships in all subjects. We investigated the differences occurring in this relationship between males and females.

Stability of Individual Correction Model Related to ECG Length

We computed the stability of the correction model when it is based on a set of measurements including N = 5–800 measurements (5 measurement increment). We assumed these measurements to be homoscedastic over a heart‐rate range equal to 60–100 bpm (R‐R = 1000–600 ms). Twenty sets of N measurements were randomly resampled with replacement from the 24‐hour pool of QT–R‐R measurements for each value of N. The stability of the correction model for a given N was computed as the standard deviation of α within these 20 estimates (STDα). Then, for a given N, we extracted the minimum and maximum values from these 20 values of α (α min and α max). The two models based on α min and α max provide two curves we used to identify the so‐called “maximum error” (Max. Err.) defined as the largest separation between the two curves at any given heart rate. Maximum error provides a quantitative assessment (expressed in milliseconds) of the effect of the variation in the design of the correction model on the correction of the QT interval.

We expect STDα to vary as a function of N following the 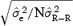model, where 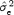is the estimate of the residual variance and 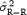is the variance of R‐R. We confirmed this variation of STDα as a function of N using 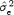and 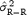computed for N = 50.

Stability of Individual Correction Model Related to Heart‐Rate Range

A 24‐hour Holter ECG (or a few‐hours recording) may have a limited range of heart rate. Thus, we studied the stability of α values according to the heart‐rate range for a fixed number of measurements (N = 200). The heart‐rate range was quantified using the variance of R‐R values used in the design of the correction model. The smallest heart‐rate range was 750 < R‐R < 850 ms, the largest was 600 < R‐R < 1000 ms. The upper and lower limits of the R‐R interval were incrementally changed by steps of 25 ms.

In addition, we investigated the stability of the models for QT–R‐R values using measurements from the entire 24‐hour recordings.

STATISTICAL METHOD

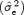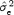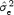The estimated residual variance of the regression line reflects the stability of the fitting model. The higher , the lower the stability is. To compare the stability between gender, we used a point estimate of the true residual variance ratio (R) where R is defined as the ratio of the residual variance of the two compared groups , where is the mean of individual estimated residual variances. On the basis of a bootstrapping technique using a number of replication equal to 1000, we empirically computed the 0.05 and 0.95 quantiles of R. Then, we tested the null hypothesis that the residual variances are equal (R = 1) at 0.05 significance level. The statistical analysis was realized using Matlab software (MathWorks).

RESULTS

QT–R‐R Relationship in 24‐Hour Holter Analysis

Table 1 provides a description of the study population for age, average heart rate, body mass index (BMI) and QTc when measured from the 12‐lead ECGs and corrected using Bazett's formula. BMI was somewhat higher in males than in females (24.9 ± 3.3 vs 23.8 ± 5.5 cm/kg², P = 0.095). The heart rate was slightly higher in females; this difference was close to the statistical threshold for significance (70 ± 11 vs 67 ± 12 bpm, P = 0.06). Ages were similar between genders. QTc intervals based on Bazett's formula were significantly higher in females than in males (0.44 ± 0.04 vs 0.42 ± 0.04 second, P = 0.016).

Table 2 reports average values of R‐R intervals, T amplitude, and α for linear and parabolic correction model for five groups (all subjects, male, female, day, and night) for lead Z. The values are in accordance with previous studies. ¹⁰ , ¹⁵ The amplitude of T wave was computed between leads (not reported in Table 2) and it was significantly higher in lead Z than in other leads (X: 0.36 ± 0.29 vs 0.30 ± 0.26 mV, P = 0.02 and Z: 0.46 ± 0.32 vs 0.30 ± 0.30 mV, P = 0.0001). The amplitude was also significantly lower in females than in males (0.26 ± 0.21 vs 0.46 ± 0.32 mV, P < 0.001).

Table 2.

Results from QT–R‐R Analysis on the Overall 24‐Hour Recordings from Lead Z.

Group	N	R‐R (ms)	T Amp (mV)	α Linear	α Parabolic
All	205	798 ± 107	0.36 ± 0.29	0.17 ± 0.08	0.34 ± 0.14
Male	104	815 ± 108	0.46 ± 0.32	0.16 ± 0.07	0.33 ± 0.13
Female	101	781 ± 105	0.26 ± 0.21	0.18 ± 0.08	0.36 ± 0.15
Day	205	759 ± 102	0.37 ± 0.29	0.16 ± 0.08	0.33 ± 0.14
Night	197	947 ± 152	0.33 ± 0.27	0.12 ± 0.12	0.26 ± 0.20

N is the number of subjects in each group, T Amp: Amplitude of T wave, α for Linear and Parabolic Models.

The variations of QT–R‐R slope between linear and parabolic models were consistent. Alpha values were significantly higher in females than in males (P = 0.047) for the linear model in accordance with previous studies. ¹⁰ For the logarithmic model, this increase did not reach significance (P = 0.13).

The autonomic nervous system affects the QT–R‐R relationship, and the slope of the linear relationship is steeper during the day than during the night revealing a sensitivity of repolarization to the vagal tone. ¹⁶ , ¹⁷ , ¹⁸ The slopes were significantly higher for both linear and parabolic models during day than during the night (P = 0.0001).

Stability of Individual Correction Model Related to ECG Length

Table 3 provides examples of the effect of the number of measurements included in the design of the individual HR correction models for both linear and parabolic models and for two values of N (N = 50 and 300). The number of subjects (n), the values of the averaged slope (α), the average standard deviation of the slope within a subject (STDα), and the maximum correction error due to instability of the model are reported for models built on a number of measurements N = 50 and 300. Figure 1 describes STDα as a function of N for linear models based on empirical and theoretical variation of α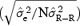. The Maximum Error values decrease in a similar manner as STDα.

Table 3.

Number of Subjects (n), the Averaged α Value and its Averaged Standard Deviation STDα Within Subjects.

	Linear	Parabolic
N = 50
n	127	128
α (n.u.)	0.17	0.36
STDα (n.u.)	0.014	0.029
Max. Err. (ms)	13.4	43.6
N = 300
n	75	74
α (n.u.)	0.18	0.37
STDα (n.u.)	0.006	0.013
Max. Err. (ms)	4.9	18.1

The Maximum Variation in milliseconds the model can generate (Max. Err.) for both linear and parabolic models in lead Z. These values are reported for a number of measurements (N) equal to 50 and 300. Values are based on the overall 24‐hour Holter recordings. n.u.: no unit.

Figure 1.

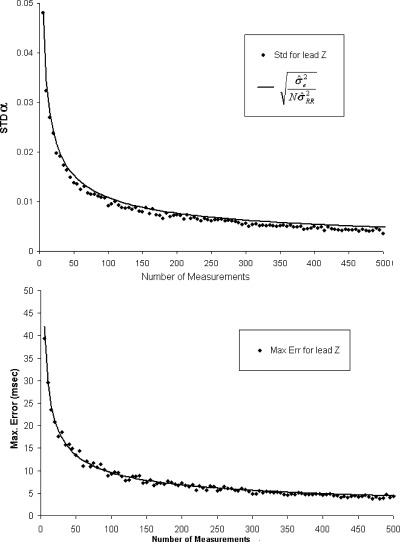
Curves describing the variation of stability (STDα) in upper panel and the variation of Max. Err. in the lower panel for lead Z, according to the number of points included in the design of the correction model. These graphs rely on the models designed with measurements spreading in a similar manner on the overall heart‐rate ranges (equal variance on heart‐rate range for all experiment). These curves follow the expected theoretical 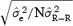pattern (bold line).

According to the lower panel in Figure 1, to insure an error less than 10 ms, more than 100 measurements must be included in the design of the linear correction model. The parabolic model leads to higher Max. Err. values according to Table 3 revealing that the parabolic model is more likely to generate on average much larger error on the QTc values.

Stability of Individual Correction Model Related to Heart‐Rate Range

The analysis of the effect of heart‐rate ranges on STDα is based on models designed using 100 QT–R‐R measurements (N = 100). The variance of R‐R values is used as a measure of the spread of the R‐R interval on which the correction model is designed.

The upper panel of Figure 2 describes the variation of STDα as in function of the variance of R‐R. The larger the R‐R variance the more stable the model is. Each point of the graph is labeled using the corresponding heart‐rate ranges expressed both in R‐R (ms) and heart rate (bpm). For N = 100 and R‐R within the range 600–1000 ms, the STDα level for a large HR range is expected to be close to 0.008 (Figs. 1 and 2). When the heart‐rate range shrinks, R‐R variance diminishes and the STDα value increases; thus the stability of the correction model decreases. Having a model based on 100 measurements spanning heart rates between 100 and 60 bpm provides two‐times higher stability than if the 100 measurements were spanning only 83 and 69 bpm.

Figure 2.

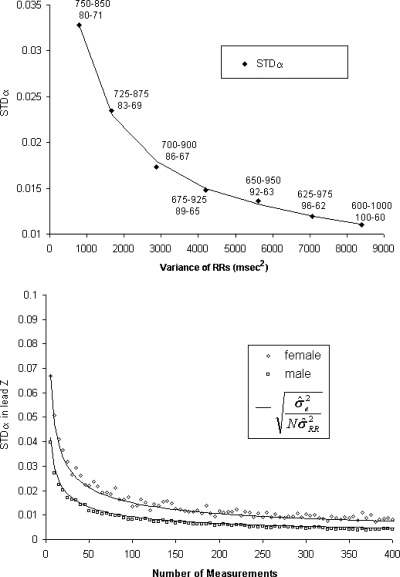
The upper panel is the evolution of stability of the slope of the linear correction model according to the R‐R ranges (expressed as the variance of the R‐Rs). Each point is labeled using the corresponding heart‐rate ranges expressed in both R‐R (ms) and HR (bpm). The smaller the R‐R variance, the less stable the correction model is. The lower panel describes the values of STDα in lead Z between genders.

Under the assumption that the QT values used for designing the QT–R‐R model are homoskedastic, the stability of a correction model is dependent on the spread of R‐R values. Limiting the heart‐rate range of QT–R‐R measurements used in the design of an individual correction model leads to a correction model with lower stability.

Role of the T‐Wave Amplitude on the Stability of the Individual Correction Model

The slope method for the identification of the end of the T wave is dependent on the morphology of the T wave and on its amplitude as well. ¹² , ¹⁹ We investigated the role of the amplitude on the stability of the correction model by computing the values of 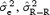and 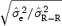for N = 200 measurements including T‐wave amplitude in two different ranges: low T amplitude <0.3 mV and high T amplitude ≥0.3 mV. Table 4 summarizes the results and demonstrates that the stability of the correction model is different between the two levels of T‐wave amplitude. QT–R‐R slopes based on low‐amplitude T waves are associated with a less stable regression line 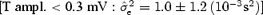than when the T‐wave amplitude is high 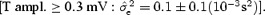Thus, the choice of leads for computing individual correction model should be based on leads where the amplitude of the T‐wave is the largest.

Table 4.

Table Providing the Averaged Values of 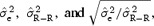in Three Groups: for All Subjects, for Subjects with T‐Wave Amplitude < 0.3 mV, and for Subjects With T‐Wave Amplitude ≥ 0.3 mV.

	All Amplitude	T Amp < 0.3 mV	T Amp ≥ 0.3 mV	P
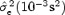
	0.5 ± 0.9	1.0 ± 1.2	0.1 ± 0.1	<0.0001
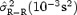
	19 ± 13	16 ± 10	20 ± 15	0.33
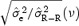
	0.16 ± 0.12	0.24 ± 0.14	0.09 ± 0.03	<0.0001

P values are given for the comparison between the third and fourth column.

Effect of Gender on the Stability of the Individual Correction Model

Differences in T‐wave amplitude have been reported between genders ²⁰ and are confirmed in our study (Table 2). This difference in amplitude is highly significant (in lead Z: 0.46 ± 0.32 vs 0.26 ± 0.21 mV, P < 0.001). In Figure 2 (lower panel), the values of STDα for an increasing number of QT–R‐R measurements are given for females and males. Again based on the ratio of variance (R), we computed Rmf (male vs female), the ratio (95% CI: 0.827–0.846) was significantly different from 1 (P < 0.0001) revealing that the stability of the models are different by gender and this difference is due to differences in the amplitude of the T wave. The theoretical variation was also modeled as in Figure 1.

DISCUSSION

The individual heart rate correction for QT interval measurements has been introduced as an alternative method to Bazett's and Fredericia's correction formulae which generally fail to provide appropriate correction. ⁹ Although the reproducibility of the QT–R‐R relationship has been studied by several authors who have reached similar conclusions, ²¹ , ²² there is no study investigating the various factors that may affect the stability of the individual QT–R‐R models. In this experiment, we demonstrated, as expected, that the stability of individual correction formula is mainly dependent on three components: (1) the number of measurements included in the model design; (2) the spread of heart rate on which the correction model has been built; and (3) the amplitude of the T wave (associated with gender). The dependence on T‐wave amplitude is linked to the method used for identifying the end of the T wave. The two other components are intrinsically related to the regression analysis and must be taken into account regardless of the technique used to measure the QT intervals. Previous publications emphasized the importance of the number of measurements but ignored the effect of the R‐R variance (or spread of heart rate into the computation of the individual regression analysis). ⁸ Our study demonstrates that these two factors (number of points and R‐R variance) affect the quality of the individual heart rate correction. Thus, both should be examined carefully before using any individual correction factor based on regression models.

The use of a filtering technique for identifying stable QT measurements discarded in average 24.8% of measurements in an overall 24‐hour recording. The range of the rejection rate was 98.7–2.0%. Which means that only few measurements were available in several ECGs due to the stringency of criteria for QT measurement selection. To decrease this rate of rejection, one could use less stringent criteria on rapid changes of heart rate or reduced the repolarization adaptation period. How this would affect the stability of the QT–R‐R measurement can only be hypothesized and could be investigated in further studies.

We studied both linear and parabolic models. Our results show that the parabolic model is less stable and can lead to larger errors in QTc than the linear model. The values of STDα for the parabolic model are higher than the linear model: 0.029 versus 0.014 for 50 measurements and 0.013 versus 0.006 for the 300 measurements (Table 3). Thus, in this discussion we will focus mainly on the linear model.

From our results, the standard deviation of α values within subjects for the linear model was close to 0.005, which is twofold lower than what was reported in Batchvarov et al. study (in males, average intrasubject standard deviation of α was 0.011). ²² The higher stability of our approach may be explained by several factors: the preselective filtering algorithm (considering only stable QT measurements), the imposed homoscedasticity of our models or simply a different number of measurements included in the design of the models. Nevertheless, the intrasubject QTc error associated with instability is not negligible and it may play a relevant role when small QT interval changes are being evaluated. For a model based on few minute recordings (300 measurements), one should note that individual‐based correction formula might lead, in the worth‐case scenario, to a 5‐ms measurement error on an individual basis, which is the level of prolongation that one might look for in certain compounds associated with polymorphique ventricular tachycardia (moxifloxacin is an example). ²³

We report α values from 205 Holter ECGs. In lead Z (highest amplitude), the average 24‐hour α value was equal to 0.18 ± 0.08 and 0.16 ± 0.07 for females and males, respectively. According to Dower's matrix, one would extend our results based on lead Z to a lead V2 in the 12‐lead system. ²⁴ Our investigation of lead X reflecting lead I and lead Y reflecting aVF were similar than in lead Z. The slight differences were associated to difference in T wave amplitude.

In the overall population, average α values are equal to 0.17 ± 0.08. When comparing our results to previous reports, Batchvarov et al. reported in 50 healthy subjects, α= 0.203 ± 0.031 in women and 0.163 ± 0.018 in men. ²² Fei et al. have found α values for their groups of healthy subjects equal to 0.12 ± 0.04 (n = 8) α and 0.14 ± 0.08 (n = 20). ²⁵ , ²⁶ Stramba‐Badiale et al. evaluated the QT–R‐R relationship in 40 healthy subjects in whom they found α values equal to 0.13 ± 0.03 in males (n = 20) and 0.16 ± 0.04 in females (n = 20). ³ Rasmussen et al. investigated the largest group of healthy with 60 subjects, average α value was 0.14 (variation between subjects was not reported). ²⁷ Malik et al. found slightly higher values (0.17) in 50 healthy subjects with 0.19 ± 0.03 and 0.15 ± 0.03 for females and males, respectively. ¹⁰ Consequently, there are slight differences in average values of QT–R‐R slopes between studies that may be explained by numerous factors (QT measurement techniques, T wave amplitude, etc.). Ensuring that QT–R‐R measurements are based (1) on the lead with the highest T‐wave amplitude and (2) on a large set of QT–R‐R measurements is important. The heart‐rate range plays an important role too. As expected, the use of ECGs including a large range of R‐R values is required to obtain a stable correction model. This means the smaller the range of R‐R values, the larger the number of QT–R‐R measurement needed to compensate for the lack of R‐R variance as shown in Figures 1 and 2.

Because the QT–R‐R slope has also been used as a potential marker for predicting an increased risk for cardiac events, ²⁸ our analysis may be relevant for any risk‐stratification method based on QT–R‐R dynamicity. Recently, Chevalier et al. reported that increased diurnal QT dynamicity (α > 0.18) could be used as a risk stratifier for sudden cardiac death in post‐MI patients. ¹⁰ , ¹⁷ Previously, Fei et al. investigated changes in α values from the overall 24‐hour recordings in patients after a sudden cardiac death, ²⁵ QT–R‐R slope was significantly increased in both groups (0.19 ± 0.07 in sudden cardiac death survivors and 0.12 ± 0.04 in healthy subjects). Thus, our recommendations for obtaining a valid evaluation of the QT–R‐R relationship might be useful for future investigation of the prognostic significance of α.

Our study demonstrates that heart‐rate ranges, number of QT–R‐R measurements and T‐wave amplitude are fundamental factors affecting the stability of the individual correction models. One would recommend insuring that there is an appropriate balance between these factors. On the basis of our experiment, designing a correction model using 400 QT–R‐R measurements (6‐hour recordings according to our method) from a lead with an average T‐wave amplitude of 0.3 mV and with heart rate ranging from 60 to 100 bpm would provide less than 5 ms error on the corrected QT at any heart rate.

LIMITATION OF THE STUDY

Our study population is one of the largest used to analyze the QT–R‐R dynamicity in normal subjects based on digital Holter recordings. However, most of our study is based on regression analyses in which the QT–R‐R measurements were chosen in order to obtain equal variance of QT values across all R‐R values (homoskedastic data) thus our experiments do not represent real data but rather ideal situations minimizing the level of stability found in our experimental models. In addition, the results are dependent on our QT algorithm that is, in this case, a derived version of the slope method.

In addition, we assessed the stability by randomly choosing QT–R‐R measurements from the 24‐hour recording without distinction between diurnal and nocturnal periods. We agree that limiting the QT–R‐R measurements to the diurnal or nocturnal period could help stabilizing the correction because the QT–R‐R relationship is different between these two periods (Table 2).

CONCLUSION

Our study investigates the stability of the QT–R‐R individual‐based correction formula in relation to the number of measurements used to design the correction model, the heart‐rate range and the T‐wave amplitude. All factors had an effect on the stability of the model. On the basis of our experiment, we recommend using the individual‐based correction formula with caution and ensure that both the number of QT–R‐R measurements (≥400) and the range of HR values (60–100 bpm) are large enough. The choice of the lead for the design of the correction model is important too. If all leads cannot be combined, the use of the lead with the highest amplitude (∼0.3 mV) of T‐wave helps in stabilizing the model.