The Measurement of the QT and QTc on the Neonatal and Infant Electrocardiogram: A Comprehensive Reliability Assessment

Abstract

Background: An electrocardiogram has been proposed to screen for prolonged QT interval that may predispose infants to sudden death in the first year of life. Understanding the reliability of QT interval measurement will inform the design of a screening program.

Methods: Three pediatric cardiologists measured the QT/RR intervals on 60 infant electrocardiograms (median age 46 days), from leads II, V5 and V6 on three separate occasions, 7 days apart, according to a standard protocol. The QTc was corrected by Bazett's (QTcB), Fridericia's (QT_CFrid), and Hodges' (QTcH) formulae. Intraobserver and interobserver reliability were assessed by intraclass correlation coefficients (ICC), limits of agreement and repeatability coefficients for single, average of two and average of three measures. Agreement for QTc prolongation (> 440 msec) was assessed by kappa coefficients.

Results: QT interval intraobserver ICC was 0.86 and repeatability coefficient was 25.9 msec; interobserver ICC increased from 0.88 for single observations to 0.94 for the average of 3 measurements and repeatability coefficients decreased from 22.5 to 16.7 msec. For QTcB, intraobserver ICC was 0.67, and repeatability was 39.6 msec. Best interobserver reliability for QTcB was for the average of three measurements (ICC 0.83, reproducibility coefficient 25.8 msec), with further improvement for QTcH (ICC 0.92, reproducibility coefficient 16.69 msec). Maximum interobserver kappa for prolonged QTc was 0.77. Misclassification around specific cut points occurs because of the repeatability coefficients.

Conclusions: Uncorrected QT measures are more reliable than QTcB and QT_CFrid. An average of three independent measures provides the most reliable QT and QTc measurements, with QTcH better than QTcB.

The importance of the QT interval measurement on the electrocardiogram (ECG) is well recognized, however, even in well‐defined populations the reliability of the measurement of the QT interval has been questioned. ¹ In this context, reliability is defined as the extent to which measured results can be replicated. ² Lack of reliability can be contributed to by the variation in the measurer, the measurement device, or the item being measured. In tests used for screening or diagnosis, poor reliability may contribute to participants being misclassified as either positive or negative for the condition of interest. ³ , ⁴

In neonates QT interval measurement has been shown to be important for the monitoring of the effects of drugs such as cisapride. ⁵ As well, an electrocardiographic screening program has been proposed for the purpose of measuring the QT interval in order to identify infants in the first or second month of life whose QT interval is prolonged and who may be at risk for sudden death. In this group of infants, sudden death due to congenital long QT syndrome (LQTS) may be incorrectly attributed to the sudden infant death syndrome (SIDS). ⁶ , ⁷ SIDS is a multifactorial disorder that occurs in between 0.3 and 1.5 per 1000 live born infants, and in which a single causative sequence has not been identified. ⁸ There is debate over the extent to which undiagnosed cardiac rhythm disorders, such as the LQTS are an important etiologic factor in SIDS. Postmortem molecular analysis has shown prevalence from 2% to 9.5% for functionally significant mutations in LQT‐associated genes. ⁹ , ¹⁰ , ¹¹

Complicating the debate over whether a neonatal electrocardiogram screening programme is practical are two major issues. First, the low prevalence of SIDS is responsible for a low positive predictive value of the ECG in identifying infants at risk, ¹² and second is the reliability of the QT interval measurement. ¹ Whether the measurement is taken manually or automatically may affect the reliability of the raw QT measurement. ¹³ Many questions have been raised about the most appropriate method for correcting the QT for heart rate. ¹⁴ Different formulas may have different impacts on the reliability of the corrected QT interval (QTc). ¹⁵

To improve the reliability, standardization of the QT measuring procedure has been recommended for more than 20 years. ¹⁶ , ¹⁷ The European Society of Cardiology (ESC) addressed this issue by establishing a Task Force that proposed a standardized method of analysis of the neonatal electrocardiogram that included specific recommendations for measuring the QT interval. ¹⁸ The Task Force also recommended repeating the ECGs during follow‐up in individuals with initially abnormal findings. Formal comprehensive analysis of the reliability of this protocol applied to infants in the first few months of life has not been published.

The purpose of this study was to: (1) perform a comprehensive reliability assessment of the recommended protocol for manual measurement of the QT interval recorded from infants in the first few months of life, ¹⁸ (2) perform a method comparison between automatic and manual measurements, and (3) analyze the impact on the reliability of different QT correction formulas that have been used in the young population. Understanding the reliability will inform the design of any proposed electrocardiogram screening program for identifying infants with prolonged QT interval.

METHODS

Subjects

Ethics approval was received from the Institutional Research Ethics Boards. The study population of 60 ECGs was drawn randomly from a convenience sample of 100 consecutive neonatal and infant ECGs stored in the local institutional database. Inclusion criteria were: (1) age less than 4 months, (2) no evidence of structural heart disease on either clinical examination or echocardiogram, (3) sinus rhythm, (4) no evidence of conduction abnormality, and (5) at least one complex in each of leads ll, V5 and V6 that was free of noise and artifact to allow determination of the end of the T wave. Measurements were obtained by three experienced pediatric cardiologist volunteers. The ECGs were obtained with GE‐Marquette 12SL carts using software versions v231, v233, or v237. All ECGs were recorded in standard format 10.00 mm/mV and at a paper speed of 25.0 mm/s, as recommended. ¹⁸

Measurements

The deidentified ECGs were measured on three separate occasions, at least 7 days apart, by the three measurers who were masked to their previous measurements. In accordance with the ESC protocol, the QT intervals were measured from the onset of the Q wave to the point where the T wave meets the isoelectric line or at its lowest visual point if the isoelectric line was not reached. ¹⁸ In circumstances where the T wave and P wave merged, a tangent was drawn from the steepest descending slope of the T wave to the isoelectric line, as recommended. The measurements from leads II, V₅ and V₆ on each ECG were obtained before measuring the next ECG. Measurements were made to a precision of one‐fourth square or 10 ms. The longest value of the three lead measurements was taken as the representative value for each measurement occasion for each ECG. ¹⁸ Two of the three participants measured five consecutive RR intervals from the lead II rhythm strip on each occasion, which were averaged. The three common correction formulas used were the methods of Bazett (QT_CB) = QT(sec)/√RR(sec), Fridericia (QT_CFrid) = QT(sec)/³√RR(sec), and Hodges (QT_CH) = QT (ms) + 1.75 × (heart rate‐60). ¹⁹ , ²⁰ , ²¹

Statistical Analysis

Commercially available statistical software packages Stata 10 (StataCorp, College Station, TX, USA) and SPSS v13 (SPSS, Chicago, IL, USA) were used for all analyses. Continuous measures are summarized by the mean and standard deviation (SD) or median and interquartile (IQR) range as appropriate. Plots of SD against mean assessed whether the assumptions for pair‐wise comparisons of observers and methods were met, and whether transformation of the variables was required. ²² Homogeneity of variance is an assumption for the derivation of intraclass correlation coefficients and was assessed by variance ratio tests.

Repeatability will describe the variability between repeated measures on the same observer (intraobserver), while reproducibility refers to the variability between different observers (interobserver). One‐way and two‐way analyses of variance, as appropriate, were used to identify the components of variance for calculation of the repeatability (and reproducibility) coefficient, and intraclass correlation coefficients (ICCs), taking the three replicated measurements into account. ²³ , ²⁴ The within‐subject standard deviation (Sw) is derived from the appropriate ANOVA model by previously described methods. ²³ The repeatability (and reproducibility) coefficient is defined as the value below which the difference between two successive measurements is expected to fall 95% of the time. ²⁵ The formula used was 2.77 × Sw and is derived from 1.96 × (√2 ×variance), which simplifies to (1.96 ×√2) × Sw and then 2.77 × Sw. ²² The results are rounded to the nearest whole number in the text. The ICC provides a measure of the proportion of the total variance that is explained by the between subject variance, and is scaled between 0 and 1. ²⁶ An ICC close to 1 indicates that only a small amount of the total variance comes from within‐subject variances. The results are presented as a point estimate and 95% confidence intervals.

Plots of difference versus mean (Bland‐Altman plots) were performed for pair‐wise comparisons between observers. Bias was assessed by whether or not the 95% CI for the mean differences included 0. Limits of agreement were calculated for pair‐wise comparisons as 1.96 × SD of the differences. Because we were interested in the effects of repeated measurements on reliability, the estimates of repeatability and reproducibility were obtained from the single (first) measurement, the average of the first two measurements and the average of all three measurements.

QT_CB measurements were dichotomized at 440 ms to reflect the use of this value for screening of whether a QTc is prolonged. ¹⁸ Kappa coefficients were calculated between and within measurers. ²⁷ The point estimates and 95% CIs are presented. Interpretation of the kappa coefficients was as near perfect (0.81–1), substantial (0.61–0.80), moderate (0.41–0.60), fair (0.21–0.40), slight (0.00–0.20), and poor agreement (<0.00). ²⁷

In order to understand the population effect of the measurement error a reference, normally distributed, data set of 1000 cases with mean 400 and SD of 20 was created. ²⁸ Two “error” data sets were created with mean of 0 and SD derived from the within‐subject standard deviations obtained from the interobserver reliability study (Sw), and added to the reference data set. The derived data sets were dichotomized at 440 ms and agreement between the two simulated observers was estimated by kappa coefficients. Each simulation was run 50 times for each Sw. The results are presented as mean, 2.5th and 97.5th percentiles for the kappa coefficient.

The probability of a “true” QTc measurement being misclassified was investigated using the “true” measurement, the 440 ms cut point, each Sw, and either the right or left hand tails of the z‐distribution. The z‐score was calculated as (QTc‐440)/Sw. Similar calculations were made for the approximate (mean + 2 SD) cut point of 460 ms for infants 1–3 months using the Hodges formula ²¹ to demonstrate the impact of a linear QT correction formula.

Sample size estimates were obtained from published power tables based on reliability between 0.8 and 0.9 with three measurers and three repeated measures, and indicated that about 45 subject ECGs were required. ²⁹ Therefore, 60 ECGs were selected to account for uncertainty in the reliability.

RESULTS

Overall, 1620 measurements of QT intervals were taken and 360 measurements of the RR intervals. The longest QT interval from each ECG and measurement occasion was taken as the representative value for further analysis, yielding 540 measurements. The pooled and averaged RR intervals were used for calculation of the QTc from the individual QT intervals.

The median age when the ECGs were taken was 46 days, with the IQR between 24.5 days and 67 days. Forty of the 60 ECGs were from male infants. The mean (SD) maximum QT and QTc for the data set are shown in Table 1. The variance ratio tests showed a common variance across all groups. Plotting SD of measurements against mean did not reveal any trends indicating the need to transform the variables.

Table 1.

Distribution of Values for Raw QT Intervals, Pooled RR Intervals (RR), and Heart Rate (HR) and Corrected QT Intervals

Variable	Mean (ms)	SD	Min	Max
QT	280	24.88	230	360
RR	416	58.33	305	574
Heart rate	147	20.19	105	197
QTCB	435	22.04	387	521
QTCFrid	375	20.78	333	452
QTCH	432	21.71	373	487

QT_CB= Bazett's correction; QT_CFrid= Fridericia's correction; AT_CH= Hodges correction.

Measured QT Intervals

Data for the intraobserver variability pooled across all measurers are shown in Table 2. The ICC indicates that the correlation between two random measurements by the measurers on the same ECG is 0.86, and that most of the variance comes from the between ECG differences. Any two measurements by the same observer on the same ECG are expected to be within 26 ms, 95% of the time. Analysis of each individual measurer shows that the ICCs range from 0.86 to 0.88 and the repeatability coefficients range between 24 and 27 ms.

Table 2.

Reliability Measures for Manually Measured QT Intervals

	Sw	Repeatability	ICC	95% CI
Intraobserver
Overall	9.34	25.87	0.86	0.81–0.91
Measurer 1	8.56	23.72	0.88	0.83–0.92
Measurer 2	8.66	23.99	0.88	0.83–0.92
Measurer 3	9.57	26.52	0.86	0.80–0.91
Interobserver
Single	8.13	22.52	0.88	0.81–0.93
Average of 2	6.60	18.29	0.93	0.87–0.96
Average of 3	6.03	16.69	0.94	0.90–0.96

Sw = within‐subject standard deviation; ICC = intraclass correlation coefficient; CI = confidence interval.

Interobserver variability was assessed for single measures, averages of the first two measures and as an average of the three independent measures (Table 2). The reproducibility coefficient decreases from 23 to 17 ms and the ICC increases from 0.88 to 0.94, showing good reliability, particularly for the average of the three measures. Pair‐wise comparisons show a small systematic bias of between 4.8 and 5.4 ms between measurer 2 and the other measurers.

Measured QT_CB Intervals

For the intraobserver analysis, the ICCs, within‐subjects SD and repeatability coefficients all show lower agreement than the QT measures. Both the pooled (Table 3) and individual ICCs (not shown) are in the range 0.66 to 0.74. The repeatability coefficients are between 37 and 41 ms for the individual measurers, indicating that two measurements taken by the same measurer on the same ECG are within 41 ms 95% of the time. The pooled estimate is 40 ms (Table 3).

Table 3.

Reliability Measures for Manually Measured QTc Intervals

	Sw	Repeatability/Reproducibility	ICC	95% CI
Pooled intraobserver
Bazett	14.29	39.58	0.67	0.58, 0.76
Fridericia	12.39	34.32	0.71	0.63, 0.79
Hodges	9.34	25.87	0.83	0.78, 0.89
Interobserver Single
Bazett	12.69	38.16	0.73	0.60, 0.83
Fridericia	10.93	30.28	0.76	0.63, 0.85
Hodges	8.13	22.52	0.88	0.81, 0.93
Average 2
Bazett	10.39	28.77	0.78	0.66, 0.87
Fridericia	8.92	24.72	0.82	0.71, 0.89
Hodges	6.60	18.29	0.91	0.84, 0.95
Average 3
Bazett	9.31	25.80	0.82	0.73, 0.89
Fridericia	8.05	22.28	0.85	0.77, 0.91
Hodges	6.02	16.69	0.92	0.88, 0.95

Sw = within‐subject standard deviation; ICC = intraclass correlation coefficient; CI = confidence interval.

The interobserver analysis for the QTc measures shows improving reliability from single measures to the average of two measures. The ICC increases from 0.73 to 0.82, and the reproducibility coefficients decrease from 38 to 26 ms.

Alternative Correction Formulas (QT_CFrid, QT_CH)

Examination of the intraobserver and interobserver analyses show that linear correction formulas provide improved reliability over the nonlinear formulas (Table 3). The ICCs increase and the Sw and repeatability/reproducibility coefficients decrease. The highest ICCs are obtained from the average of three independent measurements from three observers using the Hodges correction formula. Compared with the Bazett corrected QTc, the reproducibility coefficient is decreased by 35%. Two repeated estimates of the QT_CH on the same ECG will be within 17 ms 95% of the time.

Comparison of Measured QT and QT_CB with Automatic Measurements

There is a small but statistically significant systematic bias between manual measurements and the automatic measurements for QT and QTc, with the automatic measurements underestimating those taken manually. ICCs for the individual measurers versus automatic measures range from 0.76 to 0.84, and there are wide limits of agreement (Fig. 1). For QTc measures the ICCs are substantially lower, ranging from 0.36 to 0.45, and with wider limits of agreement (Table 4).

Figure 1.

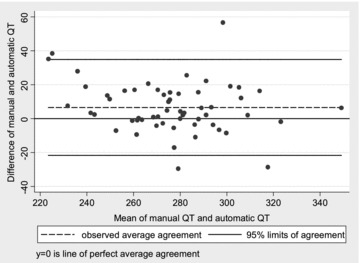
Scatterplot of difference versus average between manual QT measurements and automatic measurements, with 95% limits of agreement. There is a small systematic bias with manual measurements being longer than the automatic measurements.

Table 4.

Comparison of Individual (Average of 3) and Combined (Average of 9) Manual Measures and Automatic Measures

	ICC	95% LCL	Mean Diff	LOA
QT
m1 vs auto	0.76	0.58	7.54	−24.12, 39.20
m2 vs auto	0.84	0.74	4.1	−23.08, 31.28
m3 vs auto	0.78	0.58	8.1	−21.91, 38.11
all vs auto	0.81	0.67	6.58	−21.67, 34.84
QTc
m1 vs auto	0.36	0.12	11.37	−40.16, 62.9
m2 vs auto	0.45	0.23	5.75	−39.02, 50.52
m3 vs auto	0.38	0.13	12.06	−35.69, 59.81
all vs auto	0.45	0.22	9.73	−36.3, 53.76

ICC = intraclass correlation coefficient; LCL = lower confidence limit; LOA = limits of agreement.

Agreement for Dichotomized QT_CB at 440 ms

For the maximum QTc obtained at each measurement occasion, the intraobserver kappa coefficients are consistent with moderate to substantial agreement; however, there is reclassification between measurement occasions for each measurer (Table 5). There is substantial interobserver agreement with a combined kappa coefficient of 0.73 for the first measurement occasion, which increases to 0.77 when the longest of all three measurement occasions is used as the reference.

Table 5.

Kappa Coefficients for Agreement of Prolonged QTc (Cut Point 440 ms) for Bazett's Correction with 95% Confidence Intervals: Intraobserver Agreement, Interobserver Agreement, and Interobserver Agreement of Simulated Data Sets

	Kappa	95% CI
Intraobserver
Measurer 1	0.68	0.51–0.82
Measurer 2	0.73	0.57–0.87
Measurer 3	0.52	0.40–0.68
Interobserver m1 vs m2 vs m3
Single	0.73	0.59–0.88
Average of 3	0.77	0.61–0.90
Simulation Sw
12.69	0.36	0.25–0.50
10.39	0.43	0.31–0.54
9.31	0.46	0.31–0.59

Effects of the QT_CB Reliability

The kappa coefficients for QTc dichotomized at 440 ms in the simulated population show fair to moderate agreement, and are less than in the study group, which most likely reflects the low prevalence in the simulated population (Table 5). There is a trend for the agreement to increase as the measurement error decreases.

Similarly, the probability for misclassification at a cut point of 440 ms decreases with decreasing Sw (Table 6). For a “true” QTc of 430 ms, the probability of a single measurement of QTc misclassifying the ECG as a prolonged QTc is 21.5%. This decreases to 14.1% if the average of three measurements of the single ECG is used. The probability of misclassifying a “true” QTc of 460 ms as normal (<440 ms) is only 1.6% for the average of 3 measurements. There is a very small probability of misclassifying as <440 ms ECGs with true QTc of 470 ms, however, there is a 14.1% to 21.5% probability of misclassifying them as >480 ms.

Table 6.

Probability of Misclassifying a Theoretical “True” QTc Value as Either Prolonged (>440) or Normal (<440) for Each Level of Sw Obtained from the Interobserver Study with Bazett's Correction, and with Hodges Correction (Cut Point 460 ms)

	Sw	12.69	10.39	9.31
“True” QTCB (cut point 440 ms)		Probability of misclassification
Normal		as prolonged (%)
430		21.5	16.8	14.1
420		5.7	2.7	1.6
Prolonged		as normal (%)
450		21.5	16.8	14.1
460		5.7	2.7	1.6
470		0.1	0.02	0.001
“True” QTCH (cut point 460 ms)
	Sw	8.13	6.6	6.02
Normal		as prolonged (%)
450		10.9	6.5	4.8
440		0.07	0.01	<0.001
Prolonged		as normal (%)
470		10.9	6.5	4.8
480		0.07	0.01	<0.001

QT_CB= QTc with Bazett's correction; QT_CH= QTc with Hodges’ correction.

Best case‐worst case simulations were run using Sw (9.31, 14.29) obtained from multiple measurements/measurers versus single measurement/measurer. For a hypothetical population with 1000 live births, 22 would be expected to have a QTc >440 ms and be identified by the screening protocol. Table 7 shows the extent of the misclassification, and the improvement with multiple, independent measurements.

Table 7.

Numbers of Cases Identified or Misclassified from the Average of 50 Simulations of 1000 Cases Using Sw 14.29 (Single) and 9.31 (Multiple)

QTCB >440 ms in Simulated Screening of 1000 Infants	Detected by Single Reading	Detected by Multiple Reading
Identified	15	16
Missed	7	6
Total	22	22
False positives	37	19

Reference to a population of 100,000 live births is obtained by multiplying each number by 100.

Impact of Reliability of QT_CH

The improved reliability and resulting smaller Sw obtained by correcting with the Hodges linear formula decreases the probability of a measured value misclassifying a subject around a specific cut point. For example, the probability that a QT_CH value of 450 ms is 460 ms or more is only 4.8% (multiple measurements/measurers) compared with 14.1% for QT_CB (Table 6).

DISCUSSION

The purpose of this research was not to examine the merits of an electrocardiogram screening program of neonates/infants for a prolonged QT interval, but to investigate the reliability of the proposed measurement protocol for the purpose of informing the design of any screening program prior to implementation. ¹⁸

The overall results confirm that a fixed protocol, as described by the ESC, produces reasonable reliability and reproducibility of manually measured QT intervals in ECGs obtained from infants in the first few months of life. The high ICCs indicate that most of the variability is between the ECGs and not the measurers. However, repeatability coefficients show that there may be substantial difference between two measurements taken on the same ECG by the same or different measurers. All estimates of reliability improve when multiple measurements are taken. It is usually anticipated that intraobserver reliability is better that interobserver reliability; however, in this study the increased numbers of measurements, averaged and then pooled across all observers (nine measurements), has more than compensated for this and produced higher ICCs and smaller repeatability/reproducibility coefficients when compared with single measurements from one observer—a factor that needs to be considered in designing research studies or screening protocols utilizing manual QT measurements. “Repeated measurements” has a specific meaning in this context, and refers to measurements made independently of each other, and blind to the previous result. Taking multiple measurements at a single sitting while being aware of the measured interval (as is usually done clinically), even if averaged, results in highly correlated values that show artificially decreased variability and increased reliability.

Of more importance is that the derived (corrected) variable, QT_CB, shows poorer reliability than the directly measured values. Similar observations have been made in other patient populations, and is related to the correction formula used. ¹⁵ The implication is that the manual measurement and calculation of the QT_CB, even by a standardized protocol is potentially an unreliable measurement. From the data in this study, ICCs range from 0.62 to 0.82 and improvement in reliability is demonstrated by pooling multiple measurements of a single ECG. The best interobserver reproducibility coefficient indicates that the QT_CB calculated from an ECG by two different observers, will be within 26 ms 95% of the time. Compared to the total QTc interval (380–470 ms) this seems to be a small measurement error. However, the problem arises when decisions are being made by comparing measurements with a specific cut point that may have been determined by a number of different methods (for example, based on population SD or percentiles).

Measurement error is assumed to be normally distributed and this analysis also shows that it is independent of the magnitude of the measurement. Consequently, the z‐distribution can be used to give some guidance as to the probability of misclassification of measured values around various cut points. Using the within‐subject SD from the data, the benefits of multiple measurements are clearly shown. A QT_CB would need to be 420 ms before the possibility of incorrectly measuring it at 440 ms (or greater) is less than 2%—with multiple measurers and measurements. Of course, the true QT_CB is not known—however, the point is illustrative of the potential effects of measurement error. The number of individuals misclassified can be extrapolated to larger populations by simple multiplication. For example, in a geographical area with 100,000 live births there would potentially be 3700 false positives and 700 false negatives from a single ECG measurement occasion. This can be reduced to 1900 and 600, respectively by multiple readings. This measurement error problem is a separate and additive issue to that of the false positive rate due to low prevalence of the prolonged QT intervals.

Changing the cut point does not change the probability of misclassification. A QT_CB of 480 ms has a 14% to 21% probability of being measured as 470 ms or less depending on the protocol. The only benefit to changing the cut point is that the number of individuals misclassified is potentially smaller. This occurs because in a normally distributed population the number of individuals in the vicinity of the cut point at 2 SDs (for example, 440 ms) is more than those near the more extreme cut point at 3.5 SD (for example, 470 ms). Interestingly, the clinical consequences of misclassification are potentially more significant if the cut point is moved to 470 ms. As a further example, if it were believed that clinical risks are manifest once the QT_CB reaches 500 ms, the ECG cut point to identify all these individuals is dependent on the measuring protocol, and could be as short as 460 ms (single measurement) or as long as 480 ms (multiple measurements).

The results and conclusions from this study are not out of keeping with those described for other patient populations. De Groote and colleagues measured QT/QT_CB intervals on 53 infants of median age 3 days (range 1–65 days) and demonstrated wide limits of agreement for most comparisons, with the best reliability being shown for repeat measurements by the cardiologist. ³⁰ Their study was not a comprehensive reliability study, but demonstrated poor reliability between measurers of differing skill levels (students and trainee)—a not unexpected result. The repeatability of QT measurements in 63 healthy adult volunteers was examined by Vaidean and colleagues who reported ICCs of 0.86 (0.81–0.92) for raw QT measures, and 0.69 (0.59–0.80) for Bazett's corrected QTc.—values similar to those in this study. ¹⁵ Also shown was the benefit on the precision of estimates of change from repeated measurements that increased reliability.

The effect of different correction formulas is also of interest. The ability of the different formulas to correct for the rate dependency of QT interval has been well examined. ¹⁴ , ³¹ Variable conclusions are sometimes reached depending on the purpose and question. The formulas leave different residual relationships between heart rate and QT, which may need to be taken into account depending upon the subjects and the heart rates of interest. ³¹ The higher ICC obtained for raw QT measurements on repeat ECGs from healthy adult volunteers was previously shown, and it was postulated that lower ICCs for QTc reflects the incorporation of error from both HR and QT measurements. It was also noted that a linear correction shows higher ICCs when calculated from the same data. ¹⁵ In this study pooled RR interval data were used to isolate the QT measurement effects. For each ECG, the pooled RR interval data produced a single RR value that was then used to calculate the QTc's from each of the repeated measurements of the QT interval—although the QT intervals may have varied, the RR interval used in the calculations remained constant for each ECG. This suggests that RR variability is an untenable explanation for the differences in reliability between raw QT, and QT_CB and QT_CFrid.

The explanation, however, lies in the different mathematical effects on the variance and SD when a constant is added to or divided into the series of the three repeated measurements. For a given sequence of repeat measurements (e.g., ECG 1/measurer 1) the RR interval used was the same for all three measures (i.e., a constant), and the Hodges formula reduces to an addition of the constant RR interval. In the case of both Bazett's and Fridericia's formulas, the constant RR interval is divided into the three different QT interval measures. The variance and SD calculated from a series with a constant added is unchanged, whereas they are increased in a series calculated by division of a constant that is less than 1 (heart rates greater than 60). Because the ICC, and the Sw, are complex calculations based on the variation of the series, they change if the variance of the series changes. Adding a further source of variance (for example, the individual RR intervals for each complex) will lead to an additional (and possibly less predictable) changes in the ICC and Sw. From a purely mathematical point of view Sw's (and therefore the repeatability coefficients) for QT_CB and QT_CFrid would be expected to be worse than for raw QT at heart rates greater than 60/min, and the Sw and repeatability coefficient for QT_CH will be the same as for the raw data. The same effect will occur for the Limits of Agreement that are an essential component of a Bland‐Altman type analysis, because they are also derived from the Sw. Interestingly, the effects on the variance/SD will be the same at different RR intervals for the additive formulas (Hodge’s), however, will be affected by the RR interval for both the Bazett's and Fridericia's formulas. The change in Sw will be greater at higher heart rates, and Sw will not be affected at heart rates of 60/min (RR of 1), however, this relationship has not been explored in this study.

The different behavior of the QT‐HR relationship with different formulas has been shown in children during exercise and on prolonged recordings. ³² , ³³ The observation in this study that there is considerable variability of the average QTc's between formulas has also been made previously, and is has been shown to be more pronounced at higher heart rates. ³¹ The discrepancy would be expected to be more obvious in patient populations with higher heart rates, supporting the concept that each formula may require its own population and heart rate‐specific cut points.

The investigation of the errors in QT measurements on 50 duplicate ECGs with nine investigators was reported by Ahnve. ³⁴ The analysis revealed two important findings. First, there were significant differences between measurers. Second, random error was analyzed and it was concluded that it becomes insignificant for QT interval when nine measurements are averaged and for QTc when 11 measures are averaged. The recommendation that this factor be taken into account when designing studies has rarely been heeded. Our findings are similar for the infant ECG, and show that the reliability improved, with narrower limits of agreement and less probability of misclassification, if multiple measurements are pooled.

Study to study comparisons of reliability data are difficult to make for a few reasons. Reliability assessment methodology is not consistently applied and different indices are often presented. Although the techniques for measurement and method comparison are well described, they are not widely or correctly used in many circumstances. This problem has been specifically identified in the cardiology literature. ³⁵ As well, even when statistics such as the ICC are used, comparison of specific ICCs between studies is problematic if the populations are not similarly heterogeneous. Some would consider an ICC of 0.82 obtained for the QTc to represent good reliability; however, it only provides one part of the picture. The limits of agreement and repeatability/reproducibility coefficients provide the information that can identify the clinical consequences of the reliability and the repeatability.

Can automatic measurements be used instead of the manual measurements? Without a true gold standard, the average of many measurements can be thought of as representative of an error free estimate of a parameter. ³⁴ Our overall values of QT and QTc, which averaged nine measurements, were compared with the single automatic measures and show considerable differences. All method comparison analyses show that there is fair agreement by Landis and Koch's criteria for identifying prolonged QTc (>440 ms). ²⁷ Combined with the ICCs and limits of agreement data, it is reasonable to conclude that the manual and automatic measurements are not interchangeable, and are not providing the same information. Similar conclusions have been drawn in other patient populations. ¹³ It is therefore more likely an inherent problem with both “technologies,” rather than a specific population issue. Recently, it has been shown that there are differences in automatic QT measurement between different manufacturers and between different software versions from the same manufacturer. ³⁶ It does not seem that automatic measurements from a standard ECG cart are a viable alternative to manual measurement for screening purposes of large populations of infants at this time without standardization of technique and technology. As well, given that there appears to be a bias between manual and automatic measurements, technology appropriate normal values and cut points need to be established as an alternative to the manually derived ones in current use.

The selection of ECGs from both inpatients and outpatients could be viewed as a limitation. However, all infants had structurally normal hearts as determined by cardiovascular examination or echocardiogram, and no evidence of conduction abnormality. There is no reason to believe that the presence of any concomitant conditions makes the ECG harder to measure. The main issues are the quality of the tracing and overall heart rates, which were considered acceptable. The expected heart rates, and T‐wave morphology, are similar between the first week and 6 months of life, which is an important consideration for assessing the reliability of the measured QT and the calculated QTc intervals. ³⁷ The use of pooled RR interval measurements has removed another potential source of variability, but has concentrated the assessment on the measurement of the QT interval. The measurers in this study were all pediatric cardiologists with experience measuring intervals on the neonatal and infant ECG. It is conceivable that their measurements will be more reliable than those obtained by individuals unused to measuring infant ECGs. ¹⁸

The issue of imperfect diagnostic and screening tests is well recognized. ³⁸ , ³⁹ In the face of an imperfect test should a screening program be abandoned or should the protocol try and maximize the utility of the test? The current research study examines the reliability of a proposed methodology for measuring QT intervals as part of a screening program. The clear conclusion is that the hand measurement of the QT interval, on a single occasion, at a paper speed of 25 mm/s, using the maximum QT interval from one of leads ll, V5 or V6 and correcting the interval for heart rate by the Bazett method produces unreliable estimates of the QTc.

The major consequence of the measurement error is misclassification around a dichotomized cut‐point—regardless of the threshold chosen. It is clear from this research that the clinically important threshold needs to be identified. Only then can a screening cut point be determined that incorporates the reliability of the methodology and is appropriate for the protocol. There is little doubt that the best quality data will require multiple independent measurements if false positives and false negatives are to be minimized. The requirement for multiple, independent measurements should also be taken into account in any future cost‐effective analysis that is done. Both publications that investigated the cost‐effectiveness of a neonatal ECG screening program modeled the data on single ECG reading occasions. ⁴⁰ , ⁴¹

Overall, it should not be concluded from this study that the efforts to standardize the QT measurement is flawed. In fact, the ESC is to be commended for addressing a problem that has been identified for more than 20 years. ¹⁶ , ¹⁷ At issue is how the most reliable estimates of QTc are to be obtained while using widely applied recording methods (paper tracings recorded at 25 mm/s) hand measurement, and a formalized protocol. Appropriate cut points that take the reliability of the measurement protocol into account need to be clarified if misclassification is to be minimized. Consideration could be given to using a linear correction formula for the QTc to reduce misclassification; however, this would involve developing formula specific cut‐points of interest. The compounding effect of day‐to‐day variability in the QT intervals remains to be explored. As well, further investigation is required to elucidate the protocol that could reduce the repeatability of QT measures to less than a target value such as 10 ms (for example, how many separate observations need to be averaged). However, these low values will probably only be achievable by using measuring methods that have a precision much greater than the 10 ms of manual protocols such as the one used in this study. Digital ECGs measured at central locations may be necessary—as has been suggested for large drug studies. ⁴² The clarification of the best methodology for the standardized protocol for an infant ECG screening program that may identify infants with prolonged QT intervals and prevent death in the first year of life appears to be the next step.