Pathophysiology of Exercise Heart Rate Recovery: A Comprehensive Analysis

Abstract

Expanded use of exercise heart rate recovery (HRR) has renewed interest in the pathophysiology of heart rate control. This study uses basic physiologic principles to construct a unique model capable of describing the full time course of sympathetic and parasympathetic activity during HRR. The model is tested in a new study of 22 diverse subjects undergoing both maximal and submaximal treadmill exercise. Based on this analysis, prolongation of HRR involves changes within the sinus node, changes in sympathetic function, in parasympathetic function, and in the central mechanisms regulating autonomic balance. The methods may provide unique insight into alterations in autonomic control in health and disease.

Heart rate is determined by the intrinsic activity of the sinus node, modified by parasympathetic and sympathetic nervous system activity. At the onset of exercise, heart rate normally increases primarily by parasympathetic withdrawal. As exercise reaches more vigorous levels, sympathetic activation contributes progressively more to attaining and maintaining exercise tachycardia.1

Parasympathetic reactivation and sympathetic withdrawal begin when exercise is stopped, but the relative contribution of each during the time course of recovery is incompletely understood. Based on early studies of normal subjects exercising with and without autonomic blockade, Savin et al.2 postulated that sympathetic withdrawal contributes more to heart rate recovery (HRR) soon after peak exercise, with parasympathetic reactivation playing a greater role later in recovery. However, in a subsequent similar study, Imai et al.3 found HRR to be accelerated in athletes but blunted in patients with heart failure. They concluded that immediately postexercise, heart rate decreases primarily due to parasympathetic reactivation. This is supported by the fact that plasma norepinephrine peaks about 1 minute post high‐level exercise,4 consistent with sympathetic activity remaining high into the early stages of recovery, and implying that heart rate decrease early in recovery is, therefore, highly dependent on parasympathetic reactivation.

HEART RATE VARIABILITY

Indices of sympathetic and parasympathetic activity obtained by analyzing ambulatory heart rate variability (HRV) have been correlated with HRR in attempts to better understand the autonomic changes that alter HRR. In a relatively homogeneous population of normal college‐age men, Esco et al.5 found no relationship between the decrease in heart rate from maximum to 1‐minute post exercise (HRR1) or 2 minutes post exercise (HRR2) and measures of HRV. Similarly, in 17 healthy males, Javorka et al.6 found no correlation between HRV indices and either cardio‐acceleration at exercise onset or deceleration during recovery. In a more diverse population of normal individuals that included men and women ranging in age from 21 to 63 years, Nunan et al.7 observed some small associations of HRR with resting HRV. For example, HRR2 correlated with HF (high frequency power, an index of parasympathetic activity; r = 0.36, P < 0.05) and LF/HF (low frequency to high frequency power ratio, an index of sympathovagal balance; r = 0.41, P < 0.05). In a study group chosen specifically to include subjects with both low and normal HRR, a relationship with resting HRV was again evident, those with slower HRR having significantly lower HF and LF fluctuations.8 Similarly, HRR had some degree of correlation with resting HRV variables in elderly men with insulin resistance,9 persons with paraplegia,10 patients with coronary artery disease,11 and young people with Kawasaki Disease.12

Analysis of HRV obtained during exercise can be difficult to interpret because heart rate is changing rapidly over a short time period. Goldberger et al.,13 for example, found some variation in results depending on the time interval chosen for analysis (15, 30, or 60 seconds), but frequency domain measures (LF, HF, and LF/HF) could not differentiate between beta‐adrenergic withdrawal and parasympathetic reactivation. Ng et al.14 used 60 seconds intervals to analyze the first 5 minutes post exercise and found multiple patterns of response among HRV parameters dependent on time, and presence of selective blockade (beta blocker and/or atropine). Arai et al.15 used 64 seconds intervals in their analysis of HRR, sampling in early, mid, and late recovery. Results in normals supported a progressive withdrawal of vagal activity during exercise with a gradual increase during recovery, whereas patients with heart failure or prior cardiac transplantation demonstrated a marked reduction of autonomic modulation of heart rate. As with the studies correlating ambulatory HRV measures with HRR, the studies of HRV during exercise support the general concepts of parasympathetic reactivation and sympathetic withdrawal during HRR, but are limited in their ability to define the time course of autonomic dynamics involved.

AUTONOMIC CONTROL

To better understand the dynamics of HRR, we will review autonomic exercise physiology and incorporate the principles involved into a comprehensive model. The basic equations that comprise this model have been previously published, and can adequately describe exercise recovery curves from multiple levels of exercise.16, 17 However, how these equations relate to the fundamental properties of autonomic function has not been described, and the model has not been used to reconstruct the time course of autonomic changes during exercise recovery. This presentation will do both. Properties of the sinus node will be summarized, followed by the kinetics of parasympathetic and sympathetic stimulation and withdrawal. Central control will be included as the individual components are combined to describe the dynamics of exercise HRR. The completed model will then be applied in a new study to separate out the relative contribution of each arm of the autonomic nervous system to heart rate changes during exercise recovery.

Sinus Node

The intrinsic heart rate of the sinus node is usually measured in humans using autonomic blockade by combining atropine with a β‐adrenergic blocker. Jose and Collison18 demonstrated in normal subjects that the parasympathetic nervous system dominates at rest such that resting heart rate is lower than the intrinsic heart rate in 98% of individuals. Intrinsic heart rate decreases with age,18, 19 and this relationship has been confirmed nonpharmacologically in transplant recipients.20 There is no difference in intrinsic heart rate by gender.18 Intrinsic heart rate can be modified by physical conditioning, and is lower in athletes compared to less active individuals.21, 22

Intrinsic heart rate can also be altered by disease, and is decreased in postoperative congenital heart disease patients.23 It is also progressively lower in patients with more severe heart disease as manifest by functional class, stroke volume, and left ventricular end diastolic pressure.24 The lower intrinsic heart rate in heart failure is associated with a higher resting heart rate and a smaller difference between resting heart rate and intrinsic heart rate. These changes are consistent with a more dominant role of sympathetic tone over parasympathetic tone at rest. Sanders et al.25 further characterized changes in the in sinus node in CHF by noting a slowing of intrinsic heart rate, prolongation of corrected sinus node recovery time, prolongation of sinoatrial conduction time, and abnormal propagation of the sinus impulse. These changes are all consistent with significant sinus node remodeling. Clearly changes in intrinsic heart rate can contribute to changes in HRR.

Parasympathetic Function

The isolated effects of vagal stimulation on heart rate were well demonstrated by Warner and Cox in anesthetized dogs.26 The slowing of heart rates with sudden onset of stimulation was extremely rapid, with a decrease of over 50% within 1 second. This sudden stimulation does not mimic the progressive vagal reactivation that occurs during recovery from exercise, but insight into vagal dynamics can be gained by looking at HRR on cessation of stimulation, which was slower and smoother. If analysis is limited solely to the recovery phase, an exponential response is suggested. Figure 1A was made by digitizing the data in their graph and fitting it to an exponential equation. The curve fitting is hampered by having relatively few heart beats in the critical first few seconds, but the results suggest that exponential kinetics can adequately describe HRR from vagal stimulation under conditions where the heart is isolated from other influences.

Figure 1.

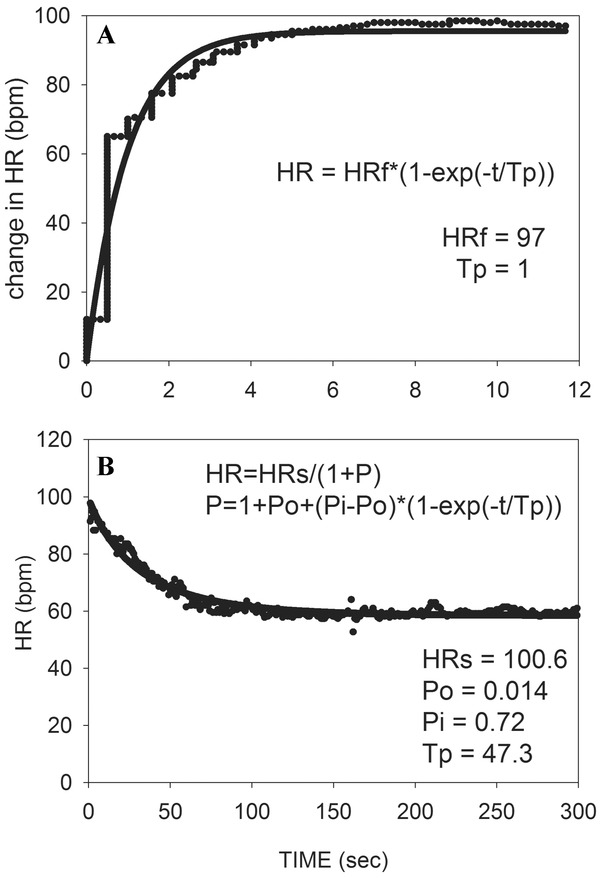
(A) Heart rate increase back to baseline levels upon stopping vagal stimulation in anesthetized dogs is fit to an exponential equation (data digitized from graph of Warner and Cox).26 (B) HRR of a healthy subject recovering from low level exercise is fit with an inverse exponential equation such that heart rate decreases as vagal activity increases. Abbreviations: HR = heart rate; HRf = final value for the change in heart rate; Tp = time constant for vagal kinetics; HRs = basal heart rate assuming constant sympathetic activity; Po = value of P at onset of recovery; Pi = value of P at infinity.

The applicability of exponential kinetics to describe the role of vagal activity in the absence of sympathetic influences in humans can be examined by taking advantage of the previously noted observation that heart rate normally increases at the onset of exercise primarily due to vagal withdrawal. As a corollary, HRR from low level exercise is normally dominated by vagal reactivation. It has previously been demonstrated that exponential decay can adequately describe HRR from low level exercise, even though recovery from high level exercise is more complex.4, 27 However, vagal activity increases to slow heart rate during exercise recovery, so a model to describe this behavior in terms of vagal activity must have heart rate decrease exponentially as parasympathetic activity (P) increases exponentially. This can be achieved by describing the exponential nature of parasympathetic effects on HRR (HRP) as,

$$\mathrm{HRP}=1/(1+\mathrm{P}),$$

where P is an exponential rise

$$\mathrm{P}=\mathrm{Po}+(\mathrm{Pi}-\mathrm{Po})\times (1-\exp (-t/\mathrm{Tp}\left)\right),$$

with Po = value of P at time zero when exercise is stopped,

Pi = value of P at infinity (end of recovery),

t = time in seconds,

and

Tp = the time constant for parasympathetic activity.

Figure 1B shows an example of this equation fit to recovery from low level exercise in a healthy subject. The model can also be tested by fitting it to patients recovering from higher levels of exercise while receiving beta blockade (see Fig. 2B described below).

Figure 2.

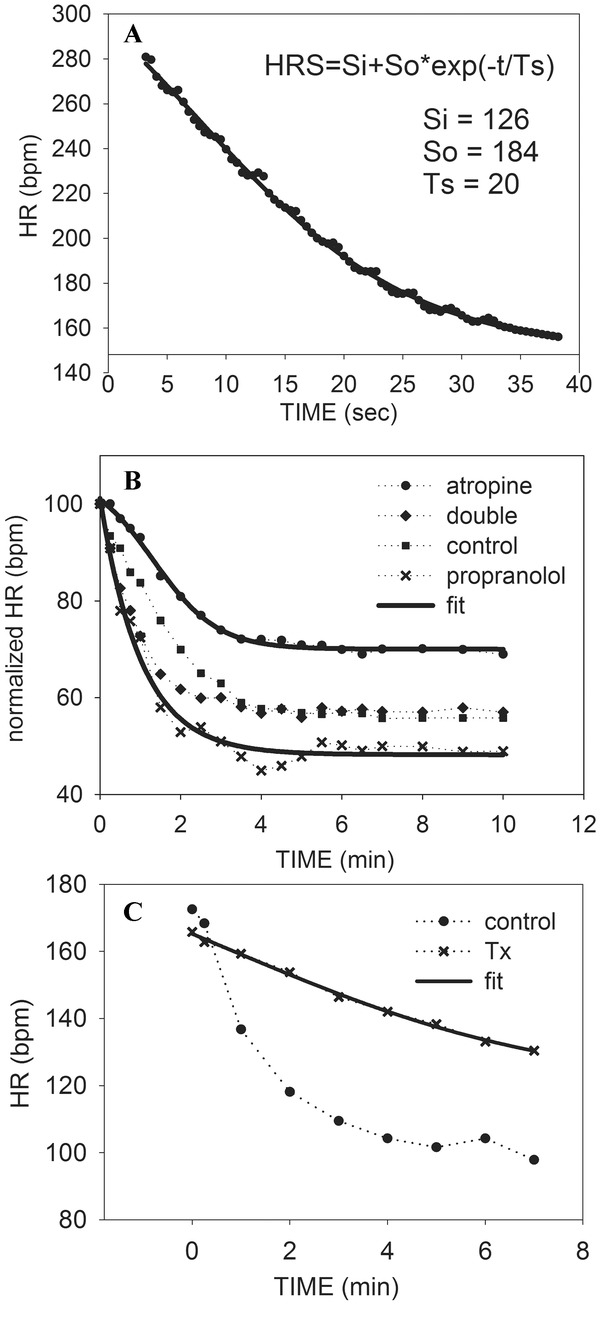
(A) Exponential decay is fit to HRR from sympathetic stimulation in anesthetized dogs (data digitized from graph of Warner and Cox).26 (B) Heart rate recovery (normalized) of healthy subjects during control, atropine, propranolol, and double blockade (data digitized from graph of Savin et al.).2 The propranolol curve is fit with exponential decay, whereas the atropine curve is fit with a sigmoidal curve for sympathetic withdrawal. (C) The sigmoidal curve is fit to heart transplant patients recovering from exercise, with normal control recovery included for contrast (data digitized from graph of Savin et al.2

Sympathetic Function

Warner and Cox26 also recorded the response of their animals to isolated sympathetic stimulation and withdrawal. Both on and off responses were slower than those obtained by vagal stimulation. As demonstrated in Figure 2A, recovery from isolated sympathetic cardiac stimulation appears exponential as well. However, recovery from the sympathetic stimulation of exercise is altered by circulating catecholamines, and this renders first order exponential decay an inadequate description of sympathetic influences in exercise recovery. This can be overcome by modifying the equation such that when sympathetic activity (S) decreases exponentially, its effect on heart rate (HRS) is more sigmoidal.17 In this equation,

$$\mathrm{HRS}=(1+\mathrm{M}\times \mathrm{S}/(\mathrm{M}+\mathrm{S})),$$

where S is an exponential decay,

$$\mathrm{S}=\mathrm{Si}+(\mathrm{So}-\mathrm{Si})\times \exp (-t/\mathrm{Ts}),$$

with

$$\mathrm{So}=\mathrm{S}\mathrm{at}\mathrm{time}\mathrm{zero}\mathrm{when}\mathrm{exercise}\mathrm{is}\mathrm{stopped},$$

$$\mathrm{Si}=\mathrm{S}\mathrm{at}\mathrm{infinity}\left(\mathrm{end}\mathrm{of}\mathrm{recovery}\right),$$

$$t=\mathrm{time}\left(\sec \right),$$

Ts = time constant for sympathetic exponential withdrawal, and

M = variable determining the upper and lower limits for HRS.

Note that this equation does not separate the effects of changes in direct sympathetic stimulation from those of circulating catecholamines, but rather describes the time course of their combined effects on heart rate.

Figure 2B demonstrates how this model can describe sympathetic recovery from exercise by fitting the equation to subjects recovering from exercise during parasympathetic blockade by atropine. The equation was fit to data digitized from the graph of Savin et al.2 In Figure 2C, adequacy of the model is further confirmed in cardiac transplant patients where the heart is denervated, and heart rate recover is thus strongly dependent on clearance of circulating catecholamines (data digitized from Savin et al.).2

The individual parasympathetic and sympathetic effects on intrinsic heart rate must now be combined. In doing so, it is important to recognize that sympathetic and parasympathetic effects on heart rate are not additive. This was demonstrated in 1969 by Levy and Zeiske28 who stimulated sympathetic and parasympathetic nerves enervating the hearts of anesthetized dogs. It became apparent that levels of stimulation to each nerve which independently produced an equal but opposite effect on heart rate produced a net result favoring dominance of the parasympathetic system when combined. These results were subsequently supported by Brack et al. in isolated rabbit heart.29 As a result, it is not appropriate to measure heart rate changes during an intervention (such as exercise), repeat the intervention during selective autonomic blockade, and then subtract to get isolated effects.

Rosenblueth and Simeone30 first described neural control of heart rate as multiplicative, using the equation R = mnR₀, where R₀ is the intrinsic heart rate, and m and n factors describing the neural influences of sympathetic effects and parasympathetic effects respectively. In view of the above considerations, this appears to be a more reasonable model, and has subsequently been used by others.17, 19

Changing the notation such that intrinsic heart rate is HRI, and using HRP and HRS as defined above for parasympathetic and sympathetic effects, respectively

$$\mathrm{HR}=\mathrm{HRI}\times \mathrm{HRS}\times \mathrm{HRP}.$$

Incorporating the expressions for HRS and HRP developed above

$$\mathrm{HR}=\mathrm{HRI}\times (1+\mathrm{M}\times \mathrm{S})/(\mathrm{M}+\mathrm{S}\left)\right)/(1+\mathrm{P}),$$

where

$$\mathrm{S}\mathrm{is}\mathrm{exponential}\mathrm{sympathetic}\mathrm{withdrawal}$$

and

$$\mathrm{P}\mathrm{is}\mathrm{exponential}\mathrm{parasympathetic}\mathrm{reactivation}.$$

Note that if S = 0, then HRS = 1 (no effective sympathetic activity). Moreover, no matter how strong sympathetic activity (S) becomes, HRS cannot exceed the value of 1 + M. Thus we have reasonable bounds on sympathetic effects, with HRS ranging from 1 (if S = 0) to 1+ M (if S is very large). Note also that since HRP = 1/(1+P), if P = 0, then HRP = 1. If P gets very large, then HRP approaches 0. This is consistent with the fact that sympathetic activity can only increase heart rate above the intrinsic rate, whereas parasympathetic activity can only decrease it.

Central Control

The two branches of the autonomic nervous system do not act independently, but are balanced under central control. A reasonable hypothesis would be that parasympathetic activity is inhibited proportional to effective sympathetic activity (i.e., HRS). This can be achieved by multiplying P by a ratio (R) that varies from 0 to 1 depending on the level of sympathetic activity: Such a ratio is,

$$\mathrm{R}=(\mathrm{HRSmax}-\mathrm{HRS})/(\mathrm{HRSmax}-1),$$

where HRSmax is the maximum attainable value for HRS.

Note that if a subject is highly motivated and reaches his/her maximal obtainable heart rate at peak exercise, then HRS = HRSmax, so R = 0, and parasympathetic activity would be fully inhibited. Indeed this is often the case, as Robinson et al. found no significant difference in maximum exercise heart rate achieved in the presence or absence of atropine.31 As sympathetic activity decreases during recovery, the ratio R would progressively increase. If sympathetic activity were totally eliminated (S = 0), HRS would reach its minimum of 1 and R would = 1, i.e., no parasympathetic inhibition. Note also that using this ratio can allow for the possibility that some individuals may not be motivated enough to reach their physiologic limits. In such a case HRS would not reach HRSmax at that level of exercise, and some parasympathetic activity would persist. Incorporating this ratio into the equation produces

$$\mathrm{HR}=\mathrm{HRI}\times (1+\mathrm{M}\times \mathrm{S})/(\mathrm{M}+\mathrm{S}\left)\right)/(1+\mathrm{P}\times \mathrm{R}),$$

$$\mathrm{with}\mathrm{R}=(\mathrm{HRSmax}-\mathrm{HRS})/(\mathrm{HRSmax}-1).$$

This approach can provide a model capable of describing HRR in normal individuals recovering from 4 levels of exercise, including maximal tolerated effort (100%) and exercises limited to heart rate heart rate increases of 80%, 60%, and 40% of that obtained with maximum effort.17 An example from this study is presented in Figure 3 for a healthy individual. The change in the shapes of the curves from maximum down to mild exercise effort is readily apparent. The curve for lowest level exercise appears much more like an exponential decay because there has been minimal sympathetic activation necessary to achieve the modest increase in heart rate attained, and thus the recovery is primarily parasympathetic reactivation.

Figure 3.

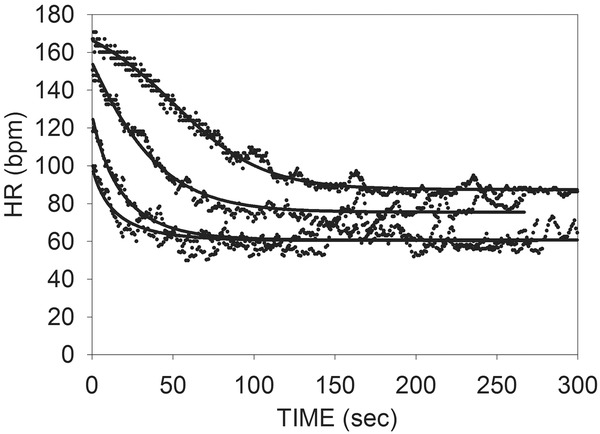
Example the equations for HR fit to data from a healthy subject recovering from 4 levels of exercise. A single time constant for sympathetic withdrawal (Ts) and for parasympathetic reactivation (Tp) is used for all curves. (Reproduced from Pierpont and Voth)17

Only the starting and ending values for sympathetic and parasympathetic activity differed between curves, thus supporting the theory that it is possible to explain HRR from all levels of exercise in terms of a fundamental time constant for the rate of change of sympathetic activity (Ts), and another for parasympathetic activity (Tp). M defines the limits of sympathetic effects, and central control (R) inhibits parasympathetic activity proportional to the level of sympathetic activity. All subjects in that study were healthy normal individuals, and this approach has not been extended to subjects with significant disease known to impair HRR. Nor has it been used in efforts to reconstruct the time course of autonomic changes controlling HRR. Consequently, we designed a study to determine if this model could be used to fully reconstruct the relative contributions of sympathetic withdrawal and parasympathetic activation during exercise recovery in a diverse group of subjects.

NEW DATA AND ANALYSIS

With the approval of the Minneapolis Veterans Administration Medical Center Investigational Research Board, we obtained informed consent from 22 subjects willing to exercise to their maximum tolerated level (100%) as well as a sub‐maximal level that increased their heart rate by 50% of the increase obtained at maximum. The subjects ranged in age from 27 to 72, with 16 males and 5 females. Their activity levels ranged from sedentary to very athletic, and their body mass index (BMI) ranged from 20 to 35. Two subjects had chronic stable congestive heart failure and one had chronic obstructive pulmonary disease. Subjects were excluded if they were taking medication known to alter heart rate (such as beta adrenergic blockers), or if their exercise was limited by symptoms other than shortness of breath or fatigue (such as arthritic pain or angina).

Graded treadmill exercise was performed according to a protocol as previously published,27 with the subjects immediately sitting down postexercise. The electrocardiogram (EKG) was recorded continuously and heart rate corresponding to each R–R interval calculated for the first 5 minutes of recovery. Premature ventricular or supraventricular beats were excluded. For each individual the HRR curves for both levels of exercise were plotted together. The above equations were fit to the curves simultaneously using a single value for Ts, Tp, and M., but the other variables differed depending on the level of exercise. The data were analyzed using Sigmaplot by Systat Software Inc. (Point Richmond, CA, USA). This analysis uses the Marquardt–Levenberg algorithm to find the least squares best fit of the equations to the data.

Note in Figure 3 that heart rate does not return to baseline by 5 minutes of recovery from higher levels of exercise. Based on analysis of HRV, delayed recovery beyond 5 minutes appears to be due to both incomplete sympathetic withdrawal and incomplete vagal reactivation.15, 32, 33 Analysis was therefore limited to the first 5 minutes postexercise because the late recovery from high level exercise likely involves mechanisms that differ from those in the early phases of recovery, and the epidemiologic data is almost exclusively limited to the first 5 minutes of recovery.

The results of this analysis were used to reconstruct the behavior of each arm of the autonomic nervous system over the 5 minute time period of recovery. Because the parasympathetic and sympathetic systems are multiplicative, this could not be done by simply using parameters obtained in the curve fitting to calculate HRS and HRP at each time point and expecting them to add together to produce the observed change in HR. Rather, the net change in HR for any given time increment caused by each is obtained by determining the total change in both variables over that time increment and calculating the proportion of that change caused by each. That percent multiplied by the net HR change for that time increment provides the net amount of heart rate change caused by the sympathetic and parasympathetic systems respectively (Fig. 4). The net change in each variable for each time increment is sequentially summed to provide a graph comparing the relative contribution of each over time.

Figure 4.

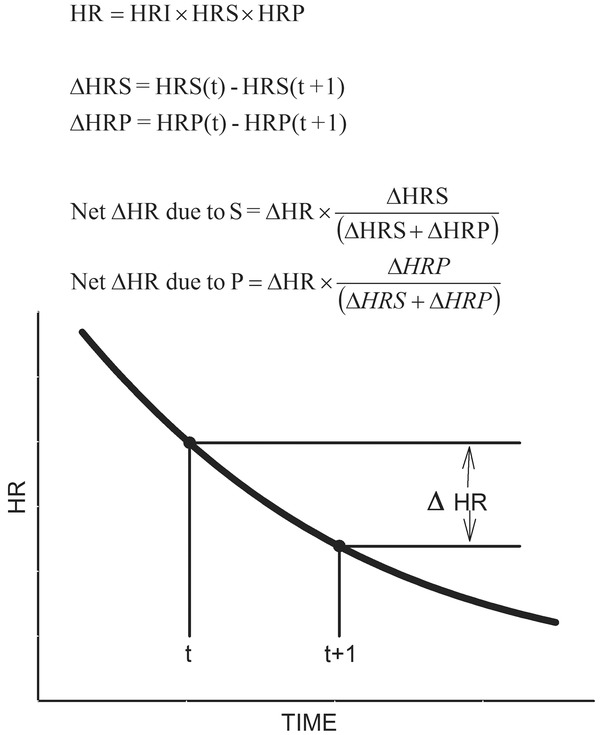
Diagram illustrating the calculations used to reconstruct the curves for parasympathetic reactivation and sympathetic withdrawal. The incremental change in heart rate (∆HR) is the sum of the net ∆HR due to S (∆HRS) and the net ∆HR due to P (∆HRP).

The results of this process for a physically fit 53 year old female with a BMI of 24 are illustrated in Figure 5. Panel A shows HRR data from 100% and 50% exercise, with the corresponding curve fits plotted on the same graph. Panel B shows the recovery from 50% exercise with the reconstructed curves demonstrating the relative contributions of the sympathetic and parasympathetic nervous system included. At any time point, the total decrease in heart rate from maximum is now equal to the decrease in the sympathetic curve plus the decrease in the parasympathetic curve. Note that there is minimal contribution of sympathetic withdrawal from this level of exercise because the increase in HR to this point was primarily due to vagal withdrawal. Panel C shows the same for recovery from 100% exercise. Here sympathetic contributions are much more significant.

Figure 5.

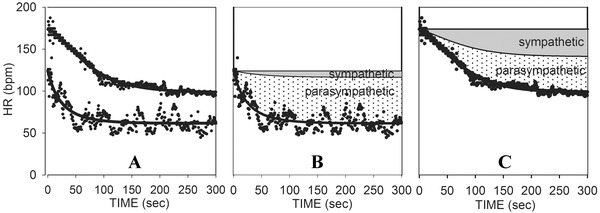
(A) Curve fits of HRR from both maximum and 50% exercise for a fit subject. (B) Curve fit for 50% exercise, with the reconstructed curves showing the net changes resulting from parasympathetic reactivation and sympathetic withdrawal. (C) Curve fit for maximum exercise, with reconstructed curves showing the net changes resulting from parasympathetic reactivation and sympathetic withdrawal.

Figure 6 shows results for a sedentary 40 year old male with a BMI of 32. Note that here there has already been significant sympathetic activation by the time that 50% submaximal level was achieved, and that sympathetic activity contributes more to attaining maximum HR than the first example. Note also that by 5 minutes of recovery, HR still remains significantly above baseline (by 43 bpm) due to both incomplete sympathetic withdrawal and incomplete parasympathetic reactivation.

Figure 6.

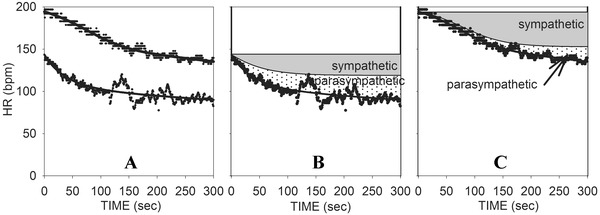
(A) Curve fits of HRR from both maximum and 50% exercise for a sedentary subject. (B) Reconstructed curves for 50% exercise showing the net changes due to parasympathetic reactivation and sympathetic withdrawal. (C) Reconstructed curves for maximum exercise showing the net changes due to parasympathetic reactivation and sympathetic withdrawal.

These examples provide results consistent with the hypotheses that HR increase at the onset of exercise is primarily due to parasympathetic withdrawal, with progressive sympathetic activation occurring at higher levels of exercise. However, when attempting to fit the data of several subjects with these equations, results occurred that did not appear consistent with these hypotheses. An explanation for this problem can be seen in the data of Francis et al., who reported changes in catecholamines during exercise in both normals and patients with CHF.34 They demonstrated that normal subjects have no (or minimal) change in plasma norepinephrine at low levels of exercise, with a large exponential increase at higher levels. In contrast, subjects with CHF have generally higher resting levels of norepinephrine that increase immediately with onset of exercise, yet fail to achieve levels of magnitude equivalent to those of normal controls These findings are consistent with the known autonomic changes in CHF, which include: a chronic increase in sympathetic activity as evidence by direct sympathetic nerve recordings and elevated circulating catecholamines, down regulation of beta adrenergic receptors, depletion of myocardial catecholamines, decreased catecholamine turnover rate, and decreased vagal tone as evidenced by decreased heart rate variability.35, 36 Conversely, during exercise, normals have a greater sympathetic response producing a more dynamic range of heart rates capable of reaching higher maximums.

All of these findings need to be incorporated into the concept of autonomic balance. In the absence of a generally accepted specific definition for the term autonomic balance, Goldberger37 proposed using the ratio of the resting RR interval to the intrinsic RR interval (the latter obtained during autonomic blockade) as a measure of “vagal‐sympathetic effect (VSE).” This is the inverse of sympathovagal balance, but captures very well the concept of balance in the autonomic nervous system. The vagal‐sympathetic effect would be 1 if there was equal balance between parasympathetic effect and sympathetic effect, >1 if vagal effects predominated, and <1 if sympathetic effects predominated. Unfortunately, because it requires autonomic blockade, it is not easily obtained. The LF/HF ratio obtained from HRV analysis is a more easily obtained index of sympathovagal balance, but not as conceptually clear. Although efferent vagal activity is considered the major contributor to the HF component, the LF contribution is more controversial.38

At rest, or with normal ambulatory activity, these definitions are straight forward, and in patients with CHF, sympathovagal balance clearly is tilted toward sympathetic predominance. However, to apply a similar statement to the heart rate response to exercise would mask the fact that normals have a greater overall change in sympathetic activity, and reach higher levels of circulating catecholamines and higher heart rates than do those with CHF.

Figure 7, from a 58‐year‐old male with CHF, illustrates these concepts. Note that there is already significant sympathetic activation at the 50% level of exercise despite the heart rate only increasing to 100 bpm. Maximum heart rate was only 121 bpm, and that was obtained primarily via sympathetic activation. Parasympathetic reactivation has a decreased overall influence on HR, including minimal effect in the first 50 seconds of recovery from peak exercise (consistent with the hypothesis of Imai et al.).3

Figure 7.

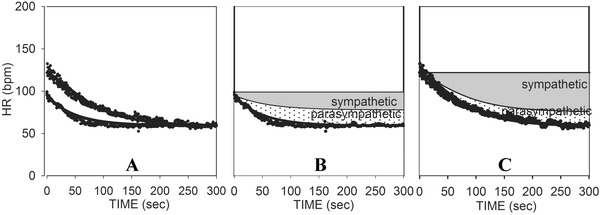
(A) Curve fits of HRR from both maximum and 50% exercise for a subject with CHF. (B) Reconstructed curves for 50% exercise showing the net changes due to parasympathetic reactivation and sympathetic withdrawal. (C) Reconstructed curves for maximum exercise showing the net changes due to parasympathetic reactivation and sympathetic withdrawal.

It is difficult to explain all of these findings without postulating major changes in central autonomic control. Central control mechanisms are not easily studied experimentally in humans, but by taking advantage of the variation in responses of HRR from different levels of exercise, the model used here may provide further insight into changes that occur with chronic disease. This may be achieved by testing alternate hypotheses about the nature of sympathetic inhibition of vagal activity by varying R in the equations above. For example, rather than have R inhibit parasympathetic reactivation in direct proportion to the level of sympathetic activity, it might inhibit sympathetic activity relatively more at lower levels, or relatively more at higher levels. The overall magnitude of sympathetic effect or the range over which the effect occurs could be altered. There may be a threshold effect at a certain level, above which parasympathetic activity is completely inhibited, but below which there is a gradual decrease of inhibition (a sigmoidal type of effect).

The method of analysis we used provides a way to examine the sympathetic and parasympathetic components contributing to heart rate changes during HRR. However, the results are not definitive. The Marquardt–Levenberg method used in the curve fitting algorithm is an iterative process that starts with an estimate of the initial values for each variable, and then systematically alters the values until the differences between the residual sums of squares no longer decreases significantly. As such, there is no definable single “solution” to the equations, as there may be more than one combination of variables capable of providing similar results. Initial estimates of the parameters that will allow the equations to best fit the data are usually provided using the investigator's best guess of the likely resultant value. Thus, for example, if the intrinsic heart rate is input as 90, output of the process might fit the equations equally well, but with slightly different values for some of the variables if 70 was chosen as the likely the intrinsic heart rate. Note that the equations in Figure 4 used to reconstruct the sympathetic and parasympathetic contributions to HRR produce a unique solution that depends only on the results of the Marquardt–Levenberg fit of the data.

It is also possible that the best possible fit could be missed. This problem is exacerbated when the number of variables in the equations is increased. The equations used here include 4 variables that share the same values at all levels of exercise (HRI, Tp, Ts, M), and 4 each that differ with the level of exercise (Po100, Pi100, So100, Si100 unique to maximal exercise, and Po50, Pi50, So50, Si50 unique to sub‐maximal exercise). Consequently, it cannot be assumed with full confidence that the results for a given individual provide the best possible explanation of the complex response involved.

More definitive results could be obtained by replacing as many of the variables involved as possible with measured or independently calculated values. This minimizes any possible differences likely to occur with differing input values. Doing this would require repeating studies such as those of Imai et al.3 and Savin et al.2 using autonomic blockade at rest and with different levels of exercise. Resting sympathovagal balance could be determined by selective blockade, and HRI obtained during dual blockade. The response to exercise during atropine infusion, both at peak and sub maximal levels, would be particularly valuable, allowing the sympathetic variables to be determined independently. Because beta blockers are competitive antagonists, circulating catecholamines during exercise would still alter HR, and parasympathetic effects of exercise would not be totally isolated. As such, the use of beta blockade is best limited to obtaining intrinsic heart rate at rest. As more variables are measured, better estimates of the remaining variables can be made, and reasonable limits imposed on their potential values. Including drug free exercise at several levels (low level, intermediate level, and peak) would then help to insure that the final model reflects a more accurate description of autonomic activity during exercise recovery.

The model of HRR used in this study demonstrates a method by which known physiologic principles of autonomic function can be applied to reconstruct hear rate recovery from exercise in a diverse population. However, because of the limitations discussed above, a quantitative summary of results is best deferred to application of these methods in a study incorporating autonomic blockade.

SUMMARY

The pathophysiology of prolonged HRR involves changes within the sinus node, changes in sympathetic function, in parasympathetic function, and in the central mechanisms regulating autonomic balance. Disease (or even deconditioning) increases basal sympathetic activity. This causes down regulation of beta receptors, depletion of myocardial catecholamines, and slower norepinephrine turnover rate. The resultant higher resting heart rate and lower peak heart rate narrow the effective range of sympathetic activity, concomitant with a slower sympathetic response time. Vagal tone and maximum vagal effects are decreased, narrowing the effective range of parasympathetic activity. Sinus node remodeling lowers intrinsic heart rate and delays overall response time. Central control contributes to a more dominant role of sympathetic activity over parasympathetic activity at rest, but at the same time limits the sympathetic response to exercise. The fact that significant changes occur in essentially every aspect of the autonomic nervous system explains the relatively poor correlations between HRR and isolated measures of a specific autonomic pathway.

The autonomic changes contributing to prolonged HRR appear to be independent of the cause of the stress as long as it is systemic and chronic. As such, this constellation of findings (as reflected in a decrease in HRR) could be considered a “chronic systemic stress syndrome.” As demonstrated in the examples presented above, the various components of these changes may vary among individuals, allowing for significant differences in the pattern of response seen in a diverse population. However, because essentially all of the autonomic changes contribute to a decrease in HRR, it is easy to understand why HRR is able to independently predict all‐cause mortality in a large variety of populations.