Automated Assessment of Cardiac Autonomic Function by Means of Deceleration Capacity from Noisy, Nonstationary ECG Signals: Validation Study

Abstract

Background

Assessment of heart rate variability by means of deceleration capacity (DC) provides a noninvasive probe of cardiac autonomic activity. However, clinical use of DC is limited by the need of manual review of the ECG signals to eliminate artifacts, noise, and nonstationarities.

Objective

To validate a novel approach to fully automatically assess DC from noisy, nonstationary signals

Methods

We analyzed 100 randomly selected ECG tracings recorded for 10 minutes by routine monitor devices (GE DASH 4000, sample size 100 Hz) in a medical emergency department. We used a novel automated R‐peak detection algorithm, which is mainly based on a Shannon energy envelope estimator and a Hilbert transformation. We transformed the automatically generated RR interval time series by phase‐rectified signal averaging (PRSA) to assess DC of heart rate (DC_auto). DC_auto was compared to DC_manual, which was obtained from the same manually preprocessed ECG signals.

Results

DC_auto and DC_manual showed good correlation and agreement, particularly if a low‐pass filter was implemented into the PRSA algorithm. Correlation coefficient between DC_auto and DC_manual was 0.983 (P < 0.0001). Average difference between DC_auto and DC_manual was ‒0.23±0.49 ms with limits of agreement ranging from ‒1.19 to 0.73 ms. Significantly lower correlations were observed when a different R‐peak detection algorithm or conventional heart rate variability (HRV) measures were tested.

Conclusions

DC can be fully automatically assessed from noisy, nonstationary ECG signals.

Cardiac autonomic function yields important prognostic information in cardiac and noncardiac diseases. Analysis of beat‐to‐beat (RR) variations by means of heart rate variability (HRV) provides a noninvasive probe of cardiac autonomic activity and is therefore used for clinical purposes.1 The RR interval time series is usually derived from Holter recordings or short‐term resting ECGs but can also be obtained from monitoring devices used in emergency rooms, intensive care units, or operating rooms. In the latter case, however, ECG signals are characterized by a substantial amount of nonstationarities and noise.

In most studies, manual preprocessing of the ECG signals is performed as a conditio sine qua non to eliminate artifacts and noise. This approach, however, is highly impracticable when HRV shall be used for fast clinical decision. Fully automated approaches to HRV analysis would therefore be of high interest.

Deceleration capacity (DC) of heart rate is a novel measure of HRV that might be particularly useful for automated approaches to HRV assessment.2 Owing to its underlying signal processing algorithm DC is largely insensitive to nonstationarities and noise.3 DC is an integral measure of periodic power within the RR interval time series and has previously been shown to be a very potent predictor of mortality after myocardial infarction.2

In the present study, we validate a fully automated approach to DC assessment from noisy, nonstationary ECG signals recorded in a large medical emergency department under routine clinical conditions.

METHODS

Patients and ECG Signals

The study included 100 patients admitted to the medical emergency department of the Eberhard‐Karls‐University, Tübingen, Germany. Patients were randomly selected from a large database. All patients were in sinus rhythm. Directly after hospital admission single lead ECG monitoring was started using a commercial device (GE DASH 4000, sampling frequency 100 Hz). Recordings were performed under routine clinical conditions. Only the first 10 minutes were used for analysis. The study has been approved by the local ethical committee.

Manual Processing of the ECG Signals

Manual processing of the ECG signals was done by an experienced technician with help of a commercial software package (Cardioday Version 2.2.0, Getemed, Teltow, Germany). The signals were carefully checked for artifacts and noise. True R peaks were identified to obtain the series of RR intervals.

Automated Processing of the ECG Signals

Automated processing of the ECG signals was done without any manual intervention. We used an optimized version of a previously published R‐peak detection algorithm.4 The sequence of filtering and R‐peak detection is illustrated in Figure 1. The original algorithm is described in detail elsewhere.4 Briefly, a Butterworth filter (second‐order, cutoff 0.5) and a band pass filter (fourth order Chebyshev type 1, bandwidth filter 6–18 Hz) were applied to the signal. The amplitudes were normalized using Equation (1):

$$\mathrm{d}\left[\mathrm{n}\right]=\mathrm{d}\left[\mathrm{n}\right]/\max \left(\mathrm{d}\right[\mathrm{n}\left]\right).$$ (1)

Figure 1.

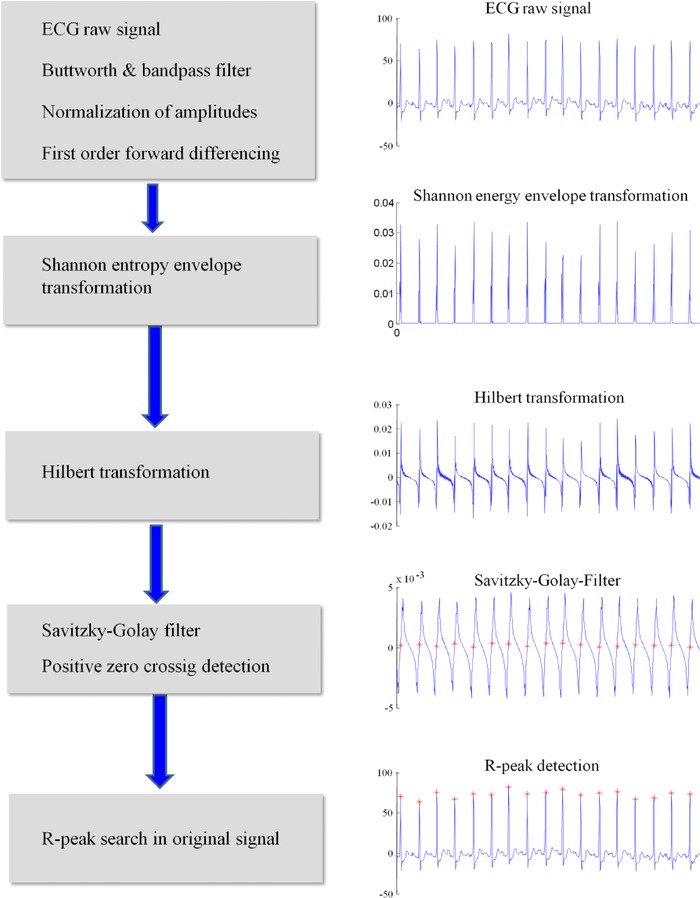
Scheme of automated R‐peak detection.

Subsequently, the signal was filtered by forward differencing filter:

$$\mathrm{d}\left[\mathrm{n}\right]=\mathrm{f}[\mathrm{n}+1]-\mathrm{f}\left[\mathrm{n}\right].$$ (2)

The signal was then nonlinearly transformed using the Shannon energy envelope:

$$\mathrm{s}\left[\mathrm{n}\right]=-{\mathrm{d}}^2\left[\mathrm{n}\right]\log \left({\mathrm{d}}^2\left[\mathrm{n}\right]\right).$$ (3)

Subsequently, a Hilbert transformation was performed and a moving average filter with a length of 250 samples was applied to the signal followed by a Savitzky‐Golay‐filter (frame 15, degree 0). Times of positive zero crossing were identified. R‐peaks were searched in the original signal within a range of ±10 samples.

We additionally evaluated an established standard method of R‐peak detection based on the Pan–Tompkins algorithm. The exact methodology of the Pan–Tompkins algorithm can be found elsewhere.5

Phase‐Rectified Signal Averaging (PRSA) and Assessment of DC

Both, the manually and automatically generated series of RR intervals were transformed by PRSA as previously described.3 Briefly, instances within the RR interval time series are identified where the heart rate decelerates (so‐called anchors). Segments around these decelerations are averaged to obtain the so‐called PRSA signal. The central part of the PRSA signal is quantified by Haar wavelet analysis to obtain an estimate of the periodic power of the signal. The wavelet coefficient is termed DC.

The PRSA technology allows for several adjustments. Here, we systematically tested the effect of the low‐pass filter T (eq. 2a in Ref. 3). The scale s of the wavelet used for quantification of the PRSA signal is adjusted to T as follows (see also eq. 8 in Ref. 3):

$$\mathrm{S}=\mathrm{T}+1\left[4\right].$$ (4)

DC obtained from manually or automatically processed ECG signals are denoted DC_manual and DC_auto, respectively.

Assessment of Standard Measures of HRV

Standard measures of HRV were calculated in time and frequency domain as proposed by the task force.1 We assessed the following measures: the standard deviation of all normal‐to‐normal intervals (SDNN), the root mean square of successive differences of normal‐to‐normal intervals (RMSSD), the frequency power in the low (0.04–0.15 Hz) and high frequency (0.15–0.40 Hz) band (HF and LF).

Statistical Analyses

Continuous variables are presented as mean and standard deviation. Qualitative data are expressed as percentages. Correlation between two continuous variables was assessed by Pearson's correlation coefficient. Agreement between two continuous variables was analyzed by the method of Bland and Altman,6 which involves plotting the signed difference between two measures against the mean of the two measures. Limits of agreement depict the mean difference of two measures ± 1.96 × the standard deviation.

RESULTS

ECG Signals

ECG tracings were characterized by substantial artifacts and noise. Typical examples are shown in Figure 2. On average, 16.6 ± 10.4% of the recording time was classified as artifacts or noise by manual review.

Figure 2.

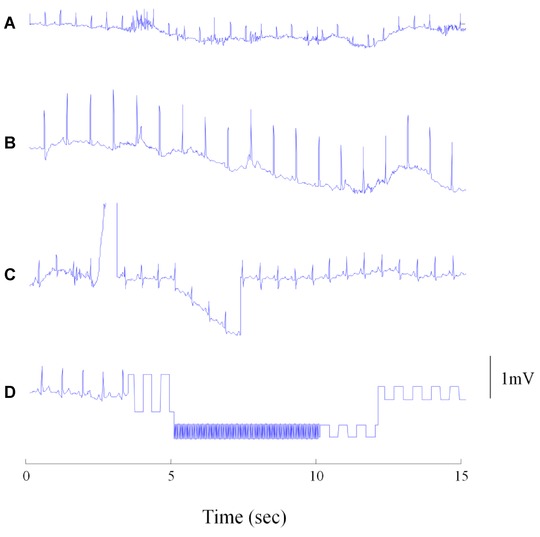
Typical problems in noisy ECG recordings. (A) High‐frequency artifacts probably due to muscular activity; B and C: different forms of baseline wandering; D: artifacts due to signal interruption.

Correlation and Agreement of DC_manual and DC_auto

DC_manual and DC_auto were highly significantly correlated. Correlation coefficients ranged from 0.903 to 0.983 depending on T used for PRSA analysis (P < 0.0001 for all). With increasing T, the correlation coefficient gradually improved and saturated when T was 5 or more (Fig. 3). Figure 4 shows the correlations of DC_manual and DC_auto for T = 1 and T = 5, respectively. Figure 5 shows the Bland–Altman plots of DC_manual and DC_auto for T1 and T5, in which the average of DC_manual and DC_auto is plotted against their difference. For T = 1, the average difference between DC_auto and DC_manual was ‒1.12±1.69 ms with limits of agreement ranging from ‒4.43 to 2.19 ms. For T = 5, the average difference between DC_auto and DC_manual was ‒0.23±0.49 ms with limits of agreement ranging from ‒1.19 to 0.73 ms.

Figure 3.

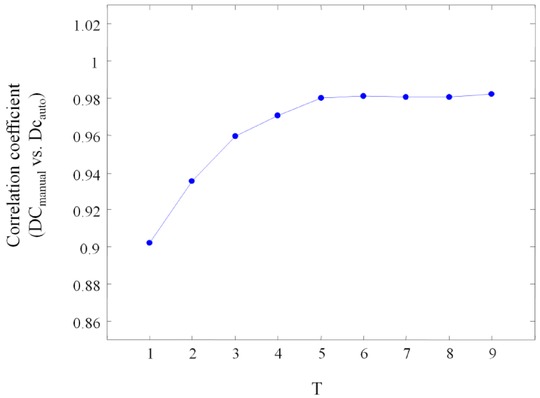
Correlation coefficients of manually and automatically generated measures of deceleration capacity using different T‐filters in the phase‐rectified signal averaging algorithm. The T‐filter acts as a low‐pass filter.

Figure 4.

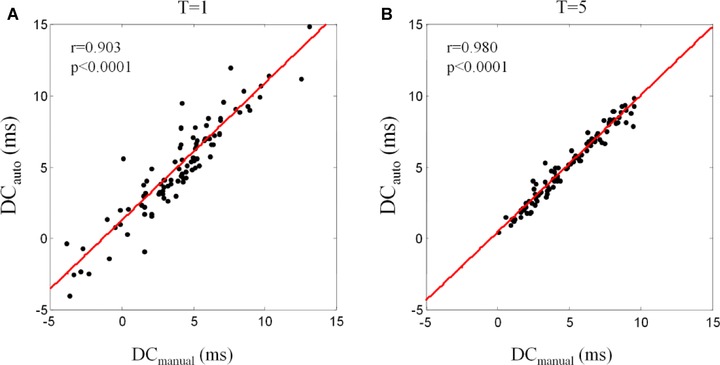
Correlation of manually and automatically generated measures of deceleration capacity. Panel A shows computation by using T = 1. Panel B shows computation by using T = 5.

Figure 5.

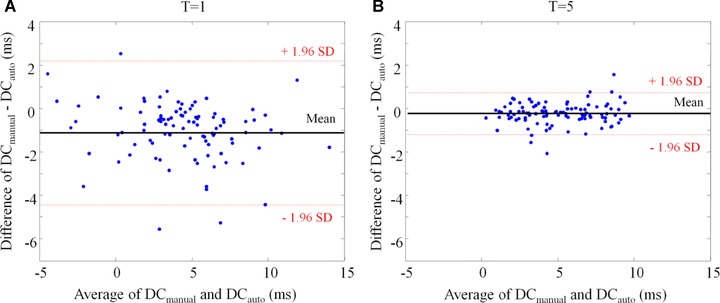
Bland‐Altman plot showing the agreement of manually and automatically generated measures of deceleration capacity DC_manual and DC_auto. The average of DC_manual and DC_auto is plotted versus the difference. A shows computation by using T = 1. Panel B shows computation by using T = 5.

Standard HRV Measures and Standard R‐Peak Detection Algorithm

We also analyzed the correlations for several other HRV measures in time and frequency domain. As shown in the left columns of Table 1, correlations were significantly lower for standard measures of HRV including SDNN, RMSSD, LF, and HF as compared to DC, demonstrating the importance of PRSA in our approach.

Table 1.

Correlations of Manually and Automatically Generated HRV Measures Using Two Different Approaches

	Manual versus Autoa		Manual versus Auto 2b
HRV Measure	R	P‐Value	R	P‐Value
DCT1	0.903	<0.001	0.371	<0.001
DCT5	0.980	<0.001	0.427	<0.001
SDNN	0.653	<0.001	0.294	0.003
RMSSD	0.761	<0.001	0.208	0.038
LF	0.278	0.005	0.148	0.145
HF	0.603	<0.001	0.105	0.304

^aAuto refers to automatic R‐peak detection as proposed in the present study mainly based on a Shannon entropy envelope estimator and a subsequent Hilbert transformation;

^bAuto 2 refers to a standard R‐peak identification based on the Pan–Tompkins algorithm.

Abbreviations as in text.

Additionally, we tested a standard method of R‐peak detection by the Pan–Tompkins algorithm. As shown in the right columns of Table 1, HRV analysis based on the standard R‐peak detection by the Pan–Tompkins algorithm resulted in significant lower correlations of manual and automated HRV analysis.

DISCUSSION

The findings of our study indicate that DC can be automatically calculated from noisy, nonstationary ECG signals with considerable agreement to DC derived from manually preprocessed ECG signals. Agreement between automatically and manually derived DC can be further enhanced by implementation of a low‐pass filter into the PRSA algorithm. Use of a standard R‐peak detection algorithm or quantification of HRV by standard measures resulted in significantly worse correlations between automatically and manually derived measures.

Automated R‐peak detection in the setting of noise and nonstationarities is challenging. R‐peak detection is mainly based on two different steps, preprocessing of the ECG signal and decision making. Aim of preprocessing is to harmonize QRS complexes and to suppress noise. In the present study, this was mainly realized by nonlinear transformation of the ECG signal using a smooth Shannon energy envelope estimator. As previously shown, this is of particular advantage when QRS complexes are characterized by sudden changes in morphology.4 After preprocessing of the ECG signal, the positions of the R peaks need to be identified. Most conventional approaches to decision making use heuristic rules which are often complex and require predefined thresholds. The Hilbert transformation as used here is a remarkably simple approach to R‐peak identification of preprocessed data. It assumes that the signal is subject to cyclic variations by calculating the phase for every time point and with phase zero corresponding to the R peak. The subsequent moving averaging filter is used to remove low‐frequency baselines shifts, which can occur when QRS amplitudes are suddenly changing. Manikandan and coworkers have recently tested the performance of this approach in 48 ECGs of the MIT‐BH database.4 The algorithm achieved an average detection accuracy of 99.80% outperforming other approaches based on linear prediction, wavelet transform,7, 8, 9 or empirical mode decomposition.10

However, even the best algorithm for automated R‐peak detection may sometimes fail when applied to noise‐polluted data. This is particularly true when ECGs are derived from low‐resolution monitoring devices in emergency rooms or intensive care units. It is therefore of great importance that HRV is assessed by a method that is most insensitive to artifacts, nonstationarities, and noise. As substantiated by rather low correlations coefficients standard approaches to HRV assessment are not particularly reliable in this setting. In contrast, PRSA is a robust technique to detect periodic patterns even in the presence of nonstationarities and noise. We have previously shown that the threshold intensity for the detection of additional quasi‐periodic components is approximately 75% lower with PRSA than with standard techniques.3 The agreement between manually derived and automatically generated PRSA signals can be further improved by implementation of a low‐pass filter into the PRSA algorithm. In previous studies on postinfarction patients, DC has been shown to yield strong and independent prognostic information.2, 11, 12 In survivors of acute MI, predictive value of DC was shown to be superior to left ventricular ejection fraction and standard measures of HRV.

The limitations of our study should be recognized. Although automatically generated measures of DC showed good agreement with manually generated measures, automated and manual analyses are still different. It is subject to further investigations to evaluate whether these differences are clinically meaningful. Implementation of a low‐pass filter into the PRSA algorithm suppresses high‐frequency oscillations of heart rate. The clinical value of low‐pass filtered DC needs to be proven by further studies.

In conclusion, we developed and validated a novel approach that allows for a fully automated assessment of cardiac autonomic function without manual intervention in noise‐polluted signals. Automatically generated DC showed good agreement to DC derived from manually preprocessed data. Future studies are needed to test the clinical usefulness of automated DC assessment in different clinical settings.