Dynamics and Rate‐Dependence of the Spatial Angle between Ventricular Depolarization and Repolarization Wave Fronts during Exercise ECG

Abstract

Background: QRS/T angle and the cosine of the angle between QRS and T‐wave vectors (TCRT), measured from standard 12‐lead electrocardiogram (ECG), have been used in risk stratification of patients. This study assessed the possible rate dependence of these variables during exercise ECG in healthy subjects.

Methods: Forty healthy volunteers, 20 men and 20 women, aged 34.6 ± 3.4, underwent an exercise ECG testing. Twelve‐lead ECG was recorded from each test subject and the spatial QRS/T angle and TCRT were automatically analyzed in a beat‐to‐beat manner with custom‐made software. The individual TCRT/RR and QRST/RR patterns were fitted with seven different regression models, including a linear model and six nonlinear models.

Results: TCRT and QRS/T angle showed a significant rate dependence, with decreased values at higher heart rates (HR). In individual subjects, the second‐degree polynomic model was the best regression model for TCRT/RR and QRST/RR slopes. It provided the best fit for both exercise and recovery. The overall TCRT/RR and QRST/RR slopes were similar between men and women during exercise and recovery. However, women had predominantly higher TCRT and QRS/T values. With respect to time, the dynamics of TCRT differed significantly between men and women; with a steeper exercise slope in women (women, −0.04/min vs −0.02/min in men, P < 0.0001). In addition, evident hysteresis was observed in the TCRT/RR slopes; with higher TCRT values during exercise.

Conclusions: The individual patterns of TCRT and QRS/T angle are affected by HR and gender. Delayed rate adaptation creates hysteresis in the TCRT/RR slopes.

Ann Noninvasive Electrocardiol 2010;15(3):264–275

Abnormal cardiac depolarization and repolarization, measured from the standard 12‐lead electrocardiogram (ECG), have been associated with adverse clinical outcomes in several populations. ¹ , ² Traditional methods in the analysis of these abnormalities have been the measurement of duration of the QRS complex and the QT interval. Methodological problems related to the measurement of these indexes and their limited view of the electrogenesis of ventricular activation and deactivation has prompted to the search of new descriptors of repolarization abnormalities. Some of these new descriptors have been shown to have predictive value, such as the “Total Cosine R to T” (TCRT) ³ , ⁴ , ⁵ and QRS/T angle. ⁶ , ⁷ Both indexes describe the spatial angle between the main vectors of ventricular depolarization and repolarization wave fronts.

The dynamics and rate dependence of the QRS/T angle and TCRT are poorly understood as these descriptors have been predominantly measured from a single QRS‐T complex of the standard 12‐lead ECG, ³ , ⁷ , ⁸ , ⁹ or from averaged complexes. ¹⁰ , ¹¹ One previous study, ¹⁰ assessing the circadian dynamics of TCRT, T‐wave residuum, and corrected QT intervals from 24‐hour Holter recordings showed that TCRT decreased at higher heart rate (HR). However, the dynamic range of the HR is limited in standard 24‐hour Holter recordings; therefore, we wanted to explore the dynamics patterns and rate dependence of TCRT and QRS/T angle in healthy men and women during a standard exercise stress test, where the dynamic range of the HR is greater. As far as we are aware, this is the first study to assess the dynamics of these descriptors from the exercise ECG.

METHODS

Study Population

This study investigated healthy men (n = 20, age: 34.5 ± 3.1 years) and women (n = 20, age: 34.7 ± 3.6 years) recruited by advertising in the local newspaper. The candidates were interviewed with a standardized scheme to ascertain their medical history and level of physical activity. All smokers, subjects with a BMI ≥ 30 kg/m², competing athletes, and subjects with diabetes mellitus, asthma, cardiovascular disorders, or having prescribed mediation were excluded. No abnormalities were observed in standard resting 12‐lead ECG in any subject.

Exercise Test Protocol

The subjects underwent maximal exercise test by a bicycle ergometer (Monark Ergomedic 839 E, Monark Exercise AB, Vansbro, Sweden). The Mason‐Likar modification with two additional leads was used in the 12‐lead ECG recording. The exercise protocol included a 2‐minute preexercise rest period during which the test subject sat still on the bicycle. The exercise period started with an initial workload of 25 watts (W), which was gradually increased in steps of 1 W every 5 seconds until voluntary exhaustion. Exercise period was followed by 1‐minute passive recovery while sitting on bicycle ergometer and 4‐minute active recovery at workload of 25 W. Continuous digital ECG at 500 Hz was recorded throughout the test with CardioSoft exercise ECG system (Version 4.14, GE Medical Systems, Freiburg, Germany).

Signal Processing and Analysis

The signal processing and the subsequent analysis were carried out with software written in Matlab (MathWorks, Inc. Natick, MA, USA). Power line interference was reduced with a notch filter at 50 Hz. Baseline wander was removed with cubic spline interpolation. High frequency noise was suppressed with a 40 Hz low‐pass filter. Ectopic and abnormally shaped beats were automatically removed from the analysis. Beats were considered to be ectopic if the preceding RR interval differed more than 20% of the last valid RR interval. Beats with deviating morphology were identified with template matching; the initial template was constructed from the first 10 normal beats. The template was updated with each accepted beat. The threshold for acceptance was 95% match.

The beginning of the QRS‐complex, R‐peak and T‐wave end were located automatically for each beat, after which all beats were aligned according to their R‐peak location. The alignment was done separately for each of the eight independent leads of the 12‐lead ECG (I, II, V₁–V₆). Subsequently, the aligned beats were filtered with a 10‐beat‐wide sliding window in order to produce representative median beats for each cardiac cycle and to further suppress the noise within the beats. This was done separately for each lead.

The TCRT and QRS/T angles were then automatically calculated from the averaged beats in a beat‐to‐beat manner. The mathematical background for the calculation of TCRT and QRS/T angle is explained in the appendix. The analysis process was visually verified in each subject. However, due to the vast number of samples, only every 20th beat was visually inspected for correct fiducial points, that is, Q‐wave, R‐ and T‐peak, and T‐wave end. The QRS/T results were modified by taking the cosine of the values. This was done in order to obtain the same range of values for both the TCRT and QRS/T angle (that is between −1 and 1). Normally, the overall vectors of depolarization and repolarization are orientated in the same direction, whereby, TCRT and QRS/T angle receive values close to 1, which corresponds to an angle of 0 degrees. When the vectors are pointing at opposite directions, the values are close to −1, which corresponds to an angle of 180 degrees.

TCRT/RR and QRST/RR Relation

The relationship between TCRT and RR intervals as well as between the QRS/T angle and RR intervals were studied separately for the exercise and recovery periods in each subject. The individual beat‐to‐beat TCRT/RR and QRST/RR patterns were fitted with seven different regression models:

• • Linear model (LIN):

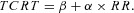
• • Hyperbolic model (HYP):

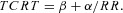
• • Parabolic model (PAR):

• • Logarithmic model (LOG):

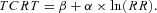
• • Shifted logarithmic model (SLOG):

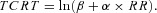
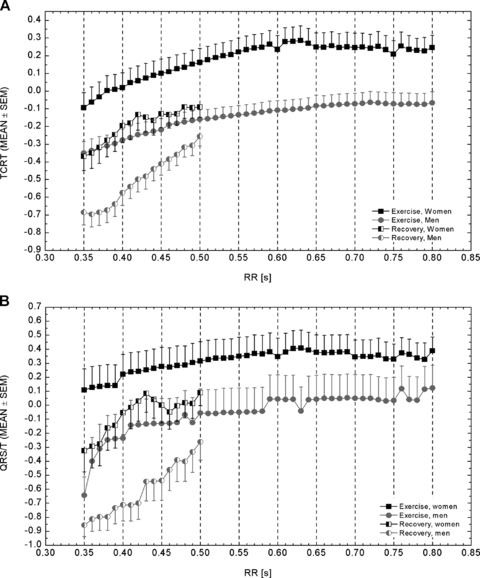
• • Exponential model (EXP):

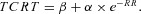
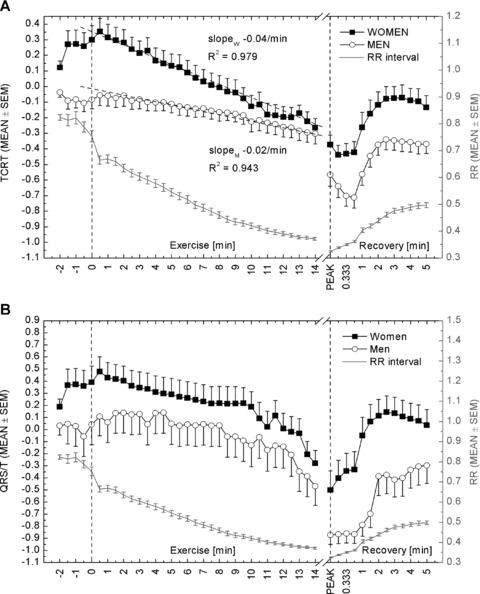
• • Second‐degree polynomial model (POL2):


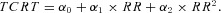
The first six regression models have two parameters (α, β) defining the regression model whereas the last, second‐degree polynomic model, is defined with three parameters. The correlation coefficient and average regression residual were also calculated for each fit. The average regression residual describes the quality of the fit; it is the root‐mean‐square of the differences between the observed and regression‐generated TCRT (QRS/T) values. In order to investigate which of the regression models fitted the overall data best, the residuals of the individual regressions were compared between models using the nonparametric paired Wilcoxon's test. In addition, for each subject, the regression model that fitted the data best was identified separately for the exercise and recovery periods.

Statistical Analysis

In order to compare the TCRT and QRS/T values occurring at the same HR, the values were sorted into RR interval bins ranging from 300 to 1000 ms (i.e., from 60 to 200 bpm), in steps of 10 ms. This sorting was performed for each subject (separately for exercise and recovery). The median value of each bin was taken to represent that bin. Subsequently, the data from each individual were then pooled and grouped for men and women.

Similarly, to analyze the dynamic patterns of TCRT and QRS/T with respect to time, the median filtered (10 beat median) values were sampled at 30‐second intervals; starting 2 minutes prior to the exercise. In addition, one sample was taken from the peak exercise. The values from the recovery period were sampled with respect to the exercise peak; the first three samples were taken at 10‐second intervals (10‐, 20‐, and 30‐second recovery) after which the samples were taken at 30‐second intervals to the end of the recovery period. The samples gathered from each individual were pooled together and grouped separately for men and women.

The averaged TCRT and QRS/T patterns were analyzed with the analysis of variance for repeated measures (RANOVA, with gender as the between‐subjects factor) to determine whether the overall change in the values was significant (main effect = RANOVA_M) and whether there were significant differences in the values (between subjects factor = RANOVA_S) or the profiles of the slopes between men and women (interaction = RANOVA_I). Post hoc comparisons were performed with Student's t‐test; the tests were corrected with Bonferroni correction in order to compensate for the multiple tests (i.e., P‐values were multiplied by the number of tests). The data were analyzed using the SPSS version 15 (SPSS, Inc., Chicago, IL, USA). All tests were 2‐sided and P‐value < 0.05 was considered statistically significant. The continuous values are presented as mean ± standard deviation (SD) in text and tables and as mean ± standard error of mean (SEM) in the figures, unless otherwise stated.

RESULTS

On average, the exercise period lasted for 1080 ± 266 seconds (men, 1313 ± 178 vs 883 ± 148 seconds, women, P < 0.001). During the exercise, an average of 2045 ± 465 individual cardiac cycles were analyzed (men, 2374 ± 373 vs 1706 ± 329 women, P < 0.001). Respectively, during the recovery, an average of 770 ± 88 separate beats were analyzed (men, 753 ± 103 vs 795 ± 64, women, P = 0.048). The maximum HR achieved during exercise was 184 ± 8.3 bpm (men, 185 ± 8.5 vs 184 ± 8.6, women, P = 0.585).

TCRT during Exercise and Recovery

The behavior of TCRT with respect to time is illustrated in Figure 1A. TCRT decreased during exercise and the overall change in the average values during the exercise was statistically significant (RANOVA_M, P < 0.001). The profiles of the TCRT curves differed significantly between men and women (RANOVA_I, P = 0.018), with steeper average slope in women (women, −0.04/min vs −0.02/min in men). On average, greater TCRT values were observed in women (RANOVA_S, P = 0.037). The difference between the groups decreased toward the exercise peak and was statistically significant only at the beginning of the exercise (P < 0.050 at each time instant from 0 to 4 minutes).

Figure 1.

Average TCRT (A) and QRS/T (B) values at different time instances throughout the measurement. Average RR intervals at corresponding time instances are included in both panels. The dotted vertical lines indicate the beginning of the exercise and the peak exercise, respectively. The first three samples after the exercise peak represent 10‐, 20‐, and 30‐seconds’ recovery. Otherwise, samples are 30 seconds apart from each other. After 3 minutes of recovery, the average TCRT and QRS/T values started to decline. Unfortunately, the recovery period was followed for only 5 minutes, and therefore the return to baseline level cannot be seen in the figure.

During recovery, the TCRT values increased (RANOVA_M < 0.001). The profiles of the slopes between men and women did not differ (RANOVA_I, P = 0.650), but the difference in the values was significant (RANOVA_S, P = 0.009); the difference between the groups was greatest at 20‐ and 30‐second recovery (P < 0.020 and P < 0.040, respectively).

QRS/T during Exercise and Recovery

Figure 1B illustrates the average dynamics of the QRS/T angle in men and women with respect to time. There was a decrease in the QRS/T values during exercise in both men and women (RANOVA_M, P< 0.001). Though women seemed to have greater QRS/T values than men throughout the measurement, the difference between men and women was not significant during exercise (RANOVA_S, P = 0.224). In addition, the profiles of the slopes were similar between the sexes (RANOVA_I, P = 0.716).

During recovery, the QRS/T values increased (RANOVA_M, P < 0.001). The profiles of the slopes did not differ between men and women (RANOVA_I, P = 0.121), but the difference in QRS/T values between sexes differed significantly (RANOVA_S, P < 0.003); the difference was significant at each time instant from 20‐ to 90‐second recovery (P < 0.050, at each), with the greatest difference at 90‐second recovery (P < 0.010).

TCRT/RR Relation

Figure 2A illustrates the pooled TCRT values over the RR interval bins ranging from 350 to 800 ms. The TCRT values decreased at higher HR (RANOVA_M, P < 0.001). The profiles of the average TCRT/RR slopes were similar (RANOVA_I, P = 0.498) during exercise. However, there was a significant difference in the average TCRT values between men and women (RANOVA_S, P < 0.001), with larger TCRT values in the women's group; the difference between sexes was significant in RR bins ranging from 450 to 700 ms (P < 0.050, in each bin). There was no significant difference in the profiles of the recovery slopes between men and women (RANOVA_I, P = 0.233). The TCRT values, however, differed significantly between the groups (RANOVA_S, P < 0.005), with the greatest difference observed in the RR bins ranging from 350 to 430 ms (P < 0.050, in each bin).

Figure 2.

TCRT (Panel A) and QRS/T (Panel B) values averaged over 10‐ms RR bins ranging from 350 to 800 ms intervals. The RR bins from recovery period were limited to the range of 350 to 500 ms due to the lack of samples in other bins.

Table 1 shows the averaged residuals of the generic models that were applied to the TCRT/RR patterns of individual subjects. In addition, the table reveals the number of cases in which the regression model in question provided the optimal fit. Table 2 shows the P‐values of the paired comparisons (Wilcoxon's test) of the regression residuals summarized in Table 1. Based on the averaged regression residuals in individual subjects and the number of optimal cases, the best regression model for both exercise and recovery was the polynomic model. The parameter values of the polynomic fit for exercise and recovery are shown in Table 3.

Table 1.

Averaged Regression Residuals of the Different Regression Models

Model	Summary for TCRT				Summary for QRS/T
	Residual		Optimal Fit		Residual		Optimal Fit
	Exercise	Recovery	Exercise	Recovery	Exercise	Recovery	Exercise	Recovery
Linear	0.080	0.083	0	0	0.231	0.194	1	0
	(0.045)	(0.035)	(0/0)	(0/0)	(0.208)	(0.190)	(1/0)	(0/0)
Hyperbolic	0.073	0.081	2	0	0.219	0.192	3	0
	(0.045)	(0.032)	(1/1)	(0/0)	(0.191)	(0.191)	(1/2)	(0/0)
Parabolic	0.086	0.087	8	1	0.258	0.226	1	0
	(0.057)	(0.037)	(7/1)	(0/1)	(0.241)	(0.230)	(0/1)	(0/0)
Logarithmic	0.076	0.082	1	0	0.224	0.193	0	0
	(0.045)	(0.033)	(1/0)	(0/0)	(0.199)	(0.190)	(0/0)	(0/0)
Shifted logarithmic	0.077	0.082	0	0	0.217	0.195	0	0
	(0.044)	(0.033)	(0/0)	(0/0)	(0.187)	(0.195)	(0/0)	(0/0)
Exponential	0.078	0.083	0	0	0.228	0.193	0	0
	(0.045)	(0.034)	(0/0)	(0/0)	(0.203)	(0.190)	(0/0)	(0/0)
2nd degree Polynomic	0.064	0.073	29	39	0.198	0.173	35	40
	(0.038)	(0.026)	(11/18)	(20/19)	(0.172)	(0.179)	(18/17)	(20/20)

Residuals are shown as mean (SD). The optimal fit is reported as number of cases for whom the particular regression model was the optimum among all models: total (men/women).

Table 2.

The P‐Values of the Paired Comparisons between the Regression Residuals of Different Regression Models

		LIN	HYP	PAR	LOG	SLOG	EXP
TCRT/RR	HYP	0.002
		(0.022)
	PAR	0.420	0.016
		(0.405)	(0.074)
	LOG	0.0002	0.027	0.096
		(0.004)	(0.09)	(0.116)
	SLOG	0.001	0.008	0.166	0.008
		(0.012)	(0.038)	(0.129)	(0.320)
	EXP	7 × 10−5	0.009	0.179	0.001	0.657
		(0.001)	(0.045)	(0.248)	(0.012)	(0.113)
	POL2	4 × 10−8	2 × 10−7	2 × 10−5	6 × 10−8	4 × 10−8	4 × 10−8
		(8 × 10−8)	(2 × 10−7)	(4 × 10−7)	(2 × 10−7)	(1 × 10−7)	(8 × 10−8)
QRST/RR	HYP	0.064
		(0.747)
	PAR	7 × 10−5	2 × 10−4
		(2 × 10−4)	(0.008)
	LOG	0.005	0.110	2 × 10−6
		(0.510)	(0.936)	(3 × 10−4)
	SLOG	0.016	0.798	6 × 10−6	0.162
		(0.856)	(0.460)	(5 × 10−4)	(0.648)
	EXP	0.004	0.088	6 × 10−6	0.037	0.013
		(0.420)	(0.835)	(2 × 10−4)	(0.667)	(0.840)
	POL2	5 × 10−8	1 × 10−7	4 × 10−8	6 × 10−8	5 × 10−8	4 × 10−8
		(4 × 10−8)	(4 × 10−8)	(4 × 10−8)	(4 × 10−8)	(4 × 10−8)	(4 × 10−8)

Paired comparisons (Wilcoxon's test) of the regression residuals summarized in Table 1. P‐values are shown as: exercise (recovery).

LIN = linear; HYP = hyperbolic; PAR = parabolic; LOG = logarithmic; SLOG = shifted logarithmic; EXP = exponential; POL2 = second order polynomic model.

Table 3.

The Average Parameters of the Individual Second‐Degree Polynomic Models for Exercise and Recovery Periods

	TCRT		QRS/T
	Men	Women	Men	Women
r	0.900 ± 0.064†	0.890 ± 0.097	0.672 ± 0.204	0.745 ± 0.203
	(0.810 ± 0.117)	(0.811 ± 0.185)	(0.644 ± 0.181)*	(0.751 ± 0.154)*
a2	−2.36 ± 1.69	−6.43 ± 11.69	−12.38 ± 17.95	−4.30 ± 13.62†
	(−7.78 ± 13.02)	(−16.09 ± 25.77)	(3.46 ± 57.71)*	(−39.30 ± 47.50)*
a1	3.25 ± 1.88†	7.31 ± 10.20	14.14 ± 18.35	5.37 ± 13.44†
	(8.92 ± 10.92)	(15.56 ± 20.24)	(0.80 ± 47.11)*	(35.08 ± 40.00)*
a0	−1.21 ± 0.67†	−1.86 ± 2.07†	−3.99 ± 4.09*	−1.27 ± 3.29*†
	(−2.86 ± 2.27)	(−3.85 ± 3.76)	(−1.55 ± 9.36)*	(−7.79 ± 8.53)*
Residual	0.048 ± 0.026†*	0.080 ± 0.041*	0.277 ± 0.186*	0.118 ± 0.113*
	(0.075 ± 0.030)	(0.070 ± 0.024)	(0.230 ± 0.210)*	(0.114 ± 0.118)*

*Significant difference between men and women (P < 0.05).

^†Significant difference between exercise and recovery (P < 0.05).

r = correlation coefficient; a0, a1, and a2 are the parameters of the second‐degree polynomic fit. Values are shown as mean ± SD. Values within brackets are parameter values for recovery.

In the TCRT/RR regression models, there was no statistically significant difference in the distribution of optimum cases between men and women during exercise (P = 0.066, chi‐square test) or recovery (P = 0.311, chi‐square test). However, the distribution of optimal cases differed between exercise and recovery in men (P = 0.009, chi‐square test) but not in women (P = 0.598, chi‐square test). The average regression residuals differed between men and women during exercise (P < 0.010 in each model), with smaller average residuals in men. The residuals did not differ between the groups during recovery. In addition, the residuals observed in men were significantly smaller during exercise when compared to those observed during recovery (P < 0.015 in each regression model). In women, the residuals did not differ between the exercise and recovery periods.

QRST/RR Relation

Figure 2B illustrates the pooled QRS/T angle values over the RR interval bins ranging from 350 to 800 ms. The QRS/T values decreased at higher HR (RANOVA_M, P < 0.001). The profiles of the average QRST/RR exercise slopes did not differ between men and women (RANOVA_I, P = 0.416). Though the women seemed to have greater QRS/T values throughout the measurement, the difference between the groups was not significant during exercise (RANOVA_S, P = 0.063). The profiles of the average QRST/RR slopes during recovery were also similar in men and women (RANOVA_I, P = 0.694). However, the QRS/T angle values differed significantly between the two groups (RANOVA_S, P < 0.005), with the greatest difference observed in the RR bins ranging from 350 to 430 ms (P < 0.050, in each RR bin).

Based on the results shown in Tables 1 and 2, the best regression model for both exercise and recovery was the polynomic model. The correlation coefficients and regression parameter values and their comparisons are shown in Table 3. The distribution of optimal cases was similar in men and women during exercise (P = 0.501, chi‐square test) and recovery (P = 1.000, chi‐square test). The distribution of optimum cases did not differ between exercise and recovery in men (P = 0.349, chi‐square test) or women (P = 0.198, chi‐square test). The average regression residuals differed between men and women during exercise (P < 0.035, in each model); women had smaller average residuals. The residuals did not differ between men and women during recovery. There was also no statistically significant difference in the regression residuals between the exercise and recovery periods in men or women.

Hysteresis

Figure 2 reveals evident hysteresis in the values of the studied descriptors; hysteresis in the sense that the descriptors at a given HR during recovery receive different values than during exercise. This deviation can be seen in both TCRT/RR and QRST/RR slopes. Further investigation revealed that the difference in the TCRT values between exercise and recovery was not similar in men and women. In women, the differences in the average TCRT values between exercise and recovery (within RR bins from 350 to 500 ms) were not statistically significant. However, in men, the difference was significant at higher HR, that is, in the RR bins ranging from 350 to 430 ms (P < 0.040, in each bin). In addition, in women the exercise and recovery TCRT/RR slopes were parallel (RANOVA_I, P = 0.452), whereas in men, the recovery slope was steeper than the exercise slope (RANOVA_I, P < 0.001).

DISCUSSION

The results emphasize the significant influence of HR on the spatial relationship between depolarization and repolarization (TCRT and QRS/T angle) in the human heart. In particular, the TCRT displayed a remarkable rate dependence in individual subjects during exercise and recovery. In individual subjects, this rate dependence was best described with a nonlinear, second‐degree polynomic model. On average, the dynamic patterns of TCRT and QRS/T angle were similar in men and women with respect to HR; however, the TCRT and QRS/T values were predominantly higher in female subjects. With respect to time, women had a steeper TCRT slope during exercise. We also found significant hysteresis in the QRS/T and TCRT values between the exercise and recovery periods; especially in men, the TCRT values differed significantly between exercise and recovery at higher HR (RR bins from 350 to 430 ms).

Relations to Previous Studies

The TCRT values measured prior to exercise were lower than previously reported for healthy subjects. ⁸ However, this can be explained with posture, as supine TCRT values are larger than TCRT values measured while sitting or standing. ¹² During the course of exercise, the TCRT and QRS/T values decreased toward the exercise peak, reaching negative values. Negative TCRT values are generally observed in cardiac patients, and they have been associated with poor clinical outcome. ³ , ⁴ , ⁹ Similarly, QRS/T values measured at the peak exercise exceeded the normal limits for QRS/T angle. ¹³

The rate dependence of TCRT has been previously reported by Smetana et al. ¹⁰ Their study indicated that TCRT achieves lower values at higher HR. The results from our study concur with this observation. However, the magnitude of individual TCRT‐RR relations shown in our study was much greater than that reported by Smetana et al. ¹¹ (women: r = 0.464 ± 0.21; men: r = 0.549 ± 0.21) versus this study during exercise (women: r = 0.890 ± 0.097; men: r = 0.900 ± 0.064) and recovery (women: r = 0.811 ± 0.184; men: r = 0.810 ± 0.117), which might be explained by the physical stress and broader dynamic range of the HR.

There were significant sex differences in the QRS/T and TCRT values as well as in the dynamics of these descriptors. On average, women had predominantly higher QRS/T and TCRT regardless of the HR. This observation is in good agreement with previous findings. ¹⁰ , ¹¹ , ¹⁴ , ¹⁵ The dynamics of the TCRT differed between men and women during exercise (Fig. 1A); that is, women exhibited steeper exercise slopes. This might attributable to the fact that women achieved higher HR earlier than men, and therefore received lower TCRT values earlier in the exercise period. This theory is supported by the fact that the pooled TCRT/RR patterns did not differ between men and women (Fig. 2A).

The physiological basis for the decrease in the QRS/T angle and TCRT at elevated HR is not well known. Smetana et al. ¹⁰ suggested that the rate dependence of the TCRT partly derives from the differences between action potential durations (APD), generated by differences within the repolarizing ionic currents, with the trend toward reduced global APD dispersion at higher HR. On the waveform level, the reason for the decrease in the TCRT and QRS/T values at higher HR can be speculated in a more straightforward manner. Previous studies on healthy subjects have shown specific, gradual changes in the ECG waveforms during and after exercise. ¹⁶ , ¹⁷ , ¹⁸ Simoons et al. ¹⁶ observed no significant change in the QRS complex duration; however, the duration of the R wave decreased whereas the S‐wave duration increased the same amount at higher HRs. Wolthuis et al. ¹⁷ reported gradually decreasing R‐waves and increasing S‐wave magnitudes during exercise. We suggest that these changes in the QRS complex combined with the changes in the T‐wave amplitude and symmetry ¹⁶ , ¹⁸ contribute largely to the behavior of QRS/T angle and TCRT during and after exercise. The decrease in the R wave and the corresponding increase in the S wave at higher HR alter the QRS loop morphology so that the contribution of S‐wave vectors in the QRS loop increase. As the S wave generally has opposite polarity to that of the T wave, the overall angle described by the TCRT decreases as more S‐wave vectors exceed the threshold for the calculation of TCRT (see the Appendix).

Figure 3 illustrates the TCRT‐RR and QRST‐RR relation of three different test subjects. Visually, it is obvious that the HR relation of the TCRT and QRS/T angle varied not only between the test subjects but also between the exercise and recovery periods of the individual subjects. This inter‐individual variation can also be seen in the regression parameters shown in Table 3. Consequently, as the TCRT and QRS/T values vary significantly between different test‐subjects at a given HR, the changes in the mean values of the pooled data (Figs. 1 and 2) seem modest over the wide range of HRs. The differences between the maximum and minimum values are generally larger in individual subjects, which can be well observed in Figure 3. Due to this variation, it might be difficult to perform the rate correction of TCRT satisfactorily with a generalized correction formula; instead individualized rate correction should be considered. Similar inter‐individual variations have been described in the rate dependence of the duration of the QT interval. ¹⁹

Figure 3.

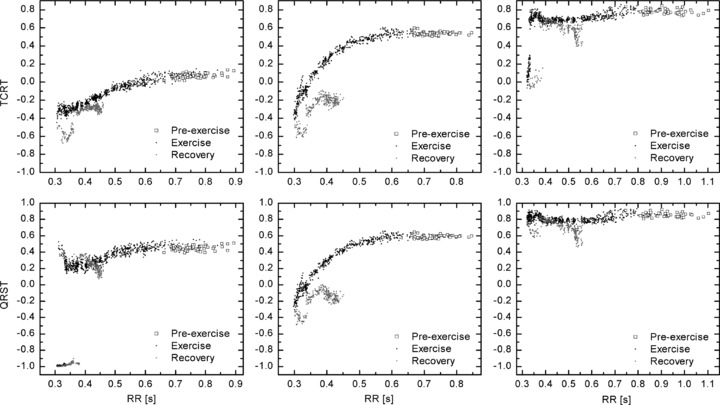
Individual TCRT‐RR patterns from three different test subjects are shown on the top row. Corresponding QRST‐RR patterns are shown on the bottom row. The first two patterns from the left represent the most typical patterns of TCRT and QRS/T behavior, whereas the subject on the right represents a rarer pattern.

During early recovery, both TCRT and QRS/T values either decreased slightly or remained at the level of the exercise peak despite the decelerating HR, thus forming a hysteresis loop in the TCRT/RR and QRST/RR loops (Fig. 2). A similar phenomenon in cardiac repolarization has been observed earlier in the RR‐QT relationship ²⁰ , ²¹ , ²² as well as in the dynamics of the APD during cardiac pacing. ²³ Due to the hysteresis, the correlation coefficients were on average lower during recovery than during exercise (Table 3); thus the hysteresis can also be seen as a delayed or reduced rate adaptation during recovery.

Limitations

This study has taken a step in the direction of defining the rate dependence and dynamics of the QRS/T angle and TCRT during exercise ECG. However, a few methodological points deserve some comment. The reliability of the analysis may sometimes be questionable due to the extensive noise present in an exercise test. The effects of noise can be reduced by filtering and with the use of averaged representative beats. In addition, our previous studies have shown that TCRT is inherently robust, as the phenomenon it describes is large and therefore less affected by noise. ²⁴ The analysis of these new morphological descriptors does not require an exact determination of T‐wave offset. Furthermore, sources of human errors are minimized with digital ECG and automated computer analysis. ⁸

Due to differences in the duration of exercise and HR dynamics between test subjects, the number of samples varied between sample points and RR bins. Therefore, the analysis was limited to specific time range and RR bins to avoid excess lack of samples. Regardless of this, some missing samples had to be replaced with group means in order to keep each individual in the analysis and to avoid unbalanced design. During the exercise, the number of test subjects per sample point dropped after 10 minute exercise, so that the total number of test subjects at 14‐minute sample point was 30 (20 men). Similarly, in the exercise RR bins, the number of subjects in the RR bins from 0.65 to 0.80 seconds dropped from 40 to 34 (20 men), respectively. During the recovery, the number of test subjects in RR bins from 0.43 to 0.50 seconds dropped from 40 to 26 (16 men), respectively. The missing values were replaced with group means at each point.

Some of the analyzed parameters do not seem to return to their normal, baseline, value during recovery (Fig. 1). This is due to limited data: recovery was only monitored for 5 minutes. A longer monitoring of recovery would have revealed the return to normal metrics.

Conclusions

These results clearly show that the TCRT value, which has been already used in risk stratification analysis of various populations, exhibits a strong correlation with HR in individual subjects, resembling that of the QT interval. Therefore, in the analysis of this index, an HR correction should be considered in an attempt to describe more specifically the global repolarization heterogeneity, not only the HR. Furthermore, it is possible that the observed association between the reduced TCRT and mortality may partly result from this rate dependency. Elevated HR, resulting in lower TCRT values, is a well‐known risk factor of mortality. ²⁵ , ²⁶ Therefore, future studies should assess the prognostic value of this index, measured both at rest, adjusted for HR, and at high HR during exercise. Furthermore, the prognostic significance of the dynamics of TCRT and QRS/T angle should be studied; the assessment of the dynamics of these descriptors might offer better and more reliable information than a single measurement of TCRT or QRS/T angle from standard supine 12‐lead ECG.

In order to calculate the morphological descriptors, singular value decomposition is applied to the eight algebraically independent leads (I, II, V₁–V₆) of the 12‐lead ECG sample. The leads are reconstructed in an orthogonal lead system so that the first lead contains the maximum energy in one direction and the second the maximum energy perpendicular to the first lead, etc. It has been shown that the first three components of the decomposition may contain up to 99% of the ECG's energy; ⁵ they are referred to as the dipolar components, which are related to the X, Y, and Z leads of the Frank's vectorcardiographic lead system.

If M is an 8 ×n matrix, where each row corresponds to an ECG lead and each column (n) represents a sample, then there are two orthogonal matrices: L =[l₁, l₂, … , l₈]∈ℜ ^{8 × 8} and R =[r₁, r₂, … , r_n]∈ℜ ^nxn so that the M = L^TΣR, where Σ=diag(σ₁, σ₂ … , σ₈) ∈ℜ ^nx8, where σ₁≥σ₂≥ … ≥σ₈≥ 0. Columns L and R are the left and right singular vectors, respectively, and σ_i are the singular values of M.

TCRT. The three‐dimensional minimum subspace is spanned by the columns of 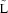^nx3, and P is the projection of matrix M onto 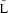, P =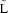Σ. P_QRS and P_T represent the projections of QRS and T‐wave loops in the three‐dimensional subspace, respectively. Unit vector U_T represents the main orientation of the T‐wave loop (P_T) in this space. As stated in Equation 1, TCRT is the average of the cosines of the angles between the U_T and each vector, P_QRS(i), of the QRS complex whose resultant exceeds 50% of the maximum value of the resultant (note the difference to the threshold in Acar et al. ⁸ where the threshold was 70%).

QRS/T. As shown in Equation 2, the QRS/T angle is the three‐dimensional angle between the largest vector of the QRS complex (P_{QRS  max}) and the main vector of the T‐wave loop (U_T). The purpose of the cosine, in Equation 2, is to make QRS/T angle values comparable with the TCRT values (i.e., to produce QRS/T values in the range of −1 and 1).

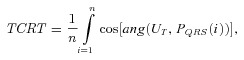(1)

(2)