Abnormalities of the Repolarization Characteristics of Patients with Heart Failure Progress with Symptom Severity

Abstract

Background: Congestive heart failure is a common condition with high mortality. Many of these deaths are sudden and unexpected. Ventricular action potential, surface repolarization (QT interval), and dispersion of repolarization are prolonged in the failing heart, contributing to arrhythmogenesis and sudden death. We studied the relationship between QT and heart rate (RR interval) from ambulatory recordings using a novel method in patients with ischemic heart disease and varying degrees of left‐ventricular impairment (IHD) and compared them to healthy subjects (HS). We compare the degree of abnormality with the functional impairment and ejection fraction.

Methods: Using a previously described automated method for continuous estimation of the QT/RR characteristic that incorporates a correction formula for compensation of QT adaptation lag (VERDA, Del Mar Reynolds Medical Ltd., Hertford, UK), we compared recordings from 41 IHD patients with age‐matched HS.

Results: IHD Patients have prolonged 24‐hour mean QTo (461 ms vs 426 ms, P < 0.01), and abnormal rate dependence relative to controls (24‐hour mean slope: 0.20 vs 0.14, P < 0.001; J: 0.38 vs 0.28, P < 0.001). There is increased temporal variation in J with respect to HS. These abnormalities of repolarization increase with worsening NYHA class, but do not correlate with ejection fraction.

Conclusions: The use of a universal correction formula to compare dynamic QT data in IHD patients is inappropriate. The observed progressive abnormalities may be responsible for the high incidence of sudden death through promotion of arrhythmias.

Congestive heart failure (CHF) is a common condition with high mortality. Many of these patients die suddenly, ¹ and often tachyarrhythmias are responsible for this. ² , ³ The failing ventricle exhibits prolongation of action potential duration (APD), ⁴ and prolongation of the surface QT interval is linked to malignant arrhythmias. ⁵ , ⁶ , ⁷ , ⁸

To allow comparisons of QT interval data between individuals and populations, it is necessary to correct the QT duration for heart rate, as this is the greatest single influence upon QT. However, QT duration is also influenced by autonomic tone and the effects of many cardiac drugs. Correcting QT for rate is problematic and has led to the development of numerous linear, logarithmic, and exponential formulae, although researchers have questioned whether any single formula can be universally applicable. ⁹

More recently, due to the developments in the field of electronics, it has become possible to analyze large quantities of data at high speed, with automated measurement of both the RR and QT intervals. This has enabled the study of long‐term ECG recordings and assessment of the relationship between QT and RR. This has the advantage that large quantities of data can be processed quickly and removes some of the problems of interobserver errors in manual QT measurement. ¹⁰ There is also the advantage that assessment of repolarization over long recordings allows a more complete assessment of the relationship between QT and heart rate throughout the day, as considerable circadian variation in repolarization characteristics is thought to occur. ¹¹ , ¹² , ¹³ Unfortunately the analysis of dynamic recordings, where heart rate is varying constantly, prompts special care when attempting to draw conclusions regarding short‐term changes in the QT/RR relationship. QT does not adapt immediately to changes in RR but tends to lag behind. This time lag has been shown in cellular and pacing studies to have two components ¹⁴ , ¹⁵ , ¹⁶ with an immediate rapid phase with a very short time constant that acts over the first or second inter‐beat interval. The second delayed component has a much longer time constant, estimated at 1 min or more, which means that several minutes are required before full adaptation of QT to the new heart rate is reached. Estimation of the QT/RR relationship over short time periods will, therefore, be influenced by incomplete QT adaptation and errors in estimation of the QT/RR slope or rate‐corrected QT (QTc) will occur. ¹⁷ Automated methods for analysis of the QT/RR relationship have circumvented this problem by only analyzing steady‐state data when heart rate has been constant within a narrow range for a period of time. This permits assessment of the steady‐state QT:RR characteristic, but removes all data when heart rate is changing. Our primary objective was to describe the QT/RR relationship from continuous 24‐hour data in patients with left ventricular impairment, and to establish whether there was a correlation between abnormalities in this relationship and the severity of the condition.

METHODS

Patient Population and Data Acquisition

Patients with ischemic heart disease and either symptoms of heart failure or left ventricular impairment (or both) who had been stable on cardiac medications for at least 1 month were suitable for inclusion in the study. Left ventricular ejection fraction was estimated by standard echocardiographic, angiographic, or radionucleide methods. Patients on agents known to prolong the QT interval were excluded. Patients with bundle branch block (BBB) or atrial fibrillation were excluded. Data from recordings in 41 patients from NYHA classes I–IV were compared with 15 age‐matched healthy volunteers. NYHA functional class was assessed by a clinician blinded to the results of the ambulatory ECG data. For the purposes of subanalyses, patients were divided into four broad groups according to ejection fraction (<15%, 16–25%, 26–40%, >40%). The characteristics of patients and controls are shown in Table 1. Twenty‐four‐hour ambulatory ECG recordings were acquired with two‐channel ambulatory ECG recorders using standard bipolar thoracic leads CM1 and CM5.

Table 1.

Characteristics of Subjects

	Healthy Volunteers	IHD
Age	53 (6)	57 (14)
Sex	10 male,	35 male,
	5 female	6 female
EF	NA	25% (14)
Mean heart rate (SD)	71 (6)	70 (11)
Beta blockers	NA	50%
ACE Inhibitors/AII antagonists	NA	90%
Diuretics	NA	90%
Digoxin	NA	5%
Class III agents	NA	0%

Data are expressed as means (SD), or as percentages; NA = not assessed.

Dynamic QT/RR Measurements

The tapes were replayed on a Pathfinder Analyzer (Del Mar Reynolds Medical Ltd., Hertford England), which excluded ectopic complexes and those that were significantly distorted by artefact. The analyzer measured each QT interval and the preceding RR interval. T_end was measured using the slope method, whereby, the end of the T wave is determined as being the point at which the current slope of the T wave drops below a predetermined proportion of the maximum slope. The accuracy of QT interval measurement has been validated independently. ¹⁸ Twenty‐four‐hour files of RR and QT intervals were then processed on a personal computer using VERDA software (Del Mar Reynolds Medical Ltd.). The three‐stage process has been described elsewhere ¹⁷ , ¹⁹ but is outlined below.

For any given change in RR, the change in QT is related to the slope of the QT/RR plot at that heart rate. If changes in RR were infinitely slow, the plot would describe the steady‐state characteristic and the change in QT (ΔQT) due to a change in RR (ΔRR) would be given by the formula

However, for more physiological changes in RR, one must incorporate a model for the lag phenomenon. The change in QT comprises an immediate undelayed fraction described as

and the remainder as the fraction

which has suffered a single‐pole lag with a time constant of τ seconds. In Laplace transform notation the lag function is thus

This model was refined electronically by adjusting the time constants and applying this lag function to the RR signal to create RR', an identically lagging version of the RR signal. From analysis of recordings from normal individuals, it was found that α remains relatively constant throughout the 24‐hour period, with a population range of 0.22 to 0.31 (mean 0.26 ± 0.02). When the proportion of the fast and slow components of the lag function are correctly adjusted, the QT/RR plot no longer has hysteresis loops but traces out a curve which is presumed to be the underlying steady‐state characteristic (Fig. 1). During analysis the operator can monitor the removal of “hysteresis loops” and manually adjust the lag‐compensation algorithm if necessary by adjusting the proportion of α.

Figure 1.

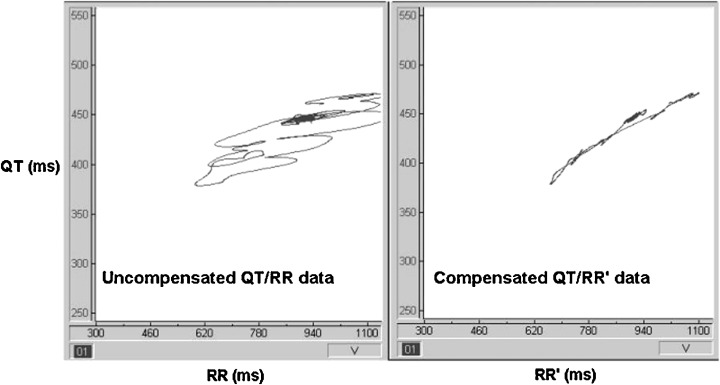
A 3‐min excerpt of data as would be seen during analysis of a Holter recording. The panel on the left is a plot of raw QT values against the preceding RR intervals (QT/RR). Hysteresis loops are seen as heart rate accelerates and decelerates. The right‐hand panel shows the same QT intervals plotted against the lag‐compensated (RR') intervals. The resultant effect is seen as removal of the hysteresis loops, enabling the fitting of data to the exponential formula.

Technically, however, this is now a QT/RR' plot as the QT data are the same, but the RR data have been delayed by applying the lag function. As these “pseudo‐steady‐state” plots are not linear but curved, the relationship is estimated by fitting the data against a general exponential formula with an X/Y intercept at zero. The curve can be described in terms of two variables—the exponent J and QTo, which is the QT interval at RRo, a reference RR interval (chosen as 1000 ms for reasons of convention).

Secondly, throughout the analysis, the RR' and QT signals are cross‐correlated within a moving 5‐min time window that is scrolled through the 24‐hour data. As long as the correlation between QT and RR' remains high (correlation coefficient r > 0.8), the slope (S) of the QT/RR plot around each successive (RR', QT) point is computed as the linear regression coefficient in the 5‐min time window currently centered on that point. Thus a continuously updated measure of the slope of the QT/RR' characteristic curve is generated. If the mean 5‐min correlation coefficient drops below 0.8, these data are automatically edited out and not used for the calculation of 24‐hour mean values of QTo, S, and J. Unlike some methods for QT/RR analysis, the data are not divided into epochs, but rather, values are continuously calculated from the mean of a continuously scrolling 5‐min window of data. Thus, if the correlation coefficient transiently drops below 0.8, only data from this period are edited out, rather than larger blocks of data. In this study, an average of 88 ± 4% and 93 ± 2% of 24‐hour data was included for analysis in the heart failure and healthy volunteer groups, respectively.

Thirdly, it is found that the slope of the curve decreases at longer RR intervals, providing evidence that the steady‐state QT/RR characteristic is curved. To avoid the necessity of reporting the value of RR at each measure of slope, a simple generic exponential formula, as adopted by both Fridericia ²⁰ and Bazett ²¹ is used. These familiar formulae have given rise to some confusion regarding the correct units for “QTc.” To avoid this difficulty the present method uses the most general expression:

Here QTo is the intercept of the curve with the ordinate at RRo, a chosen reference RR interval (e.g., 1000 ms), and J is the exponent determining the shape of the curve (using Bazett's formula J = 0.5; for Fridericia's, J = 0.33). The value of J is continuously computed from J = S (RR'/QT), where RR' is the compensated value of RR.

The overall 24‐hour variation of J is expressed as the mean 24‐hour standard deviation (SD) of J, and is derived from the mean of the continuously calculated mean SD of J from the 5‐min scrolling data window.

Statistical Analysis

To minimize the impact of noisy recordings on results, only tapes where the percentage of data analyzed was greater than 80% and the mean 24‐hour correlation between QT and RR' was greater than 0.8 were included. Mean 24‐hour parameters from Holter recordings were compared between populations by unpaired t‐test.

RESULTS

There was no significant difference in mean 24‐hour RR or QT between the two groups. The mean 24‐hour QTo was significantly prolonged in the IHD group (461 vs 426 ms, P < 0.005). The mean 24‐hour slope (S) was also steeper in IHD (0.195 vs 0.140, P < 0.01). The mean 24‐hour J (the exponent of the general formula that determines the form of the QT/RR curve) was significantly elevated in HF (0.38 vs 0.28). Constructed QT/RR curves created by using the mean population values of QTo and J are shown in Figure 2 to illustrate the different characteristics over a range of heart rates. In addition, the spread of values of J throughout the 24‐hour period indicated by the mean 24‐hour SD of J is much greater in the IHD group (0.181 vs 0.059, P < 0.01), reflecting an increased variation in the relationship between QT and heart rate. These data are summarized in Table 2. The increased variation in J cannot be explained by differences in the lag compensation as the overall correlation between QT and RR for compensated data is comparable between the two groups, as indicated by the similar‐pooled mean 24‐hour correlation (r).

Figure 2.

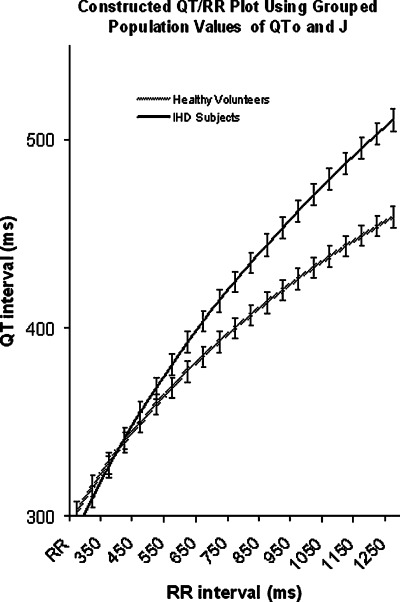
Curves generated from the mean population data in heart failure and healthy subjects. This illustrates how, at higher heart rates, little difference is observed between HF subjects and HV subjects. However, at lower heart rates, the combination of a higher J and longer QTo leads to a wider separation of the two curves. Error bars indicate standard errors of the means.

Table 2.

Characteristics of 24‐Hour Recordings

	RR (ms)	QT (ms)	QTo (ms)	S	J	24‐Hour SD of J	Pooled 24‐Hour Value
HV (n = 15)	845 (105)	402 (24)	426 (20)	0.14 (0.02)	0.28 (0.05)	0.05 (0.05)	0.742 (0.08)
IHD (n = 41)	859 (152)	420 (45)	461 (37)	0.20 (0.07)	0.38 (0.11)	0.181 (0.25)	0.77 (0.10)
P‐value	0.76	0.18	<0.01	<0.01	<0.01	<0.01	0.25

Data are expressed as mean 24‐hour values (SD).

When patients were subdivided according to NYHA class, the values of S, QTo and J increase with worsening functional class (Fig. 3). Analysis of variance (ANOVA) confirmed statistical significance (Table 3). In contrast, when patients were subgrouped according to ejection fraction (0–15%, 16–25%, 25–40%, and >40%), no significant difference is seen between the subgroups (Fig. 4).

Figure 3.

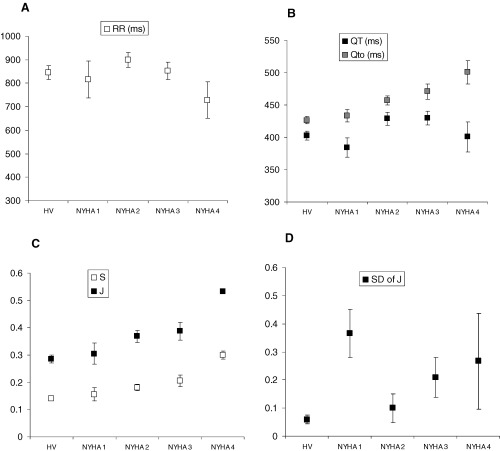
Comparison of the correlation between functional class, ejection fraction, and repolarization characteristics. Error bars indicate standard errors of the means.

Table 3.

Statistical Analysis of NYHA and EF Subgroups by Analysis of Variance (ANOVA)

	NYHA	EF
RR	0.17	<0.05
QT	0.11	0.09
QTo	<0.05	0.89
S	<0.005	0.66
J	<0.01	0.83
24‐hour SD of J	0.11	0.59

In this table, P values are shown for each parameter measured, according to whether patients were subgrouped by NYHA class or ejection fraction.

Figure 4.

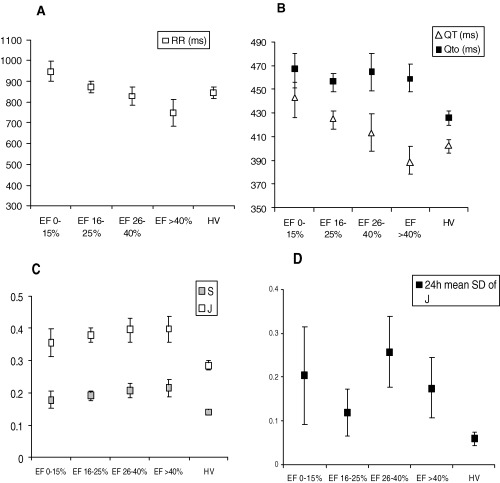
Comparison of the correlation between ejection fraction and repolarization characteristics. Error bars indicate standard errors of the means.

CONCLUSIONS

The most appropriate method for assessment of ventricular repolarization is debatable. The simplest approach would be to take a resting 12‐lead ECG and use one of the available correction formulae to correct for differences in heart rate. Unfortunately, the use of formulas to correct for heart rate are limited by the fact that most are only accurate at rest when heart rate is relatively low. In addition, they impose the same underlying QT/RR relationship on both populations, and can only be applied when heart rate has been stable for several minutes due to the significant time delay in reaching steady state. Investigators have shown that different subjects have different overall QT/RR relationships, and patient groups tend to have steeper QT/RR slopes and longer QT intervals, making direct comparison between populations using the same correction formula inappropriate. This is particularly true when using Holter data, which by nature are largely non‐steady‐state. The use of this method permits continuous assessment of the 24‐hour relationship in patients with heart failure. Several differences come to light as a result.

Differences in the QT/RR Relationship between Heart Failure Subjects and Controls

When the overall QT/RR characteristic is examined, a marked difference emerges between patients and controls. The extrapolated QTo is significantly prolonged, and the exponent, J, is greater. The resultant effect of these two abnormalities is that the curves are separated over a broad range of heart rates, with the differences most marked at low heart rates.

The ability to detect prolongation of QT is dependent on the method used for correction of rate‐related changes. Previous studies have shown that survivors of out‐of‐hospital cardiac arrests can have a normal QTc when traditional rate correction formulae are applied, but abnormal rate dependence when QT/RR plots are constructed with raw data. ²² This is an important point, because if one considers that in this study QTo is chosen arbitrarily as 1 s for no reason other than convention, it can be seen from Figure 3 that if QTo was set at, for example, 500 ms, little difference would be observed between the groups. QTo as a stand‐alone measure of repolarization may show differences between populations, but when combined with the exponent J it takes on a much more useful role, as it allows description of the entire QT/RR characteristic, regardless of heart rate. Knowing both of these variables gives more precise information about repolarization at any point in time.

Increased Variability in the QT/RR Relationship

By calculating the mean 24‐hour SD of J, information is obtained about the frequency and magnitude of changes occurring in the QT/RR characteristic throughout the day. In both healthy volunteers and HF variation is seen although the magnitude of this variation is greater in heart failure. This increased variation in the QT/RR relationship bears similarities with the work of Atiga et al. ²³ , ²⁴ They used a novel approach for the assessment of repolarization dynamics that assesses changes in QT with respect to changes in RR over relatively short time periods (256 s). When they compared healthy volunteers with patients, they found that there was decreased heart rate variance but an increase in QT variance in the patient groups. When these two parameters are combined to produce the QT variability index (QTVI) they found that it discriminated between the control and patient groups. This increased variability in the QT/RR relationship may reflect an inability of the myocardium to regulate repolarization for changes in heart rate.

Correlation with NYHA Functional Class

Although this study was small, subjects were distributed across all four NYHA classes. When subgroups were analyzed, it became apparent that the abnormalities of the QT/RR relationship show a worsening trend with functional class. NYHA functional class correlates with the degree of neurohumoral activation in heart failure. The maladaptive mechanisms of increased sympathetic tone, decreased parasympathetic activity, and activation of the renin‐angiotensin‐aldosterone system have been shown to, either directly or indirectly, influence cardiac repolarization, with downregulation of ion currents and abnormal expression of adrenergic receptors. These factors may be partly responsible for the progressive changes in repolarization dynamics that we have described. Other investigators ²⁵ , ²⁶ , ²⁷ have shown that beta‐blockade reduces the slope of the QT/RR relationship in both healthy subjects and patients, and this implies that increased sympathetic drive is at least one of the factors responsible for the increases seen in J and QTo relative to controls.

Previous studies ²⁸ have shown that sudden death is disproportionately common in relatively asymptomatic patients and our findings would seem to be discordant. However, arrhythmic death is frequently hard to determine as it is often unwitnessed and rhythms are not documented in the community. Certainly, patients with NYHA IV failure proportionately more likely to die from pump failure compared to NYHA I patients, but studies suggest that they are also very likely to die of arrhythmias. ³

In summary, as both the “corrected” QT, and the exponent describing the curve (J) are different between controls and patients with LV impairment, the use of “off the shelf” rate correction formulas to correct QT for heart rate will lead to errors in measurement, particularly if used on dynamic data. The observed progression in QT prolongation, increased rate dependence, and increased variation in the relationship may promote ventricular arrhythmias and sudden death. Further studies will demonstrate whether prognostic information can be obtained using this method.