Abstract
To date, practical application of mathematical models for model-based design of stem cell expansion processes is limited. Nevertheless, the first attempts show vast potential of this approach for the improvement of expansion process performance. This article presents the developed dynamic kinetic model of the human induced pluripotent stem cell expansion process in suspension culture. The model predicts cell growth, consumption of glucose and production of lactic acid, as well as the average aggregate size. The latter process variable is of particular importance for achieving high cell density. By adding botulinum hemagglutinin, an E-cadherin inhibitor and subsequent aggregate break-up, one can significantly increase performance of cell expansion process. After defining the appropriate optimization criteria and additional modification of the model, the latter can be further applied for model-based optimization of the final cell concentration by calculating optimal aggregate break-up and glucose/glutamine feeding strategies.
Keywords: Aggregation, Expansion, Human induced pluripotent stem cells, Kinetic model, Suspension culture
Highlights
-
•
Dynamic kinetic model of the human induced pluripotent stem cell expansion process was developed.
-
•
The model predicts cell growth, glucose consumption, lactic acid production, average aggregate size.
-
•
The average aggregate size is of particular importance for achievement of high cell density.
1. Introduction
Recently considerable attention has been paid to application of human induced pluripotent stem cells (hiPSCs) in regenerative medicine [1], [2], [3]. Depending on the therapeutic target, it is necessary to generate a quantity of 105–1010 cells [4]. Therefore a robust and high-performance culture system for successful cell expansion (maintaining efficient cell growth and preventing spontaneous differentiation) is essential, to provide sufficient quantities of undifferentiated human pluripotent stem cells (hPSCs) for further processing and differentiation [5]. Analysis of various cell cultivation technologies indicates that three-dimensional (3-D) suspension cultures in stirred-tank bioreactors provide good process scalability, controllability, and monitoring options [6], [7]. Recently it was demonstrated that sustainable growth of hPSCs can occur in the form of cell aggregates when monitoring of cell aggregate size is realized during the process [8], [9]. In addition to hPSC aggregation characteristics, advanced control systems should regulate concentrations of important substrates and metabolites within the cultivation medium, as well as homogeneous mixing, gas diffusion and exchange features [10]. As a starting point, repeated batch cultivation processes may be selected, in which cultivation medium is replaced at predefined time intervals to reduce negative impact of metabolites and restore depleted nutritional components [11], [12]. In such a cultivation mode, one can additionally control the cell aggregate size by using botulinum hemagglutinin, which can inhibit the E-cadherin-mediated cell–cell connections and break-up the aggregates into small sizes by pipetting. This approach allows reducing the average aggregate size and thus improves penetration of the nutritional components and dissolved oxygen into the aggregate kernels. The next step of the cultivation process design is to establish more precise control of the important substrates and metabolites by means of optimal feeding strategies in a fed-batch mode.
To implement the advanced control systems, it is straightforward to start with the development of simplified mathematical models for the calculation of optimal control strategies and regimes. It is important to understand both the potential of possible applications and the apparent limitations of existing mathematical models to improve pluripotent stem cell cultivation technologies. Galvanauskas et al. [5] have presented an extensive overview of existing modeling methods and techniques. To date, only a limited number of mathematical models [13], [14], [15] have been applied to optimization and control problems in stem cell expansion processes. The main limitations for such application are model complexity and lack of suitable measurements for identification of the key model parameters. At this point it is important to stress that the application of simplified models for optimization and control of stem cell expansion processes receives a skeptical reaction from biotechnologists, arguing that expansion is being influenced by many other factors that need to be taken into account. Arguably, such factors influence the expansion processes [16], [17] and may require much more complicated models [18]. In our opinion, at the beginning of process design it is important to take under control the most important process variables by means of already existing control techniques. After solving these tasks, the process can be improved with respect to the other factors. The aim of this research was to develop and validate a mathematical model describing hiPSCs expansion in suspension culture. The model predicts stem cell growth, consumption of the main substrate (glucose) and production of metabolite (lactic acid), as well as changes in average aggregate size. Later on, this model can be used for calculation of optimal timing for aggregate break-up and optimization of feeding strategy with the aim of maximizing stem cell productivity of the expansion process.
2. Materials and methods
2.1. Experimental methods
2.1.1. Cells and culture conditions
The hiPSC line, Tic, provided by Japanese Collection of Research Bioresources (JCRB1331, JCRB Cell Bank, Japan), was routinely maintained on polystyrene substrate coated with recombinant laminin-511 E8 fragments (iMatrix™-511; Nippi Inc., Japan) in commercially available medium (mTeSR™1; STEMCELL Technologies, Canada). For subculture, single cells were seeded with 10 μM Rho-associated protein kinase (ROCK) inhibitor (Y-27632; Wako Pure Chemical Industries, Japan). The initial seeding was fixed at a viable cell density of 1.0 × 104 cells cm−2. Cells were incubated at 37 °C in a humidified atmosphere with 5% CO2, and medium was replaced daily with the fresh one. On day 4, when the cells reached 80–90% confluence, cells were sub-cultured as described by Nath et al. [12].
2.1.2. Suspension culture of hiPSC
To perform suspension culture, hiPSCs were detached from the culture substrate by following a method described elsewhere [12]. In brief, for single cell preparation, cells were treated with 5 mM ethylenediaminetetraacetic acid (EDTA)/phosphate-buffered saline (PBS) for 7 min at room temperature with 10 μM ROCK inhibitor. After that, dissociation reagent (TrypLE Select™, Invitrogen, USA) with 10 μM ROCK inhibitor was applied for another 7 min at room temperature. After dissociating the hiPSC colony into single cells, 1.0 × 105 cells mL−1 were seeded in a 30 mL bioreactor (BWV—S03A, Able Co., Japan) with 10 μM ROCK inhibitor with an agitation rate of 55 rpm and incubated at 37 °C with 5% CO2. The high-density culture was performed for 192 h with and without aggregate break-up. The medium was exchanged at frequent intervals to reduce toxic effects of metabolites. Additionally, in high-density culture with aggregate break-up, botulinum hemagglutinin (His-HA, His-BHA1-FLAG: His-BHA2: Strep-BHA3, 20 nM) [19] was added to the culture medium at 87 h and incubated for 9 h [20]. After that, aggregates were broken up into smaller sizes by pipetting and all of the cells were re-seeded in a 30 mL bioreactor with 10 μM Rock inhibitor and cultured for additional 96 h.
2.1.3. Determination of cell density and aggregate size
To determine the cell density, X (cells mL−1), hiPSC aggregates were collected from the bioreactor (3 samples each time) every 24 h, and dissociated into single cells by using TrypLE Select. Then the live cells were counted by using a cell counter (Bio-Rad, USA) with the trypan blue exclusion method. To determine the aggregate size, images were captured every 24 h by using an image analyzer with a 4× objective lens (In CELL Analyzer 2000; GE Healthcare, UK) and the aggregate diameter was measured by using Image-Pro Plus software (Media Cybernetics, USA).
2.1.4. Analysis of medium components
To analyze the components of the culture medium associated with the cell cultivation, the used medium was collected during every medium change and analyzed for glucose, glutamine, lactic acid, and ammonium by using a biochemical analyzer (Bioprofile 400; Nova Biomedical, UK).
2.1.5. Statistical analysis
Data presented in this study were obtained from three independent experiments and expressed as mean ± standard deviation (SD). Statistical comparisons were evaluated using the Student's t-test and values of p < 0.01 and p < 0.05 were considered significant.
2.2. Mathematical model
Expansion of hiPSCs in suspension culture was carried out by using a repeated batch mode, i. e. periodically exchanging the medium (usually every 12–24 h). Initially, a dynamic model of the expansion process, including mass balance equations for cell density, glucose, glutamine, lactic acid, and ammonium concentrations, average aggregate size and the corresponding kinetic specific reaction rates, was developed. In the experiments performed so far, glutamine concentrations were kept within a range that does not significantly influence the specific growth rate. Also, according to the measurements performed [12], the ammonium level remained below the detection limit of 0.004 g L−1. Consequently, in the simulation studies discussed in this research, the glutamine limitation and ammonium inhibition phenomena were neglected and the corresponding equations have been omitted. If in the future the developed process model is to be applied for process optimization, e. g., of the glutamine feeding strategy, then the aforementioned model equations will be additionally included.
Finally, the following model was used in the simulation studies, which accounts for the changes in concentrations of the main components, i. e. hiPS cells X, cells mL−1, glucose G, g L−1, lactic acid Lac, g L−1, and average aggregate size Agg, μm:
| (1) |
| (2) |
| (3) |
| (4) |
where μ is the specific growth rate of the viable cells, h−1, κ is cell specific death rate, h−1, σ is specific glucose consumption rate, g (109 cells)−1 h−1, λ is specific lactic acid production rate, g (109 cells)−1 h−1, and α is a model parameter, μm, that correlates the cell specific growth rate μ with the aggregate size growth rate. The analysis of the process data has shown that the relationship of these two process variables is close to linear within the observed data range.
In general, the dynamic model Eqs. (1), (2), (3), (4) describes the mass balance of a batch process. The medium exchange was taken into account by additional modeling techniques. For that purpose, simulation of the entire cultivation process was split into several batch sub-processes that were carried out between two subsequent exchanges of the medium. The initial conditions of the cell number and average aggregate size for a sub-process are defined by the terminal states of the preceding sub-process. Initial concentrations of glucose are defined knowing the amount of glucose used in the fresh medium supplied to the sub-process. Finally, the lactic acid concentration at the beginning of a sub-process is assumed to be zero, as the fresh medium does not contain this component.
The corresponding specific reaction rates were modeled taking into account the most important phenomena and at the same time keeping the model structure as simple as possible.
The cell growth process was modeled taking into account the overall viable cell number, without splitting the cell population into the undifferentiated and differentiated cells. This decision was made taking into account the results of the flow cytometry analysis, which has shown that more than 98% of the viable cells at the end of the performed expansion processes have retained the main pluripotency markers OCT 3/4 and SSEA 4.
The specific growth rate of the viable cells μ, h−1, takes into account the rate limitation due to low glucose concentrations, the rate inhibition due to elevated lactic acid concentrations, and the rate reduction due to larger average cell aggregate size:
| (5) |
where μmax is the maximal specific growth rate, h−1, KG is a Monod-type limitation constant, g L−1, KLac is a Haldane-type inhibition constant, g L−1, and KAgg is an inhibition constant, μm3, of the 3rd order kinetics. In Eq. (5), addition of the term for the average cell aggregate size influence on the cell growth rate is based on the assumption that the efficiency of oxygen and nutrient component diffusion into the cell aggregate kernel decreases within large aggregates [10]. This leads to lower average specific growth rates in the culture. The cubic value of the exponent within this term was identified from the process data and reflects the relationship of this limiting phenomenon with the average cell aggregate volume rather than with its size (diameter). The latter quantity (Agg) was left in Eq. (5) because it is the primary measurement carried out on the process samples and is modeled by means of the differential Eq. (4).
During the process, temperature was kept constant at its optimal level. Hence, the death rate due to this reason was minimal. The toxic substances were periodically removed together with the used medium and did not accumulate up to the levels that may significantly increase the death rate. Therefore, only the death rate due to the initial adaptation stress was considered. Experimental evidence of this phenomenon was observed within the first 24 h of the expansion processes and was also reported by other researchers [11]. The cell specific death rate κ, h−1, in the cell growth Eq. (1) is modeled using an exponential decay function:
| (6) |
where Kd is a proportionality coefficient, h−1, and Td is the time constant of the exponential decay. Eq. (6) yields a maximal death rate κ equal to Kd at the beginning of the expansion process and later asymptotically decreases.
Eq. (7) for glucose specific consumption rate σ, g (109 cells)−1 h−1, accounts for glucose utilization for cell growth and lactic acid production due to overflow metabolism. The latter reaction rates are linked with σ through the average conversion yields YGX and YGLac:
| (7) |
Numerical values of the glucose/cell conversion yield YGX, g (109 cells)−1, and glucose/lactic acid conversion yield YGLac, g g−1, have been identified from the process data.
For the lactic acid specific production rate λ, g (109 cells)−1 h−1, a simple linear relationship was selected to reflect the influence of the elevated growth rate and of glucose concentration levels on the lactic acid production:
| (8) |
where KoG is a proportionality coefficient, L (109 cells)−1. The value of the model parameter KoG, which reflects the intensity of lactic acid production due to overflow metabolism, was identified from the available process data.
Average aggregate size was modeled using a dynamic model presented in Eq. (4). Due to the high noise level of the aggregate size measurements, the structure of the right-hand side of Eq. (4) was selected as simple as possible (a linear function of the specific growth rate). Despite its simplicity, the model provides a sufficiently good match of the mean value of the average aggregate size as a function of the cell specific growth rate. This relationship is of particular importance as the average aggregate size plays an important role in specific growth rate modeling. The average aggregate size is also used as a key quantity to control and significantly increase the cell density in the cultivation processes with controlled aggregate break-up.
Numerical simulations of the process model described in the paper were performed in the Matlab (Mathworks, Inc., USA) environment. To achieve high accuracy in the calculations, a variable-order solver for ordinary differential equations ode15s (stiff/NDF) was used and the relative tolerance was set to 10−12.
3. Results and discussion
The values of the most important model parameters have been identified numerically from the process data using the model Eqs. (1), (2), (3), (4), (5), (6), (7), (8) and evolutionary computation techniques. The optimization criterion to be minimized was a weighted mean absolute percentage error, MAPE (Mean Absolute Percentage Error, in the case analyzed this is the difference between the modeled variables and the corresponding process data). The dimensionless weights for the residuals of the cell density, glucose and lactic acid concentrations, as well as average aggregate size were selected empirically and in the analyzed case were [0.4, 0.1, 0.1, 0.4], respectively. The values of the dimensionless weights for residuals of the cell density (0.4) and average aggregate size (0.4) are higher since the objective of the parameter identification problem was to obtain more precise estimates for these two process variables. The parameter identification was performed using the process data from both high cell density suspension cultures with and without aggregate disruption. As a result of identification, a set of parameters was obtained that minimizes the defined MAPE criterion. The values of the process model parameters are provided in Table 1.
Table 1.
Model parameters.
| Model parameter | Value | Units |
|---|---|---|
| KAgg | 5.6 × 106 | μm3 |
| Kd | 0.4 | h−1 |
| KG | 1.27 | g L−1 |
| KLac | 5.0 | g L−1 |
| KoG | 3.24 | L (109 cells)−1 |
| Td | 5.0 | h |
| YGLac | 1.15 | g g−1 |
| YGX | 0.5 | g (109 cells)−1 |
| α | 46.6 | μm |
| μmax | 0.098 | h−1 |
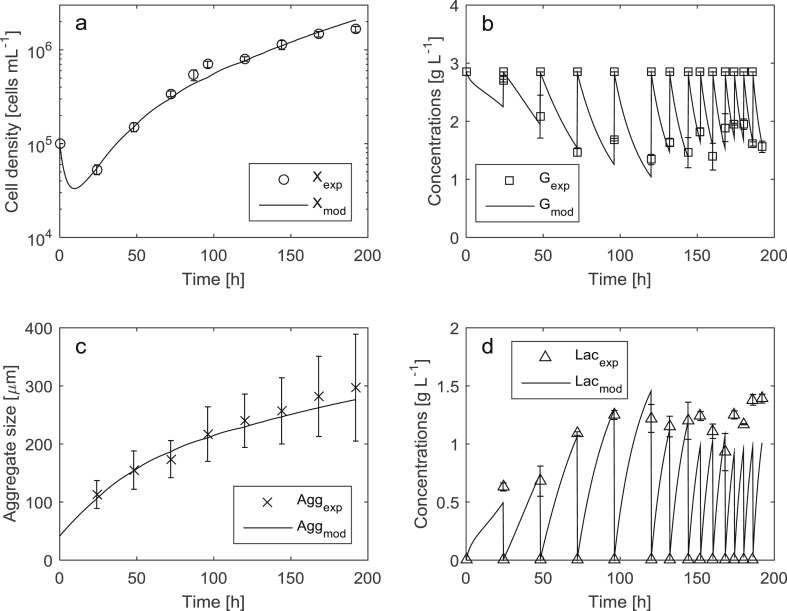
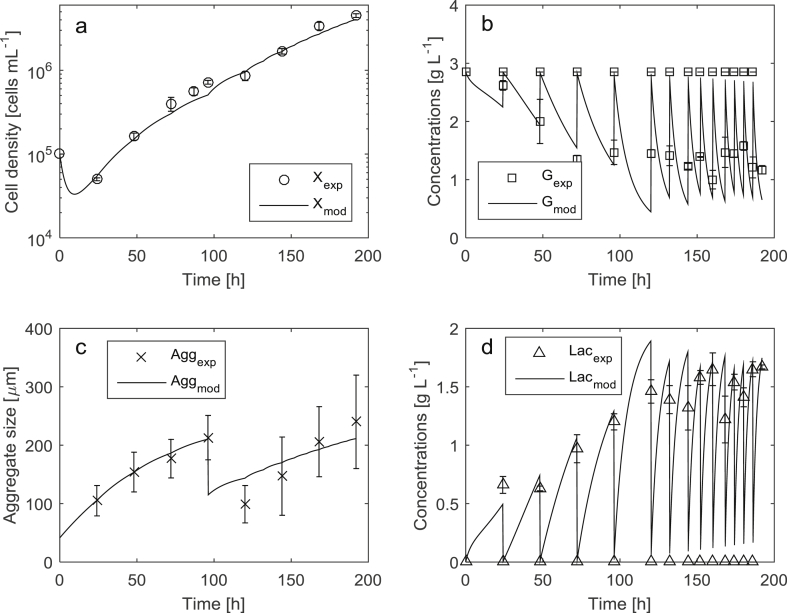
The modeling results for the cultures with and without aggregate disruption obtained using the model Eqs. (1), (2), (3), (4), (5), (6), (7), (8) and the parameters (Table 1) are depicted in Figs. 1 and 2, respectively.
Fig. 1.
Experimental data and modeling results of the hiPSCs expansion in high-cell density suspension culture without aggregate disruption.
Fig. 2.
Experimental data and modeling results of the hiPSCs expansion in high-cell density suspension culture with aggregate disruption.
The MAPE achieved for cell density was 13.6%, and for average aggregate size 9.3%. Considering the precision of the cell density and average aggregate size measurements, which is 5–10% and 20–30% respectively, the obtained modeling quality is sufficient for an adequate estimation of these process variables. MAPE for both glucose and lactic acid was approx. 15%. The modeling quality of glucose and lactic acid concentrations, as well as average aggregate size still could be improved. For example, the predicted lactic acid concentrations (Fig. 1d, process time from 150 h to 200 h) are below the measured ones. This can be explained by possible changes in metabolic pathways that affect the production rate of the lactic acid by the cells. The simulation results of the average aggregate size after break-up (Fig. 2c, process time from 100 h to 200 h) show the deviations in the aggregate growth dynamics. However, the simulated trajectory stays within the accuracy limits defined by the measurements. The deviations could be further reduced by refining and/or including more complex kinetic rate expressions. On the other hand, the impact of glucose and lactic acid concentrations on cell growth and aggregation was rather limited due to favorable cultivation conditions that were maintained (1–3 g L−1 for glucose and 0–1.5 g L−1 for lactic acid, respectively). After parameter identification, a validation of the model in terms of prediction error has been performed using new data of an expansion process with aggregate disruption and with a calculation of the corresponding MAPE. The achieved MAPE for all four key quantities was in the range of 10–15%. As the main aim was to develop a relatively simple model, it does not take into account possible variations of other important process conditions (e. g., cultivation temperature, pH and composition of the cultivation medium, etc.) that were optimized in advance and maintained during the cultivations. The model is able to predict the interactions of the modeled process variables within the working ranges investigated in the study. If the process conditions change significantly, one needs to update the model and/or perform a re-identification of the model parameters.
The average aggregate size drop (Fig. 2c) and the respective increase of the cell growth rate (Fig. 2a) at approx. 96 h of the process demonstrates the positive effect of aggregate break-up on the expansion process. The addition of HA and subsequent aggregate break-up lead to approx. 200% increase in the final cell density within the same cultivation time (as compared to high cell density process without aggregate break-up). This indicates that the aggregate break-up is an effective technique to further increase the total cell density. The ability of the developed model to predict the average aggregate size and cell density allows defining the optimal timing for break-up action(s) using model-based optimization techniques. This research is currently in progress and delivers promising results.
4. Conclusions
An important result obtained using the model is that the developed and identified functional relationships (Eqs. (4) and (5)) between the average aggregate size and the specific growth rate deliver estimates suitable for prediction of average aggregate size. This property of the model is especially important when using the model for optimization of maximal cell density by controlled aggregate break-up. In such a case, Eq. (4) needs to be updated by a term that accounts for the influence of HA concentration and current cell density on the break-up efficiency during controlled addition of HA. Such a relationship would allow prediction of the average aggregate size achieved immediately after the break-up process. Appropriate experimental investigations are currently in progress. The results could be a valuable contribution in the reaction engineering field because the kinetic expressions that describe the nature of the relationships between the cell expansion and the aggregate growth in suspension culture are identified in this research.
Future research will be focused on the model-based optimization of the controlled aggregate break-up and glucose/glutamine feeding strategy to further increase the performance of the investigated high cell density expansion process.
Declarations of interest
None.
Acknowledgement
This research was supported by the Research Council of Lithuania (Grant No. LJB-4/2015).
Footnotes
Peer review under responsibility of the Japanese Society for Regenerative Medicine.
References
- 1.Yamanaka S. Induced pluripotent stem cells: past, present, and future. Cell Stem Cell. 2012;10:678–684. doi: 10.1016/j.stem.2012.05.005. [DOI] [PubMed] [Google Scholar]
- 2.Chen K.G., Mallon B.S., McKay R.D., Robey P.G. Human pluripotent stem cell culture: considerations for maintenance, expansion, and therapeutics. Cell Stem Cell. 2014;14:13–26. doi: 10.1016/j.stem.2013.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jekins M.J., Farid S.S. Human pluripotent stem cell-derived products: advances towards robust, scalable and cost-effective manufacturing strategies. J Biotechnol. 2015;10:83–95. doi: 10.1002/biot.201400348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Serra M., Brito C., Correia C., Alves P.M. Process engineering of human pluripotent stem cells for clinical application. Trends Biotechnol. 2012;30:350–359. doi: 10.1016/j.tibtech.2012.03.003. [DOI] [PubMed] [Google Scholar]
- 5.Galvanauskas V., Grincas V., Simutis R., Kagawa Y., Kino-oka M. Current state and perspectives in modeling and control of human pluripotent stem cell expansion processes in stirred-tank bioreactors. Biotechnol Prog. 2017;33:355–364. doi: 10.1002/btpr.2431. [DOI] [PubMed] [Google Scholar]
- 6.Rodrigues C.A.V., Fernandes T.G., Diogo M.M., da Silva C.L., Cabral J.M. Stem cell cultivation in bioreactors. Biotechnol Adv. 2011;29:815–829. doi: 10.1016/j.biotechadv.2011.06.009. [DOI] [PubMed] [Google Scholar]
- 7.Liu N., Zang R., Yang S.T., Li Y. Stem cell engineering in bioreactors for large-scale bioprocessing. Eng Life Sci. 2014;14:4–15. [Google Scholar]
- 8.Abbasalizadeh S., Larijani M.R., Samadian A., Baharvand H. Bioprocess development for mass production of size-controlled human pluripotent stem cell aggregates in stirred suspension bioreactor. Tissue Eng C Methods. 2012;18:831–851. doi: 10.1089/ten.TEC.2012.0161. [DOI] [PubMed] [Google Scholar]
- 9.Chen V.C., Couture L.A. The suspension culture of undifferentiated human pluripotent stem cells using spinner flasks. Methods Mol Biol. 2015;1283:13–21. doi: 10.1007/7651_2014_118. [DOI] [PubMed] [Google Scholar]
- 10.Sart S., Agathos S.P., Li Y. Process engineering of stem cell metabolism for large scale expansion and differentiation in bioreactors. Biochem Eng J. 2014;84:74–82. [Google Scholar]
- 11.Kropp C., Kempf H., Halloin C., Robles-Diaz D., Franke A., Scheper T. Impact of feeding strategies on the scalable expansion of human pluripotent stem cells in single-use stirred tank bioreactors. Stem Cells Transl Med. 2016;5:1289–1301. doi: 10.5966/sctm.2015-0253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nath S.C., Nagamori E., Horie M., Kino-oka M. Culture medium refinement by dialysis for the expansion of human induced pluripotent stem cells in suspension culture. Bioproc Biosyst Eng. 2016;40:123–131. doi: 10.1007/s00449-016-1680-z. [DOI] [PubMed] [Google Scholar]
- 13.Bartolini E., Manoli H., Costamagna E., Jeyaseelan H.A., Hamad M., Irhimeh M.R. Population balance modelling of stem cell culture in 3D suspension bioreactors. Chem Eng Res Des. 2015;101:125–134. [Google Scholar]
- 14.Kresnowati M.T.A.P., Forde G.M., Chen X.D. Model-based analysis and optimization of bioreactor for hematopoietic stem cell cultivation. Bioproc Biosyst Eng. 2011;34:81–93. doi: 10.1007/s00449-010-0449-z. [DOI] [PubMed] [Google Scholar]
- 15.Yeo D., Kiparissides A., Cha J.M., Agullar-Gallardo C., Polak J.M., Tsiridis E. Improving embryonic stem cell expansion through the combination of perfusion and bioprocess model design. PLoS One. 2013;8 doi: 10.1371/journal.pone.0081728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kempf H., Olmer R., Kropp C., Rückert M., Jara-Avaca M., Robles-Diaz D. Controlling expansion and cardiomyogenic differentiation of human pluripotent stem cells in scalable suspension culture. Stem Cell Rep. 2014;3:1132–1146. doi: 10.1016/j.stemcr.2014.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Olmer R., Lange A., Selzer S., Kasper C., Haverich A., Martin U. Suspension culture of human pluripotent stem cells in controlled, stirred bioreactors. Tissue Eng C Methods. 2012;18:772–784. doi: 10.1089/ten.tec.2011.0717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wu J., Rostami M.R., Olaya D.P., Tzanakakis E.S. Oxygen transport and stem cell aggregation in stirred-suspension bioreactor cultures. PLoS One. 2016;9 doi: 10.1371/journal.pone.0102486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sugawara Y., Yutani M., Amatsu S., Matsumura T., Fujinaga Y. Functional dissection of the Clostridium botulinum Type B hemagglutinin complex: identification of the carbohydrate and E-cadherin binding sites. PLoS One. 2014;9:e111170. doi: 10.1371/journal.pone.0111170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nath S.C., Tomohiro T., Kim M.H., Kino-oka M. Botulinum hemagglutinin-mediated in situ break-up of human induced pluripotent stem cell aggregates for high-density suspension culture. Biotechnol Bioeng. 2018;115:910–920. doi: 10.1002/bit.26526. [DOI] [PubMed] [Google Scholar]