Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Dec 27.
Published in final edited form as: Phys Med Biol. 2015 Mar 24;60(8):3031–3043. doi: 10.1088/0031-9155/60/8/3031

Motionless electromagnetic phase stepping versus mechanical phase stepping in x-ray phase-contrast imaging with a compact source

Katherine J Harmon 1, Houxun Miao 1, Andrew A Gomella 1, Eric E Bennett 1, Barbara A Foster 2, Priya Bhandarkar 2, Han Wen 1
PMCID: PMC6933752  NIHMSID: NIHMS1064156  PMID: 25803511

Abstract

X-ray phase contrast imaging based on grating interferometers detects the refractive index distribution of an object without relying on radiation attenuation, thereby having the potential for reduced radiation absorption. These techniques belong to the broader category of optical wavefront measurement, which requires stepping the phase of the interference pattern to obtain a pixel-wise map of the phase distortion of the wavefront. While phase stepping traditionally involves mechanical scanning of a grating or mirror, we developed electromagnetic phase stepping (EPS) for imaging with compact sources to obviate the need for mechanical movement. In EPS a solenoid coil is placed outside the x-ray tube to shift its focal spot with a magnetic field, causing a relative movement between the projection of the sample and the interference pattern in the image. Here we present two embodiments of this method. We verified experimentally that electromagnetic and mechanical phase stepping give the same results and attain the same signal-to-noise ratios under the same radiation dose. We found that the relative changes of interference fringe visibility were within 3.0% when the x-ray focal spot was shifted by up to 1.0 mm in either direction. We conclude that when using x-ray tube sources, EPS is an effective means of phase stepping without the need for mechanical movement.

Keywords: x-ray phase contrast imaging, x-ray radiography, x-ray phase stepping, x-ray Talbot–Lau interferometer, motionless, x-ray scattering, x-ray dark field imaging

1. Introduction

X-ray phase contrast is a means to observe internal structures by the refractive bending and scattering of x-rays, without the need for substantial absorption of radiation energy. A few examples from a large wealth of literature over several decades demonstrate how phase contrast can be detected in x-ray imaging, either by the intrinsic properties of wave propagation (Engstrom and Finean 1953, Nugent et al 1996, Wilkins et al 1996) or enhanced with instrumentation in the beam (Bonse and Hart 1965, Mcnulty et al 1992, Davis et al 1995, Momose 1995, Chapman et al 1997, David et al 2002, Momose et al 2003, Weitkamp et al 2005, Pfeiffer et al 2006, 2008, Wen et al 2008). X-ray grating interferometers are attractive options for imaging applications since gratings generally have broad working bandwidths, thus requiring only x-ray tube sources (Clauser 1998, Pfeiffer et al 2006, Wen et al 2009). Polychromatic x-ray grating interferometry is feasible in both near-field (Pfeiffer et al 2006) and far-field (Wen et al 2013a) regimes. At its core, grating-based x-ray imaging measures the wavefront phase distortion and scattering in addition to intensity attenuation. Although wavefront measurement from a single image is possible from the earliest examples of Hartman grid (Hartmann 1900) and Shack–Hartman lens array (Platt and Shack 1971) to later x-ray methods (Takeda et al 1982, Bone et al 1986, Momose and Fukuda 1995, Wen et al 2008, 2010, Morgan et al 2011, 2013, Rand et al 2011, Ge et al 2014), they recruit an area of neighboring pixels to obtain a single measurement at a trade-off of resolution. Alternatively, pixel-wise phase measurement is obtained by phase stepping (Bruning et al 1974, Momose 1995, Momose et al 2003, Weitkamp et al 2005, Schorner et al 2012, Zanette et al 2012).

Phase stepping is a controlled stepping of the phase of the interference pattern at each image pixel, such that the intensity goes through a complete cycle of oscillation. The oscillation is recorded in multiple images, and used to determine the phase and interference amplitude at the pixel. The phase increments are either precisely controlled (Bruning et al 1974) or determined a posteriori from the images themselves (Miao et al 2013, Wen et al 2013b). A hybrid of phase stepping and single-image analysis can reduce the number of phase steps (Kondoh et al 2014). Phase stepping traditionally involves physically scanning a mirror (Bruning et al 1974), a grating (Momose 1995), the imaging device (Roessl et al 2014) or the sample (Arboleda et al 2014). For compact x-ray sources we created electromagnetic phase stepping (EPS) that eliminates mechanical movement. EPS synthesizes phase stepping by shifting the focal spot of the x-ray tube with a magnetic field coil attached to the tube (Miao et al 2013), thus removing the complexity and cost associated with precise mechanical scanning.

We developed two embodiments of EPS and tested them against mechanical phase stepping. We addressed the question of how magnetically shifting the tube focal spot may affect the interference fringe amplitude. We also compared the visibility of a fixed mouse heart specimen immersed in de-ionized water between a Talbot–Lau interferometer and a commercial digital mammography scanner under the same entrance surface dose (ESD).

2. Method

2.1. Imaging device and data processing

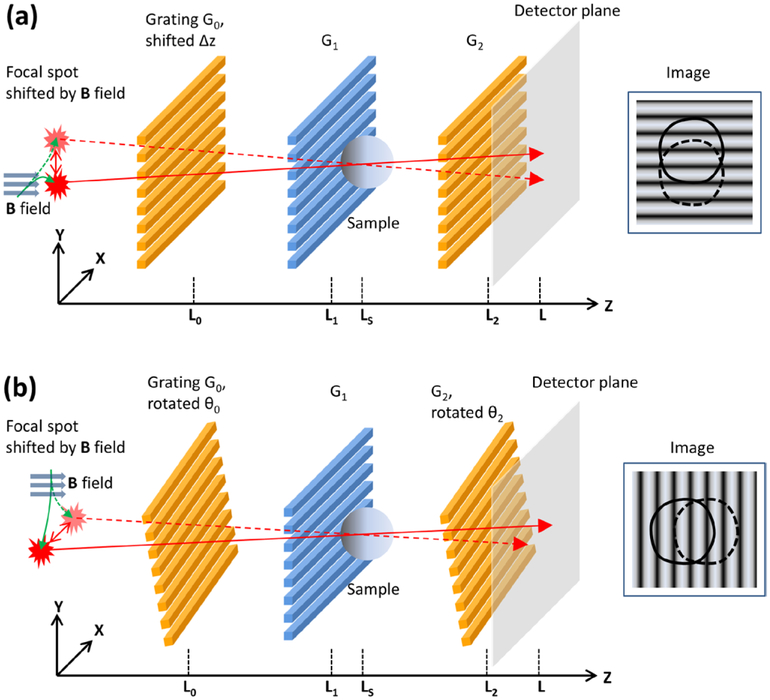
We set up a third-order Talbot–Lau interferometer as illustrated in figure 1. The x-ray source was a fixed-anode tungsten target tube operating at 40 kVp/1.0 mA (SRI-80–1k, Source-Ray Inc., Ronkonkoma, New York, USA), with a focal spot size of approximately 80 μm. The detector was a flat panel digital radiography detector with a pixel size of 83 μm (PaxScan 3024M, Varian, Palo Alto, CA, USA). The three gratings from the source towards detector were a 4.8 μm period gold absorption grating (Microworks GmbH, Karlsruhe, Germany), a silicon 2.4 μm period π/2 phase shift grating, and a 4.8 μm period gold absorption analyzer grating (Microworks GmbH). All three gratings were rotated about the vertical axis by 30° to increase their effective depths (Hoshino et al 2012). Moiré interference fringes had a visibility of 20% (defined as the coefficient of the cosine harmonic over the mean intensity). Samples were placed immediately behind the phase grating, half way between the source and the detector, resulting in a 2 × magnification in the projection.

Figure 1.

Figure 1.

Open in a new tab

Cross-grating and along-grating motionless electromagnetic phase stepping (EPS) in a Talbot–Lau Interferometer. (a) In cross-grating EPS, the x-ray focal spot is shifted by a magnetic field B along the X axis, so that the spot moves along the Y axis, perpendicular to the grating lines. The moiré fringe lines on the detector are horizontal. The sample projection is shifted vertically across the fringe lines. (b) In along-grating EPS, the x-ray focal spot is stepped along the X axis in the direction parrallel to the grating lines. Slight rotations of G0 and G2 about the Z axis result in vertical moiré fringes, and the sample projection is moved horizontally across the fringes.

For shifting the cone-beam focal spot in motionless EPS, we wound a solenoid coil with copper wire and attached it to the front surface of the x-ray tube housing. The coil had 200 turns and an inner diameter of 60 mm. The distance from the center of the coil to the location of the electron beam in the x-ray tube was approximately 30 mm. The coil was driven by a digital power supply which provided up to 3.0 A of current at 15 W of power. The corresponding peak magnetic field was calculated and verified with a magnetometer to be 4.6 mT at the location of the electron beam in the x-ray tube. The response time of the solenoid to current switching was 200 μs as determined by its resistance and inductance without impedance matching circuits. In the two-embodiments of EPS, the x-ray tube was placed either vertically or horizontally to realize focal spot movement in either direction, respectively. The deflections of the focal spot at various levels of input current were calibrated experimentally (Miao et al 2013).

The sample used for quantitative comparison between mechanical and electromagnetic phase stepping was an array of 3 × 3 borosilicate spheres of 5 mm diameter. We collected phase stepping scans of 11 steps with each method. The entrance surface dose of the sample was 1.0 mGy as measured by a Rad-Check Plus x-ray exposure meter (Fluke Biomedical, Cleveland, OH). A reference scan without sample was also collected with each method for background subtraction.

We used the same adaptive algorithm to process all data. The algorithm determines the phase increments and intensity fluctuations of each phase step retrospectively from the data images themselves and uses these as inputs to retrieve three images from a scan set—the intensity, the fringe amplitude, and the differential phase image. The processing procedure is described in detail in the references (Miao et al 2013, Wen et al 2013b).

The differential phase image was further integrated into an integrated phase shift image in a column-by-column procedure, where each column was Fourier transformed, multiplied with 1/k where k is the variable in Fourier space, inverse Fourier transformed, and corrected for any linear baseline offset in the background area. The intensity and fringe amplitude images were normalized to the corresponding reference scans. Thus, their values in blank areas were unity.

We made pair-wise comparisons among the three phase stepping methods, including mechanical phase stepping and two forms of EPS. The two forms of EPS are cross-grating EPS where the source focal spot was scanned perpendicular to the grating lines (figure 1(a)), and along-grating EPS where the focal spot was scanned along the grating lines (figure 1(b)). These are elaborated in the sections below. We evaluated the four measurements of differential phase, integrated phase, intensity and fringe amplitude.

Additionally, a formalin-fixed mouse heart specimen (1 year old male) was obtained under an Institutional Animal Care and Use Committee approved protocol. The specimen was first fixed in 10% formalin solution and then immersed in de-ionized water in a plastic chamber of a uniform thickness of 4.0 mm. The chamber was mounted in a 4.5 cm thick hollow frame. We acquired phase contrast data using both MPS and EPS methods. We also imaged the sample in a GE Senographe Essential digital mammography scanner with a fixed source-to-detector distance of 66 cm and a standard tube setting of Mo target/Mo filter operating at 26 kVp/63 mAs and the same ESD. The scanner has a CsI scintillator on an amorphous silicon detector of 100 μm pixel pitch, and a grid with a 5 : 1 aspect ratio and 36 lines cm−1. The hollow frame of the sample allowed the compression pad of the scanner to be used in a standard protocol. All three imaging experiments had an ESD of 4.7 mGy.

To assess whether shifting the source focal spot affects the moiré fringe visibility, we measured the fringe visibility as a function of the distance of the shift in both directions up to ±1.0 mm at the imaging condition of 40 kVp/1.0 mA.

2.2. Cross-grating electromagnetic phase stepping (EPSC)

In the first mode of EPS, shown in figure 1(a), the grating G0 is slightly moved along the beam axis by Δz, resulting in horizontal periodic moiré fringe lines on the detector. As the source focal spot is stepped along the Y axis by the external magnetic field, a phase shift at any location in the sample, Δφ, occurs due to a source spot shift of dy. The phase shift as a function of the source spot movement is

Δφ(dy) =2π dyLSΔzP0 (1)

where P0 is the period of the G0 grating and LS is the source-to-sample distance. Given a designed range of focal spot shift Dy and a designed range of phase shift in terms of the number of 2π cycles, a, the required offset of the G0 grating position along the beam is solved from (1) as

Δz = aLSP0 / Dy (2)

The moiré fringe period is given by

PM = LP0 / Δz (3)

where PM is the moiré fringe period and L is the source-to-detector distance. Thus, the moiré fringe period can be expressed in terms of the designed ranges of focal spot shift and phase stepping by substituting (2) into (3),

PM = (Dy / a)(L / LS) (4)

The range of focal spot shift must be at least 3 times the focal spot size for the phase steps to be distinct. Our focal spot shift range was Dy = 1.0 mm, and phase stepping range was set to a = 1.2 cycles. Substituting into (4) gave an expected moiré fringe period of 1.4 mm. Experimentally, we set up this configuration by moving the G0 grating along the beam (Z) axis to tune the moiré fringe period to this value.

2.3. Along-grating electromagnetic phase stepping (EPSA)

In the second embodiment of EPS, illustrated in figure 1(b), vertical moiré fringe lines were produced by a slight rotation θ0 of G0 about the Z axis, and a similar θ2 rotation of the G2 grating. The moiré fringe period is given by

PM = 1 / |L0Lθ0P0 + L2Lθ2P2| (5)

where L0 is the source-to-G0 grating distance, L2 is the source-to-G2 grating distance, and P0 and P2 are the periods of the G0 and G2 gratings. Then, as the source is stepped along the X axis by the external magnetic field, a phase shift Δφ occurs on a sample location due to a source spot shift of dx, with the relationship

Δφ(dx) = 2πdx(LS − L0Lθ0P0 − L2 − LSLθ2P2) (6)

Again, for a designed range of source spot shift Dx and a designed range of phase shift in terms of the number of 2π cycles, a, the grating rotation angles must meet the condition from (6) as

a = Dx(LS − L0Lθ0P0 − L2 − LSLθ2P2) (7)

Together with a desired moiré fringe PM in (5), these two linear equations are combined to solve for the grating rotation angles θ0 and θ2.

In our setting, the range of the focal spot shift was set to 1.0 mm, the phase stepping range was set to 1.2 cycles, and the moiré fringe period was set at 1.4 mm. The corresponding grating rotation angles were θ0 = 0.54°, and θ2 = 0.13°.

3. Results

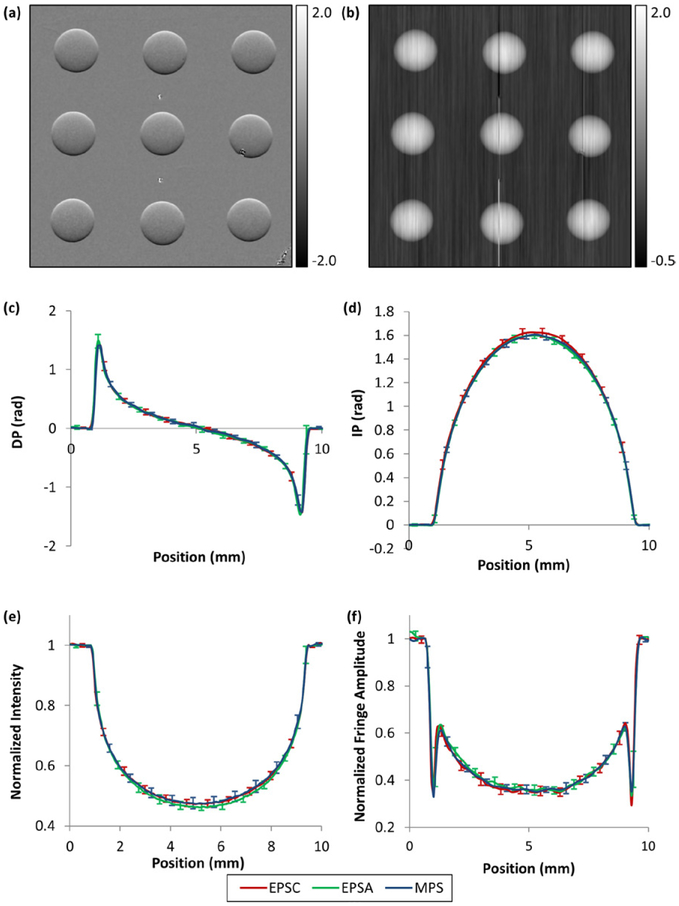
Examples of the differential phase contrast and integrated phase shift images of the borosilicate spheres are shown in figures 2(a) and (b). These were acquired with the cross-grating EPS method. For quantitative comparison among the three phase stepping methods (mechanical, cross-grating and along-grating EPS), vertical line profiles across the centers of the 9 beads were measured for the four quantities that can be extracted from each data set. These are the differential and integrated phase values, the intensity and the fringe amplitude. A total of 3 × 4 × 9 = 108 line profiles were obtained. These were separated into 12 groups, each containing the profiles of the 9 beads of the same measurement and the same phase stepping method. The mean and standard deviations of the profiles in each group are graphed according to the measured quantity in figures 2(c)–(f). The standard deviations were calculated from corresponding points along the 9 beads. We see substantial overlap of the curves from the three methods, all falling within the standard deviations among the beads.

Figure 2.

Figure 2.

Open in a new tab

Differential phase and integrated phase images, and averaged line profiles down the center of borosilicate spheres of the four measured quantities and the three methods of phase stepping. (a) Differential phase and (b) integrated phase images of an array of nine borosilicate spheres from the cross-grating EPS method (EPSC) are shown. Three small features are visible besides the spheres. These were two small tungsten beads in the middle column and a grating defect overlapping with a sphere in the right column. They caused the streak artifacts in the integrated phase image in (b). Line profiles down the center of the spheres were averaged among the nine spheres and plotted for the three phase stepping methods (EPSC in red, EPSA in green and MPS in blue). The four measured quantities were (c) the differential phase (DP), (d) the integrated phase (IP), (e) the intensity, and (f) the fringe amplitude. Standard deviation bars among the nine spheres are shown for alternating points along the curves for visual clarity. The curves of the three methods overlap with each other within the standard deviation bars. The statistics of pair-wise comparisons are provided in the text.

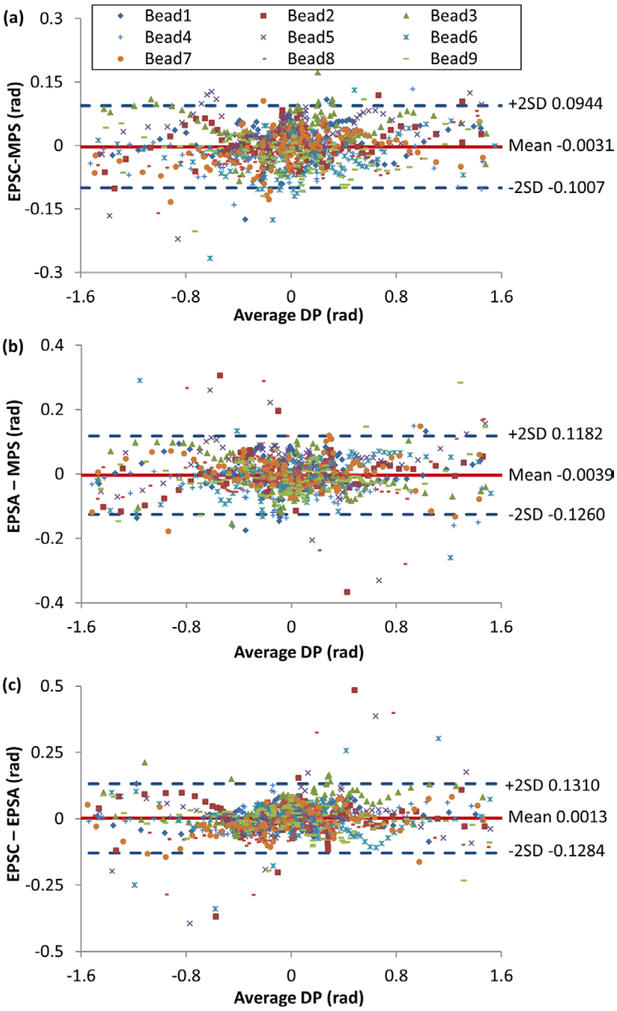
For statistical comparisons among the three methods, Bland–Altman (Bland and Altman 1986) plots (BA plots) were used to show the relationship between the difference and the average value of each pair of methods. For example, the BA plots of the differential phase measurement are constructed for the three method pairs in figure 3. Each data point in a BA plot came from one point along the differential phase line profile of one bead. The x and y values in the BA plot are the mean value and the difference of the measurements from a pair of methods, e.g. from EPSA and MPS. The total number of data points in a Bland–Altman plot was 9 beads × 105 points in a line profile = 945 points. We documented the zero bias, or the mean of the differences, in each BA plot, and the spread, or standard deviation, of the differences. These are tabulated in table 1 for the three pairs of comparison and the four measured quantities. In all cases, the zero bias was below 65% of the standard deviation of the differences. In all plots, the differences showed no trend with respect to the mean values. Additionally, for the three measurements that were directly extracted from the phase stepping procedure (differential phase, intensity and fringe amplitude), the zero biases were all below the background noise levels as detailed below.

Figure 3.

Figure 3.

Open in a new tab

Bland–Altman plots of differential phase measurements for pairs of phase stepping methods. The data points are from points along line profiles down the centers of the 9 borosilicate beads. The vertical axis is the difference between a pair of methods, the horizontal axis being the mean of the pair of methods. The mean and ±2 standard deviations of the differences are shown with horizontal lines. The three pairs of comparisons are (a) cross-grating electromagnetic phase stepping (EPSC) versus mechanical phase stepping (MPS), (b) along-grating electromagnetic phase stepping (EPSA) versus MPS, and (c) between the two EPS methods. In all three comparisons the mean of the difference was below 65% of the standard deviation.

Table 1.

Bland–Altman zero bias and standard deviation (bias/SD) measurements.

Measured quantity MPS versus EPSC MPS versus EPSA EPSC versus EPSA
Intensity 0.0023 / 0.0106 0.0093 / 0.0145 −0.0070 / 0.0113
Fringe amplitude 1.4E – 4 / 0.0379 −0.0053 / 0.0259 0.0060 / 0.0381
Differential phase −0.0031 / 0.0488 −0.0039 / 0.0611 0.0013 / 0.0648
Integrated phase 0.019 / 0.030 −0.0048 / 0.0288 0.023 / 0.038
Open in a new tab

The background noise levels were measured for the three quantities of differential phase, intensity and fringe amplitude from the three phase stepping methods. These are tabulated in table 2. A noise level was taken as the standard deviation of a measurement in a blank region of the image. Ten regions of 80 × 80 pixels each, distributed evenly across the images, were measured. The average and standard deviation of the ten regions are reported. While the EPSC and the MPS methods had the same background noise level, the EPSA method had 32% higher background noise in the differential phase and fringe amplitude measurements. This reflects ripple like artifacts in certain areas of the EPSA differential phase images, which were absent in the other two methods. The likely cause is the specific support structures in the absorption gratings, which will be further discussed in the next section.

Table 2.

Measurement noise levels of the three methods of phase stepping.

MPS EPSC EPSA
Intensity noise 0.015 ± 0.002 0.015 ± 0.001 0.014 ± 0.001
Fringe amplitude noise 0.026 ± 0.002 0.025 ± 0.001 0.032 ± 0.001
Differential phase noise 0.026 ± 0.002 0.025 ± 0.001 0.033 ± 0.002
Open in a new tab

Assuming that the noises in the fringe amplitude and differential phase images are random, since the fringe amplitude is normalized to the reference scan, its noise level should be equal to the differential phase noise. This was verified for all three phase stepping methods in table 2.

In the pair-wise comparison of the phase stepping methods described previously, the mean differences between pairs of methods were all below 70% of the background noise levels.

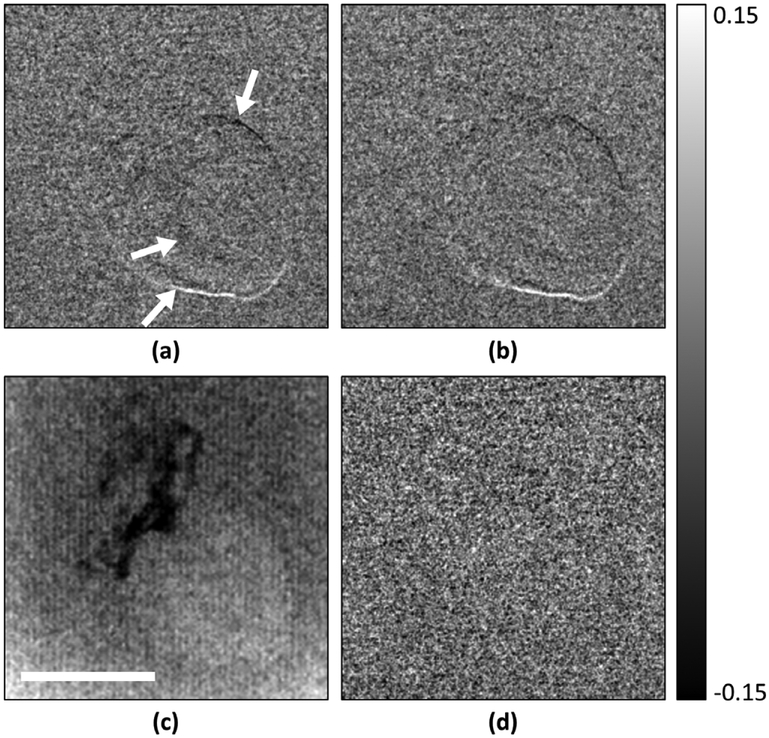
In a demonstration of phase contrast imaging of a biological specimen, a mouse heart specimen immersed in water was imaged using both mechanical and cross-grating EPS methods on the Talbot–Lau interferometer, as well as with the GE Senographe digital mammography scanner (figure 4). In the differential phase images, the surface of the specimen produced a phase signal above the noise floor, revealing its outline (figures 4(a) and (b)). The outline was strongest at the bottom and top edges of the heart, regions that produce the strongest refractive bending of the x-rays in the sensitive direction of the interferometer. In the image of the digital mammography scanner at the same entrance surface dose of 4.7 mGy (figure 4(c)), the specimen was less clearly visualized. MPS and EPS gave the same differential phase signal evidenced by the subtraction image (figure 4(d)). They also produced the same background noise level of 0.052 radians. The noise levels of the intensity, fringe amplitude and differential phase image for the two methods of phase stepping are reported in table 3 and confirm the results of the borosilicate bead test.

Figure 4.

Figure 4.

Open in a new tab

Differential phase contrast images of a mouse heart specimen immersed in water acquired with (a) cross-grating electromagnetic phase stepping and (b) mechanical phase stepping on the Talbot–Lau interferometer, and (c) the digital mammography scanner, all at the ESD of 4.7 mGy. The differential phase measures the refractive bending of the x-rays in the vertical direction. Therefore, the image shows a visible outline at the top and the bottom of the heart where the refractive index changes most rapidly from the tissue to the surrounding water. A valve within the heart also starts to become visible in (a) and (b). The outline of the heart is less distinct in the radiography image. Dark areas are low-absorption adipose tissue without sharp edges. The subtraction of (a) and (b) resulted in a random noise image (d). The scale bar is 5 mm.

Table 3.

Noise levels of mechanical and electromagnetic phase stepping in the mouse heart specimen.

MPS EPSC
Intensity noise 0.0079 ± 0.0005 0.0078 ± 0.0006
Fringe amplitude noise 0.052 ± 0.003 0.051 ± 0.003
Differential phase noise 0.052 ± 0.003 0.052 ± 0.005
Open in a new tab

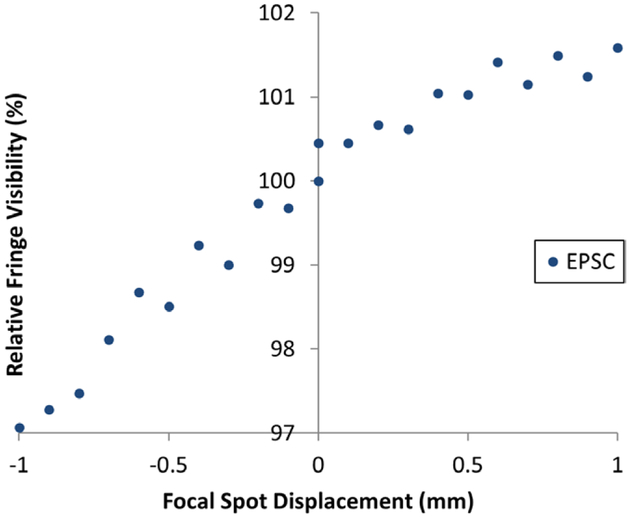
To determine how the fringe visibility is affected by magnetically shifting the focal spot of the x-ray tube, we measured the fringe visibility for the two EPS methods over a range of shifts at the imaging condition of the tube. The results of cross-grating EPS for both positive and negative spot displacements are graphed in figure 5. The relative changes of fringe visibility were from −3.0 to +1.5% over a ±1.0 mm range of shift in both directions. Similar results were seen in along-grating EPS. We found the variability to be sensitive to the precise alignment of the gratings, and it did not exceed the range shown in figure 5.

Figure 5.

Figure 5.

Open in a new tab

Relative fringe visibility as a function of x-ray tube focal spot displacement. Normalized fringe visibility values at the imaging condition of 40 kVp/1.0 mA are plotted for cross-grating electromagnetic phase stepping. The changes were within a total range of 4.5% for a bidirectional spot displacement ±1.0 mm.

4. Discussion

In this study we established quantitatively that electromagnetic phase stepping and mechanical phase stepping provide the same results in the three direct measurements and one derived measurement from grating-based x-ray phase contrast imaging, namely the differential phase, the intensity, the fringe amplitude and the integrated phase shift. The visibility of the interference fringes was not changed significantly by shifting the x-ray focal spot up to 1.0 mm. We found that the level of change depended on the alignment details of the gratings.

Under the same dose and other imaging parameters, MPS and cross-grating EPS had the same background noise levels for all measurements. The along-grating EPS had 32% higher background noise in the differential phase and fringe amplitude images, which included subtle wave-like patterns in some background areas. For an explanation, the first and last of the three gratings were absorption gratings constructed from polymer molds of linear arrays of trenches, which were filled with gold in a bottom-up electroplating process. A repeating pattern of cross-bridges between the polymer walls was built into the gratings for structural support. In direct projection images of these gratings we observed wave-like features, possibly a moiré pattern between the cross-bridge structures and the detector pixel array. In the along-grating EPS mode where the focal spot is shifted in the direction parallel to the grating lines, we saw subtle ripple artifacts in parts of the field of view in the fringe amplitude and differential phase images, which were reminiscent of the pattern in the projection images of the gratings. These were absent in the cross-grating EPS and the MPS images. They account for the increased background variability from EPSA. This effect is likely specific to the details of the support structures. Therefore, in implementing EPS with such gratings, we found it worthwhile to look at both forms and identify the one that is free of the grating artifacts.

In a limited comparison with a modern digital mammography scanner using a mouse heart specimen, our particular Talbot–Lau interferometer made the heart sample more visible under the same entrance surface dose. Although primarily a demonstration of electromagnetic phase stepping, this example showed the benefit of the Talbot–Lau interferometer for relatively thin samples.

The electromagnetic phase stepping method essentially replaces precision motors with a fixed solenoid coil. It is easier to precisely control the magnetic field strength by the coil current level than to control the motor position to a fraction of the grating period, particularly anticipating mechanical drifts in a compact system. The response time in switching the magnetic field was 200 μs and can be made substantially shorter with either an analog compensation circuit or digital waveform compensation of the input current, while mechanical motion has inherent speed limits. Lastly, comparing the solenoid coil and its digital current source with the precision motor and its power supply, the cost was substantially reduced. When considered in whole, the motionless method has distinct advantages over mechanical scanning for future clinical applications. In conclusion, EPS gives the same results and has the same sensitivity as mechanical phase stepping, with the benefits of simplified instrumentation, speed and more precise control.

Acknowledgment

Micro fabrication was performed at the Nanofab Facility of the Center for Nano Science and Technology, National Institute of Standard and Technology. We are indebted to Mr Gary Melvin who machined parts of the imaging device. We are grateful to Dr Mark Rivers, Department of Geophysical Sciences and Center for Advanced Radiation Sources, The University of Chicago, for his assistance with developing instrument control software.

References

  1. Arboleda C, Wang ZT and Stampanoni M 2014. Tilted-grating approach for scanning-mode x-ray phase contrast imaging Opt. Express 22 15447–58 [DOI] [PubMed] [Google Scholar]
  2. Bland JM and Altman DG 1986. Statistical-methods for assessing agreement between 2 methods of clinical measurement Lancet 1 307–10 [PubMed] [Google Scholar]
  3. Bone DJ, Bachor HA and Sandeman RJ 1986. Fringe-pattern analysis using a 2D Fourier-transform Appl. Opt 25 1653–60 [DOI] [PubMed] [Google Scholar]
  4. Bonse U and Hart M 1965. An x-ray interferometer Appl. Phys. Lett 6 155–6 [Google Scholar]
  5. Bruning JH, Herriott DR, Gallaghe JE, Rosenfel DP, White AD and Brangacc DJ 1974. Digital wavefront measuring interferometer for testing optical surfaces and lenses Appl. Opt 13 2693–703 [DOI] [PubMed] [Google Scholar]
  6. Chapman D, Thomlinson W, Johnston RE, Washburn D, Pisano E, Gmur N, Zhong Z, Menk R, Arfelli F and Sayers D 1997. Diffraction enhanced x-ray imaging Phys. Med. Biol 42 2015–25 [DOI] [PubMed] [Google Scholar]
  7. Clauser JF 1998. Ultrahigh resolution interferometric x-ray imaging US Patent 5,812,629 [Google Scholar]
  8. David C, Nohammer B, Solak HH and Ziegler E 2002. Differential x-ray phase contrast imaging using a shearing interferometer Appl. Phys. Lett 81 3287–9 [Google Scholar]
  9. Davis TJ, Gao D, Gureyev TE, Stevenson AW and Wilkins SW 1995. Phase-contrast imaging of weakly absorbing materials using hard x-rays Nature 373 595–8 [Google Scholar]
  10. Engstrom A and Finean JB 1953. Low-angle x-ray diffraction of bone Nature 171 564. [DOI] [PubMed] [Google Scholar]
  11. Ge YS, Li K, Garrett J and Chen GH 2014. Grating based x-ray differential phase contrast imaging without mechanical phase stepping Opt. Express 22 14246–52 [DOI] [PubMed] [Google Scholar]
  12. Hartmann J 1900. Bemerkungen über den Bau und die Justierung von Spektrographen Z. Instrumentenkunde 20 47–58 [Google Scholar]
  13. Hoshino M Uesugi K and Yagi N 2012. Phase-contrast x-ray microtomography of mouse fetus Biol. Open 1 269–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kondoh T, Date T, Yamaguchi K, Nagai K, Sato G, Handa S, Den T, Itoh H and Nakamura T 2014. Sparse phase-stepping in 2D x-ray phase contrast imaging Appl. Opt 53 2602–10 [DOI] [PubMed] [Google Scholar]
  15. Mcnulty I, Kirz J, Jacobsen C, Anderson EH, Howells MR and Kern DP 1992. High-resolution imaging by Fourier-transform x-ray holography Science 256 1009–12 [DOI] [PubMed] [Google Scholar]
  16. Miao H, Chen L, Bennett EE, Adamo NM, Gomella AA, Deluca AM, Patel A, Morgan NY and Wen H 2013. Motionless phase stepping in x-ray phase contrast imaging with a compact source Proc. Natl Acad. Sci. USA 110 19268–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Momose A 1995. Demonstration of phase-contrast x-ray computed-tomography using an x-ray interferometer Nucl. Instrum. Meth. A 352 622–8 [Google Scholar]
  18. Momose A and Fukuda A 1995. Phase-contrast radiographs of nonstained rat cerebellar specimen Med. Phys 22 375–9 [DOI] [PubMed] [Google Scholar]
  19. Momose A, Kawamoto S, Koyama I, Hamaishi Y, Takai K and Suzuki Y 2003. Demonstration of x-ray Talbot interferometry Japan. J. Appl. Phys. 2 42 L866–8 [Google Scholar]
  20. Morgan KS. et al. Measuring airway surface liquid depth in ex vivo mouse airways by x-ray imaging for the assessment of cystic fibrosis airway therapies. Plos One. 2013;8:e55822. doi: 10.1371/journal.pone.0055822. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Morgan KS, Paganin DM and Siu KKW 2011. Quantitative single-exposure x-ray phase contrast imaging using a single attenuation grid Opt. Express 19 19781–9 [DOI] [PubMed] [Google Scholar]
  22. Nugent KA, Gureyev TE, Cookson DF, Paganin D and Barnea Z 1996. Quantitative phase imaging using hard x-rays Phys. Rev. Lett 77 2961–4 [DOI] [PubMed] [Google Scholar]
  23. Pfeiffer F, Bech M, Bunk O, Kraft P, Eikenberry EF, Bronnimann C, Grunzweig C and David C 2008. Hard-x-ray dark-field imaging using a grating interferometer Nat. Mater 7 134–7 [DOI] [PubMed] [Google Scholar]
  24. Pfeiffer F, Weitkamp T, Bunk O and David C 2006. Phase retrieval and differential phase-contrast imaging with low-brilliance x-ray sources Nat. Phys 2 258–61 [Google Scholar]
  25. Platt BC and Shack RV 1971. Lenticular Hartmann-screen Opt. Sci. Center Newslett 5 15–6 [Google Scholar]
  26. Rand D, Ortiz V, Liu Y, Derdak Z, Wands JR, Taticek M and Rose-Petruck C 2011. Nanomaterials for x-ray imaging: gold nanoparticle enhancement of x-ray scatter imaging of hepatocellular carcinoma Nano Lett 11 2678–83 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Roessl E, Heiner D, Koehler T, Martens G and van Stevendaal U 2014. Slit-scanning differential phase-contrast mammography: first experimental results Proc. SPIE 9033 90330C [Google Scholar]
  28. Schorner K, Goldammer M, Stierstorfer K, Stephan J and Boni P 2012. Scatter correction method by temporal primary modulation in x-ray CT IEEE Trans. Nucl. Sci 59 3278–85 [Google Scholar]
  29. Takeda M, Ina H and Kobayashi S 1982. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry J. Opt. Soc. Am 72 156–60 [Google Scholar]
  30. Weitkamp T, Diaz A, David C, Pfeiffer F, Stampanoni M, Cloetens P and Ziegler E 2005. X-ray phase imaging with a grating interferometer Opt. Express 13 6296–304 [DOI] [PubMed] [Google Scholar]
  31. Wen H, Bennett EE, Hegedus MM and Carroll SC 2008. Spatial harmonic imaging of x-ray scattering—initial results IEEE Trans. Med. Imaging 27 997–1002 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wen H, Bennett EE, Hegedus MM and Rapacchi S 2009. Fourier x-ray scattering radiography yields bone structural information Radiology 251 910–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Wen HH, Bennett EE, Kopace R, Stein AF and Pai V 2010. Single-shot x-ray differential phase-contrast and diffraction imaging using 2D transmission gratings Opt. Lett 35 1932–4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Wen H, Gomella AA, Patel A, Lynch SK, Morgan NY, Anderson SA, Bennett EE, Xiao X, Liu C and Wolfe DE 2013a. Subnanoradian x-ray phase-contrast imaging using a far-field interferometer of nanometric phase gratings Nat. Commun 4 2659. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wen H, Miao H, Bennett EE, Adamo NM and Chen L 2013b. Flexible retrospective phase stepping in x-ray scatter correction and phase contrast imaging using structured illumination Plos One 8 e78276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wilkins SW, Gureyev TE, Gao D, Pogany A and Stevenson AW 1996. Phase-contrast imaging using polychromatic hard x-rays Nature 384 335–8 [Google Scholar]
  37. Zanette I, Bech M, Rack A, Le Duc G, Tafforeau P, David C, Mohr J, Pfeiffer F and Weitkamp T 2012. Trimodal low-dose x-ray tomography Proc. Natl Acad. Sci. USA 109 10199–204 [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES