Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Dec 12;13(12):13932–13939. doi: 10.1021/acsnano.9b05519

X-ray Imaging of Functional Three-Dimensional Nanostructures on Massive Substrates

Diana A Grishina †, Cornelis A M Harteveld †, Alexandra Pacureanu ‡, D Devashish †, Ad Lagendijk †, Peter Cloetens ‡,*, Willem L Vos †,*
PMCID: PMC6933814  PMID: 31829557

Abstract

graphic file with name nn9b05519_0007.jpg

To investigate the performance of three-dimensional (3D) nanostructures, it is vital to study their internal structure with a methodology that keeps the device fully functional and ready for further integration. To this aim, we introduce here traceless X-ray tomography (TXT) that combines synchrotron X-ray holographic tomography with high X-ray photon energies (17 keV) in order to study nanostructures “as is” on massive silicon substrates. The combined strengths of TXT are a large total sample size to field-of-view ratio and a large penetration depth. We study exemplary 3D photonic band gap crystals made by CMOS-compatible means and obtain real space 3D density distributions with 55 nm spatial resolution. TXT identifies why nanostructures that look similar in electron microscopy have vastly different nanophotonic functionality: one “good” crystal with a broad photonic gap reveals 3D periodicity as designed; a second “bad” structure without a gap reveals a buried void, and a third “ugly” one without gap is shallow due to fabrication errors. Thus, TXT serves to nondestructively differentiate between the possible reasons of not finding the designed and expected performance and is therefore a powerful tool to critically assess 3D functional nanostructures.

Keywords: 3D integration, complementary metal-oxide semiconductor, nanofabrication, photonic band gaps, silicon photonics, X-ray imaging

Three-dimensional (3D) nanostructures are drawing a fast-growing attention for their advanced functionalities in nanophotonics,1−6 photovoltaics,7−9 and 3D integrated circuits and flash memories.10−12 The functional properties of such nanostructures are fundamentally determined by their complex internal structure that consists of 3D arrangements of structural units such as spheres, rods, pores, or split rings.13 Inevitably, any fabricated nanostructure differs from its initial design, systematically in the case of structural deformations,14,15 and statistically in the case of size and positional disorder of the structural units.16,17 Consequently, the observed functionality differs from the expected one.

It is therefore critical to assess the structure of a 3D nanomaterial and verify how well it matches the design. Ideally, such an inspection technique leaves no traces, keeping the nanostructure fully functional and ready for integration. To this end, we introduce here traceless X-ray tomography (TXT) as a methodology to the world of nanotechnology in order to nondestructively assess the functionality of the nanostructures. As a representative example, we study 3D periodic silicon photonic band gap crystals made by complementary metal-oxide semiconductor (CMOS)-compatible methods (see Figure 1A).18,19 These nanostructures are powerful tools to control the propagation and the emission of light by their broad complete 3D photonic band gap20,21 (see Figure 1B). We observe that TXT is ultimately limited only by the transmission loss of the X-ray signal while propagating through the nanostructure and its substrate. A transmission T > 10% is sufficient to preserve good photon statistics and avoid artifacts. Therefore, with the X-ray energy available with TXT (17 keV), massive sample–substrate combinations can be investigated. In the case of silicon, the maximum thickness is about 1.5 mm, sufficient for CMOS wafers. There are no limitations to the internal geometry of the nanostructures under study as periodic, random, or aperiodic structures can all be resolved.

Figure 1.

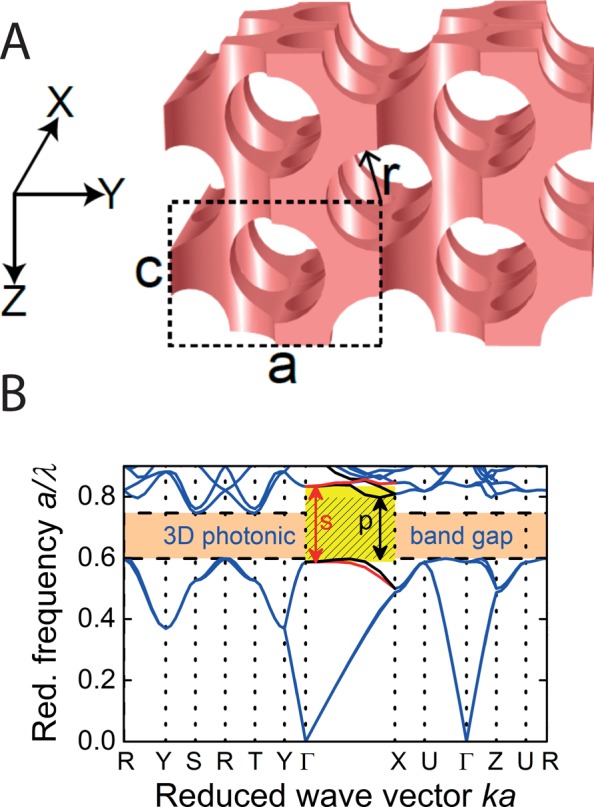
Figure 1

Open in a new tab

Design of a 3D photonic crystal and its photonic functionality. (A) Cubic 3D inverse woodpile photonic crystals have a density distribution designed as two perpendicular 2D centered rectangular arrays (lattice parameters a, c; a/c = √2) of pores with radius r. Pores in the X-direction are aligned between pores in the Z-direction.18 (B) Band diagram for an inverse woodpile crystal made from silicon reveals a broad 3D photonic band gap between a/λ = 0.60 and 0.75 (orange bar). In the experimentally probed Γ–X high-symmetry direction (panel 3× enlarged for clarity), the s-polarized stop gap (yellow) is broader than the p-polarized stop gap (black).21

Traditionally, in nanotechnology, a fabricated sample is inspected by scanning electron microscopy (SEM).22 A major limitation of SEM, however, is that only the external surface is viewed, whereas the inner structure remains hidden. Indeed, Figure 2 shows three 3D photonic crystal nanostructures whose external surfaces look closely similar and closely match the design in Figure 1A (for sample description see the Methods section). However, the corresponding nanophotonic functionality shown in Figure 2 strongly differs: the crystal shown in panel A reveals a broad photonic gap as designed (panel B), whereas the other two structures reveal no gaps and instead a surprisingly constant reflectivity (panels D and F; for the setup, see the Methods section).

Figure 2.

Figure 2

Open in a new tab

Scanning electron microscopy and nanophotonic functionality of three 3D photonic nanostructures. (A) SEM image of the external surface of a 3D inverse woodpile photonic crystal made from Si whose measured reflectivity spectrum (B) reveals a broad photonic gap in agreement with theory with input from TXT (yellow range). Horizontal black bars are estimated uncertainties in the TXT stop gap width. The blue range is the stop gap estimated from SEM data. (C) SEM image of a 3D photonic crystal whose reflectivity spectrum (D) reveals a constant low reflectivity with no gap. (E) SEM image of a 3D photonic crystal whose reflectivity spectrum (F) reveals a constant elevated reflectivity and no gap. In (A,C,E), the scale bar is 1 μm.

Functional verification, such as optical reflectivity, does not provide insights into the reasons why the performance of samples differs from design expectations. The reasons for different functional performance may be hidden in errors of the fabrication process, in errors in the design, or in errors of the functionality test itself. Therefore, to differentiate fabrication or design errors from performance test errors, it is necessary to know the actual 3D structure of the sample. In case the internal structure indeed matches the design while simultaneously the functionality differs from expectation, it is obvious that the sample should remain intact in order to perform further functionality studies, whence TXT.

To visualize 3D nanostructures, SEM is supplemented with micromachining or ion beam milling to cut away part of the structure.22 Unfortunately, however, this approach is destructive, irreversible, and not in situ, hence packaged or buried structures will inevitably be broken. Whereas transmission electron microscopy (TEM) allows for high-resolution 3D imaging, the required sample thickness of less than 1 μm is insufficient for monolithic 3D photonic nanostructures.23 X-ray techniques are well-suited due to their high penetration and high resolution.24,25 Although small-angle X-ray scattering is employed to study 3D nanoparticle arrays, it naturally operates in reciprocal space, making it hard to characterize local nanosized features.26,27 In contrast, X-ray tomography yields a real space 3D representation of the sample.28 In traditional tomography, the contrast is provided by the sample absorption that is simply related to the brightness of the transmitted image called a radiograph.29 As silicon and many materials that prevail in nanotechnology and in the CMOS industry absorb X-rays only weakly, however, advanced tomography methods are required.

Here, we obtain the relevant real space structural information directly from the optical phase change of the X-ray beam that propagates through the sample (for details, see the Methods section). The phase change is quantitatively retrieved from a set of radiographs taken at multiple sample-to-detector distances while rotating the sample.30 Following a conventional tomographic reconstruction of the retrieved phase maps, the 3D electron density ρe(X,Y,Z) is obtained in real space as a stack of equally spaced 2D slices in the plane normal to the sample’s rotation axis. To achieve nanometer spatial resolution in a structure with millimeter thick substrates that do not need to be cut away, we employ X-ray holographic tomography with hard X-rays31 (see the Methods section). Its main features are the X-ray beam that is focused and the sample that is placed at a small distance zs downstream from the focus to collect magnified Fresnel diffraction patterns on the detector.

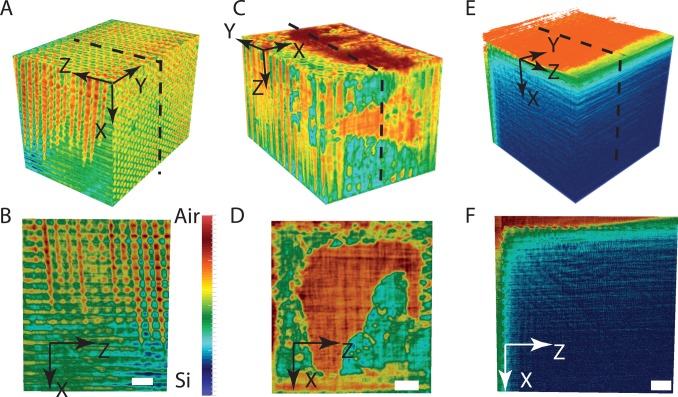
Figure 3A shows a bird’s-eye view of the reconstructed sample volume of the 3D photonic crystal shown in Figure 2A,B. The YZ top face shows the surface of the X-directed pores, similar to the SEM surface in Figure 2A. The alignment of the pores determines the 3D crystal structure and is a crucial step in the nanofabrication. In practice, the alignment is controlled by the etch mask for each pore array and by the directionality of the etching processes.32 In the XZ side face in Figure 3A, pores are running in the Z-direction, whereas in the XY front face, pores are running in the X-direction, matching the 3D design of the inverse woodpile structure (cf. Figure 1A), hence our nickname “the good”. In the XY front face, several pores appear as if they start “from nowhere” in the middle, which is simply due to their running slightly obliquely to the XY face (see Movie S2 and Movie S3), hence the top parts of the pores are not apparent.

Figure 3.

Figure 3

Open in a new tab

3D tomographic reconstructions of the three silicon nanostructures shown in the SEM images in Figure 2. (A,C,E) Bird’s-eye views of the reconstructed sample volumes, X-, Y-, and Z-axes are shown with each panel. (B,D,F) XZ cross sections taken midway through each sample; a 1 μm scale bar is shown in each slice. The common scale bar in panel (B) gives the electron density linearly interpolated between silicon (blue) and air (red). Movies S1, S2, and S3 present animations of the “good” sample shown in (A,B). Movie S4 presents cross sections of the “bad” sample shown in (C,D), and Movie S5 presents cross sections of the “ugly” sample shown in (E,F); see Supporting Information.

Figure 3B shows an XZ cross section midway through the 3D reconstructed volume that cuts through both arrays of pores and allows us to determine the maximum depths of both sets of pores (for YZ cross sections as a function of X, see Movie S2). The Z pores have a depth D = 6280 ± 20 nm and a radius r = 183 ± 10 nm, corresponding to a state-of-the-art depth-to-diameter aspect ratio of 17.15 ± 0.04, as expected from the deep reactive ion etching settings.32,33 To date, the aspect ratio of pores deeply etched in silicon could only be assessed destructively and ex situ by SEM inspection of ion-milled slices or cleaved cross sections.32,33 The deepest X pores have an even greater depth of 9460 ± 20 nm, corresponding to a high aspect ratio of 25.8 ± 0.1. This is an unequivocal observation that a second set of deep-etched pores runs even deeper than a first set. As the pore depth is a main limitation for a crystal’s size, 3D nanostructures are thus significantly larger than expected before. Clearly, TXT reveals buried structural features that are inaccessible to SEM or other nanocharacterization methods (atomic force microscopy or scanning transmission microscopy), as shown in Figure 3B, thus illustrating its power. Moreover, Figure 2B shows that the photonic gap estimated from TXT structural data agrees much better with the measured reflectivity stop band than the gap estimated from electron microscopy.

In addition to characterizing functional nanostructures, TXT allows one to identify several main deviations from the design that affect functionality. Figure 3C,D shows a bird’s-eye view and a cross section through a crystal whose external surface revealed usual crystalline features on a SEM image (cf. Figure 2C). The TXT reconstruction, however, reveals a buried internal void. The void is caused by stiction,34 that is, the structural collapse of a nanostructure due to capillary action on the nanoscale due to the evaporation of a liquid. Here, the liquid was a suspension of colloidal quantum dots that was infiltrated in order to study spontaneous emission control20 and subsequently the liquid spontaneously evaporated from the crystal. From TXT, we thus conclude that after the emission experiment, the crystal lost its functionality as a photonic band gap device, as is evident from the absence of a gap in reflectivity (see Figure 2D), and hence our nickname “the bad”.

Figure 3E,F shows a bird’s-eye view and a XZ cross section of a third sample whose external surface revealed usual periodic pore arrays in a SEM image (see Figure 2E). The tomographic reconstruction reveals a structure with pores that appear to be surprisingly shallow (about 70 nm in cross section) due to inadvertent erroneous settings during the etching process, hence our nickname “the ugly”. Thus, TXT allows us to conclude why this peculiar structure has no band gap functionality to begin with, as is apparent from the lack of gap in reflectivity (see Figure 2F), and the higher constant reflectivity (compared to Figure 2D) is obviously caused by the presence of bulk silicon.

One key feature of our TXT study is the use of X-rays with a much higher photon energy than before,35−37 namely, 17 keV (compared to 6 or 8 keV). Therefore, the 1/e attenuation length for silicon is here 640 μm, that is, 9 to 20× greater than before, and sufficient to traverse wafer-thick silicon substrates that are ubiquitous in the CMOS industry. Therefore, we have been able to study nanostructures embedded in massive substrates with cross sections up to 1.07 × 106 μm2 “as is” without the need for irreversible sample preparation. In contrast, in recent papers, samples had to be destructively milled to a much smaller size36 or had to be doped with heavy elements in order to obtain sufficient contrast.35

To characterize the TXT method, we define as a figure of merit F the ratio between the total linear sample size including substrate and the linear field of view (see Table 1). Due to the high photon energy and the holographic tomography method used here, we arrive at F = 86 (see Table 1), even without the need for extra data. In contrast, other interior or local tomography methods such as Fresnel zone plate or ptychography38 have a limited F ≤ 3.3, while also requiring extra data taken with some empty beam next to the sample. In 2D ptychography of an integrated circuit,39 the sample had to be thinned to 10 μm to allow sufficient X-ray transmission. On the contrary, a large F, as is demonstrated here, allows one to nondestructively study CMOS-compatible nanostructures “as is” and allows subsequent integration or fabrication steps.

Table 1. List of Samples Studied in This Paper with Their Nickname, Fabrication Method (First or Second Generation), Total Sample Cross Section Including Substrate As (μm)2, Figure of Merit 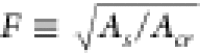Inline graphic (with Crystal Cross Section Acr = (12μm)2), and Pixel Volume in the Tomography Scans Vpix (nm3)a.

name fabrication method As F Vpix
good 1 1460(60) × 730(20) 86(4) 203
bad 1 480(20) × 410(30) 37(3) 203
ugly 2 500(50) × 530(20) 43(5) 103
Open in a new tab
a

Numbers between parentheses are estimated error margins.

Conclusion

We have performed X-ray holographic tomography of 3D silicon photonic band gap crystals on massive substrates as a generic demonstration of traceless X-ray tomography of 3D nanomaterials. The method is truly traceless since we successfully recorded optical spectra even after the X-ray experiments. We obtain the 3D electron density and observe that the structural design is faithfully realized and leads to photonic functionality as expected. We uncover several buried structural deviations that help to identify the lack of functionality of faulty structures. We thus conclude that TXT is a powerful tool to assess the functionality of any complex 3D functional nanostructure with arbitrary short or long-range order, and allowing any subsequent integration or fabrication steps.

Methods

3D Photonic Crystal Nanofabrication

The CMOS-compatible fabrication process of our 3D photonic band gap crystals was described previously.32,40,41 In brief, in our first generation of photonic crystals, a hard mask is defined on a silicon wafer (thickness up to 0.73 mm) with a centered rectangular array of apertures, with a pore radius r/a = 0.245 that gives the broadest possible band gap.15 Deep reactive ion etching of the first set of deep pores (in the Z-direction) results in a wafer with a large 2D array of deep pores.32 Next, such a wafer is cleaved and polished and cut to a millimeter width to fit in the etching machine to perform the second etching step in the perpendicular direction. The second hard mask is carefully aligned with respect to the first array of pores40 and defined in a 10 × 10 μm2 area on the side face of the wafer. By etching the second set of pores in the X-direction, the 3D nanostructure is obtained in the volume where both sets of pores overlap (see Figure 3 and the Movies S1–S3). Finally, the hard mask is removed. 3D photonic crystals shown in Figure 3A–D are fabricated in the above-mentioned way and are sitting on massive chips with large cross sections up to 0.73 × 1.46 = 1.07 mm2.

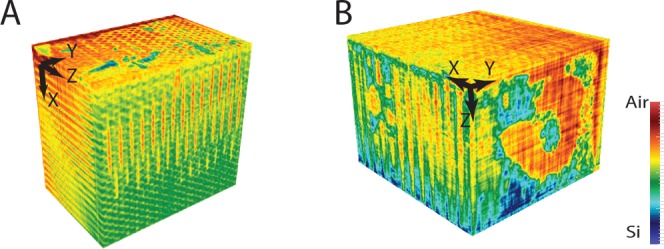
In our second generation of photonic crystals, the etch mask is deposited in a single step on both faces of a wafer edge,41 followed by deep reactive ion etching of two perpendicular arrays of pores. As substrates, we employ Si beams that are chemically etched to cross sections of 0.5 × 0.5 mm2 to obtain exactly perpendicular crystal surfaces. The 3D photonic crystal shown in Figure 3E,F is an example of a second generation photonic crystal fabricated with the single-step etch mask. Although this particular sample was unsuccessful, this fabrication route has yielded many successful samples that have the intended 3D nanostructure, as confirmed by X-ray tomography (see Figure 4). Details of all samples are listed in Table 1.

Figure 4.

Figure 4

Open in a new tab

Photographs of a typical sample studied by X-ray tomography. Top: Silicon beam with photonic crystal structures is mounted on a holder for the X-ray tomography scans. Center: Zoomed-in image of the top part of a Si beam, with a vertical row of 3D photonic crystal structures on the edge of the beam. In the defocused background, the edges of the beam-inclined surfaces are visible. Bottom: Further zoomed-in image reveals ten 3D photonic crystal structures that display a blueish iridescence due to their periodic surface structure. The edge of the beam appears as the vertical green line of scattered light.

Figure 4 shows photographs of a Si 3D nanostructured sample as it is studied in the X-ray tomography instrument “as is”, thus illustrating the power of TXT. The silicon-beam-shaped substrate measures 0.5 × 0.5 × 10 mm3 and is shown after fabrication in the MESA+ NanoLab (www.utwente.nl/mesaplus/nanolab) and mounted for X-ray holographic tomography scans at the ESRF. We emphasize that we do not mill a specific area out of the sample using, for instance, focused ion beams (FIB), as is used with other imaging techniques that require small sample volumes, such as X-ray ptychography, TEM, FIB-SEM, and so forth. We have successfully mounted all samples characterized by X-ray holographic tomography at ESRF in optical setups in Twente without further modifications and even in the same sample holder.

X-ray Holographic Tomography

Holographic tomography experiments were performed at the European Synchrotron Radiation Facility (ESRF), on the nanoimaging beamline ID16A-NI.42 The hard X-ray beam with 17 keV photon energy propagates in the Z-direction and is focused with multilayer coated Kirkpatrick-Baez optics to a 23 × 37 nm2 focus. The sample is placed at a small distance zs downstream from the focus, and the detector is placed at a distance zd downstream from the sample, as shown in Figure 5.

Figure 5.

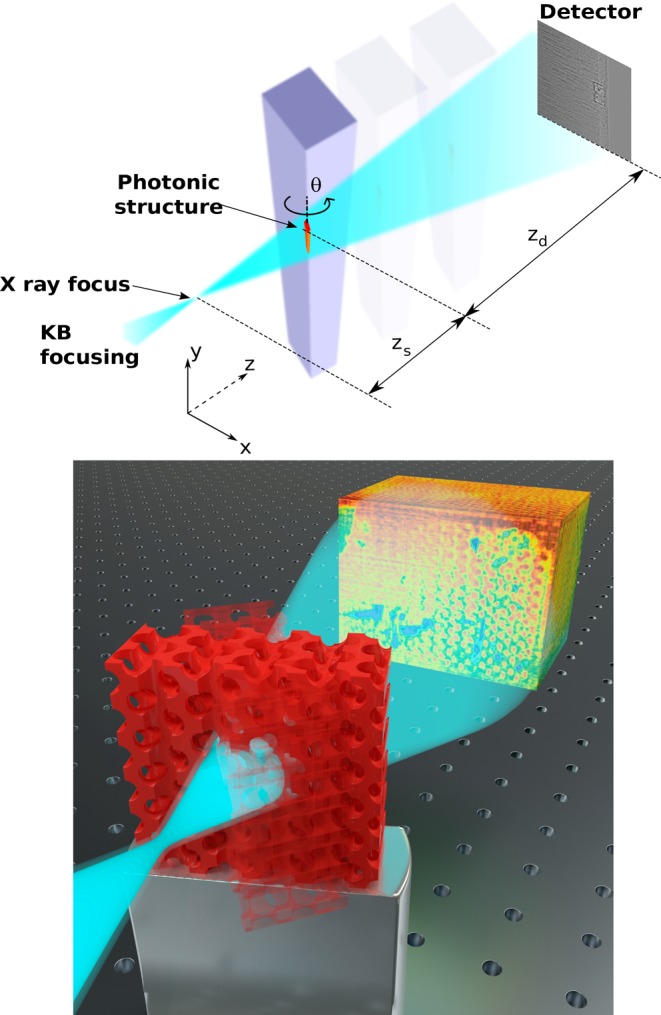
Figure 5

Open in a new tab

(Top) Scheme of the synchrotron X-ray holotomography setup. The incident X-ray beam is focused using Kirkpatrick-Baez optics into a 23 × 37 nm2 focus. The sample is placed at a small distance zs downstream from the focus, and the detector is placed at a distance zd. Radiographs (one example shown) are recorded while rotating the sample by angle θ. (Bottom) Animation of tomography: data are recorded while rotating the sample (two orientations shown). From the recorded radiographs, the tomographic reconstruction is derived that is shown in the background.

The image recorded in the detector plane is an in-line Gabor hologram or Fresnel diffraction pattern.43 Due to the focusing, the sample is illuminated with a spherical wave, unlike the plane-wave illumination in traditional tomography. According to the Fresnel scaling theorem, the spherical wave illumination gives rise to an effective propagation distance D and a magnification M given by44,45

graphic file with name nn9b05519_m001.jpg 1

Varying the focus-to-sample distance zs allows us to vary the magnification M of the diffraction patterns. It also strongly modifies the Fresnel diffraction pattern recorded on the detector through the effective propagation distance. For a phase periodic object, such as our photonic band gap crystals, the Talbot effect results in zero contrast for certain spatial frequencies at the characteristic Talbot distances.46 To obtain nonzero contrast at all spatial frequencies, data are taken at four distances zs. The first distance was chosen to obtain a desired pixel size, either 10 or 20 nm (see Table 1). At each distance zs, Ni = 1500 images were recorded with 0.3 s exposure time while rotating the sample from θ = 0 to 180° around the Y-axis of the crystal (see Figure 2). After each set of rotations, additional radiographs at angles θ = 0 and 90° were collected that revealed that no irreversible changes occurred in the sample during the experiments. The number of projections Ni was chosen as a practical compromise between limited measurement time and sufficient spatial resolution, whereas the total sample size including substrate would require on the order of 105 projections in theory, our figure of merit F decrease this number by 2 orders of magnitude. For the tomographic scans, the axis of rotation was aligned to be a few micrometers deep inside the silicon.

X-ray Data Processing

The data processing is a two-step procedure consisting of a phase retrieval step followed by a tomographic reconstruction. The phase retrieval aims at retrieving the amplitude A(x,y) and phase ϕ(x,y) of the wave exiting the sample u0 = A(x,y)eiϕ(x,y) and that are given by

graphic file with name nn9b05519_m002.jpg 2

and

graphic file with name nn9b05519_m003.jpg 3

where λ is the X-ray wavelength. The amplitude and phase are thus the projection of, respectively, the absorption index β and the refractive index decrement δ that determine the complex refractive index for hard X-rays

graphic file with name nn9b05519_m004.jpg 4

Prior to phase retrieval, all sets of radiographs are scaled to the same magnification and mutually aligned. The mutual alignment of the radiographs at different distances is perturbed by the out-of-focus information on the thick samples. This problem is alleviated by refining this alignment iteratively using the calculated radiographs of the iterative phase retrieval step as a reference and aligning the experimental radiographs with respect to this reference.

We determine a first estimate of the amplitude and phase using the approach proposed by Paganin et al.,47 extended to multiple distances. We assume a homogeneous ratio δ/β = 174 for silicon at 17 keV photon energy. This first estimate provides a blurred version of the phase map. The map is recursively improved using 15 iterations of a nonlinear least-squares optimization. Due to the interior tomography problem, the boundary conditions are unknown in the phase retrieval step and the tomography reconstruction. The padding of the images—required in the propagation operators—and the filter step of the FBP tomography reconstruction are done as follows: The image at the largest distance (largest field of view) with an original size of 2048 (h) × 2048 (v) pixels is resampled to the highest magnification and 3216 × 3216 pixels. This image is padded to a size of 6144 × 4096 pixels by extending the boundary values with a smooth cosinus-type transition from one edge to the other. The images at higher magnification (and smaller field of view) are padded with the image data from the next lower magnification. The absence of any discontinuities in the padded images obtained in this way is effective to minimize the artifacts in the final reconstruction without the use of any supplementary data. The phase retrieval was carried out with ESRF in-house software using the GNU Octave programming environment (www.octave.org) and the public domain image analysis program ImageJ (see http://rsbweb.nih.gov/ij).

Second, a standard tomographic reconstruction48 based on the filtered back-projection algorithm49 and implemented in the ESRF software PyHST250 allows us to obtain the distribution of the refractive index decrement δ(x, y, z). As the X-ray energy of 17 keV is far above any absorption edge of the materials under study, we obtain the electron density distribution from the well-known expression

graphic file with name nn9b05519_m005.jpg 5

with re is the classical electron radius.51 The resulting structure was rendered with open-source software ParaView (see www.paraview.org).

Some phase projections are singular as the phase varies tremendously over a short distance when the X-rays are parallel to a sample face: 1.5 mm of Si introduces 216 rad phase shift at 17 keV. Therefore, about 10 projections near these singular angles (parallel to the X- or Z-directions) are omitted from the tomographic reconstruction.

In our nanostructures, the surrounding material introduces additional contrast that compounds the data interpretation, notably unpolished wafer backsurfaces with micron-high step sizes, sample corners, as well as surrounding deep 2D photonic crystal structures (some of these features are apparent in Movies S2 and S3). Fortunately, our method is sufficiently robust so that the structural features of the photonic crystals are clearly visible with sufficient spatial resolution.

Spatial Resolution

To investigate the spatial resolution, we inspected cross sections of reconstructed data within the large void of the “bad” sample as this structure presents several air–silicon interfaces. One line profile across an interface is shown as refractive index decrement in Figure 6. By modeling the data with a smooth curve and taking the derivative, we arrive at a full width at half-maximum resolution of 55 nm, corresponding to two-and-a-half 20 nm pixels.

Figure 6.

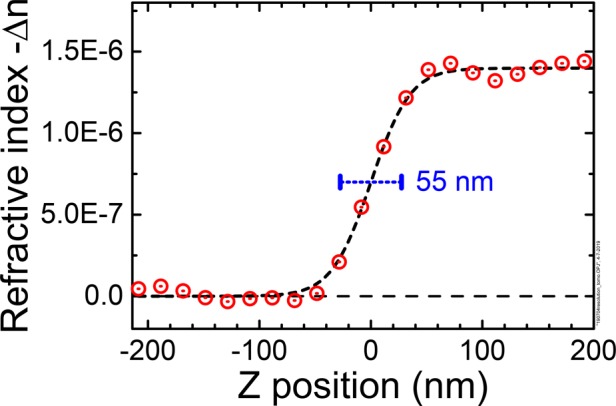
Figure 6

Open in a new tab

Line profile across an air–Si interface in the “bad” sample shown as refractive index decrement (red circles). From the drawn curve, we derive a resolution of 55 nm.

Nanophotonic Experiments and Theory

To assess the basic functionality of the photonic crystals, we performed optical reflectivity to probe the designed photonic gaps. Optical reflectivity was measured using a home-built microscope setup that employs reflective optics and operates in the near-infrared range at wavelengths beyond 800 nm, see refs (52) and (53) and Supporting Information. Photonic band structures were calculated with the plane-wave expansion method, using the MIT photonic bands (MPB) code.54 Silicon was modeled with a dielectric function ϵ = 12.1; see Supporting Information for further details.

Acknowledgments

We thank Léon Woldering, Hannie van den Broek, Willem Tjerkstra, Simon Huisman, Rajesh Nair, Elena Pavlenko, Mehdi Aas, the MESA+ Nanolab and ESRF staff for help, and Arie den Boef (ASML), Jean-Michel Gérard (Grenoble), Hans Hilgenkamp, Detlef Lohse, Allard Mosk (Utrecht), Pepijn Pinkse, Julio da Silva, and Hasan Yilmaz (Yale) for fruitful discussions and support by the “Stirring of light!” program of the “Nederlandse Organisatie voor Wetenschappelijk Onderzoek” (NWO), the NWO-domain “Toegepaste en Technische Wetenschappen” (TTW) No. 11985, the Shell-NWO/FOM programme “Computational Sciences for Energy Research” (CSER), the MESA+ Institute for Nanotechnology (Applied Nanophotonics, ANP), and (thanks to to J.M.G.) and the Descartes-Huygens Prize of the French Academy of Sciences to W.L.V. We thank ESRF for granting beamtime through experiments HC-2520 and CH-5092.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.9b05519.

  • Movie S1: Color rendering of the rotating “good” crystal (AVI)

  • Movie S2: Black and white cross sections of the “good” sample (AVI)

  • Movie S3: Black and white cross sections of the “good” sample (high resolution, emphasis on the surface) (AVI)

  • Movie S4: Black and white cross sections of the “bad” sample (AVI)

  • Movie S5: Black and white cross sections of the “ugly” sample (AVI)

  • CMOS compatibility, details of the reflectivity setup, details of the theory, features of the reconstructed crystals (PDF)

Author Present Address

§ ASML Netherlands B.V., 5504 DR Veldhoven, The Netherlands.

Author Present Address

⊥ ASML Netherlands B.V., 5504 DR Veldhoven, The Netherlands.

The authors declare no competing financial interest.

Supplementary Material

nn9b05519_si_001.avi (3MB, avi)
nn9b05519_si_002.avi (5MB, avi)
nn9b05519_si_003.avi (4.9MB, avi)
nn9b05519_si_004.avi (5MB, avi)
nn9b05519_si_005.avi (4.6MB, avi)
nn9b05519_si_006.pdf (2MB, pdf)

References

  1. Joannopoulos J. D.; Johnson S. G.; Winn J. N.; Meade R. D.. Photonic Crystals - Molding the Flow of Light; Princeton University Press: Princeton, NJ, 1995. [Google Scholar]
  2. Wijnhoven J. E. G. J.; Vos W. L. Preparation of Photonic Crystals Made of Air Spheres in Titania. Science 1998, 281, 802–804. 10.1126/science.281.5378.802. [DOI] [PubMed] [Google Scholar]
  3. Noda S.; Tomoda K.; Yamamoto N.; Chutinan A. Full Three-Dimensional Photonic Bandgap Crystals at Near-Infrared Wavelengths. Science 2000, 289, 604–606. 10.1126/science.289.5479.604. [DOI] [PubMed] [Google Scholar]
  4. Xia Y.; Gates B.; Li Z. Y. Self-Assembly Approaches to Three-Dimensional Photonic Crystals. Adv. Mater. 2001, 13, 409–413. . [DOI] [Google Scholar]
  5. Novotny L.; Hecht B.. Principles of NanoOptics; Cambridge University Press: Cambridge, 2006. [Google Scholar]
  6. Tandaechanurat A.; Ishida S.; Guimard D.; Nomura M.; Iwamoto S.; Arakawa Y. Lasing Oscillation in a Three Dimensional Photonic Crystal Nanocavity with a Complete Bandgap. Nat. Photonics 2011, 5, 91–94. 10.1038/nphoton.2010.286. [DOI] [Google Scholar]
  7. Bermel P.; Luo C.; Zeng L.; Kimerling L. C.; Joannopoulos J. D. Improving Thin-Film Crystalline Silicon Solar Cell Efficiencies with Photonic Crystals. Opt. Express 2007, 15, 16986–17000. 10.1364/OE.15.016986. [DOI] [PubMed] [Google Scholar]
  8. Atwater H. A.; Polman A. Plasmonics for Improved Photovoltaic Devices. Nat. Mater. 2010, 9, 205–213. 10.1038/nmat2629. [DOI] [PubMed] [Google Scholar]
  9. Battaglia C.; Hsu C.; Soderstrom K.; Escarre J.; Haug F.; Charriere M.; Boccard M.; Despeisse M.; Alexander D. T. L.; Cantoni M.; Cui Y.; Ballif C. Light Trapping in Solar Cells: Can Periodic Beat Random?. ACS Nano 2012, 6, 2790–2797. 10.1021/nn300287j. [DOI] [PubMed] [Google Scholar]
  10. Anthony S.IBM Creates First Cheap, Commercially Viable, Electronic Photonic Integrated Chip, 2012; http://www.extremetech.com/computing/142881-ibm-creates-firstcheap-commercially-viable-siliconnanophotonic-chip (accessed Dec 10 2016).
  11. Samsung V-NAND (vertical-NAND) Technology (white Paper), 2014; https://www.samsung.com/us/business/oem-solutions/pdfs/VNAND_technology_WP.pdf (accessed Dec 10 2016).
  12. Crippa L.; Micheloni R. In 3D Flash Memories; Micheloni R., Ed.; Springer: Dordrecht, 2016; pp 85–127. [Google Scholar]
  13. Soukoulis C. M.; Wegener M. Past Achievements and Future Challenges in the Development of Three-Dimensional Photonic Metamaterials. Nat. Photonics 2011, 5, 523–530. 10.1038/nphoton.2011.154. [DOI] [Google Scholar]
  14. Fan S. H.; Villeneuve P. R.; Joannopoulos J. D. Theoretical Investigation of Fabrication-Related Disorder on the Properties of Photonic Crystals. J. Appl. Phys. 1995, 78, 1415–1418. 10.1063/1.360298. [DOI] [Google Scholar]
  15. Woldering L. A.; Mosk A. P.; Tjerkstra R. W.; Vos W. L. The Influence of Fabrication Deviations on the Photonic Band Gap of Three-Dimensional Inverse Woodpile Nanostructures. J. Appl. Phys. 2009, 105, 093108 10.1063/1.3103777. [DOI] [Google Scholar]
  16. Hughes S.; Ramunno L.; Young J. F.; Sipe J. E. Extrinsic Optical Scattering Loss in Photonic Crystal Waveguides: Role of Fabrication Disorder and Photon Group Velocity. Phys. Rev. Lett. 2005, 94, 033903 10.1103/PhysRevLett.94.033903. [DOI] [PubMed] [Google Scholar]
  17. Koenderink A. F.; Lagendijk A.; Vos W. L. Optical Extinction Due to Intrinsic Structural Variations of Photonic Crystals. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 72, 153102. 10.1103/PhysRevB.72.153102. [DOI] [Google Scholar]
  18. Ho K. M.; Chan C. T.; Soukoulis C. M.; Biswas R.; Sigalas M. Photonic Band Gaps in Three Dimensions: New Layer-by-Layer Periodic Structures. Solid State Commun. 1994, 89, 413–416. 10.1016/0038-1098(94)90202-X. [DOI] [Google Scholar]
  19. Maldovan M.; Thomas E. L. Diamond Structured Photonic Crystals. Nat. Mater. 2004, 3, 593–600. 10.1038/nmat1201. [DOI] [PubMed] [Google Scholar]
  20. Leistikow M. D.; Mosk A. P.; Yeganegi E.; Huisman S. R.; Lagendijk A.; Vos W. L. Inhibited Spontaneous Emission of Quantum Dots Observed in a 3D Photonic Band Gap. Phys. Rev. Lett. 2011, 107, 193903. 10.1103/PhysRevLett.107.193903. [DOI] [PubMed] [Google Scholar]
  21. Devashish D.; Hasan S. B.; van der Vegt J. J. W.; Vos W. L. Reflectivity Calculated for a Three-Dimensional Silicon Photonic Band Gap Crystal with Finite Support. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 155141. 10.1103/PhysRevB.95.155141. [DOI] [Google Scholar]
  22. Goldstein J.; Newbury D. E.; Joy D. C.; Lyman C. E.; Echlin P.; Lifshim E.; Sawyer L.; Michael J. R.. Scanning Electron Microscopy and X-Ray Microanalysis; Springer: New York, 2003. [Google Scholar]
  23. Jacobsen C.; Medewaldt R.; Williams S. In X-ray Microscopy and Spectromicroscopy; Thieme J., Schmahl G., Rudolph D., Umbach E., Eds.; Springer: New York, 1998; pp 197–206. [Google Scholar]
  24. Misra S.; Liu N.; Nelson J.; Hong S. S.; Cui Y.; Toney M. In Situ X-Ray Diffraction Studies of (De)Lithiation Mechanism in Silicon Nanowire Anodes. ACS Nano 2012, 6, 5465–5473. 10.1021/nn301339g. [DOI] [PubMed] [Google Scholar]
  25. Stankevič T.; Hilner E.; Seiboth F.; Ciechonski R.; Vescovi G.; Kryliouk O.; Johansson U.; Samuelson L.; Wellenreuther G.; Falkenberg G.; Feidenhansl R.; Mikkelsen A. Fast Strain Mapping of Nanowire Light-Emitting Diodes Using Nanofocused X-Ray Beams. ACS Nano 2015, 9, 6978–6984. 10.1021/acsnano.5b01291. [DOI] [PubMed] [Google Scholar]
  26. Vos W. L.; Megens M.; van Kats C. M.; Bösecke P. X-Ray Diffraction of Photonic Colloidal Single Crystals. Langmuir 1997, 13, 6004–6008. 10.1021/la970423n. [DOI] [Google Scholar]
  27. Shabalin A. G.; Meijer J.-M.; Dronyak R.; Yefanov O. M.; Singer A.; Kurta R. P.; Lorenz U.; Gorobtsov O. Y.; Dzhigaev D.; Kalbfleisch S.; Gulden J.; Zozulya A. V.; Sprung M.; Petukhov A. V.; Vartanyants I. A. Revealing Three-Dimensional Structure of an Individual Colloidal Crystal Grain by Coherent X-Ray Diffractive Imaging. Phys. Rev. Lett. 2016, 117, 138002. 10.1103/PhysRevLett.117.138002. [DOI] [PubMed] [Google Scholar]
  28. Sakdinawat A.; Attwood D. Nanoscale X-Ray Imaging. Nat. Photonics 2010, 4, 840–848. 10.1038/nphoton.2010.267. [DOI] [Google Scholar]
  29. Pollak B. Experiences With Planography. Dis. Chest 1953, 24, 663–669. 10.1378/chest.24.6.663. [DOI] [PubMed] [Google Scholar]
  30. Cloetens P.; Ludwig W.; Baruchel J.; van Dyck D.; van Landuyt J.; Guigay J. P.; Schlenker M. Holotomography: Quantative Phase Tomography with Micrometer Resolution Using Hard Synchrotron Radiation X Rays. Appl. Phys. Lett. 1999, 75, 2912–2914. 10.1063/1.125225. [DOI] [Google Scholar]
  31. Mokso R.; Cloetens P.; Maire E.; Ludwig W.; Buffière J.-Y. Nanoscale Zoom Tomography with Hard X-Rays Using Kirkpatrick-Baez Optics. Appl. Phys. Lett. 2007, 90, 144104. 10.1063/1.2719653. [DOI] [Google Scholar]
  32. van den Broek J. M.; Woldering L. A.; Tjerkstra R. W.; Segerink F. B.; Setija I. D.; Vos W. L. Inverse-Woodpile Photonic Band Gap Crystals with a Cubic Diamond-Like Structure Made from Single Crystalline Silicon. Adv. Funct. Mater. 2012, 22, 25–31. 10.1002/adfm.201101101. [DOI] [Google Scholar]
  33. Wu B.; Kumar A.; Pamarthy S. High Aspect Ratio Silicon Etch: A Review. J. Appl. Phys. 2010, 108, 051101 10.1063/1.3474652. [DOI] [Google Scholar]
  34. Roman B.; Bico J. Elasto-Capillarity: Deforming an Elastic Structure with a Liquid Droplet. J. Phys.: Condens. Matter 2010, 22, 493101. 10.1088/0953-8984/22/49/493101. [DOI] [PubMed] [Google Scholar]
  35. Chen Y. C.; Geddes J. B.; Yin L.; Wiltzius P.; Braun P. V. X-Ray Computed Tomography of Holographically Fabricated Three-Dimensional Photonic Crystals. Adv. Mater. 2012, 24, 2863–2868. 10.1002/adma.201200411. [DOI] [PubMed] [Google Scholar]
  36. Holler M.; Guizar-Sicairos M.; Tsai E. H. R.; Dinapoli R.; Müller E.; Bunk O.; Raabe J.; Aeppli G. High Resolution Non-Destructive Three Dimensional Imaging of Integrated Circuits. Nature (London, U. K.) 2017, 543, 402–406. 10.1038/nature21698. [DOI] [PubMed] [Google Scholar]
  37. Furlan K. P.; Larsson E.; Diaz A.; Holler M.; Krekeler T.; Ritter M.; Petrov A. Y.; Eich M.; Blick R.; Schneider G. A.; Greving I.; Zierold R.; Janen R. Photonic Materials for HighTemperature Applications: Synthesis and Characterization by X-Ray Ptychographic Tomography. Appl. Mater. Today 2018, 13, 359–369. 10.1016/j.apmt.2018.10.002. [DOI] [Google Scholar]
  38. da Silva J. C.; Guizar-Sicairos M.; Holler M.; Diaz A.; van Bokhoven J. A.; Bunk O.; Menzel A. Quantitative Region-Of-Interest Tomography Using Variable Field of View. Opt. Express 2018, 26, 16752–16768. 10.1364/OE.26.016752. [DOI] [PubMed] [Google Scholar]
  39. Guizar-Sicairos M.; Johnson I.; Diaz A.; Holler M.; Karvinen P.; Stadler H. C.; Dinapoli R.; Bunk O.; Menzel A. HighThroughput Ptychography Using Eiger: Scanning X-Ray Nano-Imaging of Extended Regions. Opt. Express 2014, 22, 14859–14870. 10.1364/OE.22.014859. [DOI] [PubMed] [Google Scholar]
  40. Tjerkstra R. W.; Woldering L. A.; van den Broek J. M.; Roozeboom F.; Setija I. D.; Vos W. L. Method to Pattern Etch Masks in Two Inclined Planes for Three Dimensional Nano- and Microfabricationy. J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom. 2011, 29, 061604 10.1116/1.3662000. [DOI] [Google Scholar]
  41. Grishina D. A.; Harteveld C. A. M.; Woldering L. A.; Vos W. L. Method to Make a Single-Step Etch Mask for 3D Monolithic Nanostructures. Nanotechnology 2015, 26, 505302. 10.1088/0957-4484/26/50/505302. [DOI] [PubMed] [Google Scholar]
  42. Cesar da Silva J.; Pacureanu A.; Yang Y.; Bohic S.; Morawe C.; Barrett R.; Cloetens P. Efficient Concentration of High-Energy XRays for Diffraction-Limited Imaging Resolution. Optica 2017, 4, 492–495. 10.1364/OPTICA.4.000492. [DOI] [Google Scholar]
  43. Gabor D. A New Microscopic Principle. Nature (London, U. K.) 1948, 161, 777–778. 10.1038/161777a0. [DOI] [PubMed] [Google Scholar]
  44. Pogany D.; Gao A.; Wilkins S. W. Contrast and Resolution in Imaging with a Microfocus X-Ray Source. Rev. Sci. Instrum. 1997, 68, 2774–2782. 10.1063/1.1148194. [DOI] [Google Scholar]
  45. Paganin D.Coherent X-ray Optics; Oxford University Press: Oxford, 2006. [Google Scholar]
  46. Goodman J. W.Introduction to Fourier Optics, 3rd ed.; Roberts & Co: Englewood, CO, 2005. [Google Scholar]
  47. Paganin D.; Mayo S. C.; Gureyev T. E.; Miller P. R.; Wilkins S. W. Simultaneous Phase and Amplitude Extraction from a Single Defocused Image of a Homogeneous Object. J. Microsc. 2002, 206, 33–40. 10.1046/j.1365-2818.2002.01010.x. [DOI] [PubMed] [Google Scholar]
  48. Hounsfield G. Computerized Transverse Axial Scanning (Tomography): I. Description of System. Br. J. Radiol. 1973, 46, 1016–1022. 10.1259/0007-1285-46-552-1016. [DOI] [PubMed] [Google Scholar]
  49. Herman G. T.Fundamentals of Computerized Tomography, 2nd ed.; Springer: London, 2009. [Google Scholar]
  50. Mirone A.; Brun E.; Gouillart E.; Tafforeau P.; Kieffer J. The pyhst2 Hybrid Distributed Code for High Speed Tomographic Reconstruction with Iterative Reconstruction and a Priori Knowledge Capabilities. Nucl. Instrum. Methods Phys. Res., Sect. B 2014, 324, 41–48. 10.1016/j.nimb.2013.09.030. [DOI] [Google Scholar]
  51. Guinier A.X-ray Diffraction: In Crystals, Imperfect Crystals, and Amorphous Bodies; W.H. Freeman and Co.: San Francisco, CA, 1963. [Google Scholar]
  52. Huisman S. R.; Nair R.; Woldering L. A.; Leistikow M. D.; Mosk A. P.; Vos W. L. Signature of a Three-Dimensional Photonic Band Bap Observed on Silicon Inverse Woodpile Photonic Crystals. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 205313. 10.1103/PhysRevB.83.205313. [DOI] [Google Scholar]
  53. Adhikary M.; Uppu R.; Harteveld C. A. M.; Grishina D. A.; Vos W. L.. Experimental Probe of a Complete 3D Photonic Band Gap. arXiv.org 1909.01899 2019. [DOI] [PubMed] [Google Scholar]
  54. Johnson S. G.; Joannopoulos J. D. Block Iterative Frequency-Domain Methods for Maxwells Equations in a Planewave Basis. Opt. Express 2001, 8, 173–190. 10.1364/OE.8.000173. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn9b05519_si_001.avi (3MB, avi)
nn9b05519_si_002.avi (5MB, avi)
nn9b05519_si_003.avi (4.9MB, avi)
nn9b05519_si_004.avi (5MB, avi)
nn9b05519_si_005.avi (4.6MB, avi)
nn9b05519_si_006.pdf (2MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES