Crystal Structure, Morphology, and Surface Termination of Cyan-Emissive, Six-Monolayers-Thick CsPbBr₃ Nanoplatelets from X-ray Total Scattering

Abstract

Highly anisotropic colloidal CsPbBr₃ nanoplatelets (NPLs) represent an appealing class of colloidal quantum wells with enhanced light emissivity. Strong quantum confinement imposed by the small platelet thickness and atomic flatness gives rise to enhanced oscillator strength, higher exciton binding energy, and narrow emission linewidth. While discrete thicknesses manifest themselves in discrete bandgap energies, fine-tuning of the emission energy can be achieved by compositional modulations. Here we address one of the most debated aspects of perovskite nanoplatelets: their crystal structure. Starting with the direct imaging by high-resolution electron microscopy (providing a clue on the pseudocubic faceting of the NPLs), we focus the study on X-ray total scattering techniques, based on the Debye scattering equation (DSE) approach, to obtain better atomistic insight. The nanoplatelets are six-monolayers thick and exhibit an orthorhombic structure. A thorough structure–morphology characterization unveils a specific orientation of the axial and equatorial bromides of the PbBr₆ octahedra versus the NPLs thickness; we found that {010} and {101} planes of the orthorhombic CsPbBr₃ lattice (Pnma space group) correspond to the six facets of the NPL, with basal planes being of {101} type. The NPLs undergo a lattice relaxation in comparison to cuboidal CsPbBr₃ NCs; the major deformation is observed in the axial direction, which suggests a structural origin of the higher compliance along the b axis. The DSE-based analysis also supports a CsBr surface termination model, with half Cs sites and a half (or slightly more) Br sites vacant.

Nanocrystals (NCs) of semiconductive lead halide perovskites (LHPs, APbX₃ compounds, where A = Cs, methylammonium, or formamidinium)¹⁻²³ have recently attracted a great deal of attention for their potential use as classical light sources in light-emitting diodes²⁴⁻³¹ and LCD displays and as quantum light sources,³²⁻³⁹ lasing medium,⁴⁰⁻⁴³ or absorbers in photodetectors⁴⁴ and in photovoltaics.⁴⁵⁻⁵⁰ Thanks to the higher ionicity compared to other traditional semiconductors (chalcogenides, pnictides), these LHP NCs form faster and at lower temperatures.

Thus far, most of the research has been devoted to relatively large, cuboid-shaped CsPbX₃ NCs, exhibiting bright photoluminescence (PL) with narrow emission bandwidths (<100 meV, 12–42 nm in blue-to-red), high PL quantum yields (QYs) (up to 90–100%), and short radiative lifetimes (1–29 ns).² A possibility for tuning the optical absorption and emission features of LHPs is offered by resorting to anisotropic NCs, very much as demonstrated for cadmium chalcogenide nanoplatelets (NPLs).^51,52 By judicious adjustment of the synthesis parameters (reaction temperature, ligand ratio, or mixing long- and short-chain ligands), the morphology of CsPbBr₃ NCs can be adjusted to one-dimensional nanowires^53,54 and two-dimensional (2D) NPLs and nanosheets.⁵⁵⁻⁶⁴ In the particular case of NPLs, by exploiting the quantum confinement effect governed by the NPL thickness, blue-shifted absorption and emission features are controlled discretely. As observed in other 2D semiconductors, a thickness of just few unit cells in LHP NPLs gives rise to larger exciton binding energies (120–280 meV depending on the NPLs thickness^65,66 versus 40 meV in 10 nm cuboid NCs)⁶⁷ and reduced dielectric screening.^63,68 Moreover, the large contact area between NPLs, which have shown a clear tendency to self-assemble along the direction parallel to their thickness (as a deck of playing cards),⁵⁵ makes them particularly interesting for LED applications.⁶⁹⁻⁷¹

However, LHP NPLs remain poorly understood at the atomistic level. One immediate, highly pressing open question is to determine in which polymorphs they crystallize. This issue has been extensively investigated in CsPbX₃ NCs leading to the clear assignment of the orthorhombic crystal structure as the thermodynamic stable polymorph at ambient conditions.^72,73 The orthorhombic structure differs from the archetypal cubic structure by a small tilting of the PbX₆ octahedra, which preserves the 3D corner-shared network of octahedra while introducing structural differences between axially and equatorially coordinated halides. While these differences are of lesser importance for more isotropic cuboid shapes, when NPLs are considered, owing to the highly anisotropic morphology, knowing how the orthorhombic structural axes are aligned with respect to the NPL thickness and basal planes is of paramount significance. Therefore, determining the correct atomistic structure of these materials, in terms of the crystal polymorph, structural defectiveness, structure–morphology relationship and surface termination, is a fundamental step toward understanding and controlling their optical properties. For example, the utmost correct atomistic model is needed for accurate computing of the electronic structure by the DFT methods and for rationalization of the optical properties.^74,75

In the field of nanotechnology, transmission electron microscopy (TEM), especially in its high-resolution mode (HRTEM), is often employed to retrieve information on NCs structure, size, and morphology. In the context of LHP research, electron microscopy suffers from two major drawbacks. First, it has limited capacity to distinguish perovskite polymorphs through detection of tilting of PbX₆ octahedra, both for CsPbX₃ NCs⁷⁶⁻⁸² and NPLs.^{55,57,58,63,83} The tiny extent of the tilting is very difficult to capture with imaging techniques unless sophisticated aberration-corrected scanning TEM (STEM) coupled with phase recovering methods on ultrathin nanosheets are adopted.⁸⁴ Second, LHP NCs are structurally labile, low-melting-point semiconductors, and hence, their atomic structure might be altered by the beam of electrons. These drawbacks necessitate the reliance on forefront X-ray diffraction (XRD) techniques. Structural lability of LHPs manifests itself, most profoundly, in small nanostructures. For instance, few-nm-thin NPLs are far less robust compared to cuboid-shaped NCs.^55,85 This poses major difficulties for obtaining stable, size- and shape-uniform ensembles of LHP NPLs.^63,85 Such uniform and stable ensembles are imperative for any ensemble-averaging technique, be it optical characterization or structural characterization by XRD methods. We also would like to point that electron microscopy deposits substantial energy flux and, in the case of structurally labile NCs, this may lead to alteration or damage to the crystal structure. It is thus much desired to corroborate the electron microscopy with less invasive X-ray analysis.

In this study, we thought to shed light on the atomic structure of CsPbX₃ NPLs and on the diverse structure–morphology related questions.

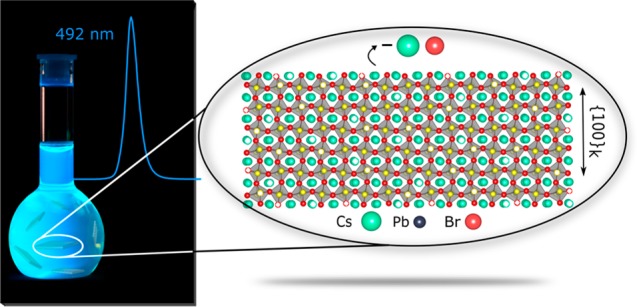
As a first step, we report the synthesis of stable and monodisperse CsPbBr₃ NPLs, six-unit-cells thick (ca. 3.5 nm) and with PL emission peaked in the sky-blue region (492 nm). High PL QYs (up to 75%) are retained in deposited films, a prerequisite for efficient light-emitting devices employing NPLs as the active medium. While preserving the size and shape of the NPLs, the emission spectra bands can be tuned from 492 to 398 nm (blue/violet) and 632 nm (red) via fast anion exchange easily performed at room temperature in air.

As a second step, we applied a powerful X-ray total-scattering based method for characterizing LHP NPLs in their native colloidal state. Conventional XRD is rather inadequate when dealing with very small NCs, characterized by extensive Bragg peaks broadening and the presence of a large amount of diffuse scattering between and below them, stemming from intermingled effects, such as reduced coherent domains, aspherical morphology, structural defects, or surface reconstruction.^86,87 Moreover, with conventional XRD methods, LHPs are typically characterized in the dry state; highly textured samples are obtained by dropping the NPLs solution on a flat holder, which introduces distorted intensity ratios of Bragg peaks, making the structural analysis even more challenging. A pertaining difficulty is also to characterize the NC surfaces. Perovskite NPLs are potentially “easier” in this regard, owing to their atomically defined thickness and atomically flat basal planes. Knowing the alignment of the NPL facets with regard to the crystal planes of the underlying lattice is an essential first step.

We present an accurate structural, morphological, and compositional characterization of CsPbBr₃ NPLs by using synchrotron X-ray data and the Debye scattering equation (DSE) approach.⁸⁸⁻⁹⁰ The method fosters a comprehensive characterization of the nanosized materials and full XRD pattern reconstruction, both in terms of Bragg peaks and diffuse scattering, which intrinsically arise from the detailed atomistic model definition of NPLs, developed in the real space. Recently, the DSE-based approach has been successfully and extensively applied to a wide range of nanomaterials, including LHP NCs, allowing the retrieval of unforeseen structural and compositional aspects.^73,91−96

We present evidence that six-monolayers-thick (6 ML) CsPbBr₃ NPLs (one monolayer being ca. 0.59 nm thick), exhibit orthorhombic structure and {100} pseudocubic facets, which correspond to two {010} and four {101} planes of the orthorhombic CsPbBr₃ lattice (Pnma space group). The basal facets of the NPL are of {101} family, whereas two remaining {101} planes and both {010} planes make for side NPL facets. Such determination of the orientation of the crystal structure of LHPs with respect to the NPLs thickness would be impossible without combining the crystal structure and the morphological descriptors within a unified modeling approach. CsBr-terminated surfaces are preferentially exposed.

Results and Discussion

Synthesis of Highly Stable Monodisperse CsPbBr₃ NPLs

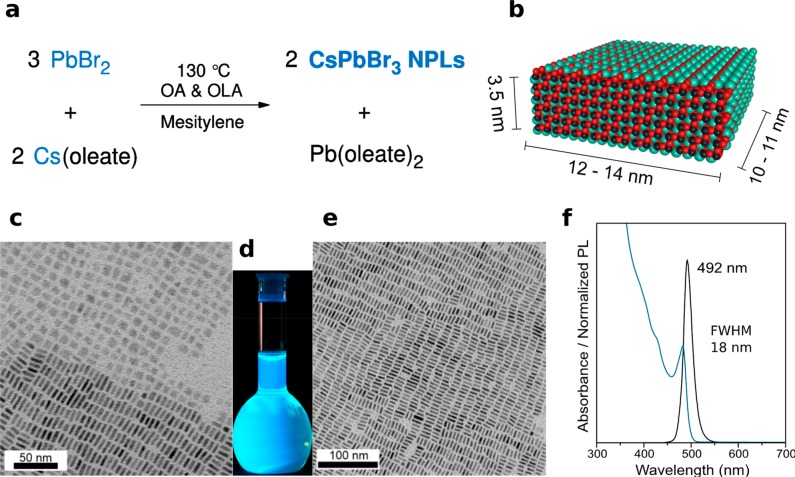
By modifying the procedure reported by Protesescu et al.,² the shape was adjusted from the cuboid to more anisotropic 6 ML CsPbBr₃ NPLs (ca. 3.5 nm thick). The factors favoring NPL formation were lower synthesis temperature and two-fold higher concentrations of reagents. As described in Figure 1a, the synthesis of CsPbBr₃ NPLs is based on the very fast coprecipitation of constituting ions. PbBr₂, along with dried oleic acid (OA) and oleylamine (OLA) in 1:1 molar ratio, was loaded in a three-neck flask in the glovebox and transferred to the Schlenk line. Mesitylene solvent was added to the reaction mixture, and the flask was flushed at room temperature with N₂ three times by quickly switching between vacuum and N₂ flow. The reaction mixture was heated to 115 °C under N₂ atmosphere, and Cs-oleate was swiftly injected (see the Methods section for the detailed procedure). Rectangularly shaped CsPbBr₃ NPLs (Figure 1b) were formed in less than 3 s, and the reaction was stopped by cooling the reaction mixture with a water-ice bath. The bright blue-emitting material was easily separated by centrifugation and further dispersed in toluene. Drying of such toluene solution results in self-assembled superstructures shown in Figure 1c–e. Similar quality NPLs were obtained when 1-octadecene or Dowtherm@A were used as solvents, but in these situations, the purification proved to be more difficult for retaining the integrity of NPLs. As shown in Figure 1c, CsPbBr₃ NPLs expose two distinct and segregated arrangements: “flat”, that is, side up, when the NPLs are exposing the basal (largest) plane (with typical edges of 10–14 nm), and side-on, laterally stacked, with a clearly visible thickness (near 3.5 nm, see Figure 1e). Also, in the latter case, large islands of equioriented NPL domains, where the 2D ordering extends over a μm size, can be envisaged.

Figure 1.

(a) Reaction scheme for the formation of CsPbBr₃ NPLs at 130 °C in mesitylene, in the presence of OA and OlAm as capping ligands. (b) Atomistic model of an average 6-monolayers-thick (6 ML) CsPbBr₃ NPL with the TEM-derived average dimensions. (c) Low-resolution TEM micrograph of CsPbBr₃ NPLs partially stacked and with the “flat” side pointing upward. (d) Photograph of CsPbBr₃ NPLs solution in toluene (under a UV lamp, λ = 365 nm) showing the bright blue–cyan emission. (e) Low-resolution TEM micrograph of CsPbBr₃ NPLs, exposing their uniform thickness. (f) Typical absorbance and PL spectra of CsPbBr₃ NPLs with a characteristic emission at 492 nm and PL QY of 70–80%.

These NPLs exhibit a bright blue emission under UV light (Figure 1d), having sharp peaks in their optical absorption (482 nm) and PL (492 nm) spectra. The PL band has a full width at half-maximum (fwhm) of about 18 nm (Figure 1f). The small Stokes shift between the absorption and the emission peak maxima (≤10 nm) is consistent with direct exciton recombination. We found that the NPLs obtained by this method preserve their structural and colloidal integrity and optical characteristics for at least 24 months. As shown in Figure S1a,b, the absorbance and PL spectra of 11 and 21 months aged NPLs, respectively, are identical. Also, the morphology of the NPLs was preserved in time (see Figure S1c,d). The quantum yields (QYs) of the NPLs embedded in polymer films were reassessed as well and found to be around 41% for the 11 months aged and decreased to 28% after 21 months. A certain instability toward the formation of a small amount of the insulating Cs₄PbBr₆ phase was also detected, as documented also by others.^83,97 The quantification of this phase, possessing a crystal structure distinctly different to that of LHPs, was carefully performed by monitoring both CsPbBr₃ colloidal solutions and films upon aging, with conventional XRD characterization (results are shown in Figure S2): the impurity amount remains very low if the LHPs are stored as colloidal suspensions (ca. 5% by weight) and slightly increases after deposition as a film (up to a maximum of 11 weight%, measured after 15 days and ca. 1 month).

With the same synthesis methodology, by lowering the injection temperature (90–110 °C), both the absorption and PL emission peaks can be blue-shifted (445–485 nm, Figure S3). These deep-blue emissions correspond to thinner nanoplatelets and, following assignments by others, correspond to two- to five-monolayers-thick NPLs.^55,66 However, we find that our NPLs of these thicknesses are prohibitively unstable against conventional isolation and purification methods.

We hence conclude that their practical utility will be limited and have focused this study on 6 ML-thick NPLs (3.5 nm, PL peak at 492 nm). We also note that, for fine-tuning the bandgap/PL peak energy, we resorted to fast Br-to-Cl or Br-to-I anion exchange reactions on these 492 nm CsPbBr₃ NPLs as parent-emitters, which enabled the coverage of a rather broad spectral range, from 398 to 632 nm (Table S1 and Figure S4), in analogy to conventional cuboid CsPbBr₃ NCs.⁹⁹ The size and shape of NPLs, and their propensity to stacking, are preserved after the anion-exchange process (Figure S5).

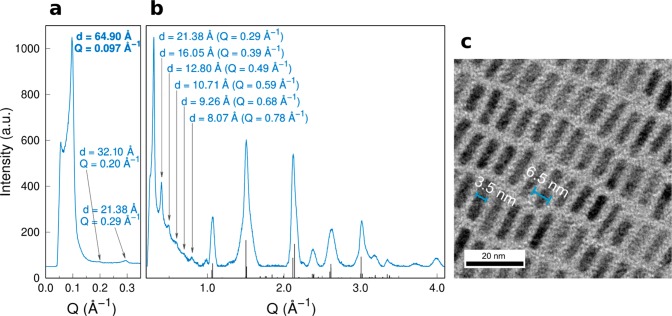
The low- and high-angle regions of the XRD patterns of dried CsPbBr₃ NPLs (collected with a laboratory instrument in transmission mode and a Cu Kα₁ source) are shown in Figure 2a and b, respectively. In Figure 2a, a first diffraction peak at Q = 0.097 Å^–1 is identified (Q = 4π sin θ/λ). This reflection corresponds to a d-spacing of 64.90 Å, attributed to the self-assembled superstructure of the NPLs, imaged in Figure 2c. The other diffraction peaks observed in the 0.1–1.0 Å^–1Q-range are consistent with the d_n = 64.90/n Å values (n = 2–7) and represent the higher harmonics of the large peak falling at 0.097 Å^–1. This rich sequence of diffraction peaks demonstrates the persistency of a long-range order of the NPLs in a dry powder, their average periodicity being in line with the sum of 3.5 nm (NPL thickness) and two 1.5 nm thicknesses of ligand coating, well matching previous reports.^55,66 Conventional XRD measurements, shown in Figure 2b, vaguely suggest that the average crystal symmetry of CsPbBr₃ NPLs is consistent with an orthorhombic structure,⁹⁸ very much like that of more conventional cuboid CsPbX₃ NCs.^72,73 This hypothesis was further corroborated by the detailed analysis with wide angle X-ray total scattering (WAXTS), discussed in the following sections.

Figure 2.

(a) Low-angle powder X-ray diffraction pattern of CsPbBr₃ NPLs displaying the first peak at d = 64.90 Å (Q = 0.097 Å^–1) corresponding to the thickness of the NPL (3.5 nm) surrounded by a shell of organic ligands, with an effective thickness of 1.5 nm (on each side). (b) High-angle region X-ray powder diffraction pattern of CsPbBr₃ NPLs showing the diffraction peaks corresponding to the stacking of the NPLs (3–15 degree) and the typical diffraction pattern matching to the orthorhombic perovskite crystal structure.^72,73,98 (c) Low-resolution TEM micrograph showing stacked NPLs exposing a thickness of ∼6.5 nm (NPL + ligand shell) corresponding with the first diffraction peak in the low-angle region (d = 64.90 Å).

On the Cubic Faceting of LHPs at the Nanoscale

APbX₃ LHPs are characterized by a 3D-perovskite structure, in which Pb²⁺ ions lie at the nodes of a pseudocubic lattice and are octahedrally coordinated by the halides, whereas the A⁺ cations (Cs⁺, FA⁺ or MA⁺) occupy the cubic cavities in the center of the pseudocubic unit cell. CsPbX₃ perovskites are known to crystallize in three different polymorphs that retain the 3D framework of PbX₆ octahedra. The transitions between the archetypal cubic α- (Pm-3m), tetragonal β- (P4/mbm), and orthorhombic γ-phases (Pnma) involve the progressive bending of the Pb-X-Pb angles (seen as mono and biaxial tilting of PbX₆ octahedra with respect to each other). Specifically, these angles are linear in the cubic structure, bent in the equatorial planes in the tetragonal polymorph and bent both in the axial and equatorial directions in the orthorhombic polymorph.

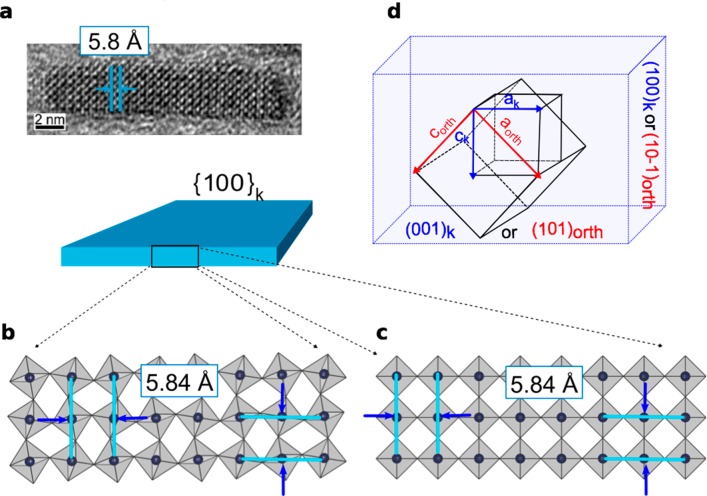
Multiple HRTEM reports ubiquitously provided direct imaging of interplanar distances of ∼5.8 Å for CsPbBr₃ and 6.2 Å for CsPbI₃, in both cuboidal NCs^76−78,100 and NPLs,^55,57,58 which well represent both the cubic cell axial lengths and also Pb–Pb distances in the orthorhombic structure. Similarly, by analyzing the HRTEM images of the CsPbBr₃ NPLs synthesized in this work (Figure 3a), the interplanar distance of ∼5.8 Å is easily detected in the directions of both NPLs thickness and elongation. Hence, d-spacing from TEM images cannot be used to directly assess the crystal polymorph of NPLs, as schematically exemplified in Figures 3b (orthorhombic structure) and c (cubic structure). The interplanar distances imaged by HRTEM relate the Pb ions of interconnected PbX₆ units, always displaying the pseudocubic framework, whereas the tilt of octahedra (detectable through the halides, not shown in Figures 3b,c) is below the resolution limit of the technique. Before validating the hypothesis of an orthorhombic structure in NPLs, as much as observed in cuboidal LHP NCs, the cubic structure was initially explored via atomistic models of NPLs and DSE simulations. We resorted to high-resolution WAXTS data, collected in transmission geometry, directly on capillaries filled with the colloidal solutions of CsPbBr₃ NPLs in toluene (details are provided in the Methods section). The cubic model provided a poor matching of the WAXTS data, as shown in Figure S6.

Figure 3.

(a) HRTEM image of CsPbBr₃ NPLs synthesized in this work, in which the cubic interplanar distance (d = 5.8 Å) is highlighted; a similar value (not shown here) is observed normal to it. Schematic representation of three-monolayers thick CsPbBr₃ NPLs in the (b) orthorhombic and (c) cubic arrangements, highlighting the identical interplanar distances measurable by HRTEM among the Pb rows in the two structures. Pb ions are the black dots inside the gray PbBr₆ octahedra, halides are not visualized. (d) Geometrical relationship between the archetypal cubic (a_k) and orthorhombic (a_orth, b_orth, and c_orth) unit cell axes and the pseudocubic and orthorhombic faces.

Worthy of note, the detection of the 5.8 Å interplanar distance measured in our prismatic NPLs (Figure 3a) provided an important initial input for the construction of a precise atomistic model: as much as observed in cuboidally shaped NCs, LHP NPLs expose {010} and {101} orthorhombic facets (in the Pnma space group), meaning that they retain a pseudocubic faceting, despite the internal arrangement of PbX₆ octahedra and the highly anisotropic morphology. To further clarify this point, we show in Figure 3d the relationship between the cubic and orthorhombic Pnma unit cell and the pseudocubic {100} morphology (hereafter labeled as {100}_k) versus orthorhombic faces, as observed both in NPLs and NCs, and also adopted in the DSE modeling discussed in the next section. Accordingly, with reference to the orientation of cell axes in Figure 3d, a_k aligns to (a_orth – c_orth), c_k to (a_orth + c_orth), and b_k is parallel to b_orth. We also recall the metric relationship between cubic (a_k) and orthorhombic axes (a_orth ≈ c_orth ≈ √2a_k; b_orth ≈ 2a_k), leading to a near equivalence of the lengths of the two orthorhombic cell axes, which is later applied.

Structure–Morphology Relationship in CsPbBr₃ NPLs with Orthorhombic Structure

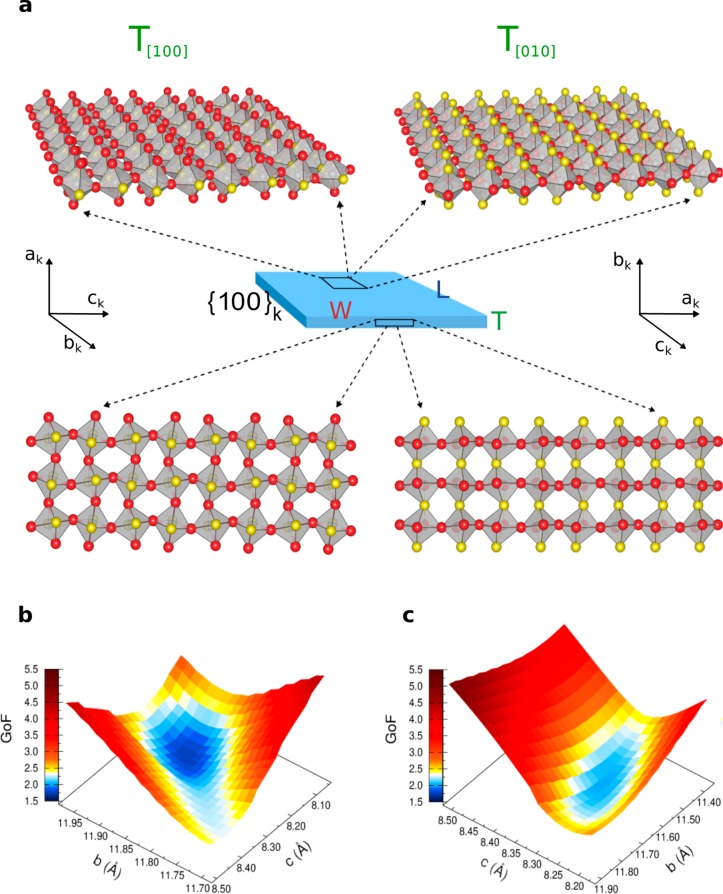
For triaxial crystal structures, such as orthorhombic CsPbBr₃, the possibility of properly orienting the three (nonequivalent) crystallographic directions (a, b, c) with respect to the morphological edges of NPLs (T = thickness, W = width, and L = length, Figure 4a), in particular to their thickness, is of fundamental importance. Matching two orthogonal crystallographic and morphological bases can be done in 3! = 6 different ways, each maintaining one crystallographic axis aligned with the T direction. However, the near equivalence of a and c axis lengths (see Figure 3d) (8.255 and 8.207 Å, as per the bulk structure),¹⁰¹ together with the similarity of the two longest morphological edges (10–12 nm) imaged by TEM (W ≈ L, as depicted in Figure 1) firmly simplifies the task, leading to two meaningful possible orientations (as shown in Figure 4a), one with T aligned with a_k (or c_k), the other with T parallel to b_k. For the sake of simplicity, we refer to the cubic crystallographic axes and adopt the notation [100], [010], and [001] to indicate a_k, b_k, and c_k in the discussion of the two configurations, hereafter labeled as T_[100] and T_[010], respectively. The two configurations are indistinguishable in bulk crystals (due to their “infinite” size) and even in nanocubes (owing to their nearly isotropic shape). However, when dealing with highly anisotropic NPLs, discriminating between them comes within reach.

Figure 4.

(a) Structure–morphology relationship in CsPbBr₃ NPLs with orthorhombic structure resulting in two meaningfully different orientations of the unit-cell (in the Pnma space group) versus the NPLs thickness: T_[100] configuration (thickness parallel to [100] or a_k axis) and T_[010] configuration (thickness parallel to [010] or b_k axis). The disposition of axial (yellow) and equatorial (red) halides of PbBr₆ octahedra versus basal and lateral faces of NPLs are schematically displayed using a single (basal) or a three-monolayers (lateral) arrangement of octahedra; Cs atoms are omitted for sake of clarity. Real NPLs thicknesses consist of six monolayers. Details on surface termination are given in Figure 5. (b, c) Goodness of fit (GoF) 3D surfaces of DSE simulations obtained by spanning the CsPbBr₃ lattice parameters using a grid search algorithm, for the T_[100] and T_[010] configurations, respectively; the surfaces are 3D projections of 4D maps (GoF vs a, b, c axes) at a selected a-value (corresponding to the minimum GoF in each configuration).

Taking the orthorhombic structure of cuboidal CsPbBr₃ NCs in ref (73) as a reference (determined by WAXTS-DSE analysis), atomistic models of NPLs (in the Pnma space group) were obtained, for the two configurations, by stacking layers of PbBr₆ octahedra while preserving the pseudocubic morphology of the exposed facets (as described in the Methods). DSE simulations of six-thick layers NPLs (10 × 10 × 3.5 nm³) and cuboidal NCs of the equivalent volume are compared in Figure S7 to illustrate the major effects of the NPLs morphology on the diffraction pattern. Bragg peaks are shifted in position from the “ideal” ones (i.e., those computed for an isotropic shape) as a consequence of different intensity ratios and widths of the inequivalent reflections hidden below each diffraction peak. T_[100] and T_[010] configurations were then explored against the experimental WAXTS data; bivariate populations of fully stoichiometric models of nanoplates up to eight layers in thickness and with adjustable basal extension were considered. Since Bragg peak positions strictly depend on the lattice parameters, misinterpretation due to wrong unit cell axes rather than morphological effects are possible; thus, we optimized the unit cell parameters through a grid search algorithm, using the statistical goodness of fit [GoF = (χ²)^1/2] indicator to measure the quality of the agreement between experimental data and DSE simulations. The GoF surfaces are shown in Figure 4b and c and were obtained by spanning the a, b, and c axes lengths while fixing the remaining structural and microstructural parameters to preadjusted reasonable values. In terms of size, the best model consisted of six-monolayers-thick NPLs, matching the TEM thickness of 3.5 nm. For the sake of clarity, instead of providing color-encoded 4D maps, we show in Figure 4b and c two GoF hypersurfaces projected at a constant a-value, in the proximity of the absolute minima for the two configurations. From the GoF indicators, we were able to dismiss the T_[010] orientation (Figure 4c, minimum GoF = 1.97), which gave a significantly worse matching with the experimental data if compared to the T_[100] configuration (Figure 4b, minimum GoF = 1.73). The DSE simulation of WAXTS data for this best model configuration is shown in Figure 5a and discussed in greater detail in the next sections. For the sake of completeness, we mention here that the atomistic model providing the fit in Figure 5a also includes slip planes, as much as reported for cuboidal CsPbX₃ NCs (details are given in the Methods), further lowering the GoF value to 1.62.⁷³ Notably, the same structure–morphology relationship has been retrieved on other two independently synthesized CsPbBr₃ samples, as shown in Figure S8; thus, the occurrence of the T_[100] structure-morphology configuration can be considered as an inherent structural feature of CsPbBr₃ NPLs. One of the most relevant structural implications of this finding refers to the structural diversity of the halides exposed at the NPLs surface for the two configurations, as highlighted in Figure 4a: the T_[100] configuration exposes only equatorial Br atoms (red) on the NPLs basal planes, while axial halides (yellow) are exposed in the T_[010] configuration. Additional interesting results are obtained from the analysis of the lattice parameters, as detailed hereafter.

Figure 5.

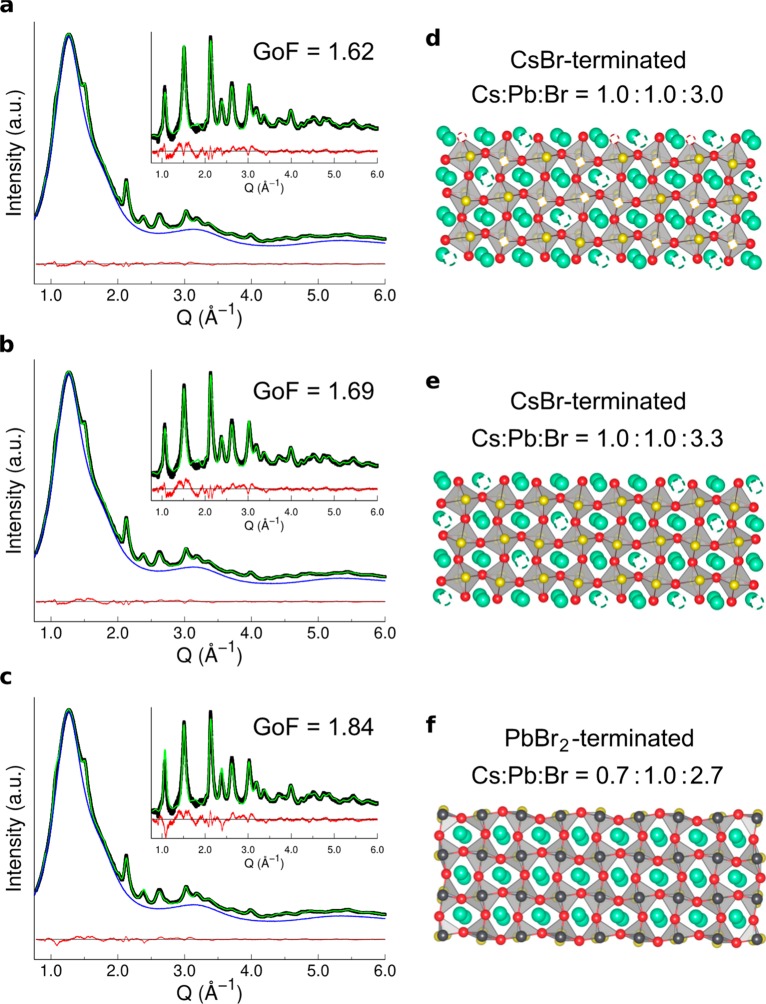
Surface-termination models in 3.5 nm-thick (six-monolayers) CsPbBr₃ NPLs investigated by atomistic models, synchrotron WAXTS data and DSE simulations. (a–c) WAXTS data (black dots) collected on colloidal solutions of the NPLs in toluene (blue trace), (d–f) DSE simulations (green trace) and difference profile (red curve) for the three surface-termination models schematically using a (simplified) three-monolayers sequence of octahedra. Ions color code: Pb (black), axial bromides (yellow), equatorial bromides (red), Cs (green). The white phantom atoms represent the Cs/Br vacant sites at the NPLs surface; the GoF of each simulation is also displayed, for comparison; (d) stoichiometric model of NPLs with CsBr-terminated surface. Cs/Br vacancies at the surface, in half sites for both ions, result in fully stoichiometric NPLs (Cs:Pb:Br = 1.0:1.0:3.0); (e) CsBr-rich model of NPLs with CsBr-terminated surfaces and no Cs/Br vacancies at the surface. This model results in a Cs:Pb:Br = 1.0:1.0:3.3 average molar ratio; (f) PbBr₂-terminated model of NPLs, resulting in a Cs:Pb:Br = 0.7:1.0:2.7 average molar ratio.

Anisotropic Lattice Relaxation

The unit cell parameters of the best T_[100] model are a = 8.31 Å; b = 11.88 Å, c = 8.21 Å. The unit cell volume (V_NPLs = 810.51 ų) exhibits a notable expansion with respect to the powder material (V_pow = 796.7 ų),¹⁰¹ with (V_NPLs – V_pow)/V_pow = 1.74%. Though weaker, a similar effect is also observed in cuboidal CsPbBr₃ NCs investigated through either pair distribution function (V_NCs = 803.13 ų)⁷² or WAXTS-DSE analysis (V_NCs = 802.74 ų); with reference to the latter, (V_NCs – V_pow)/V_pow = 0.76% and (V_NPLs – V_NCs)/V_NCs = 0.97%. Interestingly, the NPLs lattice expansion is not isotropic; if we compare the unit cell axes with those of NCs in ref (73) (in the Pnma setting), the relative changes of 0.33%, 0.64%, and −0.01% along the a, b, and c axes are obtained, respectively (those versus the powder in ref (101) are 0.67%, 1.03%, and 0.03%). The largest expansion is observed in the b axis; since the other axis lying in the basal plane (c) is almost unaffected if compared to that of both cuboid CsPbBr₃ NCs (−0.01%) and bulk (0.03%), a morphological explanation alone does not account for the large expansion. On this side, DFT calculations on MAPbX₃¹⁰² have recently indicated that LHPs exhibit markedly different elastic constants along the three crystallographic directions, the major differences occurring in particular between the axial and equatorial Pb-X directions. Thus, our experimental finding of the largest expansion in the axial direction of the PbBr₆ octahedra (running parallel to the b axis) points to the structural origin of the higher elastic compliance along b, in line with the theoretical prediction.

On the other hand, a non-negligible contribution to the volume expansion is also observed along the a-axis (0.33% vs NCs), which we consider morphologically driven and attribute to the extreme downsizing along the NPLs thickness. Such directional expansion is expected for ionic compounds, due to unsaturated coordination spheres and electrostatic repulsion between ions with the same charges at the surface.¹⁰³

As per the unit cell parameters of the best model in the T_[010] configuration, they are a = 8.42 Å, b = 11.60 Å, and c = 8.29 Å (V_NPLs = 809.70 ų); the b-axis shows a significant contraction in comparison to both CsPbBr₃ NCs (−1.73%) and bulk structure (−1.35%).¹⁰¹ Finding such large contraction along the NPLs thickness further weakens the T_[010] structure–morphology configuration. Therefore, this model not only provided a poorer match against the experimental WAXTS data but also led to rather unphysically strained values of the unit cell parameters.

On the Surface Termination of LHP NPLs Surface

Thus far, the atomistic nature of LHP NPLs and its relationship to the optical properties remain subject of intense research.^{66,74,75,104−108}

In this section, we used the best atomistic and morphological model of NPLs resulting from the previous structure–morphology analysis (Figure 5a) to shed light on the nature and composition of the CsPbBr₃ NPLs surfaces. Three different surface-terminated models were considered: (1) NPLs with CsBr-termination, fully stoichiometric (Figure 5d); (2) NPLs with CsBr-termination and excess of Br (Figure 5e); and (3) NPLs with PbBr₂-termination (Figure 5f). Parallel DSE-based simulations of each of these models are displayed in Figures 5a–c, where also the corresponding GoFs and stoichiometry are given.

Figures 5d shows the best CsPbBr₃ NPLs model obtained from the previous analysis, which was achieved by using CsBr-terminated surfaces and fully stoichiometric composition. Stoichiometric balance of Cs and Br is achieved by removing half of Br sites and half of Cs sites at the NPLs surface or, in other words, by assigning site occupancy factor (s.o.f.) of 0.5 to both ions (at the surface). The GoF value measuring the match of the DSE simulation with the experimental data is 1.62 (Figure 5a). Further relaxation of Cs and Br s.o.f.’s suggested additional slight deficiency of Br ions (sof = 0.3), resulting in nearly stoichiometric Cs:Pb:Br = 1.0:1.0:2.9) NPLs, but did not provide significant improvement of the original Gof value (1.61). Therefore, if a small deficiency of Br is considered, this would only slightly increase Br vacant sites at the surface. Indeed, a similar finding has been recently retrieved by Nenon et al.¹⁰⁷ from XPS measurements on CsPbBr₃ NCs. Additionally, a bromide-deficient surface was found to be nondetrimental for the PLQY of LHPs, introducing only shallow defects levels within the bandgap, while a Pb-rich surface would determine the formation of deep trap states.¹⁰⁷

Starting from the previous CsBr-termination model, we also explored the formation of a Br-rich surface (despite the indication of additional vacancies from the previous relaxation test), which is supported by recent experimental spectroscopic evidence¹⁰⁹ and theoretical calculations on LHP NCs.¹⁰⁴ The model is obtained by considering the Br sites at the NPLs surface as fully occupied (Figure 5e); it resulted in the average Cs:Pb:Br = 1.0:1.0:3.3 stoichiometry and provided a slight worse agreement with the experimental WAXTS data (GoF = 1.69, Figure5b). For a sake of completeness, an even worse agreement (GoF = 1.85) is obtained if also Cs vacancies at the surface are removed (leading to a Cs:Pb:Br = 1.3:1.0:3.3 stoichiometry).

Finally, we tested a PbBr₂-terminated model, pointing to an excess of Pb ions at the surface), as shown in Figure 5e. This model is consistent with a Cs:Pb:Br = 0.7:1.0:2.7 stoichiometry of the NPLs and provided a poor agreement with the experimental WAXTS data (GoF = 1.84). Accordingly, the results shown in Figure 5 suggest that our CsPbBr₃ NPLs exhibit CsBr surface termination with half Cs and half (or slightly more) Br sites vacant.

Conclusions

In this work, we have presented the synthesis of six-monolayers-thick CsPbBr₃ NPLs and their fast anion exchange reactions, which makes it possible to tune their emission properties in the whole visible region, from 398 to 632 nm. High ensemble uniformity allows the study of the atomistic structure of NPLs using reciprocal space X-ray total scattering methods.

By combining HRTEM information on the pseudocubic NPLs faceting, atomistic models of NPLs and the DSE approach of analysis, these NPLs are 3.5 nm thick (six monolayers of PbBr₆ octahedra) and exhibit a defined orientation of the underlying orthorhombic lattice with respect to the NPL facets. Specifically, the large basal facets of the NPLs belong to {101} planes of the orthorhombic CsPbBr₃ lattice (Pnma space group), whereas the side facets are of both kinds: {101} and {010}. Future studies shall concern the question as to why the NPLs form in the first place. All six NPL facets are atomistically nearly identical, explaining the common cuboid morphology of CsPbBr₃ NCs, not the NPLs. One possibility had been recently discussed by Norris et al. for another highly isotropic material–zinc-blende CdSe nanoplatelets exposing a set of identical {001} planes as both side and basal facets.¹¹⁰ The model showing the NPL-thickness-dependent kinetic instability was proposed to explain the formation of NPLs within a certain thickness range.

The lattice parameters show anisotropic relaxation along the three (nonequivalent) crystallographic directions, if compared to cuboidal LHP NCs, suggesting a directional (structurally driven) response of CsPbBr₃ to external (ligand or morphology induced) stress, leading to a major deformation in the axial direction of PbBr₆ octahedra. A plausible atomistic description of LHP NPLs surface termination was deduced as well, suggesting CsBr-terminated surfaces with Cs and Br vacancies in nearly stoichiometric proportion.

On a methodological site, this work demonstrates (1) the capability of the DSE method of unveiling relevant subtle structural features of LHP NPLs, to the same extent as previously attained for the defectiveness of cuboidal LHP NCs⁷³ and (2) the great potential of the concerted use of HRTEM and DSE-based X-ray scattering techniques, particularly useful for investigating this extremely important class of materials.

Methods

Materials and Chemicals

Cesium carbonate (Cs₂CO₃, Aldrich, 99.9%), oleic acid (OA, Sigma-Aldrich, 90%), 1-octadecene (ODE, Sigma-Aldrich, 90%), oleylamine (OLA, Acros Organics, 80–90%), lead bromide (PbBr₂, ABCR, 98%), mesitylene (Aldrich, 97%), diphyl (Dowtherm@A, eutectic mixture of 26.5% diphenyl +73.5% diphenyl oxide, Aldrich), ethanol (EtOH, Aldrich, ≥ 99.8%, GC), hydrochloric acid (HCl, Aldrich, ≥ 37%), hydroiodic acid (HI, Aldrich, 57%), toluene (Fischer Scientific, HPLC grade), hexane (Sigma-Aldrich, ≥ 95%), poly(methyl methacrylate). All materials were used without any further purification.

Preparation of Cs-Oleate

Cs₂CO₃ (0.4075 g, Aldrich, 99.9%), OA (1.25 mL, Sigma-Aldrich, 90%), and ODE (20 mL, Sigma-Aldrich, 90%) were added into a 50 mL 3-neck flask, dried for 1 h at 120 °C. Since Cs-oleate precipitates out of ODE at room-temperature, it must be preheated to 100 °C before injection.

Preparation of Oleylammonium Halides (OAmX)

Ethanol (100 mL, Aldrich) and OLA (0.038 mol, Acros Organics 80–90%) were combined in a 250 mL 2-neck flask and vigorously stirred. The reaction mixture was cooled in an ice-water bath, and HX (0.076 mol, HCl ≥ 37%, Aldrich; HI 57%, Aldrich) was added. The reaction mixture was left to react overnight under N₂ flow. The solvent was then evaporated under vacuum, and the obtained product was purified by rinsing multiple times with diethyl ether. The product was left under vacuum overnight in a vacuum oven at 80 °C resulting in a white powder.

Synthesis of CsPbX₃ NPLs

For this, 138 mg of PbBr₂, 1 mL of dried OA, and 1 mL of dried OAm were loaded into a 25 mL 3-neck flask in the glovebox. Mesitylene (5 mL) was added to the reaction mixture, and the flask was connected to the Schlenk line. The entire system was flushed three times at room temperature by quickly changing from vacuum to N₂ and left on N₂. The reaction mixture was heated up to 115 °C, and Cs-oleate (0.8 mL of a stock solution prepared as described above) was swiftly injected. In the next second from the injection, the flask was immersed in a ice-water bath to stop the reaction. After the reaction, 1 mL of crude solution was centrifuged for 3 min at 5000 rpm. The resulted precipitate was dispersed in 1 mL toluene, centrifuged again for 10 min at a maximum speed of centrifuge (13400 rpm), and, after this, the supernatant was filtrated and used further for different experiments. The typical concentration of the 492 nm emissive NPLs was about 8–10 mg/mL.

Anion-Exchange Reactions

The anion exchange reactions were conducted in air at room temperature. Then 0.2 mL of CsPbBr3 NPLs in toluene (5 mg/mL) was added in a vial, and different volumes of a solution of OAmX (X = Cl, I) 1.5 mM in toluene were added to obtain different mixed halide compositions with PL emission at different wavelengths. The anion exchange reactions are summarized in Table S1.

Characterization of CsPbX₃ NPLs

Absorbance

UV–vis absorption spectra were collected using a Jasco V670 spectrometer in transmission mode.

Photoluminescence (PL)

PL emission spectra from solutions and films were recorded by using Fluorolog iHR 320 Horiba Jobin Yvon spectrofluorimeter equipped with a PMT detector.

PL Quantum Yields (QYs) in Films

The absolute value of the PL QY was measured at room temperature on a Quantaurus QY (C11347–11, Hamamatsu) equipped with an integrating sphere.

Transmission Electron Microscopy (TEM)

TEM images were recorded using a Philips CM 12 and Hitachi HT7700 EXALENS microscope operated at 100 kV (for low-resolution TEM) and a JEOL JEM-2200FS microscope operated at 200 kV (for high-resolution TEM).

Laboratory X-ray Diffraction Measurements

Powder X-ray diffraction (XRD) patterns were collected with a STOE STADI P powder diffractometer, operating in transmission mode. A Ge(111) monochromator, Cu Kα1 radiation (λ = 1.54056 Å) and Dectris MYTHEN 1K silicon strip detector were used.

Synchrotron Wide Angle Total Scattering Experiments (WAXTS)

WAXTS measurements on CsPbBr₃ NPLs (three CsPbBr₃ samples) were performed at the X04SA-MS beamline¹¹¹ of the Swiss Light Source (Paul Scherrer Institute, Villigen, CH) on colloidal suspensions in toluene loaded in 0.8 mm-diameter certified glass capillaries (Hilgenberg GmbH G50). The operational beam energies were set at 22 keV (λ = 0.565483 and 0.565666 Å) and precisely determined using a-Si powder standard (NIST 640d, a₀ = 0.543123(8) Å nm at 22.5 °C). Total scattering data from the samples were collected in the 0.02–19 Å^–1Q-range using a single-photon counting silicon microstrip detector (MYTHEN II),¹¹² together with the X-ray pattern of the empty glass capillary and the sample environment (He/air), subtracted from the pattern of the samples. The transmitted beam intensities from the filled capillaries were independently measured to estimate the samples absorption coefficients, while the computed X-ray attenuation factors from the nominal glass composition were used for the empty capillary. Angular dependent intensities corrections to the raw data were applied, using an X-ray tracing approach.¹¹³ The inelastic Compton scattering signal was added as an additional model component during the data analysis. For the DSE-model refinements, the 0.6–16 Å^–1Q-range was used.

DSE Method

The DSE provides the average differential cross-section of a randomly oriented powder from the distribution of interatomic distances between atomic pairs, within the sample:^88,114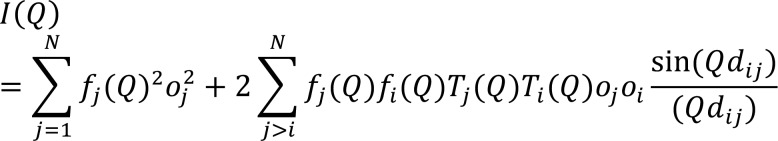where Q = 2πq, q = 2 sin θ/λ is the magnitude of the scattering vector, λ is the radiation wavelength, f_i is the X-ray atomic form factor of an element i, d_ij is the interatomic distance between atoms i and j, N is the total number of atoms, and T and o are the thermal atomic displacement parameter and the site occupancy factor associated with each atomic species, respectively.

Using locally developed routines, bivariate populations of atomistic models of NCs with two independent growth directions were generated; for each structural model, the first growth direction was chosen parallel to the NPLs basal plane and the second along an axis normal to it, describing the NPLs basal plane and thickness, respectively.

Each NC within the population is built by generating a framework of lattice nodes enclosed within a geometrical surface and by convoluting each node with the Patterson vectors within the chosen building block. To obtain the pseudocubic morphology described in the main text, a B-centered supercell based on the a_B = a_P+c_P, b_B = b_P, c_B = −a_P + c_P transformation of the primitive (P) original setting, was used. This provides four faces of the {101} type and two {010}, in the Pnma setting. Needless to say, the different T_[100] and T_[010] models require indices and axes permutations.

Each population built in this way includes all possible combinations of bases (or their equivalent diameters) and heights; the step between two consecutive clusters, along the first growth direction (NPLs basal plane), is the diameter of the circle of area equivalent to the unit cell-base; one monolayer of PbBr₆ octahedra (i.e., half of the orthorhombic unit cell parameter) was chosen as step along the thickness, and an appropriate model construction (alternating two different types of building blocks, made of one PbBr₆ monolayer each) was used. All six facets of CsPbBr3 NPLs were completely terminated with CsBr moieties, and, afterward, 50% of both Br^– and Cs⁺ surface ions have been randomly removed to ensure the charge neutrality (average model stoichiometry: Cs:Pb:Br = 1.00:1.00:3.00).

The interatomic distances of these clusters are then computed, sampled (according to a Gaussian sampling strategy, to reduce the computational times),¹¹⁵ and used to compute the model DSE, using the Debussy Program Suite.⁸⁸

First, a grid search algorithm has been employed to optimize the lattice parameters of the two NPLs morphologies (T_[100] and T_[010]) and to find the best model, matching the experimental CsPbBr₃ WAXTS data.

Once the minimum of each model has been selected, the Simplex algorithm¹¹⁶ was used to optimize the initial microstructural model parameters against the experimental data. Information from HRTEM and PL emission was used to constrain the mean value of the log-normal size distributions along the two growth directions, which are rather unstable parameters in the presence of highly defective materials, as in this case. To improve the quality of the fits and to cope with the HRTEM and PL experimental thickness, slip planes were added to the orthorhombic models of NPLs, according to the rule: 1/4 < 011>{011} (in the T_[100] setting). Further details can be found in ref (73). The DSE results suggested a final percentage of defects in the CsPbBr₃ populations of NPLs of 30%. The best fits and optimized size distributions for the minima of the T_[100] and T_[010] models are shown in Figure S9 and S10, respectively.

Starting from the refined parameters obtained for the T_[100] model, three other models with the same structure–morphology orientation, but different surfaces termination were tested: a CsBr-rich model (average molar ratio Cs:Pb:Br = 1.3:1.0:3.3), a Br-rich model (average molar ratio Cs:Pb:Br = 1.0:1.0:3.3, best fit and model shown in Figure 5b,e) and a PbBr2–terminated one (average molar ratio Cs:Pb:Br = 0.7:1.0:2.7, best fit and model shown in Figure 5c,f). These three models, however, performed poorly against the experimental WAXS data, as detailed in the pertinent paragraph of the main text.

Code Availability

The DebUsSy program suite is freely available at http://debussy.sourceforge.net.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.9b07626.

• CsPbBr₃ NPLs synthesis and PL properties, DSE-based modeling results (PDF)

Author Contributions

^# F.B. and G.N. contributed equally.

The authors declare no competing financial interest.