DISOselect: Disorder predictor selection at the protein level

Abstract

The intense interest in the intrinsically disordered proteins in the life science community, together with the remarkable advancements in predictive technologies, have given rise to the development of a large number of computational predictors of intrinsic disorder from protein sequence. While the growing number of predictors is a positive trend, we have observed a considerable difference in predictive quality among predictors for individual proteins. Furthermore, variable predictor performance is often inconsistent between predictors for different proteins, and the predictor that shows the best predictive performance depends on the unique properties of each protein sequence. We propose a computational approach, DISOselect, to estimate the predictive performance of 12 selected predictors for individual proteins based on their unique sequence‐derived properties. This estimation informs the users about the expected predictive quality for a selected disorder predictor and can be used to recommend methods that are likely to provide the best quality predictions. Our solution does not depend on the results of any disorder predictor; the estimations are made based solely on the protein sequence. Our solution significantly improves predictive performance, as judged with a test set of 1,000 proteins, when compared to other alternatives. We have empirically shown that by using the recommended methods the overall predictive performance for a given set of proteins can be improved by a statistically significant margin. DISOselect is freely available for non‐commercial users through the webserver at http://biomine.cs.vcu.edu/servers/DISOselect/.

1. INTRODUCTION

Biologically functional proteins without stable structures, known as intrinsically disordered proteins (IDPs), have been a reported phenomenon for the past few decades. IDPs have challenged the long held fundamental paradigm of the prerequisite of structure for protein function.1 IDPs and intrinsically disordered regions (IDRs) are defined as proteins or regions of protein that lack of stable tertiary structure in isolation and that form an ensemble of conformations.2, 3 IDPs associate with a number of essential biochemical activities regardless of their inability to exist in stabilized secondary or tertiary structures under conventional physiochemical conditions.3, 4, 5, 6 They contribute to signaling and regulation7, 8 and are particularly prevalent among the proteins that interact with nucleic acids.9, 10, 11, 12, 13, 14, 15 Computational studies suggest that IDPs and proteins with IDRs are widespread not only over the proteomes of all three kingdoms of life but also in viral proteomes.16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 At the same time, it has been discovered that length and abundance for IDRs and IDRs increase with complexity of the given organisms.17, 19

Experimental characterizations of IDPs2 are collected as annotations in several community databases, such as DisProt,27 MobiDB,28 and IDEAL.29 Unfortunately, the rate of accumulation of experimental data of IDPs lags far behind the rate at which new sequences are discovered; DisProt and IDEAL account for 80327 and 91329 proteins, respectively. The lack of intrinsic disorder annotations is compounded by the lack of effective homology‐based techniques analogous to those used for the structured proteins, which prevents directly leveraging existing annotations. One solution to this dearth of IDP data is use of existing annotations to build predictors that can distinguish ordered/structured from disordered regions based on a protein sequence and apply these models to unannotated proteins. This solution has been extremely successful; more than 60 predictors have been developed over the last few decades30, 31, 32, 33, 34, 35, 36 and many show high accuracy in blind, community assessments.37, 38 Intrinsic disorder predictors have a wide range of applications: from focused application for structural characterization of a few proteins, for example, References 39, 40, 41, to broad association studies, for example, References 5, 15, 17, 19, 42, 43. These research activities depend strongly on the reliability and accuracy of prediction methods, which has encouraged the continual development of improved predictors.

Intrinsic disorder predictors have been created from a wide variety of architectures and data sets, and many of them display exceptional performance on benchmark data sets.32, 36, 38, 44, 45, 46, 47 They can be categorized into three broad categories based on their underlying model for prediction35, 48: (a) ab initio methods, such as Globplot,49 IUPred50 and NORSp,51 are based on the physiochemical characteristics of proteins; (b) machine learning methods, such as DISOPRED,52, 53 DisEMBL,54 VSL2B,55 SPOT‐Disorder,56 and others,57, 58, 59, 60, 61, 62 are trained on experimental annotations using a variety of machine learning algorithms and (c) meta methods, such as ESpritz,63 MFDp,64, 65, 66 DISOPRED3,67 and others,33, 68, 69, 70, 71, 72, 73 combine multiple individual predictors and balance their strengths and weaknesses. The relative performance of intrinsic disorder predictors has been compared many times in surveys and community assessments, for example, References 32, 36, 38, 44, 45, 46, 47, 74, 75, 76. These comparisons are based on independently constructed data sets from which benchmark statistics are calculated. A common metric for predictor performance is the area under the receiver operating characteristic curve (AUC) value, which ranges from 1.0 for perfect prediction and 0.5 for random prediction. Top preforming methods in some recent assessments achieve AUCs of 0.81,46 0.89,76 and 0.91.38

A common feature of surveys and benchmark assessments is the aggregation of results across a data set with many proteins. This practice provides a single metric for each predictor that can unambiguously compare performance of several predictors. However, this contrasts with the mode in which predictors are used in practice, where predictions are used to study individual proteins or regions of proteins.77 In preliminary studies presented here, we have found that per‐protein performance varies widely from protein to protein for all predictors tested. This observation suggests that data set‐level benchmark performance evaluations are not an appropriate basis for selecting a prediction method for a specific protein. This practical problem has led us to design a novel tool, DISOselect, which estimates per‐protein performance for a range of different intrinsic disorder predictors.

DISOselect is designed to estimate AUC performance for 12 disorder predictors when applied to a specific protein sequence. The selected 12 disorder predictors uniformly cover the three categories of methods and were selected based on their computational efficiency, availability in the biggest disorder databases, MobiDB,28 and favorable predictive performance46, 56, 67; details are provided in Section 4.2. DISOselect does not require the output of individual predictors, instead it considers only the protein sequence and properties of the protein sequence to estimate the AUC performance of a given disorder predictor. With estimates of AUC values for each of the 12 predictors, DISOselect suggests the predictor that is likely to have the highest performance for a given input protein. DISOselect is freely available online as a user‐friendly web application, at http://biomine.cs.vcu.edu/servers/DISOselect/.

2. RESULTS AND DISCUSSION

2.1. Variability in per‐protein disorder predictor performance

We used the AUC measure, the most often used measure of the predictive quality of disorder predictors,32, 36, 38, 44, 46, 47, 74, 75, 78, 79 to quantify performance. We calculated the AUC values for each of the 12 predictors and for each protein in our training data set with at least four ordered and disordered residues. The minimum was imposed for a valid AUC calculation. Performance of predictors varies widely from protein to protein in our data set (Figure 1). All predictors, except GlobPlot, have a peak of highly accurately predicted proteins and a long tail of proteins predicted with poorer accuracy. The weight of this tail generally correlates with the benchmark (data set‐level) performance accuracy of the predictor; better benchmark accuracy implies fewer poorly predicted proteins. For instance, DISOPRED3 that has high data set‐level AUC (reported to equal 0.90 in38) has a smaller tail than the VSL2B that has lower data set‐level AUC (reported to be 0.82 in46). However, we note that AUC values for individual proteins vary widely from the data set‐level values. For instance, for VSL2B that has the data set‐level AUC = 0.82, Figure 1 reveals that 59.2% proteins have AUCs >0.9 while 9.3% of proteins are predicted with AUCs <0.6. Similarly, for DISOPRED3 that has the data set‐level AUC = 0.90, 9.5% of proteins are predicted with AUCs <0.8 while 68.5% have AUCs >0.95. This analysis is in agreement with the recent study on the quality of the protein‐level disorder predictions,77 and contrasts with a direct view of data set‐level predictor performance, which leads users to believe that any given protein prediction will match the benchmark accuracy. This also demonstrates the usefulness of a tool that can estimate per‐protein accuracy for an individual protein, and, if errors between prediction methods are not correlated, suggests that an optimal predictor can be selected on a per‐protein basis.

Figure 1.

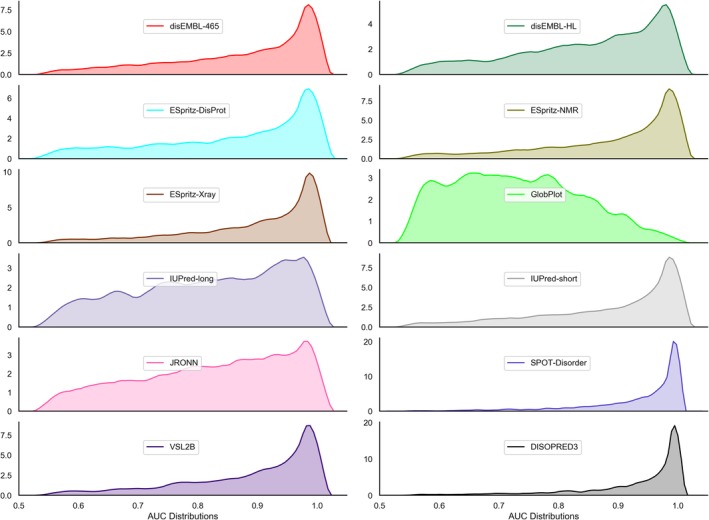
Distribution of per‐protein AUC values 12 disorder predictors. The computation was performed for the proteins in the training data set

2.2. Predictive performance of the DISOselect model

To estimate performance of each of the selected 12 disorder predictors for arbitrary proteins, we designed DISOselect using a three layered architecture (see Materials and Methods for details): (a) feature extraction, (b) extra‐tree regressor model and (c) empirical mapping from model output to AUC values. This architecture was applied to each of the 12 disorder predictors separately, using our set of experimentally annotated proteins from the training data set. Features were selected from 130 possible features generated from the input protein sequences to tailor the models for specific disorder predictors. Considered features are divided into five distinct categories: amino acid (AA) composition, secondary structure predicted from sequence, solvent accessibility predicted from sequence, sequence complexity calculated from sequence, and physicochemical properties (Table S1). The 12 sets of empirically selected features were used to train 12 different extra‐tree regressor models using cross validation over the training data set. Extra‐tree regressor models were selected based on empirical cross validation tests on the training data set over several other model types (Table S2). The outputs of the extra‐tree regressor models were mapped to AUC values using an empirical lookup table based on predicted and target AUC values in the training data set.

The performance of DISOselect was evaluated on the independent test data set (Table 1) by comparison to two controls: (a) random control, where the AUC values are taken from a randomly chosen protein in the training data set, (b) similarity‐based control, which uses AUC values taken from the most sequence similar protein in the training data set. The similarity was computed using the BLAST algorithm using its default parameters.80, 81 The random control represents the base prediction accuracy and similarity‐based control represent a homology‐based prediction of the predictor performance. We note that the test data set was designed to share low, <25%, similarity with the proteins in the training data set. These three sets of predictions—model, random control, and similarity‐based control—were evaluated by two measures (Table 1): (a) mean squared error (MSE) of estimated AUCs and (b) correlation between estimated AUCs and actual AUCs. The best performing of the two control methods, random or similarity‐based, was used to calculate the ratio of improvement between our architecture's performance and controls.

Table 1.

Performance of DISOselect for each of the 12 selected disorder predictors

Disorder predictor	MSE (mean squared error)				PCC (Pearson correlation coefficient)
	DISOselect	Random control	Similarity‐based control	Improvement ratio	DISOselect	Random control	Similarity‐based control	Improvement ratio
disEMBL‐HL	0.009	0.05 [+]	0.05 [+]	5.6	0.36	0.01 [+]	0.13 [+]	2.8
IUPred‐long	0.011	0.05 [+]	0.04 [+]	3.6	0.32	−0.01 [+]	0.18 [+]	1.8
IUPred‐short	0.011	0.05 [+]	0.05 [+]	4.6	0.32	0.03 [+]	0.07 [+]	4.6
VSL2B	0.008	0.05 [+]	0.05 [+]	6.3	0.31	0.03 [+]	0.14 [+]	2.2
disEMBL‐465	0.008	0.05 [+]	0.05 [+]	6.3	0.30	−0.03 [+]	0.14 [+]	2.1
GlobPlot	0.011	0.05 [+]	0.05 [+]	4.6	0.28	−0.13 [+]	0.09 [+]	3.1
ESpritz‐NMR	0.009	0.05 [+]	0.05 [+]	5.6	0.28	0.02 [+]	0.08 [+]	3.5
SPOT‐disorder	0.010	0.05 [+]	0.04 [+]	4.0	0.24	0.00 [+]	0.00 [+]	48.0
DISOPRED3	0.004	0.04 [+]	0.05 [+]	12.5	0.24	−0.11 [+]	0.15 [+]	1.6
ESpritz‐Xray	0.007	0.05 [+]	0.05 [+]	7.1	0.23	−0.08 [+]	0.03 [+]	7.7
JRONN	0.008	0.05 [+]	0.06 [+]	7.5	0.19	−0.01 [+]	0.00 [+]	190.0
ESpritz‐DisProt	0.007	0.05 [+]	0.04 [+]	5.7	0.12	0.00 [+]	0.05 [+]	2.4

Note: MSE and Pearson correlation coefficients (PCC) values are calculated between the estimated AUC and the actual AUC of each proteins. Control estimates of AUCs were taken from randomly picked proteins and proteins selected based on sequence similarity. Paired significance tests were performed between the DISOselect estimated AUCs and the control AUCs: [+] denotes that our model is significantly better with p‐value <.05. We used the paired t test for normal measurements and the Wilcoxon test otherwise; normality was tested with the Anderson‐Darling test at the .05 significance.

For all 12 selected predictors, the estimated AUCs generated by DISOselect are found to perform well (Table 1). Paired comparison of DISOselect's AUCs to controls shows that our tool significantly outperforms both controls for MSE‐based comparison (p‐value < .05) and correlation‐based comparison (p‐value < .05). While the raw MSE values and correlation values show modest performance, their ratios of improvement to control values show large magnitudes of the improvements. MSE evaluations of the predictions are between fourfolds and 12.5‐folds better than the best control, while correlation values are between 1.6‐folds and 7.7‐folds better than the controls. Overall, these results demonstrate that our extra‐tree regressors provide an accurate estimation of the protein‐level AUC for the 12 disorder predictors.

2.3. Analysis of the DISOselect model

We next investigated which protein features contribute to the estimation of AUCs by the DISOselect predictor. The contribution of protein features to AUC estimation was interrogated in two different ways: (a) by quantifying importance for the five categories of features (AA composition, predicted secondary structure, predicted solvent accessibility, sequence complexity, and physicochemical properties) in the extra‐tree regression models; and (b) by examining the highest ranking selected features. This two‐part analysis dissects architecture at both the first layer, feature selection, and the second layer, extra‐tree regression. It also gives two levels of feature granularity; at a coarse level, over the five feature categories, and at a fine level, over the individual features.

The feature importance was quantified with information gain, which measures decrease in the classification entropy due to the use of a given feature82 and is used to compute and optimize the extra‐tree regressor models. Examination of the contribution across the five feature categories shows a largely consistent role for each of the 12 models (Figure 2). Our analysis shows that each of the five feature categories contributes to AUC estimates; however, the degree of these contributions varies substantially. Putative secondary structure is consistently (across all 12 models) the largest contributor to our models. It is not surprising to see a close relationship between predicted local structural propensities and accuracy of disorder prediction. Disorder in the proteins with high content of the secondary structures (i.e., helices and strands) is likely harder to predict, while disorder in the proteins largely or entirely composed of coils should be easier to predict. The strong contribution of the putative secondary structure echoes its use as predictive input for many disorder predictors, such as MFDp64 MFDp2,65, 66 CSpritz,70 and Spritz,83 to name a few. The next two most important feature categories are physicochemical properties and AA composition, which are the second and third most important, depending on the predictor. These two categories are closely linked; as physicochemical properties are calculated from AA scales, they are functionally linear combinations of the composition. This reveals some bias in predictive performance in predictors for proteins with certain properties, likely related to the details of their training sets. The least contributing features are sequence complexity and solvent accessibility. While these parameters are correlated with intrinsic disorder,84, 85 they do not have a large contribution to differential predictor performance in general.

Figure 2.

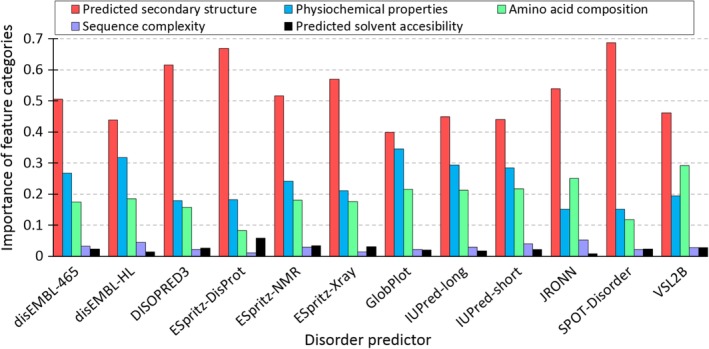
Importance the five feature categories for the DISOselect's models designed for the 12 disorder predictors. We used a three‐step process to derive the scores for each model. First, the information gain of individual features was calculated from the extra‐tree regressors. Second, features were divided into the five classes and the information gain of the features in the same category was summed up. Third, the summed values were dived by the sum of the information gain values of all features in the same model. The last step allow for directly comparison of relative contributions of each feature category

To examine specific features that contribute to the DISOselect's models, the top two features during feature selection were compiled along with their correlations to the actual AUC for each disorder predictor (Figure 3); we used this correlation to select features. The resulting feature list has 18 features, rather than 2 × 12 = 24, indicating that only a few top features are shared between multiple disorder predictors. Figure 3 reveals that the predominant features that govern the prediction for individual models are virtually exclusive to the corresponding model (dark green shading), although multiple other features contribute to the prediction in a less substantial way (light green and white shading). As expected, the predominant features primarily focus on the most important feature categories summarized in Figure 2, including putative secondary structure and physicochemical properties of AAs. A notable exception is the average accessible surface (ASA) area, which is relatively highly correlated with three disorder predictors. However, ASA is positively correlated with SPOT‐Disorder and DISOPRED3 performance, but negatively correlated with ESpritz‐DisProt performance. This reflects the general trend that no single property is consistently positively or negatively correlated with performance across multiple disorder predictors, suggesting that each disorder predictor has its own predictive bias. Individual performance biases likely reflect the makeup of the training sets and the selection of the sequence‐derived predictive inputs utilized by individual predictors.

Figure 3.

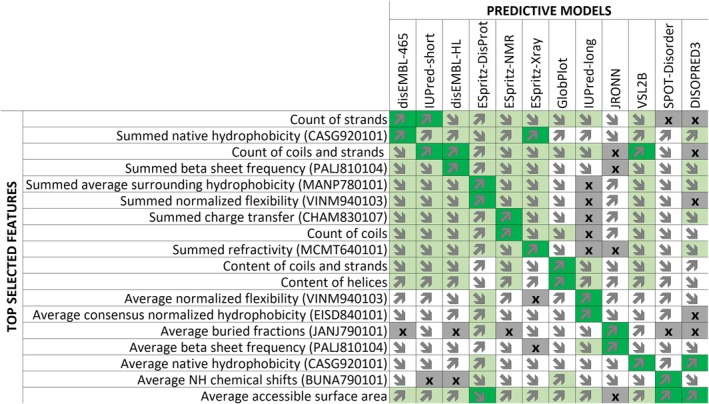
Key features used in the 12 models. The performance of individual features is quantified with the Pearson correlation coefficients (PCC) between feature values (rows) and the actual area under the receiver operating characteristic curve (AUC) for each model (columns) that were quantified on the training data set. Detailed explanation of features is available in the Table S1. PCC values are color‐coded where dark green is for |PCC| ≥ 0.3, light green for |PCC| between 0.15 and 0.30, white for |PCC| < 0.15, and gray with “x” symbol indicate the a given feature is not included in the model for that predictor. The direction of arrows reveals the sign of PCC where upwards arrows denote positive correlation while downward arrows denote negative correlation

To sum up, our analysis reveals that the estimates of the protein‐level predictive performance generated by DISOselect are primarily driven by the information extracted from the putative secondary structure, physicochemical properties and AA composition of the input protein chain. Moreover, models for individual disorder predictors are very different as they rely on largely exclusive sets of dominant predictive features. This result suggests that a particular protein, with a particular set of features, may be better predicted by some disorder predictors than others in a systematic way.

2.4. Selection of accurately predicted proteins using DISOselect

We evaluated whether the AUC values estimated by DISOselect for a specific disorder predictor can be used to accurately identify proteins that are poorly vs. well predicted by that particular method. We compared the actual AUCs of the test proteins with progressively higher values of the estimated AUCs for each of the 12 disorder predictors (Figure 4). First, we sorted all proteins by their estimated AUC values for a given disorder predictor in the ascending order. Next, we removed 5% of the test proteins with the lowest putative AUCs and evaluated the actual AUC for the remaining 95% of the test proteins for that disorder predictor. We incrementally reduced this data set by the next 5% of the sorted proteins (all the way until we ended up with the 5% of the proteins with the highest putative AUCs) to assess whether the proteins with higher estimated AUCs in fact secure higher actual AUCs. The upward trends shown in Figure 4 demonstrate that the proteins with higher estimated AUC values in fact obtain higher data set‐level AUCs. This result is consistent across all 12 disorder predictors. The differences in the actual AUC values between the results on the test data set (left‐most points in Figure 4) and the smallest set of the 5% of proteins with the highest estimated AUCs are very substantial. For instance, for DISOPRED3, the 5% of proteins with the best estimated AUCs secure AUC = 0.950 when compared to AUC = 0.918 on the test data sets, which translates to (0.950–0.918)/(1–0.918) = 39% error reduction. The largest absolute increase in AUC is for disEMBL‐HL where the 5% of the best predicted proteins secure AUC = 0.896 compared to the AUC = 0.761 on the whole test data set, which corresponds to (0.896–0.761)/(1–0.761) = 56% error reduction.

Figure 4.

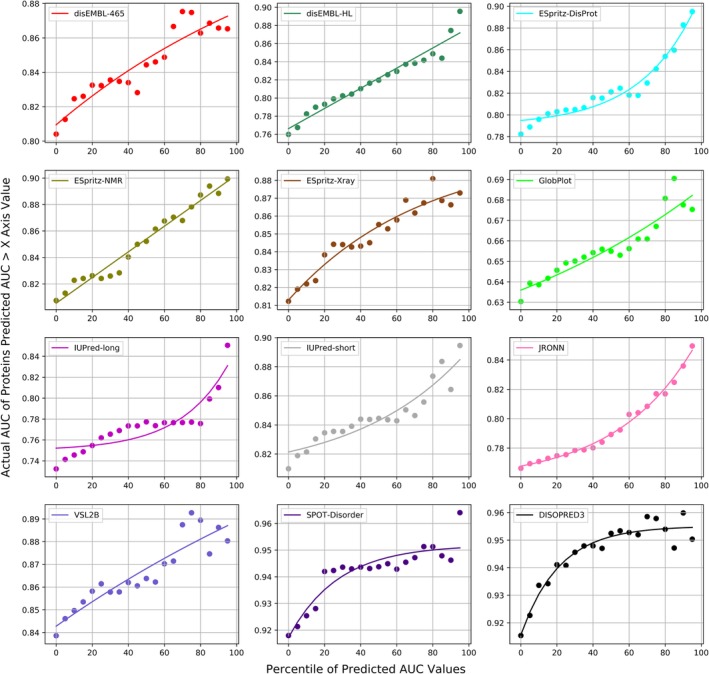
The data set‐level actual area under the receiver operating characteristic curve (AUC) values for subsets of the test proteins that are sorted based on their AUCs values estimated by DISOselect. Individual panels correspond to different disorder predictors. Points in each panel correspond to AUCs of the subsets of test proteins for which the estimated AUCs are above a given percentile of all estimated AUCs, that is, the 20 mark on the x‐axis corresponds to the 80% of the test proteins that have estimated AUCs that are above the 20th percentile of estimated AUCs generated by DISOselect. The left‐most point corresponds to the result on the complete test data set while the right‐most point corresponds to the 5% of test proteins with the highest estimated AUCs. The line is the third‐degree polynomial fit into the measured data

Figure 5 summarizes the above results by comparing AUCs between the complete test data set and the top 25% (in green), top 50% (in orange) and top 75% (in blue) of the proteins selected based on the AUCs predicted by DISOselect. The box plots represent the distribution of these differences across the 12 disorder predictors, where whiskers correspond to the minimal and maximal improvements and the boxes delineate the first, second and third quartiles. The positive values of the differences indicate that AUCs for given subsets of the test proteins are higher than for the complete test data set. The corresponding numeric values together with the results of the significance tests that compare the AUCs on the whole test data sets against the AUCs for each of the three subsets are provided in the Table S3. Figure 5 reveals that the proteins selected based on the favourable estimates from DISOselect secure AUCs that are consistently higher (over each of the 12 disorder predictors) when compared to the results on the whole test data set; this can be deduced from the fact that the minimal improvements in Figure 5 are always positive (lower whiskers point to values >0). On average (across the 12 disorder predictors) the 25% of proteins with the highest putative AUCs generated by DISOselect secure AUCs that are over 0.05 higher than the corresponding AUCs on the complete test data set. Table S3 demonstrates that the improvements in the AUCs values for the proteins selected with assistance of DISOselect are statistically significant (p‐value < .01) for each of the 12 disorder predictors. In the nutshell, our analysis provides compelling support for the claim that DISOselect accurately estimates AUCs that allow for the selection of proteins that are well‐predicted by a wide range of different disorder predictors.

Figure 5.

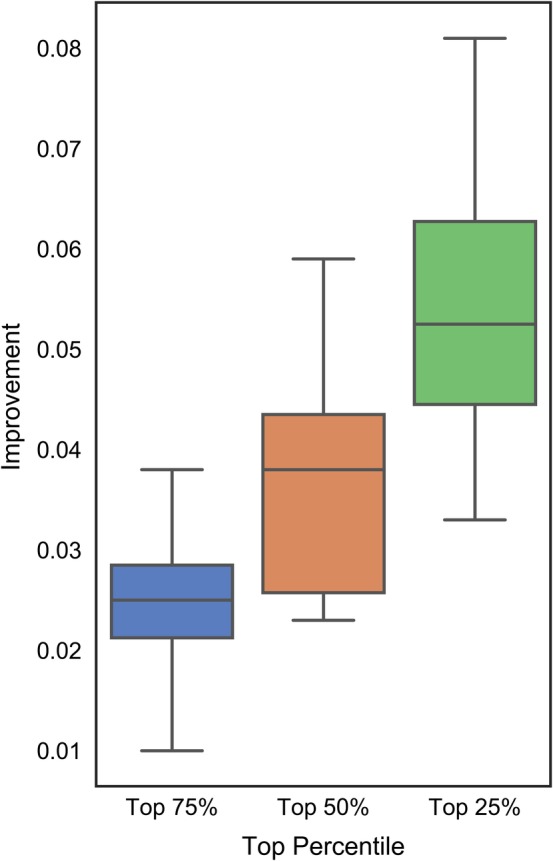
Improvements in the actual area under the receiver operating characteristic curve (AUC) values computed as the difference between the AUC for subsets of the top 25% (in green), 50% (in orange) and 75% (in blue) of the test proteins selected based on their AUCs values estimated by DISOselect and the data set‐level AUC. Positive values of the improvement indicate that AUC for the subsets of the test proteins are higher than for the complete test data set. The box plots represent the distribution of the improvements across the 12 disorder predictors where whiskers corresponding to the minimal and maximal improvements and boxes denote the first, second and third quartiles

2.5. Application of DISOselect to recommend accurate disorder predictor

The section “Selection of accurately predicted proteins using DISOselect” shows that DISOselect accurately identifies well‐predicted proteins for each of the 12 disorder predictors. Here, we investigated whether these 12 results can be used jointly to recommend a disorder predictor that produces accurate results for a given protein sequence; in other words, whether DISOselect can be used to accurately recommend a well‐performing disorder predictor. To explore that we used the disorder prediction from the method that has the highest AUC estimated by DISOselect and we compared these per‐protein estimates on the test proteins with the results of the 12 disorder predictors (Figure 6). For additional comparison, several meta‐predictors were built—based on the 12 individual predictors—that combine predictions at the residue level to provide a single prediction. Details of the design of these meta‐predictions are explained in the section “Meta‐prediction models”. The two best meta‐predictors are shown for comparison (Figure 6). We also considered an oracle approach that selects the prediction from the disorder predictor with the highest actual AUC for each test protein. Table 2 provides the corresponding numerical results and evaluates statistical significance of differences between the results of DISOselect and the other 17 methods including the 12 disorder predictors, four meta‐prediction methods, and the oracle approach. Our empirical analysis that is summarized in Table 2 reveals that the predictions selected with the help of DISOselect are significantly better than the results produced by any of the 12 disorder predictors and meta‐predictors based on these 12 predictions (P‐value <0.01). More specifically, the mean per‐protein AUC of the predictions recommended by DISOselect is 0.97, compared to the 0.94 by the best disorder predictor (SPOT‐Disorder) or 0.95 by the best meta‐prediction method. Figure 6 reaffirms that DISOselect recommends predictions that are much better than the results of the 12 methods, that is, the thick black line that represents results from DISOselect is separated from the dashed and colored lines that correspond to the 12 disorder predictors by a wide margin. Further, while meta‐prediction methods perform better than any individual method, they perform substantially worse than DISOselect. Moreover, the oracle method, which is denoted with thick red line in Figure 6, is relatively close to the results of DISOselect, particularly when compared against the margin of improvement between DISOselect and the best of the 12 disorder predictors, SPOT‐Disorder. Numerical comparison in Table 2 shows that the oracle approach secures the mean per‐protein AUC = 0.98 versus 0.97 obtained by DISOselect. While this difference is statistically significant (p‐value < .01), the magnitude of the difference is arguably small showing that DISOselect performs high‐quality selection of disorder predictors.

Figure 6.

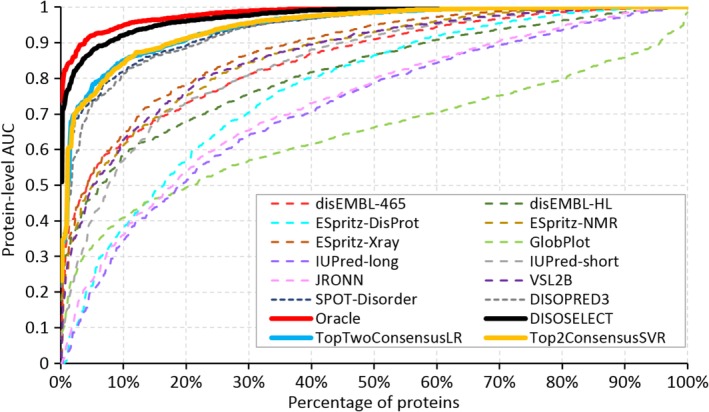
Comparison of the per‐protein area under the receiver operating characteristic curve (AUC) values on the test proteins between the 12 disorder predictors (dashed lines), the selection of the best disorder predictor using the highest estimated AUCs generated by DISOselect (solid black line), the oracle method (solid red line), and the best two consensus‐based disorder predictors constructed using a simple logistic regression (LR) and a more sophisticated support vector regression (SVR) (solid blue and yellow lines, respectively). The oracle method selects the disorder predictor with the highest AUC among the 12 disorder predictors. Lines show the per‐protein AUCs that are sorted in the ascending order for each of the 17 methods

Table 2.

Comparison of the per‐protein AUC values for the test proteins produced by the 12 disorder predictors, the oracle method that selects the predictor with the highest AUC, the selection based on the highest estimated AUC produced by DISOselect, and four different residue‐level consensus‐based disorder predictors that use logistic regression (LR) and support vector regression (SVR) models

Category	Predictor	Mean per‐protein AUC	Per‐protein AUC at the worst quartile of proteins	Significance of differences compared to DISOselect
Hypothetical method	Oracle	0.983	0.984	p‐value < .01 (significantly better)
Proposed model	DISOselect	0.974	0.971
Consensus models	Top2Predictor SVR	0.947	0.938	p‐value < .01 (significantly worse)
	Top2Predictor LR	0.947	0.936	p‐value < .01 (significantly worse)
	12Predictor SVR	0.942	0.929	p‐value < .01 (significantly worse)
	12Predictor LR	0.940	0.921	p‐value < .01 (significantly worse)
Individual predictors	SPOT‐disorder	0.940	0.927	p‐value < .01 (significantly worse)
	DISOPRED3	0.935	0.921	p‐value < .01 (significantly worse)
	ESpritz‐Xray	0.880	0.832	p‐value < .01 (significantly worse)
	ESpritz‐NMR	0.865	0.809	p‐value < .01 (significantly worse)
	VSL2B	0.864	0.816	p‐value < .01 (significantly worse)
	disEMBL‐465	0.853	0.768	p‐value < .01 (significantly worse)
	IUPred‐short	0.843	0.768	p‐value < .01 (significantly worse)
	disEMBL‐HL	0.816	0.719	p‐value < .01 (significantly worse)
	ESpritz‐DisProt	0.772	0.649	p‐value < .01 (significantly worse)
	JRONN	0.733	0.603	p‐value < .01 (significantly worse)
	IUPred‐long	0.718	0.584	p‐value < .01 (significantly worse)
	GlobPlot	0.646	0.537	p‐value < .01 (significantly worse)

Note: We compared the mean per‐protein AUCs computed over the test proteins and the AUCs for the worst (the least accurately predicted) quartile of the test proteins (i.e., the 25% point in Figure 6). Methods are sorted by their mean per‐protein AUCs. Significance of the differences in the per‐protein AUCs of the predictions selected by DISOselect and the predictions generated by the other methods (including the oracle) was assessed with the t test for normal measurements and the Wilcoxon test otherwise; normality was tested with the Anderson‐Darling test at .05 significance; we sampled 50% of proteins in the test data set 10 times at random and compared the corresponding 10 pairs of AUCs; the resulting p‐values are listed in the last column.

The analysis in Figure 6 is aggregated at the test data set level for clarity, that is, we compared re‐sorted per‐protein AUCs across different methods. Figure 7 offers a direct comparison of predictive performance of the results selected with DISOselect against the most accurate disorder predictor (SPOT‐Disorder), the best performing meta‐prediction method (Top2Predictor SVR), and an average disorder predictor. When compared against SPOT‐Disorder, DISOselect selects a better disorder prediction for 64% of proteins, the same prediction for 5% of proteins, and worse prediction for 31% of proteins, and the average improvement in AUC equals 0.035 (red line in Figure 7). In other words, DISOselect improves over SPOT‐Disorder for two out of three proteins. Similar results are obtained when comparing DISOselect with the best meta‐predictor (green line in Figure 7). DISOselect is better, the same and worse for 62, 4 and 34% of proteins, respectively, with the average improvement in AUC of 0.028. When compared against an average disorder prediction, DISOselect secures a better result for 95% of proteins with the average improvement in AUC of 0.152 (blue line in Figure 7). Overall, we conclude that DISOselect is an accurate approach for the selection of disorder predictors that provide high‐quality predictions for a given protein of interest.

Figure 7.

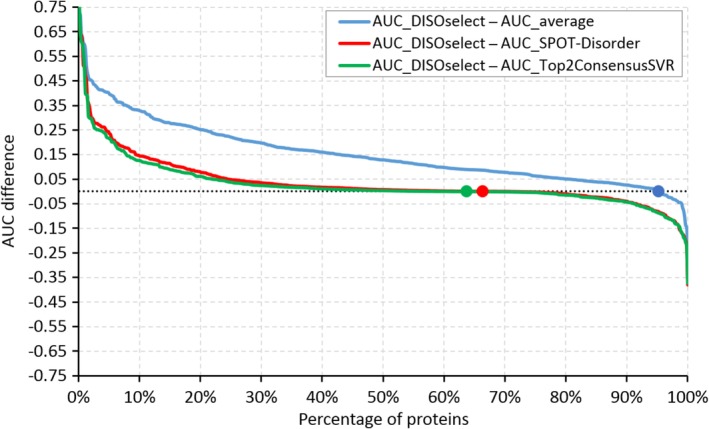
Evaluation of the differences in the protein‐level area under the receiver operating characteristic curves (AUCs) for the same test proteins between the predictions selected with DISOselect and the average AUC of the 12 disorder predictors (blue line), between the predictions selected with DISOselect and the predictions generated by the most accurate disorder predictor at the data set level, SPOT‐Disorder (red line), and between the predictions selected with DISOselect and the best consensus‐based method that relies on the support vector regression (SVR) (green line). Points indicate where the difference between protein AUCs crosses zero. The proteins are sorted by the value of the difference in the descending order

3. CONCLUSIONS

Our empirical analysis shows that the per‐protein predictive quality of popular disorder predictors varies widely between different proteins. The users cannot expect that the disorder predictor with the best benchmark‐data set level results will provide favorable results across all proteins. These results suggest that a computational tool that can accurately estimate per‐protein predictive performance for a given disorder predictor and a given protein is needed. This tool would inform the users about the expected predictive quality of a given disorder predictor and could be also used to recommend an “optimal” predictor that provides the best results for a given protein of interest.

To this end, we proposed the DISOselect method that predicts predictive performance (quantified with the AUC scores) for a representative set of 12 popular disorder predictors and which utilizes these results to recommend the predictor that provides the best predictive quality. The DISOselect's models rely on the information extracted from the putative secondary structure, physicochemical properties of residues and AA composition of the input protein chain, which can be efficiently computed from the protein sequence. Models for individual disorder predictors are very different, rely on largely exclusive sets of dominant features, and reveal that each disorder predictor has a different predictive bias.

Empirical assessment on a large test data set shows that DISOselect provides accurate estimates of the protein‐level AUC for each of the considered disorder predictors. The disorder predictions selected using DISOselect are significantly more accurate than the results produced by any of the 12 disorder predictors, including the top‐performing methods such as SPOT‐Disorder and DISOPRED3, and a selection of four disorder consensus predictors. The mean per‐protein AUC for the predictions selected with DISOselect is 0.97, compared to an average AUC of 0.82 generated by the 12 methods, and an average AUC of 0.94 for the consensus methods. We conclude that DISOselect can be used to effectively estimate predictive performance of disorder predictors and to select predictors that offer high‐quality prediction for a given input protein sequence.

A webserver that implements DISOselect is freely available for non‐commercial users at http://biomine.cs.vcu.edu/servers/DISOselect/. DISOselect requires only the FASTA‐formatted protein sequences as input. Up to 1,000 proteins can be predicted in a single run. All computations are performed on the webserver side. The webserver outputs the putative AUC and the qualitative performance (including the percentile of predicted AUC value) for each of the 12 disorder predictors, which are sorted in the descending order of the predicted AUC. The predictor at the top of the list, which has the highest estimated AUC, is recommended to the user as the best option to collect the disorder predictions. For the user's convenience, the main page of the webserver provides links to the websites of these disorder predictors under the “Help” section. The results are available via an HTML page, which can be accessed via a direct link, and a parsable text file. We will archive these results for at least 1 month.

4. MATERIALS AND METHODS

4.1. Data sets

The source data set with 25,717 proteins with the native intrinsic disorder annotations was originally collected from the MobiDB resource86 and recently published as a basis of a large‐scale disorder prediction assessment.46 In our recent work87, 88 we amended the original data set by excluding sequences with unknown/undetermined AA types, which is necessary to obtain some of the disorder predictions, and by reducing within‐data set redundancy. The latter was accomplished by clustering proteins at 25% pairwise similarity with BLASTCLUST.89 This similarity reduction ensures that the data set uniformly samples the sequence space and that training and test data sets extracted from these data share low, <25%, sequence similarity. Empirical analysis in88 demonstrates that the predictive quality of the disorder predictors on the reduced and improved data set with 6,271 proteins is similar to the quality that was evaluated on the original data set of 25,000 proteins.46 The 6,271 proteins include 105,709 disordered and 1,672,907 structured residues. We divided these proteins at random into a training data set with 5,272 proteins and test data set with 999 proteins. The two data sets are available at http://biomine.cs.vcu.edu/servers/DISOselect/. We used the training data set to design and optimize models that predict the protein‐level performance for the specific disorder predictors. We applied the test data set to assess performance of these models on an independent (i.e., sharing low sequence similarity) data set, to compare them to alternative predictive methods, and to evaluate effectiveness of the DISOselect system that recommends a well‐performing disorder predictor for a given protein sequence.

4.2. Selection of the disorder predictors

We cover a diverse set of 12 widely used disorder predictors. We selected 10 predictors from the list of 13 methods that were assessed in a recent large‐scale benchmark.46 We excluded three of the 13 predictors (SEG,90 Pfilt91 and FoldIndex92) since these older methods were ranked near the bottom in that study.46 The 10 remaining predictors include two versions of DisEMBL (DisEMBL‐465: trained using X‐ray structures, and DisEMBL‐HL: trained to predict propensity for loop conformations)54; three flavours of ESpritz (ESpritz‐Xray: trained on the disorder annotations from X‐ray structures, ESpritz‐NMR: trained on annotations from NMR structures, and ESpritz‐DisProt: trained on the annotations from the DisProt database)63; two versions of IUPred (IUPred‐short: for short disordered regions and IUPred‐long: for long disordered regions)50; GlobPlot49; RONN58; and VSL2B.55 We supplemented these 10 methods with two popular and accurate predictors: DISOPRED367 and SPOT‐Disorder.56 DISOPRED was ranked at the top in the CASP10 experiment, the last CASP that evaluated disorder predictions.38 SPOT‐Disorder represents a new class of predictors that rely on the deep learning models. The 12 methods uniformly sample the three categories of the predictive models including the ab‐initio methods (IUPred‐short, IUPred‐long and GlobPlot), the machine learning methods (RONN, DisEMBL‐HL, DisEMBL‐465, VSL2B, and SPOT‐Disorder), and the meta‐methods (DISOPRED3, ESpritz‐Xray, ESpritz‐NMR and ESpritz‐DisProt). These predictors were developed using all main sources of the disorder annotations, such as crystal structures, NMR structures and other experimental methods that are covered in the DisProt database.27

We collected the disorder predictions for the training and test data sets for the set of the 10 predictors that were included in the recent benchmark study46 from the MobiDB resource.86 We generated predictions for DISOPRED3 and SPOT‐Disorder by running the author‐provided code.

4.3. Predictive model

Selection of a well‐performing disorder predictor is a two‐step process. First, predictive quality that is quantified with AUC is estimated for each of the 12 disorder predictors. Second, the 12 estimated AUCs are compared and the method with the highest estimated AUC is recommended to the user. The first step provides the user with an estimate of the predictive quality for a given disorder predictor. This result is useful in scenarios when the user is committed to using a specific predictive tool. The second step suggests a particular, best‐performing method and this option should be utilized when the user is willing to collect prediction for any of the 12 tools. We note that the predictions of these tools can be easily collected from MobiDB at http://mobidb.bio.unipd.it/ 86 (for the 10 methods) and via the webservers for DISOPRED3 (http://bioinf.cs.ucl.ac.uk/psipred/) and SPOT‐Disorder (http://sparks-lab.org/server/SPOT-disorder/).

The architecture of DISOselect method is visualized in Figure 8a. The corresponding pseudo‐code is shown in Figure 8b. The input protein sequence is used to generate an information‐rich profile. The profile includes sequence‐derived structural and physiochemical properties such as putative solvent accessibility, putative secondary structure, sequence complexity and several selection physiochemical properties of the input AA residues. In the first layer, the sequence profile is encoded into sets of numeric features that are optimized for each of the 12 disorder predictors. The second layer uses 12 machine learning models to predict AUC values from the input features for the 12 disorder predictors. These predictions are mapped into the distribution of AUCs values from the training data sets for the corresponding 12 disorder predictors in the third layer. This ensures that the predicted AUCs are calibrated to cover the entire spectrum of AUC values that are covered by a specific disorder predictor. Finally, the 12 predicted AUCs are compared and the method with the highest putative AUCs is recommended back to the user. The outputs generated by DISOselect also include the AUC values for each of the 12 methods.

Figure 8.

Architecture of the DISOselect method (a) and pseudo code of the DISOselect implementation (b)

4.3.1. Disorder prediction evaluation measure

Disorder predictors output putative propensity for intrinsic disorder for every AA residue in the input sequence. Propensities are expressed as numeric scores where a high value denotes larger likelihood for the disordered state. The binary prediction classifies each residue as either structured or disordered, and is derived from the propensities, that is, residues with propensity scores > predictor‐specific threshold are classified as disordered while the remaining residues are classified as structured. The measure that the most commonly used to assess the predictive quality of the disorder predictors is the AUC.32, 36, 38, 44, 46, 47, 75, 79 AUC is a threshold‐agnostic measure of the putative propensities which makes it arguably more informative than the threshold‐specific measures such as sensitivity and specificity. The threshold‐specific measures depend on the threshold values and in practice their values correlate with the AUC values. In other words, methods with higher AUC values typically secure higher values of the binary measures as long as the thresholds across the different disorder predictors are adjusted to generate the same prediction rate (the same number of predicted disordered residues). AUC is computed as the area under the curve composed of the true positive rates (on the y‐axis) and false positive rates (on the x‐axis) computed for thresholds that equal to the set of all unique propensities generated by a given disorder predictor. The true positive rate is defined as the number of true positives (correctly predicted disordered residues) divided by the number of the native disordered residues. The false positive rate is defined as the number of false positives (structured residues predicted as disordered) divided by the number of all structured residues. The AUC values range between 0.5 (for random predictions) and 1 (for perfect predictions).

4.3.2. Sequence profile

The sequence profile includes a comprehensive set of structural and physiochemical protein properties which are widely recognized as influential to disorderness.93, 94, 95, 96, 97, 98, 99, 100 They include the sequence itself, solvent accessibility predicted from the input protein sequence with ASAquick,101, 102 secondary structure predicted with the single‐sequence (fast) version of PSIPRED,103, 104 sequence complexity computed using the SEG algorithm,105 and selected physiochemical properties of the input AA residues including hydrophobicity, hydropathy, charge, structural entropy, polarity, volume, size, flexibility, refractivity, transfer and solvation energies, and propensity for coil, turn, strands, helix and disordered conformations. These properties were quantified using the AA indices collected from the AAindex resource106 and the disorder propensity index from.97 The selection of the solvent accessibility and secondary structure predictors was motivated by their computational efficiently, stemming from the fact that they make predictions from a single sequence, that is, without the computationally expensive calculation of the multiple sequence alignments. The sequence profile was used to generate 130 features that aggregate the structural and physiochemical protein properties at the whole‐protein level. These features are detailed in the Table S1. They include 21 features computed directly from the input sequence (AA composition and sequence length), 3 features computed from the putative solvent accessibility, 2 features from the sequence complexity, 8 features from the putative secondary structure, and 96 features based on the physiochemical properties.

4.3.3. Empirical design of predictive models

The layers 1 and 2 of the DISOselect's architecture (Figure 8a) were designed using empirical selection of features and machine learning models to maximize quality of predictions of the per‐protein AUC scores for individual disorder predictors. The design process had two steps, where we first removed similar features (i.e., we reduced mutual similarity between features) and then we selected the best combination of models and selected predictive features. This two‐step design was done separately for each of the 12 disorder predictors, resulting in predictive models that are sensitive to the disorder predictor‐specific biases in the predictive performance. All design activities were performed exclusively on the training data set. In the first step, we quantified the mutual similarity for all pairs of the 130 features based on the Pearson correlation coefficients (PCCs). For each pair of highly correlated features (|PCC| > 0.65), we removed one of them that has lower predictive performance, that is, which has lower value of PCC with the per‐protein AUC scores of a specific disorder predictor. This step results in the removal of between 21 and 40 features, depending on the disorder predictor.

The second step relied on a wrapper‐based approach to select the best machine learning models in combination with selection of predictive feature sets. First, we quantified the predictive performance of each feature that was retained in the first step based on its PCC with windowed per‐protein AUC values of a specific disorder predictor. Second, we select a subset of features with |PCC| > threshold where the value of the threshold is selected to provide the highest predictive quality for a predictive model that relies on the corresponding feature set. Three types of regression algorithms were tested for use in our predictive model: linear regression,107 nearest neighbor regression,108 and extra tree regression.109 We did not explore deep learning regression methods because our data set that includes 5,272 proteins (data points) and 130 input features (that are used to represent the input protein sequences) would not provide enough data for this approach. The predictive quality was measured based on the threefold cross validation on the training data set and was quantified with PCC between outputs of a given machine learning model and the per‐protein AUC scores of the given disorder predictor. We started with threshold = 0 (we used all features retained in the first step) and we incremented it by 0.01 until the cross validated PCC of the given model type starts to decrease. The selected feature sets ranged in size between 24 and 38 for the extra tree regression, 29–46 for the nearest neighbor regression, and 51–64 for the linear regression, depending on the considered disorder predictor. After the feature selection was completed, we optimized parameters of the machine learning algorithms via a grid search for each of the 12 disorder predictors, with the aim to maximize the PCC for the threefold cross validation on the training data set. For instance, for the extra tree regression we parameterized the maximum depth of the trees (using 0–20 range), number of trees in the forest (100–180 range), minimum number of samples required for a split (0–30 range), and the number of features to consider when calculating best split (0–50 range). Table S2 summarizes the results secured by the three parameterized machine learning models for the selected feature sets. The average (over the 12 disorder predictors) PCC for the nearest neighbor regression, linear regression, and extra tree regression models are 0.15, 0.13 and 0.31, respectively. The corresponding MSEs between the predicted and actual AUC values equal 0.018, 0.011 and 0.007, respectively.

Our empirical results on the training data set show a clear advantage for the extra tree regression model, which we selected to implement the DISOselect methods. The extra tree regression is a supervised algorithm inspired by the decision forest algorithm. It is a version of the extremely randomized random forests where the computation of the optimal features that are used to grow the tree is done randomly,110 with the underlying aim to minimize overfitting.111 This is particularly useful in the context of our prediction task given the low (<25%) similarity between the proteins in our data sets. Moreover, the training of the extra trees regression is computationally efficient given the random nature of the tree‐building procedure, which contrasts with a more exhaustive search performed by the traditional random forests.109

4.4. Meta‐prediction models

A conventional approach to combining predictions from several different methods is meta‐prediction, where several prediction methods are combined to give a single prediction, usually at the residue level. For comparison with our predictor selection method, we developed several residue‐level meta‐prediction methods based on the 12 individual predictors examined in this study. We used several variations on meta‐predictor construction: two‐different architectures—logistic regression (LR) and support‐vector regression (SVR), and different input predictors—either all 12 predictors or only the best of the predictors. The best predictors were selected based on the data set level performance on our training set (Table 1). Based on these assessments, we selected two prediction methods—SPOT Disorder and Disopred3—as significantly better than the other individual methods. This gave four meta‐predictors: 12Predictor LR, 12Predictor SVR, Top2Predictor LR and Top2Predictor SVR.

Prediction scores from the individual predictors were initially rescaled to be in the same range of 0–1. The rescaling was based on the default thresholds of respective predictors as values from minimum to threshold to be in the range of 0–0.5 and values from threshold to maximum to be in the range of 0.5–1.

The logistic regression model was trained with the threefold cross validation on the training data set with default L2 regularization penalty by balanced class weights according to the proportions of training set using the L‐BFSG optimization algorithm. The SVR models were trained with the threefold cross validation on the training data set after subsampling 10% of each fold randomly to minimize the training time. We used the radial basis function kernel and performed a grid search for the penalty parameter C (between 2⁻⁵ and 2⁵), kernel coefficient gamma (between 0 and 1), and tolerance for stopping criteria (between 10⁻³ and 10³).

CONFLICT OF INTEREST

None declared.

Supporting information

Table S1. Description of the 130 features that were considered in the design of DISOselect.

Table S2. Predictive performance of the considered three types of machine learning models algorithms reported based on the threefold cross validation experiments on the training data set. The performance is measured with Pearson correlation coefficient (PCC), mean absolute error (MAE) and mean squared error (MSE) between the predicted and the actual area under the receiver operating characteristic curve (AUC) values. The last line shows the average values across the 12 considered disorder predictors.

Table S3. Improvements in the data set‐level area under the receiver operating characteristic curve (AUC) values based on the selection of proteins using the putative AUC values generated by DISOselect for each of the 12 considered disorder predictors. The disorder predictors are sorted by their complete test data set‐level AUCs. For each disorder predictor the results on the whole test set are compared against the 75, 50 and 25% proteins that have the highest putative AUC values. Significance of the differences between the AUCs on the whole test data set and the AUCs for each of the three subsets was evaluated with the t test for normal measurements and the Wilcoxon test otherwise; normality was tested with the Anderson‐Darling test at .05 significance. We sampled 50% of proteins in each data set ten times at random and compared the corresponding 10 pairs of AUCs; the resulting p‐values are reported in the table inside the square brackets.

Katuwawala A, Oldfield CJ, Kurgan L. DISOselect: Disorder predictor selection at the protein level. Protein Science. 2020;29:184–200. 10.1002/pro.3756