Identifying Clusters of High Confidence Homologies in Multiple Sequence Alignments

Abstract

Multiple sequence alignment (MSA) is ubiquitous in evolution and bioinformatics. MSAs are usually taken to be a known and fixed quantity on which to perform downstream analysis despite extensive evidence that MSA accuracy and uncertainty affect results. These errors are known to cause a wide range of problems for downstream evolutionary inference, ranging from false inference of positive selection to long branch attraction artifacts. The most popular approach to dealing with this problem is to remove (filter) specific columns in the MSA that are thought to be prone to error. Although popular, this approach has had mixed success and several studies have even suggested that filtering might be detrimental to phylogenetic studies. We present a graph-based clustering method to address MSA uncertainty and error in the software Divvier (available at https://github.com/simonwhelan/Divvier), which uses a probabilistic model to identify clusters of characters that have strong statistical evidence of shared homology. These clusters can then be used to either filter characters from the MSA (partial filtering) or represent each of the clusters in a new column (divvying). We validate Divvier through its performance on real and simulated benchmarks, finding Divvier substantially outperforms existing filtering software by retaining more true pairwise homologies calls and removing more false positive pairwise homologies. We also find that Divvier, in contrast to other filtering tools, can alleviate long branch attraction artifacts induced by MSA and reduces the variation in tree estimates caused by MSA uncertainty.

Introduction

Multiple sequence alignments (MSAs) and phylogenetic trees are the cornerstones of comparative sequence analysis. Our knowledge of evolution—including the tree of life, molecular dating, and adaptive evolution—all require high-quality MSAs and accurate tree estimates. It is often overlooked, however, that MSA and evolutionary inference are a joint inference problem (Kruskal and Sankoff 1983), where accurate estimation of one is dependent on the accurate estimation of the other. Joint estimation of the MSA and tree, often referred to as statistical alignment, is possible but is computationally difficult and time consuming, so the overwhelming majority of studies adopt the two-step approach for inference (Lunter et al. 2005). The first step consists of obtaining a “good enough” MSA, which infers the homology relationships between the characters in the raw sequences. The second step consists of the evolutionary analysis, which takes the MSA as a fixed set of homology assignments and uses explicit evolutionary models to extract the biologically relevant parameters from the data, such as the phylogenetic tree or the selective pressures acting upon those sequences (Yang 2014; Whelan and Morrison 2017).

Given the obvious relationship between the methods used and the desired result, the evolutionary inference step has become the focus of the majority of methodological research, with increasingly elaborate models capturing ever more complex and subtle aspects of the evolutionary process (Yang 2014). The MSA problem—and particularly the uncertainty in MSA—is relatively less studied. There are a number of established MSA methods (MSAMs), such as MAFFT (Katoh 2002) and T-Coffee (Notredame et al. 2000), that are typically used to obtain a “good enough” MSA for downstream evolutionary inference but provide few measures of confidence in the MSA in terms of either the whole MSA or the individual homology assignments contained within. The performance of MSAMs is typically benchmarked against databases of structurally derived “true” MSAs, such as BAliBASE (Thompson et al. 1999) or Prefab (Edgar 2004), with success measured solely by the number of correctly matched pairs or columns of amino acids in the inferred MSA. As a consequence, MSAM development has primarily focused on improved algorithms or speed and rarely seeks to incorporate measures of uncertainty or any explicit description of the evolutionary process (Chatzou et al. 2016).

This division of the analysis pipeline into stepwise inference of MSA and tree is known to be problematic. There are many published examples where different MSAMs lead to different tree estimates (Ogden et al. 2006; Wong et al. 2008; Blackburne and Whelan 2013), changes in branch lengths, and different levels of support for branches in the tree (Hossain et al. 2015). Inaccuracy of the MSA step can also lead to long branch attraction artifacts (Hossain et al. 2015), the systematic biases usually associate with inadequate phylogenetic modeling (Huelsenbeck 1997). These problems are even more pernicious for more sophisticated analyses, such as the detection of adaptive evolution, where small errors in the MSA can lead to large errors in the quantities of interest (Jordan and Goldman 2012). These errors leading to biased analysis outcomes are prevalent in all MSAMs, although several authors have argued that MSAMs that incorporate more of our evolutionary knowledge might be less biased than others (Notredame et al. 2000; Löytynoja and Goldman 2008; Jordan and Goldman 2012; Blackburne and Whelan 2013; Tan et al. 2015).

In order to address the bias problem, it is common practice to remove (filter) putative low-quality columns in an MSA under the assumption that removing these columns will improve the accuracy of downstream evolutionary inference. In the past, this filtering was often done by hand, but reproducibility and genome-scale data require an automated procedure. The first type of automation uses arbitrary measures of gappiness or conservation in an attempt to mimic what patterns researchers look for by eye and include popular programs such as TrimAl (Capella-Gutierrez et al. 2009) and GBlocks (Castresana 2000). There are also more advanced filtering approaches that have looked at different objective functions to score and then filter out low scoring columns. Approaches such as HoT (Landan and Graur 2007) and GUIDANCE (Penn et al. 2010) use consistency measures, which filter according to the stability of the MSA when some aspect of the MSAM is varied. An alternative is a model-based approach, such as those used in Zorro (Wu et al. 2012) and PSAR (Kim and Ma 2014), which use probabilistic pair hidden Markov models (pair-HMMs) to calculate posterior probabilities (PPs) of pairwise homology, then process these probabilities to obtain a column score that can be used for filtering. Several studies have demonstrated that these filtering methods have little effect at best, or even that they may make the evolutionary estimates worse (Jordan and Goldman 2012; Tan et al. 2015).

Here, we present a new approach to quantifying and dealing with MSA uncertainty using a graph-based clustering approach based on the PPs obtained using a pair-HMM. Our idea is different to existing approaches since it does not seek to remove entire columns from an MSA, but instead tries to identify clusters of good (and by extension bad) homologies within a column. Our approach can be used to either partially filter a column, by picking the largest high confidence set of homologous residues and removing everything else, or “divvy up” a column into a new block of columns, each representing a cluster sharing strong evidence of homology. Using an implementation in the program Divvier, we demonstrate our new approaches are extremely effective relative to existing software at identifying true and false homologies using simulations and on the alignment benchmark BAliBASE. Both divvying and partial filtering tend to result in the removal of similar proportions of residue pairs, regardless of the MSAM used. We also find that our partial filtering and divvying approaches can alleviate at least some of the phylogenetic artifacts caused by MSA uncertainty.

Results

Methodological Overview

The methods described in this study are summarized in figure 1 . The aim of our approach is to identify and remove the false homologies induced where two or more residues have no shared common descent, while maintaining as many true homologies as possible. In order to classify true and false homologies, we take a given MSA and calculate the PPs of the pairwise homologies contained within that MSA using a pair-HMM. We then proceed to examine each column in the MSA in turn and use these pairwise PPs to cluster the residues in a column. Groups of residues within high PP clusters represent high confidence homology calls, whereas pairs of residues between clusters have low evidence of homology. A high confidence column in an MSA would consist of a single cluster where residues tend to share strong evidence—high PPs—of homology, whereas a low confidence column might have many clusters each representing smaller groups with little evidence of shared homology between the groups. Our clustering step is conceptually different to other filtering approaches which attempt to identify whether a column is “good” or “bad” since it allows multiple clusters of residues to all be assigned “good.”

Fig. 1.

A schematic of our graph-based filtering method. On the left is the original MSA. First, the unaligned sequences are used to calculate PPs of shared homology between pairs of residues using a pair-HMM. Our method then considers each column in turn (middle left), with the residues arranged in a circular ordering and the gaps are set aside. The darkness of the lines linking the residues represent relative the PPs of residues being homologous. The aim of our method is to break that residue graph apart in some meaningful manner. We use a heuristic to an agglomerative clustering approach with an appropriate cut off to identify the groups of putatively homologous residues (middle right). Based on these homologous clusters, we propose two filtering schemes. The first is partial filtering (bottom right), which selects the largest cluster of residues and filters the remaining residues, resulting in a partial column in the alignment. The second is divvying (top right), which splits each cluster into its own new column in the MSA. We insert a “static” character “$=$” for sequences with a known residue in another column to represent missing data not arising as the result of an insertion of deletion event. For partial filtering and divvying, the set aside gaps are restored to the MSA in all relevant columns.

The clusters can then be processed in one of two ways: partial filtering and divvying. Partial filtering is closest to existing filtering methods and outputs only the largest cluster with characters from other clusters replaced as missing data (gaps). We have named this approach partial filtering because columns can be partially removed to keep only the largest homology cluster. Divvying, in contrast, is a new approach and takes advantage of the multiple clusters and how phylogenetic programs treat gaps as missing data rather than as a source of phylogenetic signal. In divvying, we divide (or divvy up) a column into a block consisting of a set of columns each representing a supported cluster. This approach introduces multiple missing data symbols across columns within a block (see fig. 1) representing the cases where that column has a character present in another column within the block. Instead of using “-” or “X” for these missing data we use a static symbol, “$=$,” to emphasize the difference between divvying and the methods that generate real missing data, such as alignment producing “-” and sequencing uncertainty producing “X.” These static “$=$” symbols can be replaced by other typical characters for missing data, such as “X” or “-,” when conducting phylogenetic analysis.

Divvying up an MSA column in this way leads to the concern that it might introduce “new” data into an analysis, since one column can become many more columns in a block. First, we note that the only new characters introduced into the MSA are treated as missing data by phylogenetic analysis and effectively ignored, so at the basic level divvying a column does not create additional characters to inform about the tree. Divvying a column may, however, introduce additional ancestors since each original column in an MSA with a single ancestor can result in multiple columns in a block, each with its own ancestor. For single character columns, the new ancestors introduced by divvying are constant across all trees, so for reversible models introduce a constant into the likelihood function that will will not affect topology. Moreover, these additional ancestors seem more reasonable than the alternative of forcing two nonhomologous groups of characters to artificially share a common ancestor, which may induce artificial changes on the tree.

A second concern might be how information is shared across the tree by the characters in a phylogeny. Consider a column in an MSA for the simple tree ((A, B), C, D); and how dividing a truly homologous column affects the information about that tree. Divvying the column into the clusters AB and CD means that column now has information about each external branch, but it loses information about the internal branch since no clusters span that branch. If the column ABCD were correct then this divvying would remove information about the internal branch and increase sampling error but is unlikely to cause bias to the tree estimate. In contrast if the column was clustered into AC and BD, it could potentially bias the tree topology since the information about the internal branch would be used by both the AC and BD columns. Our approach to divvying columns attempts to avoid this issue by using a guide tree to limit the number and structure of clusters examined so that they are consistent with the guide tree. Our approach is not an exact solution to this problem and falsely divvied columns might bias the downstream tree estimate toward the guide tree. In defense we highlight our approach is similar to the use of guide trees in MSAMs, which are widely used in phylogenetics. Moreover, divvying nonhomologous columns will remove a potentially more serious form of bias, caused by forcing nonhomologous groups to share an ancestor, and provided a suitable threshold is chosen then divvying will affect many more of these nonhomologous columns than truly homologous columns.

Performance of Divvying and Partial Filtering on the BAliBASE Benchmark

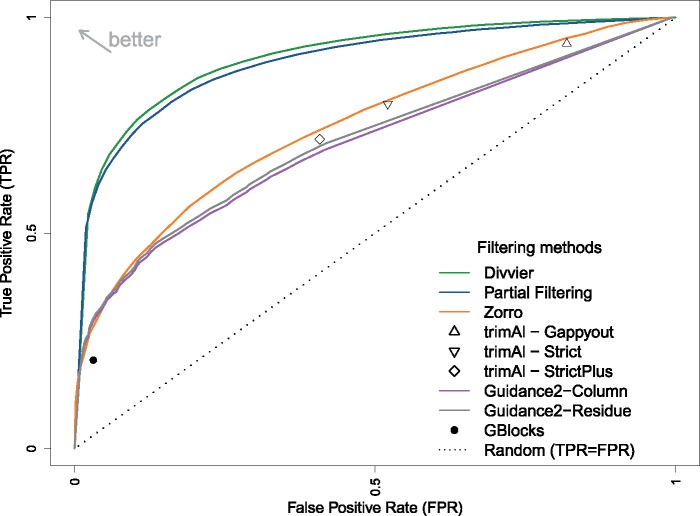
In order to investigate the effect of our new methods on MSA accuracy, we apply them to the BAliBASE benchmark (Thompson et al. 2005), which has high confidence structurally aligned regions that can be used to assess the true and false homologies inferred by MSAMs. In our comparisons, we include the entire sequence, including the C- and N-termini, when inferring the MSA and compute the confusion matrix from only the structurally aligned region. This approach is consistent with the intended use of BAliBASE, since the additional flanking sequence (or lack thereof) in some sequences represents the major challange in some of the reference sets. We note, however, that other studies have made the MSA problem easier by only examining the structurally derived region to infer the MSA and compute the confusion matrix. This difference in approach explains why the performance of other existing methods is poorer here compared with their published performance on the same data. Figure 2 shows the Receiver-Operator Characteristic (ROC) curve for pairwise homologies using our new methods (partial filtering and divvying), GUIDANCE 2 (both column filtering and residue filtering) and Zorro, as well as the point estimates for different settings of trimAl and Gblocks. The further to the top-left a method reaches, the better it is at discriminating between true and false homologies, which means it strikes the best balance between removing erroneous pairs while keeping true pairs. For the purpose of phylogeny, the most important part of the ROC curve is arguably the far left, where the maximum number of false positive (FP) pairwise homologies can be removed while removing as few true pairwise homologies (phylogenetic signal) as possible.

Fig. 2.

The ROC curve for true positive and FP homologies under a range of filtering methods applied to MAFFT MSAs across the BAliBASE benchmark.

Figure 2 shows both partial filtering and divvying perform substantially better than any existing methods and this holds true for the five analyzed reference sets of the BAliBASE benchmark, with divvying providing a marginal improvement over partial filtering. Both GUIDANCE 2 and Zorro perform similarly in the critical left hand region of the ROC curve, although Zorro performs marginally better if one is willing to accept the removal of more data during filtering. The points representing different settings of trimAl are close to different regions of the GUIDANCE 2 and Zorro curves, suggesting they have a similar tradeoff for at least those default values, whereas Gblocks appears to be the least capable of discriminating between true and false homologies, although it does at least do better than random.

The clear improvement of our partial filtering and divvying methods over existing filtering methods is partly attributable to their treatment of false homologies in a column. A column might be mostly right, containing mostly true positive (TP) pairwise homologies, but in order to remove the relatively small number of FP pairwise homologies, all of the true homologies must be discarded. An alternative way of thinking about this problem is that the only condition where column filtering can remove FP homologies efficiently occurs when the entire column is misaligned and contains no TPs. In contrast, our methods can identify the clusters of truly homologous residues in a column and remove the false homologies occurring between clusters. By keeping one (partial filtering) or more (divvying) of these clusters, we can successfully purge FP homologies without removing the large numbers of TPs they are associated with. We note that GUIDANCE 2 residue filtering can also remove only single residues, which suggests that Divvier's improved performance is due to the use of both PPs and the graph-based algorithm.

We also investigated the effect of treatment of divvying and partial filtering on alignments from various MSAMs and on true alignment. Naturally, we expect a proportion of residue pairs removed and under idealized conditions, only the misaligned residue pairs (FP) should be trimmed. However, due to the overlap between PP distributions between true and FPs homology pairs seen on ROC curves, we have to expect a number of TP pairs removed. The results depicted in table 1 show that the proportion of residue pairs remaining after applying divvier on various types of sequence alignments appears to be similar. The results across BAliBASE show that MSAMs get trimmed to a similar degree. Only treated Prank alignments appear to contain more residue pairs compared with other methods. Interestingly, the true reference alignments appear to get trimmed to the same, or even higher, degree as the inferred alignments. As noted in Bogusz (2018), BAliBASE alignments contain extensive portions of low PP residue pairs with a big fraction of reference sets containing more than 50% of pairwise homologies with PPs < 0.5. This explains why the reference alignments get trimmed to a high degree because these homologies are unlikely given the evolutionary model implemented in our piece of software. On the other hand, Prank produces more realistic gap patterns thus introducing fewer FP homology pairs compared with the other MSAMs.

Table 1.

Proportion of Pairwise Homologies Retained after Treatment in Core Regions.

Data Set	Divvying						Partial Filtering
	Reference MSA	Mafft-FFT-ns	Mafft-lin-si	Prank	Probcons	T-Coffee	Reference MSA	Mafft-FFT-ns	Mafft-lin-si	Prank	Probcons	T-Coffee
BBS11	0.22	0.23	0.23	0.24	0.23	0.23	0.18	0.19	0.18	0.19	0.18	0.18
BBS12	0.66	0.68	0.68	0.7	0.67	0.67	0.62	0.64	0.63	0.65	0.63	0.63
BBS20	0.81	0.82	0.82	0.84	0.82	0.82	0.78	0.79	0.79	0.81	0.79	0.79
BBS30	0.56	0.57	0.56	0.63	0.56	0.56	0.48	0.49	0.48	0.54	0.49	0.48
BBS50	0.5	0.52	0.51	0.58	0.51	0.51	0.41	0.43	0.41	0.48	0.42	0.41

Note.—Proportion of residue pairs after treating reference and inferred MSAs using divvier. The numbers represent fraction of pairwise homologies remaining following divvying and partial filtering.

The Effect of Divergence on Filtering Accuracy

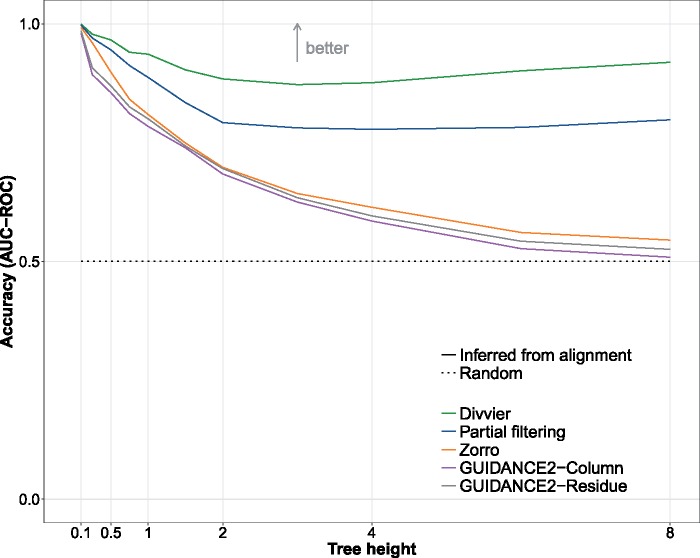
BAliBASE provides insight into the performance of filtering methods on low similarity sequences, but very few phylogenetic problems deal with such massively divergent sequences. There are no MSA benchmarks for intermediate divergences so we take a simulation approach to examine the effect of sequence divergence on filtering. Figure 3 shows the area under the curve (AUC) of the ROC curves from a range of methods, with high values representing the better methods. All filtering methods do well for low divergence (very similar) sequences since MSAMs make relatively few errors, but as the sequences diverge a clear order performance appears: divvying (best), partial filtering, Zorro, and then GUIDANCE 2 (worst). Note that the nature of trimAl and Gblocks as points in the ROC curve mean, we cannot calculate AUCs.

Fig. 3.

The performance of filtering methods on simulated data under a range of sequence divergences assessed using AUC.

The clear improvement of our new methods compared with existing methods is present even for closely related sequences, with the relatively shallow tree height of 0.5 already showing substantial differences between the methods. For massively divergent sequences, with a tree height of 8, Zorro and GUIDANCE 2 appear close to random (AUC = 0.5), whereas partial filtering and divvying are still able to discriminate between true and false homologies. The poor performance of Zorro and GUIDANCE 2 at this extreme divergence is partly due to the complete removal of columns in many data sets almost regardless of the threshold, so their AUC of 0.5 might be better interpreted as an inability to find any “good” columns to keep rather than a random assignment of “good” and “bad.”

Correcting for MSA-Induced Long Branch Attraction Artifacts

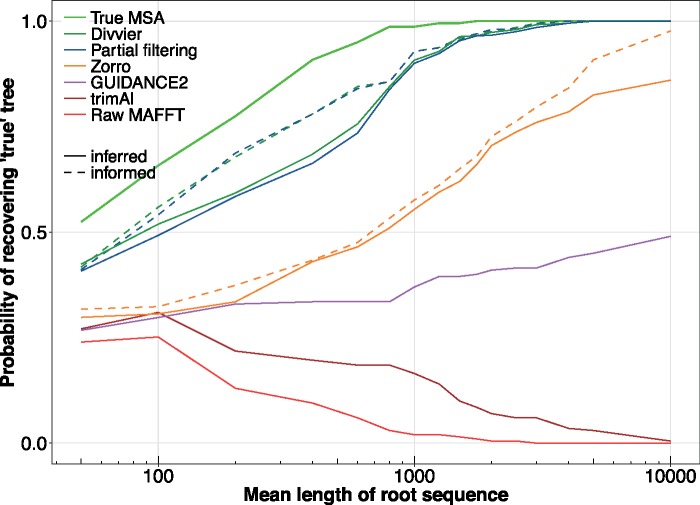
The previous sections show that our new filtering methods perform well in the context of the MSA, but filtering methods often treat the MSA as a stepping stone to the parameter of interest: the phylogenetic tree. We use a simulation approach to examine whether filtering methods can remedy the long branch attraction artifact induced by MSA introduced by Hossain et al. (2015). Figure 4 shows the probability of recovering the true tree for different sequence lengths under a range of treatments of the simulated sequences. The light green line (top) is the best case scenario where true alignment is known and shows that the the true tree can be reliably recovered for a root sequence length of around 1,000 amino acids. This observation demonstrates both that this is a difficult phylogenetic problem, but there is adequate information within a moderately long sequence to accurately recover the correct tree. The red line shows the effect of aligning with MAFFT and performing phylogenetic inference with no filtering and demonstrates the long branch attraction artifact since adding sequence data makes one less likely to recover the true tree and more certain of the LBA tree, with fewer than 5% of simulated sequences recovering the tree with a root length of 1,000 amino acids. These two results recapitulate those of Hossain et al. (2015).

Fig. 4.

The effect of filtering on the relative frequency of long branch attraction tree estimates induced by MSA. Sequences are simulated from a known “Felsenstein-zone” tree following Hossain et al. (2015) under varying root sequence lengths (x axis) and the likelihood of the three alternative topologies around the critical branch are estimated. The probability of the true tree (y axis) is computed as the fraction of the time the true (simulation) trees is recovered from 200 replicates. Inferred lines show results obtained after the application of existing methods, whereas informed lines show the best possible results obtained applying the perfect knowledge of the true (simulated) MSA.

The performance of existing filtering methods is mixed. We find that trimAl does not really help matters and only appears to slow the rate that the MAFFT MSA becomes certain of the wrong tree. A filtering approach randomly removing a fraction of columns might have a similar effect since any reduction in the amount of data might be expected to reduce certainty. GUIDANCE 2 performs somewhat better and there is a gradual upward tendency toward the correct tree as more data are added. This tendency might lead convergence, but it would require biologically unrealistically long data sets of over 10,000 amino acids. The rate that Zorro improves performance is better still, although it is still unable to recover the true tree with certainty at 10,000 amino acids. The orange dotted line above Zorro represents an informed column filtering method that uses our knowledge of the true alignment to removes all incorrect columns. This informed column filterer provides a useful point of reference to show the limits of what standard methods can achieve and is close to converging on the true tree with certainty at 10,000 amino acids.

In order to apply our new methods to data, we chose cutoffs from our BAliBASE analysis (fig. 2) based on a false discovery rate of 1.0% since incorrect homologies can have a major impact on the phylogeny. This 1% false discovery rate is relatively conservative and chosen so that ∼1/100 of pairwise homologies are incorrect. Under these cutoffs, partial filtering and divvying perform noticeably better than existing methods, with both having around a 90% chance of recovering the true topology at 1,000 amino acids and have fully converged to certainty by around 5,000 amino acids. Divvying has slightly better performance than partial filtering throughout, which is expected given it keeps more data, although the improvement in this case is small. The green and blue dotted lines above represent informed versions of partial filtering and divvying that perfectly cluster true homologies. In other words, these dotted lines represent the case of how perfect filtering and divvying would perform if our PPs perfectly predicted true and false homologies. It is noticeable that by around 1,000 amino acids both the applied and perfect versions of our algorithms are performing similarly, suggesting our clustering methods working as intended and are efficiently discriminating between true and false homologies.

The Effect of Filtering on a Bird Phylogenomic Data Set

Simulated data provide some insight into the effect of filtering methods on phylogenetic inference, but real data are often more complex with a range of biological factors affecting substitution and indel rates along the sequences and through time. These variations might affect our methods so it is useful to demonstrate some useful phylogenetic performance on real data. In order to address this problem, we will examine the tree estimates from 1,340 bird genes from MSAs inferred under MAFFT and PRANK, which are intended to be representative of similarity-based and evolutionary-based MSAMs, respectively (Blackburne and Whelan 2013). The difference between the tree estimates inferred under these two MSAs is represented by the geodesic distance between the trees (which in turn is a complex function of the true and false homologies the MSAs contain). Removing the FP homologies from the two MSAs by filtering should therefore bring the two tree estimates closer together and reduce the geodesic distance between them. Note that the key test here is a consistent shift leftward toward less difference rather than the eradication of difference itself. This is because the phylogenetic signal for these taxa will be dominated by the larger numbers of TP homologies and that these true homologies may substantially differ between MSAMs.

The red density plot in figure 5 shows in log 10-scale the geodesic distance between the trees as a measure of MSA disagreement, with the expectation that a distance of 0 represents perfect agreement between the MSAs (and therefore the trees) and >0 representing some difference in branch lengths or tree topology attributable to differences in the MSA. As expected, the majority of genes show some differences between MAFFT and PRANK and the log-scale means that there is a long tail of genes that have rather major differences between the MSAMs. Note also that the small hump of genes around 1E-5, which represents the few cases where the MSA problem is easy and that MAFFT and PRANK agree.

Fig. 5.

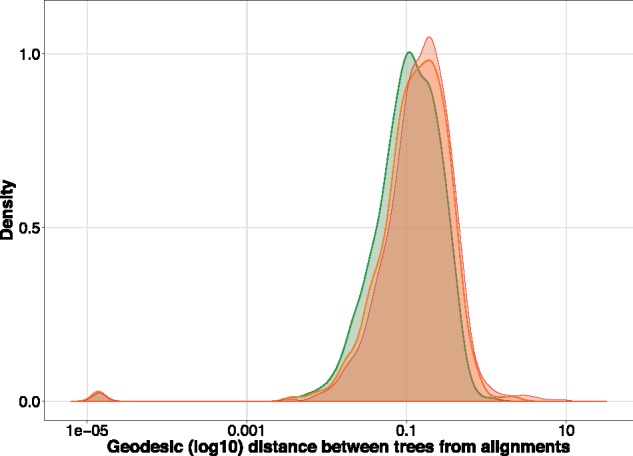
Geodesic distance between tree estimates from MAFFT and PRANK MSAs on a bird phylogenomic data set. The red curve represents trees estimated from the raw MSAs, the orange curve trees from MSAs filtered by Zorro and the green curve trees estimated from divvied MSAs. Note for clarity the curve for partial filtering is not shown since it is indistinguishable from that produced from divvying.

The orange density plot in figure 5 shows filtering under Zorro and there is some evidence of a small, but noticeable leftward shift in the distribution. (We do not filter under GUIDANCE 2 because it is too slow for this volume of data.) This shift demonstrates that filtering MAFFT and PRANK MSAs with Zorro makes their resultant trees more similar (again note the log-scale), suggesting that the filtering is working as intended and removing at least some conflicting signal introduced by the MSAM. The green density plot shows the performance of Divvier (partial filtering performs similarly; not shown for clarity) and shifts the distribution further leftward indicating greater similarity between the resultant trees when using Divvier for filtering, which is indicative of greater agreement between the MSAs from MAFFT and PRANK than observed when using Zorro. (Again, note the shift leftward is on a log 10-scale.) This result is consistent with the tree estimates from different MSAs being more consistent after Divvying, which might indicate a reduction in bias caused by either of the MSAs attributable to FP homologies.

Discussion

In this study, we propose two new graph-based approaches to MSA filtering where the characters in an individual column are split into clusters and each cluster has evidence of shared ancestry. Our approaches either present subsets of the original MSA columns by only showing the single largest cluster, which we dub partial filtering since it removes some characters from the original MSA column, or dividing the original MSA column into a block of multiple new columns each containing a cluster, which we dub divvying and retains all of the characters in the data. Our two approaches have several key benefits over existing filtering methods. First, we do not assume a whole column is “good” or “bad,” but rather whether there is evidence clustering one or more set of residues under a single shared ancestor. This approach means we do not have to remove whole columns of data when we detect errors, which allows our method to keep more of the phylogenetic signal in the data. This retention of signal might be particularly helpful for highly diverged data where standard filtering approaches would remove large portions of data, thus increasing the sampling error. Second, our approach uses a statistically justifiable approach to distinguish between the true and false homologies efficiently. Being based on an explicit probabilistic model stands in contrast to some other methods that are based on more opaque measures, such as relative position to gaps, Shannon entropy, or stability of an MSAM algorithm. The explicit probability model we currently use comes from Zorro (in part created through MAVID), but the structure of the approach means we can naturally include more sophisticated models as and when they become available, under the expectation that better models might allow more accurate estimation of PPs and improved inference of true and false homologies. Our results suggest these two benefits of our methods relative to existing approaches to MSA filtering do, indeed, lead to improvements in MSA accuracy and downstream phylogenomic analysis.

The resulting partially filtered and divvied MSAs can be used for phylogenetic inference with existing software and tools. There are, however, a few notes of caution. Our methods, particularly divvying, typically result in much longer MSAs than standard filtering methods. The computational complexity of phylogenetic inference scales linearly with the number of columns in the data, so standard programs will be of similar speed on partially filtered MSAs and potentially much slower on divvied MSAs. For individual genes, some of this slowdown might be offset by greater information to infer parameters from during maximization of the likelihood, but the increase in divvied MSA length could be a big issue for phylogenomic analyses. This computational problem can be offset by users specifying the minimum number of residues present in a column, so the smaller and less informative clusters are removed. Our Divvier software includes this solution as an option.

A second note of caution relates to the use of resampling approaches such as bootstraps or RELL-based statistics with divvied alignments. In standard phylogenetic analysis, the widely accepted unit of calculation is the MSA column, but under divvying a single column from the original MSA can be split into a block consisting of multiple columns in the divvied MSA. As a consequence, a user might be concerned that what was a single column in the original alignment might be over represented (over weighted) in the bootstrap or RELL. The same argument can, of course, be made in reverse by stating that each column should represent an evolutionary history from a common ancestor and adjusting column weights by the number of columns in a block unfairly down weights individual evolutionary histories. We can provide no unequivocal statement or recommendation in how to treat these blocks. Our weak recommendation is to treat a divvied MSA in the normal fashion for bootstrapping since this is the most practical solution for existing software. We do encourage users to treat results with caution, particularly if there are large unexpected differences between the results from divvied and partially filtered MSAs.

It is also important to appreciate the hard limitations of the methods discussed here. The total error in a phylogenetic tree estimate can be loosely considered a function of the sampling error, the modeling error, and the MSA error. In common with existing filtering methods, partial filtering and divvying only attempts to fix the problem of MSA error and makes no attempt to address the other two factors. Sampling error is of limited concern in modern phylogenetics since we have effective tools for dealing with parameter uncertainty due to limited alignment lengths, such as bootstrap proportions or PPs. In contrast, modeling error remains a major problem since inadequate substitution models are known to lead to long branch attraction artifacts and over/under confidence in tree estimates. Having a reliably filtered MSA, such as those produced from partial filtering or Divvier, in no way alleviates the need for more improved phylogenetic models, but should help to reduce MSA error.

It might appear surprising that reference structural alignments from the BAliBASE benchmark get trimmed similarly to MSAs that are known to contain errors. This means that a large fraction of true homology pairs have low PPs under the state-of-the art evolutionary models currently in use. Since divvying uses a statistically rigorous approach in its treatment of pairwise homologies, these low PP pairs, even though true, are classified as false. This behavior, however, is probably especially pronounced in BAliBASE, which contains structural alignments, mostly because similarity in structure is not necessarily to homology in evolutionary sense (Morrison et al. 2015). Furthermore, this aggressive trimming of true pairwise homologies illustrates that the models used to describe protein evolution are not sufficient to describe the complexity of evolutionary processes.

There are also several avenues that could be explored in order to improve our approaches, namely in the calculation of PPs used during clustering and the clustering algorithm itself. In order to compute PPs, our Divvier software integrates a modified version of Zorro, which in turn uses the model initially proposed by MAVID (Bray and Pachter 2004). This model is trained on data that is much more divergent than that usually used in phylogenomic analyses and the fit of that model, along with the resultant PPs, might be improved by using data dependent models such as those implemented in (e.g.,) PaHMM-Tree (Bogusz and Whelan 2017). An alternative to Zorro might also enable divvier to work on nucleotide sequences, although the inherent difficulty of aligning four character sequences means that clusters of high confidence characters might be harder to identify (Yang 2014).

In our method, we use a guide tree along with a pseudohierarchical clustering algorithm based on UPGMA to produce the clusters taken as input the divvying and partial filtering steps. We investigated a wide range of different full clustering approaches—including WPGMA, neighbor-joining and MCL—along with a range of different heuristics and found our approach provided the most accurate answers on BAliBASE benchmark. We do not, however, rule out an alternative approach providing a better way of obtaining clusters. We also note that divvier, in common with many other methods, is sensitive to the specific guide tree used during clustering. For instance, choosing a guide tree where 25% of the branches are different to the bionj default reduces the performance of divvier (partial filtering) from an AUC of 0.75 (0.70) across BAliBASE to an AUC of 0.70 (0.67). The results of our simulations do, however, suggest that the performance of our new methods is relatively close to the maximum possible performance in filtering, suggesting modifications to the clustering method or an improved way of obtaining a guide tree may offer only limited improvement.

To summarize, our new partial filtering and divvying approaches, implemented in the program divvier, offer a fast and accurate way of removing spurious homologies from sequence alignments while retaining informative data. Our results suggest Divvier is accurate and has the potential to improve phylogenetic inference, particularly in the case of divergent sequences where traditional filtering approaches tend to remove lots of data and increase sampling errors.

Materials and Methods

Clustering of Characters in MSA Columns Based on Homology

All of the methods we develop in this study require scores of pairwise homology, $S(S_i^{(1)},S_j^{(2)})$, between sequence ${\mathbf{S}}^{(1)}=\{S_1^{(1)},S_2^{(1)},\mathrm{\dots }\}$ and ${\mathbf{S}}^{(2)}=\{S_1^{(2)},S_2^{(2)},\mathrm{\dots }\}$ in order to identify clusters of characters that can be confidently identified to share a common ancestor (see fig. 1). We choose to use a modified implementation of the pair-HMM from Zorro to obtain pairwise PPs calculated by the forward-backward algorithm (Durbin et al. 1998), resulting in the distance measure between characters of $S(S_i^{(1)},S_j^{(2)})=1-P(S_i^{(1)},S_j^{(2)}|\theta )$. The pair-HMM, θ, contains states capturing matches, deletions, insertions, long insertions, and the N- and C-termini of proteins.

Given a set of n sequences, $\mathbf{S}=\left\{S^{(k)}\right\}$ the computational unit for our filtering approach is a column in the MSA, $C_x=S^1(x),\mathrm{\dots },S^n(x)$, with $S^1(x)$ representing the $S_i^{(1)}$ that maps to the xth column or a gap when no mapping exists. To form our clusters, we use UPGMA on the n × n matrix of $S(S^{(k)}(x),S^{(l)}(x))$. Note that during clustering we ignore gap characters. During UPGMA, the distance between two clusters A and B is calculated as $\frac{1}{\left|\mathbf{A}\right|+\left|\mathbf{B}\right|}\sum _{k\in \mathbf{A}}\sum _{k\in \mathbf{B}}S[S^{(k)}(x),S^{(l)}(x)]$. In practice, there is an iterative approach where the sequences in the closest cluster A and B are joined together and the distances updated. Rather than producing a complete clustering, our approach continues until a suitable threshold distance is reached at which point UPGMA terminates and returns current clusters. In order to cluster the characters in C_x using UPGMA, we would need to calculate $P[S^{(k)}(x),S^{(l)}(x)]\forall k\le n;l<m$, which has $\mathcal{O}(n^2)$ complexity. Calculating $P[S^{(k)}(x),S^{(l)}(x)|\theta ]$ is relatively slow, so to reduce the $\mathcal{O}(n^2)$ complexity we investigate an approximate clustering algorithm.

This heuristic takes two parts. First, we calculate a guide tree using bionj (Gascuel 1997) on the Poisson distances between the sequences using the original MSA. This tree provides the set of splits to be tested during the approximate clustering: $\text{split}(m)=\left\{{\mathbf{A}}_m\right|{\mathbf{B}}_m\}$ where $\left\{A_m\right\},\left\{B_m\right\}\in C_x$ and ${\mathbf{A}}_m\cap {\mathbf{B}}_m=\varnothing$. Our approximate clustering uses these splits to select a subset of PPs to calculate. For each of the splits, we select a subset of pairwise comparisons, $P(A,B|\theta )$, to include based on the pairwise distance between the sequences (closer is more informative), the length of the sequences (better coverage within sequences) and ensuring as many comparisons as possible (better coverage between sequences). We calculate a suitable list of pairwise comparisons and create new sets of $\mathbf{A}{\prime }_m$ and $\mathbf{B}{\prime }_m$ for each split m. The size of these potentially incomplete sets is $\left|\mathbf{A}{\prime }_m\right|\le \left|{\mathbf{A}}_m\right|$, meaning that fewer pairwise comparisons need to be made; potentially a much smaller number when n becomes large. In our implementation, we limit the size of this subset to 10 for each split, which reduces the complexity of the clustering algorithm to $\mathcal{O}(n)$. Extensive testing on the BAliBASE benchmark shows the ROC curve produced by this heuristic is almost indistinguishable from that produced using full UPGMA. All of the analyses presented here use this heuristic.

A Graph-Based Interpretation of Clusters

The hierarchical clustering approach described above can be interpreted in terms of the circular ordered graph shown in figure 1, which provides an intuitive insight into what the algorithm is trying to achieve. Testing all possible splits within that graph could result in a set of clusters where an individual character from a sequence occurs in multiple clusters, which would prevent the clean divvying of the column. This interpretation if accompanied by some weighting might make sense where there is uncertainty about where that character belongs, but there is no established way of incorporating that information into phylogenetic tree inference programs. Instead, the use of a hierarchical clustering, which implies a tree structure, means that none of the set of lines drawn through the circular ordering need to cross, in turn resulting in each character occurs in at most one cluster. This allows clean separation of the column into clusters, each representing a set of characters sharing evidence of shared ancestry, which can be taken as input into any phylogeny program.

The presentation of these graph-based clusters is then used to divide our methodology into divvying and partial filtering. Our divvying approach presents all of the clusters from a target column as a block in the MSA, each with its own new column within the block. Each of the new columns includes the gap characters of the target column and replaces the characters from the target column not present in the new column with static “$=$” characters (see fig. 1). Bootstrapping and other resampling techniques are still applicable to the divvied data and could take place either at the level of the column or at the level of the block. We have not investigated that problem here, but tentatively suggest that standard column based bootstrapping might be suitable for most analyses. Partial filtering instead only takes the largest cluster from the target column and replaces characters not present in that cluster with gap characters. This partial filtering approach is exactly equivalent to removing characters in the MSA where shared ancestry cannot be statistically supported. Our method is implemented in the program Divvier, which is freely available via https://github.com/simonwhelan/Divvier.

Perfect Divvying and Perfect Filtering

For the purposes of evaluating the performance of our filtering methods and our heuristics, we also define perfect divvying and perfect filtering. Rather than clustering based on our PPs we define $S[S^{(k)}(x),S^{(l)}(x)]$ as 0 for pairwise homologies that are present in the true MSA produced by simulation or 1 those that are not. For any threshold >0 and <1, the resultant clusters therefore contain no FP homologies and the maximum possible number of TP homologies contained within a target column. The resultant divvied and perfectly filtered MSAs can be used to therefore test the theoretical limit of our new methods.

Evaluating the Performance of Filtering Methods

During this study, we evaluate the performance of our and other MSA filtering methods using three broad criteria: 1) the true positive rate (TPR) and false positive rate (FPR) for identifying pairwise homologies in real and simulated data; 2) the accuracy of tree inference under simulated data; and 3) the similarity between tree estimates obtained from different MSAs using the same real data.

In order to score FPs and TPs from an inferred MSA, we require a reference MSA that represents the known truth. For real data this “truth” is the core region of the BAliBASE benchmark (although MSAs are inferred from the full sequences) and for simulated data it is the true MSA taken as output from the simulation program. A TP is defined as a pair of characters that co-occur in a column of the reference MSA and in any column of the inferred MSA. A FP is defined as a pair of characters that co-occur in any column of the inferred MSA and are both present in the reference, but not in the same column. (This implies that an alignment between an amino acid from the core region and noncore region of the BAliBASE reference is not classified as a FP.) We clarify this approach further with an example, where the reference MSA contains three sequences across three columns. The first column, R1 = {F1, F2, F3}, is in the flanking region (not the core), whereas the second column and third columns consist of the core region, R2 = {C1.1, C2.1, C3.1} and R3 = {C1.2, C2.2, C3.2}. In the inferred MSA, we have four columns, M1 = {F1, F2, -}, M2 = {C1.1, -, F3}, M3 = {C1.2, C2.1, C3.1}, and M4 = {-, C2.2, C3.2}. The treatment of the core can be considered as removing all flanking sites and replacing them with “-” characters. The resulting pairwise homologies consist of the TPs (C2.1, C3.1) and (C2.2, C3.2); the FPs (C1.2, C2.1) and (C1.2, C3.1); and (C1.1) is not aligned with anything.

These definitions are in line with the standard sum-of-pairs score that has long been used to evaluate MSAs (Thompson et al. 1999). The TPR is the fraction of TPs in the filtered reference MSA relative to the total possible TPs in the unfiltered reference MSA, whereas the FPR is the fraction of FPs in the filtered MSA relative to the total possible FPs in the unfiltered MSA. For any given reference MSA, inferred MSA and filtered inferred MSA we can calculate the TPR and FPR and varying the thresholds of the filtering method allows us to plot ROC curves. The AUC of the ROC curve is a measure of the overall TPR and FPR over a range of thresholds and is representative of the overall performance of a binary classification algorithm.

To calculate tree accuracy for the pseudo-Felsenstein-zone trees—see Hossain et al. (2015)—from simulated data we examine the three possible arrangements of subtrees around the critical branch and compute their likelihoods, with the highest likelihood arrangement(s) being the ML estimate(s). The score for each topology is the number of times each topology is the ML estimate. For ties, where several topologies score within a computational threshold of $1.0\mathrm{E}-4$, each is considered equally likely and the score is evenly distributed among the tied trees. In other words, if there were two ML estimated trees then each would gain a score of (1/2=) 0.5. The probability of the true tree is taken to be the total score for the true simulated tree divided by the total number of simulated data sets.

To assess the effect of filtering on real data, we examine the geodesic distance between trees estimated from two MSAs obtained using MAFFT-linsi and Prank aligners. Given that both MSAs were obtained from the same data, this distance is intended to measure the disagreement between the tree estimates contributed by the MSA. The geodesic distance accounts for both differences in tree topologies as well as edge lengths by using the concept of continuous tree space when comparing phylogenies (Billera et al. 2001). Tree estimates are obtained from the popular RAxML tree estimating software using mostly default parameters and LG + Γ model of sequence evolution (PROTGAMMALG option) (Stamatakis 2014), with the likelihood threshold set to 1.0E-6. Geodesic distances were calculated using Megan Owen and Scott Provan’s java implementation of their GTP algorithm (Owen and Provan 2011).

In order to establish the proportion of residue pairs retained after filtering, we apply divvying and partial filtering to a range of MSAMs. To this end, we use core protein regions (excluding N- and C-termini) from the data sets from BAliBASE sequence database. We apply our method to the reference (true) structural alignments, MAFFT in the fast FFT-NS and accurate L-INS-i mode. Furthermore, we use T-Coffee, Probcons, and Prank alignments.

Programs and Settings

This study uses out-of-the-box settings for MSA methods and filtering software, unless specified elsewhere, since this is how the majority of researchers will use them. For MSA methods, we use PRANK version 140603 (Löytynoja and Goldman 2008) and MAFFT version 7.2733 (Katoh and Standley 2013). For filtering methods, we use GUIDANCE2 (Sela et al. 2015), Zorro (Wu et al. 2012), TrimAl (Capella-Gutierrez et al. 2009), and GBlocks (Castresana 2000). For phylogenetic analysis, we use RAxML version 8.2.9 (Stamatakis 2014). For simulating data, we use INDELible version 1.03 (Fletcher and Yang 2009). All other computational analyses were conducted using custom scripts.

Real Data

We use both real and simulated data to assess the impact of filtering methods on alignment accuracy and downstream phylogenetic inference. To assess the accuracy of retaining TPs and removing FPs of filtering methods for real data, we use the data sets (Ref11, Ref12, Ref20, Ref30, and Ref50) with structurally verified regions of BAliBASE benchmark database (Thompson et al. 2005). The BAliBASE data are more highly divergent than those typically used in a phylogenetic study so can be considered an upper bound on the difficulty of the problem.

For studying effects of divvying and filtering on accuracy of phylogeny inference, we use the avian phylogenomics data set consisting of one-to-one orthologous sequences (Jarvis et al. 2014). The original data consist of 8,251 syntenic and orthologous protein families from 48 avian species and 4 outgroup species, but we selected only families with genes present in all species to allow clearer comparisons after tree inference. From the remaining 1,340 protein families, we extracted raw sequence data from the original unfiltered SATé + PRANK alignments and applied our MSA and filtering methods to those sequences.

Simulated Data

We simulate our sequence alignments using INDELible, which generates data based on a probabilistic model of substitutions and insertions/deletions. This model can be considered similar to a pair-HMM, although there are differences in the structure and parameterization of the model of insertions and deletions. For insertions and deletions, we use negative binomial gap model with the gap lengths being geometrically distributed. During this study, we use two related simulation schemes.

In the first scheme, we examine the effect of divergence on filtering methods (fig. 3) and simulate six 100-replicate data sets for each divergence examined under the LG + Γ model with 4 discrete rate categories. The divergence categories represent tree heights of 0.25, 0.5, 1.0, 2.0, 4.0, and 8.0 expected substitutions per amino acid site. The α parameter from the Γ distribution was drawn from the normal distribution $\mathcal{N}(0.8,0.2)$. The 16-taxa trees were simulated through Yule pure birth process using Dendropy (Sukumaran and Holder 2010) with the birth rate being converted to the expected tree height for each of the six categories. The remaining parameters in the simulation were inspired by BAliBASE and varied for each replicate. The length of the root sequence and the proportions of N, C, and core (structural) regions were equal to those in BAliBASE database and were drawn at random for each of the replicate from the list of lengths of core, N, and C regions in the benchmark database. The indel rate parameter was drawn from $\mathcal{N}(0.02,0.005)$ for core and $\mathcal{N}(0.025,0.0075)$ for N- and C-termini. Core gap length distribution parameter was drawn from $\mathcal{N}(0.5,0.05)$ and for N and C regions from uniform distribution between 0.5 and 0.9.

The second simulation scheme we use to measure whether filtering methods can correct for phylogenetic long branch attraction artifacts introduced through alignment. The evolutionary parameters—the tree topology, the substitutions model, and the indel rate—were chosen to match those of Hossain et al. (2015), who first demonstrated long branch attraction through alignment. In this case, we take 200 samples at different sequence lengths to examine the statistical properties of the tree estimate under different filtering schemes, specifically whether there is evidence of the estimator converging as more data (sequence length) is added. To aid reproducability we provide the INDELible control file for sequence length 5,000.