GPU-Accelerated Implementation of Continuous Constant pH Molecular Dynamics in Amber: pK_a Predictions with Single-pH Simulations

Abstract

We present a GPU implementation of the continuous constant pH molecular dynamics (CpHMD) based on the most recent generalized Born implicit-solvent model in the pmemd engine of the Amber molecular dynamics package. To test the accuracy of the tool for rapid pK_a predictions, a series of 2-ns single-pH simulations were performed for over 120 titratable residues in 10 benchmark proteins that were previously used to test the various continuous CpHMD methods. The calculated pK_a’s showed a root-mean-square deviation of 0.80 and correlation coefficient of 0.83 with respect to experiment. 90% of the pK_a’s were converged with estimated errors below 0.1 pH units. Surprisingly, this level of accuracy is similar to our previous replica-exchange simulations with 2 ns per replica and an exchange attempt frequency of 2 ps⁻¹ (Huang, Harris and Shen, J Chem Info Model, 2018). Interestingly, for the linked titration sites in two enzymes, although residue-specific protonation state sampling in the single-pH simulations was not converged within 2 ns, the protonation fraction of the linked residues appeared to be largely converged, and the experimental macroscopic pK_a values were reproduced to within 1 pH unit. Comparison with replica-exchange simulations with different exchange attempt frequencies showed that the splitting between the two macroscopic pK_a’s is underestimated with frequent exchange attempts such as 2 ps⁻¹, while single-pH simulations overestimate the splitting. The same trend is seen for the single-pH vs. replica-exchange simulations of a hydrogen-bonded aspartyl dyad in a much larger protein. A 2-ns single-pH simulation of a 400-residue protein takes about one hour on a single NVIDIA GeForce RTX 2080 graphics card, which is over 1000 times faster than a CpHMD run on a single CPU core of a high-performance computing cluster node. Thus, we envision that GPU-accelerated continuous CpHMD may be used in routine pK_a predictions for a variety of applications, from assisting MD simulations with protonation state assignment to offering pH-dependent corrections of binding free energies and identifying reactive hot spots for covalent drug design.

Graphical Abstract

INTRODUCTION

Molecular dynamics (MD) simulations are widely used in structure-based drug design and to understand biophysical processes on a molecular level,^1,2 but one weakness of the most common simulations is that they require the protonation states of the titratable sites to be fixed. Typically, the protonation states of these residues are set to match those of model compounds representing single amino acids in water at pH 7, but these states may not be correct, as the pK_a of a titratable site in the protein environment may differ significantly from the model pK_a in solution. Sometimes, structure-based pK_a prediction tools, such as the empirical method Propka³ and the Poisson-Boltzmann solver based methods APBS-PDB2PQR,⁴ H++,⁵ and DelPhiPKa,⁶ are used to obtain estimates of the protonation states prior to running simulations; however, these tools do not directly account for the dynamic flexibility of the protein, which may lead to incorrect assignment of protonation states. Most importantly, even if the initial assignment is correct, protonation states may change in the course of conformational dynamics, as demonstrated in pH-dependent protein folding,^7,8 protein-ligand binding,^9–11 enzyme catalysis,¹² and ion/substrate transport across the membrane.^13,14

One solution to the above problems is to use constant pH molecular dynamics (CpHMD) methods to determine protonation states on the fly during the MD simulation.^15–20 CpHMD methods treat the pH as a macroscopic thermodynamic variable of the simulation, similar to how temperature and pressure are commonly handled in MD simulations. By linking the protonation states of the titratable residues to the solute conformation, the effects of conformational flexibility on the pK_a estimates are explicitly taken into account. Several CpHMD methods have been developed in the past, and they generally fall into two categories: The Monte-Carlo based methods,^15,16,18,20 which maintain a constant pH by periodically attempting Metropolis Monte Carlo moves to protonate or deprotonate titratable sites and continuous CpHMD,^17,21–26 which is rooted in the λ-dynamics method for free energy calculations²⁷ and treats the protonation states of the titratable sites as continuous dynamic variables of the system. Continuous CpHMD lets systems escape local energy minima by allowing transient access to partially protonated states which are unphysical and must be discarded from the final pK_a calculations. In contrast, Monte-Carlo based CpHMD allows only fully protonated or deprotonated states, but as a result they tend to converge more slowly. Additionally, the proper way to extend these methods to fully explicit solvent is unclear.^19,20 A more extensive discussion of the various CpHMD methods can be found in the reviews.^28,29

Both Monte-Carlo and continuous CpHMD simulations have historically required some enhanced sampling technique, such as temperature-^30,31 or pH-based replica exchange,^22,32 to obtain converged pK_a estimates. However, at the present time, replica exchange is not necessarily attractive for computation on Graphics Processing Units (GPUs), as in some molecular dynamics packages, including Amber, each replica requires a separate graphics card, and to ensure frequent exchange between neighboring replicas, a large number of parallel replicas are sometimes needed. Such simulations would require a relatively expensive GPU cluster and could prevent the method from being widely used.

Here we present the first implementation of the generalized Born (GB) based continuous CpHMD method in the GPU-accelerated pmemd program³³ of the Amber molecular dynamics (MD) package.³⁴ The performance of the code was benchmarked in pK_a predictions for Asp, Glu, and His sidechains of 10 small and medium sized proteins. Considering that common users may not have access to a GPU node equipped with multiple GPU cards, single pH titration simulations were used. We restricted the simulation length to 2 ns to facilitate comparison with our previous work, where the pK_a’s were calculated using pH replica-exchange (pH-REX) titration simulations of 2 ns per replica on the CPUs.³⁵ We note that even though the time scale for conformational rearrangements in implicit solvent is much shorter than in explicit solvent, 2 ns may be insufficient for conformational relaxation to specific pH conditions, particularly for buried residues and those undergoing strong electrostatic or hydrogen-bond interactions. However, the objective of this work is to demonstrate the tool not for constant pH simulations but for pK_a predictions given a user-specified simulation time, e.g, 2 ns. Encouragingly, despite the short simulation length, the calculated pK_a values of ten benchmark proteins agree well with our previous pH-REX results and experimental data. Interestingly, although the microscopic pK_a’s for the linked residues in two enzymes were not converged, the single-pH simulations were able to reproduce the experimentally observed macroscopic pK_a’s. On a single NVIDIA 2080 graphics card, a 2-ns single-pH simulation of a 400-residue protein takes about one hour. Thus, we envision the GPU-accelerated continuous CpHMD tool will be routinely applied to predict pK_a’s on commodity hardware.

METHODS AND PROTOCOLS

The Compute Unified Device Architecture (CUDA) code of the GB molecular dynamics method in the pmemd.cuda program³³ of Amber (version 2018)³⁴ was modified. The energies, forces, and other numbers computed with the code matched those given by our CPU implementation, subject to the precision differences between the GPU and CPU code. As in the CPU implementation, the code is currently limited to using the GB-Neck2 model³⁶ for both conformational and titration dynamics. Although the method does not impose a limit on the total number of titration sites, the maximal number of titratable sites is currently set to an arbitrary number 1000 (Asp/Glu has 2 titratable groups due to double-site titration), which however can be changed in the future.

We performed single-pH simulations on 11 proteins: the 36-residue villin headpiece subdomain (HP36, pdbid 1VII), 45-residue binding domain of 2-oxoglutarate dehydrogenase multi-enzyme complex (BBL, pdbid 1W4H), 56-residue N-terminal domain of ribosomal protein L9 (NTL9, pdbid 1CQU), 56-residue turkey ovomucoid third domain (OMTKY, pdbid 1OMU), 105-residue reduced form of human thioredoxin (pdbid 1ERT), 129-residue hen egg-white lysozyme (HEWL, pdbid 2LZT), 143-residue hyperstable Δ+PHS variant of staphylococcal nuclease (SNase, pdbid 3BDC), 124-residue ribonuclease A (RNase A, pdbid 7RSA), 155-residue E. coli ribonuclease H (RNase HI, pdbid 2RN2), 185-residue oxidized form of Bacillus circulans xylanase (xylanase, pdbid 1BCX), and 389-residue unbound β-secretase 1 catalytic domain (BACE1, pdbid 1SGZ). These proteins have been previously used to validate our CPU implementation of the same continuous CpHMD method.³⁵

The initial structures for the simulations were taken from our previous paper.³⁵ We started from the PDB coordinates by adding acetylated N terminus and amidated C terminus caps, building any disulfide bonds, and adding hydrogens with the CHARMM program (version c42a1).³⁷ The protonation states of the titratable residues were set so that Asp/Glu were deprotonated and His/Lys/Arg/Cys/Tyr were protonated. The structures then underwent 50 steps of steepest descent minimization in GBSW implicit solvent³⁸ with a harmonic force constant of 50 kcal/mol/Ų applied to each heavy atom. Next, dummy atoms were added to the Asp/Glu residues, and the structure was minimized for 10 steps of steepest descent and 10 steps of Newton-Raphson minimization. These final structures were then converted to the structure files with the Leap utility in Amber.³⁴

All simulations used the Amber ff14SB force field³⁹ and the GB-Neck2 implicit-solvent model.³⁶ All bonds containing hydrogens were constrained with the SHAKE algorithm,⁴⁰ the salt concentration was set to 0.15 M, and a 2 fs timestep was used. For the 2 proteins without His residues (HP36 and NTL9), 14 single-pH simulations were run with pH 1–7.5 in 0.5 unit increments, and for the other proteins 18 simulations were run with pH 1–9.5 in 0.5 unit increments. Each simulation lasted 2 ns except for BACE1 simulations which were extended to 10 ns each. The CpHMD settings and options were the same as in our previous replica-exchange simulations,³⁵ except that the latter also employed a pH replica-exchange protocol, in which exchanges between adjacent pH replicas were attempted every 250 MD steps (exchange attempt frequency of 2 ps⁻¹). In the current work, we performed additional replica-exchange simulations for SNase and RNase H with exchanges attempted every 500 and 1000 MD steps which correspond to the exchange attempt frequencies of 1 ps⁻¹ and 0.5 ps⁻¹, respectively. Larger pH ranges were used in the replica-exchange simulations. For the 2 proteins without His, 16 replicas were used with pH 0–7.5 in increments of 0.5 units, and for the other proteins 20 replicas with pH ranging from 0–9.5 in increments of 0.5 units were used.

To calculate pK_a’s, the probability of deprotonation (unprotonated fraction) was fit to the generalized Henderson-Hasselbalch (HH) equation, as in our previous work.³⁵ For simplicity, the word generalized will be omitted in later discussions. The statistical errors in the pK_a’s were estimated from the covariances of the fit parameters. For the macroscopic pK_a of histidine, the total unprotonated fraction was used in the fitting. For the pK_a’s of HID and HIE, the fractions of the respective tautomers were used (see more explanation in the footnote of Table 1).

Table 1:

Calculated pK_a’s of the model alanine pentapeptides from the GPU single-pH simulations compared to the CPU replica-exchange results and experiment

	GPU		CPUc	Exptd
	Fita	Bootstrapb
Asp	3.7±0.03	3.7±0.10	3.8±0.05	3.67±0.04
Glu	4.2±0.02	4.2±0.06	4.1±0.05	4.25±0.05
His	6.3±0.03	6.3±0.10	6.4±0.03	6.54±0.04
HIDe	7.0±0.03	7.0±0.08	7.0±0.05	n/d
HIEf	6.4±0.03	6.4±0.11	6.5±0.02	n/d

^apK_a’s and errors from the fitting of all data points (see main text).

^bpK_a’s and errors from a bootstrap procedure (see main text).

^cpK_a’s from our previous replica-exchange simulations with errors calculated as the standard deviations of the pK_a’s from five sets of replica-exchange simulations.³⁵

^dNMR-determined pK_a’s by Thurlkill et al.⁴¹ These pK_a’s were used as the reference (model) values in our simulations.

^eThe pK_a of HID is associated with HIP ⇋ HID.

^fThe pK_a of HIE is associated with HIP ⇋ HIE.

RESULTS AND DISCUSSION

Titration simulations of model peptides.

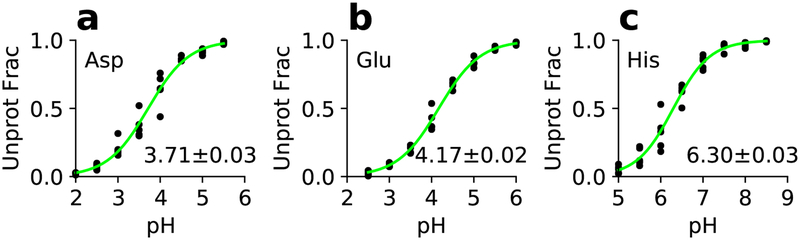
First, we verified that the GPU-based single-pH titration simulations with the model parameters from our previous work³⁵ can reproduce the reference experimental pK_a’s of model alanine pentapeptides, CH₃CO-Ala-Ala-X-Ala-Ala-NH₂, where X represents Asp, Glu, or His. These reference pK_a’s are also referred to elsewhere as model or solution pK_a’s. For each pentapeptide, 5 independent 2-ns titration simulations were performed at each of the 8 evenly spaced pH conditions with an interval of 0.5 units, in the pH ranges 2–5.5 for Asp, 2.5–6 for Glu, and 5–8.5 for His. Fig. 1 displays the unprotonated fraction versus pH (titration data) for each residue and the least-square fit to the HH equation. Fitting of all 40 data points for each peptide returned a pK_a of 3.71 for Asp, 4.17 for Glu, and 6.33 for His. These pK_a’s are within 0.1 units of the previous CPU-based replica-exchange pK_a’s and within 0.2 units of the experimental values (Table 1). This level of agreement is acceptable and therefore we decided that we could use the previously derived model parameters for the titration simulations of proteins.

Figure 1: Simulated titration data for the model alanine pentapeptides in solution.

Unprotonated fraction as a function of pH for Asp (a), Glu (b), and His (c). Green curves are the best fits to the HH equation. The calculated pK_a’s based on all five sets of titration data and the fitting errors are shown.

Error estimates for the model pK_a’s.

From the least-square fit of five titration datasets (40 data points) to a single HH equation, an error for the pK_a, i.e., fitting parameter, can be obtained. This fitting error is below 0.03 for model Asp, Glu, and His, demonstrating a high precision of the pK_a (Fig. 1). We were also interested in the error (reproducibility) of the calculated pK_a given only one titration dataset (one data point for each pH). To address this question, a bootstrap method was used, where the unprotonated fractions at different pH were combined to generate every possible combination out of 5⁸ virtual sets of titration data, where 5 is the number of simulations per pH and 8 is the number of pH conditions. Thus, 5⁸ pK_a’s were obtained, from which an average and standard deviation were calculated (Figure S3). As expected, the bootstrap procedure gave identical pK_a’s but larger errors compared to those obtained from the best fits of all five datasets (Table 1). The bootstrap errors are only somewhat larger than the standard deviations from the CPU replica-exchanges simulations,³⁵ which is surprising, as previous work based on the continuous CpHMD in CHARMM,^21,30 which uses the GBSW model³⁸ and CHARMM22 protein force field⁴² as well as the discrete CpHMD in Amber, which employs the GB-OBC model⁴³ (igb=2)^31,32 and Amber99SB force field⁴⁴ indicated that the single-pH model titration data are very noisy, with errors much larger than those from the replica-exchange simulations. We will continue the discussion of pK_a convergence and error in the context of protein titration simulations.

Timing of the GPU-accelerated simulations.

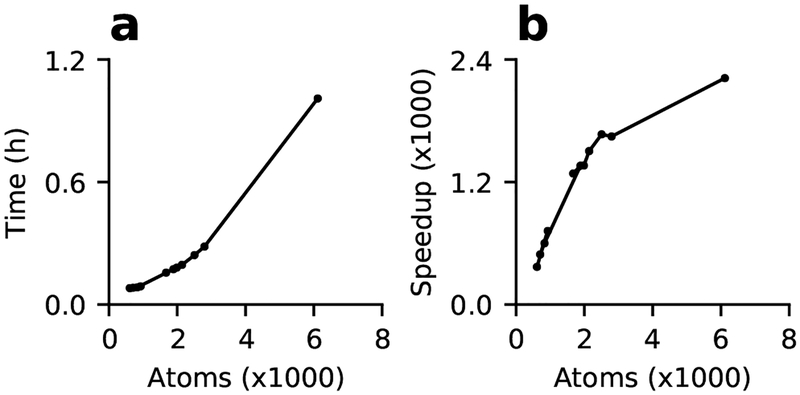
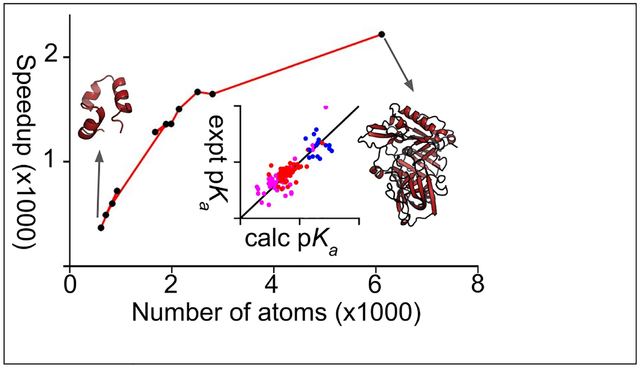
To demonstrate the feasibility of GPU CpHMD titration for routine use on a single desktop equipped with a graphics card, we examined the wall clock time of 2-ns simulations of the benchmark proteins on a Nvidia GeForce RTX 2080 graphics card. The GPU wall clock time increases with the system size, from 5 minutes for the 36-residue HP39 to 17 minutes for the 185-residue xylanase, and about one hour for the 389-residue BACE1 (Fig. 2a). Compared to a single core on the AMD Opteron 6276 processor cluster node, the wall-clock speedup on the GPU increases with system size and reaches about 2400 times. Thus, CpHMD simulations no longer require a high-performance computing cluster and are significantly more cost effective on commodity GPUs.

Figure 2: Timing of the GPU-based titration simulations.

(a) The time (in hours) required to run a 2-ns single-pH simulation on a single NVIDIA Geforce 2080 graphics card for the 11 proteins discussed in the main text. (b) GPU speedup relative to one core on the AMD Opteron 6276 processor node with 64 cores. The simulations ran on 2–8 cores and the time was extrapolated to one core.

We compared the speed of the GPU CpHMD titration with the GPU-accelerated GBSW-based continuous CpHMD^21,30 in the CHARMM-OpenMM interface.⁴⁵ The latter implementation was reported to output a trajectory of about 81 ns/day for SNase on a Nvidia GeForce GTX 780 Ti graphics card.⁴⁵ Using our implementation, SNase ran at 250 ns/day on an RTX 2080 card. Considering the difference in single-precision floating point operations per second (FLOPS) between 780 Ti and 2080 cards (5.3 vs. 10.1) and the Amber benchmark data for GB simulations on various graphics cards (http://ambermd.org/GPUPerformance.php), we estimated the speed of our GPU implementation to be slightly faster than the implementation in the CHARMM-OpenMM interface.

Protein titration simulations: overall comparison to the replica-exchange simulations and experiment.

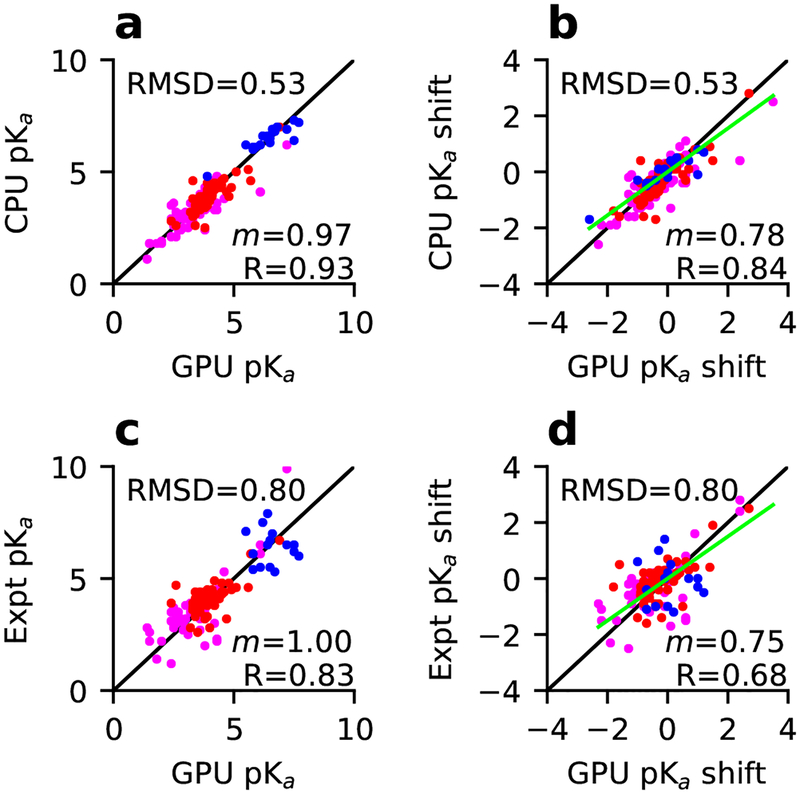
We performed single-pH titration simulations of 10 benchmark proteins, comprising 4 small proteins and 6 enzymes, on a single GPU card. Each protein was run for 2 ns at single pH values between 1 and 7.5/9.5, with a pH spacing of 0.5 units. We compared the calculated pK_a’s to our previous replica-exchange simulations on CPUs,³⁵ which used the same amount of sampling (2 ns per replica, with replicas separately by 0.5 pH units) (Table 2). Assuringly, the pK_a’s are very similar, with a root-mean-square deviation (RMSD) of 0.54, linear regression slope (m) of 0.97 and Pearson’s correlation coefficient (R) of 0.93 (Fig. 3a). The comparisons for Asp, Glu, and His pK_a’s are given in Table 3. In terms of the pK_a shifts relative to the model values, a comparison between the GPU single-pH simulations and CPU replica-exchange simulations gives m of 0.78 and R of 0.84.

Table 2:

Protein pK_a’s calculated from the GPU single-pH simulations compared to the CPU replica-exchange simulations and experiment^a

Residue	Expt	REX	Single	Residue	Expt	REX	Single	Residue	Expt	REX	Single	Residue	Expt	REX	Single
BBL				HP36				OMTKY				HEWL
Asp129	3.9	2.8	3.3(0.09)	Asp44	3.1	2.1	2.4(0.06)	Asp8	2.7	2.5	2.9(0.08)	Glu7	2.6	3.5	3.5(0.04)
Glu141	4.5	4.1	3.9(0.04)	Glu45	4.0	3.7	3.8(0.02)	Glu11	4.1	3.9	4.1(0.02)	His15	5.5	6.5	6.5(0.03)
His142	6.5	6.9	7.2(0.01)	Asp46	3.5	3.6	3.2(0.03)	Glu20	3.2	3.7	3.8(0.05)	Asp18	2.8	1.1	1.4(0.02)
Asp145	3.7	2.6	2.5(0.06)	Glu72	4.4	4.1	4.1(0.05)	Asp28	2.3	3.6	4.3(0.05)	Glu35	6.1	4.6	5.7(0.06)
Glu161	3.7	3.3	3.6(0.07)					Glu44	4.8	4.6	4.5(0.02)	Asp48	1.4	1.8	1.8(0.02)
Asp162	3.2	3.2	2.6(0.06)	RNase A				His53	7.5	6.6	6.2(0.07)	Asp52	3.6	3.3	3.8(0.03)
Glu164	4.5	4.0	4.1(0.10)	Glu2	2.8	3.2	3.2(0.09)					Asp66	1.2	2.1	2.4(0.15)
His166	5.4	6.0	5.8(0.04)	Glu9	4.0	3.4	3.8(0.03)	RNase H				Asp87	2.2	1.8	2.0(0.17)
				His12	6.2	6.4	7.5(0.04)	Glu6	4.5	4.3	4.9(0.29)	Asp101	4.5	4.8	4.3(0.06)
NTL9				Asp14	2.0	2.4	3.8(0.08)	Asp10*	6.1	4.8	7.1(0.18)	Asp119	3.5	2.4	2.7(0.10)
Asp8	3.0	2.1	2.6(0.04)	Asp38	3.5	2.8	2.6(0.08)	Glu32	3.6	3.2	3.3(0.09)
Glu17	3.6	3.4	3.5(0.04)	His48	6.0	7.2	7.7(0.06)	Glu48	4.4	2.5	3.8(0.12)	SNase
Asp23	3.1	2.9	2.9(0.08)	Glu49	4.7	2.6	2.6(0.05)	Glu57	3.2	4.1	4.7(0.06)	His8	6.5	6.5	6.4(0.06)
Glu38	4.0	3.6	3.6(0.09)	Asp53	3.9	4.3	3.8(0.02)	Glu61	3.9	2.8	2.4(0.05)	Glu10	2.8	3.7	4.0(0.02)
Glu48	4.2	3.8	4.0(0.06)	Asp83	3.5	2.9	2.4(0.07)	His62	7.0	6.9	6.6(0.07)	Asp19*	2.2	1.8	1.5(0.17)
Glu54	4.2	3.8	3.9(0.02)	Glu86	4.1	3.5	3.4(0.03)	Glu64	4.4	3.1	3.4(0.04)	Asp21*	6.5	4.1	6.1(0.17)
				His105	6.7	6.3	6.5(0.07)	Asp70*	2.6	2.6	1.7(0.17)	Asp40	3.9	2.8	3.2(0.09)
Thioredoxin				Glu111	3.5	3.5	3.6(0.03)	His83	5.5	6.2	6.1(0.05)	Glu43	4.3	3.7	3.7(0.10)
Glu6	4.8	3.9	4.8(0.11)	His119	6.1	6.1	5.8(0.03)	Asp94	3.2	3.2	3.0(0.07)	Glu52	3.9	3.9	3.8(0.04)
Glu13	4.4	4.4	4.5(0.03)	Asp121	3.1	3.5	2.4(0.02)	Asp102	<2.0	3.4	3.5(0.15)	Glu57	3.5	3.4	3.5(0.02)
Asp16	4.0	4.0	4.1(0.06)					Asp108	3.2	3.1	3.0(0.04)	Glu67	3.8	4.5	4.2(0.01)
Asp20	3.8	2.9	3.0(0.01)	Xylanase				His114	<5.0	7.0	6.8(0.05)	Glu73	3.3	3.9	3.8(0.04)
Asp26	9.9	6.2	7.2(0.27)	Asp5	3.0	3.3	4.2(0.06)	Glu119	4.1	3.9	3.8(0.04)	Glu75	3.3	2.6	3.4(0.22)
His43	n/d	6.1	5.9(0.03)	Asp12	2.5	2.5	3.1(0.06)	His124	7.1	6.2	5.5(0.06)	Asp77	<2.2	1.9	2.0(0.07)
Glu47	4.1	4.3	4.4(0.04)	Glu79	4.6	5.1	5.6(0.10)	His127	7.9	6.6	6.4(0.02)	Asp83	<2.2	2.1	2.6(0.31)
Glu56	3.3	4.5	3.9(0.21)	Asp84	<2.0	3.4	3.9(0.08)	Glu129	3.6	4.6	3.3(0.05)	Asp95	2.2	4.3	4.3(0.11)
Asp58	5.3	3.8	4.6(0.25)	Asp102	<2.0	3.3	4.3(0.08)	Glu131	4.3	4.3	4.5(0.05)	Glu101	3.8	3.5	3.9(0.08)
Asp60	2.8	3.6	2.5(0.11)	Asp107	2.7	3.1	3.6(0.14)	Asp134	4.1	4.3	4.3(0.12)	His121	5.2	6.8	6.7(0.05)
Asp61	4.2	4.6	4.1(0.05)	Asp120	3.2	4.0	3.6(0.06)	Glu135	4.3	4.2	4.2(0.04)	Glu122	3.9	3.0	3.3(0.11)
Asp64	3.2	3.1	2.8(0.03)	Asp122	3.6	3.4	3.4(0.07)	Glu147	4.2	3.9	3.7(0.09)	Glu129	3.8	4.5	4.2(0.05)
Glu68	4.9	4.3	4.2(0.05)	His150	<2.3	4.8	3.9(0.09)	Asp148	<2.0	2.4	2.8(0.05)	Glu135	3.8	4.2	3.9(0.05)
Glu70	4.6	5.0	5.1(0.02)	His157	6.5	7.3	7.5(0.03)	Glu154	4.4	3.8	3.6(0.05)
Glu88	3.7	3.8	3.3(0.04)	Glu173	6.7	7.0	6.9(0.13)					all	mud	0.64	0.60
Glu95	4.1	3.5	3.9(0.02)					BACE1					rmsd	0.87	0.80
Glu98	3.9	3.9	3.6(0.07)					Asp32*	5.2	4.2	6.6(0.25)
Glu103	4.4	4.7	4.6(0.01)					Asp228*	3.5	2.4	<1

^aExperimental pK_a’s were taken from our previous work.³⁵ The REX data were taken from our previous replica-exchange simulations with an exchange attempt frequency (EAF) of 2 ps⁻¹.³⁵ The errors in the pK_a’s estimated from the least-square fits are given in parentheses. The statistics, mean unsigned deviation (mud) and root-mean-square deviation (rmsd) from the experimental values are calculated for residues with NMR determined pK_a’s. As such the two BACE1 residues are excluded. The linked residues are indicated by _* and their pK_a’s were obtained from the best fits to the coupled titration model (Equation 1).

Figure 3: Comparison of the pK_a’s and pK_a shifts from the GPU single-pH simulations to the CPU replica-exchange simulations or experiment.

The GPU pK_a estimates compared to (a) CPU and (b) experiment and the corresponding plots ((c) and (d)) for the pK_a shifts. The model pK_a’s from Thurlkill et al.⁴¹ were used for calculating the shifts. Data for Asp, Glu, and His resides are colored magenta, dark red, and blue, respectively. The diagonal (y = x) and linear regression lines are colored black and green, respectively. RMSD, regression slope (m) and Pearson’s correlation coefficient (R) are shown. The regression was performed with a zero intercept (R only changed in the second decimal point). In c and d, only pK_a’s with NMR determined pK_a’s are included. In d, the data for Asp26 in thioredoxin are hidden for clarity (the experimental pK_a shift > 4).

Table 3:

Comparisons of Asp, Glu, and His pK_a’s from the GPU single-pH simulations and CPU replica-exchange simulations and experiment^a

Res	N	maxd	mud	rmsd	R
Single vs. REX
Asp	48	2.0	0.49	0.66	0.84
Glu	54	1.3	0.28	0.42	0.84
His	18	1.1	0.35	0.44	0.90
Single (REX) vs. experiment
Asp	42	2.7 (2.1)	0.69 (0.75)	0.92 (1.06)	0.78 (0.71)
Glu	54	2.1 (1.2)	0.45 (0.54)	0.61 (0.70)	0.64 (0.53)
His	18	1.6 (1.5)	0.90 (0.67)	1.04 (0.81)	−0.08 (0.16)b

^aThe maximum unsigned deviation (maxd), mean unsigned deviation (mud), root-mean-square deviation (rmsd), and Pearson’s correlation coefficient (R) are listed. The replica-exchange (REX) statistics for His is taken from our previous work,³⁵ and those for Asp and Glu are recalculated. Only residues with NMR determined pK_a’s are included.

^bSee main text for discussion.

A comparison between the pK_a’s calculated form the single-pH simulations and experiment yields a RMSD of 0.80, m of 1.0 and R of 0.83 (Fig. 3c). The comparisons for Asp, Glu, and His pK_a’s are given in Table 3. A comparison of the corresponding pK_a shifts to experiment yields m of 0.75 and R of 0.68 (Fig. 3d). These statistics are comparable to those for our previous replica-exchange simulations, which had a RMSD of 0.87, R of 0.81 for pK_a’s, and R of 0.61 for pK_a shifts.³⁵ This finding is surprising, as previous work based on both continuous³⁰ and discrete^31,32 constant pH MD showed that the pK_a accuracies from single-pH simulations are much lower than those from temperature or pH replica-exchange simulations. We will continue the discussion later.

Analysis of the pK_a errors by residue types.

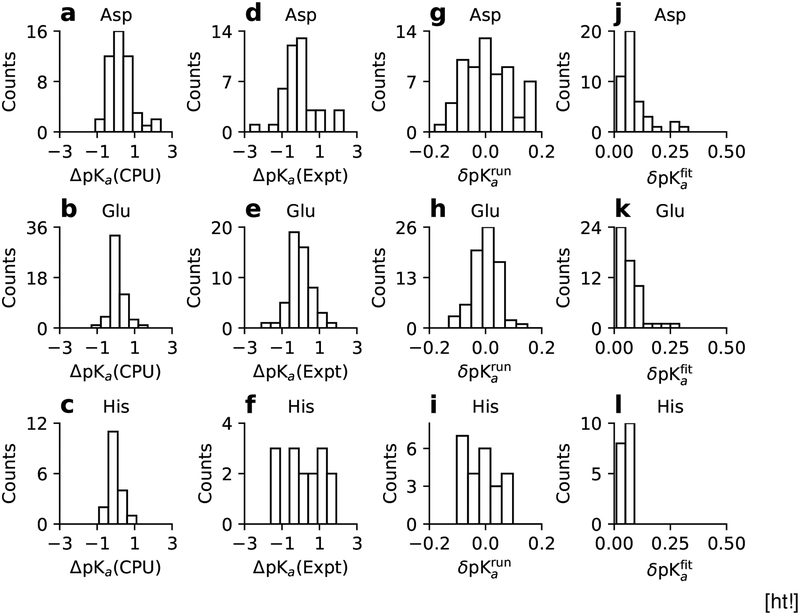
Now we examine the calculated pK_a’s of Asp, Glu, and His individually by calculating the comparison statistics (Table 3) and by plotting the histograms of the pK_a differences between the GPU single-pH and CPU replica-exchange simulations or experiment (Fig. 4). Assuringly, the histograms of the differences between the single-pH and replica-exchange pK_a’s for Asp, Glu, and His are peaked around 0 and span a range of −1 to 1 unit, with Asp showing a few data counts between 1–2. Both the comparison statistics and histograms of the differences between the single-pH and experimental pK_a’s (or pK_a errors) indicate differences among the three types of residues.

Figure 4:

(a-c) Comparisons of the Asp, Glu, and His pK_a’s from the GPU single-pH and CPU replica-exchange simulations(ΔpK_a(CPU) = GPU pK_a−CPU pK_a). (d-f) Comparisons of the single-pH results and experiment (ΔpK_a(Expt) = GPU pK_a−Expt pK_a). (g-i) Histograms of the convergence error estimates (δpK_a^run) obtained from the difference between the 2-ns and 1.5-ns pK_a’s. Asp26 of Thioredoxin (δpK_a^run =−0.34) falls off the plot. (j-l) Histograms of the statistical error estimates $\left(\delta \text{p}{K}_a^{\text{fit}}\right)$ from the pK_a fitting. The linked residues, Asp19/Asp21 in SNase and Asp10/Asp79 in RNase H, are excluded in the error estimates.

The distribution of the pK_a errors for His is broad and essentially flat, in contrast with those for Asp and Glu, which are narrower and peaked around 0. The rmsd of the His pK_a’s with respect to experiment is 1.04, larger than the rmsd of 0.92/0.61 for Asp/Glu pK_a’s. Significantly, there is essentially no correlation (correlation coefficient of −0.08 in Table 3) between the calculated and experimental pK_a’s for His, while the R value for Asp/Glu is 0.78/0.64. The performance of the single-pH simulations for His pK_a’s is slightly worse than the previous replica-exchange simulations (R of 0.16 and RMS error of 0.81).³⁵ Close examination revealed that salt bridges involving His are more persistent in single-pH as compared to replica-exchange simulations. In our previous work,³⁵ we found that the original GB-Neck2 parameters gave significantly higher pK_a’s for His involved in electrostatic interactions with acidic groups. Close examination revealed overstabilization of salt bridges involving His. Therefore, we decreased the imidazole hydrogen Born radius from 1.3 to 1.17 Å, following a similar modification of the Born radii of the guanidinium hydrogens of Arg which weakened the salt-bridge strength to a similar value as in explicit solvent.³⁶ Our modification of the His Born radius brought nearly all calculated His pK_a’s down and closer to experiment; however, for partially buried His involved in strong attractive electrostatic interactions, the pK_a’s remained somewhat overestimated. We suggested that the major source of error is the underestimation of desolvation energy, which results in an underestimated pK_a downshift (see a detailed analysis and discussion in our previous work³⁵). This is clearly an area that requires further testing and improvement.

Although Asp and Glu differ in only one methylene group, the histograms of the pK_a errors show noticeable differences. Most of the pK_a errors for Glu are within ±0.5 units and do not extend beyond ±1; however, there are several larger pK_a errors (above 2 units in magnitude) for Asp and the histogram appears to be somewhat skewed to the left (more negative errors). The sidechain of Asp is shorter than that of Glu by one methylene group and as a result, the carboxylate oxygen can form a hydrogen bond with its own or a neighbor backbone amide group. These sidechain-to-backbone hydrogen bonds were observed in our simulations with both Amber and CHARMM force fields. The hydrogen bond formation or breakage perturbs the protonation state of Asp and contributes to the larger fluctuation in the model peptide titration (Table 1) and perhaps also the protein titration simulations (Fig. 4a). In the parameterization of the GB-Neck2 model,³⁶ the strengths of the Glu· · · Lys and Glu· · · Arg salt bridges were examined; however, the strengths of the Asp· · · Lys and Asp· · · Arg salt bridges were not. As the structural differences in Asp and Glu lead to changes in the interactions formed by the sidechains, perhaps a slight adjustment is needed for the Asp parameters, which are currently the same as for Glu.

Most pK_a’s are converged within 2 ns but some require longer sampling time.

To assess the convergence of protonation-state sampling and pK_a’s, we examined the running estimates of the unprotonated fractions at different pH and the running estimates of the pK_a values (Fig. S6). The unprotonated fractions of a majority of the 120 residues with experimental values and the corresponding pK_a’s appear to stabilize within 2 ns. The convergence behavior seems comparable to the previous replica-exchange simulations,³⁵ consistent with the model peptide titration data discussed earlier. We note that pK_a, which is calculated by fitting unprotonated fractions from all pH conditions, converges more quickly than unprotonated fractions. For example, the pK_a of Asp162 in BBL is converged, although the unprotonated fraction at one of the pH conditions appears to slightly increase between 1 ns and 2 ns (Fig. S6). To quantify the convergence of the calculated pK_a’s, we plotted the histograms of the convergence error estimates, obtained as the pK_a differences between the 2-ns and 1.5-ns pK_a simulations for Asp, Glu, and His (Fig. 4g–i). The errors for Glu and His pK_a’s fall in the range of ±0.1. Except Asp19/Asp21 in SNase, Asp10/Asp70 in RNase H, and Asp26 in thioredoxin, the errors for Asp pK_a’s fall in the range of ±0.2. The slower convergence of the Asp pK_a’s compared to Glu pK_a’s is consistent with the larger deviations between the calculated and experimental pK_a’s of Asp. Curiously, the unprotonated fractions of Asp19/Asp21 in SNase and Asp10/Asp70 in RNase H are not converged and their titration data do not follow a single sigmoidal trend. We will come back to the discussion of these residues.

Higher mixed fractions are correlated with insufficient sampling.

One potential drawback of continuous CpHMD is the presence of mixed states, defined here as λ values between 0.2 and 0.8. Although mixed states are necessary and their presence can accelerate sampling, they are unphysical and a high occupancy of them may lower the accuracy of a CpHMD simulation. We were puzzled that the previous replica-exchanges simulations³⁵ showed somewhat higher mixed fractions than the continuous CpHMD simulations in CHARMM.³⁰ In contrast, the mixed fractions in the current single-pH simulations are very low, below 10% at all pH for a majority of residues (Fig. S6), consistent with the CpHMD simulations in CHARMM with a lower replica exchange frequency³⁰ (see later discussion). A few residues which showed a mixed fraction above 30% are: Asp26 of thioredoxin, Glu79/Asp84/His150 of xylanase, His114 of RNase H, and His12/His48 of RNaseA, and none of them displayed converged protonation-state sampling. The worst case is His150 of xylanase, which had a mixed fraction of 35 to 55% at pH below 6. His150 is deeply buried, with an experimental pK_a below 2.3, compared to the estimate of 3.9 from our 2-ns simulations. 2 ns is likely too short to complete the conformational rearrangement accompanying the protonation of His150. While the present data show that the mixed fractions are correlated with insufficient sampling, it remains to be seen if they decrease in much longer trajectories.

Statistical error estimates for the calculated pK_a’s.

Unlike replica-exchange titration, single-pH simulations are independent of each other and therefore the pK_a error obtained in the least-square fit of one set of titration data may be a good representation of the statistical error. To test this hypothesis, we performed an additional three sets of single-pH simulations at 9 evenly spaced pH conditions between 5 and 9 for RNase A to explore the statistical errors of the His pK_a’s. Table 4 lists the calculated pK_a’s and least-square fitting errors based on the original set of titration data and the pK_a’s and errors from the bootstrap procedure based on a total of 3⁹ virtual sets of titration data. The calculated pK_a’s deviate by 0.1 units at most and the fitting errors using one dataset are similar and highly correlated with the bootstrap errors. Although this test is not a rigorous proof, it suggests that the fitting error derived from a single set of titration simulations can be an approximate representation of the statistical error. The ease of obtaining error estimates is an advantage for single-pH over replica-exchange simulations, for which deriving error estimates is less straightforward. We list the pK_a fitting errors for all titratable residues in Table 2. The corresponding histograms are given in Figure 4j–l. Except for a handful of residues with fitting errors around 0.2–0.3, the errors are smaller than 0.1, demonstrating that the statistical noise in the calculated pK_a’s from the single-pH simulations is generally low.

Table 4:

Error analysis for the pK_a’s of histidines in RNase A.

Residue	Fita	Bootstrapb
H12	7.5±0.11	7.5±0.08
H48	7.6±0.14	7.7±0.13
H105	6.7±0.04	6.8±0.06
H119	5.6±0.07	5.7±0.06

^apK_a’s and fitting errors based on the first set of simulations.

^bpK_a’s and errors estimated from the bootstrap method using three sets of simulations.

Single-pH simulations could not converge microscopic pK_a’s but captured macroscopic pK_a’s of linked residues in SNase and RNase H.

A close examination of the residues that do not display a single sigmoidal trend, Asp19/Asp21 of SNase and Asp10/Asp70 of RNase H, revealed linked (coupled) titration, i.e., protonation of one residue is linked to the protonation of the other. As a result, the titration plot of one residue shows evidence of pH-dependent titration of the other residue and the transition from the fully protonated to the fully deprotonated persists over a very wide pH range (>4 pH units for Asp19/Asp21 in RNase and Asp10/Asp70 in RNase H, see Fig. 5 and Fig. 6). Interestingly, although the residue-specific unprotonated state fractions of of these linked residues are not converged (Fig. S6), the convergence of the total unprotonated fractions of the two linked residues is much better (Fig. S4 and S5).

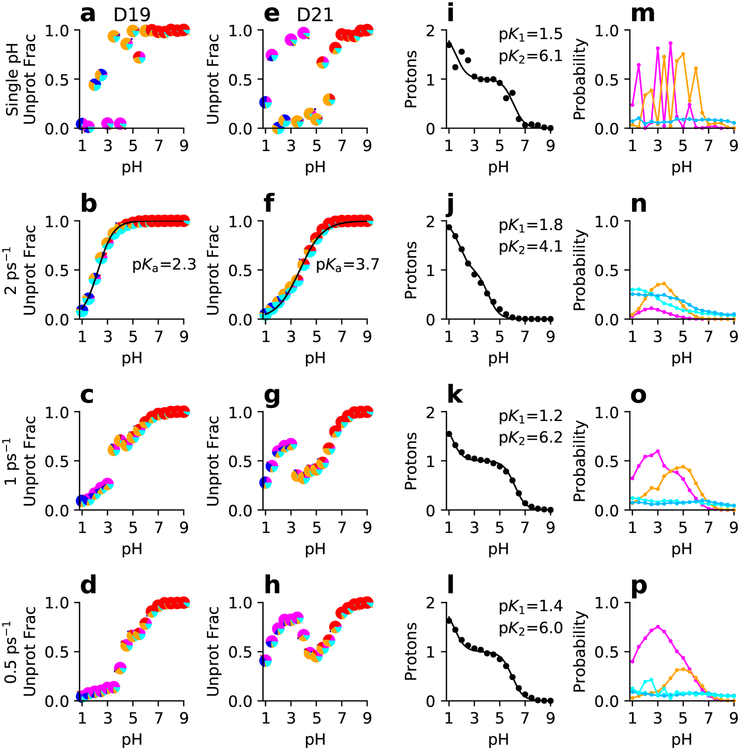
Figure 5: Titration data of the linked residues D19 and D21 in SNase from single-pH and replica-exchange simulations.

From top to bottom rows, single-pH and replica-exchange simulations with different exchange attempt frequencies are shown. (a-h) Unprotonated fraction as a function of pH and best fit to the residue-specific HH equation for D19 (a-d) and D21 (e-h). Each data point is a pie chart showing the probability of the four protonation states: D19^H/D21^H (blue), D19⁻/D21⁻ (red), D19^H/D21⁻ (magenta), and D19(−)/D21^H (orange). Cyan indicates that one of the residues is in a mixed state. (i-l) Total number of protons as a function of pH and best fit to the linked-titration model. (m-p) Probabilities of the singly-protonated (magenta for D19^H/D21⁻ and orange for D19⁻/D21^H) and mixed states (light cyan for D19 titration and dark cyan for D21 titration) as functions of pH. The macroscopic experimental pK_a’s are 2.2 and 6.5 for D19 and D21, respectively.

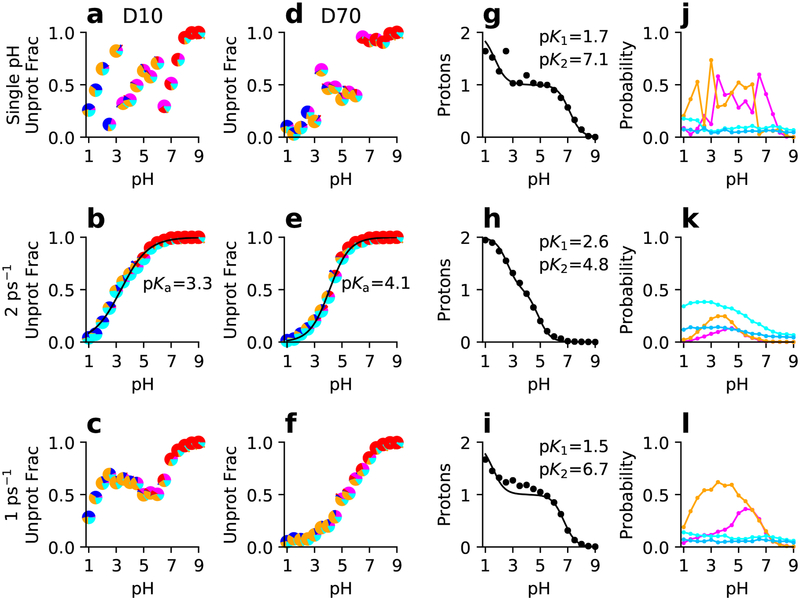
Figure 6: Simulated titration of the linked residues D10 and D70 in RNase H from single-pH and replica-exchange simulations.

From top to bottom rows, single-pH and replica-exchange simulations with different exchange attempt frequencies are shown. (a-f) Unprotonated fraction as a function of pH and best fit to the residue-specific HH equation for D10 (a-c) and D70 (d-f). Each data point is a pie chart showing the probability of the four protonation states: D10^H/D70^H (blue), D10⁻/D70⁻ (red), D10^H/D70⁻ (magenta), and D10(−)/D70^H (orange). Cyan indicates that one of the residues is in a mixed state. (g-i) Total number of protons as a function of pH and best fit to the linked-titration model. (j-l) Probabilities of the singly-protonated (magenta for D10^H/D70⁻ and orange for D10⁻/D70^H) and mixed states (light cyan for D10 titration and dark cyan for D70 titration) as functions of pH. The experimental macroscopic pK_a’s are 6.1 and 2.6 for D10 and D70, respectively.

For linked titration, the residue-specific microscopic pK_a’s cannot be experimentally determined. Rather, the signals, e.g., NMR chemical shifts, are fit to a coupled two-proton model, which results in two macroscopic pK_a’s representing the stepwise titration events.⁴⁶ To obtain macroscopic pK_a’s from simulations, the average number of protons bound to the two residues (N_prot) at different pH values can be fit to an analogous statistical mechanics model,^24,47,48

$$N_{\text{prot}}=\frac{{10}^{\text{p}{K}_2-\text{pH}}+2\times {10}^{\text{p}{K}_1+\text{p}{K}_2-2\text{pH}}}{1+{10}^{\text{p}{K}_2-\text{pH}}+{10}^{\text{p}{K}_1+\text{p}{K}_2-2\text{pH}}},$$ (1)

where the denominator is the partition function, and the fitting parameters, pK₁ and pK₂, are the macroscopic pK_a’s. The resulting macroscopic pK_a’s for the linked residues in SNase are 1.5 and 6.1 (Fig. 5i) and for those in RNase H are 1.7 and 7.1 (Fig. 6i). Note, linked titration events can also be studied by a decoupled-site model representing the sum of two HH equations.^49,50

To identify which residue should be assigned the higher pK_a, we can observe which residue becomes protonated first as pH decreases. For SNase, since the occupancy of Asp19⁻/Asp21^H is higher than Asp19^H/Asp21⁻ at pH above 4.5, i.e., Asp21 protonates first (Fig. 5m), Asp21 has the higher pK_a. Thus, we assigned Asp19 and Asp21 the pK_a’s of 1.5 and 6.1, in excellent agreement with the respective experimental assignment of 2.2 and 6.5. Similarly for RNase H, since the occupancy of Asp10^H/Asp70⁻ is higher than Asp10⁻/Asp70^H at pH above 6 (Fig. 5j), we assigned Asp10 and Asp70 the pK_a’s of 7.1 and 1.7, in good agreement with the respective experimental assignment of 6.1 and 2.6.

Comparison of single-pH and replica-exchange simulations with an exchange attempt frequency of 2 ps⁻¹.

Interestingly, the residue-specific titration data of Asp19/Asp21 in SNase (Fig. 5b and f) and Asp10/Asp70 in RNase H (Fig. 5b and e) from our previous replica-exchange simulations did not offer noticeable evidence of coupling. A comparison to the single-pH titration data reveals that the occupancies of the singly protonated states are much lower while those of the mixed states are much higher, up to 30% for SNase and up to 45% for RNase H in the pH range where two singly protonated states seem to compete in the single-pH simulations. The decreased amount of coupling seen in the replica-exchange simulations is consistent with the underestimation of the higher pK_a and the splitting between the low and high pK_a observed in experiment. Since the fraction of mixed states was much higher in the replica-exchange compared to single-pH simulations, we hypothesized that the underestimation of pK_a splitting could be due to insufficient sampling time for the conformation to relax to the specific pH conditions in the replica-exchange simulations. In these simulations,³⁵ the exchange attempt frequency (EAF) was every 250 MD steps (or 2 ps⁻¹), rather than every 500 (1 ps⁻¹) or 1000 MD steps (0.5 ps⁻¹), as used in our previous CHARMM-based CpHMD.³⁰ Our decision to increase EAF was inspired by the reported observation that high EAF improved pK_a estimates in the discrete-CpHMD simulations in Amber.³² We will come back to this discussion in Concluding Remarks.

A high frequency of exchange attempts may not allow sufficient conformational relaxation.

To test if the lack of conformational relaxation is responsible for the decreased amount of coupling in our previous replica-exchange simulations, we performed additional replica-exchange simulations with EAFs of 1 ps⁻¹ and 0.5 ps⁻¹ for SNase and EAF of1 ps⁻¹ for RNase H. As seen from Fig. 5 and 6, at the lower EAFs, the occupancies of the singly protonated states increase to similar levels as in the single-pH simulations, while the mixed fractions decrease to below 10% as in the single-pH simulations. Importantly, the higher macroscopic pK_a’s increase by about 2 units, to similar values as from the single-pH simulations of SNase and RNase H. The increased amount of coupling is also reflected in the noisier residue-specific titration data, which no longer conform to the one-proton HH equation. Additionally, the solvent-accessible surface areas (SASA) and number of hydrogen bonds of the two residues predicted by simulations with the lower EAFs of 1 and 0.5 ps⁻¹ agree more closely with the single-pH results than the simulations with the high EAF of 2 ps⁻¹ (Fig. S1 and Fig. S2), which offers a direct piece of evidence for the insufficient conformational relaxation for the coupled residue pairs with the EAF of 2 ps⁻¹. Interestingly, for both proteins, the nucleophile (residue with the lower pK_a) has a larger SASA and number of hydrogen bonds compared to the proton donor (higher pK_a), in agreement with the findings from CpHMD simulations using the CHARMM force field and the GBSW model.⁵¹

Having demonstrated that a high EAF may lead to insufficient conformational relaxation for linked residues, we wondered if the pK_a’s of other independent residues are affected as well. A comparison of the pK_a’s from the SNase simulations with different EAFs and single pH values (no exchange) showed that, although the differences are much smaller than for the couple residues, the pK_a’s from the two slower exchange (EAF of 1 and 0.5 ps⁻¹) simulations agree with each other and with the single-pH simulations much better as compared to the fast exchange (EAF of 2 ps⁻¹) simulations (Table S1). A similar trend is observed for the RNase H simulations (Table S1). These data are consistent with the findings in regards to the linked titration and support the notion that an EAF of 2 ps⁻¹ may not allow sufficient conformational relaxation. In other words, the relaxation time for adapting to changes of protonation states is likely above 0.5 ps for the tested proteins.

Hydrogen-bonded dyad in BACE1 requires enhanced sampling or significantly longer simulations.

To further test the ability of single-pH simulations to quantitatively reproduce the experimental apparent pK_a’s of coupled sites in enzymes, we performed titration simulations of BACE1, which is more than three times as large as HEWL, a frequently used benchmark protein for pK_a calculations,^16,32 and more than twice as large as xylanase, the largest protein among the 10 benchmark proteins studied here. Most importantly, the aspartyl dyad of BACE1 (Asp32 and Asp228) is subject to much stronger hydrogen bonding than the linked residues in SNase and RNase H.⁵¹ Our previous replica-exchange simulations with an EAF of 2 ps^{−1 35} and the hybrid-solvent continuous CpHMD in CHARMM¹² correctly predicted the pK_a order of the dyad but underestimated the two macroscopic pK_a’s and magnitude of their splitting. The current single-pH simulations also reproduced the experimental pK_a order; however, compared to the experimental data, the macroscopic pK_a assigned to Asp32 is too high by 1.4 units, and Asp228, which is the dyad residue with the lower pK_a did not protonate even at pH 1 (the lowest simulation pH). The latter may be attributed to a persistent hydrogen bond between the carboxylate oxygens of the dyad, whereby Asp228 was exclusively acting as a hydrogen bond acceptor (data not shown). The overestimation of the higher pK_a and underestimation of the lower pK_a, i.e, overestimation of the pK_a splitting, is consistent with the single pH simulations of the linked titration in SNase and RNase H. To attempt to break the hydrogen bond, we prolonged the single-pH simulations to 10 ns; however, while the pK_a of Asp32 remained largely unchanged, Asp228 remained deprotonated in the entire pH range (Figure S6). This data suggests that for buried, linked residues with strong hydrogen bonding, pH replica-exchange or significantly longer simulation length is required. Detailed exploration of linked titration involving strong hydrogen bonds is a topic of our future work.

Comparison of the 2-ns and 10-ns single-pH simulations of BACE1.

Although no experimental titration data are available for BACE1 except for the dyad pK_a’s, comparison of the 2-ns and 10-ns single-pH simulations may allow us to further assess the convergence behavior of pK_a calculations for larger proteins. Out of a total of 50 titratable residues, the majority showed negligible pK_a changes when extending the simulations from 2 to 10 ns; however, 10 residues showed pK_a changes of 0.5–1.5 units (Table S1). The second largest change is for Asp83; its pK_a increased from 2.2 based on the 2-ns simulations to 3.4 based on the 10-ns simulations. The latter is closer to the pK_a of 5.3 from the replica-exchange simulations (Table S1). Trajectory analysis revealed that in the first 2 ns, Asp83 sometimes formed a salt bridge with Arg96 at pH above 3, and as the simulation continued, the salt bridge became less frequently sampled. This trend continued throughout the 10-ns simulations, which explains why the calculated pK_a shows an increasing trend and it is not converged at 10 ns (Figure S6). This data suggests that for Asp83, a single-pH simulation requires longer than 10 ns to converge the pK_a, and replica-exchange simulations are effective in breaking the salt bridge and accelerating convergence.

The largest change is for His360, which has a pK_a of 4.7 based on the 2-ns simulations and the pK_a increased by 1.5 units to 6.2 based on the 10-ns simulations. Trajectory analysis showed that although starting out as largely buried, His360 became exposed to solvent in the prolonged simulations, which resulted in the pK_a increase. Curiously, the replica-exchange simulations gave a pK_a of 4.8, similar to the 2-ns single pH simulations. We hypothesize that His360 did not have sufficient time to become solvent exposed at low pH conditions due to the frequent exchange attempts, and that is why the calculated pK_a is similar to that from the 2-ns simulations. Another question is whether His360 becoming exposed to solvent is realistic. Our extensive replica-exchange simulations based on a hybrid-solvent CpHMD method in CHARMM indicated that this is not the case.^10,12 Although the GB-Neck2 model has been demonstrated to enable accurate folding of a set of small proteins,³⁶ explicit solvent representation remains more accurate and yields pK_a’s in better agreement with experiment.^18,22 Thus, prolonged CpHMD simulations may worsen the pK_a calculations as the conformational states deviate further from the crystal structure, as demonstrated by a previous discrete CpHMD simulation.¹⁸ Future work may shed more light on these issues.

CONCLUDING REMARKS

We presented and validated a GPU implementation of the generalized Born continuous CpHMD in the Amber pmemd.cuda program. A 2-ns single-pH simulation of a 400-residue protein runs in about 1 hour on a single NVIDIA Geforce 2080 graphics card, which represents a three-orders-of-magnitude speedup compared to the wall-clock time on a single CPU core of a high-performance computing cluster node (AMD Opteron 6276). Most calculated pK_a’s of Asp, Glu, and His sidechains of the 10 proteins from 2-ns single-pH simulations were converged and in close agreement (RMSD of 0.54) with our previous replica-exchange simulations on CPUs.³⁵ Compared to the experimental pK_a’s, the single-pH simulations gave a RMSD of 0.80 units, which is slightly lower than the RMSD of 0.87 from our previous replica-exchange simulations. Surprisingly, the errors in the protein pK_a’s from the single-pH simulations were generally small (below 0.2 units). This finding is in stark contrast to the reported data from the continuous CpHMD in CHARMM^21,30,52 and the discrete CpHMD in Amber,^31,32 which found that errors from single-pH simulations were much larger than those from replica-exchange simulations. Perhaps the most unexpected finding is that the single-pH simulations were able to correctly predict the pK_a order of the linked residues in SNase and RNase H and reproduce the experimental macroscopic pK_a’s to about 1 pH units, although the pK_a splitting was overestimated. By contrast, our previous replica-exchange simulations, which used an exchange attempt frequency (EAF) of 2 ps^{−1 35} underestimated the pK_a splitting and gave a significant amount of mixed states which were largely absent in the single-pH simulations. Additional replica-exchange simulations with less frequent exchange attempts gave similar pK_a’s and conformational behavior as the single-pH simulations, suggesting that an EAF of 2 ps⁻¹ may not allow sufficient conformational relaxation at specific pH conditions. A more extensive study will be carried out in the future to further investigate the topic.

We suggest that the above finding does not contradict a previous study³² using the GB-OBC⁴³ based discrete CpHMD, which found that an EAF of 50 ps⁻¹ significantly improved the pK_a of a salt-bridged residue (Asp66 in HEWL), which did not titrate with an EAF of 0.5 ps⁻¹. While our single-pH simulations did not encounter this issue (Table 2), likely because salt bridges are significantly weakened in the newer GB-Neck2 model,³⁶ we suggest that conformational relaxation time for buried residues, such as the aforementioned linked pairs, is much longer than solvent-exposed ones. As a result, too frequent exchanges may not allow internal residues to adjust themselves and the local environment to a change in pH. This may explain why the pK_a’s of buried residues are more sensitive to the EAF, while pK_a’s of solvent-exposed residues are not. For example, a deeply buried Asp26 in thioredoxin has a calculated pK_a of 6.2 from replica-exchange and 7.2 from single-pH simulations. The latter is in better agreement with the experimental pK_a of 9.9.

It is indisputable that enhanced sampling in either temperature^30,31 or pH space^22,32 accelerates protonation-state sampling and thereby the convergence of calculated pK_a’s. The analysis of the pK_a results from the 2-ns, 10-ns single-pH and replica-exchange simulations of BACE1 confirmed this point and further explored the topic of replica-exchange frequency. Although the pK_a order of the catalytic dyad, Asp32/Asp228, was correctly predicted, Asp228 did not protonate at pH 1 (the lowest simulation pH), due to a persistent hydrogen bond, which requires enhanced sampling or significantly longer sampling time to break. As a result, the extent of coupling and pK_a splitting were overestimated. By contrast, the extent of coupling and pK_a splitting were underestimated in the replica-exchange simulations with an EAF of 2 ps⁻¹. Thus, our future work will explore the usage of either much longer single-pH simulations or an optimum EAF to make the most accurate and efficient predictions of pK_a’s for tough cases, i.e., buried, salt-bridged, and linked titratable residues.

A most recent study⁵³ demonstrated the capability of replica-exchange GBNeck2-CpHMD for accurate prediction of downshifted Cys and Lys pK_a’s. Work is underway to benchmark the performance using single-pH simulations. Another area of interest is the improvement of His pK_a’s, which have the largest errors in the current dataset. Although there remains much room for improvement, our present data are encouraging and demonstrate that single-pH simulations may be routinely performed on a desktop computer equipped with a single GPU card for a variety of applications, from assisting MD stimulations with protonation state assignment to offering pH-dependent corrections of binding free energies¹⁰ and nucleophilic hot spots for covalent drug design.⁵³