COUSIN (COdon Usage Similarity INdex): A Normalized Measure of Codon Usage Preferences

Abstract

Codon Usage Preferences (CUPrefs) describe the unequal usage of synonymous codons at the gene, chromosome, or genome levels. Numerous indices have been developed to evaluate CUPrefs, either in absolute terms or with respect to a reference. We introduce the normalized index COUSIN (for COdon Usage Similarity INdex), that compares the CUPrefs of a query against those of a reference and normalizes the output over a Null Hypothesis of random codon usage. The added value of COUSIN is to be easily interpreted, both quantitatively and qualitatively. An eponymous software written in Python3 is available for local or online use (http://cousin.ird.fr). This software allows for an easy and complete analysis of CUPrefs via COUSIN, includes seven other indices, and provides additional features such as statistical analyses, clustering, and CUPrefs optimization for gene expression. We illustrate the flexibility of COUSIN and highlight its advantages by analyzing the complete coding sequences of eight divergent genomes. Strikingly, COUSIN captures a bimodal distribution in the CUPrefs of human and chicken genes hitherto unreported with such precision. COUSIN opens new perspectives to uncover CUPrefs specificities in genomes in a practical, informative, and user-friendly way.

Introduction

Translation of messenger RNAs (mRNA) into proteins is a central molecular biology process common to all forms of life. During translation, ribosomes proceed along the mRNA in steps of three nucleotides, called codons. The ribosome allows pairing of a mRNA codon against the complementary anticodon on a transfer RNA (tRNA), catalyzing the polymerization of amino acids to yield peptides and proteins (Quax et al. 2015). Sixty four nucleotide triplets are available and, in the standard genetic code, 61 codons encode for the 20 standard amino acids (Belalov and Lukashev 2013). Because of this asymmetry, certain groups of codons, known as “synonymous codons,” encode for the same amino acid (Nirenberg and Matthaei 1961; Khorana et al. 1966). Synonymous codons are not used with similar frequencies, resulting in so-called Codon Usage Preferences (CUPrefs) or Codon Usage bias. Different CUPrefs can be identified in regions within a gene, between genes within a genome and between genomes in different organisms (Grantham et al. 1980; Carbone et al. 2003).

A variety of indices have been developed since the 1980s to describe CUPrefs (Ikemura 1981; Freire-Picos et al. 1994; Urrutia and Hurst 2001; Zhang et al. 2012). Most of them compare the CUPrefs of a query either against a reference set or against a Null Hypothesis (Shields et al. 1988; Lee et al. 2010). The “Codon Adaptation Index” (CAI; Sharp and Li 1987) and the “Effective Number of Codons” (ENC; Wright 1990) are respectively the most popular indices for each category. Numerous software packages to evaluate CUPrefs have been implemented, such as INCA (Supek and Vlahovicek 2004), JCAT (Grote et al. 2005) and CodonW (Peden and Sharp 2005). Most of them compute the CAI, sometimes the ENC, and occasionally other indices (Wan et al. 2004; Angellotti et al. 2007). Still, an important number of indices, such as the scaled ${\chi }^2$ (Shields et al. 1988) or the “Maximum-likelihood Codon Bias” (MCB; Urrutia and Hurst 2001) cannot be calculated via any dedicated software.

Despite this profusion of alternatives, none of the available indices evaluates CUPrefs simultaneously against a reference and against a Null Hypothesis, thus hindering direct interpretation of the results. We conceived COUSIN (for COdon Usage Similarity INdex) as a score to estimate CUPrefs of a sequence compared with those of a reference, normalized over a Null Hypothesis of equal usage of synonymous codons. The output is normalized and allows for a straightforward biological interpretation. We have implemented COUSIN together with seven other existing indices in an eponymous Python3 software available for local or online use (http://cousin.ird.fr). To illustrate the power of COUSIN, we compare it to the well-known CAI by analyzing eight complete Coding DNA Sequence (CDSs) data sets from a range of organisms with large differences in nucleotide composition and genome organization.

Measuring CUPrefs with COUSIN

In COUSIN, the CUPrefs of a query are compared with those of a reference data set, and the results of this comparison are normalized over a Null Hypothesis of equal usage of synonymous codons. The notations used as well as the detailed calculation steps are given in table 1.

Table 1.

Notations Used to Define COUSIN and CAI Indices

Symbol	Description
c	Codon
a	Amino acid
f	Frequency
ref	Reference
que	Query
H 0	Null hypothesis
L	Query length
ka	Set of synonymous codons coding for amino acid a
$\mathcal{A}$	Amino acids present in both query and reference
$\mathcal{N}$	Number of amino acids present in both query and reference

The amino acid composition of a sequence may affect its CUPrefs (Roth et al. 2012). We therefore conceived two variants of our index: In ${\text{COUSIN}}_{18}$ each of the 18 families of synonymous codons contributes equally to the global index, whereas in ${\text{COUSIN}}_{59}$ each family contributes proportionally to the frequency of the corresponding amino acid in the query. The classical CAI score would thus correspond thus to ${\text{CAI}}_{59}$. For the sake of comparison we have defined the equivalent ${\text{CAI}}_{18}$ as described in supplementary data 1, Supplementary Material online. By comparing the “18” and “59” scores of an index, we can estimate the impact of amino acid composition on the CUPrefs of a sequence. The COUSIN score calculation involves five steps:

• 1. Calculate deviation scores (${\text{dev}}_{c,a}$) for each codon (c) of each amino acid (a) in the reference data set, compared with the Null Hypothesis:

• $${\text{dev}}_{\mathrm{c},\mathrm{a}}=f_{c,a}^{\text{ref}}-f_{c,a}^{H_0}$$ (1)

where $f_{c,a}^{\text{ref}}$ is the frequency of the codon c among its synonymous in the reference data set and $f_{c,a}^{H_0}$ the corresponding frequency under the Null Hypothesis.

• 2. Define a weight for each codon ($W_{c,a}$), by multiplying the codon frequency in the reference by its deviation score:

  $$W_{\mathrm{c},\mathrm{a}}^{\text{ref}}=f_{c,a}^{\text{ref}}\times {\text{dev}}_{c,a}$$ (2)
• 3. Repeat step 2 for the codon frequencies in the query:

  $$W_{\mathrm{c},\mathrm{a}}^{\text{que}}=f_{c,a}^{\text{que}}\times {\text{dev}}_{c,a}$$ (3)

  Using the same deviation score to calculate the weights allows us to compare the scores of the query and of the reference.

• 4. The ${\text{COUSIN}}_{18}^a$ score of each amino acid is the ratio of the sum of the weights of all synonymous codons for this amino acid in the query data set over the corresponding sum of the weights in the reference data set:

$${\text{COUSIN}}_{18}^{\mathrm{a}}=\frac{1}{\mathcal{N}}\times \frac{{\sum }_{c\in k_a}{\mathrm{W}}_{c,a}^{\text{que}}}{{\sum }_{c\in k_a}{\mathrm{W}}_{c,a}^{\text{ref}}}$$ (4)

where $\mathcal{N}$ is the number of amino acids present in both the query and the reference and k_a is the set of synonymous codons coding amino acid a.

For ${\text{COUSIN}}_{59}$:

$${\text{COUSIN}}_{59}^{\mathrm{a}}=f_a^{\text{que}}\times \frac{{\sum }_{c\in k_a}{W}_{c,a}^{\text{que}}}{{\sum }_{c\in k_a}{W}_{c,a}^{\text{ref}}}$$ (5)

where $f_a^{\text{que}}$ is the frequency of the amino acid a in the query.

• 5. The final COUSIN score is obtained by adding the individual COUSIN scores of all amino acids:

  $${\text{COUSIN}}_{18}=\sum _{a\in \mathcal{A}}{\text{COUSIN}}_{18}^a$$ (6)

  $${\text{COUSIN}}_{59}=\sum _{a\in \mathcal{A}}{\text{COUSIN}}_{59}^a$$ (7)

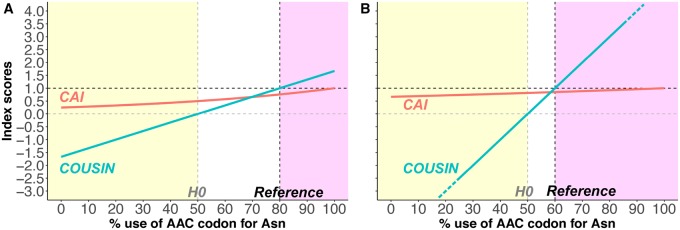
By design, the results of $\text{COUSIN}$ have an immediate biological interpretation and are directly suitable for hypothesis testing (fig. 1):

Fig. 1.

—COUSIN (blue curve) and CAI (red curve) scores (y-axis) for a set of hypothetical queries with different frequency for the AAC and AAU codons encoding the asparagine amino acid (x-axis). Values are calculated for a reference set using (A) a strong usage bias of AAC:AAU 80:20 and (B) a slight usage bias of AAC:AAU 60:40. Vertical dashed lines indicate the composition for the Null Hypothesis of equal usage of both codons (gray line) and for the corresponding reference (black line). Horizontal dashed lines show the COUSIN key values that correspond to the Null Hypothesis (gray line) and to the reference (black line). The yellow area indicates queries with CUPrefs opposite to those in the reference, white one queries with similar but weaker CUPrefs than the reference and pink one queries with similar and stronger CUPrefs than the reference. Notice that, by design, the COUSIN values are always 0 and 1 respectively for the H0 and for the reference, independently of the CUPrefs in the reference. By definition, CAI is bounded by 0 and 1. In this example, COUSIN scores below –3 and above 4 are omitted to facilitate results visualization and reading.

• a COUSIN score of 1 indicates that the CUPrefs in the query are similar to those in reference data set;

• a COUSIN score of 0 indicates that the CUPrefs in the query are similar to those in the Null Hypothesis (i.e., equal usage of synonymous codons);

• above 1, CUPrefs in the query are similar to those in the reference but of larger magnitude;

• between 0 and 1, CUPrefs in the query are similar to those in the reference but of smaller magnitude;

• below 0, CUPrefs in the query are opposite to those in the reference;

Upper and lower boundaries to COUSIN values depend on the CUPrefs of the reference: The closer the CUPrefs of the reference are to the null hypothesis, the largest the range of the possible COUSIN scores. As an example, in the case of Homosapiens, with a light global bias in CUPrefs, the range of possible COUSIN values is [–4.48; 6.13]. On the other hand, for Plasmodiumfalciparum, with a strong global bias in CUPrefs, the boundaries for COUSIN values are [0.15; 1.35]. To facilitate interpretation of CUPrefs, artificial boundaries can be given when calculating a COUSIN score. The COUSIN software, described below, proposes such solution.

COUSIN Software

We designed a Python3 software package to implement COUSIN along with other seven existing indices to facilitate CUPrefs analysis and comparisons between methods. The COUSIN software and its documentation are accessible online at http://cousin.ird.fr. A local version can be downloaded from the same website to be used on a UNIX-like Operating System via command lines. For most tasks, the COUSIN software requires query sequences in a FASTA format and a reference data set in a kazusa-like format (Nakamura et al. 2000). The global architecture of the COUSIN software is described in supplementary data 2, Supplementary Material online.

For any entry, the COUSIN software initially calculates basic nucleotide and amino acid composition statistics and estimates CUPrefs. The COUSIN software currently features eight indices that evaluate CUPrefs: COUSIN, CAI (Sharp and Li 1987), ENC (Wright 1990), FOP (Ikemura 1981), SCUO (Angellotti et al. 2007), ICDI (Freire-Picos et al. 1994), CBI (Bennetzen and Hall 1982), and scaled ${\chi }^2$ (Shields et al. 1988).

If instructed by the user, the COUSIN software performs simulations to assess whether the score of a query is statistically close to that of a standard CDS encoded by the reference (supplementary data 2, Supplementary Material online). The COUSIN software offers additional features to further analyze CUPrefs, such as a clustering analysis to group sequences according to their CUPrefs, or an optimization step to modify the CUPrefs of a sequence to adhere to those in the reference. The COUSIN software can also create a Codon Usage Table in a kazusa-like style from a set of sequences.

COUSIN Analysis

We illustrate the potential of the COUSIN and compare it to the widely used CAI by performing an analysis on the complete CDSs of eight unrelated organisms with contrasted GC content: Two prokaryotes (Escherichia coli, Streptomyces coelicolor), a plant (Arabidopsis thaliana), a yeast (Saccharomyces cerevisiae), a protist (P.falciparum), a bird (Gallus gallus), and two mammals (H.sapiens, Mus musculus). We extracted the complete nuclear CDSs from these genomes using the Emboss extractfeat function (Rice et al. 2000). To avoid redundancy, when there were alternative spliced forms of a gene, only the first isoform was kept. Only CDSs >300 nucleotides were kept for the analyses. Indeed, most CUPrefs methods show strong biases when analyzing sequences <100 amino acids (Comeron and Aguadé 1998; Roth et al. 2012). Further details about the selected sequences are in supplementary data 3, Supplementary Material online.

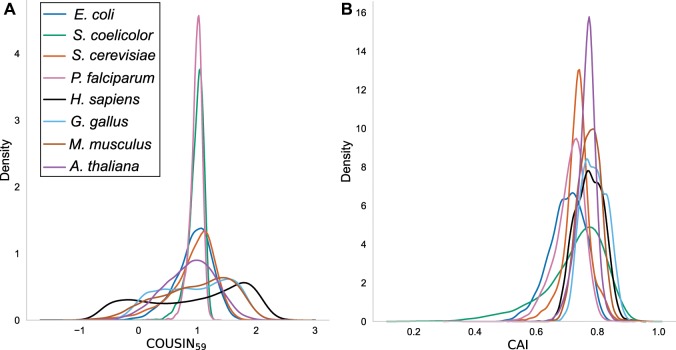
For each genome data set, we constructed a codon usage reference table using the corresponding the COUSIN software utility, and calculated the CUPrefs scores of each CDS against this reference. The resulting density curves for ${\text{COUSIN}}_{59}$ and CAI are presented in figure 2. Details about this analysis are given in supplementary data 4–6, Supplementary Material online.

Fig. 2.

—Density curves for ${\text{COUSIN}}_{59}$ (A) and CAI (B) indices for the complete CDSs of the eight organisms studied (see color legend). For each CDS the values for ${\text{COUSIN}}_{59}$ and CAI were calculated against the average codon usage reference table of the corresponding genome. The ${\text{COUSIN}}_{59}$ normalization renders curves centered around 1 allowing for rapid identification of differential dispersion in the leptokurtic curves for organisms with strong nucleotide compositional biases (e.g., Streptomyces coelicolor, in green) compared with those more platykurtic for organisms with weaker compositional biases (e.g., Escherichia coli in blue). Notice the bimodal distributions for Homo sapiens (black) and Gallus gallus (light blue) in panel A.

Analysing CDSs with COUSIN highlights shared patterns as well as differences between organisms. All COUSIN frequency curves (fig. 2, panel A) are centered around 1 (i.e., with similar CUPrefs to those of the reference), but differ strongly in terms of dispersion and of the global shape of data distribution (unimodal, bimodal, or nearly flat). For S. coelicolor and P. falciparum COUSIN distributions are unimodal and display little variance, consistent with the strong nucleotide composition bias in these genomes (respectively 92.4% GC3 and 17.8% GC3). For other organisms with unimodal distribution but less biased nucleotide composition (e.g., E. coli, with 54.9% GC3), the distributions display a larger variance. For larger genomes with strong local differences in nucleotide composition (e.g., chromosome isochores in H. sapiens, and microchromosomes in G. gallus), the COUSIN frequency curves capture a hitherto not described bimodal shape of CUPrefs (supplementary data 4, Supplementary Material online). For the CAI results obtained with the same data sets (fig. 2, panel B), all frequency curves display unimodal shapes while exhibiting differences in their central value and dispersion, preventing direct contrast with one another.

The key difference between COUSIN and CAI resides in the direct interpretation of the COUSIN results. Indeed, the correlation between CAI and COUSIN scores for each CDS is strong and positive, ranging from 0.661 in A. thaliana to 0.978 in S. coelicolor (see complete comparisons in supplementary data 6, Supplementary Material online). However, for COUSIN we compare here the CUPrefs of individuals CDSs to a reference representing the average CUPrefs of the organism, therefore expecting—and obtaining—an average score close to 1. For CAI, the central value of the obtained distribution depends on the precise CUPrefs of the reference, and are therefore not comparable between organisms. This lack of normalization hampers any direct comparison of CAI values for genes against different reference sets. Furthermore, the COUSIN score seems to better capture the impact of the query’s GC3 content on CUPrefs with, for instance, a Pearson correlation score of 0.91 between GC3 and ${\text{COUSIN}}_{59}$ and of 0.86 between GC3 and CAI for H. sapiens CDSs (supplementary data 4, Supplementary Material online).

Discussion

A large number of indices have been conceived to evaluate CUPrefs. Nevertheless, in most cases they do not allow for a straightforward interpretation. As an example, the CAI is often considered as a direct measure of CUPrefs against a reference. However, the CAI value of the reference against itself is different for each reference, preventing comparisons between genomes. Further, the CAI value of 1 is virtually never reached by any CDS in a given genome. Similarly, the different flavors of ENC (Wright 1990; Novembre 2002; Satapathy et al. 2017) allow to evaluate the presence and extent of CUPrefs against a Null Hypothesis of equal codon usage, but cannot inform on the precise trends of the detected CUPrefs.

We introduced here COUSIN, a new index to measure the CUPrefs of a sequence with respect to both a reference and a Null Hypothesis of equal usage of synonymous codons. The COUSIN value has a straightforward quantitative and qualitative meaning: It allows for an easy comparison 1) between the CUPrefs of the query CDS and those of both the reference and random CUPrefs, and 2) between queries and/or between data sets. We implemented the calculation of the COUSIN index, as well as of a number of additional features and existing indices to evaluate CUPrefs, into an eponymous bioinformatic software, available in a stand-alone as well as in an online version (COUSIN, at http://cousin.ird.fr).

We briefly illustrated the novelty and potential of the COUSIN by analyzing all CDSs in the genomes of eight divergent organisms. Taking the average genomic CUPrefs as a reference, we showed that COUSIN brings to light strong differences between CDSs within organisms, as well as between organisms. Such differences are far less obvious when using the CAI. Importantly, using the average genomic CUPrefs as a reference may or not be relevant when analyzing tissue or condition-dependent CUPrefs based on gene expression data. It remains the responsibility of the user to choose the appropriate reference and to interpret the results accordingly. Our results on differences in COUSIN values distribution and variance (exemplified by the bimodality in H. sapiens and G. gallus) demonstrate the power and utility of this novel index to identify differential heterogeneity between and within genomic data sets.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.