Abstract
Ovarian cancer has the lowest survival rate among all gynecologic cancers due to predominantly late diagnosis. Optical Coherence Tomography (OCT) has been applied successfully to experimentally image the ovaries in vivo; however, a robust method for analysis is still required to provide quantitative diagnostic information. Recently, texture analysis has proved to be a useful tool for tissue characterization; unfortunately, existing work in the scope of OCT ovarian imaging is limited to only analyzing 2D sub-regions of the image data, discarding information encoded in the full image area, as well as in the depth dimension. Here we address these challenges by testing three implementations of texture analysis for the ability to classify tissue type. First, we test the traditional case of extracted 2D regions of interest; then we extend this to include the entire image area by segmenting the organ from the background. Finally, we conduct a full volumetric analysis of the image volume using 3D segmented data. For each case, we compute features based on the grey-level co-occurrence matrix and also by introducing a new approach that evaluates the frequency distribution in the image by computing the energy density. We test these methods on a mouse model of ovarian cancer to differentiate between age, genotype, and treatment. The results show that the 3D application of texture analysis is most effective for differentiating tissue types, yielding an average classification accuracy of 78.6%. This is followed by the analysis in 2D with the segmented image volume, yielding an average accuracy of 71.5%. Both of these improve on the traditional approach of extracting square regions of interest, which yield an average classification accuracy of 67.7%. Thus, applying texture analysis in 3D with a fully segmented image volume is the most robust approach to quantitatively characterizing ovarian tissue.
Keywords: optical coherence tomography, texture analysis, ovarian cancer
1. Introduction
Despite concerted efforts to improve patient outcomes, ovarian cancer remains the deadliest gynecologic malignancy in the United States. Ovarian cancer is not particularly common, with an incidence of approximately 22,000 per year in the US. However, the disease maintains a high mortality rate, with median five-year survival less than 45% (Barnholtz-Sloan et al., 2003), due to a high proportion of advanced disease at the time of presentation. In fact, a substantial majority of patients have already experienced spread of their disease to local or distant tissues at initial diagnosis, corresponding to FIGO stages III or IV, and conferring a significantly poorer prognosis (Maringe et al., 2012). This insidious pattern of disease progression has led to strong interest in the area of ovarian cancer screening, with the goal of identifying asymptomatic tumors in their early stages and allowing more effective treatment. Screening modalities that have been investigated include physical examination, transvaginal ultrasound (TVUS), and serum tumor marker measurement (most commonly CA-125) (Carlson, 2017). Annual bimanual pelvic examination has been shown to have little value as a screening test, with low sensitivity leading to a positive predictive value (PPV) of only 1% in an asymptomatic screening population (Ebell et al., 2015). Ultrasound examination provides favorable sensitivity and specificity, but also does not reach adequate PPV in screening populations (Menon et al., 2009; van Nagell et al., 2011). Although tumor markers such as CA-125 have utility in monitoring response to treatment in previously diagnosed cancers, it is not useful as a screening test. Only 80% of early stage ovarian cancers produce an elevation in CA-125, and multiple other conditions can produce elevated levels, leading to poor sensitivity and specificity (Bast, 2003), and may prove to be useful strategies for identifying ovarian cancer in asymptomatic women. However, at this time the US Preventive Services Task Force continues to recommend no routine screening in average-risk patients (Moyer, 2012). There remains a strong need for a high-quality, minimally invasive modality for effective detection of early-stage ovarian malignancies.
Optical coherence tomography (OCT) is an interferometric imaging technique first introduced in 1991 by (Huang et al., 1991) that yields depth-resolved, high-resolution images of tissue, providing information about the tomography and microstructure. Historically, OCT has been applied with much success to biological imaging in the human eye (Swanson et al., 1993; Hee et al., 1995; Abràmoff et al., 2010), the lung (Tsuboi et al., 2005; Otte et al., 2013), the esophagus (Lightdale, 2013), the coronary artery (Ferrante et al., 2013; Abdolmanafi et al., 2017), in addition to a number of other organs including the ovaries (Hariri et al., 2010; Wang, 2015; Drexler et al., 2014). The physical principle of OCT systems is similar to that of ultrasound, except that OCT systems measure time-resolved backscattered light instead of sound waves (Schmitt, 1999). In a typical OCT configuration, a low-coherence infrared light source is coupled into a Michelson interferometer. The reference arm light is reflected by a mirror, while the sample arm light is focused onto the sample. The back-reflected light from the reference and sample arms is combined and directed to a wavelength-resolved detector. The depth-resolved reflectance of the sample is encoded in the spectral frequency information on the detector, which can be recovered with a Fourier transform. By scanning the beam across the sample, two- and three-dimensional images can be acquired. Both the axial and lateral resolution depend on the source wavelength, which commonly is in the range of 800 – 1300 nm. The axial resolution also depends on the bandwidth of the source, whereas the lateral resolution is determined by the numerical aperture of the focusing lens (Wang, 2015). Depending on the application, an OCT system can be designed for a specific axial and lateral resolution; typically these are on the order of several microns. A complicating factor of OCT is the depth dependence of the system performance. Lateral resolution varies throughout the image depth; furthermore, the signal is attenuated due to absorption and scattering, and the axial resolution is effectively degraded in deeper tissue, as the assumption of single-scattering becomes less true. Ultimately, this leads to the image statistics varying as a function of depth, which can frustrate attempts at quantitative analysis. Despite these drawbacks, OCT is an effective approach to characterizing tissue microstructure. In particular, OCT has been demonstrated to image a wealth of microstructural features in the ovaries, including the stroma, epithelium, and collagen, which show great potential for disease diagnostics and tissue classification (Hariri et al., 2010; Wang, 2015; Welge et al., 2014; Brewer et al., 2004; Watanabe et al., 2015)
While OCT provides an abundance of information about tissue health, quantitatively analyzing three-dimensional OCT data of the ovaries is challenging due to the scaling of processing time with higher-dimensional data, the depth-dependent processes described above, the presence of speckle noise (Schmitt et al., 1999), and also the large biological variation inherent to the ovaries. While recent advances in computing have enabled the rapid processing of large datasets, determining a robust analytic method that yields relevant pathological information remains a major objective. One potential approach is to characterize the microstructural features using texture analysis. Previously, texture analysis has been applied in medical imaging to classify different tissue types, in some cases with over 90% accuracy (Gossage et al., 2003; Miller and Astley, 1992; Mostaço-Guidolin et al., 2013). It follows that analyzing the texture of OCT images can potentially yield quantitative diagnostic information. With this approach, two major sources of texture features arise in OCT images: first is the biological composition of the tissue. In particular, collagen is a major source of scattering in tissue that changes throughout the progression of cancer (Wang, 2015; Saidi et al., 1995; Jacques, 1996). The physiological structure of the ovaries, such as the corpora lutea, contain a rich network of collagen, giving texture analysis high potential for tissue health assessment. Another source of texture in OCT images is the speckle inherent to the imaging modality (Schmitt et al., 1999). While speckle is a general characteristic of partially coherent imaging, previous work has shown that the speckle can be characterized with texture analysis and differentiate material media (Gossage et al., 2006). In this study, the imaging specifications are tuned such that changes in speckle are not the primary source of texture features; thus, we focus on assessing the texture changes introduced by disruption in the collagen matrix and microstructures. Other scattering processes introduced by the biological changes throughout disease progression will influence the texture as well (Beauvoit et al., 1995; Wilson et al., 2015; Jacques, 2013), making texture an attractive target for potentially differentiating objects and tissue types.
Texture analysis in image processing is a general method to describe the local variations in image brightness. Often used in conjunction with the concept of tone, which is related to the varying levels of image brightness, texture characterizes the spatial distribution of the tones in an image (Haralick et al., 1973). A number of techniques have been developed for texture analysis of images, which can be generally categorized into three groups: statistical, spectral, and structural methods. Statistical methods are based on analyzing image histograms by computing their statistical moments and other properties (Haralick, 1979). These approaches are best suited to characterize features such as inhomogeneity and contrast. Spectral methods apply autocorrelation and Fourier analysis to evaluate periodic features of an image. Finally, structural approaches decompose the image into a set of sub-patterns, arranged according to certain placement rules. To date, there has been an abundance of work investigating the application of different texture analysis methods to volumetric medical imaging (Depeursinge et al., 2014). Unfortunately, very little of this work has been focused on OCT; furthermore, the existing body of literature is either confined to two-dimensional (2D) analysis (Gossage et al., 2003, 2006; St-Pierre et al., 2017), or applied to retinal OCT imaging (Quellec et al., 2010; Kafieh et al., 2013). In particular, by confining the analysis to 2D, critical pathological information could be discarded; therefore, applying three-dimensional (3D) texture analysis could be a powerful diagnostic tool to aid physicians. A further challenge is the selection of the image area to analyze. Traditionally, this is done by selecting a square area within the region of interest. Unfortunately, due to the irregular shape of the organs, this may discard valuable information that is not captured within the selection, leading to higher variance in the analysis. Moreover, the manual selection of regions of interest can be time consuming for volumetric data, which would not lend itself well to applications in computer-aided diagnosis.
Here, we address these challenges by conducting 3D texture analysis on OCT images of a mouse model of ovarian cancer. We apply and compare three different approaches to texture analysis techniques in both 2D and 3D to examine which is has the highest accuracy for tissue classification. In all three cases, we compute features based on analyzing the Grey level co-occurrence matrix, as well as using a new method to parameterize the frequency distribution of an image. First we test the performance of the traditional approach relying on extracting 2D square regions of interest. We then apply the analysis to 2D images with a fully segmented organ area. Finally, the analysis is extended to 3D, where the fully segmented organ volume is considered. To the best of our knowledge, this is the first such study to employ these methods in 3D to analyze the ovaries. In this manuscript, we first describe the OCT system and mouse model used to in the experiment. Then, we provide an overview of the image pre-processing and texture analysis methods, followed by the classification scheme. We then report the results of the three types of analysis, showing that the 3D application of texture analysis yields higher classification accuracy than either of the 2D cases, providing features that can be used to differentiate between mouse populations with high statistical significance (p < 0.001). These results suggest that texture analysis may be useful as an aid for ovarian cancer screening.
2. Methods
2.1. OCT System
Three dimensional OCT imaging was completed with a swept source OCT system (OCS1050SS, Thorlabs). The system operates in non-contact mode with a central wavelength of 1040 nm and spectral bandwidth of 80 nm. A central wavelength of 1040 nm was chosen to balance penetration depth with resolution; while other common systems operate around 1310 nm, which penetrates more deeply, we chose a slightly shorter wavelength of 1040 nm to enable increased resolution. This allows us to capture textural features, while retaining good penetration depth. The axial scan rate was 16 kHz and the power on the sample was measured as 0.36 mW. The system was set to average 4 axial scans to increase the signal-to-noise ratio. The OCT system has 11 μm transverse resolution and 9 μm axial resolution in tissue with an approximate NA of 0.055 (focal length of 36 mm). Imaging volume was (x lateral) 4 mm × (y lateral) 4 mm × (z axial) 2 mm deep and 750 × 752 × 512 pixels (pixel size of approximately 5 μm × 5 μm). The image volume was exported as a series of 2D en face (x − y) images or slices, and saved to disk as 16-bit .tif image files.
2.2. Mouse Model
For this experiment, we used a transgenic mouse model in which females spontaneously develop bilateral epithelial ovarian cancer. The TgMISIIR-TAg (TAg) mouse was obtained from Dr. Denise Connolly and colleagues at Fox Chase Cancer Center (Connolly et al., 2003; Quinn et al., 2010). Male TAg mice were breed to female C57Bl/6 (Wild Type) mice. This resulted in producing offspring expressing either the TAg or Wild Type geneotype. Female offspring of both geneotypes were injected with Vehicle (sesame oil) or 4-Vinylcyclohexene diepoxide (VCD) dissolved in sesame oil at a concentration of 80 mg/kg for 20 days beginning at post-natal day seven. VCD was used to destroy preantral follicles, resulting in early ovarian failure. VCD has previously been used as a model for menopause (Romero-Aleshire et al., 2009). Mice were sacrificed at four and eight weeks for imaging, which was performed within 30 minutes of explant. The ovaries were rinsed with saline and covered with sterile surgical lubricant (Surgilube, HR Pharmaceuticals, York PA). Our previous investigations, as well as experience on this project support the assertion that OCT images have minimal changes over a 30 minute post-explant period. There should be minimal to no noticeable changes in tissue structure over the time required for transfer. Our previous investigations support this, as we saw minimal changes in signal over the same period of time. For brevity, we refer to different groups in figures by abbreviating (age-genotype-treatment). For example, 4WV refers to four weeks of age, Wild Type genotype treated with VCD and 8TS refers to eight weeks of age, TAg genotype treated with sesame oil.
With this procedure, we have eight different groups to compare (2×2×2 for age, genotype and treatment). Four mice in each group were imaged; each of the two ovaries are analyzed, resulting in eight samples per group except for the four-week Tag mouse injected with sesame oil, for which seven mice were analyzed, resulting in fourteen samples (Table 1). Within these eight groups we have three distinct class designations: age, genotype and treatment. This poses an interesting challenge for class separation based on image analysis, as we expect the structure of the ovary to change due to each of these three processes. Firstly, we expect the TAg mice to spontaneously develop ovarian cancer; however, this likely will not be visible until the mice are eight weeks old. Secondly, the mice treated with VCD will undergo major physiological and visible tissue changes including reduction in the number of follicles, as the treatment will mimic menopause. Attempting to classify these images based on image content provides a unique challenge, as the biological variation among each group may not be quantifiable using the same feature set; thus this provides a more complex challenge in classification than a binary comparison.
Table 1.
Number of ovaries harvested and imaged for each of the different mouse groups. Two ovaries were harvested for each mouse.
| Age | 4 Week | 8 Week | |||
|---|---|---|---|---|---|
| Treatment | VCD | Sesame oil | VCD | Sesame oil | |
| Genotype | Wild Type | 8 | 8 | 8 | 8 |
| TAg | 8 | 14 | 8 | 8 | |
2.3. Image Preprocessing
All images (both 2D and 3D) were first filtered with a median filter (3 pixel kernel), followed by a Gaussian filter (kernel sigma = 0.5 pixel) to minimize the influence of noise. The median filter removes single-pixel speckle noise, and the Gaussian filter suppresses high frequency noise. 2D analysis proceeded by selecting one en face OCT image slice from the superficial region of each ovary. For the first approach, we tested the performance of the traditional method using manually-extracted 2D square regions of interest (Figure 1a). Four regions of interest for each ovary were selected using ImageJ with no overlap, each measuring 85 × 85 pixels (425 × 425 μm) (Rasband, 2012). These regions were selected at random, but regions of fat and dark regions with no signal were excluded. The size of these squares was chosen to ensure that the 4 regions of interest could be contained entirely within the area of the smallest ovary. Images are normalized to range between a value of zero and one. This ensures that the texture features are independent of total signal strength. While the noise in the system (speckle and shot noise) depends on the signal level, the features due to tissue morphology will be independent.
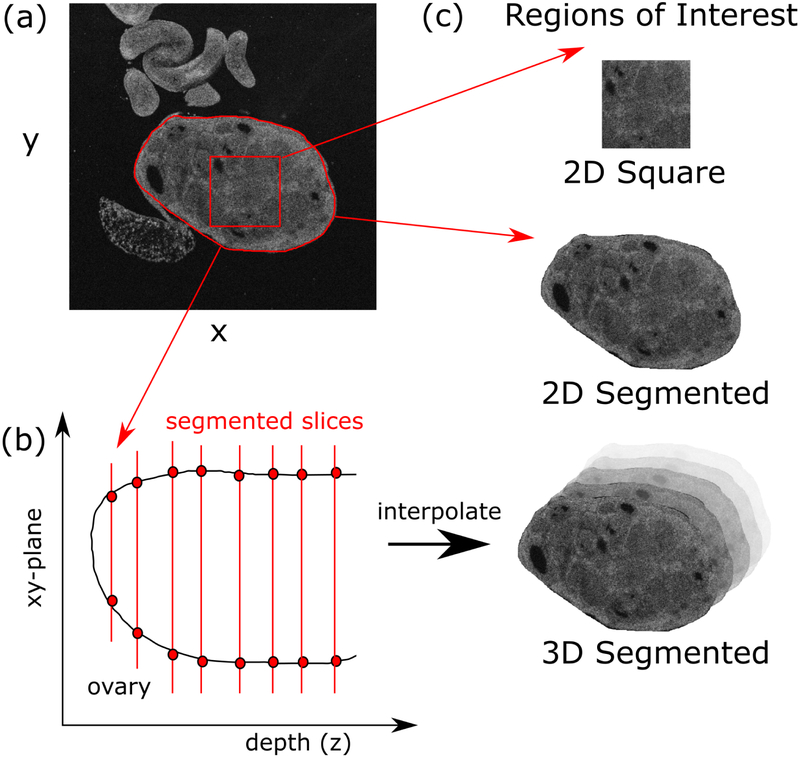
Figure 1.
The ovaries are manually segmented from the image background, selecting regions of interest (ROIs) both as square areas and as the entire ovary (a). The segmentation is done throughout the tissue depth (b), which is then interpolated to yield the 3D segmentation. This gives rise to three types of ROIs: 2D square, 2D segmented and 3D segmented (c).
The second two approaches involved analyzing the full image area (2D) and volume (3D) of the image data corresponding to the ovary. We first segmented the image to separate the organ from the background using ImageJ. The entire image stack for an ovary was loaded into the program. We located the first image at the most superficial location where the ovaries were visible and the image is not occluded by artifacts such as strong surface back reflections (approximately 40 μm deep). A mask was then drawn around the ovaries using the Create Mask tool (Figure 1a). The result was a binary mask where the value was one within the drawn region of interest and zero elsewhere. The mask was saved to disk, and the process was repeated approximately every ten slices until the average brightness within the ovary dropped below 20% of that recorded from the first superficial image. Once this step was complete, the segmentation mask was linearly interpolated between each slice to account for the sampling step of ten slices (Figure 1). Then the mask was applied to the image stack to isolate approximately only the ovarian tissue. For the 2D case, analysis was conducted on each slice individually, while for the 3D case, the entire image volume was analyzed simultaneously.
2.4. Texture Analysis
We apply two methods of texture analysis to extract features from the acquired images. First is based on constructing and analyzing the Grey-level co-occurrence matrix (GLCM) (Haralick et al., 1973). The GLCM is a spatial histogram that describes the distribution of grey-level values in an image. Each entry in the GLCM, p(i, j|d,Θ), corresponds to the probability of a pixel with a grey-level of (i) being a distance (d)pixels away from a neighboring pixel with a grey-level of (j) in the (Θ) direction (Figure 2a). With an image quantized into Ng grey levels, the GLCM is an Ng × Ng matrix. For a two dimensional image, four directions for (Θ) are possible: 0 degree, 45 degree, 90 degree, 135 degree (Figure 2b). Treating the three-dimensional case gives rise to an additional nine directions in addition to these four to total thirteen (Figure 2c). In this study, we fix (d) at one pixel, and compute the GLCM in 2D using the four relevant directions and in 3D with all thirteen possible directions.
Figure 2.
The GLCM is constructed by measuring the probability of two pixel values i and j occurring a distance d from one another (a). This can be done for four different directions in 2D (b), and thirteen directions total for 3D (c).
From the GLCM, we compute thirteen texture features originally proposed by (Haralick et al., 1973) to describe the texture of an image as follows:
| (1) |
| (2) |
| (3) |
where μx, μy, σx, σy are the mean and standard deviations of px and py, the marginal probability density functions;
| (4) |
| (5) |
| (6) |
where x and y are the row and column indices of the GLCM and px+y(i) is the probability of the two indices summing to x + y;
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
where IMC is the Information Metric of Correlation, Sxy is the Entropy in 9, Sx and Sy are the entropies of px and py, and .
We compute the thirteen features using (1) (2) for each GLCM corresponding to the thirteen possible directions for (Θ). We then average the features for the thirteen directions to produce a single set of features; by averaging over the different directions, we effectively create rotationally-invariant features, which is important when dealing with unconstrained objects such as biological tissue.
These features can be interpreted physically to understand what properties of the image are quantified. Here we describe five of the most common features used to describe image texture. The Angular Second Moment, also known as energy (1), is found by summing the squared values in the GLCM; this feature thus is a high value when the image has a small number of intensity distributions or is homogeneous, e.g, the GLCM has a few, large entries. The entropy (9), introduced by (Shannon, 1948), describes the inhomogeneity of the image. By multiplying the GLCM entries by their logarithm, smaller values are amplified, thus having the opposite effect of the Energy feature. Both the contrast and variance (2 and 4) are well-known statistical parameters that measures the variations in tone by providing higher weight to GLCM entries that are far from the diagonal. Essentially the opposite of variance, the inverse-difference moment amplifies the diagonal entries of the GLCM. Physically, this corresponds to a high feature value for low-contrast areas, such as large patches of uniform grey-level. Each of the other 13 Haralick features provides additional information regarding image texture, and are described in (Haralick et al., 1973).
2.5. Frequency Analysis
We compute a second set of features by analyzing the magnitude of the discrete Fast Fourier transform (FFT) of the image, both in 2D and 3D. For both cases, the FFT of the image data is calculated and stored in a matrix where the central value in the matrix represents the DC frequency component. We then integrate the magnitude of the spatial frequencies in a disk centered at the origin (Figure 3a). The value is normalized to the total signal magnitude, representing the percentage of the total signal contained in a given disk. The radius of this disk is then increased iteratively and the total signal proportion is recorded until the radius has reached 80% of the maximum, beyond which values are very small, and may contain mainly noise. Any artifacts caused by the edge introduced by the segmentation are also mitigated, as the edge would be characterized by very high spatial frequencies. This is effectively the cumulative distribution function of the energy density; taking the difference between the values for any two radii gives the proportion of energy contained within a specific frequency band. By differentiating the cumulative distribution function, we produce a distribution of the energy density as a function of spatial frequency. Images that are highly homogeneous would have higher energy density associated with lower spatial frequencies. On the other hand, images with more inhomogeneity would have more energy density corresponding to higher spatial frequency. We conducted an analogous procedure for the 3D case; however, as a pixel in the axial direction (z) is a smaller physical distance than the en-face axes (x, y), the area of integration was taken as an ellipse, where each radius for each axis was normalized by the total axis length (Figure 3b).
Figure 3.
The frequency analysis is done by integrating the fractional energy in a disk centered at the origin of coordinates for the FFT (a). The radius of the disk is increased until reaching 80% of the maximum value. For the 3D case, the disk becomes an ellipse, scaled by the axis lengths in x, y and z (b).
We then parameterize the distribution by fitting the energy density curve to the following equation:
| (14) |
where x is spatial frequency and y is the energy density. The frequency distribution is thus described by the two features α and β, which are combined with the thirteen Haralick features to create feature vectors with fifteen elements total. The choice of a decaying exponential was arbitrary, but visually a good fit to the data. These feature vectors were normalized along each feature axis to a value between 0 and 1 for the training set. The analyses were completed in Python using a computer with an Intel Core I-4710HQ CPU (2.50 GHz) and 16 GB DDR3L memory.
2.6. Selection of Feature Subsets
Once feature vectors were created, redundant features were removed by calculating the correlation matrix for the feature set. For each pair of features which was highly correlated (correlation > 0.85) (Lingley-Papadopoulos et al., 2008), one feature from the set was removed. For each correlated pair, we removed the feature which yielded a higher average p-value using a students t-test to discriminate between the groups. Significance was set at p < 0.05.
It is well-documented in the literature that the combination of two features may yield high performance even when the individual features do not perform well (Lingley-Papadopoulos et al., 2008; Duda et al., 2001). However, it is also understood that there is some optimal number of features that balances the information content and probability of error; thus, including an excessive number of features can in fact reduce the performance compared to the careful selection of a subset. We exhaustively tested the classification performance of feature subsets consisting of five or fewer features, as the literature suggests that high performance can typically be achieved with two to five features (Lingley-Papadopoulos et al., 2008; St-Pierre et al., 2017).
Several criteria exist to evaluate how well a set of features can separate different classes within a cluster of data. Here we use the criteria of the trace of the ratio of the between-class scatter (SB) and within-class scatter (Sw), which has previously been used to this effect with much success (Lingley-Papadopoulos et al., 2008). The within-class scatter Sw(i) for cluster i represents variance of the data points within cluster i, and can be calculated as (Duda et al., 2001):
| (15) |
where mi is the mean vector for cluster i, and x is the set of j points in cluster i. The total within-class scatter Sw for a group of clusters is the sum of the within-class scatter across all clusters .
Conversely, the between-class scatter SB for a group of classes represents the variance separating the clusters, and may be calculated as
| (16) |
where m is the mean vector for the entire data set, mi is the mean vector for cluster i, and ni is the number of points in class i. For both Sw and SB, the result is an N ×N matrix (where N is the number of features) describing the variance between each features for the data within each class (Sw) and between each class (SB). Thus, taking the ratio of SB to Sw will yield a value that is large when a given feature is consistent (low variance) within a class and different (high variance) between each class. Taking the trace of this ratio is equivalent to summing the magnitude of the eigenvectors, which represent the principal components of the matrix. In this case, these eigenvalues quantify how well a given set of features will separate two classes. Thus, maximizing this value increases the separability of the classes.
2.7. Classification
To classify the data, we use linear discriminant analysis (Welling, 2009), which has previously been applied in the scope of medical image classification (Lin et al., 2010; Reshetov et al., 2016). This approach is closely tied to the criteria used to select the feature subsets. To obtain the linear discriminants, we solve the generalized eigenvalue problem for the matrix . After this decomposition, we are left with a set of eigenvectors and eigenvalues; in this case, the eigenvectors essentially represent the axes which have highest variance between classes. The magnitude of each eigenvector represents how suitable a given axis is for class separation. Following this decomposition, we reduce the dimension of the problem by selecting the top three eigenvectors, which we found account for at least 99% of the variance in every case. We then transform the data to this new subspace and find the optimal decision boundary, which we generate by fitting the class conditional densities to the data and using Bayes rule; here we assume a Gaussian probability density distribution for each class. To validate the model, we use leave-one-out cross-validation, which is a well-documented method to evaluate the accuracy of such a model. This validation is conducted by iteratively removing a single data point, training the model on the remaining points and then testing the removed sample. By iterating through every point, we maintain independence of the test and training data since the training set never includes the point which is tested. There are eight groups, but only certain comparisons are necessary. We performed 12 comparisons: for a given age and treatment, the difference between genotypes, for a given treatment and genotype, the difference between ages, and for each genotype and age, the difference between treatments.
3. Results and Discussion
In this section, we present the results of computing the features using both the GLCM approach and the frequency analysis. We do so to illustrate that some individual features yield high statistical significant between groups, while others do not. In particular, we emphasize that the 3D analysis yields, on average, higher statistical significant for more groups than the 2D analogs. Following this, we present the results of the classification, beginning by inspecting the distribution of features determined to be most appropriate, followed by the resulting linear discriminant analysis, ultimately showing that the 3D application of texture analysis is most appropriate for tissue classification.
3.1. GLCM Features
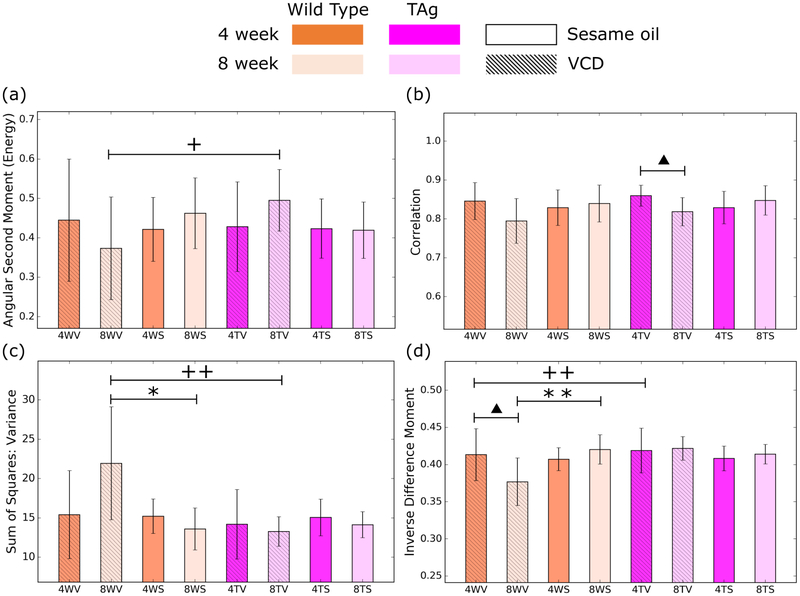
The results of computing the features from the GLCM in 2D (manually extracted squares) are illustrated in Figure 4 for a representative set of features. Using these features to perform pairwise comparison between different mouse groups, we see that the most effective feature is the inverse difference moment, which shows statistical significance for three different comparisons. Unfortunately, while the other features show significance for a select few comparisons, the majority of comparisons have no parameter that provides a statistically significant measure of difference. We observed similar results for the 2D analysis using the entire ovary.
Figure 4.
Representative features from the 2d application of the GLCM. The parameters of angular second moment (a), correlation (b), variance (c) and inverse difference moment (d) proved to be the most statistically significant for differentiating the mouse groups. Error bars are given by the standard deviation of the result evaluated over the population of mice. Significance levels are represented by a triangles for age groups, + for genotypes and * for treatments, with one and two symbols for p <0.05 and p < 0.01, respectively.
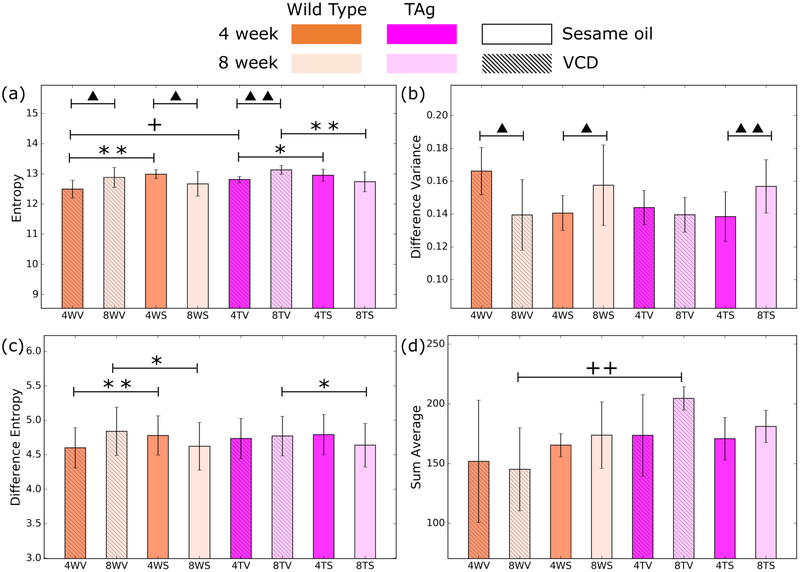
Evaluating the results in 3D, we see marked improvement over the 2D analog. In this case, we observed that for pairwise comparison between most groups, more than one feature can be used to distinguish the groups with high statistical significance. Figure 5 illustrates a representative set of features that show high potential for tissue classification. Entropy, for example can be used in seven different pairwise comparisons. Broad features such as entropy compliment other more specific features that are effective for a subset of groups, such as the difference variance for age or difference entropy for treatment.
Figure 5.
Representative features from the 3D application of the GLCM. Entropy is a powerful feature for differentiating all groups (a). Individually, difference variance (b) is useful for age, while difference entropy is powerful for treatment (c) and sum average provides statistical significance for genotype (d). Error bars are given by the standard deviation of the result evaluated over the population of mice. Significance levels are represented by a triangles for age groups, + for genotypes and * for treatments, with one and two symbols for p <0.05 and p < 0.01, respectively.
While we see tremendous improvement over the 2D analysis, it is not possible to distinguish between all groups, even with 3D analysis. In particular, no feature provided a statistically significant difference between genotype for both 4 week and 8 week mice treated with sesame oil. It is possible that this difficulty may be a result of the large changes introduced by age and treatment, which effectively mask variations that would be observed by the different genotype. Another potential cause may be the lack of any biological variability. It is possible that these mouse groups do not exhibit significant structural changes between one another, thus leading to very similar values for the texture features (Figure 6a,b). Hence, this would result in the features being a poor classifier between the two groups. In contrast, we observe that many parameters are significant for differentiating between Wild Type and TAg mice at 8 weeks treated with VCD (Figure 6c,d). This suggests that this mouse population likely has undergone a fundamental biological change that can be quantified with texture analysis. These results are highly encouraging and indicate that texture features can be used to quantitatively assess and classify tissue in the ovaries. With the large number of relevant features, it remains a challenge to determine which features are most diagnostically relevant and robust.
Figure 6.
Representative images of the ovaries for mice at 4 weeks treated with sesame oil for wild type (a) and TAg (b) genotypes. There is very little observable differences between the two, leading to very similar texture features. In contrast, wild type (c) and TAg (d) mice at 8 weeks while treated with VCD show clear differences, reflected in the variation among texture features.
3.2. Frequency Analysis
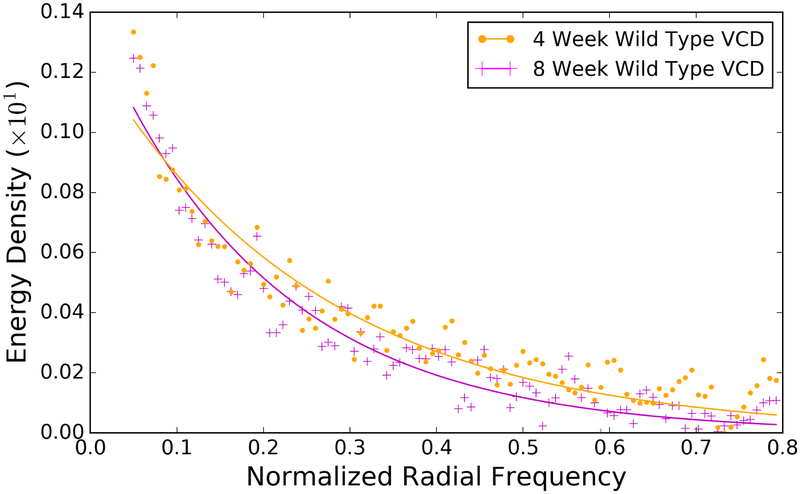
Example fits of the energy density as a function of spatial frequency are illustrated in Figure 7, which illustrates that the energy density is distributed differently for 4 week and 8 week wild type mice treated with VCD. The results for parameterizing the energy density as a function of frequency for all eight groups are illustrated in Figure 8 for both 2D and 3D. We observe statistical significance for a number of different comparisons using the parameters. The same comparisons consistently produce statistically significant results in both 2D and 3D, indicating that these groups exhibit the highest degree of change in the frequency content.
Figure 7.
The energy density is distributed differently as a function of frequency for different mouse groups, for example 4 week (magenta + symbols) and 8 week (orange dots) wild type mice treated with VCD. Fitting these curves to a two-parameter model yields an additional two features for analysis. The curves shown here are for the 3D analysis
Figure 8.
Frequency analysis results for 2D (a,b) and 3D (c,d). In both cases, the distribution is described using two parameters: α (a,c) and β (b,d). Error bars are given by the standard deviation of the result evaluated over the population of mice. Significance levels are represented by a triangles for age groups, + for genotypes and * for treatments, with one, two, and three symbols for p <0.05, p < 0.01, and p <0.0001, respectively.
We find that the there is little correlation between the feature value of alpha and beta between the 2D and 3D calculation. Furthermore, while there are more, and more highly significant, differences between groups, with 3D, the results are not highly superior to 2D analysis, as was observed with the GLCM. Also, some comparisons are significant in 2D but not in 3D. This may indicate that the frequency distribution in 2D is shaped fundamentally different than in 3D; while we observed minimal fitting error, it still may be more appropriate to parameterize the distribution using a different functional form. Nevertheless, the results shown here indicate that there is a quantifiable change in the frequency distribution as the underlying biology changes.
3.3. Feature Selection
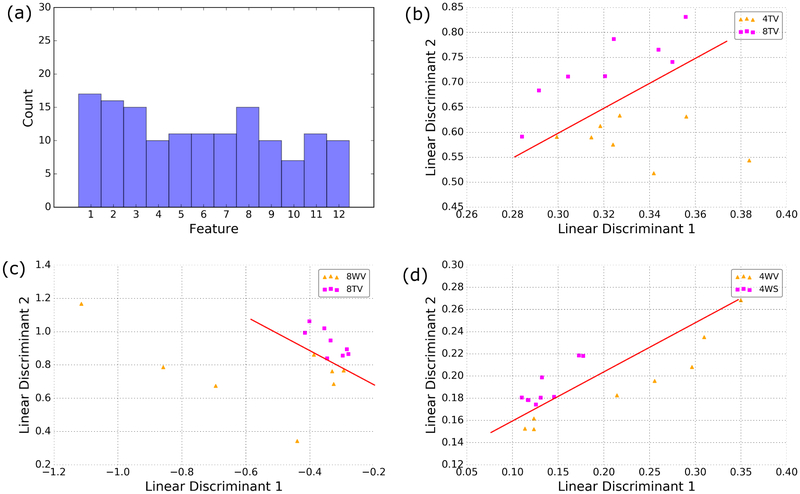
Of the fifteen original features (thirteen texture, two frequency), three pairs of features were found to share correlations with one another. In particular, we found high correlation between the inverse difference moment and the angular second moment, the sum variance and sum of squares: variance, and between the entropy and sum entropy. In each case, the feature with the higher average p-value across all twelve comparisons was removed. Using the trace metric to select the best features for discrimination, we find that the selected features are distributed relatively uniformly across the set (Figure 9). This illustrates how some features may not be suitable taken alone; however, these features may be relevant when taken with other complimentary features.
Figure 9.
Histogram of the frequency with which features were selected (a). From the best features, the linear discriminants were computed and the data were projected onto these axes. Examples for which the data can be separated with high accuracy with only 2 linear discriminants for age (b), genotype (c) and treatment (d). Red lines are a visual aid to illustrate the axis of discrimination.
Interestingly, while we see a roughly even feature distribution for classification, many of these features did not yield significant p-values for differentiating between classes individually. This validates the expectation that some features are only relevant for separation when combined with other complimentary features, further motivating the use of dimension reduction techniques such as LDA or principal component analysis. After computing the linear discriminants, we found that in every case, at least 95% of the variance was contained in the first two linear discriminants. Once the data is projected onto these axes, we could observe clear class separation when investigating age (Figure 9), treatment (Figure 9) and genotype (Figure 9). While projecting into two dimensions is useful to illustrate the class separability, we retain the top three linear discriminants during classification, which accounted for over 99% of the variance for each case.
3.4. Classification
The classification results are summarized in Table 2. We see that applying texture analysis in 3D yields the highest accuracy on average, with an overall accuracy of78.6%. This is followed by 2D analog using the entire area of the segmented ovary, with an accuracy of 71.5%. Both of these cases exceed the performance of the traditional approach, which uses 2D manually-extracted square regions of interest, yielding an accuracy of 66.7%. These results indicate that, while manually-extracted regions of interest may intentionally omit artifacts, the additional information contained within the full segmentation provides a higher degree of classification accuracy. Full segmentation, including information around the edges of the ovaries, may lead to the increased classification accuracy if physiological changes begin around the edges of the organ, or in the adjacent fallopian tubes, which is often the case in ovarian cancer (George et al., 2016). Furthermore, the substantial improvement in classification rate with 3D implies that relevant information is encoded in the depth dimension of the image data.
Table 2.
Classification results for each of the three tested approaches for each pairing of classes as well as the overall performance. On average, the 3D method yields the highest classification accuracy, followed by the 2D analysis of the segmented image area.
| 2D Squares | 2D Segmented | 3D Segmented | |
|---|---|---|---|
| Ages | 0.7376 | 0.6291 | 0.7940 |
| Genotypes | 0.5708 | 0.7292 | 0.8403 |
| Treatments | 0.6985 | 0.7872 | 0.7372 |
| Overall | 0.6779 | 0.7151 | 0.7860 |
These results are encouraging; however, several challenges remain before bringing the approach toward practical implementation as a physician aid. First, while the mouse model used here is an interesting and unique classification problem, the classification of tissue health is the ultimate goal for such a tool. Here, the mouse genotype is used as a proxy for disease, since the TAg genotype is used to induce ovarian cancer. Considering this, the classification results for genotype are of particular interest, where we see the 3D analysis is superior. Other classification approaches exist; in particular, machine learning algorithms have shown great success in recent years for tissue classification. While highly accurate, these are often tuned to a specific system configuration, reducing the ability to generalize the results. Furthermore, these often require a large amount of data for training. As our study was focused on generally assessing texture analysis for characterizing ovarian tissue, we chose to select a more general statistical model for classification. Nevertheless, using machine learning for classification remains an interesting avenue to investigate, and remains an objective of future work.
Second, developing an automated segmentation protocol is essential for streamlining the procedure. We see that using the fully segmented image area for both 2D and 3D analysis is superior to extracting regions of interest, thus a rapid and robust segmentation algorithm would greatly improve the utility of the process. Lastly, a major obstacle is the depth-dependent signal levels due to tissue absorption. Of the image depth captured in OCT, only a subset (approximately 0.5 mm) of the image data is relevant and of high enough quality to be used in analysis. In this study, we determine the boundaries by selecting the first image with no artifacts such as back reflections and the final image by finding where the mean signal inside the ovary drops to a prescribed level (20% of original). While this is suitable to conduct the study presented here, an evaluation of the optimal range of depth to include in the analysis would advance the approach toward clinical application by minimizing the noise included in the computations, thus reducing variance and maximizing the statistical power.
Another challenge that remains in the scope of clinical application is obtaining motion-free data. The respiratory rate of a human is significantly slower than mice; therefore it is possible that a patient could hold their breath for a short amount of time, allowing 3D scanning to take place. Due to the small field of view, visualizing the entire ovary would involve probing the tissue at multiple locations, requiring several breath holds. Another potential solution is to develop a probe that is in contact with the ovary, mitigating motion artifacts in the tissue region of interest.
We have demonstrated that the effectiveness of texture analysis for classifying tissue type in OCT images of ovarian tissue can be enhanced by conducting the analysis in three-dimensions. In particular, we introduce three concepts that improve upon what little work has been done to-date to apply texture analysis in this regime. In summary, these contributions include:
Utilizing the depth information in the images by computing texture parameters for all thirteen possible directions in a three-dimensional volume of data. We demonstrate that this increases classification rates over the 2D analog by approximately 7%.
By first segmenting the images to isolate the relevant image volume, we avoid the need to select a square region of interest to analyze. This provides a more true representation of the image content, leading to a more representative analysis and improving classification rates.
We introduce a new approach to frequency analysis that does not rely on isolating individual frequency bands. We characterize the frequency distribution by first computing the energy density as a function of radial frequency. By fitting this distribution to a functional form, we parameterize the full frequency content, which we see yields features with high statistical significance.
4. Conclusion
In this manuscript, we assess three implementations of texture analysis for the ability to classify ovarian tissue. First, we test the traditional case of analyzing 2D square regions of interest; then we extend this to include the entire image area by segmenting the ovary from the background. Finally, we conduct a full 3D analysis of the image volume using 3D segmented data. For each case, we compute features based on the grey-level co-occurrence matrix and also by parameterizing the frequency distribution in the image by computing the energy density. We use a transgenic mouse model that spontaneously develops ovarian cancer and attempt to use texture features to differentiate between age, genotype, and treatment. The results indicate that the 3D application of texture analysis is most effective for differentiating tissue types, yielding an average classification accuracy of 78.6%. This is followed by the analysis in 2D with the segmented image volume, yielding an average accuracy of 71.5%. Both of these improve on the traditional approach of extracting square regions of interest, which yield an average classification accuracy of 67.8%. Considering these results, we conclude that applying texture analysis in 3D with a fully segmented image volume is the most robust approach to characterize ovarian tissue. We also find that the features derived from the frequency distribution yield high statistical significance, suggesting that the method proposed here is an effective approach to quantitative tissue characterization.
Acknowledgements
This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-1143953; the National Institutes of Health under National Cancer Institute grant number 1R01CA195723; and the shared resources of the University of Arizona Cancer Center, grant number 3P30CA023074. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Appendix I: Tabulated Feature Data
Table 3.
Tabulated data for 2D GLCM texture features shown in Figure 4. Values are quoted as means ± standard deviations.
| Group | Sum of Squares: Variance | Correlation | Energy | Inverse Difference Moment |
|---|---|---|---|---|
| 4WV | 15.413 ± 5.607 | 0.8459 ± 0.0473 | 0.004448 ± 0.001552 | 0.4133 ± 0.0350 |
| 8WV | 21.953 ± 7.185 | 0.7947 ± 0.0574 | 0.003733 ± 0.001300 | 0.3767 ± 0.0321 |
| 4WS | 15.205 ± 2.192 | 0.8288 ± 0.0456 | 0.004214 ± 0.000812 | 0.4071 ± 0.0155 |
| 8WS | 13.607 ± 2.668 | 0.8397 ± 0.0473 | 0.004621 ± 0.000895 | 0.4202 ± 0.0197 |
| 4TV | 14.195 ± 4.419 | 0.8594 ± 0.0271 | 0.004282 ± 0.001137 | 0.4188 ± 0.0300 |
| 8TV | 13.283 ± 1.187 | 0.8184 ± 0.0363 | 0.004952 ± 0.000782 | 0.4216 ± 0.0159 |
| 4TS | 15.051 ± 2.336 | 0.8289 ± 0.0417 | 0.004231 ± 0.000753 | 0.4082 ± 0.0167 |
| 8TS | 14.131 ± 1.661 | 0.8473 ± 0.0378 | 0.004190 ± 0.000716 | 0.4139 ± 0.0131 |
Table 4.
Tabulated data for 3D GLCM texture features shown in Figure 5. Values are quoted as means ± standard deviations.
| Group | Entropy | Difference Variance (x 1E4)* | Difference Entropy | Sum Average |
|---|---|---|---|---|
| 4WV | 12.5039 ± 0.2944 | 1.650 ± 0.1436 | 4.7823 ± 0.1157 | 151.801 ± 51.111 |
| 8WV | 12.8917 ± 0.3332 | 1.384 ± 0.2142 | 5.0411 ± 0.1988 | 145.328 ± 34.672 |
| 4WS | 13.0166 ± 0.1442 | 1.383 ± 0.1019 | 4.9718 ± 0.0944 | 167.511 ± 7.806 |
| 8WS | 12.6742 ± 0.4114 | 1.565 ± 0.2439 | 4.8238 ± 0.1843 | 173.803 ± 27.752 |
| 4TV | 12.8208 ± 0.1053 | 1.429 ± 0.1038 | 4.9233 ± 0.1023 | 173.615 ± 34.096 |
| 8TV | 13.1429 ± 0.1458 | 1.385 ± 0.1051 | 4.9576 ± 0.0995 | 204.549 ± 9.824 |
| 4TS | 12.9653 ± 0.1991 | 1.373 ± 0.1507 | 4.9722 ± 0.1316 | 170.821 ± 17.812 |
| 8TS | 12.7475 ± 0.3325 | 1.557 ± 0.1620 | 4.8330 ± 0.1408 | 181.164 ± 13.558 |
Table 5.
Tabulated data for the 2D and 3D frequency-based texture features shown in Figure 8. Values are quoted as means ± standard deviations.
| 2D | 3D | |||
|---|---|---|---|---|
| Group | α (x 1E3) | β | α (x1E2) | β |
| 4WV | 6.341 ± 0.503 | 0.2299 ± 0.0537 | 1.329 ± 0.0536 | 0.2706 ± 0.0414 |
| 8WV | 7.038 ± 1.237 | 0.1633 ± 0.0745 | 1.245 ± 0.0333 | 0.3154 ± 0.0344 |
| 4WS | 5.940 ± 0.281 | 0.2613 ± 0.0161 | 1.323 ± 0.0532 | 0.2761 ± 0.0350 |
| 8WS | 6.456 ± 0.171 | 0.2780 ± 0.0105 | 1.346 ± 0.0580 | 0.2703 ± 0.0449 |
| 4TV | 6.704 ± 0.632 | 0.2382 ± 0.0681 | 1.330 ± 0.0299 | 0.2606 ± 0.0225 |
| 8TV | 6.433 ± 0.212 | 0.2657 ± 0.0139 | 1.345 ± 0.0222 | 0.2590 ± 0.0095 |
| 4TS | 6.064 ± 0.264 | 0.2594 ± 0.0228 | 1.318 ± 0.0333 | 0.2799 ± 0.0212 |
| 8TS | 6.419 ± 0.239 | 0.2784 ± 0.0062 | 1.383 ± 0.0378 | 0.2395 ± 0.0206 |
References
- Abdolmanafi A, Duong L, Dahdah N, Cheriet F, 2017. Deep feature learning for automatic tissue classification of coronary artery using optical coherence tomography. Biomed. Opt. Express 8, 1203 URL: https://www.osapublishing.org/DirectPDFAccess/F77DD5AD-0BC7-36D6-5C4AA4678BE906B2_357772/boe-8-2-1203.pdf?da=1&id=357772&seq=0&mobile=no%5Cnhttps://www.osapublishing.org/abstract.cfm?URI=boe-8-2-1203, doi: 10.1364d/BOE.8.001203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abràmoff M, Garvin MK, Sonka M, 2010. Retinal imaging and image analysis. IEEE Rev. Biomed. Eng 1, 169–208. URL: http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5660089, doi: 10.1109/RBME.2010.2084567.Retinal. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnholtz-Sloan JS, Schwartz AG, Qureshi F, Jacques S, Malone J, Munkarah AR, 2003. Ovarian cancer: Changes in patterns at diagnosis and relative survival over the last three decades. Am. J. Obstet. Gynecol 189, 1120–1127. doi: 10.1067/S0002-9378(03)00579-9. [DOI] [PubMed] [Google Scholar]
- Bast RC, 2003. Status of tumor markers in ovarian cancer screening. doi: 10.1200/JCO.2003.01.068. [DOI] [PubMed] [Google Scholar]
- Beauvoit B, Evans SM, Jenkins TW, Miller EE, Chance B, 1995. Correlation between the light scattering and the mitochondrial content of normal tissues and transplantable rodent tumors. Anal. Biochem 226, 167–174. doi: 10.1006/abio.1995.1205. [DOI] [PubMed] [Google Scholar]
- Brewer M.a., Utzinger U, Barton JK, Hoying JB, Kirkpatrick ND, Brands WR, Davis JR, Hunt K, Stevens SJ, Gmitro AF, 2004. Imaging of the ovary. Technol. Cancer Res. Treat 3, 617–627. doi:d=3018{\&}c=4166{\&}p=12569{\&}do= detail[pii]. [DOI] [PubMed] [Google Scholar]
- Carlson KJ, 2017. Screening for ovarian cancer. UpToDate. [Google Scholar]
- Connolly DC, Bao R, Nikitin AY, Stephens KC, Poole TW, Hua X, Harris SS, Vanderhyden BC, Hamilton TC, 2003. Female mice chimeric for expression of the simian virus 40 TAg under control of the MISIIR promoter develop epithelial ovarian cancer. Cancer Res. 63, 1389–1397. [PubMed] [Google Scholar]
- Depeursinge A, Foncubierta-Rodriguez A, Van De Ville D, Müller H, 2014. Three-dimensional solid texture analysis in biomedical imaging: Review and opportunities. Med. Imag. Anal 18, 176–196. URL: 10.1016/j.media.2013.10.005, doi: 10.1016/j.media.2013.10.005. [DOI] [PubMed] [Google Scholar]
- Drexler W, Liu M, Kumar A, Kamali T, Unterhuber A, Leitgeb RA, 2014Optical coherence tomography today: speed, contrast, and multimodality. J. Biomed. Opt 19, 071412 URL: http://biomedicaloptics.spiedigitallibrary.org/article.aspx?doi=10.1117/1.JBO.19.7.071412, doi: 10.1117/1.JBO.19.7.071412. [DOI] [PubMed] [Google Scholar]
- Duda RO, Hart PE, Stork DG, 2001. Pattern Classification. 2 ed., Wiley, NewYork. doi: 10.1007/BF01237942. [DOI] [Google Scholar]
- Ebell MH, Culp M, Lastinger K, Dasigi T, 2015. A systematic review of the bimanual examination as a test for ovarian cancer. doi: 10.1016/j.amepre.2014.10.007. [DOI] [PubMed] [Google Scholar]
- Ferrante G, Presbitero P, Whitbourn R, Barlis P, 2013. Current applications of optical coherence tomography for coronary intervention. doi: 10.1016/j.ijcard.2012.02.013. [DOI] [PubMed] [Google Scholar]
- George SHL, Garcia R, Slomovitz BM, 2016. Ovarian Cancer: The Fallopian Tube as the Site of Origin and Opportunities for Prevention. Frontiers in Oncology doi: 10.3389/fonc.2016.00108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gossage KW, Smith CM, Kanter EM, Hariri LP, Stone AL, Rodriguez JJ, Williams SK, Barton JK, 2006. Texture analysis of speckle in optical coherence tomography images of tissue phantoms. Phys. Med. Biol 51, 1563–1575. doi: 10.1088/0031-9155/51/6/014. [DOI] [PubMed] [Google Scholar]
- Gossage KW, Tkaczyk TS, Rodriguez JJ, Barton JK, 2003. Texture analysis of optical coherence tomography images: feasibility for tissue classification. J. Biomed. Opt 8, 570–575. [DOI] [PubMed] [Google Scholar]
- Haralick R, Shanmugan K, Dinstein I, 1973. Textural features for image classification. URL: http://dceanalysis.bigr.nl/Haralick73-Texturalfeaturesforimageclassification.pdf, doi: 10.1109/TSMC.1973.4309314. [DOI] [Google Scholar]
- Haralick RM, 1979. Statistical and structural approaches to texture. Proc. IEEE 67,786–804. doi: 10.1109/PROC.1979.11328. [DOI] [Google Scholar]
- Hariri LP, Liebmann ER, Marion SL, Hoyer PB, Davis JR, Brewer MA, Barton JK, 2010. Simultaneous optical coherence tomography and laser induced fluorescence imaging in rat model of ovarian carcinogenesis. Cancer. Biol. Ther 10, 438–447. URL: http://www.tandfonline.com/doi/abs/10.4161/cbt.10.5.12531, doi: 10.4161/cbt.10.5.12531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hee MR, Izatt JA, Swanson EA, Huang D, Schuman JS, Lin CP, Puliafito CA, Fujimoto JG, 1995. Optical coherence tomography of the human retina. Arch. Ophthalmol 113, 325 URL: http://archopht.jamanetwork.com/article.aspx?doi=10.1001/archopht.1995.01100030081025, doi: 10.1001/archopht.1995.01100030081025. [DOI] [PubMed] [Google Scholar]
- Huang D, Swanson E, Lin C, Schuman J, Stinson W, Chang W, Hee M, Flotte T, Gregory K, Puliafito C, et al. , 1991. Optical coherence tomography. Science 254, 1178–1181. URL: http://www.sciencemag.org/cgi/doi/10.1126/science.1957169, doi: 10.1126/science.1957169, arXiv:9809069v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacques SL, 1996. Origins of tissue optical properties in the UVA, visible, and NIR regions. OSA TOPS on Advances in Optical Imaging and Photon Migration 2, 364–371. URL: http://omlc.ogi.edu/~jacquess/papers/Jacques_OSA1996origins.pdf%5Cnhttp://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:Origins+of+Tissue+Optical+Properties+in+the+UVA,+Visible,+and+NIR+Regions#0. [Google Scholar]
- Jacques SL, 2013. Optical properties of biological tissues: a review. Phys. Med. Biol 58, 37–61. URL: http://iopscience.iop.org/article/10.1088/0031-9155/58/11/R37, doi: 10.1088/0031-9155/58/11/R37. [DOI] [PubMed] [Google Scholar]
- Kafieh R, Rabbani H, Abramoff MD, Sonka M, 2013. Intra-retinal layer segmentation of 3D optical coherence tomography using coarse grained diffusion map. Med. Imag. Anal 17, 907–928. URL: 10.1016/j.media.2013.05.006, doi: 10.1016/j.media.2013.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lightdale CJ, 2013. Optical coherence tomography in Barrett’s esophagus. Gastrointest. Endosc. Clin. N. Am 23, 549–563. doi: 10.1016/j.giec.2013.03.007. [DOI] [PubMed] [Google Scholar]
- Lin G.c., Wang W.j., Wang C.m., Sun S.y., 2010. Computerized medical imaging and graphics automated classification of multi-spectral MR images using Linear Discriminant Analysis. Comput. Med. Imaging Graph. 34, 251–268. URL: 10.1016/j.compmedimag.2009.11.001, doi: 10.1016/j.compmedimag.2009.11.001. [DOI] [PubMed] [Google Scholar]
- Lingley-Papadopoulos C.a., Loew MH, Manyak MJ, Zara JM, 2008. Computer recognition of cancer in the urinary bladder using optical coherence tomography and texture analysis. J. Biomed. Opt 13, 024003 URL: http://www.ncbi.nlm.nih.gov/pubmed/18465966, doi: 10.1117/1.2904987. [DOI] [PubMed] [Google Scholar]
- Maringe C, Walters S, Butler J, Coleman MP, Hacker N, Hanna L, Mosgaard BJ, Nordin A, Rosen B, Engholm G, Gjerstorff ML, Hatcher J, Johannesen TB, McGahan CE, Meechan D, Middleton R, Tracey E, Turner D, Richards MA, Rachet B, 2012. Stage at diagnosis and ovarian cancer survival: Evidence from the international cancer benchmarking partnership. Gynecol. Oncol 127, 75–82. doi: 10.1016/j.ygyno.2012.06.033. [DOI] [PubMed] [Google Scholar]
- Menon U, Gentry-Maharaj A, Hallett R, Ryan A, Burnell M, Sharma A, Lewis S, Davies S, Philpott S, Lopes A, Godfrey K, Oram D, Herod J, Williamson K, Seif MW, Scott I, Mould T, Woolas R, Murdoch J, Dobbs S, Amso NN, Leeson S, Cruickshank D, Mcguire A, Campbell S, Fallowfield L, Singh N, Dawnay A, Skates SJ, Parmar M, Jacobs I, 2009. Sensitivity and specificity of multimodal and ultrasound screening for ovarian cancer, and stage distribution of detected cancers: results of the prevalence screen of the UK Collaborative Trial of Ovarian Cancer Screening (UKCTOCS). Lancet Oncol. 10, 327–340. doi: 10.1016/S1470-2045(09)70026-9. [DOI] [PubMed] [Google Scholar]
- Miller P, Astley S, 1992. Classification of breast tissue by texture analysis. Image. Vis. Comput 10, 277–282. doi: 10.1016/0262-8856(92)90042-2. [DOI] [Google Scholar]
- Mostaço-Guidolin LB, Ko ACT, Wang F, Xiang B, Hewko M, Tian G, Major A, Shiomi M, Sowa MG, 2013. Collagen morphology and texture analysis: from statistics to classification. Sci. Rep 3, 2190 URL: http://www.nature.com/articles/srep02190, doi: 10.1038/srep02190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moyer VA, 2012. Screening for ovarian cancer: U.S. Preventive services task force reaffirmation recommendation statement. doi: 10.7326/0003-4819-157-11-201212040-00539. [DOI] [PubMed] [Google Scholar]
- van Nagell JR, Miller RW, DeSimone CP, Ueland FR, Podzielinski I, Goodrich ST, Elder JW, Huang B, Kryscio RJ, Pavlik EJ, 2011. Long-term survival of women with epithelial ovarian cancer detected by ultra-sonographic screening. Obstet. Gynecol 118, 1212–21. URL: http://www.researchgate.net/publication/51817152_Long-Term_Survival_of_Women_With_Epithelial_Ovarian_Cancer_Detected_by_Ultrasonographic_Screening, doi: 10.1097/AOG.0b013e318238d030. [DOI] [PubMed] [Google Scholar]
- Otte S, Otte C, Schlaefer A, Wittig L, Hüttmann G, Dromann D, Zeli A, 2013. OCT A-Scan based lung tumor tissue classification with Bidirectional Long Short Term Memory networks, in: 2013 IEEE International Workshop on Machine Learning for Signal Processing (MLSP), pp. 1–6. doi: 10.1109/MLSP.2013.6661944. [DOI] [Google Scholar]
- Quellec G, Lee K, Dolejsi M, Garvin MK, Abràmoff MD, Sonka M, 2010. Three-dimensional analysis of retinal layer texture: Identification of fluid-filled regions in SD-OCT of the macula. IEEE Trans. Med. Imag 29, 1321–1330. doi: 10.1109/TMI.2010.2047023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinn BA, Xiao F, Bickel L, Martin L, Hua X, Klein-Szanto A, Connolly DC, 2010. Development of a syngeneic mouse model of epithelial ovarian cancer. J. Ovarian Res. 3, 24 URL: http://ovarianresearch.biomedcentral.com/articles/10.1186/1757-2215-3-24, doi: 10.1186/1757-2215-3-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasband W, 2012. ImageJ. U. S. National Institutes of Health, Bethesda, Maryland, USA, //imagej.nih.gov/ij/. [Google Scholar]
- Reshetov NV, Chernomyrdin KI, Zaytsev AD, Lesnichaya KG, Kudrin OP, Cherkasova VN, Kurlov IA, Shikunova AV, Perchik SO, Yurchenko IV, 2016. Principle component analysis and linear discriminant analysis of multi-spectral autofluorescence imaging data for differentiating basal cell carcinoma and healthy skin. Proc. SPIE 9976. doi: 10.1117/12.2237607. [DOI] [Google Scholar]
- Romero-Aleshire MJ, Diamond-Stanic MK, Hasty AH, Hoyer PB, Brooks HL, 2009. Loss of ovarian function in the VCD mouse-model of menopause leads to insulin resistance and a rapid progression into the metabolic syndrome. Am. J. Physiol. Regul. Integr. Comp. Physiol 297, 587–92. URL: http://www.ncbi.nlm.nih.gov/pubmed/19439618%5Cnhttp://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC2739794, doi: 10.1152/ajpregu.90762.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saidi IS, Jacques SL, Tittel FK, 1995. Mie and Rayleigh modeling of visible-light scattering in neonatal skin. App. Opt 34, 7410–7418. doi: 10.1364/AO.34.007410. [DOI] [PubMed] [Google Scholar]
- Schmitt J, 1999. Optical Coherence Tomography (OCT): A Review. IEEE J. Sel. Top. Quantum Electron. 5, 1205–1215. doi: 10.1109/2944.796348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt JM, Xiang SH, Yung KM, 1999. Speckle in Optical Coherence Tomography. URL: http://www.mendeley.com/catalog/speckle-optical-coherence-tomography-1/%5Cnhttp://www.mendeley.com/research/speckle-optical-coherence-tomography-overview/, doi: 10.1117/1.429925. [DOI] [PubMed]
- Shannon CE, 1948. A Mathematical Theory of Communication. Bell Syst. Tech. J 27, 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x. [DOI] [Google Scholar]
- St-Pierre C, Madore WJ, De Montigny E, Trudel D, Boudoux C, Godbout N, Mes-Masson AM, Rahimi K, Leblond F, 2017. Dimension reduction technique using a multilayered descriptor for high-precision classification of ovarian cancer tissue using optical coherence tomography. J. Med. Imag 4, 41306. doi: 10.1117/1.JMI.4.4.041306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson E.a., Izatt J.a., Hee MR, Huang D, Lin CP, Schuman JS, Puliafito C.a., Fujimoto JG, 1993. In vivo retinal imaging by optical coherence tomography. Opt. Lett 18, 1864–6. URL: http://www.ncbi.nlm.nih.gov/pubmed/19829430, doi: 10.1364/OL.18.001864. [DOI] [PubMed] [Google Scholar]
- Tsuboi M, Hayashi A, Ikeda N, Honda H, Kato Y, Ichinose S, Kato H, 2005. Optical coherence tomography in the diagnosis of bronchial lesions. Lung Cancer 49, 387–394. doi: 10.1016/j.lungcan.2005.04.007. [DOI] [PubMed] [Google Scholar]
- Wang T, 2015. An overview of optical coherence tomography for ovarian tissue imaging and characterization. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol 7, 1–16. doi: 10.1002/wnan.1306.An. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe Y, Takakura K, Kurotani R, Abe H, Atanabe YUW, Akakura KEIT, Urotani REK, 2015. Optical coherence tomography imaging for analysis of follicular development in ovarian tissue. App. Opt 54, 6111 URL: https://www.osapublishing.org/abstract.cfm?URI=ao-54-19-6111, doi: 10.1364/AO.54.006111. [DOI] [PubMed] [Google Scholar]
- Welge WA, DeMarco AT, Watson JM, Rice PS, Barton JK, Kupinski MA, 2014. Diagnostic potential of multimodal imaging of ovarian tissue using optical coherence tomography and second-harmonic generation microscopy. J. Med. Imaging 1 URL: http://medicalimaging.spiedigitallibrary.org/journal.aspxhttp://ovidsp.ovid.com/ovidweb.cgi?T=JS&CSC=Y&NEWS=N&PAGE=fulltext&D=emed13&AN=2015514931http://digitaal.uba.uva.nl:9003/uva-linker?sid=OVID:embase&id=pmid:&id=doi:10.1117%2F1.JMI.1.2.025501&issn=, doi: 10.1117/1.JMI.1.2.025501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welling M, 2009. Fisher Linear Discriminant Analysis. Science 1, 1–3. URL: http://www.cs.huji.ac.il/ĉsip/Fisher-LDA.pdf, doi: 10.1109/NNSP.1999.788121. [DOI] [Google Scholar]
- Wilson JD, Cottrell WJ, Foster TH, 2015. Index-of-refraction-dependent subcellular light scattering observed with organelle-specific dyes. J. Biomed. Opt 12, 014010. doi: 10.1117/1.2437765. [DOI] [PubMed] [Google Scholar]