Meta-analytic Approaches for Examining Complexity and Heterogeneity in Studies of Adolescent Development

Abstract

Introduction.

In the field of adolescent development, meta-analysis offers valuable tools for synthesizing and assessing cumulative research evidence on the effectiveness of programs, practices, and policies intended to promote healthy adolescent development. When examining the impact of a program implemented across multiple primary studies, variation is often observed in the methodological attributes of those primary studies, such as their implementation methods, program components, participant characteristics, outcome measurement, and the systems in which programs are deployed. Differences in methodological attributes of primary studies represented in a meta-analysis, referred to as complexity, can yield variation in true effects across primary studies, which is described as heterogeneity.

Methods.

We discuss heterogeneity as a parameter of interest in meta-analysis, introducing and demonstrating both graphical and statistical methods for evaluating the magnitude and impact of heterogeneity. We discuss approaches for presenting characteristics of heterogeneity in meta-analytic findings, and methods for identifying and statistically controlling for aspects of methodological complexity that may contribute to variation in effects across primary studies.

Results.

Topics and methods related to assessing and explaining heterogeneity were contextualized in the field of adolescent development using a sample of primary studies from a large meta-analysis examining the effectiveness of brief alcohol interventions for youth. We highlighted approaches currently underutilized in the field and provided R code for key methods to broaden their use.

Conclusions.

By discussing various heterogeneity statistics, visualizations, and explanatory methods, this article provides the applied developmental researcher a foundational understanding of heterogeneity and complexity in meta-analysis.

Introduction

Meta-analysis provides valuable tools for synthesizing and assessing cumulative research evidence (Lipsey & Wilson, 2001). In the field of adolescent development, meta-analyses have been used to investigate the effectiveness of programs, practices, and policies (hereafter described as programs) intended to promote healthy development over the course of adolescence (Card & Little, 2006; Clarke, 2006; Durlak, Weissberg, & Pachan, 2010; Horowitz & Garber, 2006; Weisz, McCarty, & Valeri, 2006). Some of these meta-analyses synthesize correlational or observational evidence of risk and protective factors for healthy adolescent development (e.g., Tanner-Smith, Wilson, & Lipsey, 2013), while others synthesize evidence from controlled evaluations of program effects to answer fundamental questions about whether a program is generally helpful, harmful, or ineffective (e.g., StrØm, Adolfsen, Fossum, Kaiser, & Martinussen, 2014; Tripodi, Bender, Litschge, & Vaughn, 2010). When assessing the impact of a program implemented in multiple primary studies drawn from a systematic review of available literature, observing differences in methodological characteristics across primary studies is common. Primary studies can differ in, for instance, implementation methods, program components, participant characteristics, outcome measurement, and the systems in which a program is deployed. Differences in methodological attributes of primary studies included in a meta-analysis, referred to here as complexity, can produce variation in true effects across primary studies, which is described as heterogeneity (Borenstein, Higgins, Hedges, & Rothstein, 2017; Higgins & Thompson, 2002). Heterogeneity can considerably complicate the interpretability of meta-analytic findings, and as a result, it is recommended practice to at minimum assess the magnitude of heterogeneity among the effects of primary studies included in a meta-analysis (Higgins, 2008; Higgins & Green, 2011; Moher et al., 1999). In addition to quantifying heterogeneity, statistical and graphical tools can be used to evaluate the impact of heterogeneity on an overall effect size estimate and to investigate whether specific sources of heterogeneity can be identified (Baker, White, Cappelleri, Kluger, & Coleman, 2009; Hardy & Thompson, 1998; Higgins & Thompson, 2002; Thompson, 1994; Viechtbauer, 2007). Utilizing these approaches to examine whether aspects of methodological complexity are sources of heterogeneity in meta-analytic findings can provide a more nuanced view of when, for whom, and under what conditions program effects may vary, and yield information that can be used to identify and address differences in outcomes and to tailor programs to optimize their effectiveness across settings (Lipsey & Wilson, 2001; Viechtbauer, 2007).

This article aims to provide the applied developmental researcher with a foundational understanding of heterogeneity in meta-analysis, including methods for quantifying and assessing the impact of heterogeneity, and for explaining heterogeneity resulting from methodological complexity. Topics addressed include the historical and statistical background of heterogeneity as a parameter of interest in meta-analysis, graphical and statistical methods for evaluating the magnitude and impact of heterogeneity, and approaches for presenting characteristics of heterogeneity in meta-analytic findings.¹ We also discuss and demonstrate methods for identifying and statistically controlling for aspects of methodological complexity that may contribute to variation in effects across primary studies.²

Motivating Example

To place these topics in the context of adolescent development, key methods will be illustrated using a sample of primary studies from one of the largest meta-analyses to date of brief alcohol interventions (BAIs) for youth, which synthesized evidence from 190 randomized controlled trials and controlled quasi-experiments (Tanner-Smith & Lipsey, 2015; Tanner-Smith & Risser, 2016). BAIs are low-cost preventive interventions aimed at promoting change in alcohol use behaviors or their determinants, and while they are typically short-duration and administered in a single session, BAIs can vary in method of delivery, implementation setting, and in primary components. In the meta-analysis that serves as the motivating example for this article, participants in primary studies were adolescents and young adults ages 11–30, and included studies compared a BAI condition to an inactive comparison condition such as wait-list control, treatment-as-usual, or no treatment (Tanner-Smith & Lipsey, 2015). For the example analyses reported here, we synthesized post-intervention effects on alcohol-related consequences using the Rutgers Alcohol Problems Index (RAPI; White & Labouvie, 1989), and utilized the standardized mean difference between intervention and comparison conditions as the effect size measure. In the sections that follow, approaches for examining and explaining heterogeneity are demonstrated using the metafor package for R (version 2.0-0; Viechtbauer, 2010, 2017).³

Understanding Heterogeneity

The principal aim of many meta-analyses is to summarize the findings of multiple primary studies using an overall or average effect estimate. In the context of evaluating the effectiveness of a program using meta-analysis, the program will have an observed effect in each primary study that is assumed to reflect the true (unobserved) effect in the population; however, the true effect of the program may vary considerably across contexts, suggesting that there may be multiple true effects in the population. In the scenario where true effects vary insubstantially across contexts (that is, the true effects are homogeneous), an average effect size estimate can be a useful representation of the common true effect in the population. Conversely, in the situation where true effects vary considerably between studies (i.e., there is not a common true effect), the average effect size estimate does not have the same utility: true effects could be dispersed broadly around the average effect, ranging in magnitude (from much smaller to much larger), direction (from helpful to harmful), or both. This variation in true effects is heterogeneity, and it has clear implications for the interpretability of the overall or average effect reported in a meta-analysis. Assessing these implications, however, is complicated by the reality that we cannot directly synthesize the true effect in each primary study because each true effect is measured with error. Consequently, a meta-analysis summarizes observed effects – true effects accompanied by measurement error present in each study – rather than true effects alone.

Reliance on observed effects at the primary study level necessitates that true effects, as well as any variation among those true effects (heterogeneity), must be estimated. Over the last two decades, estimation tools for heterogeneity have become broadly available, and at the same time, there has been growing acceptance that heterogeneity in meta-analysis is often inevitable and should be anticipated (Higgins, 2008; Lorenc et al., 2016). These developments have accompanied the widespread use of random- and mixed-effects statistical models for meta-analysis, which require estimation of between-study variability in true effects, in contrast to a fixed-effect approach that assumes all primary studies share a common, or homogeneous, true effect (Riley, Higgins, & Deeks, 2011).⁴ In the field of adolescent development in particular, it is typically unreasonable to assume that all primary studies in a meta-analysis are drawn from a single homogeneous population (the assumption underlying fixed-effect models). For this assumption to hold, all included studies would need to share virtually identical methodological, contextual, and participant characteristics, and there could be no variation in the true effect of a program or intervention beyond that expected by chance.⁵ Because a more realistic assumption is often that heterogeneity is present to some degree in a sample of primary studies, random-effects models for meta-analysis are now generally recommended (Borenstein, Hedges, Higgins, & Rothstein, 2010; Lipsey & Wilson, 2001; Tanner-Smith & Grant, 2018). Alongside broader use of random-effects models, various approaches to expressing heterogeneity and assessing its impact on an overall effect size estimate have been developed, and it is now common for meta-analysts to examine heterogeneity in an effort to understand what factors may explain variation in effects across studies, contexts, and participants. There has also been increased recognition that when these factors are malleable (e.g., aspects of intervention implementation such as duration or delivery method), insight garnered from investigating heterogeneity in effects can be especially valuable to future research and practice.

Quantifying and Assessing Heterogeneity

Before investigating sources of heterogeneity in an overall effect size estimate, an important initial step is estimating the amount or magnitude of between-study variation (heterogeneity) across the true effect sizes in the population. The amount of heterogeneity is typically expressed as the parameter τ² (tau-squared), and its square-root, τ, represents the standard deviation of true effects between studies. Estimation of τ² can be accomplished using method-of-moments estimation or iterative approaches such as restricted maximum-likelihood estimation.⁶ Once estimated, τ² and τ take the unit of the effect size measure employed in a meta-analysis. This attribute can be useful in some situations, while in others, it can complicate the interpretation of the statistics as standalone measures of heterogeneity. For instance, when an effect size measure is a standardized mean difference (e.g., Cohen’s d), the estimate of τ is in the same units as the standardized mean difference, and as a result provides a straightforward index of the dispersion (standard deviation) of true effects around the overall effect size estimate. In other cases, such as when the effect size measure is a log odds or risk ratio, the estimate of τ may not offer as intuitive an interpretation because it is in the form of log-units (Borenstein et al., 2017).⁷ In a later section, we present an approach for expressing the dispersion of true effects around an overall effect size estimate that utilizes τ², but is directly interpretable regardless of the effect size measure used in a meta-analysis.

Common Presentations of Heterogeneity

In addition to τ², which represents the amount of heterogeneity in true effects, there are numerous statistical and graphical approaches that can be used for presenting characteristics of heterogeneity in meta-analytic findings. Those we introduce below are some of the most commonly used approaches. Our aim is to equip the reader with a working knowledge of the meaning, intended use, and limitations of these tools, so that when encountered, they may be interpreted accurately. We also discuss and illustrate the use of prediction intervals for expressing heterogeneity, an approach that offers great utility but is currently underutilized in meta-analyses in the field of adolescent development.

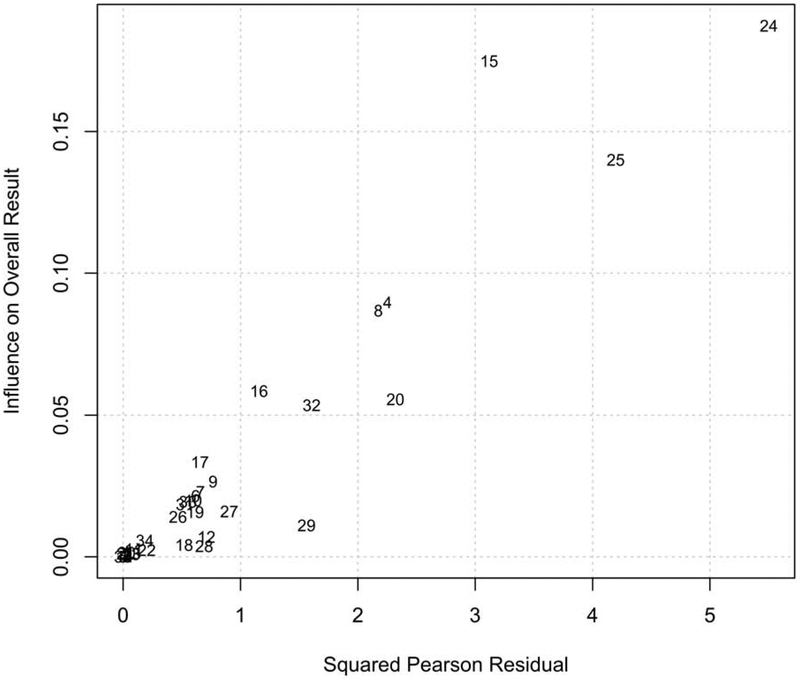
Cochran’s Q, often referred to as simply Q, summarizes the variation between each primary study’s estimated effect and the overall effect size estimate. In a random-effects meta-analysis, Q is weighted by each study’s precision (the inverse of its estimated error variance) and by between-study variation (τ²). Given these properties, Q has frequently been used to test whether the amount of between-study variation (heterogeneity) is significantly different from zero (with estimates of zero suggesting homogeneity, or no variation in true effect between studies in excess of what would be expected due to chance).⁸ Although a significance test that can be used to test for the presence or absence of heterogeneity is conceptually appealing, a serious limitation of the Q test is that it is underpowered to detect departures from homogeneity when the total number of included primary studies is small, and overpowered to detect heterogeneity when the number of studies is large (Hardy & Thompson, 1998; Higgins & Thompson, 2002; Mittlböck & Heinzl, 2006). This can result in clinically important heterogeneity that remains undetected, or clinically unimportant heterogeneity that is detected. In addition to this statistical significance test, another common use of the Q statistic is in a visual presentation of effect size heterogeneity known as a Baujat plot (Baujat, Mahé, Pignon, & Hill, 2002). Figure 1 illustrates a Baujat plot using the example BAI meta-analysis data. The primary studies that have the greatest variation from the overall effect size estimate and the most substantial contribution to the estimate are located in the upper-right corner of the plot (Anzures-Cabrera & Higgins, 2010). While a Baujat plot may be useful for identifying specific primary studies whose effects vary most substantially from those in other included studies, inspection of the plot may lead to the erroneous conclusion that the most severely-outlying studies should be removed to reduce heterogeneity. Such a practice is discouraged because doing so amounts to manipulating the eligibility criteria of a meta-analysis (Higgins, 2008). Below we discuss methods that allow for sources of heterogeneity to be identified and taken into account without study removal, such as meta-regression.

Figure 1.

Baujat plot using the BAI random-effects model. The x-axis is the squared Pearson residual of each study; a larger residual suggests a study’s estimated effect is outlying from the overall effect estimated by the model. The y-axis corresponds to the standardized squared difference between the model-estimated effect for each study, with and without each study included in the model estimation. Primary studies with the greatest variation from the overall effect size estimate and the most substantial contribution to the estimate are located in the upper-right corner of the plot.

The heterogeneity statistic I² addresses some of the limitations of Q as a measure of heterogeneity, in particular that Q is influenced by the number of primary studies included in the meta-analysis (Higgins & Thompson, 2002; Mittlböck & Heinzl, 2006). The I² statistic is a relative heterogeneity indicator, in that it expresses the proportion of true between-study variation relative to total observed variation (which is comprised of true between-study variation and within-study error). Because it is a proportion, I² takes the form of a fixed interval of 0–1 or 0–100%. A value of 0 indicates that all observed variation is attributable to within-study variation (i.e., due to error, reflecting homogeneity between studies), whereas an I² value of 1 (or 100%) denotes that all observed variation is due to true between-study variation (heterogeneity). The I² statistic has come into widespread use but has sometimes been presented as a measure of the magnitude of heterogeneity and been used to categorize heterogeneity into low, moderate, or high levels. These uses have led to some confusion in the statistic’s interpretation (Borenstein, 2018; Borenstein et al., 2017; Higgins, 2008). Namely, I² conveys the relative composition of variation in an overall effect size estimate, and not the extent (i.e., range) of variation in effect sizes between primary studies. As a result, the statistic is not suited for use as an overall statement of the impact of heterogeneity because it does not indicate the absolute magnitude of heterogeneity, and by extension, does not indicate whether effect sizes vary minimally or considerably between studies (Borenstein, 2018). For example, an I² value of 80% indicates that approximately 80% of the observed variation in an effect size estimate is due to true between-study variation (heterogeneity), and yet with no other information we cannot know if that value reflects one of two situations: the case where between-study variation makes up 80% of a substantial amount of total variation, or the case where between-study variation makes up 80% of an inconsequential amount of total variation. In both of these cases, between-study and within-study variation can contribute to the effect size estimate in the same proportion (to one another), but with the two very different conclusions of considerable heterogeneity in the former case, and minimal heterogeneity in the latter case.

To more concretely illustrate these points, including limitations of the common heterogeneity indicators we have overviewed, we can turn to the example BAI meta-analysis data. For this example, a random-effects model was used and τ² was estimated using the restricted maximum-likelihood approach (the default in the metafor package; see Footnote 6).We used an α = .05 to assess statistical significance. According to the model (see Supplement for full output), the overall effect size estimate of the post-intervention standardized mean difference (Cohen’s d) in alcohol-related problems between intervention and comparison conditions is −0.21, 95% CI [−0.28, −0.13]. This estimate indicates that, in general, BAIs are associated with lower levels of alcohol-related problems, relative to control conditions. For this estimate, just over one-third of the observed variation in the estimate is due to true between-study variation (I² = 38.75%), and the Q test suggests that the amount of heterogeneity in the effect size estimate is significantly more than would be expected due to chance (Q = 54.77, df = 34, p = .01). We might conclude from the significant Q test that heterogeneity in the overall effect size estimate is concerning. At the same time, however, it is not immediately apparent how the Q test and the I² value relate to the magnitude of heterogeneity in the estimate (τ²), which has a value of 0.02. Considering these outputs, we are left with an unclear picture of the impact of heterogeneity in the overall effect size estimate, because despite the result of the Q test and the I² value, we still do not know whether there is minimal or considerable variation in true effects between studies. We do not know this because we have not yet examined the range of true effects across primary studies.

Prediction Intervals

The distribution or range of true effects across primary studies is known as a prediction interval, and is a more direct presentation of the degree to which effects vary between studies than other commonly used heterogeneity indicators (Borenstein et al., 2017; Higgins, 2008). A prediction interval is calculated using the estimated τ² value. As mentioned above, the square-root of τ² is the standard deviation of true effects across primary studies; it is, therefore, an index of the dispersion of true effects around the overall effect size estimate. When a 95% prediction interval is calculated, it represents the range within which we would expect 95% of all primary studies’ true effect sizes to fall (Borenstein et al., 2017; Higgins, Thompson, & Spiegelhalter, 2009). Consequently, a prediction interval offers an intuitive interpretation: A narrow prediction interval indicates minimal variation in true effects between studies, and a wide prediction interval indicates extensive variation in true effects between studies. With this straightforward interpretation, we are better able to answer the key questions related to evaluating the impact of heterogeneity: How variant are effect sizes between studies, and how much concern should be raised by that variation? Put another way: If we conduct a similar study in the future, what is the reasonable range of effects we might expect to achieve?

In the previous section, we illustrated some of the challenges in assessing the impact of between-study variation in true effects using other heterogeneity indicators, and we can now return to the BAI meta-analysis example to show the utility of prediction intervals for this purpose. The overall effect size estimate was −0.21, which is accompanied by a prediction interval of −0.48 to 0.07. With this range, we can make a direct assessment of between-study variation (heterogeneity): In general, the expected effect of a BAI on alcohol-related consequences would be negative (i.e., participants receiving the BAI would have lower post-intervention levels of alcohol-related consequences than participants in comparison conditions), but there is a possibility that some studies may observe higher levels of alcohol-related consequences in the BAI (versus comparison) condition. From this assessment, we can conclude that although there is heterogeneity in effects between studies, the overall estimate is fairly representative of the distribution of true effect sizes among primary studies given that most studies would be expected to have an effect in the same direction as the overall effect size estimate (both negative, or in favor of the BAI).⁹

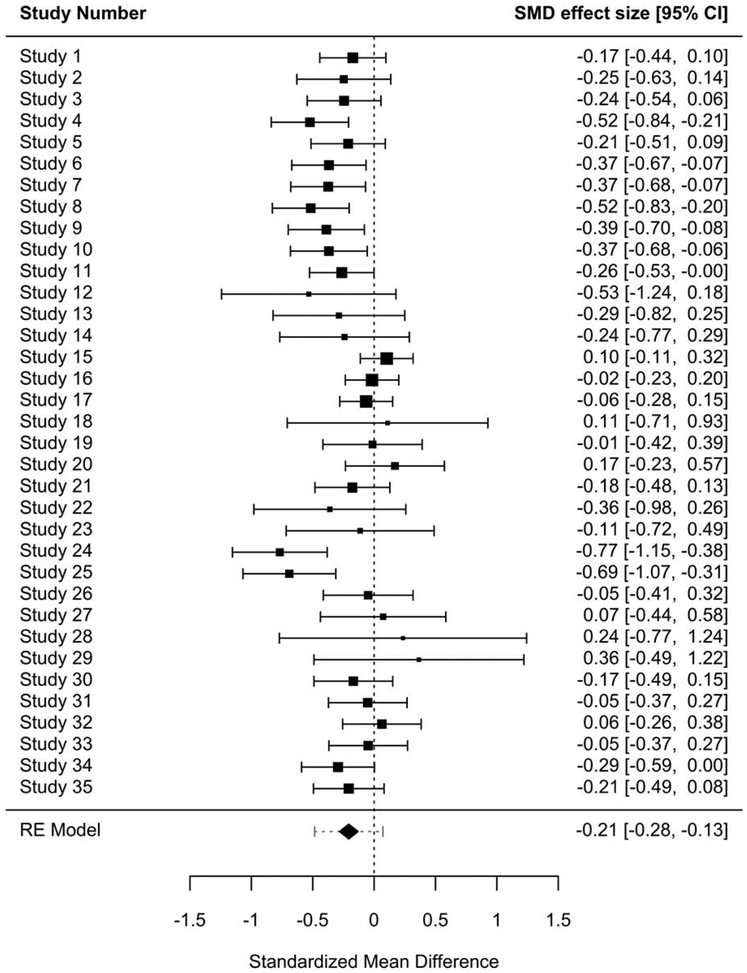
In the BAI example, the effect size measure is a standardized mean difference; as noted above, the square-root of τ² shares the same unit as the effect size measure and, in the case of a standardized mean difference, has a fairly intuitive standalone interpretation as standard deviation-unit differences between studies. We also noted that this straightforward interpretation is not the case when effect size measures such as log odds or risk ratios, prevalences, or Fisher’s-z transformed correlations are used, because τ, while still defined as a standard deviation, takes on log or other units that are not as directly interpretable as a standalone value. A benefit of the prediction interval is that the units of the interval can be returned to the unit of the effect size measure (e.g., through exponentiation), so that when, for example, an overall effect size measure is in the form of a log odds ratio, the accompanying prediction interval can express a range of odds ratios.¹⁰ Prediction intervals can also be usefully incorporated into a forest plot, one of the most frequently-used visualizations in meta-analysis. In a forest plot (see Figure 2), the estimated effect size and corresponding confidence interval of each primary study are plotted. Each study’s estimated effect size is indicated by a box (aligning with a scale of effect sizes on the x-axis), and the size of the box corresponds to the weight given to each study; studies with greater weight have a larger box. The overall effect size estimate is typically placed at the base of the plot, where it can be visually compared with the individual effect estimates. The utility of the forest plot is that it graphically summarizes the key information of a meta-analysis, namely the study-level and overall effect estimates and the precision with which those effects were estimated; as a result, the plot clearly presents the range of observed effects in a meta-analysis. Notably, however, forest plots do not typically display the estimated range of true effects, because they do not usually include a prediction interval for the overall effect size estimate. When the prediction interval is incorporated, the forest plot presents both sources of variation in the overall effect size estimate – within-study error (the confidence interval for each study’s estimated effect) and true between-study heterogeneity – and therefore displays a more informative summary of variation in a meta-analysis. The forest plot in Figure 2, which uses the BAI meta-analysis data, includes a prediction interval as the gray dashed line around the overall effect size estimate (the diamond-shaped indicator). It can be clearly seen that, despite variation in true effects between studies, most study-level effects would be in the same direction as the overall effect size estimate (i.e., in favor of the BAI). Prediction intervals, alone or included in forest plots, are currently underutilized in the field of adolescent development, and we encourage their broader use as an approach for expressing and evaluating heterogeneity in meta-analysis.

Figure 2.

Forest plot of BAI meta-analysis primary study effect size estimates with prediction interval. The overall effect size estimate is indicated by the diamond-shaped indictor at the bottom of the plot; its width corresponds to the 95% confidence interval for the estimate, which is also provided in brackets on the same line on the plot. The 95% prediction interval is denoted by gray bounding lines around the overall effect size estimate indicator.

Note. SMD = standardized mean difference. CI = confidence interval. RE = random-effects.

Explaining Heterogeneity

In the prior section, we described prediction intervals as an approach to assessing heterogeneity that provides a relatively intuitive and unambiguous means to evaluate how well an overall effect size estimate represents the distribution of true effects among primary studies. A question that naturally follows from a process of assessing heterogeneity is whether sources of heterogeneity can be identified, and in particular, whether those sources of between-study variation are related to aspects of methodological complexity among primary studies. Investigating methodological attributes of primary studies as potential sources of heterogeneity can be informative in several ways. Observing differences in effects based on program characteristics, such as method of delivery, or by aspects of study implementation, such as the duration or modality of training for interventionists, can inform program implementation in both research and applied contexts. Additionally, heterogeneity associated with major design characteristics of primary studies, such as the method of random sequence generation used or whether outcome assessors were blinded, can clarify the role of these factors in influencing overall effect size estimates, and lend support for more rigorous designs.¹¹ While there are several approaches to examining variation in effects between primary studies in a meta-analysis, in the next section we focus on meta-regression as a flexible and informative tool for this purpose.¹²

Meta-regression

Meta-regression is a versatile framework for investigating the influence of primary study characteristics on effect size heterogeneity in a meta-analysis. Meta-regression is a special case of the general linear model with heteroskedastic sampling variances that are assumed to be known; in this form of linear regression, a linear model can be fitted containing study-level variables (described here as covariates) to assess whether they are related to, or moderate, the magnitude of effect size estimates (Thompson & Higgins, 2002). Meta-regression shares many of the same features as regression in primary research, including the ability to accommodate continuous and categorical covariates, and to include covariates in main effects, polynomials, and/or multiplicative interactions. Meta-regression also bears the same considerations as linear regression in primary research, foremost of which is that the choice and number of covariates included in a model can introduce biases and yield misleading results, such as when important confounding variables have been omitted from the model or if highly collinear variables are included simultaneously in a model. When applied appropriately, however, meta-regression models that include covariates reflecting methodological complexity among primary studies can help to characterize heterogeneity in a number of ways. First, meta-regression models can provide an omnibus test of the significance of included covariates using a null hypothesis which states that none of the covariates are associated with effect size magnitude (Borenstein, Hedges, Higgins, & Rothstein, 2009). In this way, a methodological attribute of primary studies, such as differences in intervention delivery method, can be assessed as a moderator of effect size magnitude. If a covariate reflecting complexity has a significant association with effect size magnitude, meta-regression can be used to further examine how estimated effects vary relative to specific levels of the covariate (e.g., by specific types of intervention delivery methods). Finally, if after identifying a source of between-study variation, there is an interest in examining additional aspects of complexity as potentially contributing to heterogeneity, meta-regression models permit investigating other complexity-related covariates while the influence of the known sources of heterogeneity is held constant (i.e., using those covariates as control variables).

Examining heterogeneity with meta-regression.

Continuous covariates related to methodological complexity that can be incorporated into a meta-regression may be, for example, the duration of an intervention or of interventionist training, or length of time until follow-up assessment. Examples of categorical covariates might include study design (e.g., randomized controlled vs. quasi-controlled), comparison condition type (e.g., no treatment vs. treatment as usual), or risk of bias ratings (e.g., high vs. low risk of bias associated with outcome assessor blinding). In the BAI meta-analysis example, we may wish to examine the role of intervention delivery method as a source of effect size heterogeneity, as suggested above. Table 1 provides the output for a mixed-effects meta-regression model, where the outcome of interest is post-intervention differences in alcohol-related problems measured as the standardized mean difference (Cohen’s d) between intervention and comparison conditions, and the moderator (covariate) tested is intervention delivery method. In each of the primary studies, the BAI was delivered face-to-face, using a pen-and-paper modality, via a computer interface, or using a mixture of delivery methods, and these delivery methods are included in the meta-regression model using three dummy-coded indicator variables.

Table 1.

Mixed-effects Meta-regression Model of Post-Intervention Differences in Alcohol-Related Problems Moderated by Intervention Delivery Method (k = 35)

BAI Delivery Method	b	SE	95% CI
Intercept	−0.29***	0.04	[−0.36, −0.21]
Pen-and-paper	0.36*	0.16	[0.05, 0.68]
Computerized	0.25**	0.07	[0.11, 0.39]
Mixed modes	−0.25	0.36	[−0.97, 0.48]
τ2				0.005
R2				73.75
Test of Moderators				F(3, 31) = 5.65, p = .003

Note. Effect size is standardized mean difference between intervention and comparison conditions. In this output, the intercept is the coefficient for the face-to-face delivery method. k = number of primary studies. BAI = brief alcohol intervention. b = unstandardized model coefficient. SE = standard error. CI = confidence interval.

^*p < .05.

^**p < .01.

^***p < .001.

In the model output, we can first inspect the omnibus test (“Test of Moderators”), which is statistically significant at the α = .05 level, suggesting that delivery method does moderate the overall effect size estimate. We can also note two other elements of the output that are informative about delivery method as a source of heterogeneity. The first is the estimated value of τ², which now reflects residual heterogeneity after accounting for the covariates in the model. As noted above, the estimate of τ² was 0.02 before accounting for any study-level factors that might explain heterogeneity; in the current model, when we control for the effect of delivery method, the estimate of τ² is reduced to 0.005. A second useful value in the model output is the amount of heterogeneity explained, or R² (Thompson & Higgins, 2002). The R² value indicates that delivery method explains about 74% of the true between-study variation. Taken together, these three pieces of information – the significant omnibus test, the substantial reduction in the estimate of τ², and the large proportion of explained between-study variation – strongly suggest that delivery method should be viewed as a source of considerable heterogeneity in the overall effect size estimate, one that is related to methodological complexity.

Following such an assessment, we may have an interest in examining differences in the average effect size estimate across different types of delivery methods, and we can do so using the regression coefficients provided in Table 1. In this output, the intercept represents the overall effect size estimate among primary studies that used a face-to-face method for BAI delivery (the reference category for the dummy variable indicators). In these studies, RAPI scores of alcohol-related problems were on average lower $\overline{d}=-0.29$, 95% CI [−0.36, −0.21]) in the intervention versus comparison conditions. The coefficients for other delivery methods are interpreted relative to the reference category of face-to-face delivery method. If we examine the computerized delivery coefficient estimate, we can see that among studies that used this delivery method, the average standardized mean difference between intervention and comparison conditions is substantially smaller compared with face-to-face delivery ($\overline{d}=-0.29+0.25=-0.04$, 95% CI [−0.16, 0.08]). These findings suggest that delivery method is related to whether a BAI is associated with lower levels of alcohol-related problems, and that computerized delivery of BAIs may be associated with smaller beneficial effects on this type of outcome.

Additional considerations.

Employing regression analysis in meta-analytic contexts is accompanied by several considerations beyond those involved in the use of regression in primary research noted above. For one, meta-regression does not preserve primary study-level randomization, and therefore does not permit causal inference about the effects of moderators (Thompson & Higgins, 2002). Consequently, in the example interpretation provided above, we are limited to observational associations and cannot conclude unequivocally that face-to-face delivery of a BAI is more effective in reducing alcohol-related problems compared with computerized delivery. Additionally, meta-regression models are also susceptible to imbalance because the number of studies – and subgroups of studies within values of covariates – is often small. For example, in our example model output, we would exhibit caution in interpreting the coefficient representing the pen-and-paper delivery method, despite its statistical significance: As suggested by its relatively large standard error, few studies used this method in comparison to other modalities (only 2 studies used pen-and-paper delivery, in contrast to 9 using computerized delivery, and 23 employing a face-to-face approach).¹³ Furthermore, use of covariates in meta-regression that represent aggregations of study-level characteristics (e.g., demographic composition, such as proportion female) may lead to the ecological fallacy, or the incorrect overgeneralization of findings from the aggregate level to the individual participant level (Baker et al., 2009; Berlin, Santanna, Schmid, Szczech, & Feldman, 2002; Thompson & Higgins, 2002).¹⁴ In view of these limitations, meta-regression is often seen as hypothesis generating rather than as a means of hypothesis testing (Thompson & Higgins, 2002).¹⁵ When meta-regression is used to examine heterogeneity in true effects as a result of methodological complexity, findings and resulting research questions can be useful for further study of how specific methodological factors influence the effectiveness of a program.

Conclusion.

By discussing various heterogeneity statistics, visualizations, and explanatory methods, this article provides an overview of frequently employed and useful tools for assessing and explaining heterogeneity in a meta-analysis. There are other statistical and graphical approaches helpful for examining complexity and heterogeneity in meta-analyses, but we have focused on the most commonly used tools. With prediction intervals, by contrast, we have presented a currently underutilized approach. Readers interested in exploring more comprehensive treatments of options to explore heterogeneity are encouraged to examine the primary sources noted in the citations and footnotes included throughout the article. Further, the supplementary materials of this article include the full R code and data used to produce the example BAI meta-analysis results and presentations of heterogeneity we have discussed.

Our aim was also to orient the applied adolescent development researcher to examining methodological complexity as a potential source of heterogeneity in meta-analytic effect estimates. We argued that heterogeneity should be viewed as a key parameter of interest in a meta-analysis, one that can provide valuable information on how effect size estimates may vary by participant, context, and other study characteristics. Indeed, because meta-analysis can be used to synthesize evidence from a large body of primary research evidence, methods such as meta-regression can be useful for examining how a broad array of intervention ingredients or approaches may relate to variation in true effects across studies. Although methods such as meta-regression do not provide causal evidence, they can provide valuable correlational evidence that can guide future research and ultimately enhance the effectiveness of programs aimed at promoting healthy adolescent development.