Abstract
C−H∙∙∙π and N−H∙∙∙π interactions can have an important contribution for protein stability. However, direct measurements of these interactions in proteins are rarely reported. In this work, we combined the mutant cycle experiments and molecular dynamics (MD) simulations to characterize C−H∙∙∙π and N−H∙∙∙π interactions and their cooperativity in two model proteins. It is shown that the average C−H∙∙∙π interaction per residue pair is ~ −0.5 kcal/mol while the N−H∙∙∙π interaction is slightly stronger. The triple mutant box measurement indicates that N−H∙∙∙π∙∙∙C−H∙∙∙π and C−H∙∙∙π∙∙∙C−H∙∙∙π can have a positive or negative cooperativity. MD simulations suggest that the cooperativity, depending on the local environment of the interactions, mainly arises from the geometric rearrangement when the nearby interaction is perturbed.
Subject terms: Biochemistry, Biophysics
Introduction
X−H∙∙∙π interactions in biomolecules, where X can be C, N, O, or S are weak and attractive interactions between the X−H component and aromatic groups. The high incidence in biomolecules makes X−H∙∙∙π interactions an important contributor to the structure and function, and has led to an increasing number of theoretical and experimental studies devoted to characterization of such interactions1–10. Theoretical studies show that N−H∙∙∙π, O−H∙∙∙π and C−H∙∙∙π can have very different optimum geometries, with the interaction strength order O−H∙∙∙π > N−H∙∙∙π > C−H∙∙∙π4,11. The S−H∙∙∙π interaction can be weaker9 or stronger12 than O−H∙∙∙π, but is generally stronger than N−H∙∙∙π and C−H∙∙∙π9,12. The computational interaction energy of the indole-benzene dimer where the N−H∙∙∙π interaction exists can reach −5.2 kcal/mol13. The computational interaction energies between benzene and CH4, NH3, H2S, and H2O are −1.4, −2.5, −2.9 and −3.0 kcal/mol, respectively9. The computational binding energies between indole and CH4, NH3, H2S, and H2O are −2.0, −2.6, −4.9 and −3.6 kcal/mol, respectively12. The importance of the S−H∙∙∙π and C−H∙∙∙π interactions in proteins has also been highlighted by their occurrence in the PDB database search8,14,15. The C−H∙∙∙π interaction has been observed directly in proteins by nuclear magnetic resonance (NMR) spectroscopy methods where the across C−H∙∙∙π J-coupling is detected16. Quantification of C−H∙∙∙π in calix[4]pyrrole receptors yields a magnitude of −1 kcal/mol17. The C−H∙∙∙π interaction in benzene−methane, ethane, propane, and butane, increases monotonically from −1.1 to −2.7 kcal/mol18–20. The measurement of C−H∙∙∙π interactions in a cyclohexylalanine−phenylalanine pair in the core of a synthetic peptide indicates that each C−H∙∙∙π contact can contribute about −0.7 kcal/mol to peptide stability21. In real proteins, C−H∙∙∙π mainly occurs between an aliphatic side chain and an aromatic ring, or between two aromatic rings14. Although C−H∙∙∙π interactions are well documented in proteins1, direct measurements of C−H∙∙∙π and N−H∙∙∙π strength in proteins are scarce.
Another important issue about X−H∙∙∙π interactions is their cooperativity. Cooperativity is a central concept for understanding molecular recognition and supramolecular self-assembly22. By forming networks of weak interactions that compete against the entropy of flexible polypeptides, proteins fold into their biologically functional three-dimensional structures23. As a part of the interaction network, how X−H∙∙∙π interactions coexist and cooperate in proteins is an important question. Only a few studies have addressed the X−H∙∙∙π cooperativity, mainly in small molecules. The cooperativity of C−H∙∙∙π interactions in small molecules is studied using molecular torsional balances24. The average C−H∙∙∙π interaction strength increases as more C−H∙∙∙π pairs are formed, suggesting a positive cooperativity. This is opposite to the findings of an earlier computational study where the negative cooperativity is concluded for the same complexes25. The C−H∙∙∙π and N−H∙∙∙π cooperativity in proteins remains largely unexplored.
In this work, we attempt to measure the C−H∙∙∙π and N−H∙∙∙π interactions in protein GB3 and staphylococcal nuclease (SNase). GB3 is the third immunoglobulin binding domain of protein G, a model protein that has been extensively studied26. SNase is an enzyme that hydrolyzes nucleotides in DNA or RNA. A stable mutant of SNase, Δ + PHS, is selected as the test system27. It is found experimentally that the C−H∙∙∙π interaction on average is about −0.5 kcal/mol and the N−H∙∙∙π interaction on average is about −0.6 kcal/mol. N−H∙∙∙π…C−H∙∙∙π and C−H∙∙∙π…C−H∙∙∙π can have different cooperativities. Molecular dynamics (MD) simulations can reproduce N−H∙∙∙π and C−H∙∙∙π interactions and their cooperativities with reasonable accuracy. Geometric parameters that are important for C−H∙∙∙π and N−H∙∙∙π interactions are discussed. Their contribution to cooperativity is illustrated. With the combination of experimental and computational results, a better view of C−H∙∙∙π, N−H∙∙∙π and their cooperativity is obtained.
Results
Experimental C−H∙∙∙π and N−H∙∙∙π interaction energies
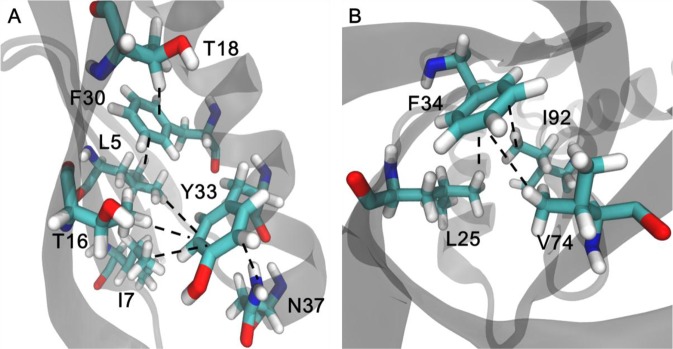
Based on the X-ray crystal structures, a series of X−H∙∙∙π interactions can be identified in GB3 and Δ + PHS (pdb code: 2OED and 3BDC, respectively). GB3 has five residue pairs that may form C−H∙∙∙π interactions, L5−F30, T18−F30, L5−Y33, I7−Y33, and T16−Y33, and one residue pair N37−Y33 that can form the N−H∙∙∙π interaction (Fig. 1A). Δ + PHS has three C−H∙∙∙π interaction residue pairs, L25−F34, V74−F34, I92−F34 (Fig. 1B). All these C−H∙∙∙π interactions are between a methyl group and an aromatic ring. A total of nine C−H∙∙∙π interactions were characterized, including L5−F30, T18−F30, L5−Y33, I7−Y33, T16−Y33, and T16−F33 of GB3, and L25−F34, V74−F34, and I92−F34 of Δ + PHS. Two N−H∙∙∙π interactions N37−Y33 and N37−F33 in GB3 were also measured. Furthermore, the introduction of triple mutant boxes (TMBs) generates additional 16 C−H∙∙∙π and 4 N−H∙∙∙π pairs (Table 1). Therefore, a total of 25 C−H∙∙∙π and 6 N−H∙∙∙π interactions were measured.
Figure 1.
Putative C−H∙∙∙π and N−H∙∙∙π interactions in GB3 (panel A, pdb code: 2OED) Δ + PHS (pdb code: 3BDC). L5 and T18 interact with F30 whereas L5, I7, T16, and N37 interact with Y33 in GB3. L25, V74 and I92 are in contact with F34 in Δ + PHS.
Table 1.
Experimental interaction energies of C−H∙∙∙π and N−H∙∙∙π interactions from double mutant cycle analysis.
| Protein | Residue pair | Interaction (kcal/mol) | Protein | Residue pair | Interaction (kcal/mol) |
|---|---|---|---|---|---|
| C−H∙∙∙π | |||||
| GB3 (WT) | L5−F30 | −0.81 ± 0.05 | GB3 (N37A) | I7−Y33 | 0.11 ± 0.06 |
| GB3 (WT) | L5−Y33 | −0.65 ± 0.06 | GB3 (N37A) | T16−Y33 | −0.85 ± 0.06 |
| GB3 (WT) | I7−Y33 | −0.13 ± 0.06 | GB3 (Y33F-N37A) | T16−F33 | −0.29 ± 0.06 |
| GB3 (WT) | T16−Y33 | −0.70 ± 0.05 | Δ + PHS (WT) | L25−F34 | −0.41 ± 0.05 |
| GB3 (WT) | T16−F33 | −0.68 ± 0.05 | Δ + PHS (WT) | V74−F34 | −0.53 ± 0.07 |
| GB3 (WT) | T18−F30 | −0.08 ± 0.05 | Δ + PHS (WT) | I92−F34 | −0.46 ± 0.06 |
| GB3 (L5V) | T16−Y33 | −0.29 ± 0.06 | Δ + PHS (L25V) | V74−F34 | −0.83 ± 0.05 |
| GB3 (L5V) | T18−F30 | 0.09 ± 0.06 | Δ + PHS (L25V) | I92−F34 | −0.84 ± 0.06 |
| GB3 (I7V) | T16−Y33 | −0.25 ± 0.06 | Δ + PHS (V74A) | L25−F34 | −0.72 ± 0.04 |
| GB3 (T16A) | L5−Y33 | −0.26 ± 0.06 | Δ + PHS (V74A) | I92−F34 | −0.51 ± 0.05 |
| GB3 (T16A) | I7−Y33 | 0.31 ± 0.05 | Δ + PHS (I92V) | L25−F34 | −0.81 ± 0.08 |
| GB3 (T18A) | L5−F30 | −0.65 ± 0.06 | Δ + PHS (I92V) | V74−F34 | −0.59 ± 0.07 |
| GB3 (N37A) | L5−Y33 | −0.34 ± 0.06 | |||
| N−H∙∙∙π | |||||
| GB3 (WT) | N37−Y33 | −0.68 ± 0.05 | GB3 (T16A) | N37−Y33 | −0.86 ± 0.06 |
| GB3 (L5V) | N37−Y33 | −0.37 ± 0.07 | GB3 (Y33F) | N37−F33 | −0.83 ± 0.06 |
| GB3 (I7V) | N37−Y33 | −0.45 ± 0.06 | GB3 (Y33F-T16A) | N37−F33 | −0.15 ± 0.06 |
The folding free energies ΔG of all proteins were derived from the denaturation curves. The values of [D]50%, m values for the wild type and mutant proteins are given in Supplementary Table S1. The magnitude of noncovalent interactions in the two proteins GB3 and Δ + PHS was obtained using the double mutant cycle (DMC) analysis28. The values of C−H∙∙∙π interactions are shown in Table 1, ranging from +0.31 (unfavorable) to −0.85 (favorable) kcal/mol, with 22 out of 25 showing favorable interactions. The three small positive interaction energies may come from the secondary interactions, i.e., the interaction changes from the surrounding residues caused by mutations (a caveat of the DMC experiment). The residual secondary interactions can contribute to the measured XH∙∙∙π energy which may change the sign of the energy (to repulsive) if it is small. The interaction energy of N−H∙∙∙π ranges from −0.15 to −0.86 kcal/mol.
According to DMC, it is preferable to mutate the two side chains x and y in the X−H∙∙∙π pair to alanine residues to completely remove the interactions between the two. However, eliminating an aromatic residue in a protein core can be detrimental to protein stability. Instead, we only mutated the aromatic side chain (y) to a leucine (y′) which is still hydrophobic but disrupts the X−H∙∙∙π interaction (see more details in Materials and Methods). For the X−H component (x), conservative mutations are introduced (x′) to remove the X−H∙∙∙π interaction and maintain the protein folding at the same time. These mutations may create residual pairwise side chain interactions in x′y′, xy′, and x′y. Furthermore, for a residue like leucine (for example, in L5−F30) which has two CH3 and one CH, it can form multiple C−H∙∙∙π interactions which complicate the interpretation of the experimental results. These problems can be solved with the assist of MD simulations.
Benchmark of MD simulations
MD simulations were performed for all the experimentally measured mutants with three commonly used force fields, Amber99sb29, Charmm2730, and Gromos53a631. The experimental C−H∙∙∙π and N−H∙∙∙π interaction energies were used as a benchmark to evaluate the accuracy of different force fields. The root mean square deviation (RMSD) between the experimental and predicted X−H∙∙∙π interactions was calculated:
| 1 |
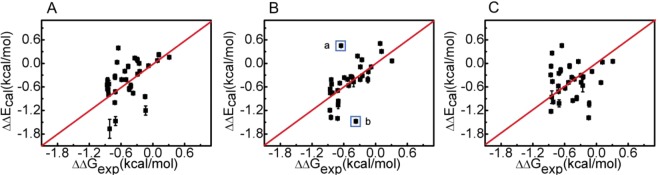
where N is 31, the total number of measured residue pairs that form X−H∙∙∙π interactions, ΔΔGexp is the experimental X−H∙∙∙π interaction energy, and ΔΔEMD is the calculated interaction energy. Charmm27 appears to perform better than the other two force fields. Its RMSD value is 0.27 kcal/mol (after removing two apparent outliers), while the RMSDs of Amber99sb and Gromos53a6 are 0.41 and 0.47 kcal/mol, respectively (Fig. 2). Thus, the trajectories produced using Charmm27 were selected for further analyses.
Figure 2.
Correlation between the experimental and calculated interaction energies from different force fields. (A) Amberff99SB, (B) Charmm27, and (C) Gromos53a6. The RMSDs from the experimental values are 0.41, 0.27 (excluding two outliers, a: L5−F30 in GB3(T18A), b: N37−Y33 in GB3(L5V)), and 0.47 kcal/mol, respectively. The red line is y = x.
Geometric parameters of C−H∙∙∙π and N−H∙∙∙π interactions
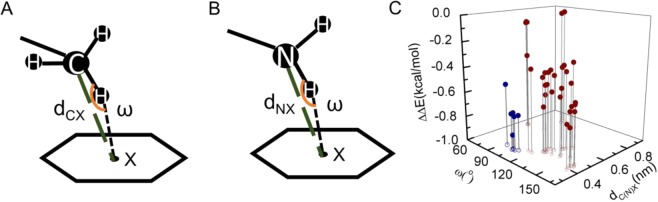
The reasonable correlation between the interaction energies from MD simulations and experiments encourages us to investigate the geometric parameters that are important for C−H∙∙∙π and N−H∙∙∙π interactions. The pairwise interaction energy ΔΔECH3∙∙∙π between a CH3 group and a aromatic ring was calculated for all the C−H∙∙∙π interactions identified above. Two geometric parameters15 dCX and ω are defined for the C−H∙∙∙π interaction, where dCX is the distance of the methyl carbon to the center of mass of the aromatic ring (X), and ω is the ∠C−H−X angle (Fig. 3A). Since there are three methyl hydrogens, the one with the largest ∠C−H−X angle is defined as ω. The same geometric parameters can also be defined for N−H∙∙∙π interactions (Fig. 3B). The 3D plot of (dCX, ω) versus ΔΔECH3∙∙∙π shows that the geometries with shorter dCX and larger ω have more negative interaction energies (Fig. 3C). The distance appears to be the most important parameter, with the energy dropping quickly as the distance decreases. Meanwhile, the angle ω can also be important. The average ΔECH3∙∙∙π for all the C−H∙∙∙π interactions is −0.36 kcal/mol. The number of N−H∙∙∙π interactions is less than that of C−H∙∙∙π, and they appear to be stronger than C−H∙∙∙π interactions with the same geometric parameters.
Figure 3.
Geometric parameters and computational interaction energies for C−H∙∙∙π and N−H∙∙∙π interactions. (A) Schematic diagram of C−H∙∙∙π. The center-of-mass of the π-system is indicated by the point X. dCX is distance between the center-of-mass of the methyl group and that of the aromatic ring, ω is the angle ∠C−H−X. (B) Schematic diagram of N−H∙∙∙π. (C) Computational ΔΔE energy scatter plot with dCX or dNX and ω. ΔΔE is the interaction energy between the methyl group and the aromatic group (red) and those between the amide group and the aromatic group (blue).
∆ΔΔGcoop from TMB measurements
On the basis of double mutant cycles we had, we established several TMBs to elucidate the cooperativity in C−H∙∙∙π∙∙∙C−H∙∙∙π and C−H∙∙∙π∙∙∙N−H∙∙∙π interactions. In protein GB3, the cooperativity is positive in L5−F30−T18, L5−Y33−T16, I7−Y33−T16, L5−Y33−N37, I7−Y33−N37, and T16−F33−N37, with ∆ΔΔGcoop varied from −0.16 to −0.55 kcal/mol (Supplementary Table S2, Fig. 4), suggesting that they are cooperative with each other. In contrast, the C−H∙∙∙π∙∙∙N−H∙∙∙π in T16−Y33−N37 of GB3, and the C−H∙∙∙π∙∙∙C−H∙∙∙π in L25−F34−V74, L25−F34−I92, and V74−F34−I92 of Δ + PHS are anticooperative, with ∆ΔΔGcoop varied from 0.04 to 0.37 kcal/mol (Supplementary Table S2). The cooperativity difference in different C−H∙∙∙π∙∙∙C−H∙∙∙π and C−H∙∙∙π∙∙∙N−H∙∙∙π suggests that it depends on the local interaction network.
Figure 4.
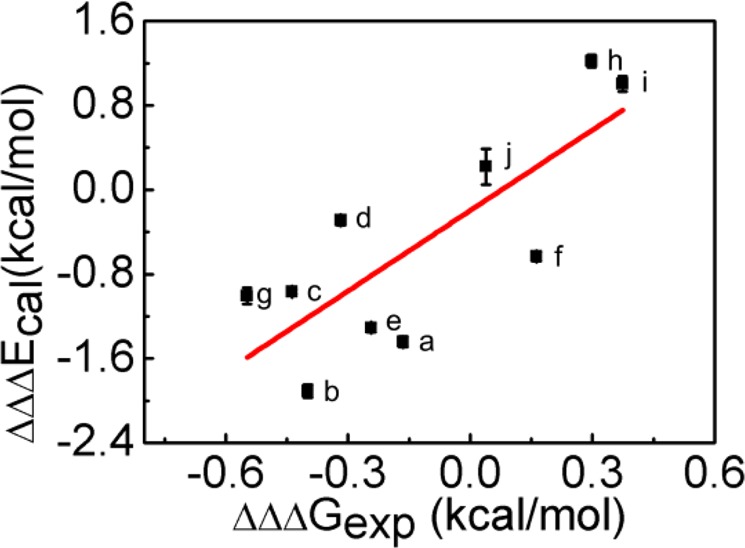
Correlation between the experimental and calculated cooperativity energies (a). L5−F30−T18, (b) L5−Y33−T16, (c) I7−Y33−T16, (d) L5−Y33−N37, (e) I7−Y33−N37, (f) T16−Y33−N37, (g) T16−F33−N37, (h): L25−F34−V74, (i): L25−F34−I92, (j): V74−F34−I92). The best fitted line is y = 2.54x − 0.2, with a correlation coefficient R of 0.79. Groups a−g are from GB3 whereas groups h−j are from Δ + PHS.
Cooperativity mechanism from MD simulations
The ∆ΔΔGcoop are in a good correlation with the computational ∆ΔΔE (cooperativity energy, see more details in Materials and Methods), although the absolute value of ∆ΔΔE is generally larger than that of ∆ΔΔGcoop (Fig. 4). One likely cause is that the entropic contribution, which is not calculated in MD simulations, may offset the large change of ∆ΔΔE. The entropy calculation is far more difficult (less reliable) and thus not pursued. As discussed above, the residual interactions caused by the experimental non-alanine mutations complicate the interpretation of ∆ΔΔGcoop. To solve this problem, we rebuilt TMBs by mutating the three side chains, for example L25, F34, and V74 in L25−F34−V74, to alanines systematically in MD simulations. The cooperativity energy ∆ΔΔE′ was calculated for the residue groups listed above with the same procedure (Fig. 5A). The cooperativity from ∆ΔΔE′ generally agrees with that from ∆ΔΔE, except that L5−Y33−T16 and I7−Y33−T16 show a weak negative instead of positive cooperativity.
Figure 5.
(A) Calculated cooperativity energy ∆ΔΔE′ for ten side chain groups (same as those in Fig. 4). (B) Percentagewise ∆ΔΔE′ defined as ∆ΔΔE′, divided by the average of the two C−H∙∙∙π/C−H∙∙∙π or C−H∙∙∙π/N−H∙∙∙π interactions. (C) ∆d, the first C−H∙∙∙π or N−H∙∙∙π distance change when the second C−H∙∙∙π or N−H∙∙∙π is removed.
The cooperativity energy ∆ΔΔE′ varies from −0.39 to 0.16 kcal/mol (Fig. 5A). Although they appear to be small, the percentagewise ∆ΔΔE′ (∆ΔΔE′ divided by the average of the two C−H∙∙∙π interactions in C−H∙∙∙π∙∙∙C−H∙∙∙π or the average of the C−H∙∙∙π and the N−H∙∙∙π interaction energy in C−H∙∙∙π∙∙∙N−H∙∙∙π) can vary from −40% (cooperative) to +60% (anticooperative) (Fig. 5B). So it is obvious that cooperativity can be very important for C−H∙∙∙π and N−H∙∙∙π interactions in an interaction network. To further understand the origin of cooperativity, the geometric changes in the TMB are investigated. It is known that dCX or dNX (Fig. 3) is an important parameter for C−H∙∙∙π or N−H∙∙∙π. Using L5−Y33−T16 as an example, Δd, the change of dCX, was calculated by
| 2 |
where dCX_WT is dCX between the methyl of L5 and the aromatic side chain of Y33 in the wild type, and dCX_MUT is dCX in the single mutant T16A. A similar Δd can be defined for C−H∙∙∙π∙∙∙N−H∙∙∙π interactions. Δd was calculated for 10 residue groups shown in Fig. 5. The positive Δd corresponds to the increase of the first C−H∙∙∙π (or N−H∙∙∙π) distance when the aliphatic side chain of the second C−H∙∙∙π (or N−H∙∙∙π) is mutated to alanine. In other words, removing the second C−H∙∙∙π (or N−H∙∙∙π) interaction weakens the first C−H∙∙∙π (or N−H∙∙∙π) interaction, suggesting a positive cooperativity. For 9 out of 10 groups, the distance change Δd predicts the cooperativity consistent with the interaction energy result (Fig. 5B,C), indicating that the cooperativity in C−H∙∙∙π∙∙∙C−H∙∙∙π or C−H∙∙∙π∙∙∙N−H∙∙∙π mainly arises from the geometric rearrangement.
Discussion
DMC experiments are commonly used to measure residue−residue interactions, such as salt bridges and hydrogen bonds32,33. However, measuring C−H∙∙∙π interactions in the protein interior using DMC can be challenging because removing an aromatic side chain can destabilize and even unfold the protein. In this work, we only mutate the aromatic residue to leucine which maintains the protein folding and removes the C−H∙∙∙π interaction. Two very stable proteins GB3 and Δ + PHS were selected for the purpose. One caveat of the F or Y to L mutation is that residual interactions with leucine complicate the data interpretation. Molecular dynamics simulations were used to decompose the various contributions and help us focus on the C−H∙∙∙π interactions. The good agreement between experimental and computational interaction energies validates the procedure which provides important insights about the C−H∙∙∙π and N−H∙∙∙π interactions.
The energy of C−H∙∙∙π interactions obtained from the DMC experiments of two proteins in this work is smaller than ~ −0.9 kcal/mol, with an average of ~ −0.5 kcal/mol. This C−H∙∙∙π interaction strength is generally weaker than those reported for small molecules17–21. It is likely that different interactions compete with each other in proteins so that the C−H∙∙∙π interaction of a specific residue pair is not in an optimum geometry. This is evident from the interaction energy landscape of methyl−aromatic ring pair (Fig. 3). The lower corner, with dCX of ~0.4 nm and ω of ~165°, has the lowest interaction energy in the plot. But many C−H∙∙∙π pairs are clustered around dCX of ~0.4−0.6 nm and ω of ~120°−150°. The optimal dCX of 0.4 nm is close to the distance obtained from the quantum mechanical calculations9. For C−H∙∙∙π pairs with larger dCX, the C−H group moves away from the top of the aromatic ring to form a side-by-side configuration which has an optimal dCX of ~0.5 nm, as suggested from the QM calculations9. The non-optimum geometry also implies that different C−H∙∙∙π interactions with the same aromatic ring are interdependent. A small perturbation of one C−H∙∙∙π pair may affect the geometry of another C−H∙∙∙π nearby which creates the cooperativity effect.
The cooperativity analysis from TMB clearly suggests that the C−H∙∙∙π…C−H∙∙∙π and C−H∙∙∙π…N−H∙∙∙π can be either cooperative or anticooperative (Fig. 4). Although in the experimental TMB analysis, the cooperativity information is contaminated by the residual interactions in the mutants, the computational TMB analysis where the residual interactions are removed suggests that the side chain C−H∙∙∙π and N−H∙∙∙π interactions have a major contribution to the experimentally determined ∆ΔΔG (Figs. 4 and 5). Moreover, the dCX or dNX distance change Δd is an important indicator for the cooperativity. But when comparing the computational cooperativity energy ∆ΔΔE′ and Δd, the linear correlation between the two is only moderate, suggesting that the distance change is not the only contributor to the cooperativity change. The change of angles such as ω may also play a role.
Two simpler cooperativity models were built using two methane and one benzene molecules, with methanes on the same side (MMB) or opposite side (MBM) of the benzene. The cooperativity energies of MMB and MBM models were calculated at the MP2/aug-cc-pvtz level34. According to the quantum mechanical (QM) calculations, the cooperativity energy of MMB is 0.74 kcal/mol, indicating that C−H∙∙∙π…C−H∙∙∙π is anticooperative in this model, while the cooperativity energy of MBM is 0.03 kcal/mol, suggesting that there is no cooperativity in this model. Similar to the result in the MD simulations, the geometric reorganization occurs in the MMB model where the two methanes compete for the binding site. No such competition exists in the MBM model where the cooperativity energy is close to zero. The QM calculations highlight the importance of geometric reorganization to cooperativity.
Conclusion
In this study, we measured the strength of C−H∙∙∙π and N−H∙∙∙π interactions in GB3 and SNase. The C−H∙∙∙π interaction is about 0.3 to −0.9 kcal/mol whereas the N−H∙∙∙π interaction is about −0.2 to −0.9 kcal/mol. The energy decomposition from MD simulations helps determine the C−H∙∙∙π and N−H∙∙∙π interactions for individual methyl−aromatic and amino−aromatic pairs and identify important geometric parameters dC(N)X and ω. The experimental TMB analysis suggests that the cooperativity of X−H∙∙∙π interactions can be either positive or negative, depending on the local environment. The cooperativity trend is successfully captured by MD simulations where the cooperativity energy can reach ~ −40% to 60% of C−H∙∙∙π or N−H∙∙∙π interactions, highlighting its importance in proteins. The geometric rearrangement is the main cause for the cooperative interactions. It is worth noting that the C−H∙∙∙π and N−H∙∙∙π interactions and the cooperativity were only measured for two proteins GB3 and Δ + PHS. More measurements will be needed to see whether the conclusions also hold for other proteins. But we expect that the mechanism behind the interactions is universal for all protein molecules.
Materials and Methods
Protein expression and purification
The wild type and mutants of GB3 and Δ + PHS were prepared with the PCR-based site-directed mutagenesis on vector pET-11b. These plasmids were transformed into the E. coli strain BL21 (DE3) cells for protein expression. The purification procedure for GB3 and its variants has been described previously35. Δ + PHS and its variants were purified using the same procedure as described by Shortle and Meeker36.
Thermodynamic stability measurements
All the denaturation measurements were performed using a HITACHI f-4600 fluorescence Spectrophotometer. Mixtures consisted of up to 6.0 M GdnHCl and 50 µM proteins (final concentration) were incubated for 30 min at 30 °C. The signal intensity at 340 nm for GB3 and 348 nm for SNase was extracted and fitted using the following equation,
| 3 |
where S is the measured Fluo340nm or Fluo348nm, αN and αU are the intercepts and βN and βU are the slopes of the Fluo340nm or Fluo348nm baselines at low (N) and high (U) denaturant concentrations, R is the Boltzmann constant, T is the temperature, [D] is the denaturant concentration, [D]50% is the denaturant concentration at which the protein is 50% denatured.
Double mutant cycle analysis
Double mutant cycle (DMC), proposed by Fersht and co-workers, can eliminate the contribution of the secondary interactions and obtain accurate binding energy for the interaction between two residues37,38. Double mutant cycles were performed to quantify C−H∙∙∙π interactions and N−H∙∙∙π interactions in this work. To build the DMC, dozens of single and double mutants were prepared. Single mutants included L5V, I7V, T16A, T18A, N37A, F30L, Y33L, Y33F in GB3 and L25V, V74A, I92V, F34L in Δ + PHS. Double mutants contained two substitutions, L5V−F30L, L5V−Y33L, I7V−Y33L, T16A−Y33F, T16A−Y33L, T18A−F30L, N37A−Y33L and N37A−Y33F in GB3, and L25V−F34L, V74A−F34L, I92V−F34L in Δ + PHS. The folding free energy for each mutant was determined from the denaturation curve monitored by fluorescence. The C−H∙∙∙π or N−H∙∙∙π interaction energy with the aromatic ring was then calculated using:
| 4 |
where ΔGxy, ΔGx′y, ΔGxy′, and ΔGx′y′ are the folding free energy for the wild type protein xy, single mutants x′y and y′x, and the double mutant x′y′, respectively. The symbols x and y denote the aliphatic and aromatic side chains in the C−H∙∙∙π or N−H∙∙∙π pair. This expression can be defined for both GB3 and Δ + PHS proteins.
Triple mutant box analysis
Two double mutant cycles can be combined to produce a TMB, which can be used for quantification of cooperative effects. Extensive studies have been performed by Hunter and co-workers using triple mutant box experiments to evaluate cooperativity in non-covalent interactions28,39. Double mutants of GB3 (L5V-I7V, L5V-T16A, L5V-T18A, I7V-T16A, L5V-N37A, I7V-N37A, and T16A-N37A) and Δ + PHS (L25V-V74A, L25V-I92V and L74A-I92V) were used to set TMBs. All of these double mutant proteins could be expressed except L5V-I7V of GB3. Triple mutants were prepared, including L5V-T16A-Y33L, L5V-T18A-F30L, I7V-T16A-Y33L, L5V-N37A-Y33L, I7V-N37A-Y33L, T16A-N37A-Y33L, and T16A-N37A-F33L for GB3, and L25V-V74A-F34L, L25V-F34L-I92V, and V74A-I92V-F34L for Δ + PHS. These mutants were used to quantify the cooperativity in C−H∙∙∙π∙∙∙C−H∙∙∙π interactions and C−H∙∙∙π∙∙∙N−H∙∙∙π interactions. The folding free energy for each mutant was measured using the same method mentioned above. The cooperativity energy was then calculated using:
| 5 |
where y represents the aromatic residue, x and z represent nonaromatic residues, ∆Gxyz, ∆Gx′yz, ∆Gxy′z, ∆Gxyz′, ∆Gx′y′z, ∆Gx′yz′, ∆Gxy′z′, and ∆Gx′y′z′ are the folding free energy of the wild type protein xyz, single mutants x′yz, xy′z and xyz′, double mutants x′y′z, x′yz′, xy′z′ and triple mutants x′y′z′, respectively.
Molecular dynamics simulations
MD simulations were performed using the GROMACS 4.5 package40 with Amber99sb29, Charmm2730, or Gromos53a631 force fields. The structures of all variants of GB3 and Δ + PHS were produced by FoldX41 with the protein backbone fixed. Each protein was solvated by adding 10.0 Å TIP3P water42 (or SPC water when the Gromos53a6 force field was used) in a rectangular box, and counter ions were used to neutralize the system. 500,000 steps of energy minimization followed by 1 ns MD simulation at constant pressure (1 atm) and temperature (303 K) were performed to equilibrate the system before the production running. Three 10 ns MD production runs with different random starting velocities were performed with snapshots saved every 50 ps which were then used in the data analysis and error estimation. All backbone heavy atoms are restrained in the equilibrium and production runs. Temperature was regulated by a modified Berendsen thermostat43 and pressure was controlled by the extended ensemble Parrinello-Rahman approach44,45. The long-range electrostatic interactions were evaluated by the Particle mesh Ewald method46,47. The nonbonded pair list cutoff was 10 Å and the list was updated every 10 fs. The LINCS algorithm48 was used to constrain all bonds linked to hydrogen in the protein, whereas the SETTLE algorithm49 was used to constrain bonds and angles of water molecules, allowing a time step of 2 fs. In the energy decomposition analysis, only the interaction energy between the paired residues of C−H∙∙∙π or N−H∙∙∙π was calculated. The computational interaction energy ΔΔE was calculated by,
| 6 |
| 7 |
where ΔExy, ΔEx′y, ΔExy′, and ΔEx′y′ are the x−y interaction energy in the wild type protein, x′−y in the single mutant x′y, x−y′ in the single mutant y′x, and x′−y′ in the double mutant x′y′, respectively. The symbols x and y are the same as those in Eq. 4. An effective dielectric constant ε of 4.0 was used for electrostatic interaction energy calculations. The computational cooperativity energy ΔΔΔE was calculated by,
| 8 |
| 9 |
where y represents the aromatic residue, x and z represent nonaromatic residues, ∆Exyz, ∆Ex′yz, ∆Exy′z, ∆Exyz′, ∆Ex′y′z, ∆Ex′yz′, ∆Exy′z′, and ∆Ex′y′z′ are the interaction energy of x−y−z, x′−y−z, x−y′−z, x−y−z′, x′−y′−z, x′−y−z′, x−y′−z′, and x′−y′−z′ in the wild type protein xyz, single mutants x′yz, xy′z and xyz′, double mutants x′y′z, x′yz′, xy′z′ and triple mutants x′y′z′, respectively.
QM calculations
Two methane and one benzene molecules were built to model the cooperativity of C−H∙∙∙π∙∙∙C−H∙∙∙π. The geometries of the two models, MMB and MBM, were optimized at the MP2/6-31 + G(d,p)50 level. The energy calculations were performed at the MP2/aug-cc-pvtz34 level. All the calculations were done using the Gaussian 09 software51.
Supplementary information
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant nos. 21773280 and 31661143036), Natural Science Foundation of Shandong Province (Grant no. ZR2018ZB0207), and the Taishan Scholars Program of Shandong Province.
Author contributions
J.W. and L.Y. conceived the project. J.W. and L.Y. planned the experiments and MD simulations. J.W performed the experiments and MD simulations. J.W. and L.Y. analyzed the data. J.W. and L.Y. wrote the paper. All authors approved the final manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
is available for this paper at 10.1038/s41598-019-56607-4.
References
- 1.Nishio M, Umezawa Y, Fantini J, Weiss MS, Chakrabarti P. CH-pi hydrogen bonds in biological macromolecules. Phys. Chem. Chem. Phys. 2014;16:12648–12683. doi: 10.1039/C4CP00099D. [DOI] [PubMed] [Google Scholar]
- 2.Neel AJ, Hilton MJ, Sigman MS, Toste FD. Exploiting non-covalent pi interactions for catalyst design. Nature. 2017;543:637–646. doi: 10.1038/nature21701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Parsons ZD, Bland JM, Mullins EA, Eichman BF. A Catalytic Role for C-H/pi Interactions in Base Excision Repair by Bacillus cereus DNA Glycosylase AlkD. J. Am. Chem. Soc. 2016;138:11485–11488. doi: 10.1021/jacs.6b07399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mohan N, Vijayalakshmi KP, Koga N, Suresh CH. Comparison of aromatic NH···π, OH···π, and CH···π interactions of alanine using MP2, CCSD, and DFT methods. J. Comput. Chem. 2010;31:2874–2882. doi: 10.1002/jcc.21582. [DOI] [PubMed] [Google Scholar]
- 5.Meyer EA, Castellano RK, Diederich F. Interactions with Aromatic Rings in Chemical and Biological Recognition. Angew. Chem. Int. Ed. 2003;42:1210–1250. doi: 10.1002/anie.200390319. [DOI] [PubMed] [Google Scholar]
- 6.Kamps JJAG, et al. Chemical basis for the recognition of trimethyllysine by epigenetic reader proteins. Nat. Commun. 2015;6:8911–8911. doi: 10.1038/ncomms9911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Al Temimi AHK, et al. Recognition of shorter and longer trimethyllysine analogues by epigenetic reader proteins. Chem. Commun. 2018;54:2409–2412. doi: 10.1039/C8CC01009A. [DOI] [PubMed] [Google Scholar]
- 8.Ringer AL, Senenko A, Sherrill CD. Models of S/pi interactions in protein structures: Comparison of the H2S-benzene complex with PDB data. Protein Sci. 2007;16:2216–2223. doi: 10.1110/ps.073002307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Alberti M, Aguilar A, Huarte-Larranaga F, Lucas JM, Pirani F. Benzene-Hydrogen Bond (C6H6-HX) Interactions: The Influence of the X Nature on their Strength and Anisotropy. J. Phys. Chem. A. 2014;118:1651–1662. doi: 10.1021/jp410917x. [DOI] [PubMed] [Google Scholar]
- 10.Tauer TP, Derrick ME, Sherrill CD. Estimates of the ab initio limit for sulfur-pi interactions: The H2S-benzene dimer. J. Phys. Chem. A. 2005;109:191–196. doi: 10.1021/jp046778e. [DOI] [PubMed] [Google Scholar]
- 11.Vaupel S, Brutschy B, Tarakeshwar P, Kim KS. Characterization of Weak NH−π Intermolecular Interactions of Ammonia with Various Substituted π-Systems. J. Am. Chem. Soc. 2006;128:5416–5426. doi: 10.1021/ja056454j. [DOI] [PubMed] [Google Scholar]
- 12.Biswal HS, Wategaonkar S. Sulfur, Not Too Far Behind O, N, and C: SH center dot center dot center dot pi Hydrogen Bond. J. Phys. Chem. A. 2009;113:12774–12782. doi: 10.1021/jp907747w. [DOI] [PubMed] [Google Scholar]
- 13.Braun J, Neusser HJ, Hobza P. N-H center dot center dot center dot pi interactions in indole center dot center dot center dot benzene-h(6),d(6) and indole center dot center dot center dot benzene-h(6),d(6) radical cation complexes. Mass analyzed threshold ionization experiments and correlated ab initio quantum chemical calculations. J. Phys. Chem. A. 2003;107:3918–3924. [Google Scholar]
- 14.Kumar M, Balaji PV. C-H…pi interactions in proteins: prevalence, pattern of occurrence, residue propensities, location, and contribution to protein stability. J. Mol. Model. 2014;20:2136–2136. doi: 10.1007/s00894-014-2136-5. [DOI] [PubMed] [Google Scholar]
- 15.Brandl M, Weiss MS, Jabs A, Suhnel J, Hilgenfeld R. C-H center dot center dot center dot pi-interactions in proteins. J. Mol. Biol. 2001;307:357–377. doi: 10.1006/jmbi.2000.4473. [DOI] [PubMed] [Google Scholar]
- 16.Plevin MJ, Bryce DL, Boisbouvier J. Direct detection of CH/pi interactions in proteins. Nat. Chem. 2010;2:466–471. doi: 10.1038/nchem.650. [DOI] [PubMed] [Google Scholar]
- 17.Aragay G, et al. Quantification of CH-pi Interactions Using Calix[4]pyrrole Receptors as Model Systems. Molecules. 2015;20:16672–16686. doi: 10.3390/molecules200916672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shibasaki K, Fujii A, Mikami N, Tsuzuki S. Magnitude of the CH/pi interaction in the gas phase: Experimental and theoretical determination of the accurate interaction energy in benzene-methane. J. Phys. Chem. A. 2006;110:4397–4404. doi: 10.1021/jp0605909. [DOI] [PubMed] [Google Scholar]
- 19.Shibasaki K, Fujii A, Mikami N, Tsuzuki S. Magnitude and nature of interactions in benzene-X (X = ethylene and acetylene) in the gas phase: Significantly different CH/pi interaction of acetylene as compared with those of ethylene and methane. J. Phys. Chem. A. 2007;111:753–758. doi: 10.1021/jp065076h. [DOI] [PubMed] [Google Scholar]
- 20.Fujii A, et al. Experimental and theoretical determination of the accurate CH/pi interaction energies in benzene-alkane clusters: correlation between interaction energy and polarizability. Phys. Chem. Chem. Phys. 2011;13:14131–14141. doi: 10.1039/c1cp20203k. [DOI] [PubMed] [Google Scholar]
- 21.Pace CJ, Kim D, Gao JM. Experimental Evaluation of CH-p Interactions in a Protein Core. Chem. - A Eur. J. 2012;18:5832–5836. doi: 10.1002/chem.201200334. [DOI] [PubMed] [Google Scholar]
- 22.Hunter CA, Anderson HL. What is cooperativity? Angew. Chem. Int. Ed. 2009;48:7488–7499. doi: 10.1002/anie.200902490. [DOI] [PubMed] [Google Scholar]
- 23.Sborgi L, et al. Interaction Networks in Protein Folding via Atomic-Resolution Experiments and Long-Time-Scale Molecular Dynamics Simulations. J. Am. Chem. Soc. 2015;137:6506–6516. doi: 10.1021/jacs.5b02324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhao C, Li P, Smith MD, Pellechia PJ, Shimizu KD. Experimental Study of the Cooperativity of CH−π Interactions. Org. Lett. 2014;16:3520–3523. doi: 10.1021/ol5014729. [DOI] [PubMed] [Google Scholar]
- 25.Ran J, Wong MW. Saturated Hydrocarbon−Benzene Complexes: Theoretical Study of Cooperative CH/π Interactions. J. Phys. Chem. A. 2006;110:9702–9709. doi: 10.1021/jp0555403. [DOI] [PubMed] [Google Scholar]
- 26.Derrick JP, Wigley DB. The 3rd IgG-binding Domain from Streptococcal Protein-G - an Analysis by X-ray Crystallography of the Structure Alone and in a Complex with Fab. J. Mol. Biol. 1994;243:906–918. doi: 10.1006/jmbi.1994.1691. [DOI] [PubMed] [Google Scholar]
- 27.Karp DA, et al. High apparent dielectric constant inside a protein reflects structural reorganization coupled to the ionization of an internal Asp. Biophys. J. 2007;92:2041–2053. doi: 10.1529/biophysj.106.090266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mahadevi AS, Sastry GN. Cooperativity in Noncovalent Interactions. Chem. Rev. 2016;116:2775–825. doi: 10.1021/cr500344e. [DOI] [PubMed] [Google Scholar]
- 29.Hornak V, et al. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Foloppe N, Mackerell AD. All-Atom Empirical Force Field for Nucleic Acids: I. Parameter Optimization Based on Small Molecule and Condensed Phase Macromolecular Target Data. J. Comput. Chem. 2000;21:86–104. doi: 10.1002/(SICI)1096-987X(20000130)21:2<86::AID-JCC2>3.0.CO;2-G. [DOI] [Google Scholar]
- 31.Oostenbrink C, Villa A, Mark AE, van Gunsteren WF. A biomolecular force field based on the free enthalpy of hydration and solvation: the GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004;25:1656–76. doi: 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
- 32.Kiel C, Serrano L, Herrmann C. A detailed thermodynamic analysis of Ras/effector complex interfaces. J. Mol. Biol. 2004;340:1039–1058. doi: 10.1016/j.jmb.2004.05.050. [DOI] [PubMed] [Google Scholar]
- 33.Bowie JU. Membrane protein folding: how important are hydrogen bonds? Curr. Opin. Struc. Biol. 2011;21:42–49. doi: 10.1016/j.sbi.2010.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kendall RA, Dunning TH, Harrison RJ. Electron affinities of the first‐row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992;96:6796–6806. [Google Scholar]
- 35.Yao L, Ying J, Bax A. Improved accuracy of 15N–1H scalar and residual dipolar couplings from gradient-enhanced IPAP-HSQC experiments on protonated proteins. J. Biomol. NMR. 2009;43:161–170. doi: 10.1007/s10858-009-9299-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Shortle D, Meeker AK. Residual structure in large fragments of staphylococcal nuclease: effects of amino acid substitutions. Biochemistry. 1989;28:936–944. doi: 10.1021/bi00429a003. [DOI] [PubMed] [Google Scholar]
- 37.Biedermann F, Schneider H-J. Experimental Binding Energies in Supramolecular Complexes. Chem. Rev. 2016;116:5216–5300. doi: 10.1021/acs.chemrev.5b00583. [DOI] [PubMed] [Google Scholar]
- 38.Horovitz A. Double-mutant cycles: a powerful tool for analyzing protein structure and function. Fold. Des. 1996;1:R121–R126. doi: 10.1016/S1359-0278(96)00056-9. [DOI] [PubMed] [Google Scholar]
- 39.Hunter CA, Jones PS, Tiger P, Tomas S. Chemical triple-mutant boxes for quantifying cooperativity in intermolecular interactions. Chemistry. 2002;8:5435–46. doi: 10.1002/1521-3765(20021202)8:23<5435::AID-CHEM5435>3.0.CO;2-V. [DOI] [PubMed] [Google Scholar]
- 40.Hess B, Kutzner C, van der Spoel D, Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory. Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 41.Guerois R, Nielsen JE, Serrano L. Predicting changes in the stability of proteins and protein complexes: a study of more than 1000 mutations. J. Mol. Biol. 2002;320:369–87. doi: 10.1016/S0022-2836(02)00442-4. [DOI] [PubMed] [Google Scholar]
- 42.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. doi: 10.1063/1.445869. [DOI] [Google Scholar]
- 43.Berendsen, H. J. C. Transport Properties Computed by Linear Response through Weak Coupling to a Bath. in Computer Simulation in Materials Science: Interatomic Potentials, Simulation Techniques and Applications (eds. Meyer, M. & Pontikis, V.) 139–155 (Springer Netherlands, Dordrecht, 1991).
- 44.Nosé S, Klein ML. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 1983;50:1055–1076. doi: 10.1080/00268978300102851. [DOI] [Google Scholar]
- 45.Parrinello M, Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981;52:7182–7190. doi: 10.1063/1.328693. [DOI] [Google Scholar]
- 46.Darden T, York D, Pedersen L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. doi: 10.1063/1.464397. [DOI] [Google Scholar]
- 47.Essmann U, et al. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. doi: 10.1063/1.470117. [DOI] [Google Scholar]
- 48.Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. doi: 10.1002/(SICI)1096-987X(199709)18:12<1463::AID-JCC4>3.0.CO;2-H. [DOI] [Google Scholar]
- 49.Miyamoto S, Kollman PA. J. Comput. Chem. 1992. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models; pp. 952–962. [Google Scholar]
- 50.Head-Gordon M, Pople JA, Frisch MJ. MP2 energy evaluation by direct methods. Chem. Phys. Lett. 1988;153:503–506. doi: 10.1016/0009-2614(88)85250-3. [DOI] [Google Scholar]
- 51.Frisch, M. J. T. et al. Gaussian 09, revision B.01; Gaussian, Inc.:(Wallingford, CT, 2010).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.