Probing the interfacial strength of novel multi-layer zirconias

Abstract

Objectives:

The rapidly increasing use of zirconia-based CAD/CAM multi-layer structures in dentistry calls for a thorough evaluation of their mechanical integrity. This work examines the effect of the multi-layering architecture as well as variations in composition and inclusion of pigments among the layers on the flexural strength of multi-layer zirconias.

Methods:

A modified 4-point bending test, aided by a Finite Element Analysis (FEA), was used to probe the interfacial strength of 3 classes of yttria-partially-stabilized zirconia: Ultra Translucent Multi-Layer (UTML—5Y-PSZ), Super Translucent Multi-Layer (STML—4Y-PSZ), Multi-Layer (ML—3Y-PSZ). In accord with the size limitation (22-mm height) of CAD/CAM pucks, test samples were prepared in the form of “long” (25×2×3 mm) and “short” (17.8×1.5×2 mm) beams. Homogeneous beams (both long and short) were produced from either the Enamel (the lightest shade) or Dentin (the darkest shade) layer, whereas multi-layer beams (short beam only) were obtained by cutting the pucks along their thickness direction, where the material components of various shades were stacked.

Results:

The Enamel and Dentin layers exhibited similar flexural strength for a given material class, with ML amassing the highest strength (800–900 MPa) followed by STML (560–650 MPa) and UTML (470–500 MPa). The 3 classes of multi-layer zirconia showed a trade-off between strength and translucency, reflecting different yttria contents in these materials. The failure stress of the cross-sectional multi-layer beams was, however, ~30% lower than that of their Enamel or Dentin layer counterparts, regardless of material tested.

Significance:

The weakness of interfaces is a drawback in these materials. Additionally, when measuring strength using short beam flexure, friction between the specimen and supporting pins and accuracy in determining loading span distances may lead to major errors.

INTRODUCTION

Over the past 2 decades, dental zirconia has evolved from the original white, opaque appearance to translucent and chromatic, and to polychromatic (multi-layered) forms [1–7]. With a wide range of translucency and shades, zirconia has now become the most versatile restorative material. Its clinical indications span from rehabilitations of a single tooth to an entire arch of teeth [7–9]. The first polychromatic zirconias released to the dental market in February 2015 are the Katana Multi-Layered zirconias by Kuraray Noritake Dental Japan (Fig. 1a), aiming for the fabrication of full contour zirconia crowns with a higher level of aesthetics. Since then, almost all major dental companies have put forward their own version of multi-layer zirconias. For example, Lava Esthetic by 3M, Cercon xt ML by Dentsply Sirona, IPS e.max ZirCAD Multi by Ivoclar Vivadent, just to name a few.

Figure 1.

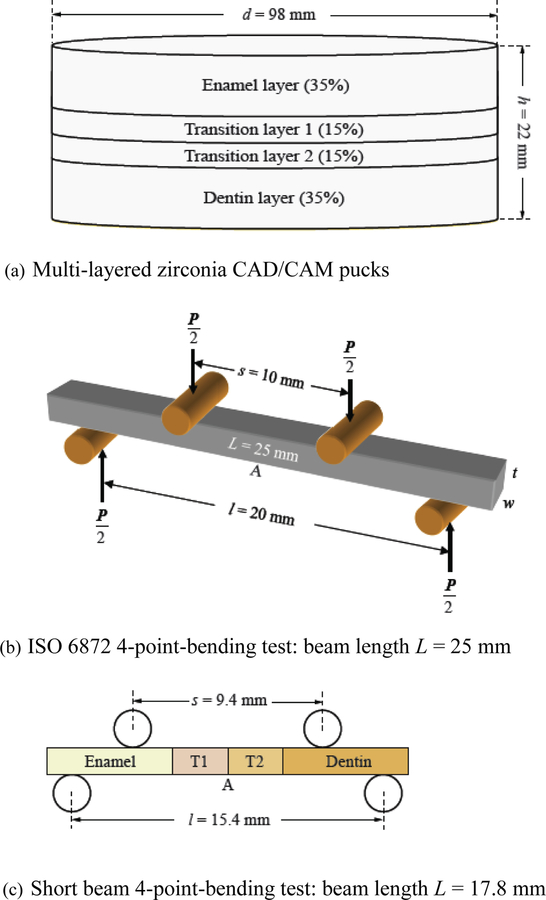
Specimen geometries and testing configurations. (a) Illustration of the multi-layer zirconia CAD/CAM puck (prior to sintering) used in this study. (b) Schematic of 4-point bending test as per beam theory and ISO 6872, where P (N) is the load at fracture, l is the span between bottom supporting pins, s the span between upper loading pins. L is the length, w the width and t the thickness of the specimen. (c) Schematic of a modified 4-point bending test set-up used to probe the interfaces of sintered multi-layer short beams.

The Katana polychromatic system includes 3 multi-layered materials: Multi-Layered zirconia (ML), Super Translucent Multi-Layered zirconia (STML), and Ultra Translucent Multi-Layered zirconia (UTML). Each material is composed of a different class of zirconia—3Y-, 4Y-, or 5Y-PSZ, corresponding to 3, 4, or 5 mol% yttria partially stabilized zirconia, respectively [10]. The yttria content within each class of zirconia plays a primary role in its translucency and strength. In general, the higher the yttria content is, the higher the cubic content, which, in turn, leads to a better translucency but lower strength [6,11–14]. However, the layered nature of the fabricated CAD/CAM puck, as well as variations in composition and inclusion of pigments among the layers, may also significantly affect the structural integrity.

Several recent studies have reported on the strength of multi-layer zirconias; the findings are summarized in Table 1. Flinn and collaborators [15] measured the flexural strength of Katana ML in 4-point bending. They reported an average value of 875 ± 130 MPa, though the layer tested was not specified. Kwon and colleagues [16] tested the flexural strength of the Enamel layer in 3-point bending, reporting for UTML a value of 688 ±159 MPa. Camposilvan et al. [17] and Pereira and coworkers [4] used the biaxial configuration, reporting 890 MPa for ML, 508 MPa for STML, and 450 – 470 MPa for UTML, yet again no description was given on the layers included within the test specimens. Wille and associates [18] evaluated the biaxial flexural strength for each layer of ML and found similar behavior among them (1048 to 1152 MPa). These rather wide ranges of strength data pertaining to identical materials raise some concerns about the data interpretation of the test results.

Table 1.

Literature flexural strength values of various Kanata multi-layer zirconia materials. Note: data shown in the parenthesis are either the standard deviation or the 95% confidence interval.

Material	Layer	Strength (MPa)	Method	Authors
ML	Unknown	875 (130)	4-point bending	Flinn et al. [15]
	Unknown	890 (852 – 930)	Piston-on-3 balls	Pereira et al. [4]
	Enamel	1048 (56)	Piston-on-3 balls	Wille et al. [18]
	Transition 1	1065 (99)	Piston-on-3 balls	Wille et al. [18]
	Transition 2	1152 (101)	Piston-on-3 balls	Wille et al. [18]
	Dentin	1095 (93)	Piston-on-3 balls	Wille et al. [18]
STML	Unknown	508 (488 – 529)	Piston-on-3 balls	Pereira et al. [4]
UTML	Enamel	688 (159)	3-point bending	Kwon et al. [16]
	Unknown	470 (431 – 513)	Piston-on-3 balls	Pereira et al. [4]
	Unknown	450 (100)	Piston-on-3 balls	Camposilvan et al. [17]

The main aim of this work is to examine the strength of the interface between the various layers in emerging designs, specifically the effect of stacking different layers of zirconia, an important factor controlling the structural performance that has received only scant attention. To accommodate size limitations and to probe all the interfaces in a multi-layer specimen, the experimental data need to be examined in light of a proper stress analysis. Accordingly, this study combines experiments and FEA to systematically investigate the structural integrity of 3 classes of multi-layer zirconias.

THEORY

The fracture stress of the material was determined with the aid of the 4-point bending specimen shown in Fig. 1b, similarly to [19]. The beam is supported by 2 stainless steel cylinders placed a distance l while loaded by 2 similar cylinders over a span s. The axial force P applied on the beam produces a uniform bending moment M = P(l – s)/4 over the beam portion enclosed by the loading points. For a slender beam, the tensile stress σ at the lower part of the beam where fracture occurs is given by [19]:

$${\sigma }_{BT}=\frac{1.5P\left(l-s\right)}{w{t}^2}$$ (1)

where the subscript BT stands for beam theory, and w and t denote the beam width and thickness, respectively.

According to ISO 6872 [20], for the beam theory to apply, the beam length (L) should be at least 2 mm longer than the bottom span l and the thickness to bottom span ratio t/l should be at least 0.1. In addition, a ratio s/l = 0.5 is recommended. Because of the unconventional dimensions used to probe the interfaces of the new multi-layer zirconia materials in the present study, some of these conditions could not be met. Accordingly, a finite element analysis (FEA) was conducted to evaluate the effect of available sample dimensions and interface locations (Fig. 1c) on the failure stress.

FINITE ELEMENT ANALYSIS

The failure stress in the 4-point bending specimen was determined with the aid of a commercial finite element (FEM) code (Ansys, Inc., version 13), specified to 2-D plane-stress conditions. All materials were assumed isotropic and linearly elastic with Young’s modulus E = 210 GPa and Poisson’s ratio ν = 0.3. Load per unit specimen width w of 100 and 200 N were used. The load transmitted to the specimens by the supporting pins was evaluated using a built-in contact routine in the FEM code, assuming a Coulomb friction law with friction coefficient μ. The latter varied from 0 to 0.6. The FEM mesh was refined to insure convergence of all stresses of interest to better than 0.1%.

EXPERIMENTS

Materials and specimens

The Katana (Kuraray, Japan – Shade A2) multi-layer zirconia system was used in this study. This zirconia system includes 3 multi-layer materials constructed from 3 classes of zirconia:

1. Multi-Layered zirconia (ML) – 3Y-PSZ

2. Super Translucent Multi-Layered zirconia (STML) – 4Y-PSZ

3. Ultra Translucent Multi-Layered zirconia (UTML) – 5Y-PSZ

The thickest CAD/CAM puck (h = 22 mm) was used. It consists of 4 distinctive layers with progressively darker shades: the Enamel layer (7.7 mm thickness or 35% of the total thickness), Transition layer 1 (T1), Transition layer 2 (T2) (both T1 and T2 are 3.3 mm thick or 15% of the total thickness), and Dentin layer (7.7 mm thickness or 35% of the total thickness) (Fig. 1a). This arrangement resulted in a relatively short multi-layer beam (across the puck thickness) of length L = 17.8 mm after sintering, accounting for a ~20 vol.% shrinkage following densification. In accord with the beam theory requirement of t/l ≤ 0.1, our beams were 1.5 mm thick (t) and 2 mm wide (w). Short beams were also prepared from the homogeneous Enamel or Dentin layer for a direct comparison with the multi-layer short beams. In addition, long beams (as per ISO 6872) [20] measuring 25 (L) × 3 (w) × 2 (t) mm were prepared from the homogeneous Enamel and Dentin layers.

All specimens were sectioned using a low speed diamond saw (IsoMet 1000, Buehler, Lake Bluff, IL, USA), with water cooling. The cutting speed was maintained below 250 rpm at all time while no extra weight applied on the cutting blade to prevent undesirable chipping of the green zirconia beams. Specimens were dry-grinded with abrasive SiC papers 320-grit and then 800-grit to near-targeted green body sizes. A fine brush was used to remove any excess zirconia powder. The specimens were then kept in a desiccator to allow them dry completely for at least 2 days prior to sintering. After that, the green beams were sintered at 1550°C with 2 hours dwell time for UTML and STML, or at 1500°C with 2 hours holding time for ML, following the manufacturer’s instructions.

The sintered beams were polished on an automated machine (AutoMet 250, Buehler, Lake Bluff, IL) using diamond discs under water irrigation. High abrasive diamond discs of 70, 45, and 15 μm were used successively to flatten the specimens. Fine polishing was obtained using diamond discs of 9, 6, 3, and 0.5 μm. The final dimensions of the specimens were documented to the accuracy within 0.2 mm with a digital caliper. After the polishing process, the long edges of the beams were beveled to a 45° angle using 6 μm and then 3 μm diamond discs, according to ASTM standard C1161–13 [21]. The prepared beam specimens were set aside for the 4-point bending test. To help determine the fracture origin (interface or bulk) in the cross-sectional multi-layer beams, the interfaces of the 4 layers were indexed based on their shades and in accord with the manufacturer’s specifications.

Tests

Flexural strength was determined using 4-point bending (n = 10) according to the test setups described in Figure 1. The beams were supported by 2 mm diameter stainless steel cylinders. (In view of the smallness of the distance between the supporting cylinders in the short beam, no ball bearing support could be used for reducing frictional effects). To insure accurate measures, the distances between the supporting pins and loading pins were measured prior to testing by using a carbon paper on a mock zirconia sample. The load rate was 1 mm/min under the displacement control mode [20]. Long versus short beam comparison was performed to experimentally validate our FEA predictions. Fracture conclusively occurred catastrophically, mostly in the middle of the specimens for homogeneous beams and at the weakest interface in the multi-layer beams. The apparent flexural strength (without consideration of friction between the specimen and supporting pins) was calculated using Equation 1. The actual strength (taking friction into account) was then computed for all beams with the aid of the FEA as detailed below.

Fractured samples were analyzed in a scanning electron microscope (SEM, EVO 50, Carl Zeiss, Gottingen, Germany) to establish the fracture origin, crack propagation direction, as well as distribution of flaws and defects on the broken surfaces.

The strength data of different layers were compared using 1-way analysis of variance (ANOVA), separately for each material. Multiple comparisons were performed using the Tukey test. The strength data of different types of beams (short or long) were compared using the t-test, within each layer and material. The significance level was set at 5% and power of analyses at 80%.

RESULTS

Finite element analysis

We ran several cases corresponding to Figures 1b and 1c to probe the effect of beam slenderness ratio, friction coefficient, interface position and load level on beam theory prediction (Eq. 1). The results are summarized in Figure 2. The first case considered was (s, l, L, t) = (10, 20, 25, 2), (9.4, 15.4, 17.8, 1.5) or (7.7, 15.4, 17.8, 1.5) mm, using a homogeneous beam configuration (Fig. 1b) and without incorporating friction between the bearing pins and the tensile surface of the specimen. The maximum tensile stress at the lower surface of the beam was within a fraction of one percent of that given by Eq. 1. In the second test, we ran the multi-layer beam configuration (Fig. 1c), again without accounting for friction. We found that the stress at the interface between all layers was similarly well predicted.

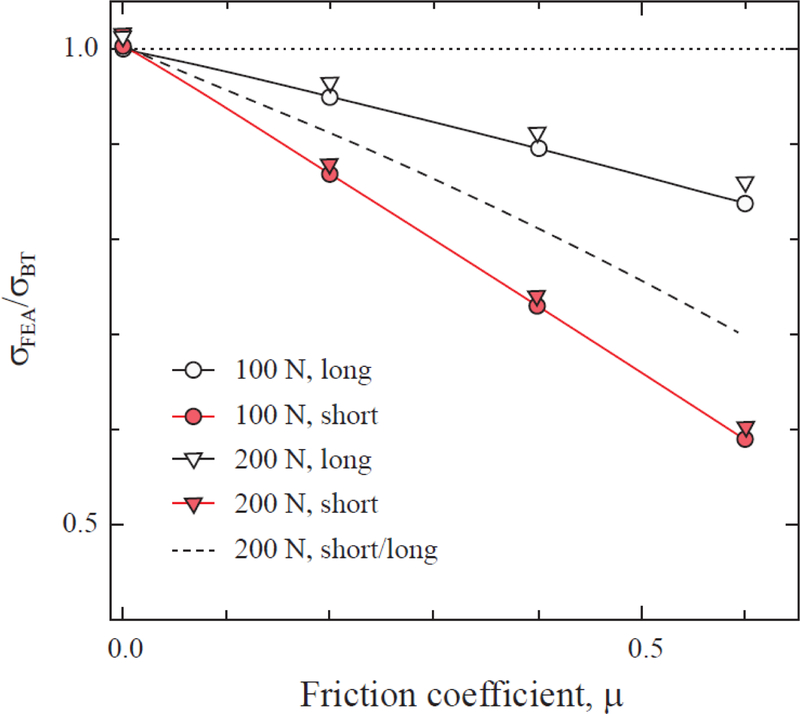
Figure 2.

Predicted tensile stress at point A of Figs. 1b and c from the FEA normalized by that of beam theory (BT, Eq. 1) vs. friction coefficient μ. The beam dimensions and experimental parameters used in the calculations are:

Short beam: s = 9.4 mm, l = 15.4 mm, L = 17.8 mm, t = 1.5 mm, w = 1 mm.

Long beam: s = 10 mm, l = 20 mm, L = 25 mm, t = 1.5 mm, w = 1 mm.

In the third test, we studied the effect of friction coefficient μ over the range 0 to 0.6 on predicted tensile stresses for the following 2 configurations: the long and short beams with dimensions specified in Figures 1b and 1c, respectively. As shown in Figure 2 the maximum tensile stress is greatly reduced with increasing μ, the more so for the short beam. Thus, if unaccounted for, friction would lead to larger apparent failure stress value. One also observes a slight reduction in predicted failure stress with increasing applied force P, attributed to geometric nonlinearity effects. The dashed line in this figure corresponds to the ratio of short to long beam configuration. As can be seen, the discrepancy increases with μ.

Test results

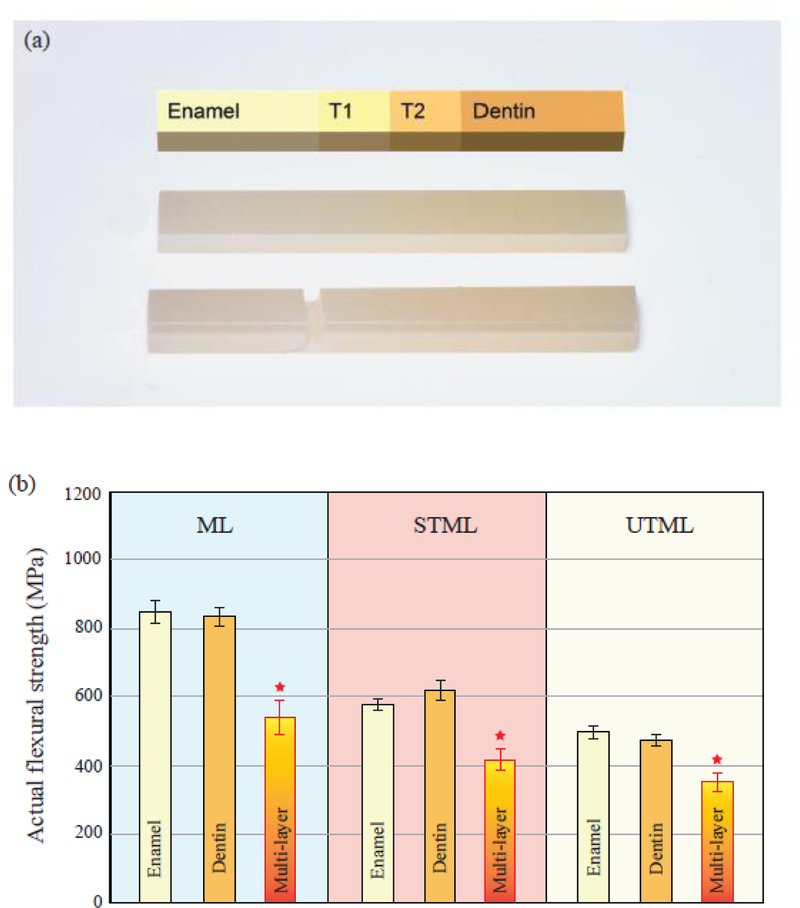
Homogeneous Enamel and Dentin beams fractured near the center of the beam, while multi-layer beams tended to break at the Enamel/T1 interface (Fig. 3a). As a first cut, all strength data were derived using the beam theory prediction (no friction, Eq. 1). The resulting apparent flexural strengths are given in Table 2 (mean and standard error of the mean). With regards to material comparison, ML shows the highest average flexural strength followed by STML and UTML. For all 3 materials, the cross-sectional multi-layer beams exhibited ~30% smaller apparent flexural strength than that of the Enamel and Dentin short homogeneous beams (p ≤ 0.03). No significant difference was observed between the Enamel and Dentin layers (p ≥ 0.4), regardless of material.

Figure 3.

Images of the flexure beams and the actual flexural strength values. (a) Schematic of beam length and layer thicknesses according to manufacturer description (Top). A digital image of an intact multi-layer beam (middle), and a representative multi-layer beam fractured at the Enamel/T1 interface (tensile surface facing up in the photo). (b) The actual flexural strength data for all specimen configurations (long and short beams, homogeneous and multi-layer beams), computed using the friction coefficient of 0.21. The star symbol (★) refers to statistical difference of multi-layer beams relative to the homogeneous Enamel and Dentin layer beams.

Table 2.

Summary of apparent flexural strength results (mean ± standard error of the mean), calculated by the classical beam theory (Equation 1) without the consideration of friction between the specimen and supporting pins.

Apparent strength (MPa)		UTML	STML	ML
Enamel layer	Short	599 ± 41	704 ± 38	1003 ± 46
	Long	532 ± 24	601 ± 17	944 ± 54
Dentin layer	Short	565 ± 27	781 ± 49	958 ± 46
	Long	512 ± 29	646 ± 32	931 ± 37
Multi-layer	Short	429 ± 28	508 ± 38	656 ± 56

To determine the actual strength data (taking into account the effect of friction), we calculated the mean ratio of failure stress (σ_FEA/σ_BT) between all short and long beams to be 0.89. With reference to the dashed line in Figure 2, this would correspond to a friction coefficient of about 0.21. In support of this choice we note a friction study between a conventional steel ball AISI 52100 and zirconia ZrO₂, which gave a friction coefficient in the range 0.1 to 0.3 [22]. Using μ = 0.21, the actual strength data were generated and depicted in Table 3 (mean and standard error of the mean). Now, the difference between short and long beam results virtually disappear, with the actual data being lower than the apparent data. Therefore, we plotted the actual strength data of the Enamel and Dentin layers in Figure 3b, for the 3 classes of zirconias. Data were presented as mean and standard error of the mean from the flexural strength data of both the short and long homogeneous beams. For comparison, the actual strength data of the cross-sectional multi-layer beams are also shown in Figure 3b. Again, there was no significant difference in actual strength between the homogeneous Enamel and Dentin layers for a given material (p ≥ 0.3). However, the flexural strength of the cross-sectional multi-layer beams were ~30% lower than their homogeneous Enamel and Dentin beams (p ≤ 0.04).

Table 3.

Summary of actual flexural strength results (mean ± standard error of the mean), calculated using a friction coefficient of μ = 0.21 between the specimen and supporting pins.

Actual strength (MPa)		UTML	STML	ML
Enamel layer	Short	497 ± 34	584 ± 32	833 ± 38
	Long	500 ± 22	565 ± 16	887 ± 51
Dentin layer	Short	469 ± 19	649 ± 41	795 ± 38
	Long	481 ± 27	608 ± 30	875 ± 35
Multi-layer	Short	356 ± 23	421 ± 31	544 ± 47

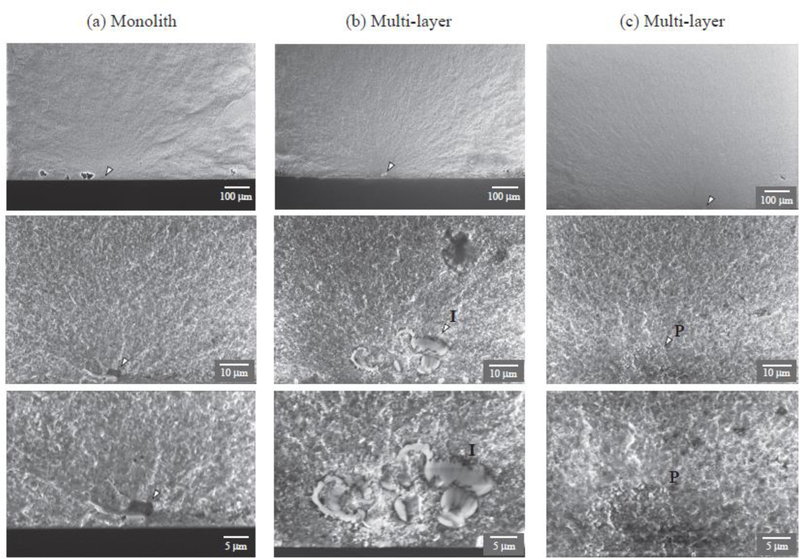
Fig. 4 shows typical SEM images of the fracture surface of monolith (a) and interface (b & c) in ML flexure beam specimens, each given at three different magnifications centered at the origin of fracture (indicated by arrows). While impurities (I) and poorly sintered regions (P) are apparent in both sequences, those for the interfaces (b & c) seem more extensive, being approximately 10 μm in these particular examples. These impurities (I) or poorly sintered regions (P) act as the source of fracture. In contrast, the dominant flaw size at the fracture origin in the monolith ML beam is around 5 μm. Detailed SEM analysis revealed that the incidence of impurities and poorly sintered regions is much higher in multi-layer cross-sectional beams relative to monolithic beams. To assess the effect of impurities or poorly sintered regions on flexural strength, we considered the well-known edge crack relationship K_C = 1.12σF(πc_F)^1/2, where K_C is the fracture toughness and c_F the flaw size. Introducing by the way of example a nominal toughness value K_C = 4 MPa m^1/2 for zirconia [7] and two flaw sizes c_F = 5 and 10 μm, the larger flaw would reduce the apparent failure σ_F by about 30%, i.e. from 900 MPa to 630 MPa.

Figure 4.

SEM images of the fracture surface of a monolith (a) and interface (b & c) flexure beam specimens of ML, given at three different magnifications centered at the fracture origin. The interface morphology exhibit large impurities (I) or poorly sintered regions (P), which help solicit fracture. Note that arrows indicate fracture origin.

DISCUSSION

This study examined the effect of multi-layering on residual strength of dental structures used for enhancing esthetics. Three multi-layer dental zirconia compositions with different translucencies were investigated, focusing on the flexural strength within and between the layers. The results revealed that ML has the highest flexural strength followed by STML and UTML. No significant difference between the Enamel and Dentin layers or short and long beams was found. However, the flexural strengths associated with cross-sectional multi-layer beams were lower than that of the longitudinal homogeneous beams.

Consistent with the least yttria content and thus the smallest cubic fraction, ML showed the highest flexural strength, whereas UTML, which had the most yttria additives or the highest cubic content was the weakest. Also, the mechanical properties of Enamel and Dentin layers were similar, in accord with their similar yttria content and cubic fraction [10]. In our study, the flexural strength of Enamel and Dentin layers was determined according to the ISO standard to allow for a direct comparison to other studies. However, due to limited thickness of available CAD/CAM pucks, we used the multi-layer short beam configuration to investigate the interlay strength. Thus, homogeneous short beams were fabricated from the Enamel and Dentin layers to experimentally prove the certainty of the method. The observed difference between short and long beams data was accounted for by incorporating friction between the supporting pins and the tensile surface of the specimen. Such a friction effect is more pronounced in short beams relative to their long beam counterparts.

The systematic evaluation performed in our study indicates that the layered manufacturing technique compromises the bulk strength of the material, with a reduction of ~30%, due to weak interfaces, in comparison to the strength of the individual layers. This is consistent with the fact that the fracture site in cross-sectional multi-layer beams was located at the interface of Enamel/T1. These weaknesses could be explained by the production process of the multi-layer. Normally, CAD/CAM zirconia pucks are fabricated by pressing ZrO₂ powder to obtain the blank. The multi-layer pucks consist of layers with different shades and compositions. Therefore, the common approach is to press different powder compositions in increments. This pressing technique is likely to create interfacial defects, such as large impurities and/or poorly sintered regions (Fig. 4), making the interfaces more susceptible to fracture.

Dental CAD/CAM blocks and pucks often come with dimensions smaller than ISO 6872 recommended beam sizes for flexure testing [20], especially the length of the beam (22 – 25 mm) [23]. To accurately determine the flexural strength using a short beam, it is essential to reduce the friction between the supporting pins and the tensile surface of the test beam. While the use of roller bearing with adjustable span distances can be helpful, for short beams this requires extensive design and labor in order to accurately measure the span distances between both loading and supporting pins. A seemly trivial error of ~1 mm in span distance could result in as much as 20% to 25% error in calculated flexural strength. Use a carbon paper to register the contact positions of the bearing pins prior to flexural testing may ensure an accurate determination of the span distances.

CONCLUSIONS

1. ML exhibits the highest flexural strength (800 – 900 MPa), followed by STML (560 – 650 MPa) and UTML (470 – 500 MPa).

2. The Enamel and Dentin layers possess similar flexural strength for a given class of zirconia.

3. There is no significant difference in actual strength derived from long beam and short beam flexure.

4. The failure stress of the multi-layer beams is ~30% lower than that of their Enamel or Dentin layer counterparts regardless of material tested, indicating weaker interfaces between various chromatic layers.

5. FEA reveals that friction between the specimen and supporting pins can be an important factor in the calculation of tensile stress, and such an effect is more pronounced for short beams.

6. Errors in determining the span distances can play a major role in calculating the flexural strength of short beams.

Highlights.

• The interfacial strength between various layers of multi-layer zirconias has been examined.

• Multi-layer zirconias with different yttria contents showed a trade-off between strength and translucency.

• The Enamel and Dentin layers exhibited similar flexural strength for a given material class.

• The strength of the cross-sectional multi-layer beams was ~30% lower than that of Enamel or Dentin layers.

• When measuring strength using short beam flexure, friction between the specimen and supporting pins and accuracy in determining loading span distances could lead to major errors.