Abstract
Broadband ultrasound attenuation (BUA) in cancellous bone is useful for prediction of osteoporotic fracture risk, but its causes are not well understood. In order to investigate attenuation mechanisms, nine cancellous-bone-mimicking phantoms containing nylon filaments (simulating bone trabeculae) embedded within soft-tissue-mimicking fluid (simulating marrow) were interrogated. The measurements of frequency-dependent attenuation coefficient had three separable components: 1) a linear (with frequency) component attributable to absorption in the soft-tissue-mimicking fluid, 2) a quasi-linear (with frequency) component, which may include absorption in and longitudinal-shear mode conversion by the nylon filaments, and 3) a nonlinear (with frequency) component, which may be attributable to longitudinal-longitudinal scattering by the nylon filaments. The slope of total linear (with frequency) attenuation coefficient (sum of components #1 and #2) versus frequency was found to increase linearly with volume fraction, consistent with reported measurements on cancellous bone. Backscatter coefficient measurements in the nine phantoms supported the claim that the nonlinear (with frequency) component of attenuation coefficient (component #3) was closely associated with longitudinal-longitudinal scattering. This work represents the first experimental separation of these three components of attenuation in cancellous bone-mimicking phantoms.
Keywords: attenuation cancellous bone phantom
I. INTRODUCTION
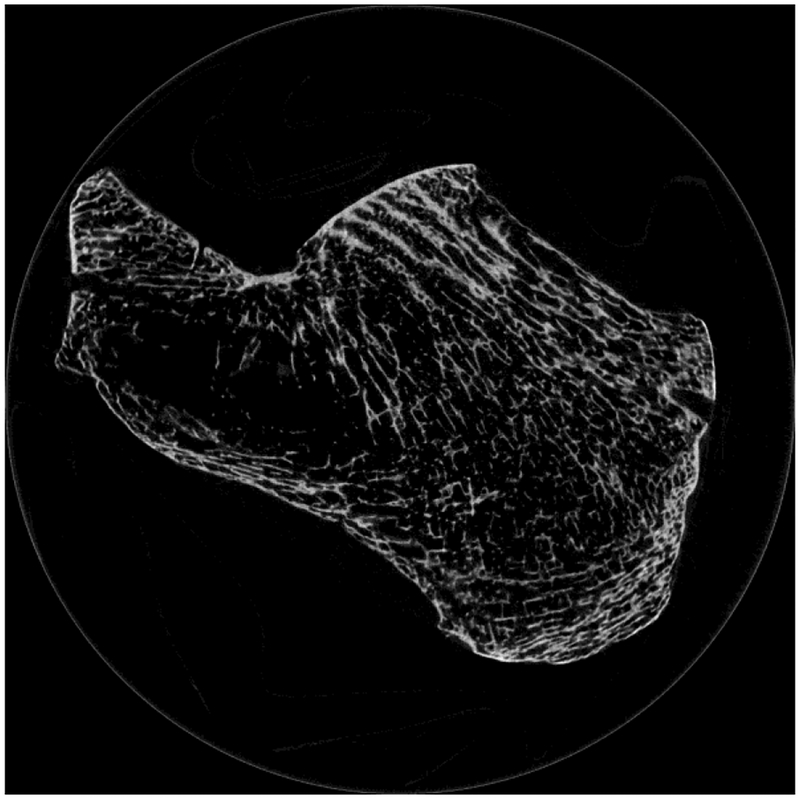
Prospective clinical trials [1–8], retrospective clinical trials [9–19], and pre-clinical experiments [20–57] have established that broadband ultrasound attenuation (BUA) (the slope of attenuation coefficient vs. frequency) and speed of sound (SOS) in calcaneus are effective for prediction of osteoporotic fracture risk. However, the mechanisms responsible for BUA in cancellous bone are not well understood. BUA is the combined result of absorption and scattering [58–94]. Cancellous bone contains approximately cylindrically-shaped scatterers (trabeculae) and plate-like structures arrayed in a mesh. See Figure 1. The spaces between the trabeculae are filled with marrow (in vivo) or water (in vitro).
Figure 1.
Micro Computed Tomogram of calcaneus. Some trabeculae appear to terminate as they move into and out of the imaging plane. Image acquired by Andres Laib, Scanco Medical AG, Brüttisellen, Switzerland.
2D simulation studies in human cancellous calcaneus suggest that scattering is greater in magnitude than absorption between 300 and 900 kHz [46, 83]. 3D simulation studies in human cancellous femur suggest that 1) absorption is greater than scattering at low frequencies but is less than scattering at high frequencies (with equality achieved around 600 kHz) and 2) longitudinal-shear (LS) mode conversion may be a significant source of attenuation [79, 84, 85, 95, 96]. The 3D studies therefore suggest that absorption is probably the largest component of clinical (300–700 kHz) BUA. 3D simulation studies also suggest the presence of a significant scattering mechanism that varies approximately linearly with frequency [95]. These 2D and 3D simulation studies appear to include LS mode conversion as a form of scattering. If shear waves are rapidly absorbed as they propagate (as has been suggested [97, 104]), LS mode conversion could alternatively be regarded as effectively an absorptive mechanism, with ultrasonic energy briefly taking the form of a transient shear wave prior to absorption. (See Discussion section.)
In the diagnostic frequency range (300 – 700 kHz), attenuation coefficient in cancellous bone is approximately proportional to frequency to the first power [20–57] while longitudinal-longitudinal (LL) backscatter coefficient is approximately proportional to frequency to the third power [60, 61, 64]. If LL total scattering (i.e., the integral of LL scattering over all angles) also varies substantially nonlinearly with frequency, then LL scattering could only represent a minor contribution to attenuation coefficient in the diagnostic frequency range [60, 64, 68]. (Evidence for nonlinear total scattering is provided by the Faran Cylinder model, which predicts that total LL scattering, like LL backscatter, varies approximately as frequency to the third power [60]).
Experiments on graphite-fiber-in-gelatin phantoms may help elucidate mechanisms of attenuation in cancellous bone. Graphite-fiber-in-gelatin phantoms [97] resemble cancellous bone somewhat in that they contain a mixture of hard scatterers (graphite fibers) embedded in a fluid (gelatin). Measurements of attenuation coefficient in graphite-fiber-in-gelatin phantoms [97] have shown that the combination of absorption within the fluid (gelatin) and LS mode conversion from the graphite fibers produces a quasi-linear frequency dependence of attenuation when ultrasound propagates parallel to the fibers and a slightly higher than linear frequency dependence of attenuation when ultrasound propagates perpendicular to the fibers (consistent with theoretical predications [98]). See Ref. 97, Figure 8.
The objective of the work described below was to experimentally separate three components of attenuation in cancellous-bone-mimicking phantoms: 1) a linear (with frequency) component attributable to absorption in the soft-tissue-mimicking fluid, 2) a quasi-linear (with frequency) component, which may include absorption in and LS mode conversion by the nylon filaments, and 3) a nonlinear (with frequency) component, which may be closely associated with LL scattering from the nylon filaments.
II. METHODS
A. Phantoms
Nine phantoms containing nylon wires (simulating trabeculae) in proprietary soft tissue-mimicking material (simulating marrow) (CIRS Inc., Norfolk, VA) were interrogated. Two reference phantoms containing only soft tissue-mimicking material were also interrogated. Table 1 shows the phantom properties. Two different kinds of nylon wire (designated below by their colors “green” and “clear” in Table 1) were used. Two batches of proprietary soft tissue-mimicking material (“CIRS #1” and “CIRS #2”) were used. Three of the phantoms used nylon filaments with diameter equal to 152 μm, which is reasonably close to the mean trabecular thickness in human calcananeus, 127 μm [102]. Figure 2 shows the phantom containing green nylon wires along with its reference phantom.
Table 1.
Properties of phantoms.
| Nylon | Fluid Filler | Diameter (μm) | Length (mm) | Scatter Number Density (# per cc) | Volume Fraction (%) | Frequency Range for Linear Fit (MHz) |
|---|---|---|---|---|---|---|
| - | CIRS #1 | - | - | - | - | 0.5 – 0.8 |
| Green | CIRS #1 | 203 | 12 | 100 | 3.9 | 0.5 – 0.8 |
| - | CIRS #2 | - | - | - | - | 0.3 – 0.7 |
| Clear | CIRS #2 | 152 | 10 | 100 | 1.8 | 0.3 – 0.7 |
| Clear | CIRS #2 | 203 | 10 | 100 | 3.2 | 0.3 – 0.7 |
| Clear | CIRS #2 | 229 | 10 | 100 | 4.1 | 0.3 – 0.7 |
| Clear | CIRS #2 | 330 | 10 | 100 | 8.5 | 0.3 – 0.5 |
| Clear | CIRS #2 | 356 | 10 | 100 | 9.9 | 0.3 – 0.5 |
| Clear | CIRS #2 | 152 | 12 | 100 | 2.2 | 0.3 – 0.7 |
| Clear | CIRS #2 | 229 | 12 | 100 | 3.3 | 0.3 – 0.7 |
| Clear | CIRS #2 | 152 | 12 | 200 | 4.4 | 0.3 – 0.7 |
Figure 2.
Phantoms. Both phantoms contained soft-tissue-mimicking material. The phantom on the right also contained green nylon filaments to simulate trabeculae.
B. Ultrasonic Methods
The phantoms containing clear nylon filaments were interrogated in through-transmission mode in a water tank using 3 pairs of coaxially-aligned Panametrics (Waltham, MA) focused transducers. See Table 2. The phantom containing green nylon filaments was only interrogated at 2.25 MHz. The propagation path between transducers was twice the focal length. Attenuation coefficient and group velocity were measured as described previously [63].
Table 2.
Transducers.
| Transducer | Center Frequency (MHz) | Diameter (mm) | Focal Length (mm) |
|---|---|---|---|
| V391 | 0.5 | 29 | 53 |
| V302 | 1 | 25 | 51 |
| V305 | 2.25 | 19 | 51 |
In order to investigate the contribution of LL scattering to attenuation coefficient, the phantoms containing clear nylon filaments were also interrogated in pulse-echo mode in a water tank using a 2.25 MHz center frequency transducer. The phantom was placed at the focal plane of the transducer. A reference-phantom method was used to compensate for transducer electro-mechanical properties and diffraction so that backscatter coefficient could be computed [60].
A Panametrics 5800 pulser/receiver was used. Received radio frequency (RF) signals were digitized (8 bit, 10 MHz) using a LeCroy (Chestnut Ridge, NY) 9310C Dual 400 MHz oscilloscope and stored on computer (via GPIB) for off-line analysis.
Frequency-dependent attenuation coefficients, α(f), were decomposed into 3 components.
where αFL(f), the linear (with frequency) absorption in the soft-tissue-mimicking fluid, was measured directly in the reference phantoms (i.e., phantoms without nylon filaments). The attenuation above and beyond that due to absorption in the soft-tissue-mimicking fluid was decomposed into linear and nonlinear components, αL2(f) and αNL(f). αL2(f) was measured by performing a least-squares linear regression fit to measured α(f) in the low-frequency linear regime and then subtracting αFL(f). αNL(f) was then computed from αNL(f) = α(f) – αFL(f) - αL2(f). Attenuation slope was defined as the sum of the slopes of linear regressions to αFL(f) vs. frequency and αL2(f) vs. frequency.
The low frequency range for the linear fit was usually the clinical range of 300 – 700 kHz. See Table 2. For phantoms containing clear nylon filaments with diameters 330 and 356 μm, however, the upper limit was reduced to 500 kHz because their nonlinear (with frequency) attenuation components became prominent at lower frequencies. For the phantom containing green nylon filaments, the range was 500 – 800 kHz, which corresponded to the low end of the usable frequency band obtainable with the 2.25 MHz center frequency transducer.
III. RESULTS
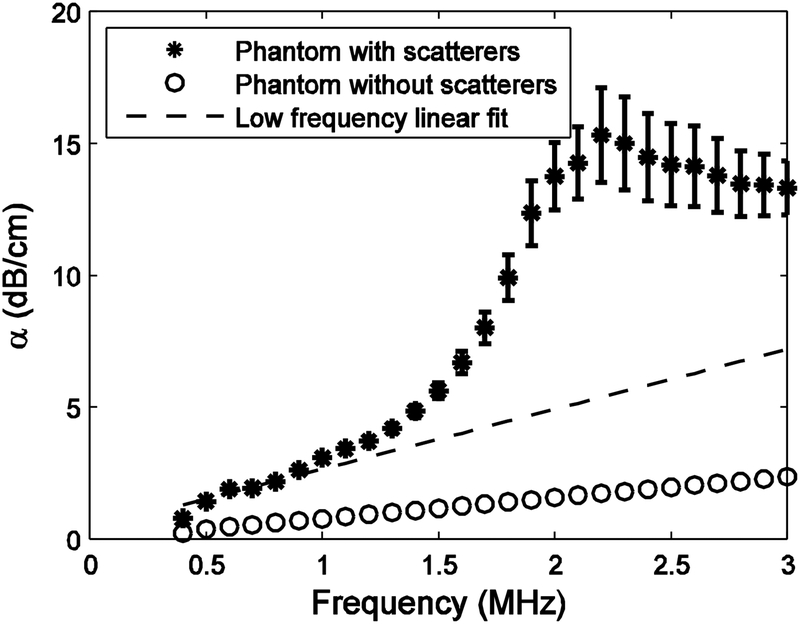
Figure 3 shows measurements of attenuation coefficient vs. frequency for the phantom containing green nylon filaments (*’s) and its reference phantom (i.e., phantom without nylon filaments) (o’s). The attenuation coefficient for the reference phantom appeared to be approximately linear with frequency up to at least 3 MHz. The slope of the linear least-squares regression fit to the reference phantom attenuation coefficient data vs. frequency was 0.7 ± 0.1 dB/cmMHz (mean ± standard error). The slope of the linear least-squares regression fit to the attenuation coefficient data from the phantom containing green nylon filaments over the range from 0.5 to 0.8 MHz was 2.3 ± 0.2 dB/cmMHz, or about three times the value for its reference phantom (see dashed line in Fig. 3). Therefore, there seems to have been a substantial quasi-linear (with frequency) attenuation mechanism operating in the phantom containing green nylon filaments, in addition to the linear (with frequency) attenuation attributable to absorption in the proprietary soft-tissue mimicking material. The group velocities were 1555 ± 5 m/s (phantom containing green nylon filaments) and 1545 ± 1 m/s (reference phantom).
Figure 3.
Attenuation coefficient vs. frequency in the phantom containing green nylon filaments (*) and in the reference (i.e. without nylon filaments) phantom (o). The dashed line corresponds to a linear regression fit at low frequencies.
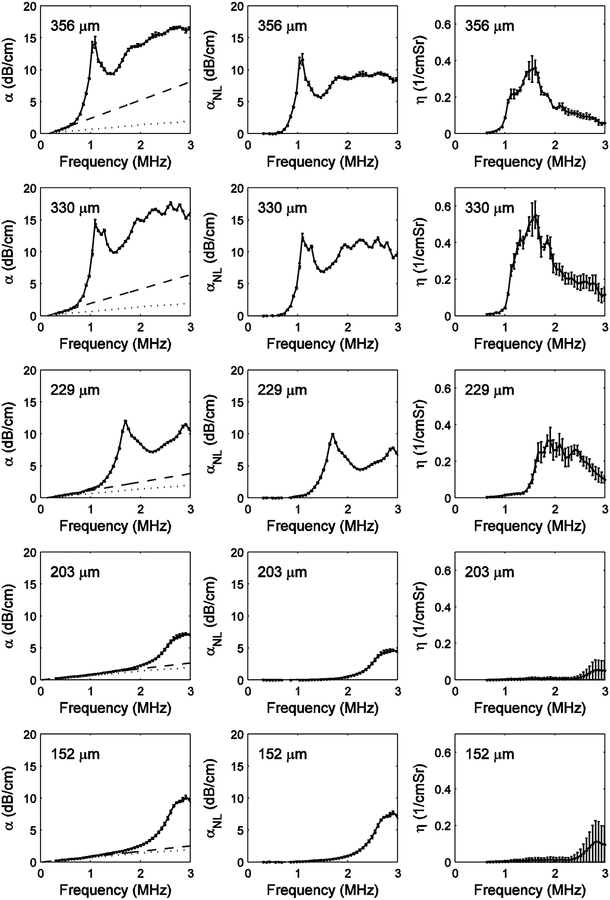
Figure 4 shows results for 5 phantoms containing 10-mm-long clear nylon filaments. The left panel shows measurements of total attenuation coefficient vs. frequency. The dotted lines correspond to frequency dependent attenuation coefficients measured from the reference phantom (i.e. phantom without nylon filaments). The dashed lines correspond to linear fits of attenuation coefficient vs. frequency at low frequencies. It can be seen that there was a substantial quasi-linear (with frequency) component of attenuation above and beyond the attenuation due to the soft-tissue-mimicking fluid (dotted line), especially for the phantoms with filaments with diameters of 229, 330, and 356 μm. The middle column of Figure 4 shows the nonlinear component of attenuation coefficient, αNL(f), which is the difference between α(f) (left panel) and the low-frequency linear fit to α(f) (left panel, dashed line). The right column of Figure 4 shows measurements of backscatter coefficient, η(f). Comparison of the middle and right columns of Figure 4 shows that for each filament diameter, the frequencies of rapid onset of αNL(f) and η(f) are very similar, suggesting that LL scattering may be a significant source of αNL(f).
Figure 4.
Results for the 5 phantoms containing 10 mm clear nylon filaments. The left panel shows measurements of attenuation coefficient vs. frequency. The dotted lines correspond to frequency-dependent attenuation coefficients measured from the reference phantom (i.e., phantom without nylon filaments). The dashed lines correspond to linear fits of attenuation coefficient vs. frequency at low frequencies. The middle panel shows the nonlinear component of attenuation coefficient, αNL(f), which is the difference between α(f) (left panel) and the low-frequency linear fit to α(f) (left panel, dashed line). The right panel shows measurements of backscatter coefficient, η(f).
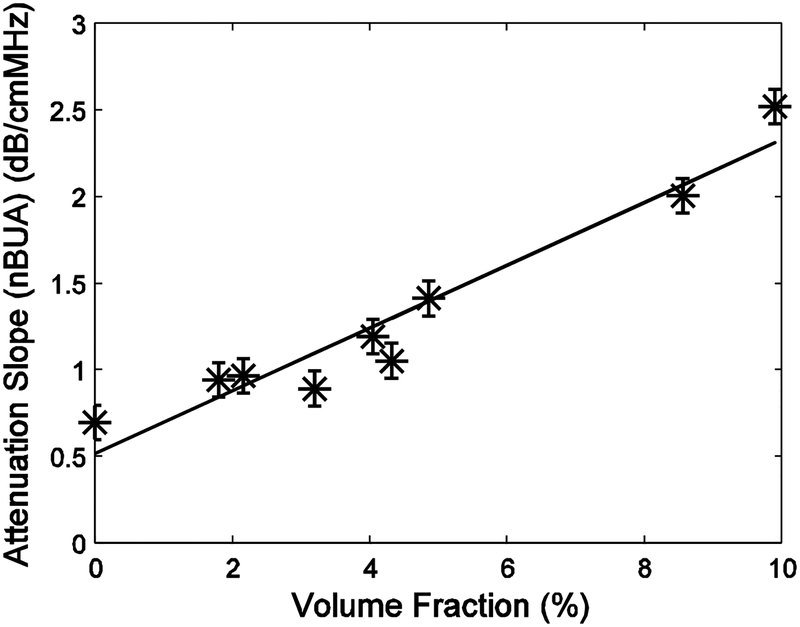
Figure 5 shows attenuation slope plotted vs. volume fraction for the phantoms containing clear nylon filaments. A least-squares linear regression fit is also shown. The correlation coefficient to the least-squares fit was r = 0.96. The 95% confidence interval for r was (0.82, 0.99).
Figure 5.
Attenuation slope plotted vs. volume fraction for the phantoms containing clear nylon filaments. A least-squares linear regression fit is also shown.
IV. DISCUSSION
This work represents the first experimental separation of three distinct components of attenuation in cancellous bone-mimicking phantoms. The rate of change of the total linear (with frequency) attenuation coefficient, αFL(f) + αL2(f), with frequency was found to increase linearly with volume fraction, consistent with previous measurements on cancellous bone.
Figures 3 and 4 show that some phantoms exhibited a substantial quasi-linear (with frequency) component of attenuation above and beyond the absorption in the soft-tissue-mimicking fluid. This quasi-linear (with frequency) excess attenuation may include absorption in and LS mode conversion by the nylon filaments. The latter source of quasi-linear (with frequency) attenuation is consistent with 1) 3D simulations that consider only non-absorptive mechanisms [95], and 2) measurements on graphite-fiber-in-gelatin phantoms that include absorption within the fluid (gelatin) and LS mode conversion from the graphite fibers [97].
Differences between the cancellous-bone-mimicking phantoms interrogated here and cancellous bone should be acknowledged:
First, the longitudinal sound speed in nylon (2600 m/s) is somewhat lower than that for mineralized bone material (2800 – 4000 m/s, near 500 kHz) [100] (but still far greater than that for water or marrow—near 1500 m/s). However, nylon may still be a reasonable material to simulate trabeculae for this application because previous studies have shown that phantoms consisting of parallel nylon wires in water exhibit similar dependences of LL scattering [77] and phase velocity [101] on frequency and scatterer thickness as cancellous bone.
Second, the cancellous bone phantom investigated here lacked cross-links that can connect nearby trabeculae in cancellous bone. However, again, the parallel-nylon-wire phantoms mentioned in the previous paragraph also lacked cross-links but still exhibited similar acoustic properties to cancellous bone [77, 101].
Third, while scatterers were essentially randomly oriented in the phantom, they tend to align along preferred directions in cancellous bone. However, the phantom may still be a useful model for this application because attenuation due to LS mode conversion tends to be quasi-linear with frequency regardless of whether ultrasound propagates parallel or perpendicular to the scatterers, according to theory [98] and measurements on phantoms containing graphite fibers in gelatin [97].
Fourth, nylon wires may have lower absorption than trabeculae. However, as stated earlier, this may not be a serious limitation because simulations that ignore absorption are able to reproduce experimental results for trabecular bone [79].
The present study is more relevant to cancellous bone than the previously-mentioned graphite-fiber-in-gelatin study [97] (which was intended to model soft tissue, not bone) in terms of scatterer diameter (152 – 356 vs. 8 μm), scatterer length (10 – 12 mm vs. 100μm), and volume fraction (1.8 – 9.9% vs. unspecified). (The mean trabecular thickness in human calcaneus is 127 μm [102]. Volume fractions in human calcaneus range from 3% to 14% [103]) Another advantage of the present study over the previous study [97] is that LL backscattering was measured independently of attenuation in order to investigate the effects of LL scattering on frequency-dependent attenuation.
Although shear waves may arise from mode conversion at scatterer interfaces, they may be extremely transient. For example, shear attenuation coefficients in bovine cancellous bone have been estimated to be approximately 17 dB/mm (at 1 MHz) [104], implying that shear wave power is reduced by approximately 98% for each mm of propagation. Similarly, shear waves generated from graphite particles suspended in gelatin have been described as “evanescent” [97]. Therefore, the relative roles of absorption and scattering in cancellous bone will depend on the relative roles of absorption and scattering of mode-converted shear waves. If the rapid attenuation of mode-converted shear waves is primarily due to absorption, then absorption would be the dominant loss mechanism, albeit with the caveat that the ultrasonic energy briefly takes the form of a very short-lived shear wave prior to absorption.
ACKNOWLEDGEMENTS
The author thanks 1) Professor James Miller, Physics Department, Washington University, St. Louis, MO, for helpful discussions, 2) Laura Perfetti and Heather Pierce, C.I.R.S., Norfolk, VA, for assistance in phantom design and construction, and 3) Andres Laib, Scanco Medical AG, Brüttisellen, Switzerland, for providing the micro computed tomogram in Figure 1. The mention of commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or implied endorsement of such products by the Food and Drug Administration.
Biography
Keith A. Wear graduated from the University of California at San Diego with a B.A. in Applied Physics in 1980. He received his M.S. and Ph.D. in Applied Physics with a Ph.D. minor in Electrical Engineering from Stanford University in 1982 and 1987.
He was a post-doctoral research fellow with the Physics department at Washington University, St. Louis from 1987–1989. He has been a research physicist at the FDA Center for Devices and Radiological Health since 1989. His research has included measurements of ultrasonic scattering properties from tissues, high-resolution spectral estimation, magnetic resonance spectroscopic image reconstruction methods, analysis of statistical properties of ultrasonic echoes from tissues, and improved measurement methodology in bone sonometry.
He is an adjunct professor of Radiology at Georgetown University. He is a Fellow of the American Institute for Medical and Biological Engineering (AIMBE) and the American Institute of Ultrasound in Medicine (AIUM). He is a senior member of IEEE. He is a member of the Acoustical Society of America, IEEE Ultrasonics Society and the AIUM Technical Standards Committee. He served as Vice-Chairman (2002–2004) and Chairman (2004–2006) of the AIUM Basic Science and Instrumentation Section. He is an associate editor of IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control.
REFERENCES
- [1].Hans D, Dargent-Molina P, Schott AM, Sebert JL, Cormier C, Kotzki PO, Delmas PD, Pouilles JM, Breart G, and Meunier PJ. “Ultrasonographic heel measurements to predict hip fracture in elderly women: the EPIDOS prospective study,” Lancet, 348, pp. 511–514, 1996. [DOI] [PubMed] [Google Scholar]
- [2].Bauer DC, Glüer CC, Cauley JA, Vogt TM, Ensrud KE, Genant HK, and Black DM. “Broadband ultrasound attenuation predicts fractures strongly and independently of densitometry in older women,” Arch. Intern, Med 157, pp. 629–634 1997. [PubMed] [Google Scholar]
- [3].Miller PD, Siris ES, Barrett-Connor E, Faulkner KG, Wehren LE, Abbott TA, Chen Y, Berger ML, Santora AC, and Sherwood LM, “Prediction of fracture risk in postmenopausal white women with peripheral bone densitometry: evidence from the national osteoporosis risk assessment,” J. Bone & Miner. Res, 17, pp. 2222–2230, 2002. [DOI] [PubMed] [Google Scholar]
- [4].Hans D, Schott AM, Duboeuf F, Durosier C, and Meunier PJ, “Does follow-up duration influence the ultrasound and DXA prediction of hip fracture? The EPIDOS prospective study,” Bone, 35, 357–363, 2004. [DOI] [PubMed] [Google Scholar]
- [5].Huopio J, Kroger H, Honkanen R, Jurvelin J, Saarikoski S, and Alhava E, “Calcaneal ultrasound predicts early postmenopausal fractures as well as axial BMD. A prospective study of 422 women,” Osteo. Int, 15, pp. 190–195, 2004. [DOI] [PubMed] [Google Scholar]
- [6].Khaw KT, Reeve J, Luben R, Bingham S, Welch A, Wareham N, Oakes S, and Day N, “Prediction of total and hip fracture risk in men and women by quantitative ultrasound of the calcaneus: EPIC-Norfolk prospective population study,” Lancet, 363, 197–202, 2004. [DOI] [PubMed] [Google Scholar]
- [7].Schott AM, Hans D, Duboeuf F, Dargent-Molina P, Hajri T, Breart G, and Meunier PJ, “Quantitative ultrasound parameters as well as bone mineral density are better predictors of trochanteric than cervical hip fractures in elderly women. Results from the EPIDOS study,” Bone, 37, 858–863, 2005. [DOI] [PubMed] [Google Scholar]
- [8].Krieg M, Cornuz J, Ruffieux C V. Melle G, Buche D, Dambacher MA, Hans D, Hartl F, Hauselmann HJ, Kraenzlin M, Lippuner K, Neff M, Pancaldi P, Rizzoli R, Tanzi F, Theiler R, Tyndall A, Wimpfheimer C, and Burckhardt P., “Prediction of hip fracture risk by quantitative ultrasound in more than 7000 Swiss women ≥ 70 years of age: comparison of three technologically different bone ultrasound devices in the SEMOF study,” J. Bone. Miner. Res, 21, 1456–1463, 2006. [DOI] [PubMed] [Google Scholar]
- [9].Schott M, Weill-Engerer S, Hans D, Duboeuf F, Delmas PD, and Meunier PJ, “Ultrasound discriminates patients with hip fracture equally well as dual energy X-ray absorptiometry and independently of bone mineral density,” J. Bone Min. Res, 10, pp. 243–249 1995. [DOI] [PubMed] [Google Scholar]
- [10].Turner CH, Peacock M, Timmerman L, Neal JM, and Johnston CC Jr., “Calcaneal ultrasonic measurements discriminate hip fracture independently of bone mass,” Osteo. International, 5, pp. 130–135 1995. [DOI] [PubMed] [Google Scholar]
- [11].Mautalen C, Vega E, Gonzalez D, Carrilero P, Otano A, and Silberman F, “Ultrasound and dual x-ray absorptiometry densitometry in women with hop fracture,” Calcif. Tissue Int, 57, 441–449, 1995. [DOI] [PubMed] [Google Scholar]
- [12].Glüer CC, Cummings SR, Bauer DC, Stone K, Pressman A, Mathur A, and Genant HK. “Osteoporosis: Association of recent fractures with quantitative US findings”, Radiology, 199, pp. 725–732, 1996. [DOI] [PubMed] [Google Scholar]
- [13].Thompson P, Taylor J, Fisher A, and Oliver R, “Quantitative heel ultrasound in 3180 women between 45 and 75 years of age: compliance, normal ranges and relationship to fracture history,” Osteo. Int’l, 8, pp. 211–214, 1998. [DOI] [PubMed] [Google Scholar]
- [14].Frost ML, Blake GM, and Fogelman I, “Contact quantitative ultrasound: an evaluation of precision, fracture discrimination, age-related bone loss and applicability of the WHO criteris,” Osteo. Int, 10, 441–449, 1999. [DOI] [PubMed] [Google Scholar]
- [15].Njeh CF, Hans D, Li J, Fan B, Fuerst T, He YQ, Tsuda-Futami E, Lu Y, Wu CY, and Genant HK, “Comparison of six calcaneal quantitative ultrasound devices: precision and hip fracture discrimination,” 11, Osteo. Int, pp. 1051–1062, 2000. [DOI] [PubMed] [Google Scholar]
- [16].Krieg MA, Cornuz J, Ruffieux C, Sandini L, Buche D, Dambacher MA, Hartl F, Hauselmann HJ, Kraenzlin M, Lippuner K, Neff M, Pancaldi P, Rizzoli R, Tanzi F, Theiler R, Tyndall A, Wimpfheimer C, and Burckhardt P., “Comparison of three bone ultrasounds for the discrimination of subjects with and without osteoporotic fractures among 7562 elderly women,” J. Bone Miner. Res 18, 1261–1266, 2003. [DOI] [PubMed] [Google Scholar]
- [17].Glüer CC, Eastell R, Reid DM, Felsenberg D, Roux C, Barkmann R, Timm W, Blenk T, Armbrecht G, Stewart A, Clowes J, Thomasius FE, and Kolta S, “Association of five quantitative ultrasound devices and bone densitometry with osteoporotic vertebral fractures in a population-based sample: the OPUS study,” J. Bone & Miner. Res, 19, pp. 782–793, 2004. [DOI] [PubMed] [Google Scholar]
- [18].Welch A, Camus J, Dalzell N, Oakes S, Reeve J, and Khaw KT, “Broadband ultrasound attenuation (BUA) of the heel bone and its correlates in men and women in the EPIC-Norfolk cohort: a cross-sectional population-based study,” Osteo. Int, 15, 217–225, 2004. [DOI] [PubMed] [Google Scholar]
- [19].Maggi S, Naole M, Giannini S, Adami S, Defeo D, Isaia G, Sinigaglia L, Filipponi P, and Crepaldi G., “Quantitative heel ultrasound in a population-based study in Italy and its relationship with fracture history: the ESOPO study,” Osteo. Int, 17, 237–244, 2006. [DOI] [PubMed] [Google Scholar]
- [20].Langton CM, Palmer SB, and Porter RW. “The measurement of broadband ultrasonic attenuation in cancellous bone.” Eng. in Med 13, pp. 89–91, 1984. [DOI] [PubMed] [Google Scholar]
- [21].Rossman P, Zagzebski J, Mesina C, Sorenson J, and Mazess R, “Comparison of Speed of Sound and Ultrasound Attenuation in the Os Calcis to Bone Density of the Radius, Femur and Lumbar Spine,” Clin. Phys. Physiol. Meas, 10, pp. 353–360, 1989. [DOI] [PubMed] [Google Scholar]
- [22].Tavakoli MB and Evans JA. “Dependence of the velocity and attenuation of ultrasound in bone on the mineral content.” Phys. Med. Biol, 36, pp. 1529–1537, 1991. [DOI] [PubMed] [Google Scholar]
- [23].Zagzebski JA, Rossman PJ, Mesina C, Mazess RB, and Madsen EL, “Ultrasound transmission measurements through the os calcis,” Calcif. Tissue Int’l, 49, pp. 107–111, 1991. [DOI] [PubMed] [Google Scholar]
- [24].Kaufman JJ and Einhorn TA, “Perspectives: Ultrasound Assessment of Bone”, J. Bone. Min. Res, 8, pp. 517–525, 1993. [DOI] [PubMed] [Google Scholar]
- [25].Laugier P, Giat P, Droin P, Saied A, and Berger G, “Ultrasound images of the os calcis: a new method of assessment of bone status,” Proc. IEEE Ultrason. Symp¸Baltimore, MD, pp. 989–992, 1993. [Google Scholar]
- [26].Langton CM, Njeh CF, Hodgskinson R, and Carrey JD, “Prediction of Mechanical Properties of the Human Calcaneus by Broadband Ultrasonic Attenuation,” Bone, 18, pp. 495–503, 1996. [DOI] [PubMed] [Google Scholar]
- [27].Alves JM, Xu W, Lin D, Siffert RS, Ryaby JT, and Kaufman JJ, “Ultrasonic assessment of human and bovine trabecular bone: a comparison study,” IEEE Trans. Biomed. Eng, 43, 249–258, 1996. [DOI] [PubMed] [Google Scholar]
- [28].Alves JM, Ryaby JT, Kaufman JJ, Magee FP, and Siffert RS, “Influence of marrow on ultrasonic velocity and attenuation in bovine trabecular bone,” Calcif. Tissue Int, 58, 362–367, 1996. [DOI] [PubMed] [Google Scholar]
- [29].Njeh CF, Hodgskinson R, Currey JD, and Langton CM. “Orthogonal relationships between ultrasonic velocity and material properties of bovine cancellous bone.” Med. Eng. Phys, 18, pp. 373–381, 1996. [DOI] [PubMed] [Google Scholar]
- [30].Strelitzki R and Evans JA, “On the measurement of the velocity of ultrasound in the os calcis using short pulses,” Euro. J. Ultrasound, 4, 205–213, 1996. [Google Scholar]
- [31].Strelitzki R, Clarke AJ, and Evans JA, “The measurement of the velocity of ultrasound in fixed trabecular bone using broadband pulses and single-frequency tone bursts,” Phys. Med. Biol, 41, 743–753, 1996. [DOI] [PubMed] [Google Scholar]
- [32].Nicholson PHF, Lowet G, Langton CM, Dequeker J, and Van der Perre G, “A comparison of time-domain and frequency-domain approaches to ultrasonic velocity measurement in trabecular bone,” Phys. Med. Biol, 41, 2421–2435, 1996. [DOI] [PubMed] [Google Scholar]
- [33].Nicholson PHF, Lowet G, Cheng XG, Boonen S, Van der Perre G, and Dequeker J, “Assessment of the strength of the proximal femur in vitro: relationship with ultrasonic measurements of the calcaneus,” Bone, 20, 219–224, 1997. [DOI] [PubMed] [Google Scholar]
- [34].Njeh CF, Hodgskinson R, Currey JD, and Langton CM, “Orthogonal relationships between ultrasonic velocity and material properties of bovine cancellous bone,” Med. Eng. Phys, 18, 373–381, 1996. [DOI] [PubMed] [Google Scholar]
- [35].Serpe L and Rho JY, “The nonlinear transition period of broadband ultrasound attenuation as bone density varies,” J. Biomech, 29, pp. 963–966, 1996. [DOI] [PubMed] [Google Scholar]
- [36].Chappard C, Laugier P, Fournier B, Roux C, and Berger G, “Assessment of the relationship between broadband ultrasound attenuation and bone mineral density at the calcaneus using BUA Imaging and DXA,” Osteo. Int, 7, pp. 316–322, 1997. [DOI] [PubMed] [Google Scholar]
- [37].Njeh CF and Langton CM, “The effect of cortical endplates on ultrasound velocity through the calcaneus: an in vitro study,” Brit. J. Radiol, 70, 504–510, 1997. [DOI] [PubMed] [Google Scholar]
- [38].Njeh CF, Kuo CW, Langton CM, Atrah HI, and Boivin CM, “Prediction of human femoral bone strength using ultrasound velocity and BMD: an in vitro study,” Osteo. Int, 7, 471–477, 1997. [DOI] [PubMed] [Google Scholar]
- [39].Bouxsein ML and Radloff SE. “Quantitative ultrasound of the calcaneus reflects the mechanical properties of calcaneal trabecular bone,” J. Bone Miner. Res 12, pp. 839–846, 1997. [DOI] [PubMed] [Google Scholar]
- [40].Laugier P, Droin P, Laval-Jeantet AM, and Berger G. “In vitro assessment of the relationship between acoustic properties and bone mass density of the calcaneus by comparison of ultrasound parametric imaging and quantitative computed tomography.” Bone, 20, pp. 157–165, 1997. [DOI] [PubMed] [Google Scholar]
- [41].Hosokawa A and Otani T “Ultrasonic wave propagation in bovine cancellous bone,”, J. Acoust. Soc. Am, 23, pp. 405–418, 1997. [DOI] [PubMed] [Google Scholar]
- [42].Nicholson PHF, Muller R, Lowet G, Cheng XG, Hildebrand T, Ruegsegger P, Van Der Perre G, Dequeker J, and Boonen S. “Do quantitative ultrasound measurements reflect structure independently of density in human vertebral cancellous bone?” Bone. 23, pp. 425–431, 1998. [DOI] [PubMed] [Google Scholar]
- [43].Droin P, Berger G, and Laugier P, “Velocity dispersion of acoustic waves in cancellous bone,” IEEE Trans. Ultrason. Ferro. Freq. Cont, 45, 581–592, 1998. [DOI] [PubMed] [Google Scholar]
- [44].Hans D, Wu C, Njeh CF, Zhao S, Augat P, Newitt D, Link T, Lu Y, Majumdar S, and Genant HK. “Ultrasound velocity of trabecular cubes reflects mainly bone density and elasticity.” Calcif. Tissue Intl 64, pp. 18–23, 1999. [DOI] [PubMed] [Google Scholar]
- [45].Trebacz H, and Natali A. “Ultrasound velocity and attenuation in cancellous bone samples from lumbar vertebra and calcaneus.” Osteo. Int’l, 9, pp. 99–105, 1999. [DOI] [PubMed] [Google Scholar]
- [46].Luo G, Kaufman JJ, Chiabrera A, Bianco B, Kinney JH, Haupt D, Ryaby JT, and Siffert RS, “Computational methods for ultrasonic bone assessment,” Ultrasound Med. Biol, 25, 823–830, 1999. [DOI] [PubMed] [Google Scholar]
- [47].Wear KA, “The effects of frequency-dependent attenuation and dispersion on sound speed measurements: applications in human trabecular bone,” IEEE Trans. Ultrason. Ferro. Freq. Cont, 47, 265–273, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Wear KA, “Measurements of phase velocity and group velocity in human calcaneus,” Ultrasound Med. Biol, 26, 641–646., 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Nicholson PHF and Bouxsein ML, “Bone marrow influences quantitative ultrasound measurements in human cancellous bone,” Ultrasound Med. & Biol, 28, 369–375, 2002. [DOI] [PubMed] [Google Scholar]
- [50].Lee KL, Roh H, and Yoon SW, “Correlations between acoustic properties and bone density in bovine cancellous bone from 0.5 to 2 MHz,” J. Acoust. Soc. Am, 113, 2933–2938, 2003. [DOI] [PubMed] [Google Scholar]
- [51].Lee KL, Rho H, and Yoon SW, “Acoustic wave propagation in bovine cancellous bone: application of the modified Biot-Attenborough model,” J. Acoust. Soc. Am, 114, 2284–2293, 2003. [DOI] [PubMed] [Google Scholar]
- [52].Hakulinen M, Day JS, Töyräs J, Timonen M, Kröger K, Weinans H, Kiviranta I, and Jurvelin JS, “Prediction of density and mechanical properties of human trabecular bone in vitro by using ultrasound transmission and backscattering measurements at 0.2–6.7 MHz frequency range,” Phys. Med. Biol, 50, pp. 1629–1642, 2005. [DOI] [PubMed] [Google Scholar]
- [53].Chen P, Chen T, Lu M, and Yao W, “The measurements of ultrasound parameters on calcaneus by two-sided interrogation techniques,” Meas. Sci. Technol, 16, 1349–1354, 2005. [Google Scholar]
- [54].Haϊat G, Padilla F, Barkmann R, Kolta S, Latremouille C, Glüer CC, and Laugier P, “In vitro speed of sound measurement at intact human femur specimens,” Ultrasound in Med. & Biol, 31, 987–996, 2005. [DOI] [PubMed] [Google Scholar]
- [55].Haϊat G, Padilla F, Cleveland RO, and Laugier P, “Effects of frequency-dependent attenuation and velocity dispersion on in vitro ultrasound velocity measurements in intact human femur specimens,” IEEE Trans. Ultrason. Ferro. Freq. Cont, 53, 39–51, 2006. [DOI] [PubMed] [Google Scholar]
- [56].Yamoto Y, Matsukawa M, Otani T, Yamazaki K, and Nagano A, “Distribution of longitudinal wave properties in bovine cortical bone in vitro,” Ultrasonics, 44, e233 – e237, 2006. [DOI] [PubMed] [Google Scholar]
- [57].Xia Y, Lin W, and Qin Y, “Bone surface topology mapping and its role in trabecular bone quality assessment using scanning confocal ultrasound,” Osteo. Int, 18, 905–913, 2007. [DOI] [PubMed] [Google Scholar]
- [58].Roberjot V, Laugier P, Droin P, Giat P, and Berger G, “Meaurement of integrated backscatter coefficient of trabecular bone. Proc. 1996 IEEE Ultrason. Symp Vol. 2, pp. 1123–1126, 1996. [Google Scholar]
- [59].Strelitzki R, Nicholson PHF, and Paech V, “A model for ultrasonic scattering in cancellous bone based on velocity fluctuations in a binary mixture,” Physiol. Meas, 19, 189–196, 1998. [DOI] [PubMed] [Google Scholar]
- [60].Wear KA. “Frequency dependence of ultrasonic backscatter from human trabecular bone: theory and experiment.” J. Acoust. Soc. Am 106, pp. 3659–3664, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Wear KA. “Anisotropy of ultrasonic backscatter and attenuation from human calcaneus: Implications for relative roles of absorption and scattering in determining attenuation.” J. Acoust. Soc. Am, 107, pp. 3474–3479, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Wear KA and Armstrong DW, “The relationship between ultrasonic backscatter and bone mineral density in human calcaneus,” IEEE Trans. Ultrason. Ferro. Freq. Cont, 47, pp. 777–780, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Wear KA, Stuber AP, and Reynolds JC, “Relationships of ultrasonic backscatter with ultrasonic attenuation, sound speed, and bone mineral density in human calcaneus,” Ultrason. Med. Biol, 26, 1311–1316, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Chaffai S, Roberjot V, Peyrin F, Berger G, and Laugier P. “Frequency dependence of ultrasonic backscattering in cancellous bone: Autocorrelation model and experimental results.” J. Acoust. Soc. Am 108, pp. 2403–2411, 2000. [DOI] [PubMed] [Google Scholar]
- [65].Nicholson PHF, Strelitzki R, Cleveland RO, and Bouxsein ML, “Scattering of ultrasound in cancellous bone: predictions from a theoretical model,” J. Biomech 33, pp. 503–506, 2000. [DOI] [PubMed] [Google Scholar]
- [66].Hoffmeister BK, Whitten SA, and Rho JY, “Low megahertz ultrasonic properties of bovine cancellous bone,” Bone, 26, pp. 635–642, 2000. [DOI] [PubMed] [Google Scholar]
- [67].Wear KA “Fundamental precision limitations for measurements of frequency dependence of backscatter: applications in tissue-mimicking phantoms and trabecular bone,” J. Acoust. Soc. Am 110(6), pp. 3275–3282, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Padilla F and Laugier P, “Prediction of ultrasound attenuation in cancellous bones using poroelasticity and scattering theories,” Proc. IEEE Ultrason. Symp, 1201–1204, 2001. [Google Scholar]
- [69].Laugier P, Padilla F, and Jenson F, “Ultrasonic scattering models for cancellous bone,” 143rd meeting of the Acoustical Society of America, J. Acoust. Soc. Am, 111(5), May, p. 2412, 2002, Pittsburgh, PA. [Google Scholar]
- [70].Hoffmeister BK, Whitten SA, Kaste SC, and Rho JY, Effect of collagen and mineral content on the high frequency ultrasonic properties of human cancellous bone, Bone, Osteo. Int, 13:26–32, 2002. [DOI] [PubMed] [Google Scholar]
- [71].Hoffmeister BK, Auwarter JA, and Rho JY, “Effect of marrow on the high frequency ultrasonic properties of cancellous bone,” Phys. Med. Biol, 47, 3419–3427, 2002. [DOI] [PubMed] [Google Scholar]
- [72].Wear KA, “Characterization of Trabecular Bone Using the Backscattered Spectral Centroid Shift,” IEEE Trans. Ultrason., Ferro. Freq. Cont, 50, 402–407, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Wear KA, “The effect of trabecular material properties on the frequency dependence of backscatter from cancellous bone,” J. Acoust. Soc. Am, 113, 62–65, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Wear KA and Laib A, “The Dependence of Ultrasonic Backscatter on Trabecular Thicknes in Human Calcaneus: Theoretical and Experimental Results,” IEEE Trans. Ultrason., Ferro. Freq. Cont, 50, 979–986, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Padilla F, Peyrin F, and Laugier P, “Prediction of backscatter coefficient in trabecular bones using a numerical model of three-dimensional microstructure,” J. Acoust. Soc. Am, 113, 1122–1129, 2003. [DOI] [PubMed] [Google Scholar]
- [76].Jenson F, Padilla F, and Laugier P, “Prediction of frequency-dependent ultrasonic backscatter in cancellous bone using statistical weak scattering model,” Ultrasound. Med. & Biol, 29, 455–464, 2003. [DOI] [PubMed] [Google Scholar]
- [77].Wear KA, “Measurement of frequency dependence of scattering from cylinders using focused transducers—with applications in trabecular bone,” J. Acoust. Soc. Am, 115, 66–72, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Periera WCA, Bridal SL, Coron A, and Laugier P, “Singular spectrum analysis applied to backscattered ultrasound signals from in vitro human cancellous bone specimens,” IEEE Trans. Ultrason. Ferro. Freq. Cont, 51, 302–312, 2004. [PubMed] [Google Scholar]
- [79].Bossy E, Padilla F, Peyrin F, and Laugier P, “Three-dimensional simulation of ultrasound propagation through trabecular bone structures measured by synchrotron micro-tomography,” Phys. Med. Biol, 50, 5545–5556, 2005. [DOI] [PubMed] [Google Scholar]
- [80].Wear KA, “Fred Lizzi’s statistical framework and the interpretation of ultrasound backscatter from bone,” Ultrasonic Imaging, 27, 41–42, 2006. [DOI] [PubMed] [Google Scholar]
- [81].Padilla F, Jenson F, and Laugier P, “Estimation of trabecular thickness using ultrasonic backscatter,” Ultrasonic Imaging, 28, 3–22, 2006. [DOI] [PubMed] [Google Scholar]
- [82].Jenson F, Padilla F, Bousson V, Bergot C, Laredo JD, and Laugier P, “In vitro ultrasonic characterization of human cancellous femoral bone using transmission and backscatter measurements: relationships to bone mineral density,” J. Acoust. Soc. Am, 119, 654–663, 2006. [DOI] [PubMed] [Google Scholar]
- [83].Kaufman JJ, Luo G, and Siffert RS, “On the relative contributions of absorption and scattering to ultrasound attenuation in trabecular bone: a simulation study,” Proc. 2003 IEEE Ultrason. Symp, Honolulu, HI, 1519–1523, 2003. [Google Scholar]
- [84].Padilla F, Bossy E, Haϊat G, Jenson F, and Laugier P, “Numerical simulation of wave propagation in cancellous bone,” Ultrasonics, 44, e239–e243, 2006. [DOI] [PubMed] [Google Scholar]
- [85].Haϊat G, Padilla F, Barkmann R, Glüer CC, and Laugier P, “Numerical simulation of the dependence of quantitative ultrasonic parameters on trabecular bone microarchitecture and elastic constants,” Ultrasonics, 44, e289–e294, 2006. [DOI] [PubMed] [Google Scholar]
- [86].Padilla F, Jenson F, and Laugier P, “Influence of the precision of spectral backscatter measurements on the estimation of scatterers size in cancellous bone,” Ultrasonics, 44, e57–e60, 2006. [DOI] [PubMed] [Google Scholar]
- [87].Hoffmeister BK, Jones III CI, Caldwell GJ, and Kaste SC, “Ultrasonic characterization of cancellous bone using apparent integrated backscatter,” Phys. Med. Biol, 51, 2715–2727. 2006. [DOI] [PubMed] [Google Scholar]
- [88].Wear KA and Garra BS. “Assessment of bone density using broadband ultrasonic backscatter,” Proc. 22nd Int. Symp. Ultrason. Imag. and Tissue Char, Washington, DC., p. 14 (Abstract), 1997. [Google Scholar]
- [89].Giat P, Chappard C, Roux C, Laugier P, and Berger G. Preliminary clinical assessment of the backscatter coefficient in osteoporosis, Proc. 22nd Int. Symp Ultrason. Imag. and Tissue Char, Washington, DC, p. 16 (Abstract), 1997. [Google Scholar]
- [90].Laugier P, Giat C, Chappard C, Roux C, and Berger G, “Clinical assessment of the backscatter coefficient in osteoporosis,” Proc. 1997 IEEE Ultrason. Symp, pp. 1104–1105, October, 1997. [Google Scholar]
- [91].Wear KA and Garra BS. Assessment of bone density using ultrasonic backscatter. Ultrason. Med. & Biol 24, pp. 689–695, 1998. [DOI] [PubMed] [Google Scholar]
- [92].Roux C, Roberjot V, Paorcher R, Kolta S, Dougados M, and Laugier P, “Ultrasonic backscatter and transmission parameters at the os calcis in postmenopausal osteoporosis,” J. Bone & Mineral Res, 16, pp. 1353–1362, 2001. [DOI] [PubMed] [Google Scholar]
- [93].Wear KA and Armstrong DW, “Relationships among calcaneal backscatter, anttenuation, sound speed, hip bone mineral density, and age in normal adult women.” J. Acoust. Soc. Am, 110, pp. 573–578, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94].Deligianni DD and Apostolopoulos KN, “Characterization of dense bovine cancellous bone tissue microstructure by ultrasonic backscattering using weak scattering models,” J. Acoust. Soc. Am, vol. 122 pp. 1180–1190, 2007. [DOI] [PubMed] [Google Scholar]
- [95].Bossy E, Laugier P, Peyrin F, and Padilla F, “Attenuation in trabecular bone: a comparison between numerical simulation and experimental results in human femur,” J. Acoust. Soc. Am, vol. 122, pp. 2469–2475, 2007. [DOI] [PubMed] [Google Scholar]
- [96].Haϊat G, Padilla F, Lonne S, Lhémery A, Laugier P, and Naili S, “Modeling of velocity dispersion in trabecular bone: effect of multiple scattering and viscous absorption,” Proc. Euro. Symp. Ultrason. Char. Bone, page 11, 2007. [Google Scholar]
- [97].Mottley JG and Miller JG, “Anisotropy of the ultrasonic attenuation in soft tissues: measurements in vitro,” J. Acoust. Soc. Am, vol. 88, pp. 1203–1210, 1990. Appendix 2. [DOI] [PubMed] [Google Scholar]
- [98].Ahuja AS and Hendee WR, “Effects of particle shape and orientation on propagation of sound in suspension,” J. Acoust. Soc. Am, vol. 63, pp. 1074–1080, 1978. Section II. B. [Google Scholar]
- [99].Faran JJ, “Sound scattering by solid cylinders and spheres,” J. Acoust. Soc. Am, vol. 23, pp. 405–418, 1951. [Google Scholar]
- [100].Duck FA, Physical Properties of Tissue. University Press, Cambridge, UK, 1990. [Google Scholar]
- [101].Wear KA, “The dependences of phase velocity and dispersion on trabecular thickness and spacing in trabecular bone-mimicking phantoms,” J. Acoust. Soc. Am, vol. 118, pp. 1186–1192, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102].Ulrich D, van Rietbergen B, Laib A, and Ruegsegger P, “The ability of three-dimensional structural indices to reflect mechanical aspects of trabecular bone,” Bone, vol. 25, pp. 55–60, 1999. [DOI] [PubMed] [Google Scholar]
- [103].Wear KA, Laib A, Stuber AP, and Reynolds JC, “Comparison of measurements of phase velocity in human calcaneus to Biot theory,” J. Acoust. Soc. Am, vol. 117, pp. 3319–3324, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104].Hosokawa A, “Simulation of ultrasound propagation through bovine cancellous bone using elastic and Biot’s finite-difference time-domain methods,” J. Acoust. Soc. Am, vol. 118, pp. 1782–1789, (2005). [DOI] [PubMed] [Google Scholar]