Abstract
Many pathogens are able to replicate or survive in abiotic environments. Disease transmission models that include environmental reservoirs and environment-to-host transmission have used a variety of functional forms and modelling frameworks without a clear connection to pathogen ecology or space and time scales. We present a conceptual framework to organize microparasites based on the role that abiotic environments play in their lifecycle. Mean-field and individual-based models for environmental transmission are analysed and compared. We show considerable divergence between both modelling approaches when conditions do not facilitate well mixing and for pathogens with fast dynamics in the environment. We conclude with recommendations for modelling environmentally transmitted pathogens based on the pathogen lifecycle and time and spatial scales of the host–pathogen system under consideration.
Keywords: environmental transmission, mean-field models, individual-based models, infectious diseases
1. Introduction
Non-host environments such as water, decaying organic matter and abiotic surfaces are important components of the lifecycle of pathogens. These environments provide habitats in which pathogens may replicate or survive, facilitating transmission. Even when environments only serve as fomites, environment-to-host transmission may determine invasion and long-term persistence pathogen dynamics [1,2]. In addition to influencing pathogen ecology, the need to survive in two distinct habitats—host and non-host environments—shapes pathogen evolution [3,4]. Therefore, environmental transmission often warrants explicit consideration in population biology models.
In representing environmental transmission in models, linking host and pathogen scales can be particularly challenging. Processes on these two populations often act at different temporal and spatial scales. Depending on the survival strategies, survival times of pathogens in the environment can be several magnitudes smaller or larger than the duration of infection in hosts. For example, for pathogens that produce spores, the persistence of spores in the environment can last months or years, while infection lasts days [5,6]. Similarly, while transmission is a local process, mobility and hydrologic processes can facilitate long-range pathogen dispersion [7]. Population biology models that explicitly incorporate environmental reservoirs and environment-to-host transmission vary both in their representation of the pathogen dynamics in the environment, as well as in the modelling approaches and mathematical expressions used to describe the per capita rate of infection (also referred to as the force of infection) [8–12]. With few exceptions [13], modellers often have not provided the rationale behind their choices in representing environment-to-host transmission. Mean-field (top-down) models are commonly used to address environmental transmission [8–12]. In mean-field models, individuals are aggregated and, instead of tracking individuals, global population densities are represented. Mean-field models assume individuals randomly interact and are well mixed. When considering environmental transmission, these assumptions may not hold across host–pathogen systems and scales, particularly if the system is highly structured in space with local interactions. Individual-based (bottom-up) models (IBMs) explicitly represent individuals interacting in their local environment. As such, there is no assumption of mixing at the population level, but instead, of local interactions that result in aggregate patterns. IBMs are implemented in code. The aggregate behaviour of an IBM is obtained by summarizing large number of replicated simulations. Compared to mean-field models, fewer IBMs for environmental transmission have been developed [7,14].
Our objective is to compare mean-field models and IBMs for environmental transmission. First, we provide a framework to classify pathogens based on the role of non-host environments in the lifecycles of those pathogens as a guide to further considering environmental pathogen dynamics in the models. Then we present and analyse a mean-field model and an IBM representing environment-to-host transmission. We evaluated under what conditions and life histories the temporal dynamics of the global populations of infected hosts and pathogen level in the environment as predicted by both approaches are in agreement. Lastly, we conclude with recommendations for modelling environmentally transmitted pathogens. We show that for certain life histories and conditions, IBMs may be a better choice for modelling environmental transmission.
2. Pathogen classification based on the role of non-host environments in pathogen lifecycles
Non-host environments are ubiquitous components of most pathogen lifecycles. To address the question of when pathogen dynamics should be explicitly modelled, here we propose a pathogen classification based on the role that non-host environments play in pathogen lifecycles (table 1). The importance of non-host environments in a pathogen lifecycle is determined by the pathogen’s ability to replicate or survive in environments outside the host and by the relative importance of environment-to-host versus other transmission modes (e.g. direct host-to-host, airborne or vector-borne). This classification is a useful first step to consider whether to include environmental processes in epidemiological models as it divides pathogens into four discrete categories. Each category can be represented by a specific model structure as shown in table 1.
Table 1.
The inclusion of environmental processes in epidemiological models depends on the pathogen lifestyle (sapronotic versus parasitic) and relative contribution of different transmission pathways. Flow diagrams for epidemiological models based on these two criteria are presented. Hosts are categorized in two epidemiological states: susceptible (S) and infected (I). For simplicity, a recovered (R) is not represented. Pathogens in the environment are represented by the compartment P. Solid lines represent flows among variables and dashed arrows indicate when a compartment I or P contributes to new infections.
| pathogen classification | examples | model structure |
|---|---|---|
| (a) sapronotic only: | Legionella pneumonia | 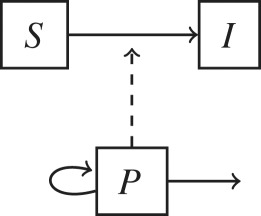 |
| reproduce in the environment | Mycobacterium ulcerans | |
| environment-to-host transmission | Fusarium solani | |
| (b) sapronotic and parasitic: | Vibrio cholera | 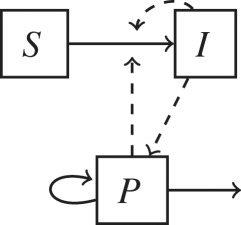 |
| reproduces in the environment/host | Bacillus anthracis | |
| environment-to-host transmission | Geomyces destructans | |
| other transmission modes | ||
| (c) parasitic only: | chronic wasting disease (prions) | 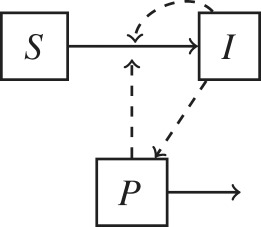 |
| reproduces in the host | Cryptosporidium parvum | |
| environment-to-host transmission | Clostridioides difficile | |
| other transmission modes | Salmonella enterica | |
| hantavirus | ||
| influenza | ||
| (d) no environmental role: | Chlamydia trachomatis | 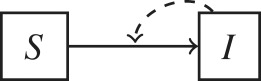 |
| reproduces in the host | human immunodeficiency virus | |
| other transmission modes | Treponema pallidum |
At one end of the organismal spectrum, sapronotic pathogens use environments such as soil, water or decaying matter as their replication site and hence non-host environments are disease reservoirs [5,6] (table 1a). Sapronotic pathogens are fungi, protozoa and bacteria that can cause opportunistic infections, particularly in immunocompromised individuals, through inhalation, ingestion and open wounds or trauma. In general, infected hosts do not contribute to new infections; therefore, host-centric interventions such as isolation, quarantine or immunization are not effective to control these pathogens [15]. Furthermore, because hosts are incidental environments, the evolution of sapronotic pathogens is not influenced by trade-offs between transmission and virulence [16]. On the contrary, traits that favour fitness in the environment may also accidentally increase virulence in the infected host. For example, Legionella pneumophila is a sapronotic organism that thrives in hot water systems, cooling towers and humidifiers. Legionella pneumophila uses the same mechanisms to parasitize freshwater protozoa as it does to attack human macrophages [15,17]. Overall, epidemiological and evolutionary dynamics are driven by pathogen processes taking place at non-host environments.
Some pathogens have a predominant sapronotic lifestyle, but can also revert to a parasitic lifestyle, causing disease in immunocompetent hosts (table 1b). These organisms' life history may reflect trade-offs on traits associated with sapronotic and parasitic lifestyles. These pathogens can also sustain both environment-to-host and host-to-host direct transmission. A particularly well-studied pathogen in this group is the organism that causes cholera in humans, Vibrio cholerae. Vibrio lives in estuarine and costal environments as free-living organisms and in association with plankton and detritus. Two serogroups of V. cholerae, O1 and O139, have both sapronotic and parasitic lifestyles and cause epidemics sustained by host-to-host transmission [18]. To increase pathogen fitness in the host, these serogroups carry virulence factors such as cholera toxin, which disrupts ion transport in enteric cells, causing secretory diarrhoea and severe dehydration [19]. Epidemic serogroups are more likely than other serogroups to transition into a dormant state in the environment suggesting a trade-off between sapronotic and parasitic lifestyles [18]. However, some traits facilitate both environmental growth and host infection. For example, V. cholerae forms biofilms (i.e. a matrix of cells and secreted polysaccharides) under a variety of environmental and physiological conditions [18] that increase both environmental persistence and infectivity as the infective dose is increased [20]. For these group of pathogens, the pathogen interaction with the biotic community and abiotic conditions in the environment still determine at large their ecology and evolutionary dynamics, and therefore environmental dynamics need to be explicitly accounted for in addressing long-term dynamics [21].
Most parasitic pathogens only have a parasitic lifestyle, and therefore they do not replicate in the environment (table 1c). Although these pathogens do not replicate in the environment, they are able to transiently survive and maintain viable populations that can infect hosts. The environmental lifespan of these pathogens is highly variable as they can use diverse strategies to prolong survival. Environmental persistence depends on multiple environmental factors such as temperature, humidity, salinity or radiation [22]. Most viruses fall into this category as they require living cells to replicate, but they also transiently reside in non-host environments. For example, avian influenza viruses only multiply within the relatively high and stable temperature conditions of hosts, but because of their ability to survive in the environment, traits that favour tolerance to the variable, and relatively lower temperature of the environment may represent an evolutionary trade-off [23]. For pathogens that survive in the environment (table 1c), the relative temporal scales between the pathogen dynamics in the environment and the epidemiological host dynamics influence the model structure.
Finally, environments play no role in the transmission of some pathogens with well-defined contacts for transmission, such as sexual contacts or vector bites (table 1d). Most sexually transmitted pathogens are often highly labile and require close sexual encounters for transmission. Environment-to-host transmission is an uncommon mode for pathogens transmitted mainly through biological vectors. Environmental variables are important drivers of the population dynamics of biological vectors, but because transmission occurs through direct contact between hosts and arthropods (e.g. via biting), environment-to-host transmission does not play a main role in pathogens transmitted by biological vectors.
3. Environmental transmission in mean-field models
In mean-field models, the functional form representing the force of infection has embedded assumptions regarding how the host and pathogen populations interact without explicitly modelling interactions at the lower hierarchical levels. In directly transmitted diseases, the terminology and use of the different functional forms for the force of infection has been extensively debated [24–26]. In this section, we discuss the assumptions behind a few forms used in environmental transmission, listed as Cases 1–4 in table 2. Although different terms for the force of infection may lead to different model-derived expressions such as the basic reproduction number, the force of infection expressions are often scalable one to each other. As a consequence, models with different force of infections may be mostly indistinguishable when fitting to population-level data.
Table 2.
Transmission functions, units of the transmission parameter β, suggested scaling of β to produce similar or identical dynamics across all four cases and associated basic reproduction number, R0. The scalings listed are used throughout this work; however other values can be used for scaling to obtain similar results, as discussed in §3. Area is assumed fixed.
| case | H (S, I, R, P) | scaling with N | units of β | β scaling | R0 |
|---|---|---|---|---|---|
| 1 | β1PS | c ⫫ N | 1/(pathogen × day) | β1 | |
| 2 | individuals/(pathogen × day) | β2 = Nβ1 | |||
| 3 | c ⫫ N | 1/day | β3 = 2Kmβ1 | ||
| 4 | individuals/day | β4 = 2Km Nβ1 |
Following the heuristic derivation used for directly transmitted diseases by Begon et al. [26], the term describing environment-to-host transmission can be thought of as the product of (i) the rate of contact between the host population and the environment, (ii) the exposure dose associated with that contact and (iii) the probability that an exposure to a given infectious dose leads to infection. Thus, the transmission term has implicit assumptions regarding the scaling of contact rates with the host population density, and the scaling of the probability of infection given an exposure dose.
Anderson & May [8] presented one of the first models that explicitly included a transmission term for free-living stages of a pathogen in the environment. The transmission term was assumed to be proportional to the number of infective stages in the environment (P), the number of susceptible (S) and a proportionality constant representing transmission efficiency (ν). This expression is analogous to the density-dependent (mass-action) term used for directly transmitted diseases (Case 1, table 2). Since then, a variety of other expressions have been used in modelling environmental transmission, including frequency-dependent type formulations [11,13] and nonlinear formulations [9,10,12,13]. Cases 2 and 4 in table 2 assume the contact rate is inversely proportional to the host population. Almberg et al. [13] suggested that contact may relate inversely with population density as an increased population size may reduce the home range of individuals, reducing effectively the proportion of encountered landscape. Lastly, Cases 3 and 4 assume a dose-dependent probability of infection. Here, we apply the different cases to a modified form of a model proposed by Cortez et al. [27]:
| 3.1 |
In this system of equations, the state variables S(t), I(t) and R(t) are the expected number of susceptible, infectious and recovered individuals in a population, respectively. The state variable P(t) is a measure of the pathogen in the environment. The recovery rate is γ, m is the natural mortality rate and ξ is the shedding rate of pathogens into the environment by the host. Functions governing the population structure of the host, transmission and environmental dynamics are represented by F, H and E, respectively. The formulation of the transmission and environmental functions H and E can accommodate a wide variety of transmission and pathogen lifestyle conditions as shown in table 1.
In order to explore the different cases for the transmission functions H presented in table 2, we choose a special case of the generalized model (3.1) that represents pathogens categorized in table 1 within the C group (parasitic only). We choose E(P) = −δP as the pathogen decay rate. For simplicity, host-to-host transmission is not included, and we choose the total birth rate for the host population to be equal to the total mortality rate, that is, F(S, I, R) = mN. As such, the total population N remains constant.
When assuming constant population, the four transmission functions can yield similar dynamics when they are properly scalable to each other. Table 2 shows suggested scalings for β to achieve this. We define βi to correspond to Case i; we choose β1 as a base and scale the other cases relative to this. Since we are considering a constant population N, the functional form of Cases 1 and 2 is simply given by PS. Cases 3 and 4 have different functional forms due to the variable P in their denominators, representing a nonlinear probability of infection. In these instances, having the solution to Case 3 be an identical curve to Case 1 (with linear probability of infection) is unlikely; however, there will exist some scaling β3 = αβ1, such that the difference between the cases is minimized (with an analogous scaling for β4). Km is the pathogen load yielding 50% chance of infection. We note that Km < Km + P < Km + Pmax and throughout the paper we chose Km = Pmax/2. For simplicity, we use α ≈ 2Km. The value 2Km is the midpoint of the upper and lower bounds of the denominator and is used as a simple substitution for α. For any choice of Km, there exist different exact values of α. Under this scaling, there will be minimal to no difference between each of the different cases.
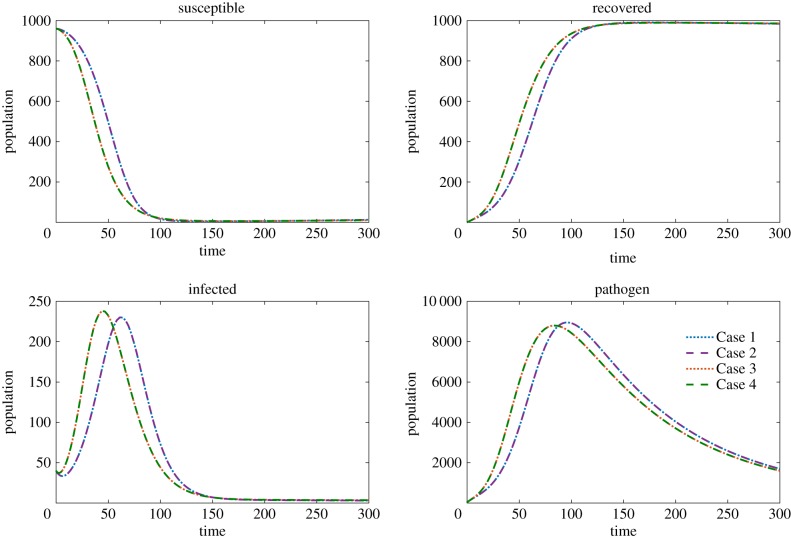
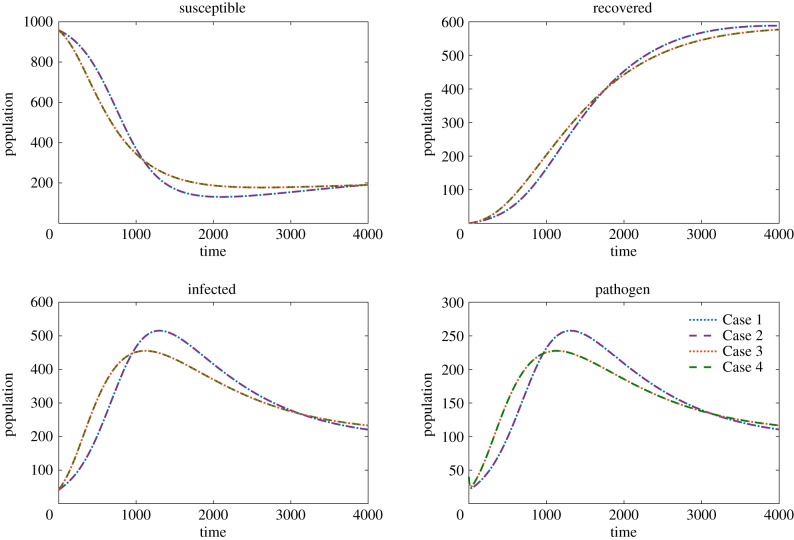
Using these scalings, we solve the system for each of our four transmission functions for two distinct parameter sets representing two environmentally transmitted pathogens with different life histories based on the time scales of pathogen and host dynamics (see parameter sets A and B in table 3). In parameter set A, the decay rate of the pathogen in the environment is slow relative to the recovery rate and the shedding rate. In parameter set B, the decay rate of the pathogen is fast relative to the recovery rate and the shedding rate. Despite both cases yielding different long-term dynamics (population recovers for parameter set A, infection persists in parameter set B) we observe little to no difference between the overall dynamics of Cases 1–4 with reasonable scaling factors as shown in figures 1 and 2.
Table 3.
Parameters used for parameter set A and parameter set B.
| parameter | description | A | B | units |
|---|---|---|---|---|
| tmax | maximum time of simulation | 300 | 4000 | days |
| m | population birth/death rate | 3 × 10−5 | 3 × 10−5 | 1/day |
| β1 | transmission coefficient | 1 × 10−5 | 1 × 10−5 | see table 2 |
| γ | recovery rate | 7 × 10−2 | 8 × 10−4 | 1/day |
| ξ | pathogen shedding rate | 1 | 0.05 | pathogen/(individuals × day) |
| δ | pathogen decay rate | 0.01 | 0.1 | 1/day |
| Km | dose yielding 50% infection chance | 4456 | 128 | pathogen |
| S0 | initial susceptible population | 960 | 960 | individuals |
| I0 | initial infected population | 40 | 40 | individuals |
| R0 | initial recovered population | 0 | 0 | individuals |
| P0 | initial pathogen population | 40 | 40 | pathogen |
Figure 1.
The solutions to model (3.1) using parameter set A. The initial conditions are S0 = 960, I0 = 40, R0 = 0, P0 = 40. The susceptible, infected, recovered and pathogen are compared where Case 1 (dotted blue), Case 2 (dashed purple), Case 3 (dotted red) and Case 4 (dashed green) are plotted in each panel. (Online version in colour.)
Figure 2.
The solutions to model (3.1) using parameter set B. The initial conditions are S0 = 960, I0 = 40, R0 = 0, P0 = 40. The susceptible, infected, recovered and pathogen are compared where Case 1 (dotted blue), Case 2 (dashed purple), Case 3 (dotted red) and Case 4 (dashed green) are plotted in each panel. (Online version in colour.)
In comparing transmission across populations with different host and pathogen densities, transmission functions can, however, yield very different simulation and analytical results including different threshold expressions for invasion and persistence of the diseases. For example, the basic reproduction number, R0, is an invasion threshold representing the average number of secondary infections produced by a single infectious host introduced into a totally susceptible population. Transmission functions yield R0 expressions with different qualitative implications (table 2). For example, Cases 1 and 3 have host density population invasion thresholds and thus there is a minimum population size below which disease cannot invade. Cases 3 and 4 have infective dose invasion thresholds.
4. Environmental transmission in a spatially explicit individual-based model
In this section, we explore the transmission terms in the context of an IBM for environmental transmission in which the physical location of individuals and pathogen is considered, and transmission only occurs locally. We construct a two-dimensional spatial domain with M = 25 sites, in the form of a 5 by 5 grid. The grid is occupied by individuals, who take on either a susceptible, infected or recovered state, and by pathogen units. The dynamics of the system are driven by events described by the ODE model (3.1). The full details of the model construction and simulation are presented in appendix A. Both parameter sets A and B are considered (table 3)
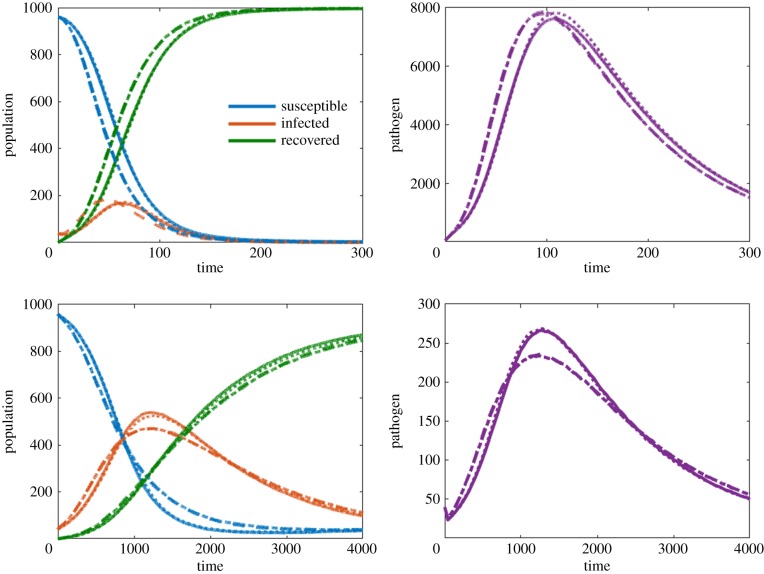
We analyse the IBM using the transmission terms outlined as Cases 1–4. The IBM assumes homogeneous mixing only within each site. This means that all susceptible individuals and pathogen within the same site will interact with each other locally. Therefore, in order to get consistent results across transmission functions, scaling needs to consider that transmission is local, not global. A derivation and discussion of appropriate scalings for the IBM are given in appendix B, with the summary given in table 4. Figure 3 shows the resulting number of susceptible, infected and recovered individuals, as well as the number of pathogen units in the system for the two different parameter sets (other simulation details are given in the figure caption) while using the scalings given in table 4. While the IBM has some important differences in implementation compared to the ODE model (see table 4 and appendix B) we are still able to find consistent results across transmission terms. Cases 1 and 2, and Cases 3 and 4, are almost identical with all four cases yielding similar transient and long-term results.
Table 4.
For Cases 1–4, we show the transmission functions for the ODE model and the spatial model. We wish to highlight the scaling between the ODE model and the spatial model derived in appendix B. Note Sj, Ij, Rj are the number of susceptible, infected and recovered individuals at site j, respectively, while Pj is the number of pathogen units at site j.
| case | ODE model | spatial model | β scaling | Km scaling |
|---|---|---|---|---|
| 1 | β1 SP | — | ||
| 2 | — | |||
| 3 | ||||
| 4 |
Figure 3.
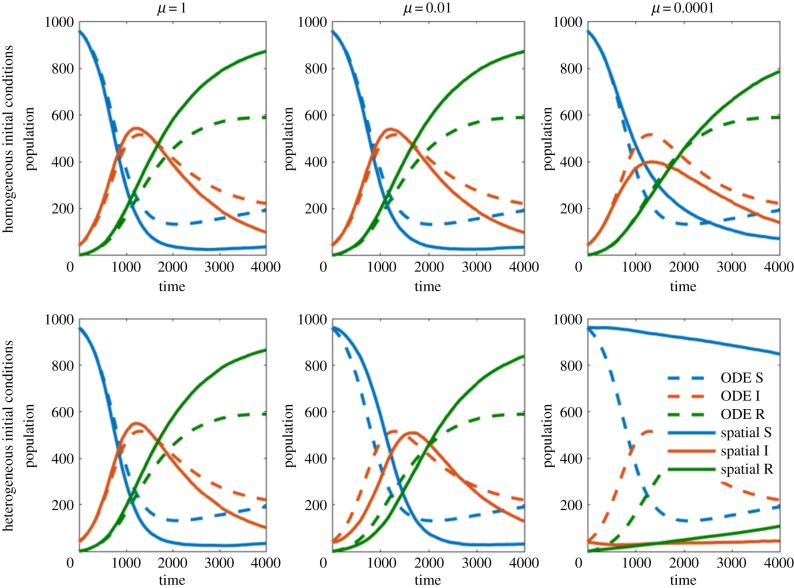
Comparison between four different transmission terms implemented in an individual-based model. Simulation A uses parameter set 1 with a movement rate μ = 0.01 and homogeneous initial condition. Simulation B uses parameter set 2 with μ = 0.01 and heterogeneous initial condition. Left-hand panels compare S, I, R populations while right-hand panels compare pathogen units P. (Online version in colour.)
5. Comparison of mean-field and individual-based models for environment-to-host transmission
To finalize our analysis, we compare the mean-field model to the IBM. Since there are no substantial differences between the four cases when scaling parameters appropriately, for brevity, we will only be comparing results for Case 1 in this section.
Under a number of simplifying assumptions, the IBM can be reduced such that it exactly matches the mean-field ODE model. If the simplifying assumptions are reasonable, the ODE model can be used to predict the dynamics of the IBM. The simplifying assumptions include the assumptions of spatial homogeneity, independence between host and pathogen, continuum approximation and deterministic rates. We discuss the independence and homogeneity assumptions which produce all notable differences between the IBM and ODE models, highlighting when these assumptions are reasonable. Note that other assumptions such as comparing a discrete model to a continuous model, or comparing a stochastic model to a deterministic model result in negligible differences. These assumptions become negligible when averaging over sufficiently many realizations of the IBM.
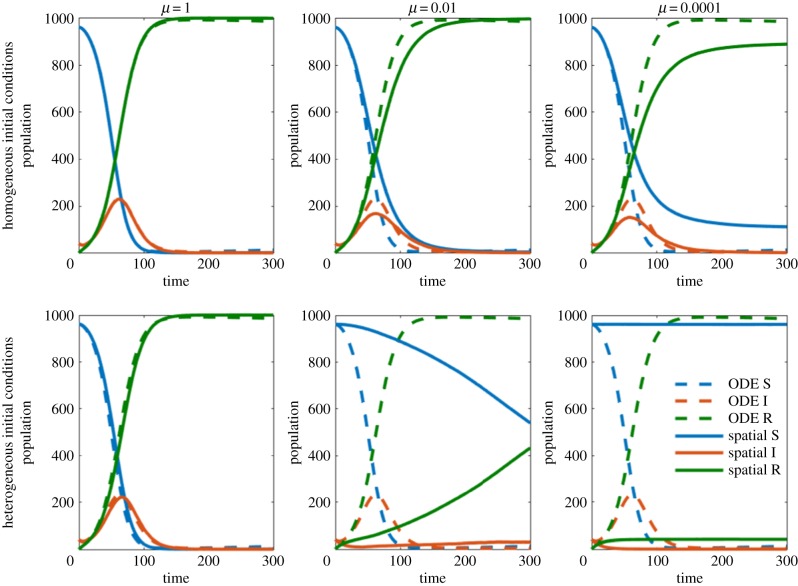
We first compared the models varying the assumption that host and pathogen are spread equally throughout the spatial domain (homogeneity assumption). As the movement rate is increased (relative to the other event rates), the random movement of host individuals causes them to diffuse throughout the domain becoming homogeneously distributed. This is observable in figures 4 and 5 where higher movement rates (left column) decrease the error between the ODE model and the spatial model. Unsurprisingly, our homogeneous initial condition is beneficial to the homogeneity assumption. Alternatively, our heterogeneous initial condition contradicts this assumption and worsens the agreement between the ODE model and IBM. This is easily observable in figures 4 and 5, where under the homogeneous initial condition (top row), the ODE model and IBM are more in agreement than under the heterogeneous initial condition (bottom row). When the movement rate is sufficiently high, the diffusive element of movement makes the initial positions of individuals irrelevant. Both low movement and heterogeneous initial conditions can yield drastically different results from the ODE model. This can result in the two models having different steady-state solutions. In some cases, we observe the eradication of a pathogen in the IBM while the ODE model predicts an endemic solution. These results are similar for both parameter sets.
Figure 4.
Comparisons between ODE model and IBM for parameter set A, for a variety of movement rates, μ, and initial conditions. The dashed ODE line is shown in each panel for comparison.(Online version in colour.)
Figure 5.
Comparisons between ODE model and IBM for parameter set B, for a variety of movement rates, μ, and initial conditions. The dashed ODE line is shown in each panel for comparison. (Online version in colour.)
We now consider the independence assumption, which has little effect on parameter set A but a substantial effect on parameter set B. The independence assumption used to construct the ODE model is
This assumption ignores the correlation between the number of susceptible and the number of pathogen units at a given site. Hence, in instances with high correlation, we expect the difference between the ODE model and the IBM to be large. In instances with low correlation, we expect consistent results between both models. To best observe the error due to the independence assumption, we consider cases with high movement rates. In these cases, the homogeneity assumption is valid, hence all error produced is a result of the independence assumption. High movement rates can be observed in the left columns of figures 4 and 5.
Parameter set A demonstrates an example of consistent results, while parameter set B demonstrates an example in which the ODE model and the spatial IBM never converge. The parameter set A was chosen so that recovery time and shedding are quick relative to the decay rate. As such, each pathogen unit has high survivability allowing individuals to move or change state frequently before the pathogen decays. This results in low correlation between the states of individual hosts and the pathogen units at a given site. The parameter set B was chosen so that recovery time is slow, and pathogen decay is quick relative to shedding. Quick pathogen decay means that the presence of pathogen will likely imply the presence of an infected individual, hence resulting in high correlations between the states of individuals and the pathogen units.
6. Discussion and conclusion
We have discussed several aspects to consider when formulating models for environmentally transmitted pathogens, including pathogen natural history, environmental transmission terms, and spatial and temporal scales of the system. The explicit role of the environment within the pathogen natural history should guide the model structure. The pathogen natural history has additional implications for the modelling framework. As shown in §5, the assumption of independence between pathogen and host individuals underlying the mean-field models may not be met for pathogens with faster environmental decay dynamics compared to the duration of the infectious period, independently of the spatial scope or level of mixing between pathogen and hosts. When environmental decay was rapid relative to other dynamics, it created a dependence between the state of individual hosts and the pathogen present at site. These components are assumed to be independent in the mean-field model, hence the IBM never converges to the mean-field model. Additional complications for pathogens with fast environmental dynamics are the inability of estimating individual parameters related to environmental transmission, such as the transmission coefficient β and pathogen shedding rate ξ, and the difficulty in discerning between transmission pathways [28,29]. Host-to-host direct and environment-to-host transmission pathways cannot easily be distinguished when the time scales of the pathogen dynamics in the environmental compartment are fast compared to the epidemiological host dynamics [12,27,28]. For such pathogens, environmental transmission is often combined with host-to-host direct transmission in mean-field models [12]. Additional measurements such as environmental pathogen loads can also improve parameter identifiability [28]. However, if transmission pathways need to be independently represented (e.g. to identify control strategies), then IBMs may be a more appropriate approach as this modelling framework can incorporate local hierarchical level data to describe processes underlying transmission. These data may be more readily available from different sources than population-level data alone. Although parametrization of complex models like IBMs is challenging, recent approaches on model calibration such as approximate Bayesian computation have been successfully applied [30].
Selecting a suitable functional form to characterize the transmission term is challenging. Selection of functional forms is based on suitable assumptions for the specific system or by fitting the model to available empirical data [31–33]. When selecting a transmission term for characterizing transmission in a single host–pathogen population, the support generated by the goodness of fit yields limited evidence in favour or against different transmission functions. As shown in §§3 and 4, by scaling β to the appropriate units, the model dynamics between different functional forms can be made to converge. We showed that the dynamics between models with dose-dependent (Cases 3 and 4) and non-dose-dependent transmission functions (Cases 1 and 2) could be made to come into close agreement with each other by selecting particular scalings of β. As the functional forms for transmission include varying assumptions regarding the scaling of contact rate with host population, care should, therefore, be exercised in the selection of the transmission function for a varying population or across populations. Empirical data collected across populations are recommended to elucidate the transmission form [32]. However, this type of data may be not be available. In addition, differences in spatial scale may obscure the transmission mechanisms underlying local transmission [34].
Our comparison between mean-field model and IBM for environmental transmission demonstrates that whether exposure is modelled in a global or local way has a significant impact on model dynamics, particularly when the assumptions of homogeneity and independence embedded in the mean-field models are not met. The distribution of the pathogen, the movement and distribution pattern of hosts, and the spatial scope of the system should all be considered to determine whether spatial heterogeneity needs to be considered into the model. In general, the distribution of most pathogens and hosts is expected to be heterogeneous at broader spatial scales. However, some pathogen distribution in the environment can be heterogeneous even at small scales [35,36]. In those conditions, modelling environmental transmission within an IBM framework and transmission as local process—with a transmission term based on suitable assumptions—may be the most accurate approach.
The relationship of patterns, scale and processes is central to ecology and is particularly relevant to the ecology of infectious diseases [37]. Patterns of pathogen transmission arise from complex interactions between local transmission and the broader spatial and temporal scales of the system [34]. These aspects are even more critical for environmentally transmitted pathogens because of the explicit consideration of both host and pathogen levels and their associated demographic and epidemiological processes. First, we suggest that the development of a model begin with a careful consideration of pathogen life-history characteristics, particularly as they relate to the temporal scales of pathogen dynamics relative to host dynamics. This should be followed by the consideration of whether the distribution of the pathogen, the movement and distribution pattern of hosts, and the spatial scope of the model system warrant the incorporation of spatial heterogeneity and local transmission into the structure of the model.
Appendix A. Individual-based model description and simulation
We construct a two-dimensional spatial domain with M = 25 sites, in the form of a 5 by 5 grid. The grid is occupied by individuals, who take on either a susceptible, infected or recovered state, and by pathogen units. Our model initially has N0 = 1000 individuals, made up of 960 susceptible individuals and 40 infected individuals, as well as 40 pathogen units. Each individual and pathogen unit is initially distributed to one of the 25 sites based on the initial condition. The number of individuals or pathogen units at a given site can change based on the dynamics of the system. The Matlab code for the model is available at github.com/lanzaslab/environmentalmodels.
We consider seven different events in our spatial model. The birth event is implemented by each individual at rate m and adds a new individual to the corresponding site. The death event is implemented by each individual at rate m and removes that individual from the system. The recovery event is implemented by each infected individual at rate γ and changes their state from infected to recovered. The shedding event is implemented by each infected individual at rate ξ and adds a new pathogen unit to the corresponding site. The decay event is implemented by each pathogen unit at rate δ and removes that pathogen unit from the system.
The final two events are somewhat more complex. The movement event is implemented by each individual at rate μ/4 with each site that is currently adjacent to their current site. We describe adjacent as being the four surrounding sites (above, below, left and right). As such, an individual at a non-edge site has four directions to move, and can move to each one at rate μ/4, for a total movement rate of μ. On an edge (or corner) site, the total movement rate is reduced. For example, if no site exists to the left of an individual's current site, then a movement event cannot be performed to the left and hence the total rate of movement for that site is 3μ/4.
Finally, the infection event is implemented between pairs of susceptible individuals and pathogen units so long as the pair are occupying the same site. We consider each of the four cases of transmission functions discussed in §4, hence the rate at which this occurs will vary. We discuss this in more detail in appendix B, but in general, each interacting susceptible individual and pathogen unit perform an infection event at rate β. Results for this are summarized in table 4. Note that our model assumes homogeneous mixing within each site. This means that all susceptible individuals and pathogen units within the same site will interact with each other continuously and equally.
Each event in the spatial model is implemented based only on the current state of the model. As such, this model is an example of continuous-time Markov chain. This implies the existence of a matrix Q, which describes the transition from each state to each other state. In this case, the state refers to all possible configurations of the spatial domain. We can simulate realizations of the system in continuous time using a process known as the Gillespie algorithm.
The procedure of the Gillespie algorithm is as follows:
-
(1)
calculate the total rate λ of all possible events from the current state,
-
(2)
generate a time step that is exponentially distributed with parameter 1/λ,
-
(3)
randomly select an event to implement, proportional to the rate at which each event can occur,
-
(4)
implement the event and the time step and repeat the process.
It is convenient to define Sj, Ij and Rj as the number of susceptible, infected and recovered individuals at site j, and Pj as the number of pathogen units at site j.
The total rate λ is the sum of all possible transition rates for each event from the current state to any other state. Consider the example of a birth event. Each individual has a rate m of performing a birth event. This event will increase the number of susceptible individuals at a given site by one, hence changing the state of the system. If we sum over all individuals, we find that the total rate of birth is mN(t). Calculating this rate is relatively simple because it does not depend on interactions between individuals or the pathogen. We now consider the example of an infection event, which is more complicated due to the nonlinear nature of the event. Due to the interaction between susceptible individuals and pathogen units, summing over each case does not result in a simple expression as it did for the birth rate. If we consider the Case 1 transmission function for infection, the total infection rate is found by calculating the rate β1 Sj Pj for each site, and then summing over all sites. Once the rates of all events have been calculated, we sum all of these in order to obtain the total rate λ.
Upon calculating λ, its inverse is used as the parameter for an exponential distribution. By randomly generating a number from this, we simulate the time until the next event. We now select which event will occur. By considering each event as a proportion of the total rate, we can calculate the probability of each event occurring. For instance, mN(t)/λ is the probability of a birth event occurring. Upon choosing an event, we must select which individual performs the event. As each individual within a given site is essentially identical, we need only choose which site will perform the event. The probability of each site performing the event is proportional to the total rate of that event occurring. For instance, site j will perform a birth event with probability m(Sj + Ij + Rj)/mN. Once a site has been chosen, the event is performed and the process can continue to the next time step.
Upon reaching some maximum time, we wish to obtain the total number of susceptible, infected and recovered individuals in the system, , and , and the total number of pathogen units in the system . These total populations can be calculated directly from the site-wise totals
We can then compare these variables for each of our different cases and to the corresponding ODE variables.
Appendix B. Transmission terms and scaling for individual-based model
Recall that for the birth event, we could sum over all the rates to obtain mN(t). As a result, the ODE model and IBM have (on average) an equal birth rate. If we consider the total rate of the infection event for the IBM, using Case 1 as an example, we obtain
This lack of equivalence appears due to the nonlinear nature of these terms and is present in all four transmission functions considered throughout the paper. As a result, it is difficult for us to directly relate the rates of the ODE model and IBM.
In order to relate the ODE model and the IBM, we use the homogeneous mixing assumption. Essentially, this assumption states that each population is spread equally among each site, that is Xj = Xk for all sites j and k, and X ∈ {S, I, R, P}. From here, we can define the total number of susceptible, infected and recovered individuals, and the total number of pathogen units under the homogeneity assumption by the following equations:
recalling that M is our number of sites. For convenience, we also define Nj = Sj + Ij + Rj as the total number of individuals at site j.
To relate the rates in our two models, let us consider the exact equation for the rate of change of the number of infected individuals on site j (this can be derived directly from the continuous-time Markov chain)
where Iadj is the rate of moving into site j from any of the adjacent sites. Note that the movement expression is slightly different at boundaries, but does not affect the scaling idea presented. Upon applying the homogeneous mixing assumption to this equation and multiplying by M, we can make the following substitution:
| B 1 |
If we now consider each of our individual cases, we can understand the appropriate β scaling between the ODE model and the IBM.
We consider each case individually from this point, starting with Case 1:
recalling that for the IBM, is the rate of infection for Case i. In order to compare results between the ODE model and IBM, we require . We can find the appropriate scalings for each case using this process. For Case 2, we obtain the following:
resulting in the scaling .
For Case 3, we obtain the following:
resulting in the scaling and . Note that here, the half infectious dose parameter must be scaled in order to give consistent results.
For Case 4, we obtain the following:
resulting in the scaling and . A summary of the major results of this appendix is shown in table 4.
Data accessibility
This article has no additional data.
Authors' contributions
C.L. conceived paper ideas. K.D. and S.E. implemented and simulated the models. C.L., K.D., S.E. and D.D. wrote, discussed and edited the manuscript.
Competing interests
We declare we have no competing interests.
Funding
This work was supported by US National Institutes of Health (NIH) grant no. R01GM117618 as part of the joint National Science Foundation (NSF)-NIH-United States Department of Agriculture (USDA) Ecology and Evolution of Infectious Diseases Program and by the joint NSF/NIGMS Mathematical Biology Program through NIH award no. R01GM113239. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
References
- 1.King AA, Ionides EL, Pascual M, Bouma MJ. 2008. Inapparent infections and cholera dynamics. Nature 454, 877–880. ( 10.1038/nature07084) [DOI] [PubMed] [Google Scholar]
- 2.Rohani P, Breban R, Stallknecht DE, Drake JM. 2009. Environmental transmission of low pathogenicity avian influenza viruses and its implications for pathogen invasion. Proc. Natl Acad. Sci. USA 106, 10 365–10 369. ( 10.1073/pnas.0809026106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Roche B, Drake JM, Rohani P. 2011. The curse of the pharaoh revisited: evolutionary bi-stability in environmentally transmitted pathogens. Ecol. Lett. 14, 569–575. ( 10.1111/j.1461-0248.2011.01619.x) [DOI] [PubMed] [Google Scholar]
- 4.Brown SP, Cornforth DM, Mideo N. 2012. Evolution of virulence in opportunistic pathogens: generalism, plasticity, and control. Trends Microbiol. 20, 336–342. ( 10.1016/j.tim.2012.04.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hubálek Z. 2003. Anthroponoses, zoonoses, and sapronoses. Emerg. Infect. Dis. 9, 403–404. ( 10.3201/eid0903.020208) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cangelosi GA, Freitag NE, Riley-Buckley MS. 2004. From outside to inside: environmental microorganisms as human pathogens. Washington, DC: American Society for Microbiology. [PubMed] [Google Scholar]
- 7.Mari L, Bertuzzo E, Righetto L, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A. 2011. Modelling cholera epidemics: the role of waterways, human mobility and sanitation. J. R. Soc. Interface 9, 376–388. ( 10.1098/rsif.2011.0304) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Anderson RM, May RM. 1981. The population dynamics of microparasites and their invertebrate hosts. Phil. Trans. R. Soc. Lond. B 291, 451–524. ( 10.1098/rstb.1981.0005) [DOI] [Google Scholar]
- 9.Codeço CT. 2001. Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect. Dis. 1, 1 ( 10.1186/1471-2334-1-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Joh RI, Wang H, Weiss H, Weitz JS. 2009. Dynamics of indirectly transmitted infectious diseases with immunological threshold. Bull. Math. Biol. 71, 845–862. ( 10.1007/s11538-008-9384-4) [DOI] [PubMed] [Google Scholar]
- 11.Andraud M, Dumarest M, Cariolet R, Aylaj B, Barnaud E, Eono F, Pavio N, Rose N. 2013. Direct contact and environmental contaminations are responsible for HEV transmission in pigs. Vet. Res. 44, 102 ( 10.1186/1297-9716-44-102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Breban R. 2013. Role of environmental persistence in pathogen transmission: a mathematical modeling approach. J. Math. Biol. 66, 535–546. ( 10.1007/s00285-012-0520-2) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Almberg ES, Cross PC, Johnson CJ, Heisey DM, Richards BJ. 2011. Modeling routes of chronic wasting disease transmission: environmental prion persistence promotes deer population decline and extinction. PLoS ONE 6, e19896 ( 10.1371/journal.pone.0019896) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen S, Sanderson MW, White BJ, Amrine DE, Lanzas C. 2013. Temporal-spatial heterogeneity in animal-environment contact: implications for the exposure and transmission of pathogens. Sci. Rep. 3, 3112 ( 10.1038/srep03112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Heymann DL, et al. 2008. Control of communicable diseases manual, 19 edn Washington, DC: American Public Health Association. [Google Scholar]
- 16.Walther BA, Ewald PW. 2004. Pathogen survival in the external environment and the evolution of virulence. Biol. Rev. 79, 849–869. ( 10.1017/S1464793104006475) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kwaik YA, Gao L-Y, Stone BJ, Venkataraman C, Harb OS. 1998. Invasion of protozoa by legionella pneumophila and its role in bacterial ecology and pathogenesis. Appl. Environ. Microbiol. 64, 3127–3133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Conner JG, Teschler JK, Jones CJ, Yildiz FH. 2016. Staying alive: Vibrio cholerae's cycle of environmental survival, transmission, and dissemination. In Virulence mechanisms of bacterial pathogens (eds Kudva I. et al.), pp. 593–633. Washington, DC: ASM Press; ( 10.1128/microbiolspec.VMBF-0015-2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pruzzo C, Huq A, Colwell RR, Donelli G. 2005. Pathogenic vibrio species in the marine and estuarine environment. In Oceans and health: pathogens in the marine environment, pp. 217–252. Berlin, Germany: Springer.
- 20.Faruque SM, Biswas K, Nashir Udden SM, Ahmad QS, Sack DA, Balakrish Nair G, Mekalanos JJ. 2006. Transmissibility of cholera: in vivo-formed biofilms and their relationship to infectivity and persistence in the environment. Proc. Natl Acad. Sci. USA 103, 6350–6355. ( 10.1073/pnas.0601277103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Anttila J, Laakso J, Kaitala V, Ruokolainen L. 2016. Environmental variation enables invasions of environmental opportunist pathogens. Oikos 125, 1144–1152. ( 10.1111/oik.2016.v125.i8) [DOI] [Google Scholar]
- 22.Brown JD, Goekjian G, Poulson R, Valeika S, Stallknecht DE. 2009. Avian influenza virus in water: infectivity is dependent on pH, salinity and temperature. Vet. Microbiol. 136, 20–26. ( 10.1016/j.vetmic.2008.10.027) [DOI] [PubMed] [Google Scholar]
- 23.Handel A, Brown J, Stallknecht D, Rohani P. 2013. A multi-scale analysis of influenza a virus fitness trade-offs due to temperature-dependent virus persistence. PLoS Comput. Biol. 9, e1002989 ( 10.1371/journal.pcbi.1002989) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.McCallum H, Fenton A, Hudson PJ, Lee B, Levick B, Norman R, Perkins SE, Viney M, Wilson AJ, Lello J. 2017. Breaking beta: deconstructing the parasite transmission function. Phil. Trans. R. Soc. B 372, 20160084 ( 10.1098/rstb.2016.0084) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.de Jong MCM, Bouma A, Diekmann O, Heesterbeek H. 2002. Modelling transmission: mass action and beyond. Trends Ecol. Evol. 17, 64–65. ( 10.1016/S0169-5347(01)02399-0) [DOI] [Google Scholar]
- 26.Begon M, et al. 2002. A clarification of transmission terms in host-microparasite models: numbers, densities and areas. Epidemiol. Infect. 129, 147–153. ( 10.1017/S0950268802007148) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cortez MH, Weitz JS. 2013. Distinguishing between indirect and direct modes of transmission using epidemiological time series. Am. Nat. 181, E43–E54. ( 10.1086/668826) [DOI] [PubMed] [Google Scholar]
- 28.Eisenberg MC, Robertson SL, Tien JH. 2013. Identifiability and estimation of multiple transmission pathways in cholera and waterborne disease. J. Theor. Biol. 324, 84–102. ( 10.1016/j.jtbi.2012.12.021) [DOI] [PubMed] [Google Scholar]
- 29.Lee EC, Kelly MR Jr, Ochocki BM, Akinwumi SM, Hamre KES, Tien JH, Eisenberg MC. 2017. Model distinguishability and inference robustness in mechanisms of cholera transmission and loss of immunity. J. Theor. Biol. 420, 68–81. ( 10.1016/j.jtbi.2017.01.032) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.van der Vaart E, Beaumont MA, Johnston ASA, Sibly RM. 2015. Calibration and evaluation of individual-based models using approximate Bayesian computation. Ecol. Modell. 312, 182–190. ( 10.1016/j.ecolmodel.2015.05.020) [DOI] [Google Scholar]
- 31.Begon M, Feore SM, Bown K, Chantrey J, Jones T, Bennett M. 1998. Population and transmission dynamics of cowpox in bank voles: testing fundamental assumptions. Ecol. Lett. 1, 82–86. ( 10.1046/j.1461-0248.1998.00018.x) [DOI] [Google Scholar]
- 32.McCallum H, Barlow N, Hone J. 2001. How should pathogen transmission be modelled? Trends Ecol. Evol. 16, 295–300. ( 10.1016/S0169-5347(01)02144-9) [DOI] [PubMed] [Google Scholar]
- 33.Fenton A, Fairbairn JP, Norman R, Hudson PJ. 2002. Parasite transmission: reconciling theory and reality. J. Anim. Ecol. 71, 893–905. ( 10.1046/j.1365-2656.2002.00656.x) [DOI] [Google Scholar]
- 34.Ferrari MJ, Perkins SE, Pomeroy LW, Bjørnstad ON. 2011. Pathogens, social networks, and the paradox of transmission scaling. Interdiscip. Perspect. Infect. Dis. 2011, 267049 ( 10.1155/2011/267049) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Li S, Eisenberg JNS, Spicknall IH, Koopman JS. 2009. Dynamics and control of infections transmitted from person to person through the environment. Am. J. Epidemiol. 170, 257–265. ( 10.1093/aje/kwp116) [DOI] [PubMed] [Google Scholar]
- 36.Faires MC, Pearl DL, Berke O, Reid-Smith RJ, Weese JS. 2013. The identification and epidemiology of meticillin-resistant Staphylococcus aureus and Clostridium difficile in patient rooms and the ward environment. BMC Infect. Dis. 13, 342 ( 10.1186/1471-2334-13-342) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Levin SA. 1992. The problem of pattern and scale in ecology. Ecology 73, 1943–1967. ( 10.2307/1941447) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.