A general method for multiscale modelling of vector-borne disease systems

Abstract

The inability to develop multiscale models which can describe vector-borne disease systems in terms of the complete pathogen life cycle which represents multiple targets for control has hindered progress in our efforts to control, eliminate and even eradicate these multi-host infections. This is because it is currently not easy to determine precisely where and how in the life cycles of vector-borne disease systems the key constrains which are regarded as crucial in regulating pathogen population dynamics in both the vertebrate host and vector host operate. In this article, we present a general method for development of multiscale models of vector-borne disease systems which integrate the within-host and between-host scales for the two hosts (a vertebrate host and a vector host) that are implicated in vector-borne disease dynamics. The general multiscale modelling method is an extension of our previous work on multiscale models of infectious disease systems which established a basic science and accompanying theory of how pathogen population dynamics at within-host scale scales up to between-host scale and in turn how it scales down from between-host scale to within-host scale. Further, the general method is applied to multiscale modelling of human onchocerciasis—a vector-borne disease system which is sometimes called river blindness as a case study.

1. Introduction

Vector-borne diseases are infectious disease systems which arise because the infectious agent (viruses, bacteria, protozoa and helminth) has a complex life cycle so that there is need for at least two hosts: (i) a vertebrate host—which is usually a human host or other animal host and (ii) a vector host—which include mosquitoes, flies (sand flies and black flies), ticks, bugs and snails for the pathogen to complete its life cycle. The vector acts both as a carrier and as an organism within which the parasite develops to an infectious stage before it is transmitted to the vertebrate host. Major vector-borne diseases include malaria, dengue, lymphatic filariasis, Chagas disease, onchocerciasis, leishmaniasis, chikungunya, Zika virus disease, yellow fever, Japanese encephalitis and schistosomiasis [1]. An estimated 17% of the global disease burden of infectious diseases is attributed to vector-borne diseases [1]. In general, we can roughly demarcate the transmission mechanisms of vector-borne diseases into two types which are:

• (a)Type I vector-borne disease systems. These are vector-borne diseases in which part of the life cycle of the infectious agent (the pathogen) is external to the two hosts that are implicated in the transmission of these multi-host infections (usually a vertebrate host and a vector host). For these vector-borne diseases the infection of both the vertebrate host and the vector host is caused by a free-living infective pathogen life stage in the environment. Examples of such vector-borne diseases are human schistosomiasis [2] and Guinea worm [3].
• (b)Type II vector-borne disease systems. These are vector-borne diseases in which the whole pathogen life cycle is strictly internal to the two hosts that are implicated in the transmission of these multi-hosts infections. For these vector-borne diseases, there is no free-living pathogen life stage in the environment that causes infection to either the vertebrate host or the vector host. Infection of these hosts is caused by pathogens which only survive in the internal environment of the two hosts (i.e. at within-host scale). The majority of these type II vector-borne diseases are transmitted by blood-feeding arthropods, such as mosquitoes, ticks and fleas. Two groups of type II vector-borne diseases can be identified. (i) Those in which there is no pathogen replication cycle at within-host scale (within-vertebrate host and within-vector host). For such type II vector-bone diseases, the pathogen load at the within-host scale (within-vertebrate host and within-vector host) increases only through super-infection (i.e. repeated infection before the host recovers from the infectious episode). In this article, we develop a general multiscale modelling method for such type II vector-borne diseases and then apply it to human onchocerciasis as an example. (ii) Those in which the pathogen has a life stage with a pathogen replication cycle at within-host scale. For such type II vector-borne diseases, the pathogen load at within-host scale increases mainly through the life stage which has a pathogen replication cycle. Malaria is a classic example of such type II vector-born diseases where the merozoite life stage has a replication cycle at within-host scale in the vertebrate host. The multiscale modelling of such vector-borne diseases is considered elsewhere. In this article, we present a general method for development of multiscale models of type II vector-borne diseases in which there is no pathogen replication cycle at within-host scale.

There are five main different generic categories of multiscale models of infectious disease systems that can be developed at the different levels of organization of an infectious disease system (the cell level, the tissue level, the host level, etc.) by integrating two adjacent scales at a time. These five main generic categories are [2,4]: (i) individual-based multiscale models (IMSMs), (ii) nested multiscale models (NMSMs), (iii) embedded multiscale models (EMSMs), (iv) hybrid multiscale models (HMSMs) and (v) coupled multiscale models (CMSMs) with each of these categories having several different classes of multiscale models. For vector-borne diseases, the multiscale models developed at host level (i.e. those integrating the within-host scale and the between-host scale) are categorized as CMSMs [4].

The general multiscale modelling method for type II vector-borne diseases presented in this paper, which is a coupled multiscale model, is an extension of two of our previous papers [5,6]. The first of these papers [5] introduced a method for development of multiscale models of type I vector-borne diseases at host level (i.e. linking within-host scale and between-host scale) using human schistosomiasis as an example. The paper demonstrated in a practical way the idea of scaling up and down in linking scales of an infectious disease system by identifying within-host scale and between-host scale variables and parameters and design a feedback of these variables and parameters through down-scaling and up-scaling across the within-host scale and the between-host scale. For this multiscale model, the development of between-host scale submodel was based on principles of modelling environmentally transmitted infectious diseases [7]. The main distinction between modelling of directly transmitted infectious disease systems and environmentally transmitted infectious disease systems is that the latter usually have at least one extra equation describing the dynamics of pathogen in the environment. The paper [5] established the role this extra equation plays in the development of multiscale models of type I vector-borne diseases that link the within-host scale and between-host scale. The second of these papers [6] established a multiscale modelling science base for directly transmitted infectious disease systems similar to the multiscale modelling method for environmentally transmitted infectious disease systems in [5] using HIV/AIDS as a case study by introducing the concept of community pathogen load (CPL) as a new public health measure in multiscale modelling of directly transmitted infectious disease systems. CPL is defined as an aggregation of individual pathogen loads of hosts (humans, animals, vectors, plants) infected with a particular pathogen (virus, protozoan, helminth, bacteria, fungus, prion, etc.) in a particular geographical location or community at a particular time [6]. Thus, in this article the word pathogen refers to any biological infectious agent (virus, protozoan, helminth, bacteria, fungus, prion). Although we use the term ‘community pathogen load’ in the development of the general multiscale model of vector-borne diseases when the infectious agent is not specified, we shall assume, for purposes of development of specific multiscale models from the general multiscale (i.e. when the infectious agent is specified), that the word ‘pathogen’ is implied to mean the actual pathogen name. For example, if the infectious agent considered in the multiscale model is a worm (for some helminth infections), the term ‘community pathogen load’ is interpreted to mean ‘community worm load’. Similarly, if the infectious agent considered in the multiscale model is a virus, the term ‘community pathogen load’ is interpreted to mean ‘community viral load’.

The introduction of CPL as an additional variable at between-host scale entails the incorporation of an extra equation describing this variable in the modelling of directly transmitted infectious disease systems. Incidentally, this converts models of directly transmitted infectious disease systems which are developed by compartmentalizing the host population into susceptible, exposed, infected, recovered (SEIR) and variations of this paradigm (SI, SIS, SEI, SEIS, SIR, SIRS, SEIRS, etc.) into those which are equivalent to environmentally transmitted infectious disease models which are developed based on compartmentalizing the host population into susceptible, exposed, infected, recovered, together with an extra variable describing pathogen load in the environment (SEIRP), and variations of this paradigm (SIP, SISP, SEIP, SEISP, SIRP, SIRSP, SEIRSP, etc.). For details of single-scale modelling of environmentally transmitted infectious diseases at host level, see [7] and references therein. The paper [6] gave a scientific rationale and justification for the use of CPL in multiscale modelling of directly transmitted infectious disease systems so that the science and accompanying theory for multiscale modelling of environmentally transmitted infectious disease systems in [5] can be applied to multiscale modelling of directly transmitted infectious disease systems. Our goal in this article is to extend the ideas in [5,6] to develop a general method for multiscale modelling of type II vector-borne disease systems. The general multiscale modelling method is applied to human onchocerciasis (river blindness) as a case study. The approach is quite general and avoids the complications of using HMSMs [8,9] and IMSMs [10] as sub-models of coupled multiscale models [4] in multiscale modelling of vector-borne diseases which require more computational resources to solve.

2. The general method for multiscale modelling of type II vector-borne disease systems

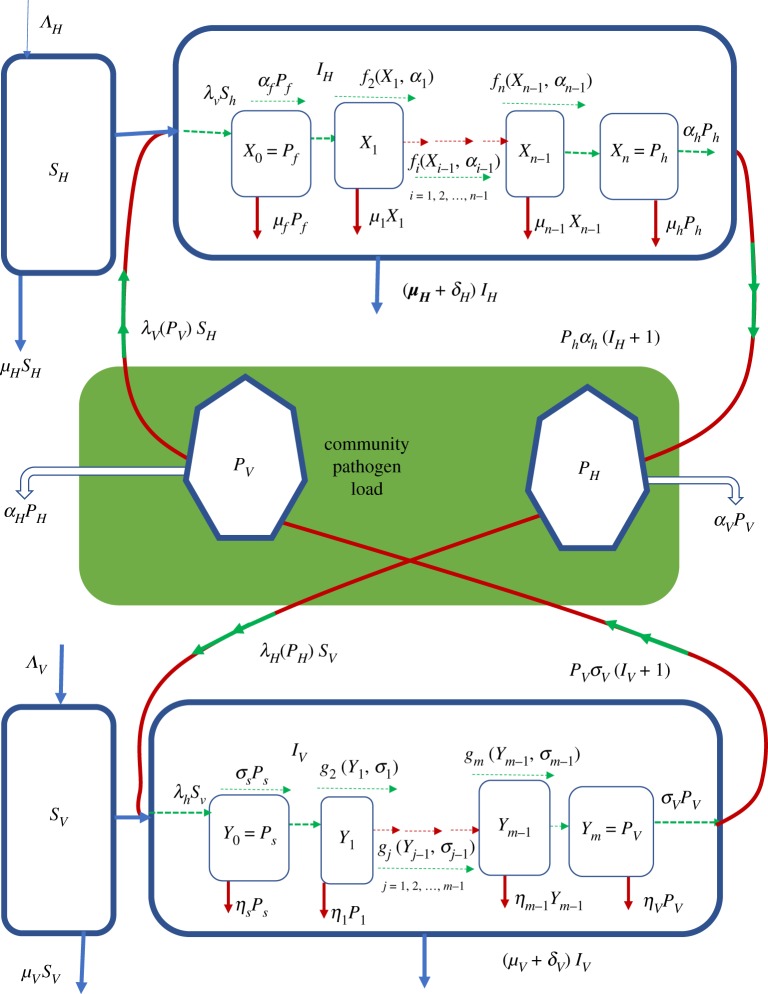
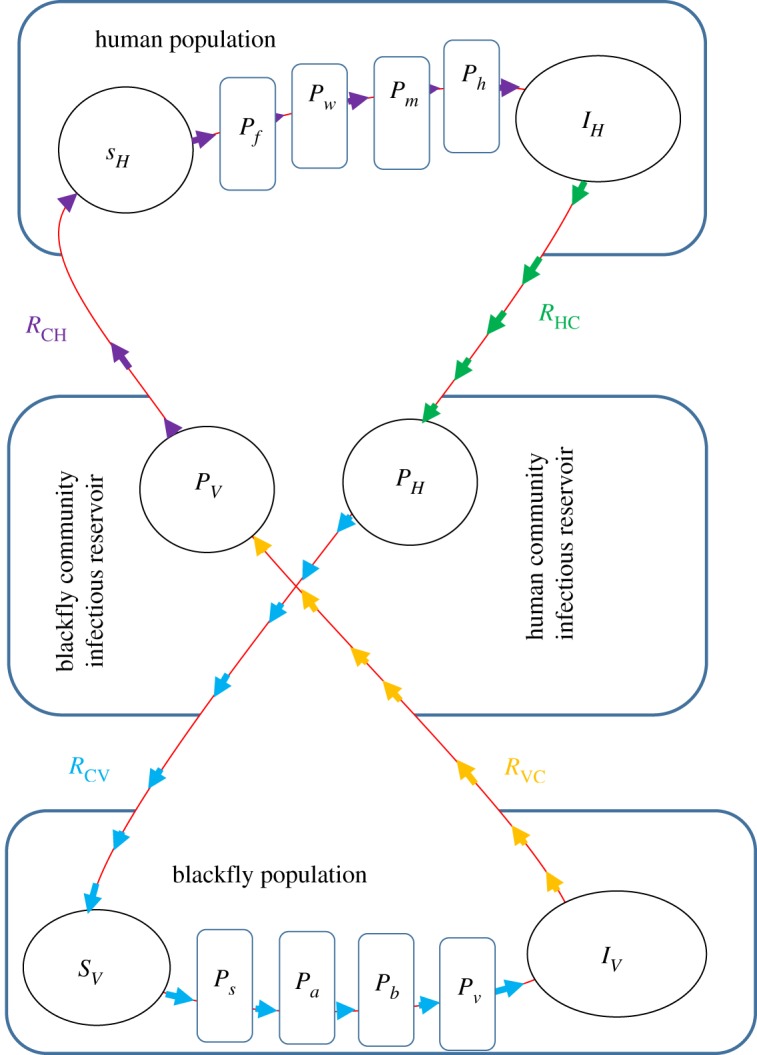
In this section, we present the general method for multiscale modelling of type II vector-borne diseases in which there is no pathogen replication cycle at both the within-vertebrate host scale and the within-vector host scale. The general multiscale model of such type II vector-borne diseases is shown in a flow diagram in figure 1. Details of the mathematical derivation of this multiscale model are given in appendix A. We introduce the general multiscale model first so that those who want to develop their own multiscale model of a type II vector-borne disease system know where to start. In the general multiscale model for type II vector-borne diseases shown in figure 1, infection of the vertebrate host usually begins with a bite of vertebrate host by an infected vector host to draw a blood meal. In the course of obtaining a blood meal, the pathogen in the vector host enters the vertebrate host and constitutes the pathogen population in the first life stage at within-vertebrate host scale denoted by X₀ = P_f in figure 1 and may increase through super-infection at a rate λ_vs_h, or die naturally in vertebrate host at rate μ₀ = μ_f or proceed to the first intermediate life stage at rate α₀ = α_f which is assumed to have a pathogen population X₁. The pathogen will then typically develop through multiple intermediate life stages denoted i = 1, 2, 3, …, n − 1 within the vertebrate host with pathogen populations denoted X₁, X₂, …, X_n−1 in each of the life stages as shown in figure 1. During these intermediate life stages, the pathogen is assumed to transition from one life stage to the next at rates f_i(X_i−1, α_i−1) or die naturally at a rates μ_i, i = 1, 2, 3, …, n − 1 until it reaches the last life stage with pathogen population denoted X_n = P_h which causes infection to the vector hosts. This last life stage is then shed/excreted into the vertebrate host’s specific anatomical compartments such as cells, tissues, organs, body fluids at an assumed rate α_h to constitute the vertebrate host reservoir of infective pathogen in the community or die there naturally at a rate μ_h. Thus, the variables X₀, X₁, X₂, …, X_n constitute the within-vertebrate scale sub-model.

Figure 1.

A conceptual diagram of the general multiscale model of a type II vector-borne disease system. All the terms associated with arrows in this flow diagram are the actual rates of flow and not per capita rates.

At within-vector scale, the first life stage of the pathogen also begins with a bite of an infected vertebrate host by a vector host to draw a blood meal. The pathogen in the infected vertebrate host then enters the vector host and also constitutes the pathogen population in the first life stage at within-vector host scale denoted by Y₀ = P_s in figure 1 and may increase through super-infection at a rate λ_hs_v, or die naturally in the vector host at rate η₀ = η_s or proceed to the first intermediate life stage at rate σ₀ = σ_s, which is assumed to have a pathogen population Y₁. The pathogen will also typically develop through multiple intermediate life stages denoted j = 1, 2, 3, …, m − 1 in the vector host with pathogen populations denoted Y₁, Y₂, …, Y_m−1 in each of the life stages as shown in figure 1. During the intermediate life stages, the pathogen is assumed to transition from one life stage to the next life stage at rates g_j(Y_j−1, σ_j−1) or die naturally at rates η_j, j = 1, 2, 3, …, m − 1 until it reaches the last life stage with pathogen population denoted Y_m = P_v that causes infection to the vertebrate hosts. This last life stage is then shed/excreted into specific anatomical compartments of the vector host such as salivary glands or the head at an assumed rate σ_v to constitute the vector host reservoir of infective pathogen in the community or die there naturally at a rate η_v. Thus, the variables Y₀, Y₁, Y₂, …, Y_m also constitute the within-vector scale sub-model.

The variables for the sub-model that describe the transmission and spread of pathogen at between-host scale from vertebrate host-to-vertebrate host or from vector host-to-vector host consist of two parts. In the multiscale model represented by figure 1, the part that describes the transmission of pathogen from vector host to vertebrate host is an SIP sub-model with variables which are susceptible vertebrate hosts (S_H), infected vertebrate hosts (I_H) and community vector host pathogen load (P_V) so that the transmission of pathogen at between-host scale from community infectious reservoir of vector hosts to vertebrate hosts happens at a rate β_Vλ_V(P_V)S_H. Similarly, the part that describes the transmission of pathogen from vertebrate hosts to vector hosts is also an SIP sub-model with variables which are susceptible vector hosts (S_V), infected vector hosts (I_V) and community vertebrate host pathogen load (P_H) so that the transmission of pathogen at between-host scale from community infectious reservoir of vertebrate hosts to vector hosts happens at a rate β_Hλ_H(P_H)S_V. In these between-host scale variables, the susceptible host populations (S_H and S_V) as well as the infected host populations (I_H and I_V) experience natural death at rates μ_H and μ_V while the infected host populations (I_H and I_V) suffer additional mortality at rates δ_H and δ_V due to infection. Further, since the most sure way to eliminate an infectious disease is to eliminate the infectious agent (since P_H = P_V = 0 would imply that a vector-borne disease is eliminated in a community), then 1/α_H and 1/σ_V are the average times it would take to eliminate the community vertebrate host pathogen load (CHPL) and community vector pathogen load (CVPL), respectively, and render the community non-infectious to the vertebrate hosts and vector hosts. The mathematical details of how these sub-models are integrated to give the general multiscale model of type II vector-borne diseases are given in appendix A. The general multiscale model represented schematically in figure 1 and mathematically in appendix A contains the main components of the dynamics of vector-borne disease which include: (i) pathogen dynamics at within-vertebrate host scale; (ii) vector-borne disease dynamics in the vector host population at between-host scale, (iii) pathogen dynamics at within-vector host scale, and (iv) vector-borne disease dynamics in the vertebrate host population at between-host scale. However, the general multiscale model (A 2) offers many opportunities for stronger links between biologists/epidemiologists and mathematical modelers for improvements and extensions when applied to specific type II vector-borne diseases. Some of the extensions and improvements that can be realized through such collaborations include incorporating the following: (i) the effects of immune response, (ii) the effects of health interventions, (iii) the effects of environmental change, (iv) the effects of life cycle of the vector host, and (v) the age structure of the vertebrate host population.

3. Application of the general multiscale model to human orchocerciasis as a paradigm

In this section, we apply the general multiscale model given schematically in figure 1 and represented mathematically by multiscale model (A 2) in appendix A for type II vector-borne diseases to human onchocerciasis as a case study. This vector-borne disease is caused by Onchocerca volvulus parasite and humans are the only vertebrate host, while the vector host are the blackflies of the genus Simulium. Human onchocerciasis is a type II vector-borne disease in which the Onchocerca volvulus parasite does not have a replication cycle in both the human host and the blackfly vector. This multi-host infectious disease causes visual impairment, blindness, skin disease and excess mortality in humans [11]. To adapt the general multiscale model (A 2) in appendix A to human onchocerciasis, the sub-models at between-host scale (for both the human host and vector host) are developed based on compartmentalizing the host population into susceptible, infected, together with the extra variable describing CPL (SIP). Since there is no pathogen replication cycle at within-host scale (for both the human host and blackfly vector host), the within-host sub-models for human onchocerciasis can be established by representing the transitions of pathogen populations from one life stage to another using linear transition functions specified in the general multiscale model (A 2) in the form f_i(X_i−1, α_i−1) = α_i−1X_i−1 for i = 1, 2, …, n and g_j(Y_j−1, σ_j−1) = σ_j−1Y_j−1 for j = 1, 2, …, m. Further, from the general multiscale model (A 2) in appendix A, we choose λ_H(P_H) = (β_HP_H(t))/(H₀ + P_H(t)) and λ_V(P_V) = (β_V P_V(t))/(V₀ + P_V(t)) from the infectivity response functions (A 3) and (A 4) specified for the general multiscale model (A 2) in appendix A. Then the super-infection that introduces the population of first life stage of Onchocerca volvulus parasite at the within-blackfly vector scale (denoted Y₀ = P_s) is modelled by

$$\begin{array}{rl}{\lambda }_h(t)s_v(t)& =\frac{{\beta }_H{\lambda }_H(P_H)[S_V(t)-1]}{{\mathit{\Phi }}_{\mathit{V}}\mathit{[}{\mathit{I}}_{\mathit{V}}\mathit{(}\mathit{t}\mathit{)}\mathit{+}\mathit{1}\mathit{]}}\\ & =\frac{{\beta }_H{P}_H(t)[S_V(t)-1]}{[H_0+P_H(t)]{\mathit{\Phi }}_{\mathit{V}}[{\mathit{I}}_{\mathit{V}}\mathit{(}\mathit{t}\mathit{)}\mathit{+}\mathit{1}]}.\end{array}$$ 3.1

Therefore, this expression links the between-host scale to the within-blackfly vector host scale. Similarly, the super-infection that introduces the population of first life stage of Onchocerca volvulus parasite at the within-human host scale (denoted X₀ = P_f) is modelled by

$$\begin{array}{rl}{\lambda }_v(t)s_h(t)& =\frac{{\beta }_V{\lambda }_V(P_V)[S_H(t)-1]}{{\mathit{\Phi }}_{\mathit{H}}\mathit{[}{\mathit{I}}_{\mathit{H}}\mathit{(}\mathit{t}\mathit{)}\mathit{+}\mathit{1}\mathit{]}}\\ & =\frac{{\beta }_V{P}_V(t)[S_H(t)-1]}{[V_0+P_V(t)]{\mathit{\Phi }}_{\mathit{H}}[{\mathit{I}}_{\mathit{H}}\mathit{(}\mathit{t}\mathit{)}\mathit{+}\mathit{1}]}.\end{array}$$ 3.2

This expression also links the between-host scale to the within-human host scale. Taking into account all these specifications based on the general multiscale model (A 2) in appendix A, the multiscale model for human onchocerciasis becomes

$$\begin{array}{rl}& \hspace{0.17em}1.\hspace{0.17em}\frac{\mathrm{d}{S}_H(t)}{\mathrm{d}t}={\mathit{\Lambda }}_{\mathit{H}}\mathit{-}\frac{{\beta }_{\mathit{V}}{\mathit{P}}_{\mathit{V}}\mathit{(}\mathit{t}\mathit{)}{\mathit{S}}_{\mathit{H}}\mathit{(}\mathit{t}\mathit{)}}{{\mathit{V}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{V}}\mathit{(}\mathit{t}\mathit{)}}\mathit{-}{\mu }_{\mathit{H}}{\mathit{S}}_{\mathit{H}}\mathit{(}\mathit{t}\mathit{)}\mathit{,}\\ & \hspace{0.17em}2.\hspace{0.17em}\frac{\mathrm{d}{I}_H(t)}{\mathrm{d}t}=\frac{{\beta }_V{P}_V(t)S_H(t)}{V_0+P_V(t)}-({\mu }_H+{\delta }_H)I_H(t),\\ & \hspace{0.17em}3.\hspace{0.17em}\frac{\mathrm{d}{P}_{\hspace{0.17em}f}(t)}{\mathrm{d}t}=\frac{{\beta }_V{P}_V(t)[S_H(t)-1]}{[V_0+P_V(t)]{\mathit{\Phi }}_{\mathit{H}}[{\mathit{I}}_{\mathit{H}}\mathit{(}\mathit{t}\mathit{)}\mathit{+}\mathit{1}]}-({\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f})P_{\hspace{0.17em}f}(t),\\ & \hspace{0.17em}4.\hspace{0.17em}\frac{\mathrm{d}{P}_w(t)}{\mathrm{d}t}={\alpha }_{\hspace{0.17em}f}{P}_{\hspace{0.17em}f}(t)-({\alpha }_w+{\mu }_w)P_w(t),\\ & \hspace{0.17em}5.\hspace{0.17em}\frac{\mathrm{d}{P}_m(t)}{\mathrm{d}t}={\varphi }_w{\alpha }_w{P}_w(t)-{\mu }_m{P}_m(t),\\ & \hspace{0.17em}6.\hspace{0.17em}\frac{\mathrm{d}{P}_h(t)}{\mathrm{d}t}=N_m{\alpha }_m{P}_m(t)-({\alpha }_h+{\mu }_h)P_h(t),\\ & \hspace{0.17em}7.\hspace{0.17em}\frac{\mathrm{d}{P}_H(t)}{\mathrm{d}t}=(I_H+1){\alpha }_h{P}_h(t)-{\alpha }_H{P}_H(t),\\ & \hspace{0.17em}8.\hspace{0.17em}\frac{\mathrm{d}{S}_V(t)}{\mathrm{d}t}={\mathrm{\Lambda }}_V-\frac{{\beta }_H{P}_H(t)S_V(t)}{H_0+P_H(t)}-{\mu }_V{S}_V(t),\\ & \hspace{0.17em}9.\hspace{0.17em}\frac{\mathrm{d}{I}_V(t)}{\mathrm{d}t}=\frac{{\beta }_H{P}_H(t)S_V(t)}{H_0+P_H(t)}-({\mu }_V+{\delta }_V)I_V(t),\\ & \hspace{0.17em}10.\hspace{0.17em}\frac{\mathrm{d}{P}_s(t)}{\mathrm{d}t}=\frac{{\beta }_H{P}_H(t)[S_V(t)-1]}{[H_0+P_H(t)]{\mathit{\Phi }}_{\mathit{V}}[{\mathit{I}}_{\mathit{V}}\mathit{(}\mathit{t}\mathit{)}\mathit{+}\mathit{1}]}-({\eta }_s+{\sigma }_s)P_s(t),\\ & \hspace{0.17em}11.\hspace{0.17em}\frac{\mathrm{d}{P}_a(t)}{\mathrm{d}t}={\sigma }_s{P}_s(t)-({\eta }_a+{\sigma }_a)P_a(t),\\ & \hspace{0.17em}12.\hspace{0.17em}\frac{\mathrm{d}{P}_b(t)}{\mathrm{d}t}={\sigma }_a{P}_a(t)-({\eta }_b+{\sigma }_b)P_b(t),\\ & \hspace{0.17em}13.\hspace{0.17em}\frac{\mathrm{d}{P}_v(t)}{\mathrm{d}t}={\sigma }_b{P}_b(t)-({\eta }_v+{\sigma }_v)P_v(t),\\ & \hspace{0.17em}14.\hspace{0.17em}\frac{\mathrm{d}{P}_V(t)}{\mathrm{d}t}=(I_V+1){\sigma }_v{P}_v(t)-{\sigma }_V{P}_V(t).\end{array}\}$$ 3.3

The multiscale model (3.3) for human onchocerciasis was established from the general multiscale model (A 2) in appendix A by incorporating details of the Onchocerca volvulus parasite life cycle which can roughly be demarcated into two major life stages as follows:

• (a)The human host life stage: at the within-human scale, Onchocerca volvulus parasite has four main life stages. These life stages are represented in the multiscale model (3.3) in terms of rates of change of the parasite population in each life stage which are as follows. (i) X₀ = P_f, which is the parasite population in the first life stage at within-human scale. This consists of L₃ larvae introduced by an infected blackfly during a blood-meal at rate λ_vs_h and experiences natural death at rate μ₀ = μ_f. (ii) X₁ = P_w, which is the parasite population in the first intermediate life stage at within-human scale. This consists of immature worms which have developed from the L₃ larvae at an assumed rate of α₀ = α_f and can die naturally at an assumed rate of μ₁ = μ_w. (iii) X₂ = P_m, which is the parasite population in the second intermediate life stage at within-human scale. This consists of mature female worms (which are a proportion ϕ_w of the total population of mature worms) which have developed from immature worms at an assumed rate of α₁ = α_w and also experience natural death at rate μ₂ = μ_m. (iv) X₃ = P_h, which is the parasite population in the final life stage at within-human scale. This parasite population consists of microfilariae produced by mature female worms at a rate α₂ = α_m. This last life stage of the Onchocerca volvulus parasite is infectious to blackfly vector. The microfilariae are then shed/excreted into the dermis layer of the skin and eyes at a rate α₃ = α_h where they constitute the infectious reservoir of humans in the community at within-human host scale (waiting to begin a second life stage in the blackfly vector host) or die naturally in the dermis layer of the skin and eyes at a rate μ₃ = μ_h.
• (b)The blackfly vector host life stage: at the within-blackfly vector scale, Onchocerca volvulus parasite also has four main life stages. These life stages are represented in the multiscale model (3.3) in terms of rates of change of the parasite population in each life stage as follows. (i) Y₀ = P_s, which is the parasite population in the first life stage at within-blackfly vector scale. This consists of microfilariae ingested by a blackfly at rate λ_hs_v during a bloodmeal from an infected human host. These microfilariae experience natural death at rate η₀ = η_s at within-blackfly vector scale. (ii) Y₁ = P_a, which is the parasite population in the first intermediate life stage at within-blackfly vector scale. This consists of L₁ larvae which have developed from the microfilariae at an assumed rate of σ₀ = σ_s. These L₁ larvae also experience natural death at rate η₁ = η_a at within-blackfly vector scale. (iii) Y₂ = P_b, which is the parasite population in the second intermediate life stage at within-blackfly vector scale and experiences natural death at an assumed rate of η₂ = η_b. This consists of L₂ larvae which have developed from L₁ larvae at an assumed rate of σ₁ = σ_a. (iv) Y₃ = P_v, which is the parasite population in the final life stage at within-blackfly vector scale. This parasite population consists of L₃ larvae which have developed from L₂ larvae at an assumed rate of σ₂ = σ_b. The L₃ larvae are then shed/excreted into the saliva at rate σ₃ = σ_v of the blackfly’s proboscis where they constitute the infectious reservoir of blackfly vector at within-blackfly vector scale (waiting to begin a second life stage in the human host) or die naturally in the saliva at rate η₃ = η_v.

In the multiscale model (3.3) for human onchocerciasis, we interpret the quantities 1/H₀ and 1/V₀ as measures of a specific geographical area/community/country’s susceptibility to human onchocerciasis. We assume that every geographical area/community/country’s human onchorececiasis dynamics is characterized by a different set of susceptibility coefficients 1/H₀ and 1/V₀ to human onchocerciasis infection which is intrinsic to that community and that these susceptibility coefficients are dependent on many factors which include: (i) temperature and rainfall, (ii) structure and topography of the rivers, (iii) strength of the health system and (iv) vegetation in and around river beds. Together, these characteristics will lead to particular human onchocerciasis susceptibility coefficients 1/H₀ and 1/V₀, which determine the human onchocerciasis baseline burden (the level of human onchocerciasis burden that would exist in a given geographical area/community/country if no interventions are implemented to control it). These two quantities (1/H₀ and 1/V₀) indicate the extent to which conditions are favourable for human onchocerciasis disease transmission in a specific geographical area. Because of the dependence of super-infection in the multiscale model (3.3) on two sets of parameters which are contact rates (β_V and β_H) with community pathogen load and the susceptibility coefficients (1/H₀ and 1/V₀), the multiscale model for human onchocerciasis (3.3) can be used to formalize and test the assumptions that underlie the observed age distribution of pathogen loads in human onchocerciasis [11], by extending the multiscale model (3.3) into an age-structured multiscale model in which contact rates (β_V, β_H) and the susceptibility coefficients (1/H₀ and 1/V₀) are different for each age group to identify mechanisms that produce observed distribution of pathogen burden in infected hosts. Table 1 in appendix B gives a summary of the variables of the multiscale model (3.3). A summary of the description of the parameters in multiscale model (3.3) is given in table 2 in appendix B. The mathematical analysis of the multiscale model (3.3) is given in appendix C. In what follows we present results of the numerical study of the multiscale model (3.3).

Table 1.

A summary of the variables of the human onchocerciasis multiscale model given by (3.3).

no.	variable	description
1	SH(t)	population of susceptible human hosts at time t
2	IH(t)	population of infected human hosts at time t
3	Pf(t)	mean population of L3 larvae per infected human host at time t
4	Pw(t)	mean population of immature worms per infected human host at time t
5	Pm(t)	mean population of mature worms per infected human host at time t
6	Ph(t)	mean population of microfilariae per infected human host at time t
7	PH(t)	community microfilariae pathogen load (CMPL) at time t
8	SV(t)	population of susceptible blackfly vector hosts at time t
9	IV(t)	population of infected blackfly vector hosts at time t
10	Ps(t)	mean population of microfilariae per infected blackfly vector at time t
11	Pa(t)	mean population of L1 larvae per infected blackfly vector at time t
12	Pb(t)	mean population of L2 larvae per infected blackfly vector at time t
13	Pv(t)	mean population of L3 larvae per infected blackfly vector at time t
14	PV(t)	community L3 larvae pathogen load (CLPL) at time t

Table 2.

Description of parameters.

no.	parameter	description of parameter
1	ΛH	supply rate of susceptible humans through birth
2	βH	contact rate of susceptible blackfly vector with infectious reservoir of humans
3	μH	natural death rate of humans
4	δH	disease-induced death rate of humans
5	αH	rate of human community microfilariae load elimination
6	H0	half saturation constant associated with infection of blackfly
7	ΦH	proportion of new infected humans in the total infected human population
8	ΛV	supply rate of susceptible blackfly vector through birth
9	βV	contact rate of susceptible humans with infectious reservoir of blackfly vector
10	μV	natural death rate of blackfly vector
11	δV	infection-induced death rate of blackfly vector
12	αV	rate of blackfly community microfilariae load elimination
13	V0	half saturation constant associated with infection of humans
14	ΦV	proportion of new infected blackfly vector in the total infected blackfly vector population
15	αf	average progression rate from L3 larvae to immature worm in the human host
16	μf	natural death rate of L3 in the human host
17	αw	average progression rate from immature worm to mature worm in the human host
18	μw	natural death rate of immature worm in the human host
19	αm	rate at which female worms become fertilized in the human host
20	μm	natural death rate of worm to mature female worm in the human host
21	αh	rate at which microfilariae are shed/excreted into the human host’s dermis layer of the skin and eyes
22	μh	natural death rate of microfilariae in the human host’s skin and eyes
23	σs	average progression rate from microfilariae to L1 larvae in the thoracic flight muscle of the blackfly vector
24	ηs	natural death rate of microfilariae in gut of the blackfly vector
25	σa	average progression rate from L1 larvae to L2 larvae and migration to the proboscis of the blackfly vector in the saliva
26	ηa	natural death rate of L1 in the thoracic flight muscle of the blackfly vector
27	σb	average progression rate from L2 larvae to L3 larvae in the blackfly vector
28	ηb	natural death rate of L2 in the blackfly’s proboscis
29	σv	rate at which L3 are shed/excreted into saliva of blackfly’s proboscis
30	ηv	natural death rate of infectious stage L3 larvae in the blackfly’s proboscis
31	Nm	number of microfilariae produced per female worm
32	ϕw	proportion of female worms among the total adult population of worms

4. Numerical study of the multiscale model

In the previous section, we presented the multiscale model (3.3) of human onchoceriasis as an example application of the general multiscale model (A 2) in appendix A of vector-borne diseases. However, not all modelling is without limitations. The biological mechanisms involved in the multiscale model (3.3) for human onchoceriasis have many inherent complexities. To begin with, most of the parameters are usually best measured only approximately. Secondly, there normally exists substantial variation in these parameters depending on geographical region, demographic factors and several other factors. Also, some of the parameters may essentially be stochastic. As a consequence of such complexities, the multiscale model (3.3) is inherent of epistemic uncertainty which derives from lack of knowledge about the value of parameters that are assumed to be constant throughout the model analysis [12]. We therefore need to investigate the uncertainty in the model output generated from uncertainty in unknown parameter inputs whose values are approximated so that reasonable qualitative features of the expected output trajectories are simulated. An interval is created with minimum and maximum values so that the chosen parameter value is within the interval. Interval analysis using the uniform distribution is used to assess how the variations of each of the parameters, after discounting the effects of the rest of the parameters, can be apportioned to the variation in the model output. To get insight on how some of the estimated parameters affect the output of the model and for reasonable inference of model simulations, we use the Latin hypercube sampling technique which is one technique that is used to detect such epistemic uncertainties. It is a reliable and efficient technique which allows an unbiased estimate of the average model output and requires fewer samples than simple random sampling to achieve the same accuracy. The technique is combined with the partial rank correlation coefficients (PRCCs) which measure the strength of the relationship between each input variable and each output variable [13]. The qualitative predictive results from variations of these parameters are generic in nature and the baseline values used in simulations are representative of the overall effects of the parameters within the specified ranges. Since these parameters are unknown, one way of determining their values is through the use of data, and different datasets may generate different parameter values but the qualitative effects of these parameters remain the same if the parameters fall in the intervals suggested in this study.

The numerical values of the parameters used in the numerical simulations are given in table 3 in appendix B. The multiscale model (3.3) for human onchocerciasis is categorized as a CMSM [2,4]. An important feature of CMSMs is that they use other categories of multiscale as sub-models. These categories of multiscale models which are used as sub-models are [2,4]: (i) IMSMs, (ii) NMSMs, (iii) EMSMs and (iv) HMSMs. In the case of the CMSM (3.3), EMSMs are used as sub-models. A key feature of EMSMs developed at host level is that the within-host scale and the between-host influence each other in a reciprocal way (i.e. both ways) continuously throughout the period when infected hosts are infectious [4]. In this section, we use numerical simulations to illustrate and verify this structure of the coupled multiscale model (3.3) and indicate the implications for control and elimination of human onchocerciasis. Of critical importance to this verification is (a) to investigate the influence of the within-host scale on between-host scale human onchocerciasis disease and (b) the influence of the between-host scale on the within host scale. We include scenarios which usually emanate from the standard decoupled within-vector host scale dynamics, within-human host scale dynamics and between-host scale dynamics, the fundamental difference being that these scenarios are extracted from the full coupled multiscale model.

Table 3.

Parameter values used in the multiscale model.

no.	parameter	value [range explored]	units	source/rationale
1	ΛH	0.165 [0.083–0.2475]	d−1	[19]
2	βH	0.114 [0.057–0.171]	d−1	[19]
3	μH	0.000055 [0.000046–0.000068]	d−1	[11]
4	δH	0.00001 [5 × 10−6–1.5 × 10−5]	d−1	s.a
5	αH	0.0000546 [2.73 × 10−5–8.19 × 10−5]	d−1	s.a
6	H0	30000.00 [1000.00–50000.00]	d−1	s.a
7	ΦH	0.0001 [5 × 10−5–1.5 × 10−4]	d−1	s.a
8	ΛV	712.33 [356.1650–1.0685 × 103]	d−1	[19]
9	βV	0.00111 [0.000555–0.0017]	d−1	[19]
10	μV	0.071233 [0.032877–0.142466]	d−1	[11]
11	δV	0.001068 [0.000685–0.001644]	d−1	[11]
12	σV	0.10000 [0.050000–0.150000]	d−1	s.a
13	V0	5000.00 [2500.00–7500.00]	d−1	s.a
14	ΦV	0.0001 [0.00005–0.00015]	d−1	s.a
15	αf	0.0001 [0.00005–0.00015]	d−1	s.a
16	μf	0.00027 [1 × 10−4–3 × 10−4]	d−1	[20]
17	αw	0.0003 [5 × 10−5–1.5 × 10−4]	d−1	s.a
18	μw	0.0002 [1 × 10−4–3 × 10−4]	d−1	s.a
19	αm	0.001836 [9.18 × 10−4–0.0028]	d−1	s.a
20	μm	0.000274 [0.000249–0.000304]	d−1	[21]
21	αh	0.000546 [0.000384–0.002740]	d−1	[11]
22	μh	0.002192 [0.001370–0.008219]	d−1	[11]
23	σs	0.0105 [0.0060–0.0150]	d−1	s.a
24	ηs	0.0012 [0.0006–0.0018]	d−1	s.a
25	σa	0.200411 [0183178–0.213041]	d−1	[22]
26	ηa	0.200411 [0.183178–0.213041]	d−1	s.a
27	σb	0.365595 [0.333534–0.403863]	d−1	[22]
28	ηb	0.010000 [0.005–0.0150]	d−1	s.a
29	σv	0.10000 [0.05–0.15]	d−1	s.a
30	ηv	0.142466 [0.071233–0.284932]	d−1	[11]
31	Nm	100 [1−1000]	worm−1 d−1	s.a
32	ϕw	0.5 [0.1−0.9]	d−1	[23]

^s.aRange of values adapted from sensitivity analysis using the Latin hypercube sampling technique.

4.1. The influence of within-host scale on between-host scale human onchoceriasis dynamics

In this section, we investigate the influence of the average progression rates σ_s, σ_v, α_f and α_h at within-blackfly vector scale and within-human host scale on the (i) between-host scale variables (P_H, P_V, I_H, I_V), (ii) within-human scale variables (P_f, P_h) and (iii) within-vector scale variables (P_s, P_v).

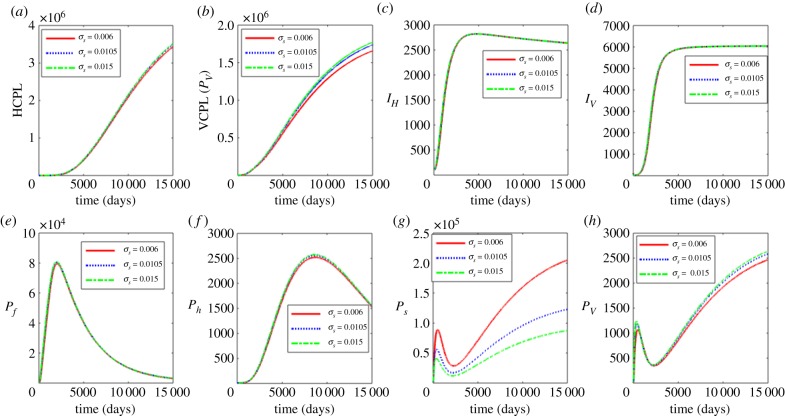
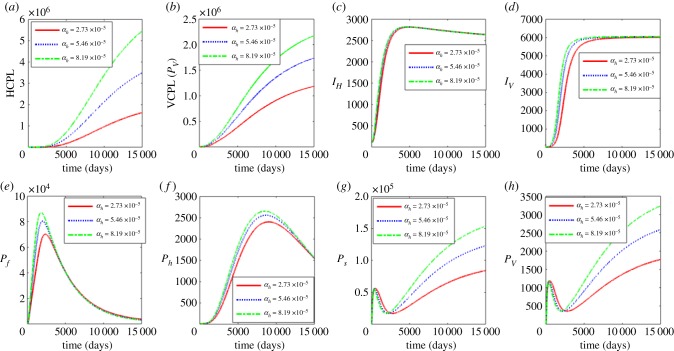
Figure 2 shows the influence of the average progression rate from microfilariae to L₁ larvae with σ_s = 0.006, 0.0105 and 0.015. Figure 2a–d shows the effects of the variation of σ_s on the between-host scale variables (P_H, P_V, I_H, I_V), while figure 2e–h shows the effects of variation of σ_s on within-human host scale variables (P_f, P_h) and within-vector host scale variables (P_s, P_v). The results in figure 2 show that an increase in σ_s results in very minimal increases in vector community pathogen load P_V as well as the microfilariae load P_s. Currently, there is no intervention that we know of that targets this life stage. However, these results suggest that control strategies that target the first life stages of the pathogen at within-vector scale will have minimal benefits in reducing parasite load at within-host scale and human onchocerciasis burden at vector pathogen community scale.

Figure 2.

Influence of average progression rate from microfilariae to L₁ larvae (σ_s) on the between-host scale variables (P_H, P_V, I_H, I_V), within-human host scale variables (P_f, P_h) and within-vector host scale variables (P_s, P_v). (Online version in colour.)

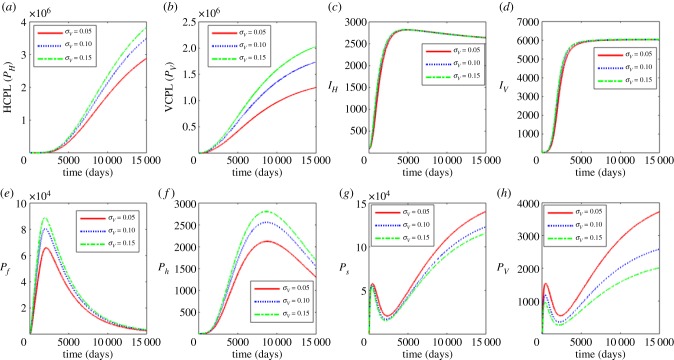
In figure 3, we show the results of investigating the influence of the average excretion/shedding rate (σ_v) of L₃ larvae into the saliva of the blackfly’s proboscis where σ_v = 0.05, 0.1 and 0.15. Figure 3a–d shows the effects of variation of σ_v on the between-host scale variables (P_H, P_V, I_H, I_V) and figure 3e–h shows the effects of the variation of σ_v on within-human host scale variables (P_f, P_h) as well as within-vector host scale variables (P_s, P_v). The results show that an increase in σ_v is associated with the increase in the between-host scale variables (P_H, P_V), the within-human host microfiliariae population P_h and the mean population of L₃ larvae per infected human host P_f. The within-vector populations (P_s, P_v) decrease with the increase in σ_v. These results indicate that use of interventions that hinder growth and development of the Onchocerca volvulus parasite at within-blackfly scale will reduce parasite load at within-host scale and human onchoceriasis burden in the community. However, care should be taken when using such strategies as they may have a positive effect of possibly increasing the within vector parasite load.

Figure 3.

Influence of average progression rate from microfilariae to L₃ larvae to infectious stage (σ_v) on the between-host scale variables (P_H, P_V, I_H, I_V), within-human host scale variables (P_f, P_h) and within-vector host scale variables (P_s, P_v). (Online version in colour.)

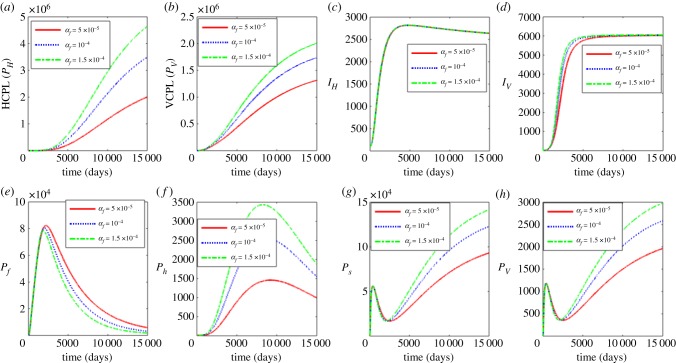
Figure 4 shows the effects of increasing the average progression rate from L₃ larvae to immature worm at within-human host scale for parameter values α_f = 0.00005, 0.00001 and 0.000015. Figure 4a–d shows the effects of the variation of α_f on the between-host scale variables (P_H, P_V, I_H, I_V) and figure 4e–h shows the effects of variation of α_f on within-human host scale variables (P_f, P_h) as well as within-vector host scale variables (P_s, P_v). The results show that the between-host scale variables (P_H, P_V, I_V) as well as the within-human scale parasite load (P_h) and within-vector scale parasite loads (P_s, P_v) increase with the increase in α_f while the within human stage P_f decreases. We deduce from these results that vaccines which induce protective immunity against incoming L₃ larvae have potential individual and community scale level benefits in controlling human onchoceriasis.

Figure 4.

Influence of average progression rate from L₃ larvae to infectious stage (α_f) on the between-host scale variables (P_H, P_V, I_H, I_V), within-human host scale variables (P_f, P_h) and within-vector host scale variables (P_s, P_v). (Online version in colour.)

Figure 5 shows the effects of varying the rate of microfiliariae shedding/excretion into the human host’s dermis layer of the skin and eyes α_h where α_h = 0.0000273, 0.0000546 and 0.0000819. Figure 5a–d shows the effects of variation of α_h on the between host variables (P_H, P_V, I_H, I_V) and figure 5e–h shows the effects of variation of α_h on within human host variables (P_f, P_h) and within vector host variables (P_s, P_v). We observe from figure 5 that the between host variables (P_H, P_V, I_V) increase significantly in response to the increase in the rate of microfiliariae shedding/excretion into the human host’s dermis layer of the skin and eyes. The within human and within vector dynamics show some switching dominance after the population peaks are reached with the within human dynamics dominating before the peaks and the within vector dynamics after. These switches can be associated with the change in correlation of α_h (figure 10) over time. The results suggest control strategies such as the use of ivermectin, a highly effective microfilaricide that inhibits the female worm microfilarial production, may have individual level benefits such as prevention of visual impairment, blindness, skin disease and excess mortality to infected individuals and community level benefits due to reduced burden of the disease in the population.

Figure 5.

Influence of rate of microfilariae migration to the human host’s skin and eyes (α_h) on the between-host scale variables (P_H, P_V, I_H, I_V), within-human host scale variables (P_f, P_h) and within-vector host scale variables (P_s, P_v). (Online version in colour.)

Figure 10.

(a–d) The measure contribution of between host parameters (β_V, β_H, H₀, V₀) on within host dynamics (P_f, P_h) and within vector (P_s, P_v). (e–h) The measure of contribution of within host parameters (σ_s, σ_v, α_f, α_v) on between host dynamics (P_H, P_V, I_H, I_V). The ranges of values used are as indicated in table 3 in appendix B. The PRCCs of each parameter are tracked over time. (Online version in colour.)

4.2. The influence of between-host scale on within-host scale human onchocerciasis dynamics

In this section, we investigate the influence of the between-host scale parameters β_V, V₀, H₀ and β_H on (i) the within-host scale variables (P_s, P_v, P_f, P_h), (ii) between-human host scale variables (P_H, I_H) and (iii) between-vector host scale variables (P_V, I_V). Figures 6–9a–d show the effects of variation of each of the between-host scale parameters β_V, β_H, H₀ and V₀ on the between host variables (P_H, P_V, I_H, I_V) and figures 6–9e–h show the effects of variation of each of the between-host scale parameters β_V, β_H, H₀ and V₀ on within-human host scale variables (P_f, P_h) as well as within-vector host scale variables (P_s, P_v).

Figure 6.

Influence of contact rate of susceptible humans with infectious reservoir of blackfly vector (β_V) on the between-host scale variables (P_H, P_V, I_H, I_V), within-human host scale variables (P_f, P_h) and within-vector host scale variables (P_s, P_v). (Online version in colour.)

Figure 9.

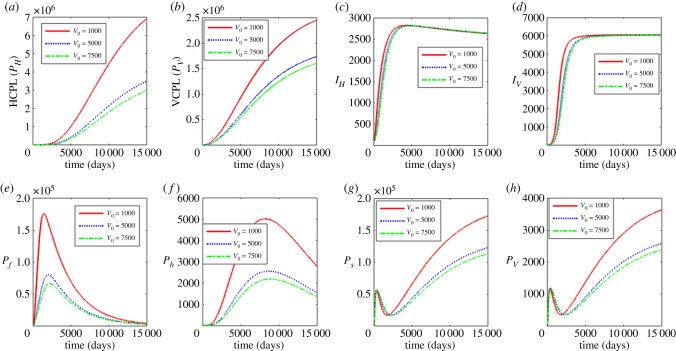
Influence of half saturation constant associated with infection of humans (V₀) on the between-host scale variables (P_H, P_V, I_H, I_V), within-human host scale variables (P_f, P_h) and within-vector host scale variables (P_s, P_v). (Online version in colour.)

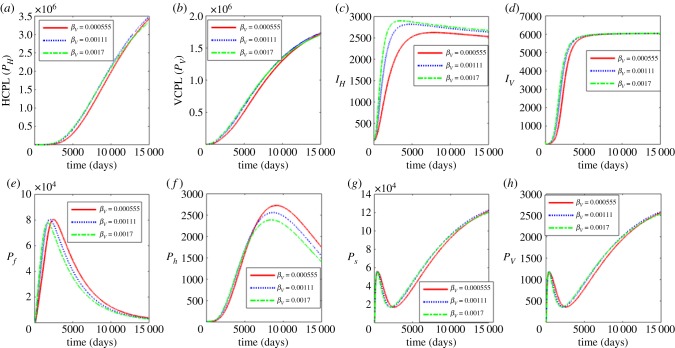
Figure 6 shows the effects of the contact rate of susceptible humans with infectious reservoir of blackflies β_V. The values used for the parameter β_V are β_V = 0.00055, 0.00111 and 0.0017. The results in figure 6 show that an increase in β_V increases the between-host scale variable (I_H). On the rest of between-host dynamics, the increase in β_V ultimately leads to the reduction of their populations. A similar trend is observed on the within human dynamics and within vector dynamics with significant decreases observed in the within human dynamics. Therefore, behavioural interventions such as reducing outdoor activities during peak periods of blackfly activity and applying insect repellent containing DEET, wearing protective clothing and minimizing openings such as buttonholes through which blackflies crawl in an attempt to feed and wearing of fine-mesh head nets, similar to those worn by beekeepers would benefit both individuals and the community.

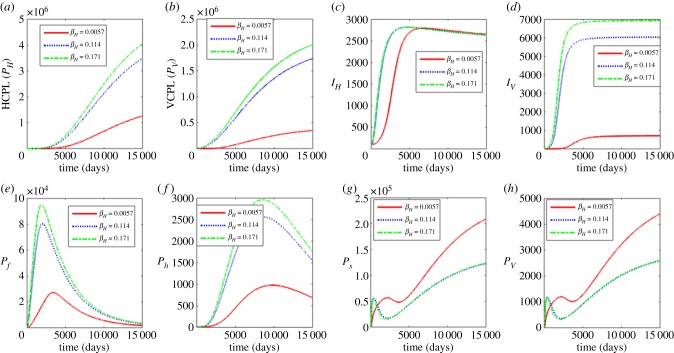
The results in figure 7 show the influence of the variation of the contact rate of susceptible blackfly vector with infectious reservoir of humans β_H. The values used in this variation are β_H = 0.0057, 0.114 and 0.171. The results show that as β_H increases, there is also a noticeable increase in the between-host scale variables (P_H, P_V, I_H, I_V), and the within-human variables (P_f, P_h). The increase of β_H leads to the decrease in within vector dynamics (P_s, P_v). This implies that interventions that include reducing outdoor activities during peak periods of blackfly activity, applying insect repellent containing DEET, wearing protective clothing, minimizing openings such as buttonholes through which blackflies crawl in an attempt to feed and wearing of fine-mesh head nets, similar to those worn by beekeepers would benefit both individuals and the community.

Figure 7.

Influence contact rate of susceptible black fly vector with infectious reservoir of humans (β_H) on the between-host scale variables (P_H, P_V, I_H, I_V), within-human host scale variables (P_f, P_h) and within-vector host scale variables (P_s, P_v). (Online version in colour.)

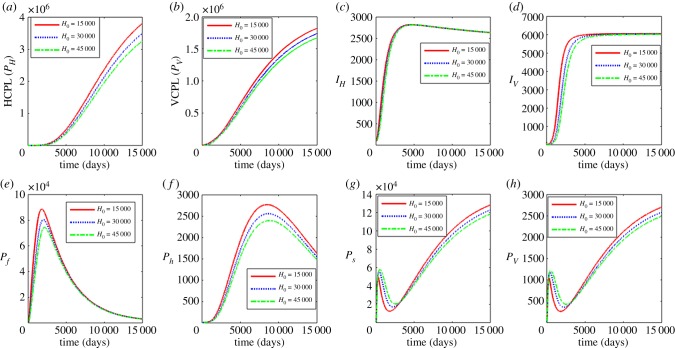
In figure 8, we show the effects of increasing the half saturation constant associated with infection of blackflies H₀ using the values H₀ = 15000, 30 000 and 45 000. The results show that an increase in H₀ results in a significant decline of the between host variables (P_H, P_V, I_V) and the within human variables (P_f, P_h) while the within vector variables initially increase but ultimately decrease over time. As stated earlier, the parameter H₀ is associated with a measure of susceptibility of a community’s human onchocerciasis burden through a susceptibility coefficient 1/H₀. The increase in H₀ corresponds to the reduction in susceptibility coefficient while the reduction in H₀ corresponds to the increase in susceptibility coefficient. Thus, the results in figure 8 suggest interventions that reduce susceptibility of blackfly vectors to infectious reservoir of humans (P_H) reduce the burden of human onchocerciasis at community level and reduce parasite load at within-host scale for both human host and blackfly.

Figure 8.

Influence of half saturation constant associated with infection of black flies (H₀) on the between-host scale variables (P_H, P_V, I_H, I_V), within-human host scale variables (P_f, P_h) and within-vector host scale variables (P_s, P_v). (Online version in colour.)

In figure 9, we show the effects of the variation of the half saturation constant associated with infection of humans V₀ with V₀ = 1000, 5000 and 7500. Increasing V₀ is associated with the decrease in the between host variables (P_H, P_V) and the within human variables (P_f, P_h) while the within vector variables (P_s, P_v) also decrease over time. As in the case of H₀, the measure of susceptibility of the blackflies is through a susceptibility coefficient 1/V₀. The increase in V₀ corresponds to the reduction in susceptibility coefficient while the reduction in V₀ corresponds to the increase in susceptibility coefficient. Similarly, the results in figure 9 suggest interventions that reduce susceptibility of humans to infectious reservoir of blackflies (P_V) such as vaccines reduce the burden of human onchocerciasis at community level and reduce parasite load at within-host scale for both human host and blackfly.

4.3. Sensitivity analysis

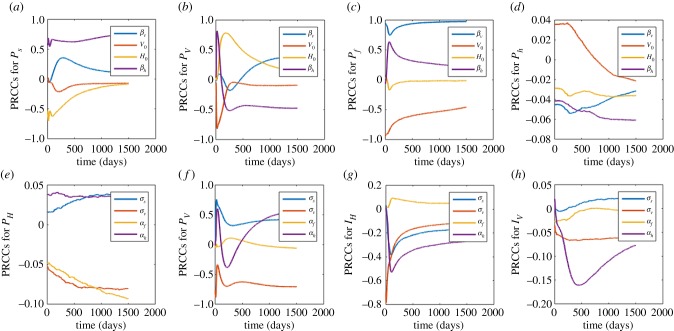
In this section, figure 10a–d is used to investigate the contribution of the between host parameters (β_V, β_H, H₀, V₀) on within host dynamics and figure 10e–h the within host parameters (σ_s, σ_v, α_f, α_v) on between host dynamics. The ranges of values used are as indicated in table 3 in appendix B. The PRCCs of each parameter are tracked over time.

Figure 10a shows that β_H and β_V are positively correlated to P_s while H₀ and V₀ are negatively correlated. Over time, the correlation of β_V, H₀ and V₀ changes towards zero correlation. Positive correlation of β_H and β_V on P_s indicates that if we increase the parameters, the variable P_s increases (and vice versa). The negative correlation of H₀ and V₀ to P_s indicates that if we increase the parameter, the variable P_s decreases (and vice versa). The change in correlation of V₀ and H₀ from negative correlation towards zero correlation suggests that the parameters were initially responsible for lowering P_s then over time the parameters lose that effect on P_s. A change in correlation of β_V from positive towards zero correlation indicates that the parameter was initially responsible for increasing P_s and over time the parameter loses these effects on P_s. A similar interpretation holds for figure 10b–h.

In figure 10b, the parameters β_H and H₀ are initially positively correlated to P_v with β_H changing its correlation to negative correlation over time and H₀ changing its correlation towards zero. The parameters β_V and V₀ are initially negatively correlated to P_v with β_V changing to positive correlation and V₀ changing to zero correlation over time. The change of correlation of β_H from positive to negative indicates that the parameter was initially responsible for the increase in P_v and then over time responsible for the lowering of P_v. The change of correlation of β_V from negative to positive suggests that the parameter was initially responsible for the lowering of P_v and later for the increase in P_v. The other two scenarios of either changing from negative to zero or from positive to zero correlation are as explained in figure 10a.

Figure 10c shows that the parameters β_H and β_V are positively correlated to P_f with β_V having near perfect correlation and β_H changing correlation towards zero correlation, H₀ changes correlation from negative to near zero and V₀ changes from negative to zero correlation over time. Thus, the parameters β_H and β_V will be associated with the increase in P_f with much contribution coming from β_V and the effects of β_H becoming insignificant over time while the parameter H₀ will initially be associated with the lowering of P_f but losing the effects over time.

In figure 10d, the parameter V₀ is negatively correlated to P_h, β_V, H₀ and β_H are positively correlated to P_h. The parameter V₀ will be associated with the decrease in P_h, β_V, H₀ and β_H increase will result in the increase of P_h. The PRCC values are, however, small, and thus their influence may not be significant against P_h over all.

Figure 10e shows that the parameters σ_s and α_h are negatively correlated to P_H and σ_v and α_f are positively correlated to P_H. This indicates that the parameters σ_s, σ_v and α_h are associated with lowering P_H while the parameter α_f is associated with increasing P_H. In figure 10f, the parameter σ_s is positively correlated to P_V, σ_v is negatively correlated to P_V, α_f changes from positive to zero correlation and α_h changes correlation from positive to negative and finally positive. This means that increasing the parameter σ_s results in the increase in P_V, σ_v will be responsible for lowering the population P_V, α_f increase will result in the initial increase of P_V losing its effects over time and increasing α_h is associated with initial increase in P_V followed by lowering and finally an increase in P_H. Figure 10g shows that the parameters σ_s, σ_v and α_h are negatively correlated to I_H and α_f changes from positive to negative correlation with all the four parameters changing to a zero correlation over time. All the parameters with be associated with the decrease in I_H but since the PRCCs are mostly close to zero, their effects are almost always insignificant on I_H. In figure 10h, the parameter σ_s changes from negative to zero correlation, σ_v and α_f are negatively correlated to I_V, and α_h changes from positive to negative and to zero correlation. This suggests that increasing σ_s initially lowers the I_V population while the effects become insignificant over time. The increase of σ_v and α_f will be associated with lowering I_V and the increase in α_h will initially increase then decrease and eventually its effects on I_V will become less significant over time. The PRCC values of all the four parameters are also small and thus, the effects of these parameters may not be so significant.

The results in this section indicate potential drivers of between-host scale dynamics as well as within-host scale dynamics that could be targeted with the available prevention and control measures for human onchoceriasis.

5. Discussion and conclusion

In this article, we presented a new method for the development of multiscale models of type II vector-borne diseases in which there is no pathogen replication cycle at both the within-vertebrate host scale and the within-vector host scale. For such type II vector-borne diseases, the pathogen load in the infected host (both the vertebrate host and the vector host) can only increase through super-infection (that is, repeated infection before the host recovers from the infectious episode). The method is based on making assumptions about how individual infectiousness is scaled up to define population/community infectiousness, which determines the probability that a random vector bite on a random vertebrate will infect the vector host or the vertebrate host. Therefore, the multiscale models developed through this method includes the actual parasite load (in the various life stages of the parasite life cycle) at within-host scale and between-host scale instead of just tracking the number of infected hosts. The multiscale model for human onchocerciasis suggests a number of control points, which are suitable for trying out strategies for controlling the spread of this vector-borne disease. The control strategies can be divided into two categories: those targeting the vector host associated with control of P_V (which may include control of the vector population or which reduce the parasite load at within-vector host scale) and those targeting the human host associated with modifying P_H (which may include control of the contact of human host with the vector, or which reduce the parasite load in the various life stages of the parasite life cycle at within-human host scale). Overall, the results in this study confirm that there is reciprocal influence between public health interventions to control human onchocerciasis which are focused on communities and populations (at between-host scale) on the one hand and medical interventions to treat diseases which are focused on the well-being of the individual (at within-host scale) on the other hand. These findings suggest that there are important medical and public health planning consequences to consider during the processes of planning of control and elimination of human onchocerciasis.

Appendix A. Derivation of the general multiscale model for type II vector-borne diseases

In this appendix, we present details for the derivation of the general multiscale model for type II vector-borne disease systems in which the pathogen does not have a replication cycle at within-host scale of any of the two hosts required to complete its life cycle (the vertebrate host and the vector host). For such type II vector-borne diseases, the pathogen load at within-host scale increases only through super-infection (i.e. repeated infection before the host recovers from an infectious episode). To develop the general multiscale model, consider a general type II vector-borne disease in which both the vector hosts and the vertebrate hosts are compartmentalized into two compartments according to their disease status, that is, susceptible vertebrate hosts S_H and infected vertebrate hosts I_H as well as susceptible vector hosts S_V and infected vector hosts I_V, with no natural recovery of infected hosts in both populations (for simplicity). Suppose that the mean pathogen populations at within-vertebrate host scale in life stages 0, 1, …, n are X₀, X₁, X₂, …, X_n, with X₀ = P_f being the pathogen population in the first life stage and X_n = P_h being mean pathogen population in last life stage (which is infectious to the vector hosts) while X₁, X₂, …, X_n−1 are the mean pathogen populations in the intermediate life stages at within-vertebrate scale. Suppose also that the mean pathogen populations at within-vector scale in life stages 0, 1, …, m are Y₀, Y₁, Y₂, …, Y_m, with Y₀ = P_s being the pathogen population in the first life stage and Y_m = P_v being mean pathogen populations in the last life stage (which is infectious to the vertebrate hosts) while Y₁, Y₂, …, Y_m−1 are the mean pathogen populations in the intermediate life stages at within-vector scale. The most critical challenge in the development of multiscale models that integrate the two sets of variables, which are (i) S_H, I_H at the between-vertebrate host scale and X₀, X₁, …, X_n at the within-vertebrate host scale as well as (ii) S_V, I_V at the between-vector host scale and Y₀, Y₁, …, Y_m at within-vector host scale, is to establish methods for linking/coupling sub-models across the between-host scale and the within-host scale for the two host populations implicated in the transmission of the vector-borne disease. From a biological point of view, the linking of the within-host scale and the between-host scale for type II vector-borne diseases without pathogen replication cycle within the two hosts consists of both super-infection, that is, repeated infection before the host recovers from an infectious episode (for linking of between-host scale to the within-host scale) and pathogen excretion/shedding (for linking of within-host scale to the between-host scale). However, from a mathematical point of view, the linking/coupling/integration of sub-models across scales involves up-scaling (for linking of within-host scale to the between-host scale) and down-scaling (for linking between-host scale to the within-host scale) of variables associated with the two disease processes (super-infection and pathogen shedding/excretion). Therefore, each of these two linking mechanisms involves exchange of pathogen between the within-host scale and between-host scale through super-infection (which involves movement of the pathogen from the community scale to the within-host scale) and pathogen shedding/excretion (which involves movement of the pathogen from the within-host scale to the community scale). Extending the ideas in [5,6] to type II vector-borne diseases, the linkage between the scales can be established as follows.

• (a)
  Linking within-host scale to the between-host scale. This is achieved by upscaling individual infectiousness P_h (for each infected vertebrate host) and P_v (for each infected vector host) to community infectiousness P_H(t) = P_h(t)I_H(t) (for all infected vertebrate hosts) and P_V(t) = P_v(t)I_V(t) (for all infected vector hosts) in a particular community. In this study, we refer to P_H and P_V as the CHPL and CVPL, respectively. Thus, the total infectious reservoir of vertebrate hosts (P_H) and vector hosts (P_V) in the community (which we collectively call CPL) is a product of the vertebrate host population I_H(t) and the infectious within-vertebrate host pathogen load P_h (for the CHPL) as well as a product of the vector host population I_V(t) and the infectious within-vector pathogen load P_v(t) (for the CVPL). Following [6], the CVPL and the CHPL are modelled by

  $$\begin{array}{rl}& \hspace{0.17em}\frac{\mathrm{d}{P}_H(t)}{\mathrm{d}t}=[I_H(t)+1]{\alpha }_h{P}_h(t)-{\alpha }_H{P}_H(t)\\ \mathrm{and}& \hspace{0.17em}\frac{\mathrm{d}{P}_V(t)}{\mathrm{d}t}=[I_V(t)+1]{\sigma }_v{P}_v(t)-{\alpha }_V{P}_V(t),\end{array}\}$$ A 1

  where α_h and σ_v are the rates at which the infectious pathogen populations in the last life stages of the pathogen life cycle are shed/excreted into specific anatomical compartments of the vertebrate host and vector host to constitute the CHPL and CVPL, respectively. Even though there is no actual movement of pathogen (as happens in environmentally transmitted infectious diseases) from within-host scale to between-host scale (population/community scale) at rates α_h and σ_v in equations (A 1), the fact that P_h and P_v at within-host scale are aggregated to re-constitute P_H and P_V, respectively at between-host scale (population/community scale), is in this study interpreted to imply that P_h and P_v moved from within-host scale (where they constitute individual host infectious pathogen load) at rates α_h and σ_v to between-host scale (population/community scale)—where they constitute community/population infectious pathogen load. In equations (A 1), 1/α_H and 1/α_V are the average times to eliminate the total CHPL and CVPL, respectively, and render a particular community non-infectious to all vertebrate hosts and vector hosts. The addition of 1 in the infected classes in equations (A 1) is due to the fact that the infection of a single host happens through a single transition defined by $(S_H(t),I_H(t),P_V(t))⟶(S_H(t)-1,I_H(t)+1,P_V(t))$ with probability λ_V(P_V) and $(S_V(t),I_V(t),P_H(t))⟶$ $(S_V(t)-1,I_V(t)+1,P_H(t))$ with probability λ_H(P_H). The subtraction of a one from the susceptible class and the addition of a one to the infected class is supported by the theory of transition probabilities [14]. The contributions of different hosts (the vertebrate host and the vector host) to vector-borne disease burden has been a key gap in our knowledge of vector-borne disease dynamics. An important feature of the multiscale model proposed in this article is that P_V and P_H can be used to give us a formal way of quantifying the contribution of each of the two hosts (the vertebrate host and the vector host) to vector-borne disease burden in a specific community. Since P_H = P_V = 0 would imply that a vector-borne disease is eliminated in a particular community, then CHPL (P_H) and CVPL (P_V) can be operationalized in the evaluation of the path from control to elimination for a vector-borne disease system in a particular community as: (i) an indicator of a community’s level of infectiousness and transmission probability of disease from vector hosts to vertebrate hosts (for CVPL) as well as an indicator of a community’s level of infectiousness and transmission probability of disease from vertebrate hosts to vector hosts (for CHPL), (ii) a measure of the effectiveness of vector-borne disease interventions targeted at the vector host (for CVPL) as well as a measure of the effectiveness of vector-borne disease interventions targeted at the vertebrate host (for CHPL) and (iii) a proximal marker of vector-borne disease incidence among vector hosts and their potential to propagate vector-borne disease to vertebrate hosts (for CVPL) as well as a proximal marker of vector-borne disease incidence among vertebrate hosts and their potential to propagate vector-borne disease to vector hosts (for CHPL). Currently, single scale models of infectious disease systems at host level define disease burden in terms of incidence and prevalence. However, for some infectious diseases prevalence is not very informative, as the infectivity of individuals depends more on pathogen load than on whether one is infected or not. Incidence is difficult to measure directly. More importantly, the use of CPL as a measure of disease burden also enables us to use a common metric for disease dynamics and burden across scales. Further, community pathogen also combines information from prevalence.
• (b)Linking between-host scale to the within-host scale. The incorporation of CPL (CHPL and CVPL) described by equations (A 1) enables us to specify the forces of the transmission of the vector-borne disease in the two hosts so that the force of infection of disease transmission from vector hosts to vertebrate hosts in terms of CVPL becomes β_Vλ_V(P_V) and the force of infection for the transmission of the disease from vertebrate hosts to vector hosts in terms of CHPL becomes β_Hλ_H(P_H). The linking of the between-host scale to the within-host scale through super-infection can be modelled by down-scaling population-level vector-borne transmission which is β_Hλ_H(P_H)S_V (for the vector host) and β_Vλ_V(P_V)S_H (for the vertebrate host) to individual host level vector-borne disease transmission so that super-infection that introduces the population of the first life stage of vector-borne parasite from the between-vertebrate host scale to the within-vector host scale (denoted Y₀ = P_s) is modelled by λ_h(t)s_v(t) = (β_Hλ_H(P_H)[S_V(t) − 1])/(Φ_V [I_V(t) + 1]). Similarly, the super-infection that introduces the population of the first life stage of vector-borne parasite from the between-vector host scale to the within-vertebrate host scale (denoted X₀ = P_f) is modelled by λ_v(t)s_h(t) = (β_Vλ_V(P_V)[S_H(t) − 1])/(Φ_H [I_H(t) + 1]). However, this representation of super-infection is a refinement of the approach in [5] in two ways. First, the approach in [5] specifies the functional forms of λ_H(P_H) and λ_V(P_V). Here λ_H(P_H) and λ_V(P_V) are a general class of functions whose properties will be specified later. Second, the approach in [5] over-estimates the number of new infections, while here the number of new infections is assumed to be a proportion Φ_H of the existing cumulative number of infected vertebrate hosts and a proportion Φ_V of the existing cumulative number of infected vector hosts.

We now develop a general multiscale model of a type II vector-borne disease system that integrates the two sets of variables which are (i) S_H, I_H, P_V at the between-vertebrate host scale and X₀, X₁, …, X_n at the within-vertebrate host scale as well as (ii) S_V, I_V, P_H at the between-vector host scale and Y₀, Y₁, …, Y_m at within-vector host scale. Based on the linking mechanisms we have just described, which represent an extension of the work in [5,6] to vector-borne disease transmission theory, then the casual links between the state variables at the within-host scale and the between-host scale for the vertebrate hosts and the vector hosts can be recast into a general multiscale model for type II vector-borne diseases in the form

$$\begin{array}{rl}& \hspace{0.17em}1.\hspace{0.17em}\frac{\mathrm{d}{S}_H(t)}{\mathrm{d}t}={\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\beta }_{\mathit{V}}{\lambda }_{\mathit{V}}\mathit{(}{\mathit{P}}_{\mathit{V}}\mathit{)}{\mathit{S}}_{\mathit{H}}\mathit{(}\mathit{t}\mathit{)}\mathit{-}{\mu }_{\mathit{H}}{\mathit{S}}_{\mathit{H}}\mathit{(}\mathit{t}\mathit{)}\mathit{,}\\ & \hspace{0.17em}2.\hspace{0.17em}\frac{\mathrm{d}{I}_H(t)}{\mathrm{d}t}={\beta }_V{\lambda }_V(P_V)S_H(t)-({\mu }_H+{\delta }_H)I_H(t),\\ & \hspace{0.17em}3.\hspace{0.17em}\frac{\mathrm{d}{P}_{\hspace{0.17em}f}(t)}{\mathrm{d}t}=\frac{{\beta }_V{\lambda }_V(P_V)[S_H(t)-1]}{{\mathit{\Phi }}_{\mathit{H}}\mathit{[}{\mathit{I}}_{\mathit{H}}\mathit{(}\mathit{t}\mathit{)}\mathit{+}\mathit{1}\mathit{]}}-({\alpha }_{\hspace{0.17em}f}+{\alpha }_{\hspace{0.17em}f})P_{\hspace{0.17em}f}(t),\\ & \hspace{0.17em}4.\hspace{0.17em}\frac{\mathrm{d}{X}_i(t)}{\mathrm{d}t}=f_i(X_{i-1},{\alpha }_{i-1})-({\alpha }_i+{\mu }_i)X_i(t),\\ & i=1,2,3,\dots ,n-1,\\ & \hspace{0.17em}5.\hspace{0.17em}\frac{\mathrm{d}{P}_h(t)}{\mathrm{d}t}=f_n(X_{n-1},{\alpha }_{n-1})-({\alpha }_h+{\mu }_h)P_h(t),\\ & \hspace{0.17em}6.\hspace{0.17em}\frac{\mathrm{d}{P}_H(t)}{\mathrm{d}t}=(I_H+1){\alpha }_h{P}_h(t)-{\alpha }_H{P}_H(t),\\ & \hspace{0.17em}7.\hspace{0.17em}\frac{\mathrm{d}{S}_V(t)}{\mathrm{d}t}={\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\beta }_{\mathit{H}}{\lambda }_{\mathit{H}}\mathit{(}{\mathit{P}}_{\mathit{H}}\mathit{)}{\mathit{S}}_{\mathit{V}}\mathit{(}\mathit{t}\mathit{)}\mathit{-}{\mu }_{\mathit{V}}{\mathit{S}}_{\mathit{V}}\mathit{(}\mathit{t}\mathit{)}\mathit{,}\\ & \hspace{0.17em}8.\hspace{0.17em}\frac{\mathrm{d}{I}_V(t)}{\mathrm{d}t}={\beta }_H{\lambda }_H(P_H)S_V(t)-({\mu }_V+{\delta }_V)I_V(t),\\ & \hspace{0.17em}9.\hspace{0.17em}\frac{\mathrm{d}{P}_s(t)}{\mathrm{d}t}=\frac{{\beta }_H{\lambda }_H(P_H)[S_V(t)-1]}{{\mathit{\Phi }}_{\mathit{V}}\mathit{[}{\mathit{I}}_{\mathit{V}}\mathit{(}\mathit{t}\mathit{)}\mathit{+}\mathit{1}\mathit{]}}-({\eta }_s+{\sigma }_s)P_s(t),\\ & \hspace{0.17em}10.\hspace{0.17em}\frac{\mathrm{d}{Y}_{\hspace{0.17em}j}(t)}{\mathrm{d}t}=g_{\hspace{0.17em}j}(Y_{\hspace{0.17em}j-1},{\sigma }_{\hspace{0.17em}j-1})-({\eta }_{\hspace{0.17em}j}+{\sigma }_{\hspace{0.17em}j})Y_{\hspace{0.17em}j}(t),\\ & j=1,2,3,\dots ,m-1,\\ & \hspace{0.17em}11.\hspace{0.17em}\frac{\mathrm{d}{P}_v(t)}{\mathrm{d}t}=g_m(X_{m-1},{\sigma }_{m-1})-({\eta }_v+{\sigma }_v)P_v(t),\\ & \hspace{0.17em}12.\hspace{0.17em}\frac{\mathrm{d}{P}_V(t)}{\mathrm{d}t}=(I_V+1){\sigma }_v{P}_v(t)-{\sigma }_V{P}_V(t).\end{array}\}$$ A 2

In the general multiscale model (A 2), the transmission rates of the vector-borne disease from the community to the vertebrate hosts and from community to vector hosts are modelled by some general functions β_Vλ_V(P_V) and β_Hλ_H(P_H), respectively. The functions λ_V and λ_H have the following specifications:

• (a)${\lambda }_V\hspace{0.17em}:\hspace{0.17em}[0,\mathrm{\infty })⟶[0,1]$ represents the probability that a random bite of a vertebrate host by a vector host in a particular community with a CVPL P_V(t) will infect the vertebrate host with a vector-borne disease in that community.
• (b)${\lambda }_H\hspace{0.17em}:\hspace{0.17em}[0,\mathrm{\infty })⟶[0,1]$ represents the probability that a random bite of a vertebrate host by a vector host in a particular community with a CHPL P_H(t) will infect the vector host with a vector-borne disease in that community.

Since the functions λ_V(P_V) and λ_H(P_H) are probabilities, they must have the following desirable properties [15]:

• (i)Property I: the probabilities of infection vanish in the absence of pathogen (i.e. λ_V(0) = 0, λ_H(0) = 0) and approach 1 as the community pathogen load becomes large (i.e. $\underset{P_V\to \mathrm{\infty }}{lim}{\lambda }_V(P_V)=1$, $\underset{P_H\to \mathrm{\infty }}{lim}{\lambda }_H(P_H)=1$).
• (ii)Property II: the probabilities of infection λ_V(P_V) and λ_H(P_H) increase with the community pathogen loads P_V and P_H, that is, λ_V′(P_V) > 0 and λ_H′(P_H) > 0, where prime denotes derivative with respect to the argument.

Several possible functions λ_V(P_V) and λ_H(P_H), which we refer to as infectivity response functions, can satisfy the above listed two properties including the following two classic examples:

• (a)
  The negative exponential infectivity response function. This function has the form [15]

  $${\lambda }_V(P_V)=1-{\mathrm{e}}^{-{\gamma }_V{P}_V}\mathrm{and}{\lambda }_H(P_H)=1-{\mathrm{e}}^{-{\gamma }_H{P}_H}.$$ A 3
• (b)
  The sigmoid infectivity response function. This function has the form [16]

  $$\begin{array}{rl}{\lambda }_V(P_V)& =\frac{P_V^k}{V_0^k+P_V^k}\mathrm{and}\\ {\lambda }_H(P_H)& =\frac{P_H^k}{H_0^k+P_H^k},\hspace{0.17em}k=1,2,\dots ,n,\end{array}$$ A 4

  where the parameter k defines the steepness of the sigmoid infectivity response.

In (a) and (b) above, V₀ and H₀ are quantities of CPL which give 50% probability of infection and γ_V = ln(2/V₀), γ_H = ln(2/H₀) [17]. For more information on other forms of infectivity response functions, see [18]. However, the multiscale modelling method for type II vector-borne disease systems presented in this article is still in its foundation stages. Currently data on type II vector-borne disease systems are still not yet available to select analytic forms of λ_V(.) and λ_H(.) on the basis of empirical evidence. Therefore, our selection of analytic forms of λ_V(.) and λ_H(.) is limited to them being able to satisfy property I and property II above.

In the general multiscale model (A 2), equations (1) and (2) describe the dynamics of a type II vector-borne disease system from the vector host to the vertebrate host where the force of infection specified is based on equations (3) and (4) in terms of the community vector pathogen (CVPL) load given by equation (12) of the general multiscale model (A 2). In these equations, μ_H and δ_H are the natural death rate and disease induced death rate, respectively. Equations (3–5) of the general multiscale model (A 2) describe the dynamics of the various pathogen populations in the different life stages at within-vertebrate host scale. In these equations, equation (3) describes the dynamics of the pathogen population in the first life stage at within-vertebrate host scale, while equation (5) describes changes in the pathogen population in the last life stage at within-vertebrate host scale (which is infectious to the vector hosts). Equations (4) describe the pathogen populations in the intermediate life stages at within-vertebrate host scale. In all the three equations (i.e. (3–5)), the transition of pathogen populations from one life stage to another (modelled by f_i(X_i−1, α_i−1), i = 1, 2, …, n, where f₁(X₀, α₀) = f₁(P_f, α_f)) is either through developmental changes to the next life stage or through reproduction of the next life stage from the previous life stage since we assumed a type of vector-borne disease system that does not have a pathogen replication cycle at within-vertebrate host scale. These pathogen populations in the different life stages i = 0, 1, 2, …, n suffer natural death at rates μ_i where μ₀ = μ_f and μ_n = μ_h.

Similarly, in the general multiscale model (A 2), equations (7) and (8) describe the transmission of the vector-borne disease system from the vertebrate host to the vector host where the force of infection specified is based on equations (3) and (4) in terms of the community vertebrate host pathogen (CHPL) load given by equation (6) of the general multiscale model (A 2). The other three equations in the general multiscale model (A 2), that is, equations (9–11), describe the dynamics of the pathogen population in the different life stages at within-vector host scale. In these equations, equation (9) describes the dynamics of the pathogen population in the first life stage at within-vector host scale, while equation (11) describes changes in the pathogen population in the last life stage at within-vector host scale (which is infectious to the vertebrate hosts). Equations (10) describe the pathogen populations in the intermediate life stages at within-vector host scale. Equally, in all the three equations (i.e. (9–11)), the transition from one life stage to another (modelled by g_j(Y_j−1, σ_j−1) j = 1, 2, …, m, where g₁(Y₀, σ₀) = g₁(P_s, α_s)) is either through developmental changes to the next life stage or through production of the next life stage from the previous life stage for the same reason that we assumed a type of vector-borne disease system that does not involve a pathogen replication cycle at within-vector host scale. The pathogen populations in the different life stages j = 0, 1, 2, …, m also suffer natural death at rates η_j where η₀ = η_s and η_m = η_v. A conceptual diagram of the general multiscale model (A 2) is given in figure 1. Following [5], we can easily derive two important results which are:

• (a)For positive parameters, the variables of the general multiscale model (A 2) with positive initial conditions will remain non-negative for all t ≥ 0 and for Λ_H > μ_H and Λ_V > μ_V, so that they do not violate a basic property of biological reality.
• (b)For a specified λ_H(P_H) and λ_V(P_V) chosen from the possible list of infectivity response functions (A 3) and (A 4), the solutions of the general multiscale model (A 2) are bounded for Λ_H > μ_H and Λ_V > μ_V.

Therefore, the general multiscale model (A 2) is mathematically and biologically well posed for Λ_H > μ_H and Λ_V > μ_V. We shall assume in all that follows (unless stated otherwise) that Λ_H > μ_H and Λ_V > μ_V.

Appendix B. Variables and parameters of the human ochocerciasis multiscale model

Table 1 gives a description of the variables in multiscale model (3.3), while table 2 gives a description of the parameters in multiscale model (3.3).

Appendix C. Analysis of the multiscale model

(a) The reproductive number of human ochocerciasis

The model system (3.3) has a disease-free equilibrium given by

$$\begin{array}{rl}{E}^0& =(S_H^0,I_H^0,S_V^0,I_V^0,P_H^0,P_V^0,P_{\hspace{0.17em}f}^0,P_w^0,P_m^0,P_h^0,P_s^0,P_a^0,P_b^0,P_v^0)\hspace{0.17em}\\ & =(\frac{{\mathit{\Lambda }}_{\mathit{H}}}{{\mu }_{\mathit{H}}},0,\frac{{\mathit{\Lambda }}_{\mathit{V}}}{{\mu }_{\mathit{V}}},0,0,0,0,0,0,0,0,0).\end{array}$$ C 1

The basic reproduction number denoted as ${\mathcal{R}}_0$ is a threshold value that is often used in public health to measure the spread of a disease. Using the next generation operator approach [24], the multiscale model (3.3) can be written in the form

$$\begin{array}{rl}& \frac{\mathrm{d}X}{\mathrm{d}t}=f(X,Y,Z),\\ & \frac{\mathrm{d}Y}{\mathrm{d}t}=g(X,Y,Z)\\ \mathrm{and}& \frac{\mathrm{d}Z}{\mathrm{d}t}=h(X,Y,Z),\end{array}\}$$ C 2

where

$$\begin{array}{rl}X& =(S_H,S_V),\\ Y& =(I_H,P_{\hspace{0.17em}f},P_w,P_m,P_h,I_V,P_s,P_a,P_b,P_v)\\ \mathrm{and}Z& =(P_H,P_V).\end{array}\}$$ C 3

Components of X denote the number of susceptibles, while components of Y represent the number of infected individuals that do not transmit the disease. Components of Z represent the number of individuals capable of transmitting the disease. Following [24], we define $\tilde{g}(X^{\ast },Z)$ by

$$\begin{array}{rl}\tilde{g}(X^{\ast },Z)=\hspace{0.17em}& ({\tilde{g}}_1(X^{\ast },Z),{\tilde{g}}_2(X^{\ast },Z),{\tilde{g}}_3(X^{\ast },Z),{\tilde{g}}_4(X^{\ast },Z),\\ & {\tilde{g}}_5(X^{\ast },Z),{\tilde{g}}_6(X^{\ast },Z),{\tilde{g}}_7(X^{\ast },Z),{\tilde{g}}_8(X^{\ast },Z)),\end{array}$$ C 4

with

$$\begin{array}{rl}& \hspace{0.17em}1.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_1(X^{\ast },Z)=\frac{{\beta }_V{\mathit{\Lambda }}_{\mathit{H}}{\mathit{P}}_{\mathit{V}}}{{\mu }_{\mathit{H}}\mathit{(}{\mu }_{\mathit{H}}\mathit{+}{\delta }_{\mathit{H}}\mathit{)}\mathit{(}{\mathit{V}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{V}}\mathit{)}},\\ & \hspace{0.17em}2.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_2(X^{\ast },Z)=\frac{1}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_V({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}{\mathit{P}}_{\mathit{V}}}{{\mu }_{\mathit{H}}\mathit{(}{\mu }_{\mathit{H}}\mathit{+}{\delta }_{\mathit{H}}\mathit{)}{\mathit{\Phi }}_{\mathit{H}}\mathit{(}{\mathit{V}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{V}}\mathit{)}\mathit{[}{\stackrel{\mathit{~}}{\mathit{g}}}_{\mathit{1}}\mathit{(}{\mathit{X}}^{\ast }\mathit{,}\mathit{Z}\mathit{)}\mathit{+}\mathit{1}\mathit{]}},\\ & \hspace{0.17em}3.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_3(X^{\ast },Z)=\frac{1}{{\alpha }_w+{\mu }_w}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_V({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}{\mathit{P}}_{\mathit{V}}}{{\mu }_{\mathit{H}}\mathit{(}{\mu }_{\mathit{H}}\mathit{+}{\delta }_{\mathit{H}}\mathit{)}{\mathit{\Phi }}_{\mathit{H}}\mathit{(}{\mathit{V}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{V}}\mathit{)}\mathit{[}{\stackrel{\mathit{~}}{\mathit{g}}}_{\mathit{1}}\mathit{(}{\mathit{X}}^{\ast }\mathit{,}\mathit{Z}\mathit{)}\mathit{+}\mathit{1}\mathit{]}},\\ & \hspace{0.17em}4.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_4(X^{\ast },Z)=\frac{1}{{\mu }_m}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\varphi }_w{\alpha }_w}{{\alpha }_w+{\mu }_w}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_V({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}{\mathit{P}}_{\mathit{V}}}{{\mu }_{\mathit{H}}\mathit{(}{\mu }_{\mathit{H}}\mathit{+}{\delta }_{\mathit{H}}\mathit{)}{\mathit{\Phi }}_{\mathit{H}}\mathit{(}{\mathit{V}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{V}}\mathit{)}\mathit{[}{\stackrel{\mathit{~}}{\mathit{g}}}_{\mathit{1}}\mathit{(}{\mathit{X}}^{\ast }\mathit{,}\mathit{Z}\mathit{)}\mathit{+}\mathit{1}\mathit{]}},\\ & \hspace{0.17em}5.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_5(X^{\ast },Z)=\frac{1}{{\alpha }_h+{\mu }_h}\hspace{0.17em}\cdot \hspace{0.17em}\frac{N_m{\alpha }_m}{{\mu }_m}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\varphi }_w{\alpha }_w}{{\alpha }_w+{\mu }_w}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_V({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}{\mathit{P}}_{\mathit{V}}}{{\mu }_{\mathit{H}}\mathit{(}{\mu }_{\mathit{H}}\mathit{+}{\delta }_{\mathit{H}}\mathit{)}{\mathit{\Phi }}_{\mathit{H}}\mathit{(}{\mathit{V}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{V}}\mathit{)}\mathit{[}{\stackrel{\mathit{~}}{\mathit{g}}}_{\mathit{1}}\mathit{(}{\mathit{X}}^{\ast }\mathit{,}\mathit{Z}\mathit{)}\mathit{+}\mathit{1}\mathit{]}},\\ & \hspace{0.17em}6.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_6(X^{\ast },Z)=\frac{{\beta }_H{\mathit{\Lambda }}_{\mathit{V}}{\mathit{P}}_{\mathit{H}}}{{\mu }_{\mathit{V}}\mathit{(}{\mu }_{\mathit{V}}\mathit{+}{\delta }_{\mathit{V}}\mathit{)}\mathit{(}{\mathit{H}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{H}}\mathit{)}},\\ & \hspace{0.17em}7.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_7(X^{\ast },Z)=\frac{1}{{\sigma }_s+{\eta }_s}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_H({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}{\mathit{P}}_{\mathit{H}}}{{\mu }_{\mathit{V}}\mathit{(}{\mu }_{\mathit{V}}\mathit{+}{\delta }_{\mathit{V}}\mathit{)}{\mathit{\Phi }}_{\mathit{V}}\mathit{(}{\mathit{H}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{H}}\mathit{)}\mathit{[}{\stackrel{\mathit{~}}{\mathit{g}}}_{\mathit{6}}\mathit{(}{\mathit{X}}^{\ast }\mathit{,}\mathit{Z}\mathit{)}\mathit{+}\mathit{1}\mathit{]}},\\ & \hspace{0.17em}8.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_8(X^{\ast },Z)=\frac{1}{{\sigma }_a+{\eta }_a}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_H({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}{\mathit{P}}_{\mathit{H}}}{{\mu }_{\mathit{V}}\mathit{(}{\mu }_{\mathit{V}}\mathit{+}{\delta }_{\mathit{V}}\mathit{)}{\mathit{\Phi }}_{\mathit{V}}\mathit{(}{\mathit{P}}_{\mathit{1}}\mathit{+}{\mathit{P}}_{\mathit{H}}\mathit{)}\mathit{[}{\stackrel{\mathit{~}}{\mathit{g}}}_{\mathit{6}}\mathit{(}{\mathit{X}}^{\ast }\mathit{,}\mathit{Z}\mathit{)}\mathit{+}\mathit{1}\mathit{]}},\\ & \hspace{0.17em}9.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_8(X^{\ast },Z)=\frac{1}{{\sigma }_b+{\eta }_b}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_a}{{\sigma }_a+{\eta }_a}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_H({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}{\mathit{P}}_{\mathit{H}}}{{\mu }_{\mathit{V}}\mathit{(}{\mu }_{\mathit{V}}\mathit{+}{\delta }_{\mathit{V}}\mathit{)}{\mathit{\Phi }}_{\mathit{V}}\mathit{(}{\mathit{H}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{H}}\mathit{)}\mathit{[}{\stackrel{\mathit{~}}{\mathit{g}}}_{\mathit{6}}\mathit{(}{\mathit{X}}^{\ast }\mathit{,}\mathit{Z}\mathit{)}\mathit{+}\mathit{1}\mathit{]}},\\ & \hspace{0.17em}10.\hspace{0.17em}\hspace{0.17em}{\tilde{g}}_9(X^{\ast },Z)=\frac{1}{{\sigma }_v+{\eta }_v}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_b}{{\sigma }_b+{\eta }_b}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_a}{{\sigma }_a+{\eta }_a}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_H({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}{\mathit{P}}_{\mathit{H}}}{{\mu }_{\mathit{V}}\mathit{(}{\mu }_{\mathit{V}}\mathit{+}{\delta }_{\mathit{V}}\mathit{)}{\mathit{\Phi }}_{\mathit{V}}\mathit{(}{\mathit{H}}_{\mathit{0}}\mathit{+}{\mathit{P}}_{\mathit{H}}\mathit{)}\mathit{[}{\stackrel{\mathit{~}}{\mathit{g}}}_{\mathit{6}}\mathit{(}{\mathit{X}}^{\ast }\mathit{,}\mathit{Z}\mathit{)}\mathit{+}\mathit{1}\mathit{]}}.\end{array}\}$$ C 5

Let

$$\begin{array}{rl}{N}_h& =\frac{1}{{\alpha }_h+{\mu }_h}\hspace{0.17em}\cdot \hspace{0.17em}\frac{N_m{\alpha }_m}{{\mu }_m}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\varphi }_w{\alpha }_w}{{\alpha }_w+{\mu }_w}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}\\ \mathrm{and}{N}_v& =\frac{1}{{\sigma }_v+{\eta }_v}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_b}{{\sigma }_b+{\eta }_b}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_a}{{\sigma }_a+{\eta }_a}.\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}\hspace{0.17em}\cdot \hspace{0.17em}\end{array}\}$$ C 6

Then,

$$\begin{array}{rl}{h}_1& =\frac{N_h{\alpha }_h{\beta }_V({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}}{{\mu }_{\mathit{H}}\mathit{(}{\mu }_{\mathit{H}}\mathit{+}{\delta }_{\mathit{H}}\mathit{)}{\mathit{\Phi }}_{\mathit{H}}}\hspace{0.17em}\cdot \hspace{0.17em}\frac{P_V}{(V_0+P_V)}-{\alpha }_H{P}_H\\ \mathrm{and}{h}_2& =\frac{N_v{\sigma }_v{\beta }_H({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}}{{\mu }_{\mathit{V}}\mathit{(}{\mu }_{\mathit{V}}\mathit{+}{\delta }_{\mathit{V}}\mathit{)}{\mathit{\Phi }}_{\mathit{V}}}\hspace{0.17em}\cdot \hspace{0.17em}\frac{P_H}{(H_0+P_H)}-{\sigma }_V{P}_V.\end{array}\}$$ C 7

Let $A=D_{Z}h(X^{\ast },\tilde{g}(X^{\ast },0),0)$ and further assume that A can be written in the form A = M − D, where M ≥ 0 and D > 0, a diagonal matrix. Then A becomes

$$A=\left[\begin{array}{cc}-{\alpha }_H& \hspace{0.17em}\frac{{\displaystyle N_h{\alpha }_h{\beta }_V({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}}}{{\displaystyle {\mu }_{\mathit{H}}\mathit{(}{\mu }_{\mathit{H}}\mathit{+}{\delta }_{\mathit{H}}\mathit{)}{\mathit{\Phi }}_{\mathit{H}}{\mathit{V}}_{\mathit{0}}}}\\ \frac{N_v{\sigma }_v{\beta }_H({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}}{{\mu }_{\mathit{V}}\mathit{(}{\mu }_{\mathit{V}}\mathit{+}{\delta }_{\mathit{V}}\mathit{)}{\mathit{\Phi }}_{\mathit{V}}{\mathit{H}}_{\mathit{0}}}& \hspace{0.17em}-{\sigma }_V\end{array}\right].$$ C 8

Since A = M − D, we deduce matrices M and D to be

$$\begin{array}{rl}& M=\left[\begin{array}{cc}0& \hspace{0.17em}\frac{N_h{\alpha }_h{\beta }_V({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}}{{\mu }_{\mathit{H}}\mathit{(}{\mu }_{\mathit{H}}\mathit{+}{\delta }_{\mathit{H}}\mathit{)}{\mathit{\Phi }}_{\mathit{H}}{\mathit{V}}_{\mathit{0}}}\\ \frac{N_v{\sigma }_v{\beta }_H({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}}{{\mu }_{\mathit{V}}\mathit{(}{\mu }_{\mathit{V}}\mathit{+}{\delta }_{\mathit{V}}\mathit{)}{\mathit{\Phi }}_{\mathit{V}}{\mathit{H}}_{\mathit{0}}}& \hspace{0.17em}0\end{array}\right]\mathrm{and}\\ & D=\left[\begin{array}{cc}{\alpha }_H& \hspace{0.17em}0\\ 0& \hspace{0.17em}{\sigma }_V\end{array}\right].\end{array}$$ C 9

The basic reproductive number is the spectral radius (dominant eigenvalue) of the matrix MD⁻¹, that is,

$$\begin{array}{rl}{\mathcal{R}}_0& =\rho (M{D}^{-1})\\ & =\sqrt{[\frac{N_h{\alpha }_h}{({\mu }_H+{\delta }_H)}\frac{({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}{\beta }_{\mathit{H}}}{{\mu }_{\mathit{V}}{\alpha }_{\mathit{H}}{\mathit{H}}_{\mathit{0}}}][\frac{N_v{\alpha }_v}{({\mu }_V+{\delta }_V)}\hspace{0.17em}\cdot \hspace{0.17em}\frac{({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}{\beta }_{\mathit{V}}}{{\mu }_{\mathit{H}}{\sigma }_{\mathit{V}}{\mathit{V}}_{\mathit{0}}}]}.\end{array}$$ C 10

In this case,

$${\mathcal{R}}_0=\sqrt{{\mathcal{R}}_{\mathrm{HV}}\hspace{0.17em}\cdot \hspace{0.17em}{\mathcal{R}}_{\mathrm{VH}}},$$ C 11

where

$$\begin{array}{rl}{\mathcal{R}}_{\mathrm{HV}}& \hspace{0.17em}=\frac{N_h{\alpha }_h}{({\mu }_H+{\delta }_H)}\hspace{0.17em}\cdot \hspace{0.17em}\frac{({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}{\beta }_{\mathit{H}}}{{\mu }_{\mathit{V}}{\alpha }_{\mathit{H}}{\mathit{H}}_{\mathit{0}}}\\ & \hspace{0.17em}=\frac{{\alpha }_h}{{\alpha }_h+{\mu }_h}\hspace{0.17em}\cdot \hspace{0.17em}\frac{N_m{\alpha }_m}{{\mu }_m}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\varphi }_w{\alpha }_w}{{\alpha }_w+{\mu }_w}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}\\ & \hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_H({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}}{{\mu }_{\mathit{V}}\mathit{(}{\mu }_{\mathit{V}}\mathit{+}{\delta }_{\mathit{V}}\mathit{)}{\mathit{\Phi }}_{\mathit{V}}{\alpha }_{\mathit{H}}{\mathit{H}}_{\mathit{0}}}.\end{array}$$ C 12

Similarly,

$$\begin{array}{rl}{\mathcal{R}}_{\mathrm{VH}}& \hspace{0.17em}=\frac{N_v{\sigma }_v}{({\mu }_V+{\delta }_V)}\hspace{0.17em}\cdot \hspace{0.17em}\frac{({\mathit{\Lambda }}_H-{\mu }_H){\beta }_V}{{\mu }_H{\sigma }_V{V}_0}\\ & \hspace{0.17em}=\frac{{\sigma }_v}{{\sigma }_v+{\eta }_v}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_b}{{\sigma }_b+{\eta }_b}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_a}{{\sigma }_a+{\eta }_a}\hspace{0.17em}\cdot \hspace{0.17em}\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}\\ & \hspace{0.17em}\cdot \hspace{0.17em}\frac{{\beta }_V({\mathit{\Lambda }}_H-{\mu }_H)}{{\mu }_H({\mu }_H+{\delta }_H){\mathit{\Phi }}_H{\sigma }_V{V}_0}.\end{array}$$ C 13

Therefore, basic reproductive number ${\mathcal{R}}_0$ has four main components which are: (i) the human-to-community partial reproductive number (${\mathcal{R}}_{\mathrm{HC}}$), (ii) the community-to-vector partial reproductive number (${\mathcal{R}}_{\mathrm{CV}}$), (iii) the blackfly-to-community partial reproductive number (${\mathcal{R}}_{\mathrm{VC}}$) and (iv) the community-to-human partial reproductive number (${\mathcal{R}}_{\mathrm{CH}}$) so that ${\mathcal{R}}_{\mathrm{HV}}={\mathcal{R}}_{\mathrm{HC}}.{\mathcal{R}}_{\mathrm{CV}}$ and ${\mathcal{R}}_{\mathrm{VH}}={\mathcal{R}}_{\mathrm{VC}}.{\mathcal{R}}_{\mathrm{CH}}$. These partial reproductive numbers in the transmission cycle of human onchocerciasis are shown in a schematic diagram in figure 11.

Figure 11.

A conceptual diagram of the four partial reproductive numbers that constitute the human onchocerciasis reproductive number. (Online version in colour.)

Therefore, the basic reproductive number ${\mathcal{R}}_0$ in the human-to-human or blackfly-to-blackfly for human onchocerciasis transmission is made up of the following four partial reproductive numbers.

• (i)
  The human-to-community partial reproductive number (${\mathcal{R}}_{\mathrm{HC}}$). This partial reproductive number is given by

  $${\mathcal{R}}_{\mathrm{HC}}=\frac{N_h{\alpha }_h}{({\mu }_H+{\delta }_H)}.$$ C 14

  This is the average amount of infectious reservoir contributed to the community microfilariae load by each infected human host during his or her entire period of infectiousness. This quantity depends on the average number of microfilariae N_h produced by female worms in each infected human, which is available for ingestion by a blackfly during her uptake of blood meals from an infected human during his or her entire period of infectiousness and is a composite parameter given by

  $$N_h=\frac{1}{{\alpha }_h+{\mu }_h}.\frac{N_m{\alpha }_m}{{\mu }_m}.\frac{{\varphi }_w{\alpha }_w}{{\alpha }_w+{\mu }_w}.\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}.$$ C 15

  In the expression for ${\mathcal{R}}_{\mathrm{HC}}$, α_h is the rate at which microfilariae are shed/excreted into the dermis layer of the skin. Therefore, N_hα_h is the rate that describes how much each infected human host contributes to the community microfilariae load (the total infectious reservoir of humans in the community) during his/her entire period of infectiousness while 1/(μ_H + δ_H) is the average microfilariae carriage time by each infected human host.
• (ii)
  The community-to-blackfly vector partial reproductive number (${\mathcal{R}}_{CV}$). This partial reproductive number is given by

  $${\mathcal{R}}_{\mathrm{CV}}=\frac{({\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{)}{\beta }_{\mathit{H}}}{{\mu }_{\mathit{V}}{\alpha }_{\mathit{H}}{\mathit{H}}_{\mathit{0}}}.$$ C 16

  It describes the average number of infected blackflies arising from each infectious dose of microfilariae ingested from the total infectious reservoir of humans in the community. This partial reproductive number depends on the effective supply rate of susceptible blackflies (Λ_V − μ_V), the average life span of each susceptible blackfly 1/μ_V, the rate of contact of the susceptible blackflies with the infectious reservoir of humans β_H, the average time it takes to eliminate the infectious reservoir of humans in the community 1/α_H and the susceptibility coefficient 1/H₀ of blackfly vectors to infection by the total human infectious reservoir in the community.
• (iii)
  The blackfly-to-community partial reproductive number (${\mathcal{R}}_{VC}$). This partial reproductive number is given by

  $${\mathcal{R}}_{\mathrm{VC}}=\frac{N_v{\sigma }_v}{({\mu }_V+{\delta }_V)}.$$ C 17

  This is also the average amount of infectious reservoir contributed to the community L₃ larvae load (CLL) by each infected blackfly vector during her entire period of infectiousness. This quantity depends on the average number of L₃ larvae produced in each infected blackfly vector N_v, which is available for injection into a human host by a blackfly during uptake of blood meals from a human during her entire period of infectiousness and is a composite parameter which is also given by

  $$N_v=\frac{1}{{\sigma }_v+{\eta }_v}.\frac{{\sigma }_b}{{\sigma }_b+{\eta }_b}.\frac{{\sigma }_a}{{\sigma }_a+{\eta }_a}.\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}.$$ C 18

  In the expression for ${\mathcal{R}}_{VC}$, σ_v is the rate at which L₃ larvae are excreted/shed into the saliva in the proboscis of the blackfly. Therefore, N_vσ_v is the rate that describes how much an infected blackfly contributes to the CLL (the total infectious reservoir of blackflies in the community) during her entire period of infectiousness while 1/(μ_V + δ_V) is the average L₃ larvae carriage time by each infected blackfly.
• (iv)
  The community-to-human partial reproductive number (${\mathcal{R}}_{CH}$). This reproductive number is given by

  $${\mathcal{R}}_{\mathrm{CH}}=\frac{({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}{\beta }_{\mathit{V}}}{{\mu }_{\mathit{H}}{\sigma }_{\mathit{V}}{\mathit{V}}_{\mathit{0}}}.$$ C 19

  It describes the average number of infected humans arising from each infectious dose of L₃ larvae injected from the total infectious reservoir of blackflies in the community. This partial reproductive number depends on the effective supply rate of susceptible blackflies (Λ_H − μ_H), the average life span of each susceptible humans 1/μ_H, the rate of contact of the susceptible humans with the infectious reservoir of blackflies β_V, the average time it takes to eliminate the infectious reservoir of blackflies in the community 1/σ_V and the susceptibility coefficient 1/V₀ of human hosts to infection by the CLL (the total blackfly infectious reservoir in the community).

Another informative way of interpreting ${\mathcal{R}}_0$ is to consider it as a product of two partial reproductive numbers which are the human-to-blackfly partial reproductive number ${\mathcal{R}}_{\mathrm{HV}}$ and the blackfly-to-human partial reproductive number ${\mathcal{R}}_{\mathrm{VH}}$ so that

$$\begin{array}{rl}{\mathcal{R}}_0& =\sqrt{[\frac{N_h{\alpha }_h}{({\mu }_H+{\delta }_H)}\frac{({\mathit{\Lambda }}_V-{\mu }_V){\beta }_H}{{\mu }_V{\alpha }_H{H}_0}][\frac{N_v{\alpha }_v}{({\mu }_V+{\delta }_V)}\hspace{0.17em}\cdot \hspace{0.17em}\frac{({\mathit{\Lambda }}_H-{\mu }_H){\beta }_V}{{\mu }_H{\sigma }_V{V}_0}]}\\ & =\sqrt{R_{\mathrm{HV}}\cdot R_{\mathrm{VH}}}.\end{array}$$ C 20

In equation (C 20), the quantity ${\mathcal{R}}_{\mathrm{HV}}$ is interpreted as follows. Consider a single newly infected human host entering a disease-free population of blackflies at equilibrium. This individual is still present and infectious and the expected number of blackflies infected by this human host is approximately

$$\begin{array}{rl}{\mathcal{R}}_{\mathrm{HV}}& =\frac{N_h{\alpha }_h}{({\mu }_H+{\delta }_H)}\frac{({\mathit{\Lambda }}_V-{\mu }_V){\beta }_H}{{\mu }_V{\alpha }_H{H}_0}\\ & =\frac{{\alpha }_h}{{\alpha }_h+{\mu }_h}\cdot \frac{N_m{\alpha }_m}{{\mu }_m}\cdot \frac{{\varphi }_w{\alpha }_w}{{\alpha }_w+{\mu }_w}\cdot \frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}\\ & \cdot \frac{{\beta }_H({\mathit{\Lambda }}_V-{\mu }_V)}{{\mu }_V({\mu }_V+{\delta }_V){\mathit{\Phi }}_V{\alpha }_H{H}_0}.\end{array}$$ C 21

Therefore, the human-to-blackfly transmission coefficient ${\mathcal{R}}_{\mathrm{HV}}$ is composed of between-host disease parameters and within-human parameters. Similarly, in equation (C 20) the quantity ${\mathcal{R}}_{\mathrm{VH}}$ is interpreted as follows. Consider a single newly infected blackfly vector entering a disease-free population of humans at equilibrium. This blackfly is still present and infectious and the expected number of humans infected by this blackfly is approximately

$$\begin{array}{rl}{\mathcal{R}}_{\mathrm{VH}}& =\frac{N_v{\sigma }_v}{({\mu }_V+{\delta }_V)}.\frac{({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}{\beta }_{\mathit{V}}}{{\mu }_{\mathit{H}}{\sigma }_{\mathit{V}}{\mathit{V}}_{\mathit{0}}}\\ & =\frac{{\sigma }_v}{{\sigma }_v+{\eta }_v}.\frac{{\sigma }_b}{{\sigma }_b+{\eta }_b}.\frac{{\sigma }_a}{{\sigma }_a+{\eta }_a}.\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}.\frac{{\beta }_V({\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{)}}{{\mu }_{\mathit{H}}\mathit{(}{\mu }_{\mathit{H}}\mathit{+}{\delta }_{\mathit{H}}\mathit{)}{\mathit{\Phi }}_{\mathit{H}}{\sigma }_{\mathit{V}}{\mathit{V}}_{\mathit{0}}}.\end{array}$$ C 22

From equation (C 22), we deduce that the blackfly-to-human transmission coefficient ${\mathcal{R}}_{\mathrm{VH}}$ is also composed of between-host disease parameters and within-blackfly parameters.

(b) Feasible region of the equilibria of the model

All parameters and state variables for model system (3.3) are assumed to be non-negative to be consistent with human and animal populations. Further, it can be verified that for model system (3.3), all solutions with non-negative initial conditions remain bounded and non-negative.

Letting N_H = S_H + I_H and adding equations (1) and (2) in system (3.3) gives

$$\frac{\mathrm{d}{N}_H}{\mathrm{d}t}\le {\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}{\mathit{N}}_{\mathit{H}}\mathit{.}$$

This implies that

$$\underset{t\to \mathrm{\infty }}{lim}\text{sup}(N_H(t))\le \frac{{\mathit{\Lambda }}_{\mathit{H}}}{{\mu }_{\mathit{H}}}.$$ C 23

Similarly, letting N_V = S_V + I_V and adding equations (8) and (9) in system (3.3) gives

$$\frac{\mathrm{d}{N}_V}{\mathrm{d}t}\le {\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}{\mathit{N}}_{\mathit{V}}\mathit{.}$$ C 24

This implies that

$$\underset{t\to \mathrm{\infty }}{lim}\text{sup}(N_V(t))\le \frac{{\mathit{\Lambda }}_{\mathit{V}}}{{\mu }_{\mathit{V}}}.$$ C 25

Using equations (C 23) and (C 25) similar expressions can be derived for the remaining model variables. Hence, all feasible solutions of system (3.3) are positive and eventually enter the invariant attracting region

$$\begin{array}{rl}\mathit{\Omega }& =((S_H,I_H,S_V,I_V,P_{\hspace{0.17em}f},P_w,P_m,P_h,P_H,P_s,P_a,P_b,P_v,P_V):\\ & \hspace{0.17em}0\le S_H+I_H\le M_1,\\ & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\le S_V+I_V\le M_2,\hspace{0.17em}0\le P_{\hspace{0.17em}f}\le M_3,\hspace{0.17em}0\le P_w\le M_4,\\ & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\le P_m\le M_5,\hspace{0.17em}0\le P_h\le M_6,\hspace{0.17em}0\le P_H\le M_7,\\ & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\le P_s\le M_8,\hspace{0.17em}0\le P_a\le M_9,\hspace{0.17em}0\le P_b\le M_{10}\hspace{0.17em}0\le P_v\le M_{11},\\ & \hspace{0.17em}0\le P_V\le M_{12}),\end{array}$$ C 26

where

$$\begin{array}{rl}& \hspace{0.17em}{M}_1=\frac{{\mathit{\Lambda }}_{\mathit{H}}}{{\mu }_{\mathit{H}}},\\ & \hspace{0.17em}{M}_2=\frac{{\mathit{\Lambda }}_{\mathit{V}}}{{\mu }_{\mathit{V}}},\\ & \hspace{0.17em}{M}_3=\frac{1}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}.\frac{{\beta }_V[{\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{]}}{{\varphi }_{\mathit{H}}\mathit{[}{\mathit{\Lambda }}_{\mathit{H}}\mathit{+}{\mu }_{\mathit{H}}\mathit{]}}.\frac{{\alpha }_H{H}_0[{\mathcal{R}}_0^2-1]}{[{\sigma }_V{V}_0{\mathcal{R}}_{\mathrm{VH}}+{\alpha }_H{H}_0{\mathcal{R}}_0^2]},\\ & \hspace{0.17em}{M}_4=\frac{1}{{\alpha }_w+{\mu }_w}.\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}.\frac{{\beta }_V[{\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{]}}{{\varphi }_{\mathit{H}}\mathit{[}{\mathit{\Lambda }}_{\mathit{H}}\mathit{+}{\mu }_{\mathit{H}}\mathit{]}}.\frac{{\alpha }_H{H}_0[{\mathcal{R}}_0^2-1]}{[{\sigma }_V{V}_0{\mathcal{R}}_{\mathrm{VH}}+{\alpha }_H{H}_0{\mathcal{R}}_0^2]},\\ & \hspace{0.17em}{M}_5=\frac{1}{{\mu }_m}.\frac{{\varphi }_w{\alpha }_w}{{\alpha }_w+{\mu }_w}.\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}.\frac{{\beta }_V[{\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{]}}{{\varphi }_{\mathit{H}}\mathit{[}{\mathit{\Lambda }}_{\mathit{H}}\mathit{+}{\mu }_{\mathit{H}}\mathit{]}}.\frac{{\alpha }_H{H}_0[{\mathcal{R}}_0^2-1]}{[{\sigma }_V{V}_0{\mathcal{R}}_{\mathrm{VH}}+{\alpha }_H{H}_0{\mathcal{R}}_0^2]},\\ & \hspace{0.17em}{M}_6=\frac{1}{{\alpha }_h+{\mu }_h}.\frac{N_m{\alpha }_m}{{\mu }_m}.\frac{{\varphi }_w{\alpha }_w}{{\alpha }_w+{\mu }_w}.\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}.\frac{{\beta }_V[{\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{]}}{{\varphi }_{\mathit{H}}\mathit{[}{\mathit{\Lambda }}_{\mathit{H}}\mathit{+}{\mu }_{\mathit{H}}\mathit{]}}.\frac{{\alpha }_H{H}_0[{\mathcal{R}}_0^2-1]}{[{\sigma }_V{V}_0{\mathcal{R}}_{\mathrm{VH}}+{\alpha }_H{H}_0{\mathcal{R}}_0^2]},\\ & \hspace{0.17em}{M}_7=\frac{{\alpha }_h}{{\alpha }_h+{\mu }_h}.\frac{N_m{\alpha }_m}{{\mu }_m}.\frac{{\varphi }_w{\alpha }_w}{{\alpha }_w+{\mu }_w}.\frac{{\alpha }_{\hspace{0.17em}f}}{{\alpha }_{\hspace{0.17em}f}+{\mu }_{\hspace{0.17em}f}}.\frac{{\beta }_V[{\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{]}}{{\varphi }_{\mathit{H}}{\mu }_{\mathit{H}}{\alpha }_{\mathit{H}}}.\frac{{\alpha }_H{H}_0[{\mathcal{R}}_0^2-1]}{[{\sigma }_V{V}_0{\mathcal{R}}_{\mathrm{VH}}+{\alpha }_H{H}_0{\mathcal{R}}_0^2]},\\ & \hspace{0.17em}{M}_8=\frac{1}{{\sigma }_s+{\eta }_s}.\frac{{\beta }_H[{\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{]}}{{\varphi }_{\mathit{V}}\mathit{[}{\mathit{\Lambda }}_{\mathit{V}}\mathit{+}{\mu }_{\mathit{V}}\mathit{]}}.\frac{{\sigma }_V{V}_0[{\mathcal{R}}_0^2-1]}{[{\alpha }_H{H}_0{\mathcal{R}}_{\mathrm{HV}}+{\sigma }_V{V}_0{\mathcal{R}}_0^2]},\\ & \hspace{0.17em}{M}_9=\frac{1}{{\eta }_a+{\eta }_a}.\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}.\frac{{\beta }_H[{\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{]}}{{\varphi }_{\mathit{V}}\mathit{[}{\mathit{\Lambda }}_{\mathit{V}}\mathit{+}{\mu }_{\mathit{V}}\mathit{]}}.\frac{{\sigma }_V{V}_0[{\mathcal{R}}_0^2-1]}{[{\alpha }_H{H}_0{\mathcal{R}}_{\mathrm{HV}}+{\sigma }_V{V}_0{\mathcal{R}}_0^2]},\\ & \hspace{0.17em}{M}_{10}=\frac{1}{{\sigma }_b+{\eta }_b}.\frac{{\sigma }_a}{{\sigma }_a+{\eta }_a}.\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}.\frac{{\beta }_H[{\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{]}}{{\varphi }_{\mathit{V}}\mathit{[}{\mathit{\Lambda }}_{\mathit{V}}\mathit{+}{\mu }_{\mathit{V}}\mathit{]}}.\frac{{\sigma }_V{V}_0[{\mathcal{R}}_0^2-1]}{[{\alpha }_H{H}_0{\mathcal{R}}_{\mathrm{HV}}+{\sigma }_V{V}_0{\mathcal{R}}_0^2]},\\ & \hspace{0.17em}{M}_{11}=\frac{1}{{\sigma }_v+{\eta }_v}.\frac{{\sigma }_b}{{\sigma }_b+{\eta }_b}.\frac{{\sigma }_a}{{\sigma }_a+{\eta }_a}.\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}.\frac{{\beta }_H[{\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{]}}{{\varphi }_{\mathit{V}}\mathit{[}{\mathit{\Lambda }}_{\mathit{V}}\mathit{+}{\mu }_{\mathit{V}}\mathit{]}}.\frac{{\sigma }_V{V}_0[{\mathcal{R}}_0^2-1]}{[{\alpha }_H{H}_0{\mathcal{R}}_{\mathrm{HV}}+{\sigma }_V{V}_0{\mathcal{R}}_0^2]},\\ & \hspace{0.17em}{M}_{12}=\frac{{\sigma }_v}{{\sigma }_v+{\eta }_v}.\frac{{\sigma }_b}{{\sigma }_b+{\eta }_b}.\frac{{\sigma }_a}{{\sigma }_a+{\eta }_a}.\frac{{\sigma }_s}{{\sigma }_s+{\eta }_s}.\frac{{\beta }_H[{\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{]}}{{\varphi }_{\mathit{V}}{\mu }_{\mathit{V}}{\sigma }_{\mathit{V}}}.\frac{{\sigma }_V{V}_0[{\mathcal{R}}_0^2-1]}{[{\alpha }_H{H}_0{\mathcal{R}}_{\mathrm{HV}}+{\sigma }_V{V}_0{\mathcal{R}}_0^2]},\end{array}\}$$ C 27

where

$$\begin{array}{rl}& \hspace{0.17em}{\mathcal{R}}_{\mathrm{VH}}=\frac{N_v{\sigma }_v{\beta }_V[{\mathit{\Lambda }}_{\mathit{H}}\mathit{-}{\mu }_{\mathit{H}}\mathit{]}}{{\varphi }_{\mathit{H}}{\mu }_{\mathit{H}}{\sigma }_{\mathit{V}}{\mathit{V}}_{\mathit{0}}}\\ \mathrm{and}& \hspace{0.17em}{\mathcal{R}}_{\mathrm{HV}}=\frac{N_h{\alpha }_h{\beta }_H[{\mathit{\Lambda }}_{\mathit{V}}\mathit{-}{\mu }_{\mathit{V}}\mathit{]}}{{\varphi }_{\mathit{V}}{\mu }_{\mathit{V}}{\alpha }_{\mathit{H}}{\mathit{H}}_{\mathit{0}}},\end{array}\}$$ C 28

for Λ_H > μ_H, Λ_V > μ_V. Thus, whenever Λ_H > μ_H and Λ_V > μ_V then Ω is positively invariant and attracting and it is sufficient to consider solutions of model system (3.3) in Ω. Existence, uniqueness and continuation results for system (3.3) hold in this region and all solutions starting in Ω remain there for all t ≥ 0. Hence, model system (3.3) is mathematically and epidemiologically well posed, and it is sufficient to consider the dynamics of the flow generated by model system (3.3) in Ω. We shall assume in all that follows (unless stated otherwise) that Λ_H > μ_H, Λ_V > μ_V and ${\mathcal{R}}_0>1$.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

W.G. acknowledges with thanks financial support from South Africa National Research Foundation (NRF) grant no. IPRR (UID 81235).